On the Laplace Residual Series Method and Its Application to Time-Fractional Fisher’s Equations
Abstract
:1. Introduction
2. Fundamental Concepts
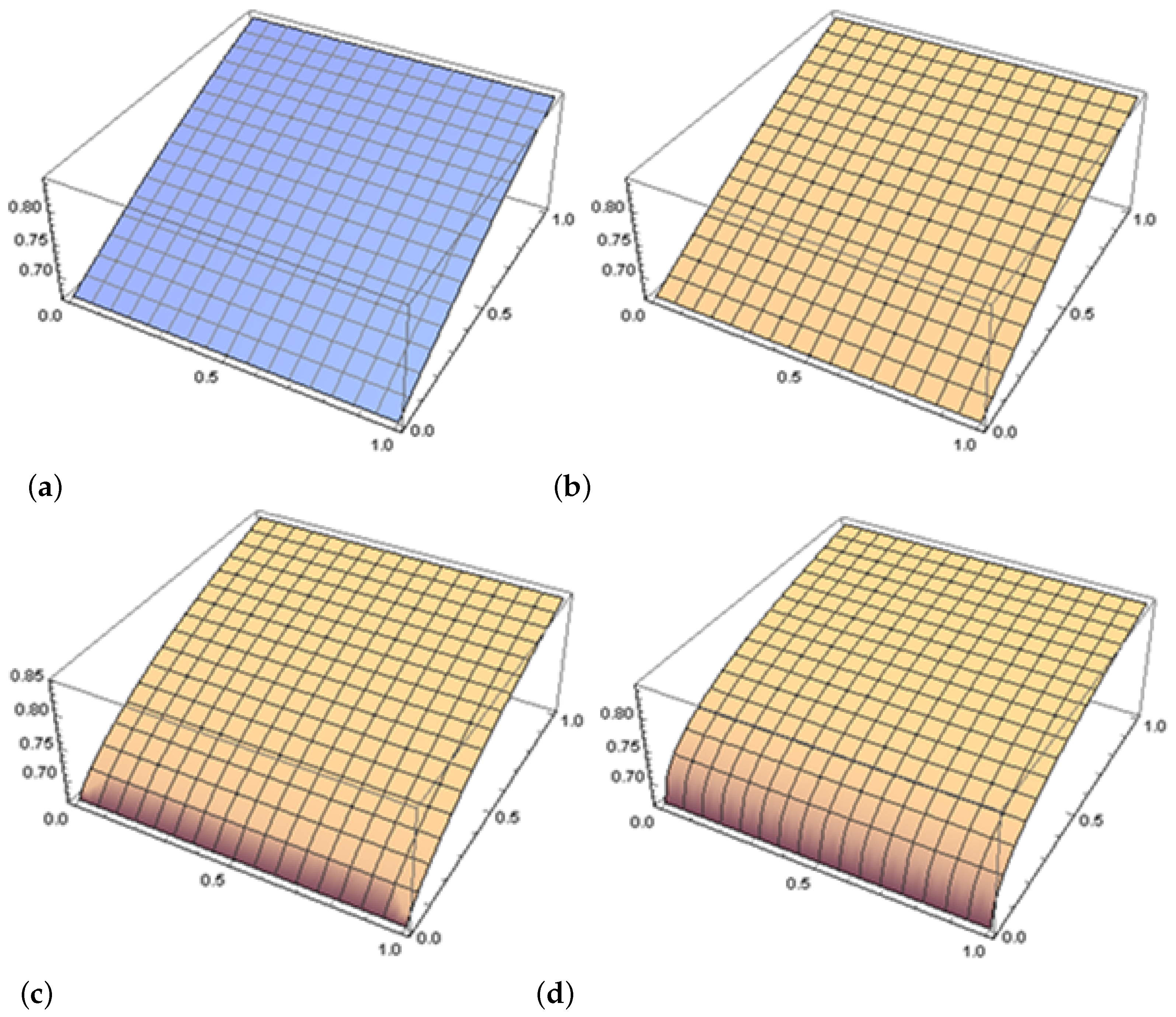
- (a)
- (b)
- (c)
- (d)
- (e)
3. The LRPS Method
- First:
- Let , and using property from Lemma 1, the Laplace transform can be applied to both sides of Fisher’s problem (1) to obtainSince . Thus, (10) can be reformulated as:
- Second:
- According to Theorem 2, let the approximate solution of (11) have the expansion series formSubsequently, to determine the coefficients , of (12), let be the i-th term of the series solution of (12). That is,For , we have , which yields
- Third:
- The i-th term of the series solution (14) can be obtained after evaluating the coefficients , by identifying the i-th-Laplace residual function of (10) asHere, the ∞-th Laplace residual function of (10) can be given byEvidently, and for each and . Furthermore, , which implies that .
- Fourth:
- After substituting the i-th term of the series solution (14) into the i-th Laplace residual function, both sides of the resulting equation are multiplied by the factor .
- Fifth:
- To determine the coefficients , we solve . Subsequently, by collecting the obtained coefficients into the expansion series (14), the i-th Laplace series solution of (11) is derived.
- Sixth:
- The approximate solution of the IVPs (1) and (2) can be obtained by applying the Laplace transform inversion formula to both sides of the i-th Laplace solution .
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Magin, R.L.; Ingo, C.; Colon-Perez, L.; Triplett, W.; Mareci, T.H. Characterization of anomalous diffusion in porous biological tissues using fractional order derivatives and entropy. Microporous Mesoporous Mater. 2013, 178, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Ghanbari, B.; Atangana, A. A new application of fractional Atangana-Baleanu derivatives: Designing ABC-fractional masks in image processing. Phys. Stat. Mech. Its Appl. 2020, 542, 123516. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Alaroud, M.; Al-Smadi, M.; Rozita Ahmad, R.; Salma Din, U.K. An Analytical Numerical Method for Solving Fuzzy Fractional Volterra Integro-Differential Equations. Symmetry 2019, 11, 205. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional differential equations. Math. Sci. Eng. 1999, 198. Available online: https://cir.nii.ac.jp/crid/1573950399205663360 (accessed on 11 February 2025).
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Almeida, R.; Tavares, D.; Torres, D.F. The Variable-Order Fractional Calculus of Variations; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Hasan, S.; Al-Smadi, M.; Freihet, A.; Momani, S. Two computational approaches for solving a fractional obstacle system in Hilbert space. Adv. Differ. Equ. 2019, 2019, 55. [Google Scholar] [CrossRef]
- El-Ajou, A. A modification to the conformable fractional calculus with some applications. Alex. Eng. J. 2020, 59, 2239–2249. [Google Scholar] [CrossRef]
- Gao, G.; Sun, Z.; Zhang, H. A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 2014, 259, 33–50. [Google Scholar] [CrossRef]
- Kazem, S. Exact solution of some linear fractional differential equations by Laplace transforms. Int. J. Nonlinear Sci. 2013, 16, 3–11. [Google Scholar]
- Wang, Q. Numerical solutions for fractional KdV-Burgers equation by Adomian decomposition method. Appl. Math. Comput. 2006, 182, 1048–1055. [Google Scholar] [CrossRef]
- Alkresheh, H.A.; Ismail, A.I. Multi-step fractional differential transform method for the solution of fractional order stiff systems. Ain Shams Eng. J. 2021, 12, 4223–4231. [Google Scholar]
- Das, S. Analytical solution of a fractional diffusion equation by variational iteration method. Comput. Math. Appl. 2009, 57, 483–487. [Google Scholar]
- He, J.H. Approximate analytical solution for seepage flow with fractional derivatives porous media. Comput. Methods Appl. Mech. Eng. 1998, 167, 57–68. [Google Scholar]
- Gumah, G.; Naser, M.F.M.; Al-Smadi, M.; Al-Omari, S.K.Q.; Baleanu, D. Numerical solutions of hybrid fuzzy differential equations in a Hilbert space. Appl. Numer. Math. 2020, 151, 402–412. [Google Scholar] [CrossRef]
- Aychluh, M.; Ayalew, M. The Fractional Power Series Method for Solving the Nonlinear Kuramoto-Sivashinsky Equation. Int. J. Appl. Comput. Math. 2025, 11, 29. [Google Scholar]
- Nikan, O.; Avazzadeh, Z.; Machado, J.T. An efficient local meshless approach for solving nonlinear time-fractional fourth-order diffusion model. J. King Saud Univ. 2021, 33, 101243. [Google Scholar]
- Gao, X.; Jiang, X.; Chen, S. The numerical method for the moving boundary problem with space-fractional derivative in drug release devices. Appl. Math. Model. 2015, 39, 2385–2391. [Google Scholar]
- Nikan, O.; Machado, J.T.; Golbabai, A. Numerical solution of time-fractional fourth-order reaction-diffusion model arising in composite environments. Appl. Math. Model. 2021, 89, 819–836. [Google Scholar]
- Shqair, M.; El-Ajou, A.; Nairat, M. Analytical solution for multi-energy groups of neutron diffusion equations by a residual power series method. Mathematics 2019, 7, 633. [Google Scholar]
- Saadeh, R.; Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Salma Din, U.K. Application of Fractional Residual Power Series Algorithm to Solve Newell-Whitehead-Segel Equation of Fractional Order. Symmetry 2019, 11, 1431. [Google Scholar] [CrossRef]
- Ali, A.I.; Kalim, M.; Khan, A. Solution of Fractional Partial Differential Equations Using Fractional Power Series Method. Inter. J. Differ. Equ. 2021, 2021, 6385799. [Google Scholar] [CrossRef]
- Area, I.; Nieto, J.J. Power series solution of the fractional logistic equation. Phys. A Stat. Mech. Its Appl. 2021, 573, 125947. [Google Scholar] [CrossRef]
- El-Ajou, A. Adapting the Laplace Transform to Create Solitary Solutions for the Nonlinear Time-Fractional Dispersive PDEs Via a New Approach. Eur. Phys. J. Plus 2021, 136, 229. [Google Scholar]
- Karatas Akgul, E.; Akgul, A.; Baleanu, D. Laplace Transform Method for Economic Models with Constant Proportional Caputo Derivative. Fractal Fract. 2020, 4, 30. [Google Scholar] [CrossRef]
- Baihi, A.; Kajouni, A.; Hilal, K.; Lmou, H. Laplace transform method for a coupled system of (p,q)-Caputo fractional differential equations. J. Appl. Math. Comput. 2025, 71, 511–530. [Google Scholar] [CrossRef]
- Gomez, C.A.; Salas, A.H. Exact solutions for the generalized BBM equationwith variable coefficients. Math. Probl. Eng. 2010, 4, 394–401. [Google Scholar]
- Estevez, P.G.; Kuru, S.; Negro, J.; Nieto, L.M. Traveling wave solutions ofthe generalized Benjamin-Bona-Mahony equation. Chaos Sol. Fract. 2009, 40, 2031–2040. [Google Scholar] [CrossRef]
- Gomez, C.A.; Salas, A.H.; Frias, B.A. New periodic and soliton solutions for the generalized BBM and Burgers-BBM equations. Appl. Math. Comput. 2010, 217, 1430–1434. [Google Scholar]
- Hanna, J.; Rowland, J. Fourier Series, Transforms, and Boundary Value Problems; John Wiley and Sons, Inc.: New York, NY, USA, 1990. [Google Scholar]
- Al-Deiakeh, R.; Abu Arqub, O.; Al-Smadi, M.; Momani, S. Lie symmetry analysis, explicit solutions, and conservation laws of the time-fractional Fisher equation in two-dimensional space. J. Ocean. Eng. Sci. 2022, 7, 345–352. [Google Scholar]

| 0.15 | 0.0011616462485873247 | 0.0011616462334527696 | 1.51345550675197 × 10−11 |
| 0.30 | 0.0013493867127497216 | 0.0013493857242148680 | 9.88534853583675 × 10−10 |
| 0.45 | 0.0015674214008082911 | 0.0015674099064100775 | 1.149439821362258 × 10−8 |
| 0.60 | 0.0018206220327889478 | 0.0018205560898476433 | 6.594294130451289 × 10−8 |
| 0.75 | 0.0021146379659695570 | 0.0021143810570989283 | 2.569088706286249 × 10−7 |
| 0.90 | 0.0024560182992063697 | 0.0024552346605740850 | 7.836386322845022 × 10−7 |
| 0.2 | 0.533333333 | 0.563133166 | 0.666743301 | 0.752959158 | |
| 0.4 | 0.7333333333 | 0.730677032 | 0.647817002 | 1.729984040 | |
| 0 | 0.6 | 0.6624999999 | 0.601221814 | 0.773199786 | 5.627232401 |
| 0.8 | 0.3833333333 | 0.380901655 | 2.296503479 | 14.43633998 | |
| 1.0 | 0.4583333334 | 0.868175353 | 7.100230119 | 29.99511468 | |
| 0.2 | 0.2500655487 | 0.282636442 | 0.461938500 | 0.198465800 | |
| 0.4 | 0.5162760640 | 0.543258410 | 0.108256800 | −4.62753690 | |
| 1 | 0.6 | 0.4323501300 | 0.204044800 | −3.30214140 | −18.3144920 |
| 0.8 | −1.181739800 | −2.27878010 | −13.1558670 | −44.2210390 | |
| 1.0 | −6.581913800 | −9.63100700 | −33.7865670 | −85.4023980 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-deiakeh, R.; Alhazmi, S.; Al-Omari, S.; Al-Smadi, M.; Momani, S. On the Laplace Residual Series Method and Its Application to Time-Fractional Fisher’s Equations. Fractal Fract. 2025, 9, 275. https://doi.org/10.3390/fractalfract9050275
Al-deiakeh R, Alhazmi S, Al-Omari S, Al-Smadi M, Momani S. On the Laplace Residual Series Method and Its Application to Time-Fractional Fisher’s Equations. Fractal and Fractional. 2025; 9(5):275. https://doi.org/10.3390/fractalfract9050275
Chicago/Turabian StyleAl-deiakeh, Rawya, Sharifah Alhazmi, Shrideh Al-Omari, Mohammed Al-Smadi, and Shaher Momani. 2025. "On the Laplace Residual Series Method and Its Application to Time-Fractional Fisher’s Equations" Fractal and Fractional 9, no. 5: 275. https://doi.org/10.3390/fractalfract9050275
APA StyleAl-deiakeh, R., Alhazmi, S., Al-Omari, S., Al-Smadi, M., & Momani, S. (2025). On the Laplace Residual Series Method and Its Application to Time-Fractional Fisher’s Equations. Fractal and Fractional, 9(5), 275. https://doi.org/10.3390/fractalfract9050275






