Chaotic Analysis and Wave Photon Dynamics of Fractional Whitham–Broer–Kaup Model with β Derivative

Abstract

This study uses a conformable derivative of order $\beta$ to investigate a fractional Whitham–Broer–Kaup ($\mathcal{FWBK}$) model. This model has significant uses in several scientific domains, such as plasma physics and nonlinear optics. The enhanced modified Sardar sub-equation $\mathcal{EMSSE}$ approach is applied to achieve precise analytical solutions, demonstrating its effectiveness in resolving complex wave photons. Bright, solitary, trigonometric, dark, and plane waves are among the various wave dynamics that may be effectively and precisely determined using the $\mathcal{FWBK}$ model. Furthermore, the study explores the chaotic behaviour of both perturbed and unperturbed systems, revealing illumination on their dynamic characteristics. By demonstrating its validity in examining wave propagation in nonlinear fractional systems, the effectiveness and reliability of the suggested method in fractional modelling are confirmed through thorough investigation.

1. Introduction

Fractional models enable physically complex systems to be established that are capable of precisely modelling memory effects and phenomena of nonlocal behaviour, which are reflected by the order difference and cannot be properly simulated by integer-order differential equations. With fractional derivatives, these models can better and more elastically describe inaccurate phenomena in the real world, such as fluid mechanics, anomalous diffusion, and viscoelasticity [1,2,3]. Fractional derivatives enhance the modelling of phenomena with history-dependent dynamics by bringing new ideas into modelling. They are, thus, very useful for both theoretical understanding and practical applications, particularly in physics, economics, and other engineering disciplines [4,5]. A prime objective is to obtain a fractional representation of the standard $\mathcal{FWBK}$ model to model nonlinear wave propagation [6].

Fractional orders are useful characteristics in classical derivatives while considering fractional orders when employing $\beta$-conformable derivatives [7,8]. This application of the $\mathcal{FWBK}$ model can capture variations in the propagation medium and derive new wave dynamics like plane and singular waves and dark and bright solitons [9,10,11,12,13]. Sophisticated analytical methods are needed to solve fractional mathematical models [14,15]. Techniques like the sub-equation method [16], Adomian Decomposition Method [17], Homotopy Analysis [18], bilinear transformation [19], F-expansion [20], and symmetry-based methods [21], among others [22,23,24], have received much attention because of their flexibility and strong convergence characteristics in solving nonlinear and fractional systems. A comparison with standard numerical approaches points out the effectiveness and reliability of these methods in representing the intricate behaviour of fractional-order systems [25,26,27]. The study examines an $\mathcal{EMSSE}$ approach to extracting novel wave patterns and carrying out a dynamical analysis to analyse the perturbed and unperturbed behaviours of the $\mathcal{FWBK}$ model. With the incorporation of $\beta$-conformable derivatives, the $\mathcal{FWBK}$ model [28] can be expressed as follows:

$$\begin{array}{cc}\hfill & D_t^{\beta }Q+D_x^{\beta }R+Q{D}_x^{\beta }Q+\delta D_x^{2\beta }Q=0,\hfill \\ \hfill & D_t^{\beta }R+D_x^{\beta }\left(QR\right)+\gamma D_x^{3\beta }Q-\delta D_x^{2\beta }R=0,\hfill \end{array}$$

(1)

x illustrates the spatial term, and t illustrates the temporal term, with dependent variables being functions of spatial and temporal terms; $\delta$ and $\gamma$ are the frequency and amplitude parameters. The $\mathcal{FWBK}$ model finds many applications in physics, especially in fields that investigate intricate wave propagation and nonlocal interactions. In the study of optical fibres, it is widely used to model wave propagation and study soliton dynamics under Kerr law nonlinearity. Optical communication system design requires improving optical communication system architecture, which calls for the efficient dispersion control of signals. In plasma physics [29], the $\mathcal{FWBK}$ model captures soliton dynamics with the inclusion of the effects of nonlinearity and nonlocality. It also models the dynamics of Heisenberg spin chains and birefringent fibres and provides useful insights into complex magnetic interactions and wave interference effects. Applications include magnetic resonance imaging and materials with spin-orbit coupling. A unique feature of this research is its use of a modified approach [30] to computationally solve the $\mathcal{FWBK}$ model, establish new conclusions, and corroborate them via dynamic analysis.

Although fractional models have been investigated recently to explain nonlinear wave propagation, the majority of these works ignore memory effects in chaotic regimes in favour of classical derivatives. A more comprehensive method that more accurately captures intricate dynamics is provided by the $\beta$ derivative. Its use in the $\mathcal{EMSSE}$ approach has not yet been investigated, though. By employing the $\beta$ derivative to analyse chaotic behaviours and wave-photon interactions in the $\mathcal{FWBK}$ model, this study closes this gap and offers fresh perspectives on its dynamical structure. The paper is organised as follows. The $\beta$ derivative is covered in Section 2. The mathematical analysis of the $\mathcal{EMSSE}$ approach is covered in Section 3. The in-detail implementation of the analytical method to regulate the model and validate the findings can be seen in Section 4. The dynamical structures of chaotic systems with perturbed and non-perturbed portraits are covered in Section 5. The simulations and discussions concerning the physical structures are covered in Section 6. The results obtained are concluded in Section 7.

2. $\beta$-Conformable Derivative

The conformable fractional derivative is a modern method of fractional calculus designed to improve and facilitate the properties of classical fractional derivatives [31]. Proposed as a different definition from the conventional ones, it is most appreciated for maintaining basic rules of calculus, such as linearity, the product rule, and the chain rule, making it easier to apply to differential equations and engineering problems. By making sure fractional differentiation behaves like regular calculus, the conformable derivative presents a neatly constructed and intuitive framework. Usually presented as a limit, it still possesses fundamental mathematical properties that are typical fractional derivatives.

This derivative has been found to be useful in the solving of ordinary and partial differential equations in a host of areas, ranging from physics and biology to finance, and it provides solutions to real problems with memory effects and hereditary properties. Its main benefit is that it conforms to classical rules of the derivative, making the analysis of analytical solutions straightforward and allowing fractional calculus to be efficiently used in areas such as signal processing and anomalous diffusion systems.

Definition 1.

Consider the function $R\left(t\right):(0,+\infty )\to \mathfrak{R}.$ so that a conformable fractional order β to $R\left(t\right)$ is stated as

$$D_t^{\beta }f\left(t\right)=\underset{c\to 0}{lim}{\displaystyle \frac{R(t+c{t}^{1-\beta })-R\left(t\right)}{\beta }},$$

(2)

as $t>0,\beta \in (0,1].$

Theorem 1.

Let $S_1$ and $S_2$ be the matching solution sets of the related fractional-order system described in Equation (2), and let $R_1\left(t\right)$ and $R_2\left(t\right)$ be two continuous functions on the interval. After that, the solutions show boundedness, convergence, etc., under appropriate beginning circumstances and assumptions. In $R_1\left(t\right)$ and $R_2\left(t\right)$, continuity plays a crucial role in determining the system’s stability. The characteristics of conformable derivatives are defined as follows.

Properties:

• $D_t^{\beta }(R_1{S}_1+R_2{S}_2)=R_1{D}_t^{\beta }{S}_1+R_2{D}_t^{\beta }{S}_2$;
• $D_t^{\beta }\left(t^{R_1}\right)=R_1{t}^{R_1-\beta }$;
• $D_t^{\beta }\left(c\right)=0$;
• $D_t^{\beta }\left(R_1{R}_2\right)=R_1{D}_t^{\beta }{R}_2+R_2{D}_t^{\beta }{R}_1$;
• $D_t^{\beta }\left({\displaystyle \frac{R_1}{R_2}}\right)={\displaystyle \frac{R_2{D}_t^{\beta }{R}_1-R_1{D}_t^{\beta }{R}_2}{R_2^2}}$;
• $R_1$ is differentiable $D_t^{\beta }\left(R_1\right)\left(t\right)=t^{1-\beta }{\displaystyle \frac{d{R}_1}{dt}}.$

Theorem 2.

Assume that for every $t>0$, $R_2\left(t\right)$ in the range of $R_1\left(t\right)$, and $R_1\left(t\right)$ is a conformable derivative. Then,

$$D_t^{\beta }(R_1\left(t\right)\circ R_2\left(t\right))=t^{1-\beta }{\displaystyle \frac{d{R}_2}{dt}}{\displaystyle \frac{d}{dt}}\left(R_1\left(R_2\left(t\right)\right)\right).$$

(3)

3. Overview of Enhanced Modified Sardar Sub-Equation Approach

Consider the generic fractional nonlinear model.

$$Q_x,Q_{xx},Q_{xt},Q_{xxxt},..=0,$$

(4)

$Q=Q(x,t)$ is a function of x and is spatial, and t is temporal. Use the transformation with variable parameters to convert Equation (8) into an ordinary differential equation ($\mathcal{ODE})$.

$$Q(x,t)=q\left(\eta \right),\eta ={\displaystyle \frac{x^{\beta }}{\beta }}-p{\displaystyle \frac{t^{\beta }}{\beta }},$$

(5)

q is the transforming dependent parameter, x is a spatial variable, and t is a temporal variable. By inserting Equation (5), Equation (4) reduces to the following $\mathcal{ODE}$:

$$q,q^{\prime },q^{″}+ ...=0.$$

(6)

Consider the following generic solution to Equation (6) as

$$q\left(\eta \right)=s_0+\sum _{w=1}^W{s}_w{H}^w\left(\eta \right).$$

(7)

In this case, $s_j$ represents arbitrary terms, and $s_W$ and $H\left(\eta \right)$ are unknown functions that must be found for our necessary results. The higher-order derivative terms and higher-order nonlinear terms in the nonlinear system must be balanced to determine the positive integer W. At this point, we will use the following differential equation to determine $q,q^{\prime },q^{″},...$ of Equation (7).

$$H^{\prime }\left(\eta \right)=\sqrt{v_0+v_1{H}^2\left(\eta \right)+v_2{H}^4\left(\eta \right)}.$$

(8)

Equation (8) obeys the following solutions, where K is the integration constant.

• Set-1: When $v_0=v_1=0$ and $v_2>0,$ we acquired the solutions in the rational form:

  $$H_1^{\pm }\left[\eta \right]=\pm {\displaystyle \frac{1}{\sqrt{v_2}(\eta +K)}}.$$

  (9)
• Set-2: When $v_0=0$ and $v_1>0,$ we acquired the solutions in the exponential form:

  $$H_2^{\pm }\left[\eta \right]={\displaystyle \frac{4v_1{e}^{\pm \sqrt{v_1}(\eta +K)}}{e^{\sqrt{v_1}\pm 2(\eta +K)}-4v_1{v}_2}},$$

  (10)

  $$H_3^{\pm }\left[\eta \right]=\pm {\displaystyle \frac{4v_1{e}^{\pm \sqrt{v_1}(\eta +K)}}{1-4v_1{v}_2{e}^{\sqrt{v_1}\pm 2(\eta +K)}}}.$$

  (11)
• Set-3: When $v_0=0,v_1>0$ and $v_2\ne 0,$ we acquired the solutions in the hyperbolic form:

  $$H_4^{\pm }\left[\eta \right]=\pm \sqrt{-{\displaystyle \frac{v_1}{v_2}}}\sec \mathrm{h}\left(\sqrt{v_1}(\eta +K)\right),$$

  (12)

  $$H_5^{\pm }\left[\eta \right]=\pm \sqrt{{\displaystyle \frac{v_1}{v_2}}}\csc \mathrm{h}\left(\sqrt{v_1}(\eta +K)\right),$$

  (13)

  when $v_0={\displaystyle \frac{v_1^2}{4v_2}},v_1<0$ and $v_2>0,$ we acquired the solutions in the hyperbolic form:

  $$H_6^{\pm }\left[\eta \right]=\pm \sqrt{-{\displaystyle \frac{v_1}{2v_2}}}tanh\left(\sqrt{-{\displaystyle \frac{v_1}{2}}}(\eta +K)\right),$$

  (14)

  $$H_7^{\pm }\left[\eta \right]=\pm \sqrt{-{\displaystyle \frac{v_1}{2v_2}}}coth\left(\sqrt{-{\displaystyle \frac{v_1}{2}}}(\eta +K)\right),$$

  (15)

  $$H_8^{\pm }\left[\eta \right]=\pm \sqrt{-{\displaystyle \frac{v_1}{2v_2}}}\left(tanh\left(\sqrt{-2v_1}(\eta +K)\right)\pm i\mathrm{sech}\left(\sqrt{-2v_1}(\eta +K)\right)\right),$$

  (16)

  $$H_9^{\pm }\left[\eta \right]=\pm \sqrt{-{\displaystyle \frac{v_1}{2v_2}}}\left(coth\left(\sqrt{-2v_1}(\eta +K)\right)\pm i\mathrm{csch}\left(\sqrt{-2v_1}(\eta +K)\right)\right),$$

  (17)

  $$H_{10}^{\pm }\left[\eta \right]=\pm \sqrt{-{\displaystyle \frac{v_1}{8v_2}}}\left(tanh\left(\sqrt{-{\displaystyle \frac{v_1}{8}}}(\eta +K)\right)\pm icoth\left(\sqrt{-{\displaystyle \frac{v_1}{8}}}(\eta +K)\right)\right).$$

  (18)
• Set-4: When $v_0=0,v_1<0$ and $v_2\ne 0,$ we acquired the solutions in the trigonometric form:

  $$H_{11}^{\pm }\left[\eta \right]=\pm \sqrt{-{\displaystyle \frac{v_1}{v_2}}}sec\left(\sqrt{-v_1}(\eta +K)\right),$$

  (19)

  $$H_{12}^{\pm }\left[\eta \right]=\pm \sqrt{-{\displaystyle \frac{v_1}{v_2}}}csc\left(\sqrt{-v_1}(\eta +K)\right),$$

  (20)

  when $v_0={\displaystyle \frac{v_1^2}{4v_2}},v_1>0$ and $v_2>0,$ we acquired the solutions in the hyperbolic form:

  $$H_{13}^{\pm }\left[\eta \right]=\pm \sqrt{-{\displaystyle \frac{v_1}{2v_2}}}tan\left(\sqrt{{\displaystyle \frac{v_1}{2}}}(\eta +K)\right),$$

  (21)

  $$H_{14}^{\pm }\left[\eta \right]=\pm \sqrt{{\displaystyle \frac{v_1}{2v_2}}}cot\left(\sqrt{{\displaystyle \frac{v_1}{2}}}(\eta +K)\right),$$

  (22)

  $$H_{15}^{\pm }\left[\eta \right]=\pm \sqrt{{\displaystyle \frac{v_1}{2v_2}}}\left(tan\left(\sqrt{2v_1}(\eta +K)\right)\pm sec\left(\sqrt{2v_1}(\eta +K)\right)\right),$$

  (23)

  $$H_{16}^{\pm }\left[\eta \right]=\pm \sqrt{{\displaystyle \frac{v_1}{2v_2}}}\left(cot\left(\sqrt{2v_1}(\eta +K)\right)\pm csc\left(\sqrt{2v_1}(\eta +K)\right)\right),$$

  (24)

  $$H_{17}^{\pm }\left[\eta \right]=\pm \sqrt{{\displaystyle \frac{v_1}{8v_2}}}\left(tan\left(\sqrt{{\displaystyle \frac{v_1}{8}}}(\eta +K)\right)-cot\left(\sqrt{{\displaystyle \frac{v_1}{8}}}(\eta +K)\right)\right).$$

  (25)
  Then, in Equation (6), substitute Equation (7) and the necessary derivatives using Equation (8) and equate all of the coefficients of $H\left(\eta \right)$ to obtain a system of algebraic equations. Solve these equations in Mathematica to obtain the necessary solutions by using the solution sets of Equations (9)–(25).

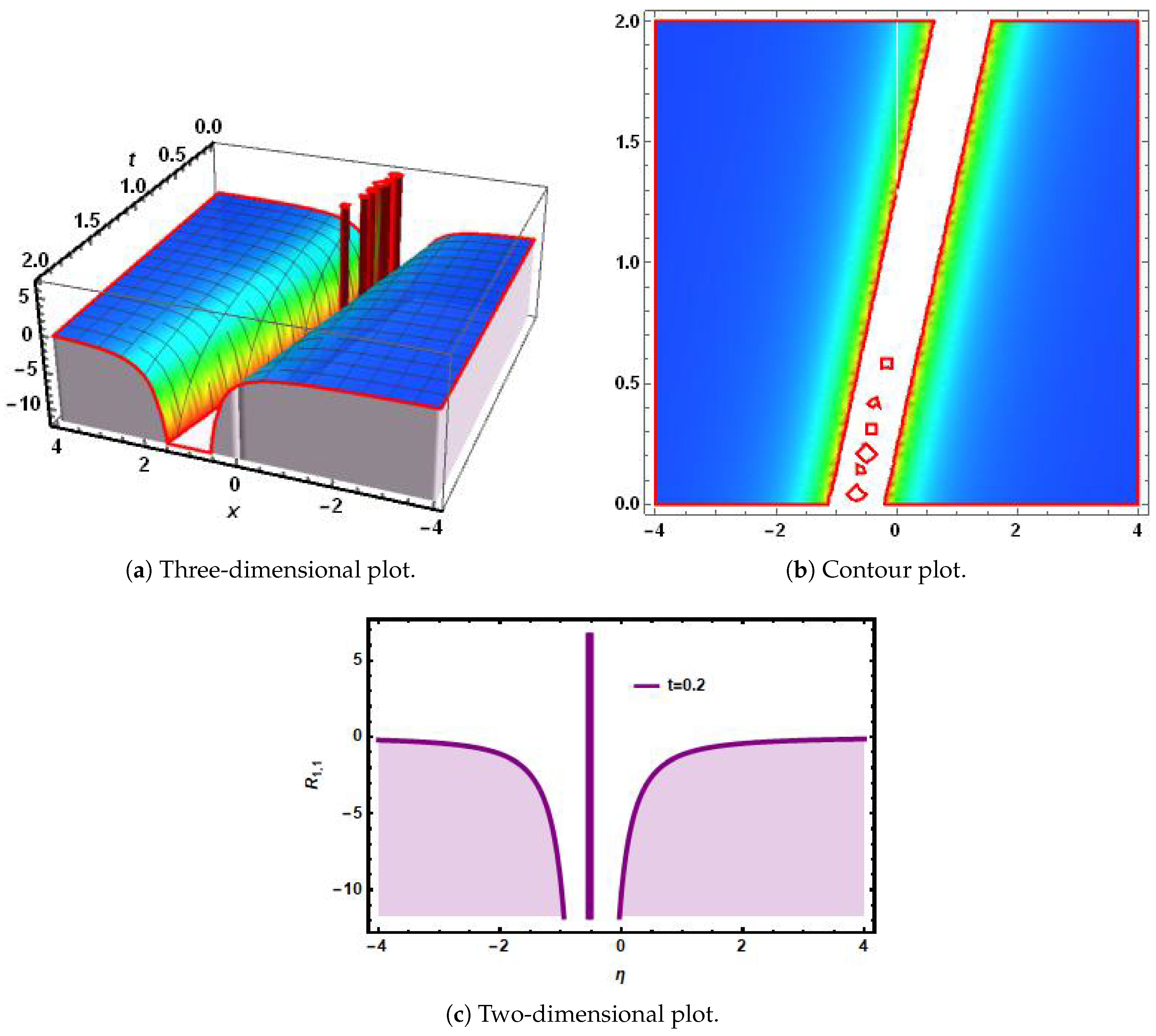
4. Application of $\mathcal{EMSSE}$ Approach to $\mathcal{FWBK}$ Model

In this section, we solve the reduced fractional-order differential equations exactly using the $\mathcal{EMSSE}$ approach. To solve for unknown parameters, the method entails establishing solution structures, substituting them into the transformed equation, and equating the coefficients. The $\mathcal{EMSSE}$ approach incorporates the $\beta$ derivative to precisely depict the system’s memory-dependent dynamics. To guarantee the analytical process’s transparency and reproducibility, comprehensive procedures and execution are given. We acquired the soliton solutions of Equation (1) using the $\mathcal{EMSSE}$ approach combined with $\beta$ derivative. Firstly, the $\mathcal{FWBK}$ system is converted into an $\mathcal{ODE}$. Now, by inserting Equation (5) into Equation (1), with the $\beta$ derivative of Equations (2) and (3), we obtain

$$\begin{array}{c}\hfill -p{q}^{\prime }\left(\eta \right)+r^{\prime }\left(\eta \right)+f{q}^{\prime }\left(\eta \right)+\delta q^{″}\left(\eta \right)=0,\end{array}$$

(26)

$$\begin{array}{c}\hfill -p{r}^{\prime }\left(\eta \right)+q^{\prime }\left(\eta \right)r^{\prime }\left(\eta \right)+\gamma q^{‴}\left(\eta \right)-\delta r^{″}\left(\eta \right)=0.\end{array}$$

(27)

After the simplification of Equations (26) and (27), we obtain the following equation:

$$\begin{array}{c}\hfill r\left(\eta \right)=pq\left(\eta \right)-{\displaystyle \frac{1}{2}}{\left(q\left(\eta \right)\right)}^2-\delta q^{\prime }\left(\eta \right),\end{array}$$

(28)

$$\begin{array}{c}\hfill -pr\left(\eta \right)+q\left(\eta \right)r\left(\eta \right)+\gamma q^{″}\left(\eta \right)-\delta r^{\prime }\left(\eta \right)=0.\end{array}$$

(29)

By substituting Equation (28) into Equation (29), we obtain the required $\mathcal{ODE}$.

$$-p^{2}q\left(\eta \right)+{\displaystyle \frac{3}{2}}p{\left(q\left(\eta \right)\right)}^2-{\displaystyle \frac{1}{2}}{\left(q\left(\eta \right)\right)}^3+(\delta +{\gamma }^2)q^{″}\left(\eta \right)=0.$$

(30)

We acquire the homogeneous balance principle $w=1$. We then derive the reduced form appropriate for additional analysis by inserting the necessary derivatives of $q^{\prime }\left(\eta \right)$, as stated in Equation (6), into Equation (7). Now, we collect all the coefficients of $H\left(\eta \right)$ to acquire solutions. In order to acquire the Family-1 of the solutions, we now solve the equation in Mathematica.

Family-1

$$\left\{\delta \to -{\gamma }^2-{\displaystyle \frac{p}{3v_1}},s_0\to p,s_1\to {\displaystyle \frac{i\sqrt{2}p\sqrt{v_2}}{\sqrt{v_1}}}\right\}.$$

(31)

As Family-1, we obtain the necessary soliton solutions by using all the cases in Equations (9)–(25), inserting all the values into Equation (5) and then Equations (7) and (8), and finally, putting this into Equation (1).

$$\begin{array}{c}\hfill Q_{1,1}(x,t)=p+{\displaystyle \frac{i\sqrt{2}p}{\sqrt{v_1}(\eta +K)}},\end{array}$$

(32)

$$\begin{array}{c}\hfill R_{1,1}(x,t)={\displaystyle \frac{i\sqrt{2}p\left(-{\gamma }^2-\frac{p}{3v_1}\right)}{\sqrt{v_1}{(\eta +K)}^2}}-{\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{i\sqrt{2}p}{\sqrt{v_1}(\eta +K)}}\right){}^2+p\left(p+{\displaystyle \frac{i\sqrt{2}p}{\sqrt{v_1}(\eta +K)}}\right),\end{array}$$

(33)

$$\begin{array}{c}\hfill Q_{1,2}(x,t)=p+{\displaystyle \frac{4i\sqrt{2}p\sqrt{v_1}\sqrt{v_2}{e}^{(\eta +K)\left(\pm \sqrt{v_1}\right)}}{e^{\sqrt{v_1}(\pm 2)(\eta +K)}-4v_1{v}_2}},\end{array}$$

(34)

$$\begin{array}{cc}\hfill R_{1,2}(x,t)=& -\left(-{\gamma }^2-{\displaystyle \frac{p}{3v_1}}\right)({\displaystyle \frac{4i\sqrt{2}p\sqrt{v_1}\sqrt{v_2}\left(\pm \sqrt{v_1}\right)e^{(\eta +K)\left(\pm \sqrt{v_1}\right)}}{e^{\sqrt{v_1}(\pm 2)(\eta +K)}-4v_1{v}_2}}\hfill \\ & -{\displaystyle \frac{4i\sqrt{2}p{v}_1\sqrt{v_2}(\pm 2)exp\left((\eta +K)\left(\pm \sqrt{v_1}\right)+\sqrt{v_1}(\pm 2)(\eta +K)\right)}{\left(e^{\sqrt{v_1}(\pm 2)(\eta +K)}-4v_1{v}_2\right){}^2}})\hfill \\ & -{\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{4i\sqrt{2}p\sqrt{v_1}\sqrt{v_2}{e}^{(\eta +K)\left(\pm \sqrt{v_1}\right)}}{e^{\sqrt{v_1}(\pm 2)(\eta +K)}-4v_1{v}_2}}\right){}^2+p\left(p+{\displaystyle \frac{4i\sqrt{2}p\sqrt{v_1}\sqrt{v_2}{e}^{(\eta +K)\left(\pm \sqrt{v_1}\right)}}{e^{\sqrt{v_1}(\pm 2)(\eta +K)}-4v_1{v}_2}}\right),\hfill \end{array}$$

(35)

$$\begin{array}{c}\hfill Q_{1,3}(x,t)=p+{\displaystyle \frac{4i\sqrt{2}p\sqrt{v_1}\sqrt{v_2}{e}^{(\eta +K)\left(\pm \sqrt{v_1}\right)}}{1-4v_1{v}_2{e}^{\sqrt{v_1}(\pm 2)(\eta +K)}}},\end{array}$$

(36)

$$\begin{array}{cc}\hfill R_{1,3}(x,t)=& -\left(-{\gamma }^2-{\displaystyle \frac{p}{3v_1}}\right)({\displaystyle \frac{16i\sqrt{2}p{v}_1^2{v}_2^{3/2}(\pm 2)exp\left((\eta +K)\left(\pm \sqrt{v_1}\right)+\sqrt{v_1}(\pm 2)(\eta +K)\right)}{\left(1-4v_1{v}_2{e}^{\sqrt{v_1}(\pm 2)(\eta +K)}\right){}^2}}+\hfill \\ & {\displaystyle \frac{4i\sqrt{2}p\sqrt{v_1}\sqrt{v_2}\left(\pm \sqrt{v_1}\right)e^{(\eta +K)\left(\pm \sqrt{v_1}\right)}}{1-4v_1{v}_2{e}^{\sqrt{v_1}(\pm 2)(\eta +K)}}})-\hfill \\ & {\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{4i\sqrt{2}p\sqrt{v_1}\sqrt{v_2}{e}^{(\eta +K)\left(\pm \sqrt{v_1}\right)}}{1-4v_1{v}_2{e}^{\sqrt{v_1}(\pm 2)(\eta +K)}}}\right){}^2+p\left(p+{\displaystyle \frac{4i\sqrt{2}p\sqrt{v_1}\sqrt{v_2}{e}^{(\eta +K)\left(\pm \sqrt{v_1}\right)}}{1-4v_1{v}_2{e}^{\sqrt{v_1}(\pm 2)(\eta +K)}}}\right),\hfill \end{array}$$

(37)

$$\begin{array}{c}\hfill Q_{1,4}(x,t)=p+{\displaystyle \frac{i\sqrt{2}p\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\mathrm{sech}\left(\sqrt{v_1}(\eta +K)\right)}{\sqrt{v_1}}},\end{array}$$

(38)

$$\begin{array}{cc}\hfill R_{1,4}(x,t)=& i\sqrt{2}p\sqrt{-{\displaystyle \frac{v_1}{v_2}}}\sqrt{v_2}\left(-{\gamma }^2-{\displaystyle \frac{p}{3v_1}}\right)tanh\left(\sqrt{v_1}(\eta +K)\right)\mathrm{sech}\left(\sqrt{v_1}(\eta +K)\right)\hfill \\ & -{\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{i\sqrt{2}p\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\mathrm{sech}\left(\sqrt{v_1}(\eta +K)\right)}{\sqrt{v_1}}}\right){}^2+p\left(p+{\displaystyle \frac{i\sqrt{2}p\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\mathrm{sech}\left(\sqrt{v_1}(\eta +K)\right)}{\sqrt{v_1}}}\right),\hfill \end{array}$$

(39)

$$\begin{array}{c}\hfill Q_{1,5}(x,t)=p+{\displaystyle \frac{i\sqrt{2}p\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\mathrm{csch}\left(\sqrt{v_1}(\eta +K)\right)}{\sqrt{v_1}}},\end{array}$$

(40)

$$\begin{array}{cc}\hfill R_{1,5}(x,t)=& i\sqrt{2}p\sqrt{{\displaystyle \frac{v_1}{v_2}}}\sqrt{v_2}\left(-{\gamma }^2-{\displaystyle \frac{p}{3v_1}}\right)coth\left(\sqrt{v_1}(\eta +K)\right)\mathrm{csch}\left(\sqrt{v_1}(\eta +K)\right)\hfill \\ & -{\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{i\sqrt{2}p\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\mathrm{csch}\left(\sqrt{v_1}(\eta +K)\right)}{\sqrt{v_1}}}\right){}^2+p\left(p+{\displaystyle \frac{i\sqrt{2}p\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\mathrm{csch}\left(\sqrt{v_1}(\eta +K)\right)}{\sqrt{v_1}}}\right),\hfill \end{array}$$

(41)

$$\begin{array}{c}\hfill Q_{1,6}(x,t)=p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}tanh\left(\frac{\sqrt{-v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{v_1}}},\end{array}$$

(42)

$$\begin{array}{cc}\hfill R_{1,6}(x,t)=& -{\displaystyle \frac{ip\sqrt{-v_1}\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(-{\gamma }^2-\frac{p}{3v_1}\right){\mathrm{sech}}^2\left(\frac{\sqrt{-v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{2}\sqrt{v_1}}}\hfill \\ & -{\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}tanh\left(\frac{\sqrt{-v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{v_1}}}\right){}^2+p\left(p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}tanh\left(\frac{\sqrt{-v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{v_1}}}\right),\hfill \end{array}$$

(43)

$$\begin{array}{c}\hfill Q_{1,7}(x,t)=p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}coth\left(\frac{\sqrt{-v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{v_1}}},\end{array}$$

(44)

$$\begin{array}{cc}\hfill R_{1,7}(x,t)=& {\displaystyle \frac{ip\sqrt{-v_1}\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(-{\gamma }^2-\frac{p}{3v_1}\right){\mathrm{csch}}^2\left(\frac{\sqrt{-v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{2}\sqrt{v_1}}}-\hfill \\ & {\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}coth\left(\frac{\sqrt{-v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{v_1}}}\right){}^2+p\left(p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}coth\left(\frac{\sqrt{-v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{v_1}}}\right),\hfill \end{array}$$

(45)

$$\begin{array}{c}\hfill Q_{1,8}(x,t)=p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(tanh\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)+i\mathrm{sech}\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}},\end{array}$$

(46)

$$\begin{array}{cc}\hfill R_{1,8}(x,t)=& -{\displaystyle \frac{\left(\sqrt{2}\sqrt{-v_1}{\mathrm{sech}}^2\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)-i\sqrt{2}\sqrt{-v_1}tanh\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)\sec \mathrm{h}\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}}\hfill \\ & -{\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(tanh\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)+i\sec \mathrm{h}\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}}\right){}^2\hfill \\ & +p\left(p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(tanh\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)+i\sec \mathrm{h}\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}}\right),\hfill \end{array}$$

(47)

$$\begin{array}{c}\hfill Q_{1,9}(x,t)=p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(coth\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)+i\mathrm{csch}\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}},\end{array}$$

(48)

$$\begin{array}{cc}\hfill R_{1,9}(x,t)=& -{\displaystyle \frac{\left(-\sqrt{2}\sqrt{-v_1}{\mathrm{csch}}^2\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)-i\sqrt{2}\sqrt{-v_1}coth\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)\mathrm{csch}\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}}\hfill \\ & +{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(-{\gamma }^2-\frac{p}{3v_1}\right)}{\sqrt{v_1}}}-{\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{\left(coth\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)+i\mathrm{csch}\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}}\right){}^2\hfill \\ & +p\left(p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(coth\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)+i\csc \mathrm{h}\left(\sqrt{2}\sqrt{-v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}}\right),\hfill \end{array}$$

(49)

$$\begin{array}{c}\hfill Q_{1,10}(x,t)=p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(tanh\left(\frac{\sqrt{-v_1}(\eta +K)}{2\sqrt{2}}\right)+icoth\left(\frac{\sqrt{-v_1}(\eta +K)}{2\sqrt{2}}\right)\right)}{2\sqrt{v_1}}},\end{array}$$

(50)

$$\begin{array}{cc}\hfill R_{1,10}(x,t)=& -{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(-{\gamma }^2-\frac{p}{3v_1}\right)\left(\frac{\sqrt{-v_1}{\mathrm{sech}}^2\left(\frac{\sqrt{-v_1}(\eta +K)}{2\sqrt{2}}\right)}{2\sqrt{2}}-\frac{i\sqrt{-v_1}{\csc \mathrm{h}}^2\left(\frac{\sqrt{-v_1}(\eta +K)}{2\sqrt{2}}\right)}{2\sqrt{2}}\right)}{2\sqrt{v_1}}}\hfill \\ & -{\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(tanh\left(\frac{\sqrt{-v_1}(\eta +K)}{2\sqrt{2}}\right)+icoth\left(\frac{\sqrt{-v_1}(\eta +K)}{2\sqrt{2}}\right)\right)}{2\sqrt{v_1}}}\right){}^2\hfill \\ & +p\left(p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(tanh\left(\frac{\sqrt{-v_1}(\eta +K)}{2\sqrt{2}}\right)+icoth\left(\frac{\sqrt{-v_1}(\eta +K)}{2\sqrt{2}}\right)\right)}{2\sqrt{v_1}}}\right),\hfill \end{array}$$

(51)

$$\begin{array}{c}\hfill Q_{1,11}(x,t)=p+{\displaystyle \frac{i\sqrt{2}p\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}sec\left(\sqrt{-v_1}(\eta +K)\right)}{\sqrt{v_1}}},\end{array}$$

(52)

$$\begin{array}{cc}\hfill R_{1,11}(x,t)=& -{\displaystyle \frac{i\sqrt{2}p\sqrt{-v_1}\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(-{\gamma }^2-\frac{p}{3v_1}\right)tan\left(\sqrt{-v_1}(\eta +K)\right)sec\left(\sqrt{-v_1}(\eta +K)\right)}{\sqrt{v_1}}}-\hfill \\ & {\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{i\sqrt{2}p\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}sec\left(\sqrt{-v_1}(\eta +K)\right)}{\sqrt{v_1}}}\right){}^2+p\left(p+{\displaystyle \frac{i\sqrt{2}p\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}sec\left(\sqrt{-v_1}(\eta +K)\right)}{\sqrt{v_1}}}\right),\hfill \end{array}$$

(53)

$$\begin{array}{c}\hfill Q_{1,12}(x,t)=p+{\displaystyle \frac{i\sqrt{2}p\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}csc\left(\sqrt{-v_1}(\eta +K)\right)}{\sqrt{v_1}}},\end{array}$$

(54)

$$\begin{array}{cc}\hfill R_{1,12}(x,t)=& {\displaystyle \frac{i\sqrt{2}p\sqrt{-v_1}\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(-{\gamma }^2-\frac{p}{3v_1}\right)cot\left(\sqrt{-v_1}(\eta +K)\right)csc\left(\sqrt{-v_1}(\eta +K)\right)}{\sqrt{v_1}}}-\hfill \\ & {\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{i\sqrt{2}p\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}csc\left(\sqrt{-v_1}(\eta +K)\right)}{\sqrt{v_1}}}\right){}^2+p\left(p+{\displaystyle \frac{i\sqrt{2}p\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}csc\left(\sqrt{-v_1}(\eta +K)\right)}{\sqrt{v_1}}}\right),\hfill \end{array}$$

(55)

$$\begin{array}{c}\hfill Q_{1,13}(x,t)=p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}tan\left(\frac{\sqrt{v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{v_1}}},\end{array}$$

(56)

$$\begin{array}{cc}\hfill R_{1,13}(x,t)=& -{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}\left(-{\gamma }^2-\frac{p}{3v_1}\right){sec}^2\left(\frac{\sqrt{v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{2}}}-\hfill \\ & {\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}tan\left(\frac{\sqrt{v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{v_1}}}\right){}^2+p\left(p+{\displaystyle \frac{ip\sqrt{-\frac{v_1}{v_2}}\sqrt{v_2}tan\left(\frac{\sqrt{v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{v_1}}}\right),\hfill \end{array}$$

(57)

$$\begin{array}{c}\hfill Q_{1,14}(x,t)=p+{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}cot\left(\frac{\sqrt{v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{v_1}}},\end{array}$$

(58)

$$\begin{array}{cc}\hfill R_{1,14}(x,t)=& {\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(-{\gamma }^2-\frac{p}{3v_1}\right){csc}^2\left(\frac{\sqrt{v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{2}}}-\hfill \\ & {\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}cot\left(\frac{\sqrt{v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{v_1}}}\right){}^2+p\left(p+{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}cot\left(\frac{\sqrt{v_1}(\eta +K)}{\sqrt{2}}\right)}{\sqrt{v_1}}}\right),\hfill \end{array}$$

(59)

$$\begin{array}{c}\hfill Q_{1,15}(x,t)=p+{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(tan\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)+sec\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}},\end{array}$$

(60)

$$\begin{array}{cc}\hfill R_{1,15}(x,t)=& -{\displaystyle \frac{\left(\sqrt{2}\sqrt{v_1}{sec}^2\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)+\sqrt{2}\sqrt{v_1}tan\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)sec\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}}\hfill \\ & +{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(-{\gamma }^2-\frac{p}{3v_1}\right)}{\sqrt{v_1}}}-{\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(tan\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)+sec\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}}\right){}^2\hfill \\ & +p\left(p+{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(tan\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)+sec\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}}\right),\hfill \end{array}$$

(61)

$$\begin{array}{c}\hfill Q_{1,16}(x,t)=p+{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(cot\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)+csc\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}},\end{array}$$

(62)

$$\begin{array}{cc}\hfill R_{1,16}(x,t)=& -{\displaystyle \frac{\left(\left(-\sqrt{2}\right)\sqrt{v_1}cot\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)csc\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)-\sqrt{2}\sqrt{v_1}{csc}^2\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}}-\hfill \\ & +{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(-{\gamma }^2-\frac{p}{3v_1}\right)}{+}}\sqrt{v_1}{\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(cot\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)+csc\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}}\right){}^2\hfill \\ & +p\left(p+{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(cot\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)+csc\left(\sqrt{2}\sqrt{v_1}(\eta +K)\right)\right)}{\sqrt{v_1}}}\right),\hfill \end{array}$$

(63)

$$\begin{array}{c}\hfill Q_{1,17}(x,t)=p+{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(tan\left(\frac{\sqrt{v_1}(\eta +K)}{2\sqrt{2}}\right)-cot\left(\frac{\sqrt{v_1}(\eta +K)}{2\sqrt{2}}\right)\right)}{2\sqrt{v_1}}},\end{array}$$

(64)

and

$$\begin{array}{cc}\hfill R_{1,17}(x,t)=& -{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(-{\gamma }^2-\frac{p}{3v_1}\right)\left(\frac{\sqrt{v_1}{csc}^2\left(\frac{\sqrt{v_1}(\eta +K)}{2\sqrt{2}}\right)}{2\sqrt{2}}+\frac{\sqrt{v_1}{sec}^2\left(\frac{\sqrt{v_1}(\eta +K)}{2\sqrt{2}}\right)}{2\sqrt{2}}\right)}{2\sqrt{v_1}}}-\hfill \\ & {\displaystyle \frac{1}{2}}\left(p+{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(tan\left(\frac{\sqrt{v_1}(\eta +K)}{2\sqrt{2}}\right)-cot\left(\frac{\sqrt{v_1}(\eta +K)}{2\sqrt{2}}\right)\right)}{2\sqrt{v_1}}}\right){}^2+\hfill \\ & p\left(p+{\displaystyle \frac{ip\sqrt{\frac{v_1}{v_2}}\sqrt{v_2}\left(tan\left(\frac{\sqrt{v_1}(\eta +K)}{2\sqrt{2}}\right)-cot\left(\frac{\sqrt{v_1}(\eta +K)}{2\sqrt{2}}\right)\right)}{2\sqrt{v_1}}}\right).\hfill \end{array}$$

(65)

Different soliton solution types, such as dark, periodic, bright, and bell-shaped structures, are represented by the above soliton solutions, which were obtained using the $\mathcal{EMSSE}$ approach under various parametric conditions. These solitons maintain their shape and energy during propagation, reflecting the fact that the governing model has stable, localised wave behaviour. Understanding nonlinear wave dynamics in dispersive media influenced by memory effects induced via the $\beta$ derivative requires such qualities.

5. Dynamical System

In this section, we will explore bifurcation and chaotic analysis of the $\mathcal{FWBK}$ model. The primary objective of this section is to convert Equation (30) into planar dynamical systems by utilising the Galilean transformation. Then, we explore the bifurcation and chaotic structures of the governing model.

5.1. Dynamical System

By using the Galilean transformation, we simplify an $\mathcal{ODE}$ into a planar dynamical system. This transformation reduces the number of independent variables by reducing their relative position or simplifying their relationships. For instance, we reduced a model with two spatial variables and one temporal variable to a system of equations that only depends on time. Equation (30) can be written as below.

$$\begin{array}{c}\hfill L_2\left(\eta \right)=E_1\left(L_1\left(\eta \right)-{\displaystyle \frac{3}{2}}{\left(L_1\left(\eta \right)\right)}^2\right)+E_2{\displaystyle \frac{1}{2}}{L}_1{\left(\eta \right)}^3,\end{array}$$

(66)

where

$$\begin{array}{cc}\hfill & E_1={\displaystyle \frac{p^2-p}{\delta +{\gamma }^2}},E_2={\displaystyle \frac{1}{\delta +{\gamma }^2}}.\hfill \end{array}$$

Then, the dynamical system of Equation (66) is described as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}q\left(\eta \right)=\hfill & L_1\left(\eta \right),\hfill \\ q^{″}\left(\eta \right)=\hfill & L_2\left(\eta \right)=E_1\left(L_1\left(\eta \right)-{\displaystyle \frac{3}{2}}{\left(L_1\left(\eta \right)\right)}^2\right)+E_2{\displaystyle \frac{1}{2}}{L}_1{\left(\eta \right)}^3.\hfill \end{array}\right.\end{array}$$

(67)

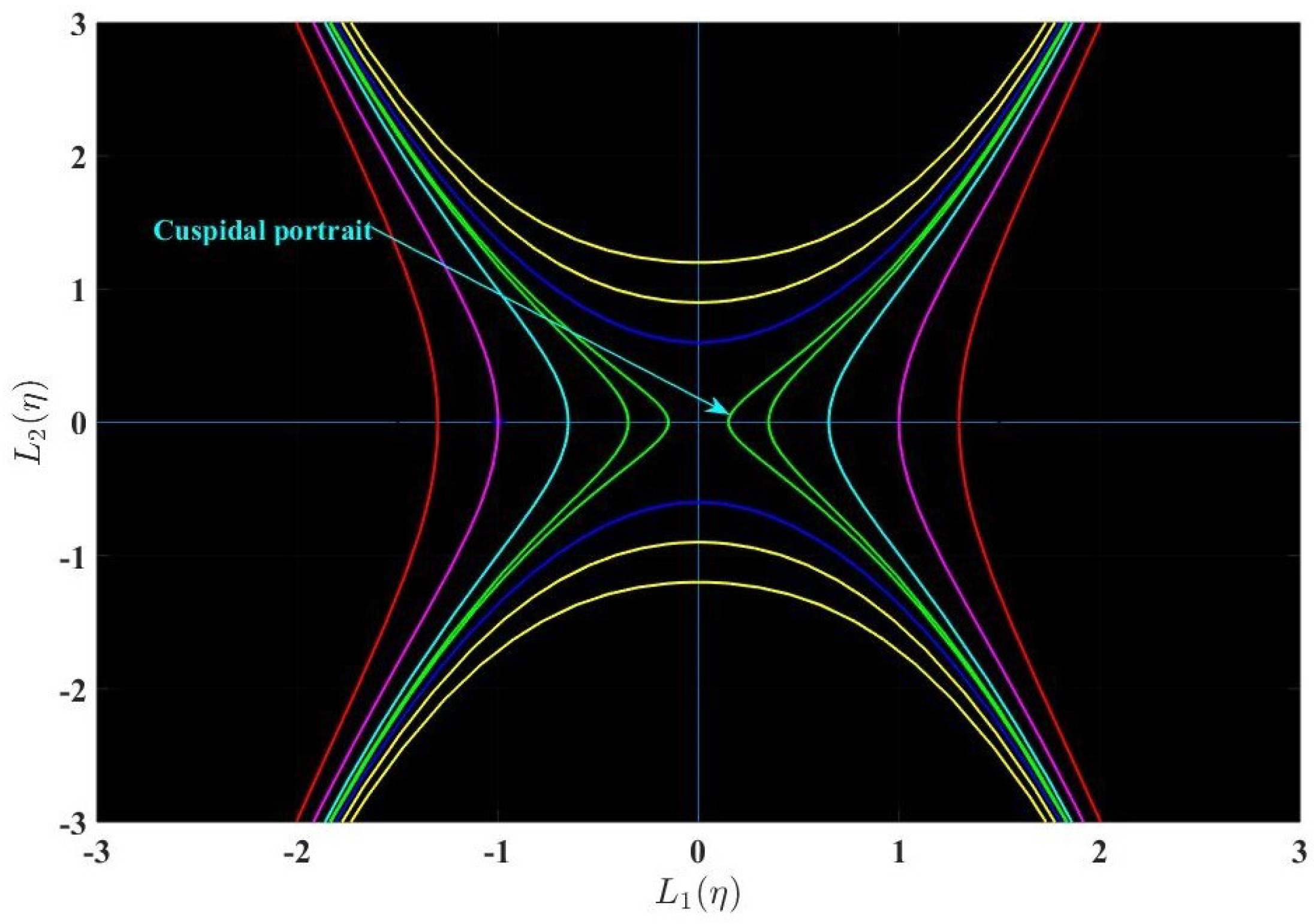
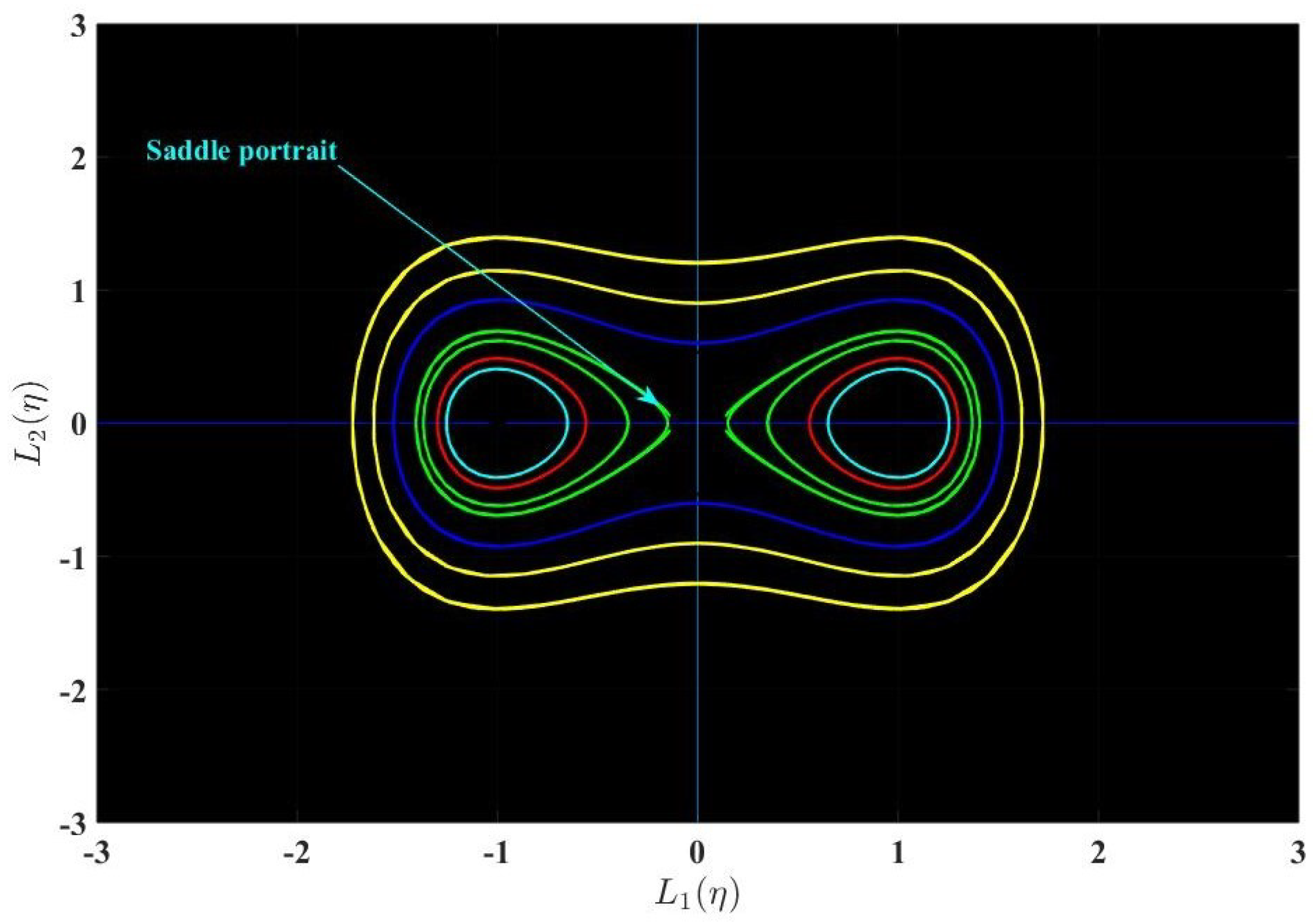
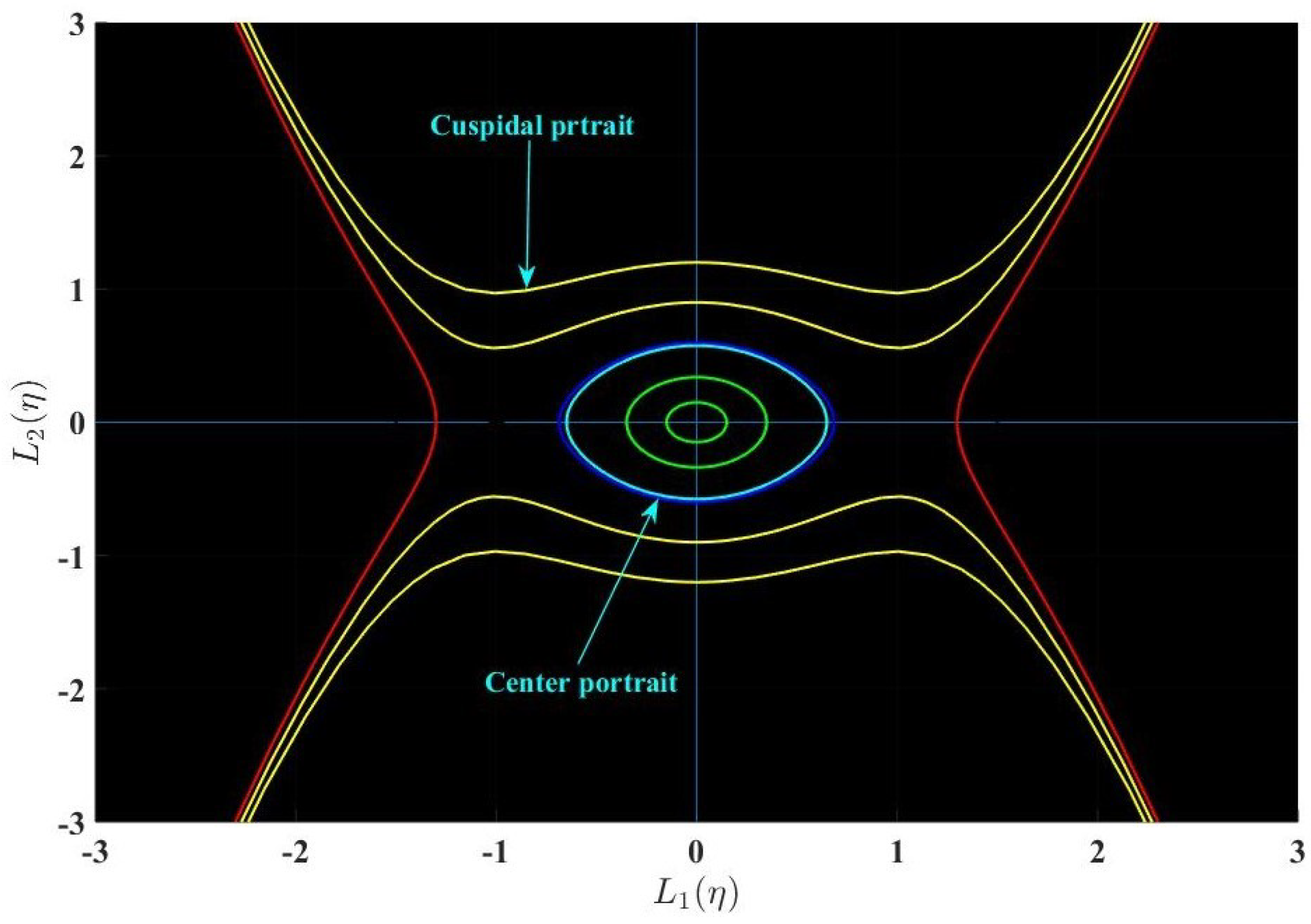
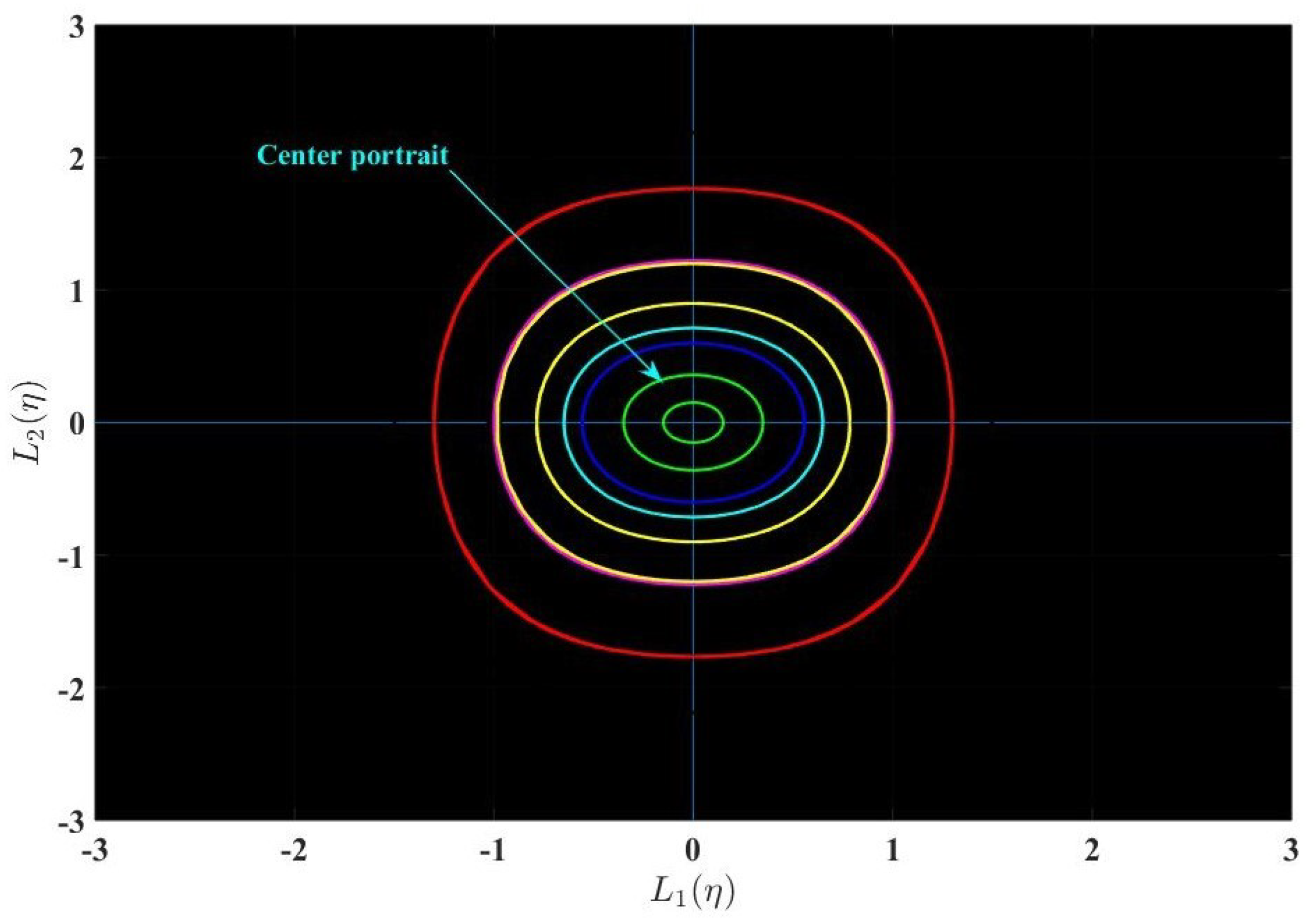
5.2. Bifurcation Analysis

Bifurcation refers to sudden changes in a system’s dynamics caused by varying parameters. Bifurcation analysis can explain variations in ocean wave formation patterns, including changes in wave speed and wavelength. By studying bifurcation processes, we can forecast and explain wave behaviour under various parameter settings. This provides a framework for ocean wave simulation and prediction. Firstly, we will represent the Hamiltonian function for Equation (67) as follows:

$$\begin{array}{c}\hfill \mathcal{H}(L_1\left(\eta \right),L_2\left(\eta \right))=+E_2{\displaystyle \frac{1}{2}}{L}_1{\left(\eta \right)}^3+E_1\left(L_1\left(\eta \right)-{\displaystyle \frac{3}{2}}{\left(L_1\left(\eta \right)\right)}^2\right).\end{array}$$

Equation (67) can be solved to determine the equilibrium points.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{L}_2\left(\eta \right)=0,\hfill \\ E_1\left(1-3\left(L_1\left(\eta \right)\right)\right)+E_2{\displaystyle \frac{3}{2}}{L}_1{\left(\eta \right)}^2=0.\hfill \end{array}\right.\end{array}$$

so that the points are

$$\begin{array}{c}\hfill {\mathcal{N}}_1=(-\sqrt{{\displaystyle \frac{E_2}{E_1}}},0),{\mathcal{N}}_2=(0,0),{\mathcal{N}}_3=(\sqrt{{\displaystyle \frac{E_2}{E_1}}},0).\end{array}$$

We calculate the determinant of Equation (30).

$$\begin{array}{c}\hfill =\left|\begin{array}{cc}0& 1\\ E_1\left(1-3\left(L_1\left(\eta \right)\right)\right)+E_2{\displaystyle \frac{3}{2}}{L}_1{\left(\eta \right)}^2& 0\end{array}\right|=E_1\left(1-3\left(L_1\left(\eta \right)\right)\right)+E_2{\displaystyle \frac{3}{2}}{L}_1{\left(\eta \right)}^2.\end{array}$$

• When $\mathit{J}\left(L_1\left(\eta \right),L_2\left(\eta \right)\right)>0$, then $\left(L_1\left(\eta \right),L_2\left(\eta \right)\right)$ behaves as a cuspidal point;
• When $\mathit{J}\left(L_1\left(\eta \right),L_2\left(\eta \right)\right)<0$, then $\left(L_1\left(\eta \right),L_2\left(\eta \right)\right)$ behaves as a center point;
• When $\mathit{J}\left(L_1\left(\eta \right),L_2\left(\eta \right)\right)=0$, then $\left(L_1\left(\eta \right),L_2\left(\eta \right)\right)$ behaves as a saddle point;
• When $\mathit{J}\left(L_1\left(\eta \right),L_2\left(\eta \right)\right)>0\&<0$, then $\left(L_1\left(\eta \right),L_2\left(\eta \right)\right)$ behaves as cuspidal and center points.

We examine the qualitative behaviour of the system’s solutions in the phase space in order to examine it from the viewpoint of a phase picture in Equation (67). We consider changes in bifurcation behaviour when parameters are being altered. It is possible to comprehend the effect of bifurcation by representing the phase portrait of the system for distinct parameter settings. This detailed investigation of multiple parameter settings allows us to better comprehend the dynamics of the system and changing behaviour. The following are the results that can be achieved by varying the concerned parameters.

Case I: When $E_1>0$ and $E_2>0$

By setting the specific parameter values $\delta =1and\gamma =1$, we obtain three equilibrium points: (−1.1291,0), (0,0), and (1.1291,0), as represented in Figure 1.

Case II: When $E_1>0$ and $E_2>0$

By setting the specific parameter values $\delta =1and\gamma =1$, we obtain three equilibrium points: (−1.1291,0), (0,0), and (1.1291,0), as represented in Figure 2.

Case III: When $E_1>0$ and $E_2>0$

By setting the specific parameter values $\delta =1and\gamma =1$, we obtain three equilibrium points: (−1.1291,0), (0,0), and (1.1291,0), as represented in Figure 3.

Case IV: When $E_1>0$ and $E_2>0$

By setting the specific parameter values $\delta =1and\gamma =1$, we obtain three equilibrium points: (−1.1291,0), (0,0), and (1.1291,0), as represented in Figure 4.

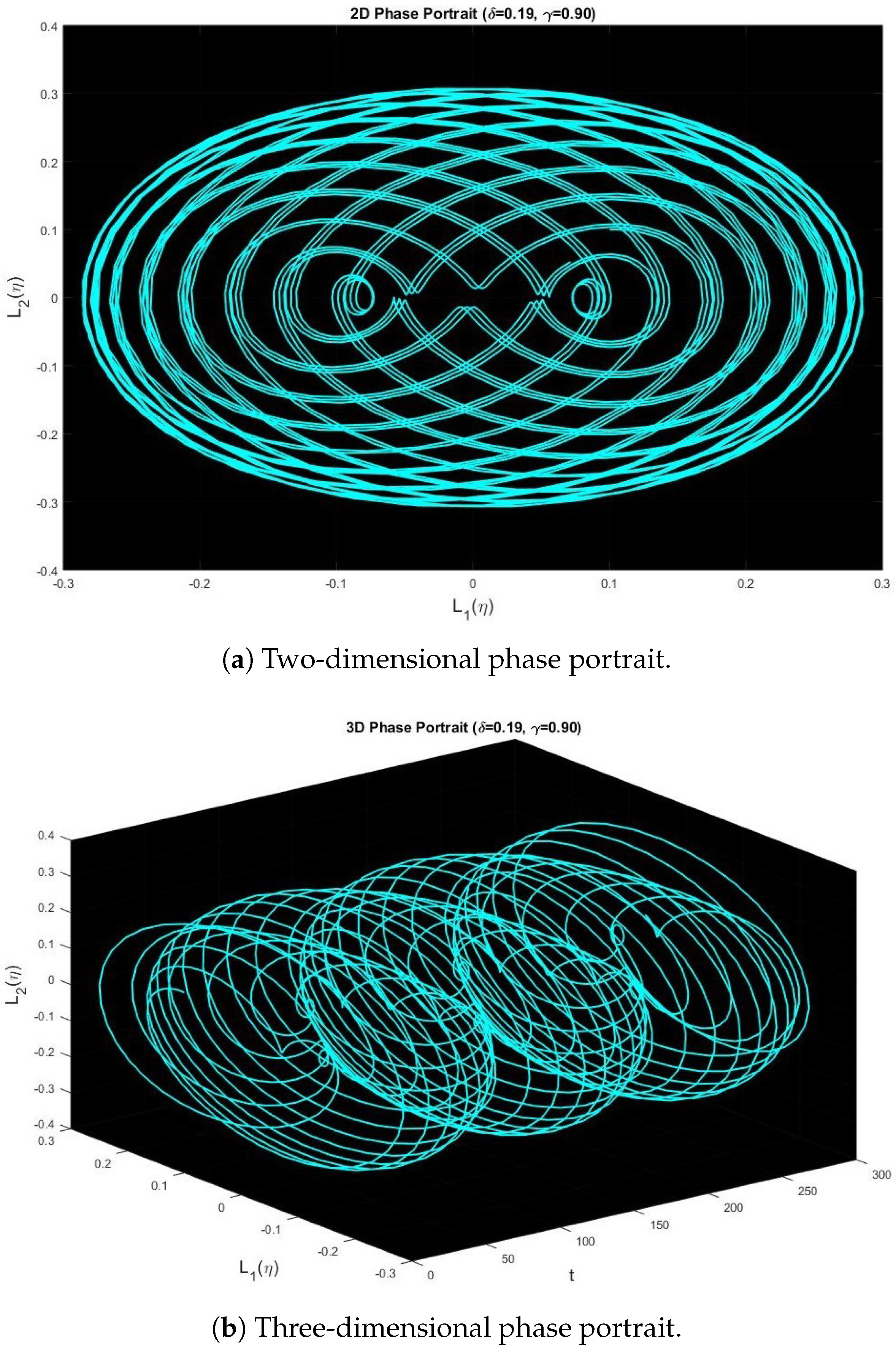
5.3. Chaotic Analysis

The sudden changes in a system’s dynamics brought on by shifting parameters are known as bifurcation. Changes in ocean wave creation patterns, including variations in wave speed and wavelength, can be taken into account via bifurcation analysis. We can forecast and take into consideration wave behaviour under various parameter situations by using bifurcation procedures. This provides us with a foundation for simulating and forecasting ocean waves. First, we will use the following expression to represent the Hamiltonian function for Equation (67).

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}q\left(\eta \right)=\hfill & L_1\left(\eta \right),\hfill \\ q^{″}\left(\eta \right)=\hfill & L_2\left(\eta \right)=E_1\left(L_1\left(\eta \right)-{\displaystyle \frac{3}{2}}{\left(L_1\left(\eta \right)\right)}^2\right)+E_2{\displaystyle \frac{1}{2}}{L}_1{\left(\eta \right)}^3+\delta (cos\left(\gamma \eta \right)).\hfill \end{array}\right.\end{array}$$

(68)

Figure 5, Figure 6, Figure 7 and Figure 8 show the chaotic dynamics of a governing model with varying amplitudes and frequencies.

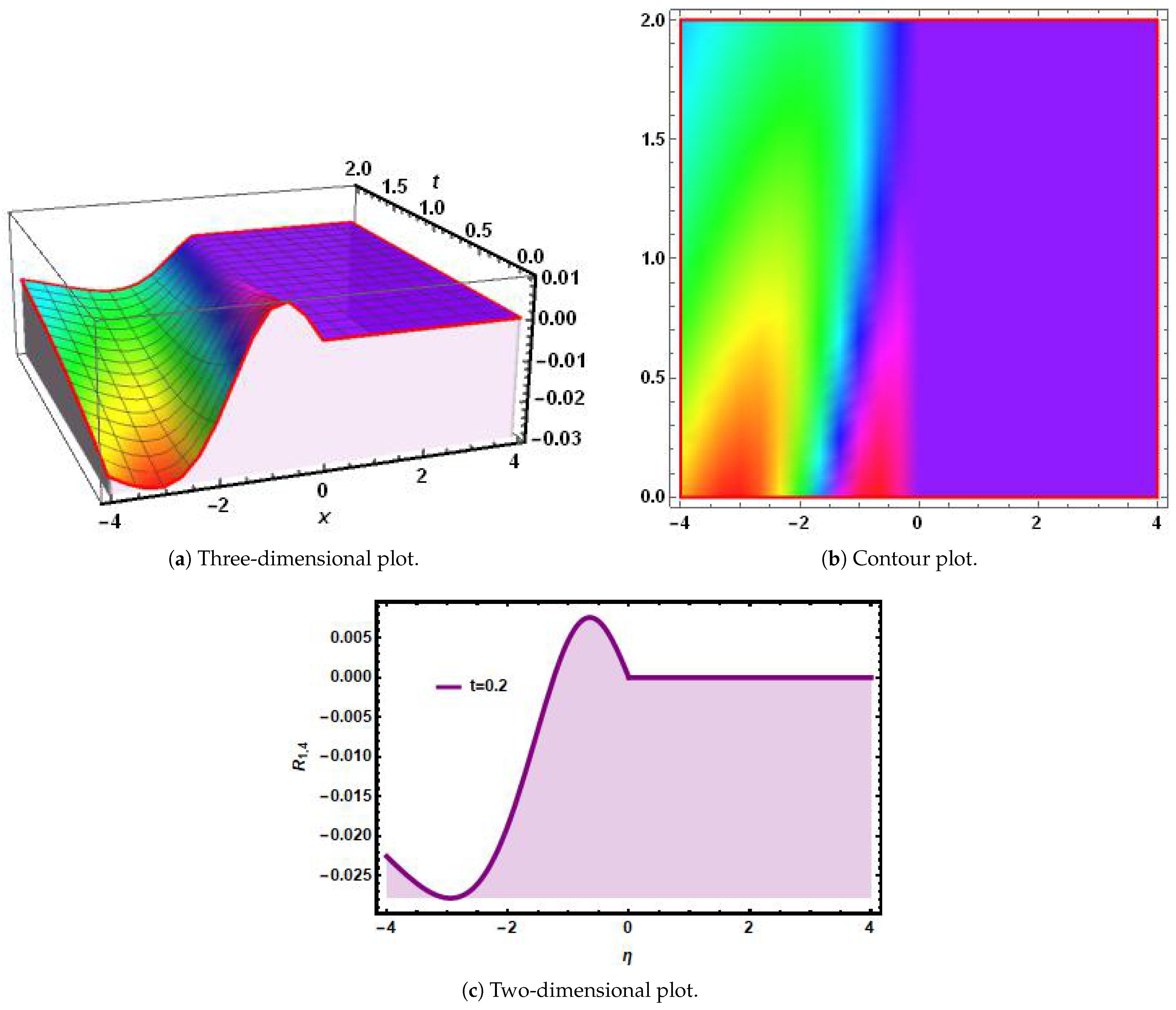
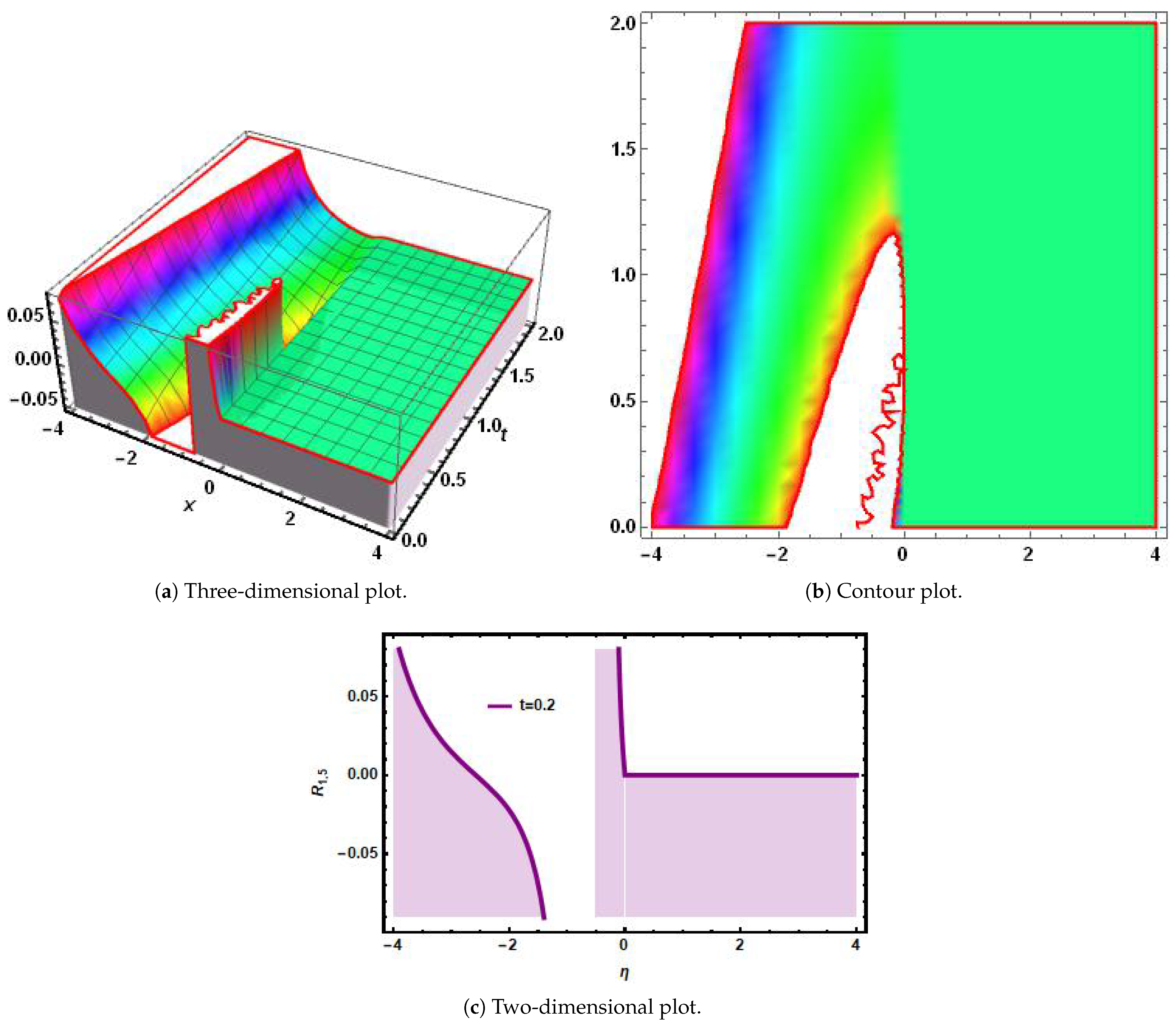
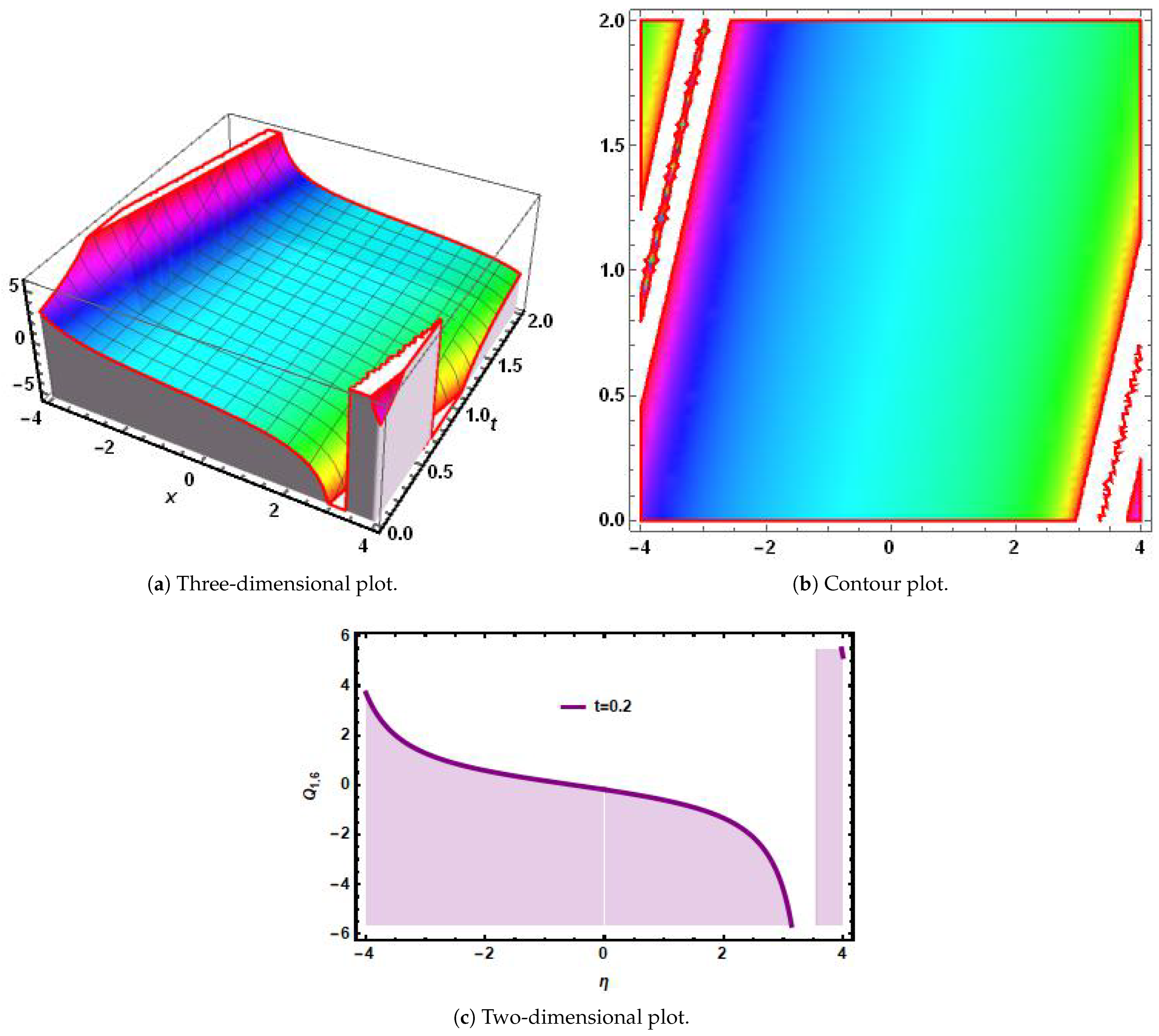
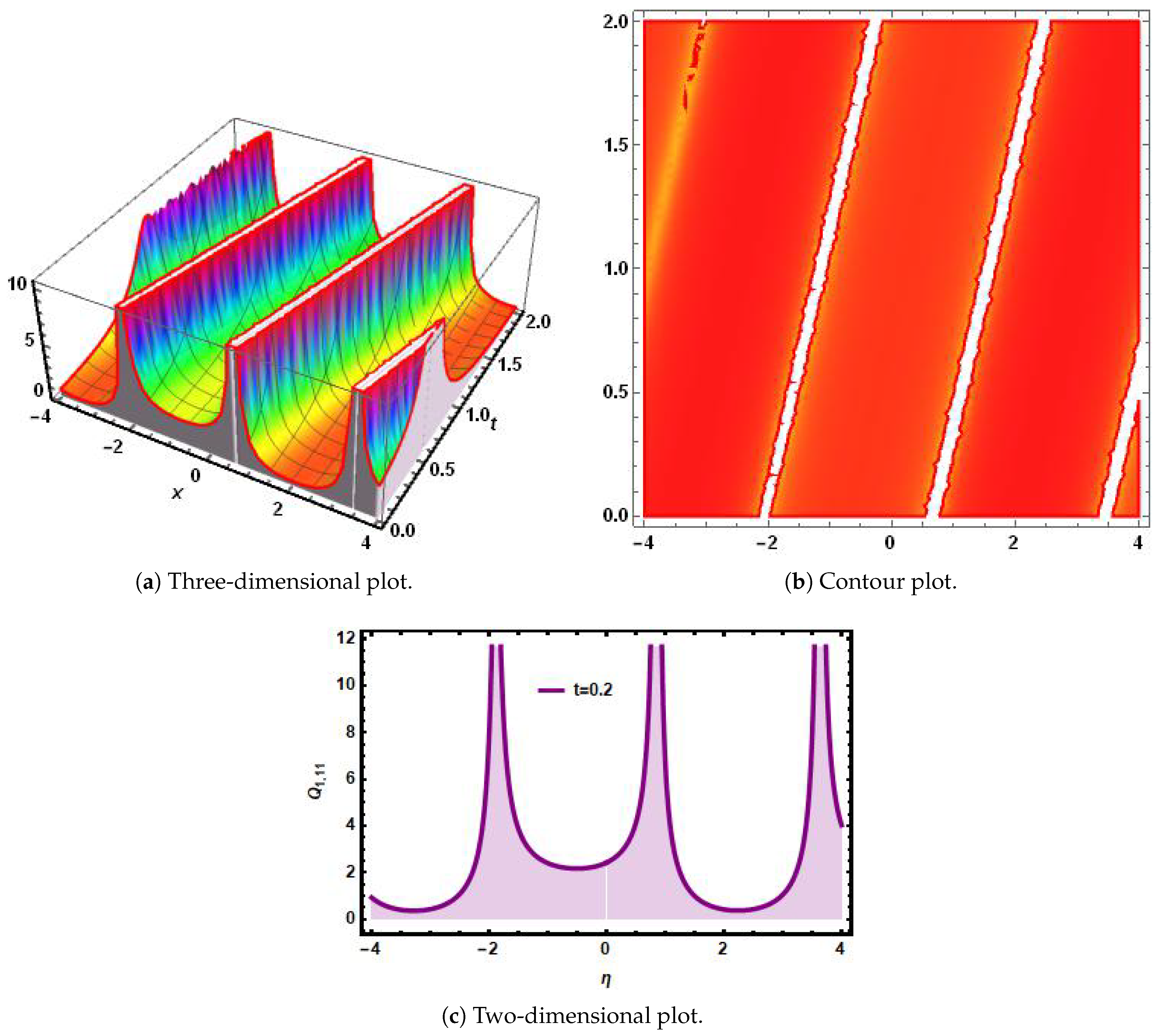
6. Simulations and Discussions

In this section, we highlight the enhancements, new features, and wider applications brought about by our technique by contrasting our analytical and numerical results with those published in the recent literature. We analysed Model (1) in [28] to obtain the dynamical outcomes. In contrast to earlier research that primarily used classical or conformable derivatives to study exact travelling wave solutions, our work uses the $\beta$ derivative to investigate chaotic dynamics and wave-photon interactions in a more comprehensive fractional context. For instance, research like [28] looks at periodic behaviour and stability, but it does not discuss how chaos can arise or how $\beta$ order affects physical interpretations. Our findings uncover previously unreported, richer dynamical properties, such as sensitivity to beginning conditions and intricate attractor structures. In the current study, we analyse new results using the $\mathcal{EMSSE}$ approach on Model (1). Various soliton solutions and mixtures of these types of solutions all possess some unique features and uses. In this study, we examined the various types of soliton, their characteristics, and their applications in science and technology. A soliton is a self-sustaining solitary wave that preserves its form as it moves at a fixed velocity. Solitons are produced by a sensitive balance between nonlinear and dispersive processes within a material and are typically explained in areas such as quantum physics, fluid dynamics, and optics. Solitons have fascinated physicists for centuries. From optical fibre wave propagation to quantum field theories, they are vital to the comprehension and modelling of a wide range of scientific phenomena. Solitons’ robustness and longevity make them well-suited for applications requiring exact and long-lasting wave behaviours. There is no single solution for solitons. Both types can be used in various contexts because of their distinctive features. Let us look at each in more detail: Dark solitons are found as individual areas of reduced intensity in a continuous, wider wave; they are useful in communications technology, especially for long-distance data transmission, because of their stability; bright solitons are used to represent localised energy or intensity; they are a feature of Bose-Einstein condensates; applications that greatly benefit from the use of these solitons in particle interaction studies require localised, high intensity.

Because they behave similarly to waves but have the added stability of soliton solutions, they are ideal for situations that require rhythm. Periodic solitons are used to study wave patterns and oscillations in controlled environments in photonics and fluid dynamics. These solitons offer a starting point for studying rhythmic wave behaviour and resonance phenomena. Unlike other solitons, which have smoother outlines, singular solitons have abrupt peaks of amplitude inside their structure. Certain boundary limitations are frequently necessary for the existence of such solitons. Pressure values are analysed using singular solitons in fluid dynamics and high-energy physics. They simulate processes involving abrupt, drastic changes in energy, such as shock waves. Hyperbolic solitons, or solutions to hyperbolic partial differential equations, are typically strong and exponential. In media where the direction of the signal affects its speed, they are helpful for characterising waves. These solitons aid in controlling the directions and speeds of waves in signal processing and are used to depict the transmission of gravitational waves in general relativity. Several soliton kinds, notably dark/bright, have their traits combined in combined solitons. The dynamical properties of the figures are used to group and interpret them. Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 illustrate how memory effects affect wave amplitude and width by displaying the evolution of soliton profiles for various fractional-order $\beta$ values. Phase portraits are shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, where periodic and chaotic behaviour is indicated by the existence of closed loops and attractor patterns. Important changes in stability and wave shape are highlighted, and each figure is examined in relation to parameter sensitivity. These interpretations demonstrate the complexity of fractional wave dynamics and validate the theoretical analysis.

These hybrid systems provide complex behaviours and customised applications in physics and engineering. When multiple soliton types are combined, scientists can study more complex and precise models of wave events. This fusion method is especially helpful for simulations that require many wave behaviours in a single scenario. In fibre optics, solitons prevent signals from spreading, enabling quick, long-distance communication without sacrificing data integrity. In particular, dark and bright solitons help maintain signal clarity. Solitons may be useful in quantum computing because stable, isolated wave packets can encode and transmit quantum information via secure, long-distance networks. Chaotic and bifurcation analysis is essential for the understanding of the complex dynamics of fractional-order systems. Here, the $\mathcal{FWBK}$ model is investigated in perturbed and non-perturbed cases to reveal its chaotic behaviour and bifurcation patterns. The use of fractional derivatives enables a more generalised description of wave evolution with memory effects and nonlocal interactions that are commonly omitted in conventional integer-order models. Bifurcation analysis shows how the system undergoes a change in dynamical states with varying parameters. The stability and type of equilibrium points can be analysed to determine conditions under which periodic, quasi-periodic, or chaotic behaviour occurs. For the occurrence of period-doubling bifurcations, these phenomena are vital for nonlinear wave interactions in applications in optical and plasma physics. Chaotic patterns in the fractional model also illustrate the sensitivity of wave dynamics to initial conditions and perturbations. The intricacy of chaotic attractors, Lyapunov exponents, and phase space analysis verifies the presence of deterministic chaos in the system. Through numerical simulations, the chaotic evolution of wave patterns is observed, differentiating between stable solitary wave solutions and random, unpredictable behaviour. The influence of fractional-order parameters on chaos transition is of special interest since it determines the level of dissipation and memory effects in the system.

7. Conclusions

In recent studies, the $\mathcal{FWBK}$ model, which is produced by a conformable derivative of order $\beta$, has been successfully examined using the $\mathcal{EMSSE}$ approach. Bright, dark, solitary, trigonometric, and planar waveforms are among the obtained solutions, demonstrating the model’s adaptability in explaining complicated wave dynamics. Furthermore, the $\mathcal{FWBK}$ model structure is included to show the reliability and effectiveness of the proposed method in fractional modelling. By proving that chaotic structures may be applied to both disturbed and non-perturbed situations, the study offers a broader understanding of wave behaviour. The results validate the resilience of the approach and enhance its potential for further analytical investigations of fractional-order wave propagation in various physical fields, including optics and plasma physics. In the future, this study might be expanded to include higher dimensions, coupling effects, and practical applications in fluid systems and optics.