Pointwise Error Analysis of the Corrected L1 Scheme for the Multi-Term Subdiffusion Equation
Abstract
1. Introduction
2. The Construction of the Corrected L1 Scheme
3. Optimal Pointwise-in-Time Error Estimate of the CL1-FEM
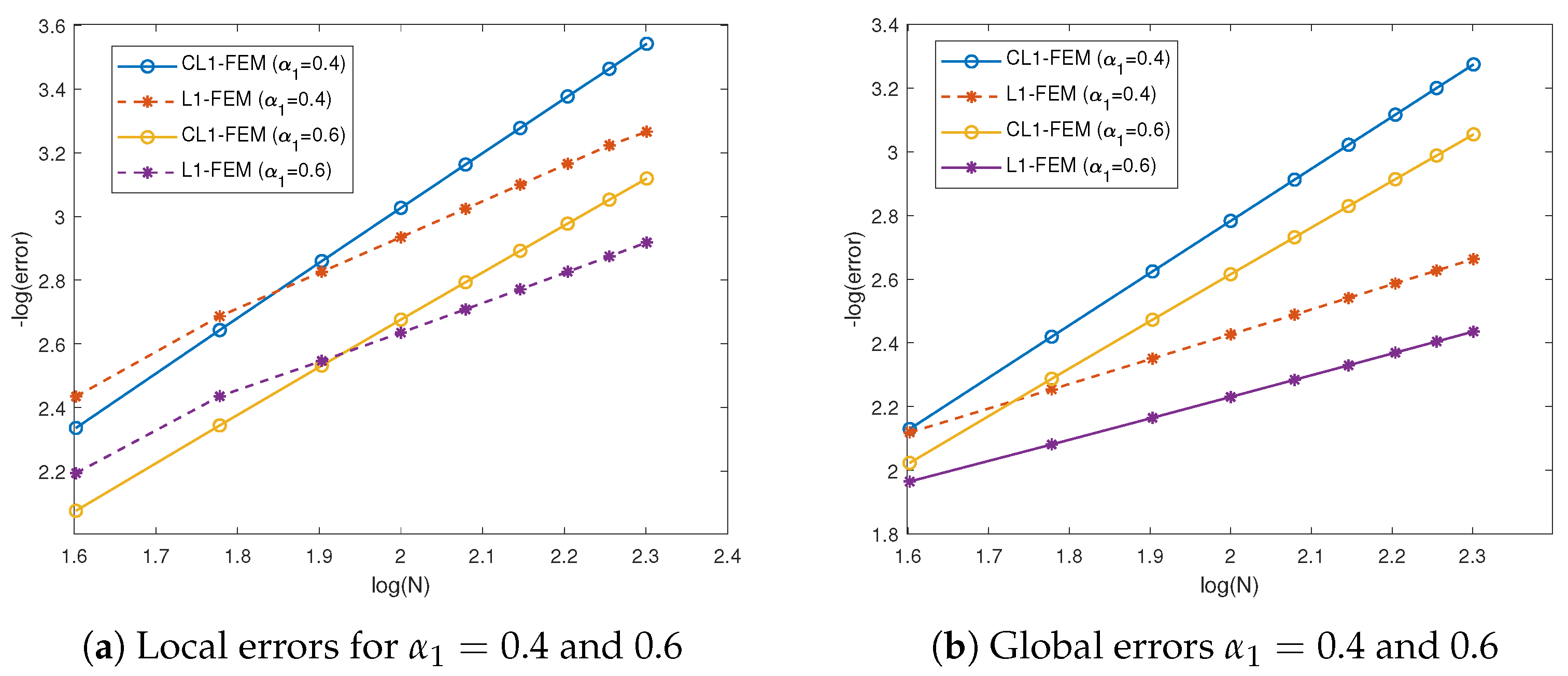
4. Numerical Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CL1 | Corrected L1 schemes |
| FEMs | Finite element methods |
| ADIs | Alternating-direction implicit schemes |
| CQ | Convolution quadrature |
| BDFs | Backward differentiation formulas |
References
- Jin, B.; Li, B.; Zhou, Z. Correction of high-order BDF convolution quadrature for fractional evolution equations. SIAM J. Sci. Comput. 2017, 39, A3129–A3152. [Google Scholar] [CrossRef]
- Bu, W.; Guan, S.; Xu, X.; Tang, Y. Finite element method for a generalized constant delay diffusion equation. Commun. Nonlinear Sci. Numer. Simul. 2024, 134, 108015. [Google Scholar] [CrossRef]
- Kopteva, N. Error analysis of the L1 method on graded and uniform meshes for a fractional-derivative problem in two and three dimensions. Math. Comp. 2019, 88, 2135–2155. [Google Scholar] [CrossRef]
- Liao, H.; Li, D.; Zhang, J. Sharp error estimate of the nonuniform L1 formula for linear reaction-subdiffusion equations. SIAM J. Numer. Anal. 2018, 56, 1112–1133. [Google Scholar] [CrossRef]
- Stynes, M.; O’Riordan, E.; Gracia, J.L. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 2017, 55, 1057–1079. [Google Scholar] [CrossRef]
- Chen, H.; Stynes, M. Error analysis of a second-order method on fitted meshes for a time-fractional diffusion problem. J. Sci. Comput. 2019, 79, 624–647. [Google Scholar] [CrossRef]
- Liao, H.; McLean, W.; Zhang, J. A discrete Grönwall inequality with applications to numerical schemes for subdiffusion problems. SIAM J. Numer. Anal. 2019, 57, 218–237. [Google Scholar] [CrossRef]
- Kopteva, N. Error analysis of an L2-type method on graded meshes for a fractional-order parabolic problem. Math. Comp. 2021, 90, 19–40. [Google Scholar] [CrossRef]
- Hou, D.; Hasan, M.T.; Xu, C. Müntz spectral methods for the time-fractional diffusion equation. Comput. Methods Appl. Math. 2018, 18, 43–62. [Google Scholar] [CrossRef]
- Korobenko, L.; Kamrujjaman, M.; Braverman, E. Persistence and extinction in spatial models with a carrying capacity driven diffusion and harvesting. J. Math. Anal. Appl. 2013, 399, 352–368. [Google Scholar] [CrossRef]
- Magin, R. Fractional calculus in bioengineering. Crit. Rev. Biomed. Eng. 2004, 32, 1–104. [Google Scholar] [CrossRef]
- Scalas, E.; Gorenflo, R.; Mainardi, F. Fractional calculus and continuous-time finance. Physica A 2000, 284, 376–384. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Dynamics. Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Nonlinear Physical, Science; Springer: Berlin/Heidelberg, Germany; Higher Education Press: Beijing, China, 2010. [Google Scholar]
- Uchaikin, V.; Sibatov, R. Fractional Kinetics in Solids. Anomalous Charge Transport in Semiconductors, Dielectrics and Nanosystems; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity—An Introduction to Mathematical Models, 2nd ed.; World Scientific Publishing Co., Pte. Ltd.: Hackensack, NJ, USA, 2022. [Google Scholar]
- Ciarlet, P.G. The finite element method for elliptic problems. In Classics in Applied Mathematics; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2002; Volume 40, Reprint of the 1978 Original [North-Holland, Amsterdam; MR0520174 (58 #25001)]. [Google Scholar]
- Caputo, M.; Fabrizio, M. On the notion of fractional derivative and applications to the hysteresis phenomena. Meccanica 2017, 52, 3043–3052. [Google Scholar] [CrossRef]
- Novozhenova, O.G. Life and science of Alexey Gerasimov, one of the pioneers of fractional calculus in Soviet union. Fract. Calc. Appl. Anal. 2017, 20, 790–809. [Google Scholar] [CrossRef]
- Huang, C.; Liu, X.; Meng, X.; Stynes, M. Error analysis of a finite difference method on graded meshes for a multiterm time-fractional initial-boundary value problem. Comput. Methods Appl. Math. 2020, 20, 815–825. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, Y.; Wang, J. Grünwald-Letnikov scheme for a multi-term time fractional reaction-subdiffusion equation. Commun. Nonlinear Sci. Numer. Simul. 2024, 132, 107930. [Google Scholar] [CrossRef]
- Meng, X.; Stynes, M. Barrier function local and global analysis of an L1 finite element method for a multiterm time-fractional initial-boundary value problem. J. Sci. Comput. 2020, 84, 5. [Google Scholar] [CrossRef]
- Cao, D.; Chen, H. Pointwise-in-time error estimate of an ADI scheme for two-dimensional multi-term subdiffusion equation. J. Appl. Math. Comput. 2023, 69, 707–729. [Google Scholar] [CrossRef]
- Hu, Z.; Li, X. Analysis of a fast element-free Galerkin method for the multi-term time-fractional diffusion equation. Math. Comput. Simul. 2024, 223, 677–692. [Google Scholar] [CrossRef]
- Roul, P.; Sundar, S. Two efficient non-uniform mesh numerical techniques for a multi-term time-fractional advection-diffusion equation: Moving mesh method. In Numerical Algorithms; Springer: Berlin/Heidelberg, Germany, 2025; pp. 1–30. [Google Scholar]
- Wu, L.; Zhang, H.; Yang, X. The finite difference method for the fourth-order partial integro-differential equations with the multi-term weakly singular kernel. Math. Methods Appl. Sci. 2023, 46, 2517–2537. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, X.; Tang, Q.; Xu, D. A robust error analysis of the OSC method for a multi-term fourth-order sub-diffusion equation. Comput. Math. Appl. 2022, 109, 180–190. [Google Scholar] [CrossRef]
- Thomée, V. Galerkin Finite Element Methods for Parabolic Problems, 2nd ed.; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2006; Volume 25. [Google Scholar]
- Bramble, J.H.; Pasciak, J.E.; Steinbach, O. On the stability of the L2 projection in H1(Ω). Math. Comp. 2002, 71, 147–156. [Google Scholar] [CrossRef]
- Huang, C.; Stynes, M. Superconvergence of a finite element method for the multi-term time-fractional diffusion problem. J. Sci. Comput. 2020, 82, 10. [Google Scholar] [CrossRef]
- Chen, H.; Stynes, M. Using complete monotonicity to deduce local error estimates for discretisations of a multi-term time-fractional diffusion equation. Comput. Methods Appl. Math. 2022, 22, 15–29. [Google Scholar] [CrossRef]
- Huang, C.; Stynes, M. α-robust error analysis of a mixed finite element method for a time-fractional biharmonic equation. Numer. Algorithms 2021, 87, 1749–1766. [Google Scholar] [CrossRef]
- Gracia, J.L.; O’Riordan, E.; Stynes, M. A fitted scheme for a Caputo initial-boundary value problem. J. Sci. Comput. 2018, 76, 583–609. [Google Scholar] [CrossRef]
- Farrell, P.A.; Hegarty, A.F.; Miller, J.J.H.; O’Riordan, E.; Shishkin, G.I. Robust Computational Techniques for Boundary Layers; Applied Mathematics; Chapman & Hall/CRC: Boca Raton, FL, USA, 2000; Volume 16. [Google Scholar]
| 1.4780 | 1.4910 | 1.4962 | ||
| 1.2692 | 1.3011 | 1.3077 | ||
| 1.2248 | 1.2294 | 1.2272 |
| 1.4415 | 1.4759 | 1.4894 | ||
| 1.2333 | 1.2861 | 1.3087 | ||
| 1.2121 | 1.2269 | 1.2285 |
| 1.7344 | 1.7112 | 1.6909 | ||
| 1.5089 | 1.4765 | 1.4530 | ||
| 1.2604 | 1.2354 | 1.2207 |
| 1.6384 | 1.6311 | 1.6253 | ||
| 1.4890 | 1.4620 | 1.4427 | ||
| 1.2604 | 1.2354 | 1.2207 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Huang, C. Pointwise Error Analysis of the Corrected L1 Scheme for the Multi-Term Subdiffusion Equation. Fractal Fract. 2025, 9, 529. https://doi.org/10.3390/fractalfract9080529
Li Q, Huang C. Pointwise Error Analysis of the Corrected L1 Scheme for the Multi-Term Subdiffusion Equation. Fractal and Fractional. 2025; 9(8):529. https://doi.org/10.3390/fractalfract9080529
Chicago/Turabian StyleLi, Qingzhao, and Chaobao Huang. 2025. "Pointwise Error Analysis of the Corrected L1 Scheme for the Multi-Term Subdiffusion Equation" Fractal and Fractional 9, no. 8: 529. https://doi.org/10.3390/fractalfract9080529
APA StyleLi, Q., & Huang, C. (2025). Pointwise Error Analysis of the Corrected L1 Scheme for the Multi-Term Subdiffusion Equation. Fractal and Fractional, 9(8), 529. https://doi.org/10.3390/fractalfract9080529







