Electromechanical Modelling of a Piezoelectric Stack Energy Harvester †
Abstract
:1. Introduction
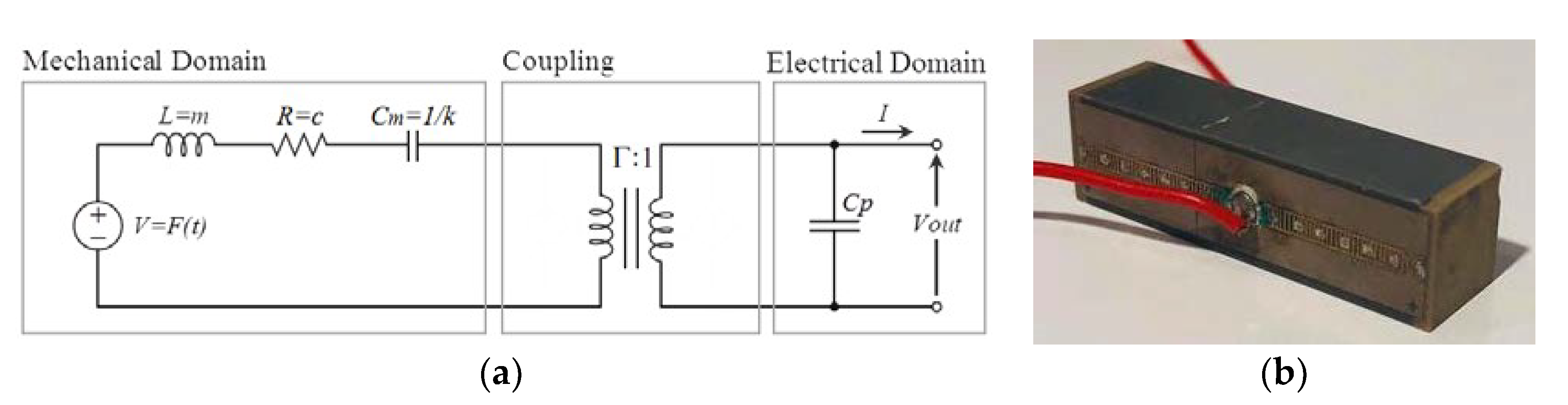
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Raghunathan, V.; Chou, P.H. Design and power management of energy harvesting embedded systems. In Proceedings of the ISLPED ’06 Proceedings of the 2006 International Symposium on Low Power Electronics and Design, Tegernsee, Germany, 4–6 October 2006. [Google Scholar]
- Ali, W.G.; Nagib, G. Design considerations for piezoelectric energy harvesting systems. In Proceedings of the 2012 International Conference on Engineering and Technology (ICET), Cairo, Egypt, 10–11 October 2012. [Google Scholar]
- Sodano, H.A.; Park, G.; Inman, D. Estimation of electric charge output for piezoelectric energy harvesting. Strain 2004, 40, 49–58. [Google Scholar] [CrossRef]
- Tao, K.; Tang, L.; Wu, J.; Lye, S.W.; Chang, H.; Miao, J. Investigation of multimodal electret-based MEMS energy harvester with impact-induced nonlinearity. J. Microelectromech. Syst. 2018, 27, 276–288. [Google Scholar] [CrossRef]
- Khaligh, A.; Zeng, P.; Zheng, C. Kinetic energy harvesting using piezoelectric and electromagnetic technologies—State of the art. IEEE Trans. Ind. Electron. 2010, 57, 850–860. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 2011, 330, 2339–2353. [Google Scholar] [CrossRef]
- Toprak, A.; Tigli, O. Piezoelectric energy harvesting: State-of-the-art and challenges. Appl. Phys. Rev. 2014, 1, 031104. [Google Scholar] [CrossRef]
- Jasim, A.; Wang, H.; Yesner, G.; Safari, A.; Maher, A. Optimized design of layered bridge transducer for piezoelectric energy harvesting from roadway. Energy 2017, 141, 1133–1145. [Google Scholar] [CrossRef]
- Li, H.; Tian, C.; Deng, Z.D. Energy harvesting from low frequency applications using piezoelectric materials. Appl. Phys. Rev. 2014, 1, 041301. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Renaud, M.; Karakaya, K.; Sterken, T.; Fiorini, P.; Van Hoof, C.; Puers, R. Fabrication, modelling and characterization of MEMS piezoelectric vibration harvesters. Sens. Actuators A Phys. 2008, 145, 380–386. [Google Scholar] [CrossRef]
- Hehn, T.; Manoli, Y. Piezoelectricity and Energy Harvester Modelling. In CMOS Circuits for Piezoelectric Energy Harvesters; Springer: Dordrecht, The Netherlands, 2015; pp. 21–40. [Google Scholar]
- Jaffe, B. Piezoelectric Ceramics; Elsevier: Amsterdam, The Netherlands, 2012; Volume 3. [Google Scholar]


| Property | Piezo Stack A | Piezo Stack B | Units |
|---|---|---|---|
| d33 | 480 | 480 | ×10−8 m/V |
| AS | 7.85 | 15.4 | ×10−5 m2 |
| t | 0.5 | 0.5 | mm |
| N | 98 | 98 | - |
| LS | 62 | 62 | mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Evans, M.; Tang, L.; Bowen, C.; Hu, A.P.; Tao, K.; Aw, K. Electromechanical Modelling of a Piezoelectric Stack Energy Harvester. Proceedings 2018, 2, 733. https://doi.org/10.3390/proceedings2130733
Evans M, Tang L, Bowen C, Hu AP, Tao K, Aw K. Electromechanical Modelling of a Piezoelectric Stack Energy Harvester. Proceedings. 2018; 2(13):733. https://doi.org/10.3390/proceedings2130733
Chicago/Turabian StyleEvans, Matthew, Lihua Tang, Chris Bowen, Aiguo P. Hu, Kai Tao, and Kean Aw. 2018. "Electromechanical Modelling of a Piezoelectric Stack Energy Harvester" Proceedings 2, no. 13: 733. https://doi.org/10.3390/proceedings2130733
APA StyleEvans, M., Tang, L., Bowen, C., Hu, A. P., Tao, K., & Aw, K. (2018). Electromechanical Modelling of a Piezoelectric Stack Energy Harvester. Proceedings, 2(13), 733. https://doi.org/10.3390/proceedings2130733








