Understanding the Aerodynamic Benefits of Drafting in the Wake of Cyclists †
Abstract
:1. Introduction
2. Methodology
3. Experimental Setup and Procedures
Experimental Setup
4. Results
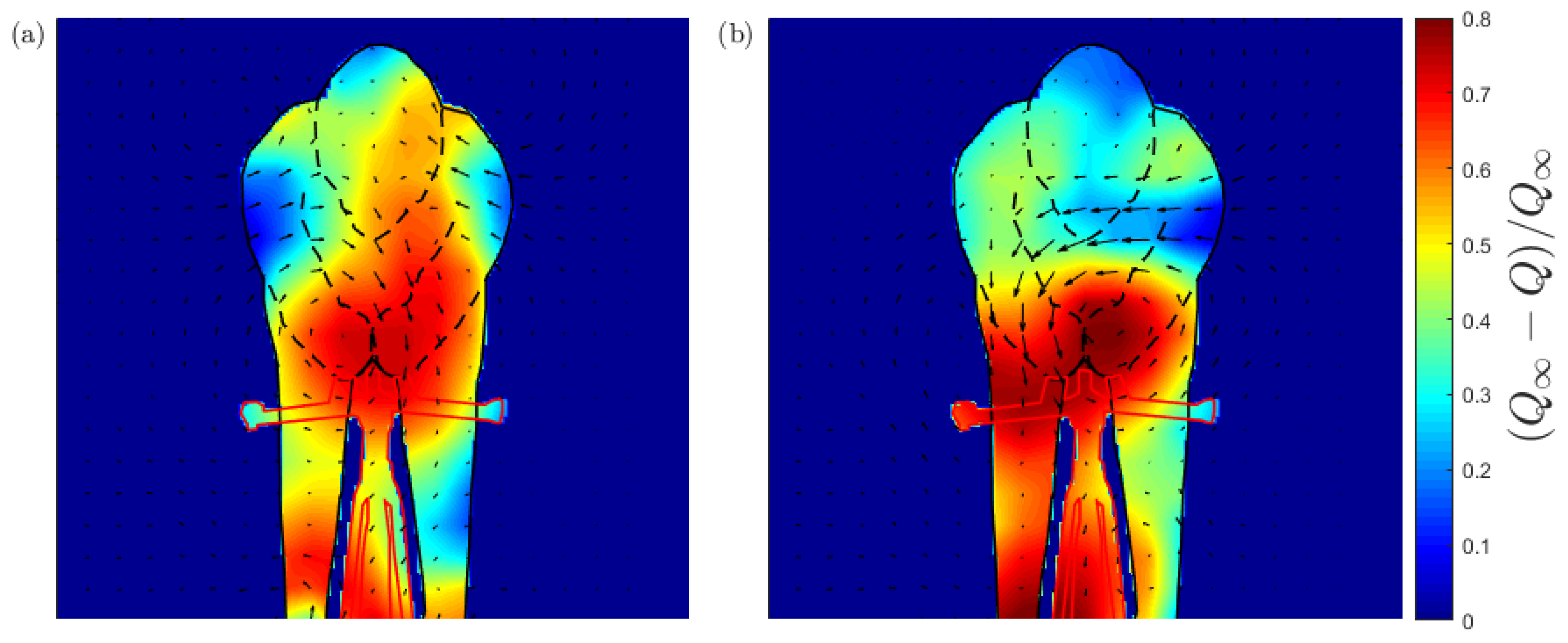
4.1. Wake Development
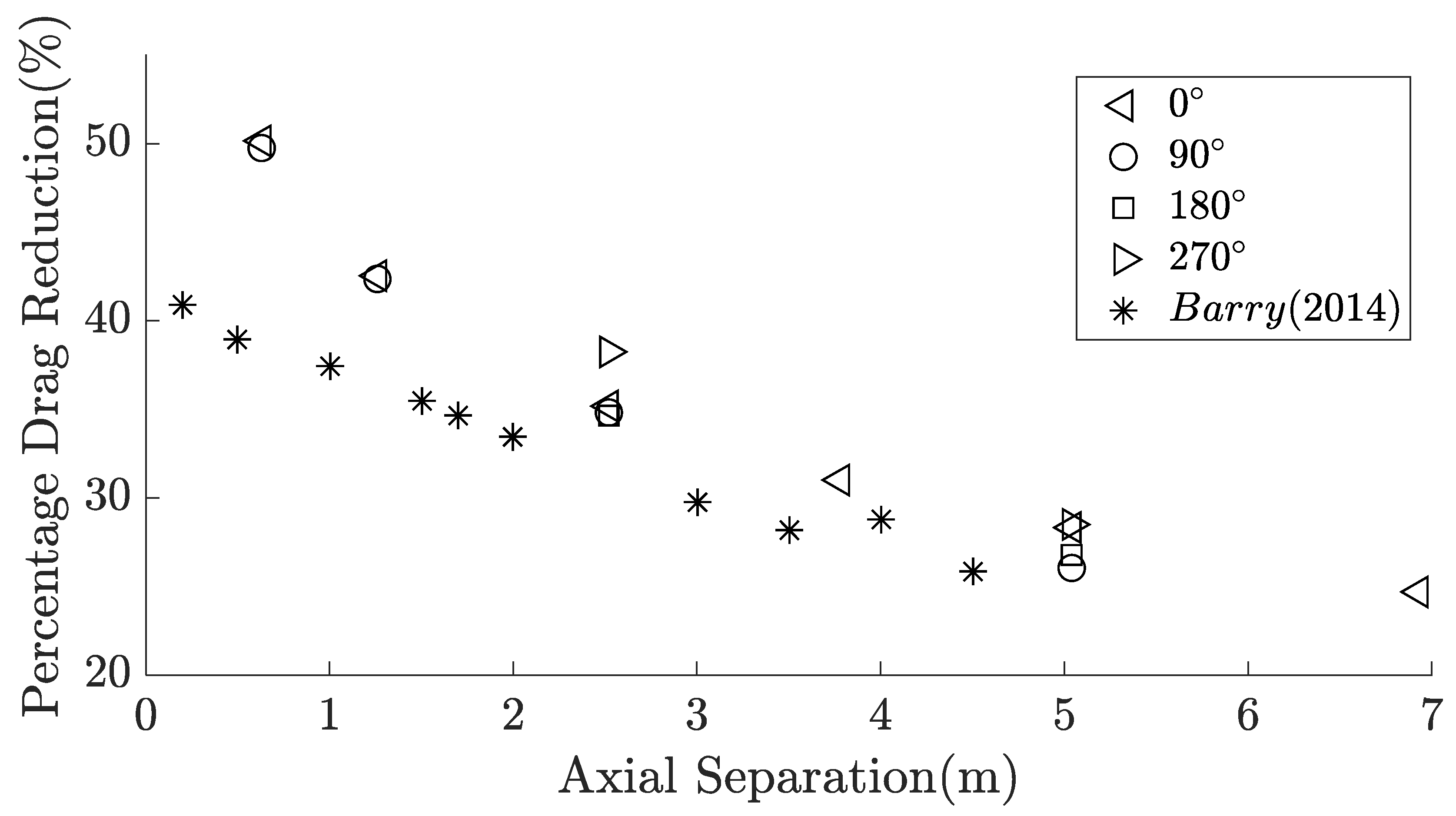
4.2. Drag Reduction (%)
5. Conclusions
Conflicts of Interest
References
- Defraeye, T.; Blocken, B.; Koninckx, E.; Hespel, P.; Carmeliet, J. Aerodynamic study of different cyclist positions: CFD analysis and full-scale wind-tunnel tests. J. Biomech. 2010, 43, 1262–1268. [Google Scholar] [CrossRef] [PubMed]
- Barry, N.; Burton, D.; Sheridan, J.; Thompson, M.; Brown, N. Aerodynamic drag interactions between cyclists in a team pursuit. Sports Eng. 2015, 18, 93–103. [Google Scholar] [CrossRef]
- Fitzgerald, S.; Kelso, R.; Grimshaw, P.; Warr, A. Measurement of the air velocity and turbulence in a simulated track cycling team pursuit race. J. Wind. Eng. Ind. Aerodyn. 2019, 190, 322–330. [Google Scholar] [CrossRef]
- Barry, N. Aerodynamic Interactions between Multiple Cyclists. Ph.D. Thesis, Monash University, Clayton, Australia, 2015. [Google Scholar]
- Blocken, B.; Toparlar, Y.; Van Druenen, T.; Andrianne, T. Aerodynamic drag in cycling team time trials. J. Wind. Eng. Ind. Aerodyn. 2018, 182, 128–145. [Google Scholar] [CrossRef]
- Martin, J.C.; Davidson, C.J.; Pardyjak, E.R. Understanding Sprint-Cycling Performance: The Integration of Muscle Power, Resistance, and Modeling. Int. J. Sports Physiol. Perform. 2007, 2, 5–21. [Google Scholar] [CrossRef] [PubMed]
- Crouch, T.; Burton, D.; Brown, N.; Thompson, M.C.; Sheridan, J. Flow topology in the wake of a cyclist and its effect on aerodynamic drag. J. Fluid Mech. 2014, 748, 5–35. [Google Scholar] [CrossRef]
- Crouch, T.; Burton, D.; Thompson, M.C.; Brown, N.; Sheridan, J. Dynamic leg-motion and its effect on the aerodynamic performance of cyclists. J. Fluids Struct. 2016, 65, 121–137. [Google Scholar] [CrossRef]
- Griffith, M.D.; Crouch, T.; Thompson, M.C.; Burton, D.; Sheridan, J.; Brown, N. Computational Fluid Dynamics Study of the Effect of Leg Position on Cyclist Aerodynamic Drag. J. Fluids Eng. 2014, 136, 101105. [Google Scholar] [CrossRef]
- Bearman, P.; Morel, T. Effect of free stream turbulence on the flow around bluff bodies. Prog. Aerosp. Sci. 1983, 20, 97–123. [Google Scholar] [CrossRef]



| Leg Position | X Location (m) | Y Limits(m) | Z Limits (m) |
|---|---|---|---|
| 0° | 0.63, 1.26, 2.52, 3.78, 5.04, 6.93 | [−0.50 0.50] | [0.45 1.40] |
| 90° | 0.63, 1.26, 2.52, 3.78, 5.04 | [−0.50 0.50] | [0.45 1.40] |
| 180° | 1.26,2.52 | [−0.50 0.50] | [0.45 1.40] |
| 270° | 1.26,2.52 | [−0.50 0.50] | [0.45 1.40] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brown, C.; Crouch, T.; Burton, D.; Thompson, M.C. Understanding the Aerodynamic Benefits of Drafting in the Wake of Cyclists. Proceedings 2020, 49, 32. https://doi.org/10.3390/proceedings2020049032
Brown C, Crouch T, Burton D, Thompson MC. Understanding the Aerodynamic Benefits of Drafting in the Wake of Cyclists. Proceedings. 2020; 49(1):32. https://doi.org/10.3390/proceedings2020049032
Chicago/Turabian StyleBrown, Christopher, Timothy Crouch, David Burton, and Mark C. Thompson. 2020. "Understanding the Aerodynamic Benefits of Drafting in the Wake of Cyclists" Proceedings 49, no. 1: 32. https://doi.org/10.3390/proceedings2020049032
APA StyleBrown, C., Crouch, T., Burton, D., & Thompson, M. C. (2020). Understanding the Aerodynamic Benefits of Drafting in the Wake of Cyclists. Proceedings, 49(1), 32. https://doi.org/10.3390/proceedings2020049032





