Detection and Velocimetry of Floating Wood for Flood Disaster Risk Management Using Electromagnetic Imaging †
Abstract
:1. Introduction
2. Experimental Setup and Methodology
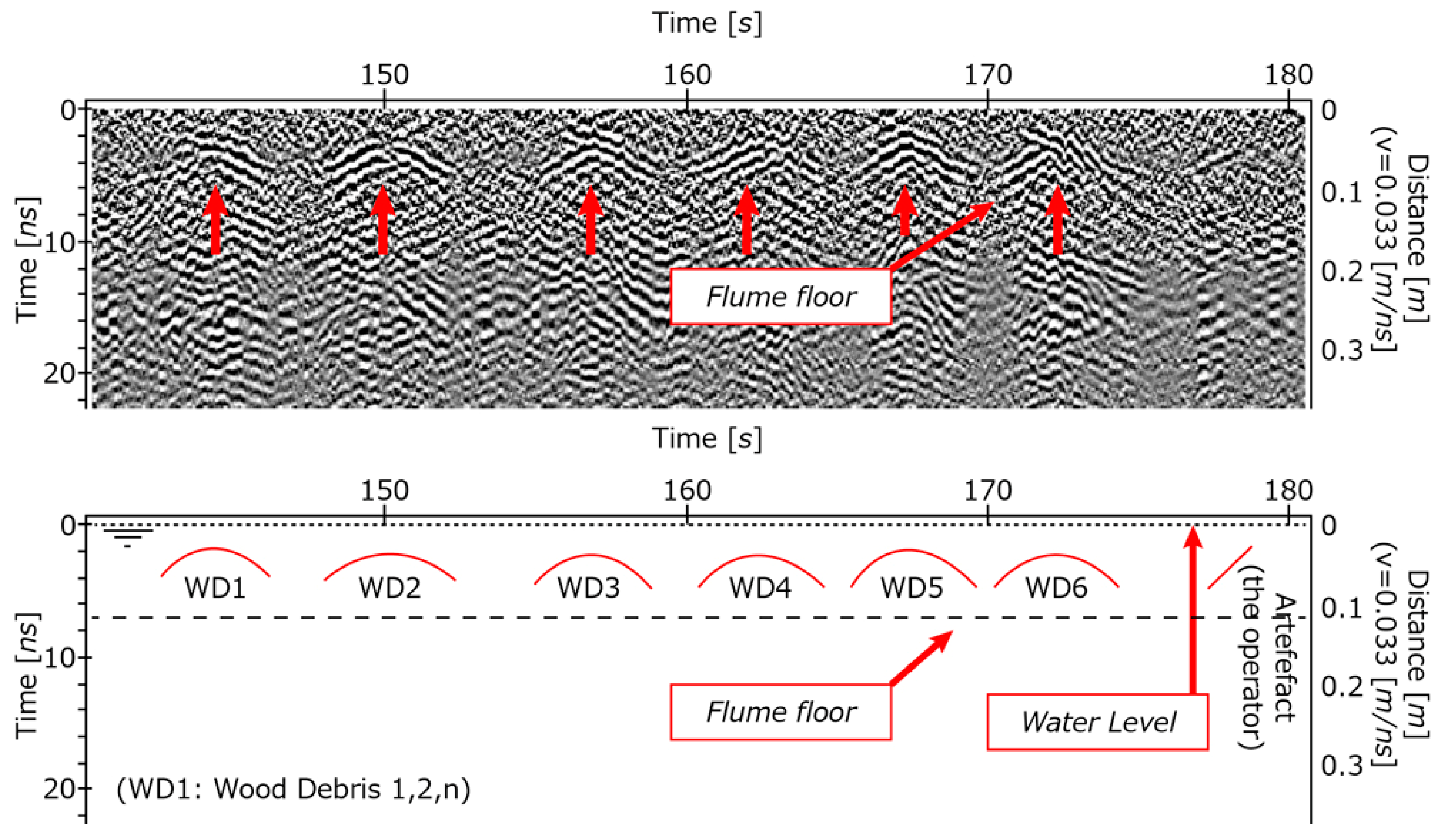
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gunnell, A.M.; Petts, G.E.; Gregory, K.J. The role of coarse woody debris in forest aquatic habitats: Implications for management. Aquat. Conserv. 1995, 5, 143–166. [Google Scholar] [CrossRef]
- Bisson, P.A.; Bilby, R.E.; Bryant, M.D.; Dollof, C.A.; Grette, G.B.; House, M.L.; Murphy, M.L.; Koski, K.V.; Sedell, J.R. Large woody debris in forested streams in the pacific northwest: Past, present and future. In Streamside Management: Forestry and Fishery Interactions; Saleo, E.O., Cunty, T.W., Eds.; University of Washington Publisher: Washington, DC, USA, 1987. [Google Scholar]
- Abbe, T.M.; Montgommery, D.R. Patterns and processes of wood debris accumulation in the Queets river basin, Washington. Geomorphology 2003, 51, 81–107. [Google Scholar] [CrossRef]
- Nakamura, F.; Swanson, F.J. Effects of coarse woody debris on morphology and sediment storage of a mountain stream system in western Oregon. Earth Surf. Process. Landf. 1993, 18, 46–61. [Google Scholar] [CrossRef]
- Seo, J.; Nakamura, F.; Chun, K. Dynamics of large wood at the watershed scale: A perspective on current research limits and future directions. Landsc. Ecol. Eng. 2010, 6, 271–287. [Google Scholar] [CrossRef]
- Chen, S.-C.; Chao, Y.-C.; Chan, H.-C. Typhoon-dominated influence on Wood Debris Distribution and Transportation in a High Gradient Headwater Catchment. J. Mt. Sci. 2013, 10, 509–521. [Google Scholar] [CrossRef]
- Moulin, B.; Piegay, H. Characteristics and temporal variability of large woody debris trapped in a reservoir on the river Rhone (Rhone): Implications for river basin management. Riv. Res. Appl. 2004, 20, 79–97. [Google Scholar] [CrossRef]
- Thevenet, A.; Citterio, A.; Piegay, H. A new methodology for the assessment of large woody debris accumulations on highly modified rivers (example of two French piedmont rivers). Regul. Rivers Res. Mgmt. 1998, 14, 467–483. [Google Scholar] [CrossRef]
- Shimizu, M.; Kanai, S.; Hotta, N.; Lissak, C.; Gomez, C. Spatial Distribution of Drifted-wood Hazard following the July 2017 Sediment-hazards in the Akatani river, Fukuoka Prefecture, Japan. For. Geo 2020, 34, 96–111. [Google Scholar] [CrossRef]
- Pettit, N.E.; Warfe, D.M.; Kennard, M.J.; Pusey, B.J.; Davies, P.M.; Douglas, M.M. Dynamics of in-stream wood and its importance as fish habitat in a large tropical floodplain river. River Res. Appl. 2013, 29, 864–875. [Google Scholar] [CrossRef]
- Bocchiola, D.; Rulli, M.C.; Rosso, R. Flume experiments on wood entrainment in rivers. Adv. Water Resour. 2006, 29, 1182–1195. [Google Scholar] [CrossRef]
- Panici, D. An Experimental and Numerical Approach to Modeling Large Wood Displacement in Rivers. Water Resour. Res. 2012, 57, e2021WR029860. [Google Scholar] [CrossRef]
- Spreitzer, G.; Gibson, J.; Tang, M.; Tunnicliffe, J.; Friedrich, H. SmartWood: Laboratory experiments for assessing the effectiveness of smart sensors for monitoring large wood movement behaviour. Catena 2019, 182, 104145. [Google Scholar] [CrossRef]
- Ravazzolo, D.; Mao, L.; Pico, L.; Lenzi, M.A. Tracking log displacement during floods in the Tagliamento River using RFID and GPS tracker devices. Geomorph 2015, 228, 226–233. [Google Scholar] [CrossRef]
- Ghaffarian, H.; Piegay, H.; Lopez, D.; Riviere, N.; MacVicar, B.; Antonio, A.; Mignot, E. Video-monitoring of wood discharge: First inter-basin comparisonand recommendations to install video cameras. Earth Surf. Process Landforms 2020, 45, 2219–2234. [Google Scholar] [CrossRef]
- MacVicar, B.; Piegay, H. Implementation and validation of video monitoring for wood budgeting in a wandering piedmont river, the Ain River (France). Earth Surf. Process Landforms 2012, 37, 1272–1289. [Google Scholar] [CrossRef]
- Galley, R.J.; Trachtenberg, M.; Langlois, A.; Barber, D.G.; Shafai, L. Observations of geophysical and dielectric properties and ground penetrating radar signatures for discrimination of snow, sea ice and freshwater ice thickness. Cold Reg. Sci. Technol. 2009, 57, 29–38. [Google Scholar] [CrossRef]
- Jaedicke, C. Snow mass quantification and avalanche victim search by ground penetrating radar. Surv. Geophys. 2003, 24, 431–445. [Google Scholar] [CrossRef]
- Huber, E.; Birte, A.; Huggenberger, P. Imaging scours in straightened and braided gravel-bed rivers with ground-penetrating radar. Near Surf. Geophys. 2019, 17, 263–276. [Google Scholar] [CrossRef]
- Bakker, M.A.J.; Maljers, D.; Weerts, H.J.T. Ground-penetrating radar profiling on embanked floodplains. Neth J. Geosci. 2007, 86, 55–61. [Google Scholar] [CrossRef]
- Wyatt, D.E.; Temples, T.J. Ground-penetrating radar detection of small-scale channels, joints and faults in the unconsolidated sediments of the Atlantic Coastal Plain. Environ. Geol. 1999, 27, 219–225. [Google Scholar] [CrossRef]
- Lissak, C.; Maquaire, O.; Malet, J.-P.; Lavigne, F.; Virmoux, C.; Gomez, C.; Davidson, R. Ground-penetrating radar observations for estimating the vertical displacement of rotational landslides. Nat. Hazards Earth Syst. Sci. 2015, 15, 1399–1406. [Google Scholar] [CrossRef]
- Kain, C.; Gomez, C.; Wassmer, P.; Lavigne, F.; Hart, D. Truncated dunes as evidence of the 2004 tsunami in North Sumatra and environmental recovery post-tsunami. N. Z. Geogr. 2014, 70, 165–178. [Google Scholar] [CrossRef]
- Starheim, C.A.; Gomez, C.; Harrison, J.; Kain, C.; Brewer, N.J.; Owen, K.; Hadmoko, D.S.; Purdie, H.; Zawar-Reza, P.; Owens, I.; et al. Complex internal architecture of a debris-flow deposit revealed using ground-penetrating radar, Cass, New Zealand. N. Z. Geogr. 2013, 69, 26–38. [Google Scholar] [CrossRef]
- Gomez, C.; Lavigne, F.; Lespinasse, N.; Hadmoko, D.S.; Wassmer, P. Longitudinal structure of pyroclastic-flow deposits, revealed by GPR survey, at Merapi Volcano, Java, Indonesia. J. Volcanol. Geotherm. Res. 2008, 176, 439–447. [Google Scholar] [CrossRef]
- Guo, S.; Xu, Z.; Li, X.; Zhu, P. Detection and Characterization of Cracks in Highway Pavement with the Amplitude Variation of GPR Diffracted Waves: Insights from Forward Modeling and Field Data. Remote Sens. 2022, 14, 976. [Google Scholar] [CrossRef]
- Hugenschmidt, J. Concrete bridge inspection with a mobile GPR system. Constr. Build. Mat. 2002, 16, 147–154. [Google Scholar] [CrossRef]
- Granlund, N.; Lundberg, A.; Feiccabrino, J.; Gustafsson, D. Laboratory test of snow wetness influence on electrical conductivity measured with ground penetrating radar. Hydrol. Res. 2009, 40, 33–44. [Google Scholar] [CrossRef]


| Floating Wood Characteristics | Manning Calculation of Velocity and Discharge | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Total Length | Wood ϕ | Wood L. | Wood Area | Velocity | Area | Wetted Perimeter | Slope | n (Artificial Laminated Chow, 1959) | Velocity | Discharge |
| [m] | [m] | [m] | [m2] | [m/s] | [m2] | [m] | [m/m] | [/] | [m/s] | [m3/s] |
| 1.15 | 0.008 | 0.2 | 0.01 | 0.25 | 0.0285 | 0.485 | 0.00435 | 0.02 | 0.50 | 0.01 |
| 1.15 | 0.008 | 0.2 | 0.01 | 0.2 | 0.0285 | 0.485 | 0.00435 | 0.02 | 0.50 | 0.01 |
| 1.15 | 0.008 | 0.2 | 0.01 | 0.25 | 0.0285 | 0.485 | 0.00435 | 0.02 | 0.50 | 0.01 |
| 1.15 | 0.008 | 0.2 | 0.01 | 0.25 | 0.0285 | 0.485 | 0.00435 | 0.02 | 0.50 | 0.01 |
| 1.15 | 0.008 | 0.2 | 0.01 | 0.25 | 0.0285 | 0.485 | 0.00435 | 0.02 | 0.50 | 0.01 |
| 1.15 | 0.008 | 0.2 | 0.01 | 0.2 | 0.0285 | 0.485 | 0.00435 | 0.02 | 0.50 | 0.01 |
| Wood Velocity from Videos | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Nb | GPR | M Setup | Water Depth | Wood Velocity | In | Out | Distance | Time | Upstream Depth | Downstream Depth |
| [/] | [/] | [/] | [m] | [m/s] | [s] | [s] | [m] | [s] | [m] | [m] |
| 1 | 8 | 75 | 0.1425 | 0.25 | 14 | 18 | 1 | 4 | 0.145 | 0.14 |
| 2 | 8 | 75 | 0.1425 | 0.2 | 19 | 24 | 1 | 5 | 0.145 | 0.14 |
| 3 | 8 | 75 | 0.1425 | 0.25 | 26 | 30 | 1 | 4 | 0.145 | 0.14 |
| 4 | 8 | 75 | 0.1425 | 0.25 | 31 | 35 | 1 | 4 | 0.145 | 0.14 |
| 5 | 8 | 75 | 0.1425 | 0.25 | 36 | 40 | 1 | 4 | 0.145 | 0.14 |
| 6 | 8 | 75 | 0.1425 | 0.2 | 41 | 44 | 0.6 | 3 | 0.145 | 0.14 |
| Wood nb | Depth 1 | Depth 2 | x1 | x2 | Start | Timelapse | Triangulated Horizontal | Halved (Return to Single) | Nanosec. to Distance Using Light-Speed | Velocity |
|---|---|---|---|---|---|---|---|---|---|---|
| [/] | [ns] | [ns] | [1/100 s] | [1/100 s] | s | s | [ns] | ns | [m] | [m/s] |
| 1.000 | 5.045 | 3.550 | 14,283 | 14,421 | 0.000 | 1.380 | 3.585 | 1.792 | 0.520 | 0.377 |
| 1.000 | 4.718 | 3.177 | 14,270 | 14,403 | 0.000 | 1.330 | 3.489 | 1.744 | 0.506 | 0.380 |
| 2.000 | 4.205 | 2.663 | 14,839 | 14,977 | 0.000 | 1.380 | 3.254 | 1.627 | 0.472 | 0.342 |
| 2.000 | 4.251 | 2.616 | 14,837 | 14,975 | 0.000 | 1.380 | 3.351 | 1.675 | 0.486 | 0.352 |
| 3.000 | 4.999 | 2.990 | 15,531 | 15,699 | 0.000 | 1.680 | 4.006 | 2.003 | 0.581 | 0.346 |
| 3.000 | 4.111 | 2.336 | 16,051 | 16,211 | 0.000 | 1.600 | 3.383 | 1.692 | 0.491 | 0.307 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez, C.; Hotta, N.; Miyata, S.; Bradak, B.; Kataoka, M.; Ashikaga, K.; Persendt, F.C. Detection and Velocimetry of Floating Wood for Flood Disaster Risk Management Using Electromagnetic Imaging. Proceedings 2023, 87, 1. https://doi.org/10.3390/IECG2022-14264
Gomez C, Hotta N, Miyata S, Bradak B, Kataoka M, Ashikaga K, Persendt FC. Detection and Velocimetry of Floating Wood for Flood Disaster Risk Management Using Electromagnetic Imaging. Proceedings. 2023; 87(1):1. https://doi.org/10.3390/IECG2022-14264
Chicago/Turabian StyleGomez, Christopher, Norifumi Hotta, Shusuke Miyata, Balazs Bradak, Mikito Kataoka, Kensuke Ashikaga, and Frans C. Persendt. 2023. "Detection and Velocimetry of Floating Wood for Flood Disaster Risk Management Using Electromagnetic Imaging" Proceedings 87, no. 1: 1. https://doi.org/10.3390/IECG2022-14264
APA StyleGomez, C., Hotta, N., Miyata, S., Bradak, B., Kataoka, M., Ashikaga, K., & Persendt, F. C. (2023). Detection and Velocimetry of Floating Wood for Flood Disaster Risk Management Using Electromagnetic Imaging. Proceedings, 87(1), 1. https://doi.org/10.3390/IECG2022-14264







