Dynamic Modeling and Control for Tilt-Rotor UAV Based on 3D Flow Field Transient CFD

Abstract

The tilt-rotor unmanned aerial vehicle (TRUAV) is characterized by both multi-rotor vertical takeoff or landing and fixed-wing long-duration flight. Not only the structure of TRUAV is complex, but also the aerodynamic coupling is severe. Especially when the TRUAV is in the transition mode, the rotor flow field and wake are complicated. The abnormal variation of the aerodynamic force of the rotor blades will directly affect the balance and manipulation of the aircraft. The downwash flow generated by the rotor spiral propeller tip vortex interference will impact the wing from every direction, forming a blocked three-dimensional effect flow field on the wing surface, which seriously affects the stability of the UAV. In this paper, the transient CFD (Computational Fluid Dynamics) numerical simulation was applied to examine the flow fields of the fuselage and rotor under the transition modal of TRUAV as well as the aerodynamic disturbance. In addition, the dynamics model of the TRUAV was established based on the change of the tilt angle state, and considering the effect of rotor slip flow, we analyzed the three-dimensional flow field distribution of TRUAV in the transition mode under the aerodynamic disturbance of the fuselage and rotor, and we identified each aerodynamic parameter required for modeling. A cascade PID control strategy is designed for the TRUAV, and the results verify that the proposed TRUAV model can remain stable even when the maximum roll angle is 20 degrees. At last, the simulation results provide data support for the optimization of the TRUAV aerodynamic profile and the design of subsequent flight control methods.

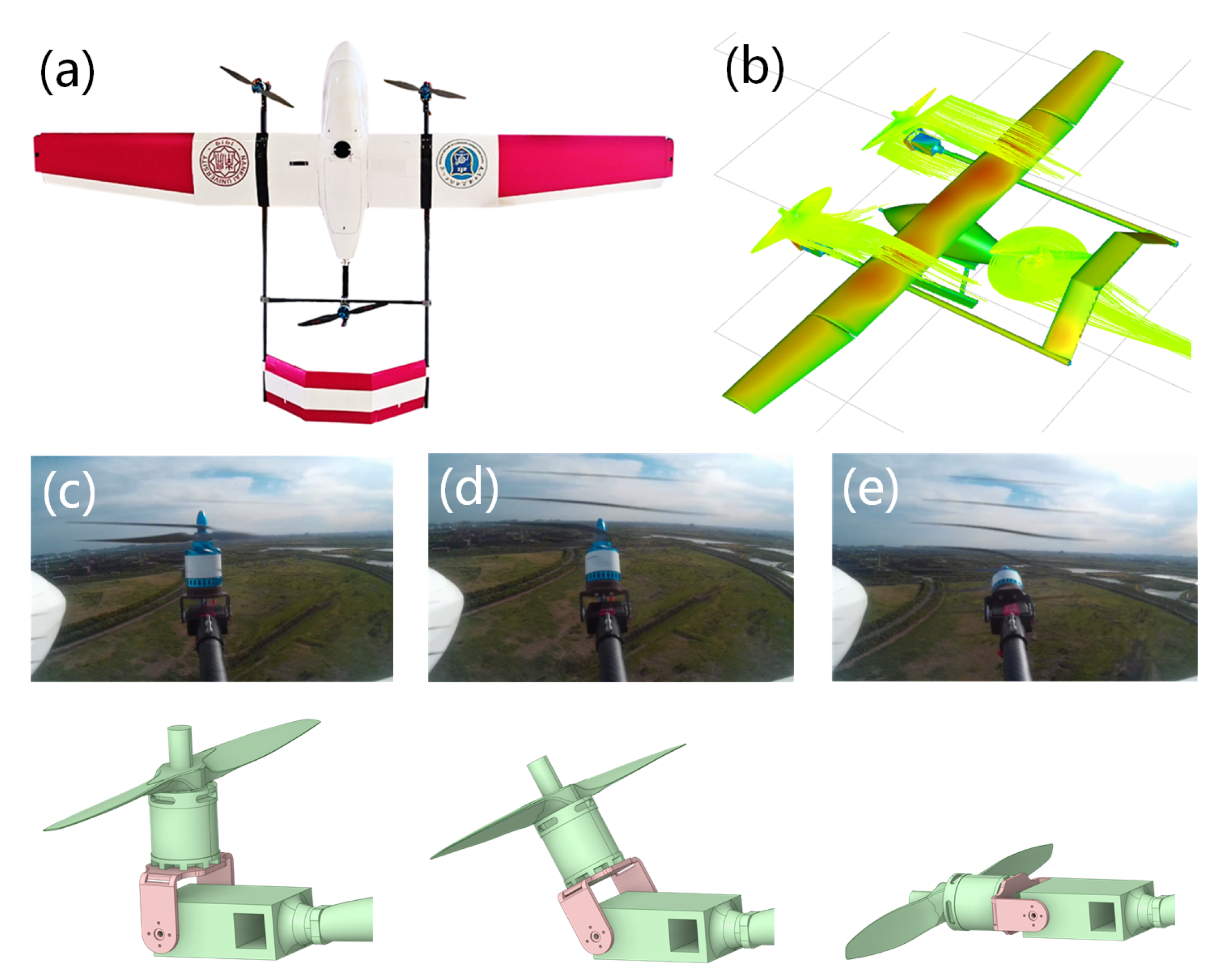
1. Introduction

Multi-rotor UAVs provide vertical takeoff and landing capabilities and can therefore operate in a variety of complex terrain environments, but multi-rotor UAVs are limited in battery capacity, and the traditional fixed-wing UAVs require specialized runways for deployment. Hence, the tilt-rotor UAV (TRUAV), which combines the advantages of both forms of UAVs, has the characteristics of flexible takeoff/landing and long-time operations [1]. The TRUAV combines the airframe structure of fixed-wing and multi-rotor UAVs, as shown in Figure 1, with a rotating mechanism designed for rotor tilting to achieve conversion between multiple modalities.

In recent years, researchers have applied various effective control methods to complete the flight of TRUAVs. While the study of dynamic modeling of TRUAV is equally essential, describing a more accurate mathematical model is especially critical for the flight of TRUAV, Govdeli et al. used a concentrated vortex model to establish a nonlinear non-constant dynamics model for the tilt-rotor UAV to simulate unsteady lift and drag, and the PID control method was applied to achieve positive control results [2]. Yang et al. studied the aerodynamic characteristics of tilt-rotor UAVs in the tilt-transition state through wind tunnel tests and numerical simulations. The experimental results showed that the “windmill” phenomenon occurs under high-speed airflow and relatively low-speed rotation, and the tilt of the rotor increases the thrust coefficient; for rotor type 8038 with a maximum efficiency of 0.567 and an advance ratio of 0.43, the rotor thrust coefficient increases as the Reynolds number increases [3].

The results of extensive wind tunnel experiments are more credible, but it cannot be ignored that this experimental equipment is expensive and time-consuming. With the high-speed development of computer technology, CFD methods have gained considerable attention, and CFD methods are more flexible for the dynamic modeling of similar complex objects such as TRUAV. Peng et al. performed CFD analysis of the virtual blade model (VBM) and an accurate blade model (RBM), indicating the presence of distorted blade tip wake and larger unsteady aerodynamic forces in the transition modal [4].

Jiang et al. studied the power and lift efficiency of an annular-ducted fan lift system in hover modal, lift and drag in transition modal, drag and flight speed of the aircraft in cruise modal, and aerodynamic coupling of nose turbine and jet exhaust, but they did not give the corresponding dynamics model [5]. Wu et al. also discretized by the Chimera grid technique and then solved the rotor aerodynamic interaction of a tilt-rotor aircraft in multi-rotor and transition modals using the Reynolds averaged Navier–Stokes (RANS) equations. They experimentally adopted quasi-steady state and transient methods to simulate the tilting motion in transition modal, discussing both qualitative and quantitative results, again without examining its mathematical model [6]. Joshi et al. developed a mathematical model of a Hybrid Aerial Vehicle Combining VTOL. They performed simple CFD simulations but only applied the simulation results for the design verification phase, although they intended to obtain aerodynamic coefficients through CFD experiments in their subsequent work [7]. This paper analyzed both the dynamic dynamics modeling of TRUAV and its complex coupled aerodynamic relationships, and the main contributions of this paper are as follows:

• Established the TRUAV unsteady dynamics model of the transition modal based on the transient computational fluid dynamics numerical simulations, and adding the aerodynamic parameters of the tilting angle state change, also considering the influence of different tilting angle slipstream flow regions.
• Conducted the numerical simulations on the rotor thrust, pitch moment of TRUAV, analysis of transition modal’s three-dimensional flow field distribution, and the corresponding conclusions were drawn.
• The TRUAV modal transition simulations are in airborne flight mode without considering ground effects.

The rest of this paper is organized as follows: Section 2 establishes aerodynamic modeling of the TRUAV transition modal based on the change of tilt angle state, and it provides the essential explanation of the notations and the assumptions prior to the research. Section 3 describes in detail the CFD numerical simulation method for the TRUAV, including sections on meshing, turbulence model, rotating domain, etc. Section 4 analyzes the experimental results, calculates the aerodynamic parameters necessary for modeling through the transient CFD simulation of TRUAV, and presents numerical simulations on the transition modal of TRUAV with three-dimensional flow field analysis to provide data support for the optimal design of a TRUAV structure and unsteady state control. Section 5 presents the simulation of the TRUAV cascade PID control strategy. Section 6 summarizes the conclusions of this paper.

2. Dynamics Model and Identification

2.1. Assumptions

The TRUAV transition modal modeling mechanism is very complex, and various aerodynamic coupling disturbances are severe [8]; it is necessary to make the following assumptions before performing the TRUAV transition modal modeling:

• The TRUAV was treated as a rigid body, neglecting the elastic deformation of the fuselage, while the aerodynamic center and the center of mass were consistent;
• The pendulum and flapping motions of the propeller were not considered;
• The mass of the TRUAV and the mass distribution were constant, the cruise speed of the TRUAV was limited, and the atmospheric density was fixed, ignoring the air compression properties.

2.2. TRUAV Dynamics Model

The six degrees of freedom dynamics equations for the TRUAV containing unsteady aerodynamics are designed for the translational and rotational motions of the TRUAV separately utilizing the Newtonian Euler equations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{\overrightarrow{p}}}^{\mathcal{W}}=R{\overrightarrow{v}}^{\mathcal{B}},{\dot{\overrightarrow{v}}}^{\mathcal{B}}=R{\overrightarrow{g}}^{\mathcal{W}}+\frac{1}{\overline{m}}\Sigma {\overrightarrow{F}}_{sum}^{\mathcal{B}}-\overrightarrow{\Omega }\times {\overrightarrow{v}}^{\mathcal{B}}\hfill \\ J\dot{\overrightarrow{\Omega }}=-\overrightarrow{\Omega }\times J\overrightarrow{\Omega }+\Sigma {\overrightarrow{M}}_{sum}\hfill \end{array}\right.\end{array}$$

(1)

where $\mathcal{W}=\left(X_e,Y_e,Z_e\right)$ specififies the world coordinate system, $\overrightarrow{p}$ represents the position vector of TRUAV, $R\in SO\left(3\right)$ is the rotation matrix of the body coordinate system $\mathcal{B}=\left(X_b,Y_b,Z_b\right)$ relative to $\mathcal{W}$ as shown in Figure 2, ${\overrightarrow{v}}^{\mathcal{B}}\in {\mathbb{R}}^3$ represents the velocity of the TRUAV body coordinate system, $\overline{m}=diag\left(m\right)\in {\mathbb{R}}^{3\times 3}$ is the whole weight of the TRUAV, $\overrightarrow{\Omega }\in {\mathbb{R}}^3$ is the angular velocity of the body coordinate system, $J\in {\mathbb{R}}^{3\times 3}$ specififies the inertial matrix of the TRUAV, ${\overrightarrow{F}}_{\mathrm{sum}}^{\mathcal{B}}$ is the sum of the rotor thrust and the aerodynamic lift of the wing, and $\Sigma {\overrightarrow{M}}_{\mathrm{sum}}$ is the vector of external torque.

The thrust of the three motors is expressed as ${\overrightarrow{F}}_{th}^{\mathcal{B}}$, where k is the motor thrust coefficient, w is the rotor speed, and ${\tau }_{*}$ is the tilt angle of the two motors in front of the fuselage:

$${\overrightarrow{F}}_{th}^{\mathcal{B}}=\left[\begin{array}{ccc}{s}_{{\tau }_1}& s_{{\tau }_2}& 0\\ 0& 0& 0\\ -c_{{\tau }_1}& -c_{{\tau }_2}& -1\end{array}\right]\left[\begin{array}{c}k{w}_1^2\hfill \\ k{w}_2^2\hfill \\ k{w}_3^2\hfill \end{array}\right]$$

(2)

The wing lift expression is ${\overrightarrow{F}}_{wing}^{\mathcal{B}}$, where $\rho$ is the air density, S represents the projected area of the wing, $V_{\infty }$ specifies the TRUAV velocity relative to air fluid, and $C_L\left(\tau \right)$ and $C_D\left(\tau \right)$ are the aerodynamic lift and drag coefficients, respectively. Considering the influence of rotor slipstream on the wing surface, this paper divides the wing into two parts: one part is affected by the rotor airflow, namely the Wing Slipstream Area (WSA), and the other part is not affected by rotor airflow, which belongs to Wing Freestream Area (WFA); the two areas are labeled in Figure 3. The size of the Wing Slipstream Area size varies with the tilting angle, the exact calculation of the area of the slipstream area is more complicated, and the formula in the GTRS (Generic Tilt-Rotor Simulator) model is applied to approximate the estimate [9,10,11], the formula for calculating the slipstream area is as follows:

$$S_{wsa}=S_{wsamax}\left[sin\left(a\ast {\tau }_{*}\right)+cos\left(b\ast {\tau }_{*}\right)\right]\frac{u_{max}-u}{u_{max}}$$

(3)

where a and b are correction factors, which satisfy $sin\left(a\frac{\pi }{2}\right)+cos\left(b\frac{\pi }{2}\right)=1$, $sin\left(a\frac{\pi }{3}\right)+cos\left(b\frac{\pi }{3}\right)=0$, that $a=1.386$ and $b=3.114$, $S_{wsamax}$ represents the maximum slipstream area, $u_{max}$ and $u_{min}$ are the critical velocity ratios when the wing is not affected by the rotor wake in the multi-rotor modal, and the rotor wake radius can be calculated using the formula [9]:

$$R_W=R\left\{0.78+0.22e^{-\left(0.3+2Z_r\sqrt{2C_T}+120C_T\right)}\right\}$$

(4)

where $\mathrm{Zr}$ is the distance between the rotor to the wing in dimensionless form, and the Wing Slipstream Area can be calculated as:

$$S_{wsa}=S-S_{wfa}$$

(5)

The dynamic pressure in the wing slipstream area and wing freestream area is expressed as:

$${\overline{q}}_{(wfa,wsa)}=\frac{1}{2}{\rho }_{air}{V}_{(wfa,wsa)}$$

(6)

where $V_{wfa}$ and $V_{wsa}$ are the combined velocity of the Wing Freestream Area and Wing Slipstream Area aerodynamic pressure centers, respectively, and the aerodynamic forces and moments of the air on the wing in the slipstream and free-flow areas can be calculated as follows:

$${\overrightarrow{F}}_{\mathrm{wing}}^{\mathcal{B}}=\sum _{(i=wfa,wsa)}\frac{1}{2}{\rho }_{air}{V}_i^2{S}_i{\left[C_D\left(\tau \right)0C_L\left(\tau \right)\right]}^T$$

(7)

$${\overrightarrow{M}}_{\mathrm{wing}}^{\mathcal{B}}=\sum _{(i=wfa,wsa)}{\overline{q}}_i{S}_i{\left[\begin{array}{ccc}0\hfill & \overline{c}{C}_M\left(\tau \right)\hfill & 0\hfill \end{array}\right]}^T$$

(8)

The moment generated by the pulling force when the rotor rotates is ${\overrightarrow{M}}_{th}^{\mathcal{B}}$ [12], where ${\overrightarrow{E}}_z$ specifies the Z-axis unit vector of $\mathcal{B}$, and $l_i$ is the distances from the motor to the TRUAV mass center, respectively:

$$\begin{array}{c}\hfill {\overrightarrow{M}}_{th}^{\mathcal{B}}=\sum _{i=1}^{2}k{w}_i^2\left[l_i\times {\left[\begin{array}{ccc}{\mathrm{s}}_{\tau i}\hfill & 0\hfill & -c_{\tau i}\hfill \end{array}\right]}^T\right]+l_3\times k{w}_3^2{\overrightarrow{E}}_z\end{array}$$

(9)

The moment generated by the rotor gyro effect is ${\overrightarrow{M}}_{rotor}^{\mathcal{B}}$, where $J_r$ is the rotational inertia of the rotor, and ${\mu }_1=1$, ${\mu }_2=-1$.

$$\begin{array}{c}\hfill {\overrightarrow{M}}_{rotor}^{\mathcal{B}}=\sum _{i=1}^2{J}_r\left[{\mu }_i{\overrightarrow{\Omega }}_i\times {\left[\begin{array}{ccc}{s}_{\tau i}\hfill & 0\hfill & -c_{\tau i}\hfill \end{array}\right]}^T\right]\end{array}$$

(10)

The anti-tilt moment from rotor tilting is ${\overrightarrow{M}}_{tilt}^{\mathcal{B}}$:

$$\begin{array}{c}\hfill {\overrightarrow{M}}_{tilt}^{\mathcal{B}}=\sum _{i=1}^2\left[\begin{array}{ccc}0\hfill & -J_r{\ddot{\tau }}_i\hfill & 0\hfill \end{array}\right]\end{array}$$

(11)

${\overrightarrow{M}}_{rotate}^{\mathcal{B}}$ is the back torsional moment of the blade, which is generated by the blade drag when the rotor rotates:

$$\begin{array}{c}\hfill {\overrightarrow{M}}_{rotate}^{\mathcal{B}}=\sum _{\mathrm{i}=1}^2\left[k_{\mathrm{i}}{\overrightarrow{\Omega }}_i^2{\left[\begin{array}{ccc}-{\mathrm{s}}_{\tau i}\hfill & 0\hfill & c_{\tau i}\hfill \end{array}\right]}^T\right]+k_3{\overrightarrow{\Omega }}_3^2{\overrightarrow{E}}_z\end{array}$$

(12)

In the TRUAV dynamics equation, there are some aerodynamic coefficients that need to be confirmed, such as lift, drag, and moment coefficient, which are calculated as follows:

$$C_L^{*}\left(\tau \right)=\frac{L\left(\tau \right)}{\frac{1}{2}\rho V^2{S}_{\omega }}$$

(13)

$$C_D^{*}\left(\tau \right)=\frac{D\left(\tau \right)}{\frac{1}{2}\rho V^2{S}_{\omega }}$$

(14)

$$C_M^{*}\left(\tau \right)=\frac{M\left(\tau \right)}{\frac{1}{2}\rho V^2{S}_{\omega }{c}_a}$$

(15)

In several related works, such aerodynamic coefficients tend to be treated as a single angle-of-attack variations function, which are acceptable in smooth motion or non-agile flight conditions [13,14], but the TRUAV transition state is heavily aerodynamically coupled, while numerical calculations applying CFD simulations can dynamically determine the aerodynamic parameters needed for modeling the TRUAV when it is in transition modal, providing data to support the control system design for the transition modal.

3. Methods

3.1. Mesh System

CFD simulation analysis requires the construction of the approximate solution space of the differential equations through the mesh division; for the transient CFD simulation analysis of a complex geometric object such as a TRUAV, a good mesh division can reduce the consumption of computing resources, shorten the calculation cycle, for different calculation domains, choose different mesh scales, in which the number of meshes will directly affect the accuracy and size of the numerical simulation results. The ploy-hexcore meshing is adopted for TRUAV, which accelerates the meshing speed to ensure faster and more accurate simulation solutions, and it improves the mesh quality by reducing the number of mesh faces. For the problem of data variation gradient and mesh division scale, we have the following settings:

• The maximum global constrained size of the mesh for TRUAV is set to 0.1 m, the minimum global constrained size is set to 0.002 m and the growth rate is set to 1.2;
• The curvature normal angle is set to 9°, which is used to rationally mesh this complex geometric model of TRUAV, implying the generation of 40 nodes within each geometric circumference;
• To ensure the quality and distribution of the mesh, check the TRUAV mesh for the initial division and repair part of the mesh for smoothness, and the minimum skewness of the TRUAV model is 0.8.

After the mesh density of the TRUAV simulation reaches a certain level, the impact of continuing to increase the mesh density on the calculation results is very small; at this point, it can be considered that the impact of increasing the number of calculated meshes on the calculation results can be ignored. In the subsequent calculation process, the number of calculated meshes at the location where the calculation results no longer change is used as the base for the number of meshes, if the relative rate of change is within a small range, the meshes are considered independent. A 45° tilt angle was selected for the TRUAV simulation, and the lift of the No. 1 rotor was used as the test point. Five different mesh densities were selected for testing. When the number of meshes reached $1.0\times {10}^8$ orders of magnitude, the error in results from encrypted meshes was within $5.0\%$, so the number of mesh nodes was chosen to be $1.0\times {10}^8$ as shown in Figure 4.

In the TRUAV numerical simulations, the total nodes number of the mesh system is about $1\times {10}^8$, where the polygonal wall faces of the rotational computational domain are $3\times {10}^4$, and the total number of rack polygonal wall faces is $1.5\times {10}^5$. The TRUAV numerical simulation blockage rate is $3.7\%$ to reduce the adverse effects on the UAV from the sides and top of the wind tunnel environment modeling. Boundary layer grids are generated by projecting surface grids normally to capture boundary layer flow phenomena. The height of the first floor of TRUAV is $2.0\times {10}^{-3}$ m. The papers on blockage rate and mesh size can be found in [15,16,17,18,19]. The TRUAV simulation flow is shown in Figure 5.

3.2. Boundary Conditions

In conducting the calculation model of TRUAV, there were three types of calculation domains, and the first was the air-fluid region, as shown in Figure 6. The volume of the area was set at 14 m in length, 9 m in width, and 6.8 m in height, which was adopted to wrap the fuselage as well as the rotor part. In CFD numerical analysis, the boundary conditions guide and limit the fluid motion. The second was the fuselage (excluding the three rotors) part, and the third was the rotor part. The complex geometric model of the tilting mechanism will additionally increase the computer’s arithmetic power consumption; in order to simplify the calculation, the rotation calculation domain and the tilting mechanism are isolated from each other. The rotating domain column area was set as the interface, the flow field information was interpolated and transferred in the part where the interface overlaps, the rotor part adopted a column-shaped region with a diameter of 0.6 m, the column-shaped calculation domain that wrapped the rotor was called the rotational calculation domain, and the fuselage part was named as stationary computational domain. The selection of the rotational computational domain dynamic mesh method was different in the steady-state calculation and transient calculation. In the steady-state calculation, the dynamic mesh was chosen as the MRF method (Moving Reference Frame). In the calculation where we applied the MRF model, the entire computational domain solved the flow field control equations in each subdomain and exchanged the flow field information by converting the velocity to absolute velocity at the intersection of the subdomains. The results of the MRF method were used as the initial values for the transient calculations, and the Moving Mesh method was chosen for the transient calculations.

At the intersection between the stationary and rotational computational domains of TRUAV, the velocity vectors of a point with respect to the stationary reference system and the moving reference system can be interconverted by the following equation:

$$v_{\mathrm{r}}=v-u_{\mathrm{r}}$$

(16)

where ${\mathcal{V}}_{\mathrm{r}}$ denotes the relative velocity, i.e., the velocity with respect to the moving reference system, $\mathcal{V}$ is the absolute velocity, i.e., the velocity with respect to the stationary reference system, and $u_{\mathrm{r}}$ is the velocity of the moving reference system with respect to the stationary reference system.

$$u_{\mathrm{r}}=v_{\mathrm{t}}+\mathbf{w}\times \mathbf{r}$$

(17)

In the above equation, ${\mathcal{V}}_{\mathrm{t}}$ is the translational velocity of the moving reference system, $\mathbf{W}$ is the angular velocity, and $\mathbf{r}$ denotes the position vector from the stationary reference system to the moving reference system. In the relative reference system, the absolute velocity u is calculated applying the control equation in the relative coordinate system:

$$\left\{\begin{array}{c}\frac{\partial \rho }{\partial t}+\nabla ·\rho \mathbf{v}=0\\ \frac{\partial }{\partial t}\rho \mathbf{v}+\nabla ·\left(\rho {\mathbf{v}}_{\mathrm{r}}\mathbf{v}\right)+\rho \left[\omega \times \left(\mathbf{v}-{\mathbf{v}}_{\mathrm{t}}\right)\right]=-\nabla p+\nabla ·\overline{\tau }+\mathbf{F}\\ \frac{\partial }{\partial t}\rho E+\nabla ·\left[\rho {\mathbf{v}}_{\mathbf{r}}\left(E+\frac{p}{\rho }\right)+p\left({\mathbf{v}}_{\mathrm{t}}+\omega \times \mathbf{r}\right)\right]=\nabla ·(k\nabla T+\overline{\tau }·\mathbf{v})+{\mathbf{S}}_h\end{array}\right.$$

(18)

In the momentum equation, $\rho \left[\omega \times \left(\mathbf{v}-{\mathbf{v}}_{\mathrm{t}}\right)\right]$ includes the Koch and centrifugal forces generated by the rotating reference system, $\overline{\overline{\tau }}$ denotes the viscous stress, and no relative motion is generated between the stationary and rotating computational domains under the MRF model.

3.3. Turbulence Model

The TRUAV numerical simulation is carried out using ANSYS Fluent© as the solver. With its rich physical models, advanced numerical methods and powerful pre- and post-processing capabilities, it has a wide range of applications in aerospace and aircraft aerodynamic analysis, which also includes the aerodynamic characteristics of TRUAV under different flight conditions.

With regard to the TRUAV transient and steady CFD simulation, the SST k-$\omega$ turbulence model was selected to simulate the viscous effects, and the SST k-$\omega$ model could be written as [20]:

$$\frac{\mathrm{D}\rho k}{\mathrm{D}t}={\tau }_{ij}\frac{\partial u_i}{\partial x_j}-{\beta }^{*}\rho \omega k+\frac{\partial }{\partial x_j}\left[\left(\mu +{\sigma }_k{\mu }_t\right)\frac{\partial k}{\partial x_j}\right]$$

(19)

$$\frac{\mathrm{D}\rho \omega }{\mathrm{D}t}=\frac{\gamma }{v_t}{\tau }_{ij}\frac{\partial u_i}{\partial x_j}-\beta \rho {\omega }^2+\frac{\partial }{\partial x_j}\left[\left(\mu +{\sigma }_{\omega }{\mu }_t\right)\frac{\partial \omega }{\partial x_j}\right]+2\left(1-F_1\right)\rho {\sigma }_{\omega 2}\frac{1}{\omega }\frac{\partial k}{\partial x_j}\frac{\partial \omega }{\partial x_j}$$

(20)

where Equation (19) is the turbulent kinetic energy transport equation, and Equation (20) is the turbulent specific dissipation equation, where $\rho$ is the fluid density; u represents the velocity; t is the time; x is the coordinate axis ($i,j=1,2,3$, denoting the x, y, z spatial coordinates, respectively), k represents the turbulent kinetic energy, and $\omega$ is the specific dissipation rate.

In Equations (19) and (20), the vortex viscosity model for Reynolds stress is:

$${\tau }_{tij}=2{\mu }_t\left(S_{ij}-S_{nn}{S}_{ij}/3\right)-2\rho k{S}_{ij}/3$$

(21)

where ${\mu }_t=\rho k/\omega$ is the vortex viscosity, $S_{ij}$ is the average velocity strain rate tensor, $S_{nn}$ is the Kronecker operator, and $P_{\omega }$ represents the generated item:

$$P_{\omega }=2\gamma \rho \left(S_{ij}-\omega S_{nn}{S}_{ij}/3\right)S_{ij}$$

(22)

In Equations (19)–(22), $\beta ,\gamma ,{\sigma }_k,{\sigma }_{\omega }$ represents the model parameters, the values of the model coefficients satisfy $\varphi =F_1{\varphi }_1+\left(1-F_1\right){\varphi }_2$, and the specific values of the parameters are mentioned in [20].

The SST k-$\omega$ two-equation model proposed by Menter combines the advantages of the Wilcox k-$\omega$ two-equation model and the high Reynolds number k-$\omega$ two-equation model. The SST k-$\omega$ two-equation model avoids the drawbacks of the k-$\omega$ model, which requires applying the dissipation functions, and it also eliminates the susceptibility to the free incoming flow environment. This makes the SST k-$\omega$ two-equation model a great advantage in dealing with wall flow, rotating mechanical flow field properties and jet flow [21]. In this paper, the SST k-$\omega$ model was adopted for the numerical simulation of TRUAV.

3.4. Termination Conditions

When solving incompressible fluid problems, the immediate joint solution of the Navier–Stokes (N-S) equation will undoubtedly generate a large amount of computational effort. The pressure correction method uses the continuity equation to correct the pressure term, which significantly reduces the computational memory. Therefore, the TRUAV numerical computation applies the SIMPLE (Semi-Implicit Methods for Pressure Linked Equations) [22] pressure correction method proposed by Patankar et al.

The TRUAV system has conducted several field flight experiments, and the data recorded in the actual flight have substantial noise interference and vibration, which cannot be directly applied in the calculation of the working condition point, so on the basis of the field flight experimental data, the working condition point parameters are also integrated with data from other related studies [23] to supplement the specific parameters shown in

Table 1. TRUAV Calculation Working Point.

Tilting Angles (deg)	Forward Flight Speed ($\mathbf{m}·{\mathbf{s}}^{-1}$)	Front Rotor Speed (rpm)	Rear Rotor Speed (rpm)	Time Steps (s)	Number of Time Steps
0.0°	5.0	3500	3500	0.001	2000
7.5°	8.0	3550	3500	0.001	2000
15.0°	11.0	3600	3500	0.001	2000
22.5°	12.0	3750	3500	0.001	2000
30.0°	13.0	3900	3500	0.001	2000
37.5°	14.0	3950	3400	0.001	2000
45.0°	15.0	4000	3300	0.001	2000
52.5°	17.5	3800	3750	0.001	2000
60.0°	20.0	3600	2400	0.001	2000
67.5°	21.5	3300	2900	0.001	2000
75.0°	23.0	3000	1400	0.001	2000
82.5°	24.0	2700	700	0.001	2000
90.0°	25.0	2400	0	0.001	2000

.

In conducting TRUAV numerical simulations, the criteria for the termination of the steady-state computation include the computation reaching convergence or reaching a specified number of iterations times, in the steady-state calculation, and the residual convergence criterion is set to $1\times {10}^{-3}$ when the data residuals will converge to the specified level. At this points, we consider that the steady-state experiment of TRUAV under the operating point has been carried out, and the number of convergence steps is set to $1\times {10}^4$. However, the number of iteration steps is normally below 500 steps in each operating point experiment, as shown in Figure 7, and the several computational parameters often involved in transient calculations, including the number of time steps, time step length, and the number of sub-step iterations, are given in Table 1.

TRUAV simulations are modeled using k-$\omega$ models with $y+\sim 1$. ANSYS FLUENT has taken steps to provide a more advanced wall format to allow mesh refinement without deterioration of results. These $y+$ independent formats are the default $\omega$-equation-based turbulence mode model. The model can be solved down to the viscous flow floor. For the implicit algorithm in the ANSYS Fluent solver, the default for Courant number is 50, taking a Courant number of 15, a minimum incoming velocity of 5 m/s, a maximum incoming velocity of 25 m/s and a minimum mesh size of 2 mm, according to equation:

$$\Delta t=\frac{\mathrm{Courant}{}^{*}\Delta x}{u}$$

(23)

The time step required for the maximum incoming flow rate is 0.006 s, and the time step required for the minimum incoming flow rate is 0.0012 s, which is satisfied with a time step of 0.001 s.

In the transient calculation, the TRUAV transient experiment results fluctuate within $\pm 2.0\%$ and reach the specified number of iteration steps, the experiment is considered complete as shown in Figure 8, and the average value of lift is taken as the calculated value for that calculation working point.

4. Numerical Simulation

Experimental Results Analysis

For the transition modal of TRUAV, we set different working condition points for transient CFD simulation calculation. Then, a series of flight aerodynamic coefficients can be obtained, these aerodynamic parameters data are used to generate an aerodynamic coefficients table. Then, we use the flight modeling simulation experiments to interpolate these data tables and calculate the aerodynamic forces and moments of different flight states, providing data support for subsequent numerical simulations and actual flight experiments.

Figure 9a plotted the velocity contours of the airframe along the incoming flow axis (XY plane) under different tilt angle changes of the TRUAV front rotor, which is due to the velocity increase of the rotor to produce a low-pressure area on the lower surface of the wing. In contrast, the wing’s upper surface is subjected to the strong downwash effect of the rotor, resulting in the induction of a substantial download and a higher drag growth rate of the TRUAV before the tilt angle of 45°. In comparison, after the tilt angle of 60°, as the tilt angle of TRUAV increases, the low pressure generated on the lower surface of the rotor gradually decreases, and the downwash effect of the rotor on the upper surface also becomes weaker. The drag growth rate starts to decay. The disturbing effect of the rotor wake can increase the pressure on the upper surface of the wing, while the greater the tilt angle, the less the effect of the rotor wake on the wing. Therefore, as the tilt angle increases, the area of low pressure at the leading edge of the wing also increases. This phenomenon results in a gradual increase in the positive lift area of the wing and a gradual increase in the lift of the wing.

Figure 9b plots the three-dimensional flow field of airframe velocity and pressure distribution on the fuselage surface under different tilt angle changes of the TRUAV front rotor. The airflow caused by the rotor affects the upper wing, creating a large area of high pressure, and the area of influence varies with the angle of inclination. The spiral slipstream generated by the high-speed rotation of the TRUAV rotor changed the original flow state of the air around the wing, within the slipstream area, affecting the pressure on the wing. The pressure on the surface of the wing increased, and because the TRUAV wing was installed behind the rotor, the slip flow field will be influenced by the wing and change, thus producing a side wash phenomenon and a blockage phenomenon. At the same time, it will make the flow field uneven, and the blockage utility will be applied to the rotor reaction force through the pressure field to increase the rotor tension. In addition, the slipstream flow field distribution was not uniform, which is mainly due to the influence of the wing and tilting mechanism and support structure behind the rotor, and the non-symmetric flow field will lead to the existence of different pressure distribution in different phases of the rotor.

The transient CFD simulation selected thirteen typical tilt angles and their respective operating points. The specific parameters of the calculation working point are shown in Table 1. Figure 10a plotted the wing aerodynamic coefficient change curve with the tilt angle. The wing suffered a drag force of 0.34 N along the X-axis direction (opposite to the cruise speed direction) at a tilt angle of 0°, and it suffered a drag force of about 13.96 N at a tilt angle of 90°. The drag coefficient of the TRUAV wing decreased at the tilt angle of 30° and leveled off at 75°, while the change curve of the drag coefficient of the wing with the tilt angle is plotted in Figure 10a. The drag coefficient of the wing increases with the increase of the tilt angle and the cruise speed. The moment coefficient of the TRUAV wing rises at a tilt angle of 0° to 22.5° and remains steady after 52.5°, as shown in Figure 10a.

The lift brought by the rotor wing started to decrease gradually with the change of rotational speed and the tilt angle of the TRUAV, and at the tilt angle of 0°, i.e., when the TRUAV was in the fixed wing mode, the three rotors provided almost all the lift of about 71.05 N, which was just the same as the lift of the whole aircraft. In contrast, as shown in Figure 10b, with the change of tilt angle, the lift from the wing was obviously in an upward trend, providing 3.01 N of lift at 0° and finally providing about 158.3 N at 90° of tilt angle, fully satisfying the lift requirement of TRUAV.

The rotor inlet airflow velocity is in the same direction as the rotor rotation axis, and the value of thrust is related to the airspeed and rotor speed. The thrust reduces with the increase of airspeed; as shown in Figure 11a, under the same rotor speed, the ratio of the maximum airspeed thrust to the initial airspeed single-rotor thrust is $19.1\%$, and the maximum thrust of the single-rotor at 4000 rpm is 36.3 N. The thrust characteristics generated by the airflow velocity of the TRUAV rotor inlet at different rotational speeds are shown, and the individual rotor thrust results are consistent with the TRUAV numerical simulation rotor thrust.

As shown in Figure 11b, the TRUAV tilts at a fixed angle, and the experiments at different airspeeds match the values of lift at the calculation working point, and the larger the TRUAV tilting angle (approaching the fixed-wing modal), the lower the lift at a certain airspeed. Conversely, at a fixed tilt angle, the airspeed and lift exhibit a positive relationship. For example, in the fixed wing modal, the minimum airspeed lift is 8.4 N and the maximum airspeed lift is 161.3 N. In Figure 11c, in the transition modal of TRUAV, the pitch down moment reduces as the tilt angle decreases, and the less forward flight speed, the lower the pitch down moment. At the higher flight speed, TRUAV is more unstable; on the contrary, the pitch moment is almost zero in the low-speed condition of the fixed-wing modal. When the TRUAV fixed tilt angle is 0°, the ratio of pitching moment at minimum airspeed and maximum airspeed is $51.2\%$, while at a tilt angle of 90°, this ratio is $2.5\%$, which indicates that the TRUAV is the most unstable when flying at high speed while in the transition from multi-rotor modal to fixed-wing modal. Instead, when TRUAV is in fixed-wing modal and cruising at low speed, the pitch moment can be kept relatively stable to the greatest extent.

When the TRUAV is hovering, the forward flight speed is relatively low, and the rotor blades are responsible for the lift required by the whole aircraft. The rotor blades are almost parallel to the fixed section of the wing plane, resulting in under-rotor wash flow hitting the wing and fuselage surfaces and not being able to move downwards smoothly. So, there is serious aerodynamic interference between the rotor blades and the fuselage and wings of the tilt-rotor in hover. The under-rotor wash flow hitting the fuselage and wing will rise back up and be re-absorbed into the rotor blades, resulting in the typical “fountain effect” aerodynamic disturbance phenomenon. The downflow caused by the rotor is blocked by the wing and part of the airflow flows inwards along the wingspan before concentrating near the symmetrical area of the fuselage. Eventually, it deflects upwards, creating a rotor fountain flow, which dissipates as the angle of tilt increases because the TRUAV is in low-speed flight. The pressure difference between the upper and lower wing sections increases as the angle of inclination increases; i.e., the wake effect diminishes as the angle of inclination increases.

5. Controller Strategy

After establishing the TRUAV dynamics model and calibration of the relevant aerodynamic coefficients, for the TRUAV control, the state variables are controlled by a PID controller, and Figure 12 shows the block diagram of the control scheme. Forces and moments due to trirotor and wing aerodynamics are calculated separately. The overall control framework consists of two cascade PID controllers, which receive the errors from speed and attitude and give corresponding control quantities. The control of TRUAV is realized by using the negative feedback mechanism [24,25,26,27,28,29].

Using Matlab Simulink© as the simulation software, the corresponding dynamic model was established as shown in Figure 13. For the dynamic aerodynamic coefficient of the tilt-rotor UAV, the signal generation module is used to add it, and the mode switching of TRUAV takes time as the trigger signal.

For the four conditions of trajectory planning, Figure 14a shows the planning of the TRUAV tilt angle: the starting absolute value is set to 0, the starting speed is also 0 m/s, the ending absolute value is $\pi /2$, and the ending speed is 0 m/s, the start time is 0 s, the end time is 20 s, and the final formula after the trajectory planning of the cubic polynomial is as follows:

$$\begin{array}{c}\mathrm{x}\left({\mathrm{t}}_{\mathrm{s}}\right)={\mathrm{c}}_0+{\mathrm{c}}_1{\mathrm{t}}_{\mathrm{s}}+{\mathrm{c}}_2{\mathrm{t}}_{\mathrm{s}}^2+{\mathrm{c}}_3{\mathrm{t}}_{\mathrm{s}}^3={\mathrm{x}}_{\mathrm{s}}\hfill \\ \mathrm{x}\left({\mathrm{t}}_{\mathrm{e}}\right)={\mathrm{c}}_0+{\mathrm{c}}_1{\mathrm{t}}_{\mathrm{e}}+{\mathrm{c}}_2{\mathrm{t}}_{\mathrm{e}}^2+{\mathrm{c}}_3{\mathrm{t}}_{\mathrm{e}}^3={\mathrm{x}}_{\mathrm{e}}\hfill \\ \mathrm{v}\left({\mathrm{t}}_{\mathrm{s}}\right)={\mathrm{c}}_1+2{\mathrm{c}}_2{\mathrm{t}}_{\mathrm{s}}+3{\mathrm{c}}_3{\mathrm{t}}_{\mathrm{s}}^2={\mathrm{v}}_{\mathrm{s}}\hfill \\ \mathrm{v}\left({\mathrm{t}}_{\mathrm{e}}\right)={\mathrm{c}}_1+2{\mathrm{c}}_2{\mathrm{t}}_{\mathrm{e}}+3{\mathrm{c}}_3{\mathrm{t}}_{\mathrm{e}}^2={\mathrm{v}}_{\mathrm{e}}\hfill \end{array}$$

(24)

Each constraint corresponds to an equation, and the matrix equation is as follows:

$$\left[\begin{array}{cccc}1& {\mathrm{t}}_{\mathrm{s}}& {\mathrm{t}}_{\mathrm{s}}^2& {\mathrm{t}}_{\mathrm{s}}^3\\ 1& {\mathrm{t}}_{\mathrm{e}}& {\mathrm{t}}_{\mathrm{e}}^2& {\mathrm{t}}_{\mathrm{e}}^3\\ 0& 1& 2{\mathrm{t}}_{\mathrm{s}}& 3{\mathrm{t}}_{\mathrm{s}}^2\\ 0& 1& 2{\mathrm{t}}_{\mathrm{e}}& 3{\mathrm{t}}_{\mathrm{e}}^2\end{array}\right]\left[\begin{array}{c}{\mathrm{c}}_0\hfill \\ {\mathrm{c}}_1\hfill \\ {\mathrm{c}}_2\hfill \\ {\mathrm{c}}_3\hfill \end{array}\right]=\left[\begin{array}{c}{\mathrm{x}}_{\mathrm{s}}\hfill \\ {\mathrm{x}}_{\mathrm{e}}\hfill \\ {\mathrm{v}}_{\mathrm{s}}\hfill \\ {\mathrm{v}}_{\mathrm{e}}\hfill \end{array}\right]$$

(25)

For pose planning, the TRUAV input is the second derivative of the attitude. For the planning of the second-order differential trajectory, a cubic polynomial is also used, and the total simulation time is set to 40 s. Before 20 s, the tilt-rotor UAV is in the transition mode, and the latter 20 s is in the fixed-wing flight modal, as shown in Equation (26), where $t_0=0$ s, $t_1=20$ s. The simulation curve is shown in Figure 14b.

$$\left\{\begin{array}{c}q\left(t\right)=a_0+a_1\left(t-t_0\right)+a_2{\left(t-t_0\right)}^2+a_3{\left(t-t_0\right)}^3,t_0\le t\le t_1\hfill \\ q\left(t\right)=q\left(t_1\right),t\ge t_1\hfill \end{array}\right.$$

(26)

Figure 15 is the experimental graph of the Euler angle of the tilt-rotor UAV attitude. For the attitude roll angle, a cubic polynomial plan is made, and the yaw and pitch angles are 0 degrees by default. From the experimental results, for the roll angle, the planning is successful. At 20 s, that is, the transition mode, because the roll angle and the pitch angle are coupled with each other, the pitch angle is jittery. However, the controller successfully maintains the stability of the tilt-rotor UAV. After 20 s in the fixed-wing modal, the jitter of the pitch angle is significantly improved, and the control strategy is successful.

The simulation results show that our proposed TRUAV dynamic modeling and control strategy is effective, the static position error does not exceed $5\%$, and the TRUAV remains stable despite the jitter in the transition mode.

6. Conclusions

In this paper, the dynamics modeling based on the change of tilt angle was performed for the TRUAV. The relevant aerodynamic parameters required for the modeling were obtained using transient CFD numerical simulations. The non-constant dynamics model of the TRUAV under typical operating conditions was established. In addition, the three-dimensional flow field and the curves of each aerodynamic parameter under the transition modal of the TRUAV were also analyzed, and we conducted experiments on the single rotor thrust, pitching moment, and TRUAV lift at different Reynolds numbers. The results demonstrated that the TRUAV is severely disturbed by aerodynamic forces during the transition phase. However, the whole lift can still counteract the full gravity in the cruise condition and achieve the flight conditions. Finally, the control simulation of TRUAV was completed by cascade PID control strategy.

The aerodynamic parameters simulated through the calculation points are directly fitted and updated into the TRUAV dynamic model. The calculation points chosen in this paper are discrete and future work plans include the use of active modeling control methods to observe, predict, and dynamically adjust TRUAV model parameters for more accurate control by using model predictors such as the EKF (Extended Kalman Filter) [30,31,32,33,34], with the TRUAV discrete state parameters as a reference.