Investigating and Analyzing the Potential for Regenerating Excess Energy in a Helicopter UAV
Abstract
:1. Introduction
2. Modeling and Methods
2.1. Numerical Approach
2.1.1. Numerical Model
2.1.2. Numerical Method
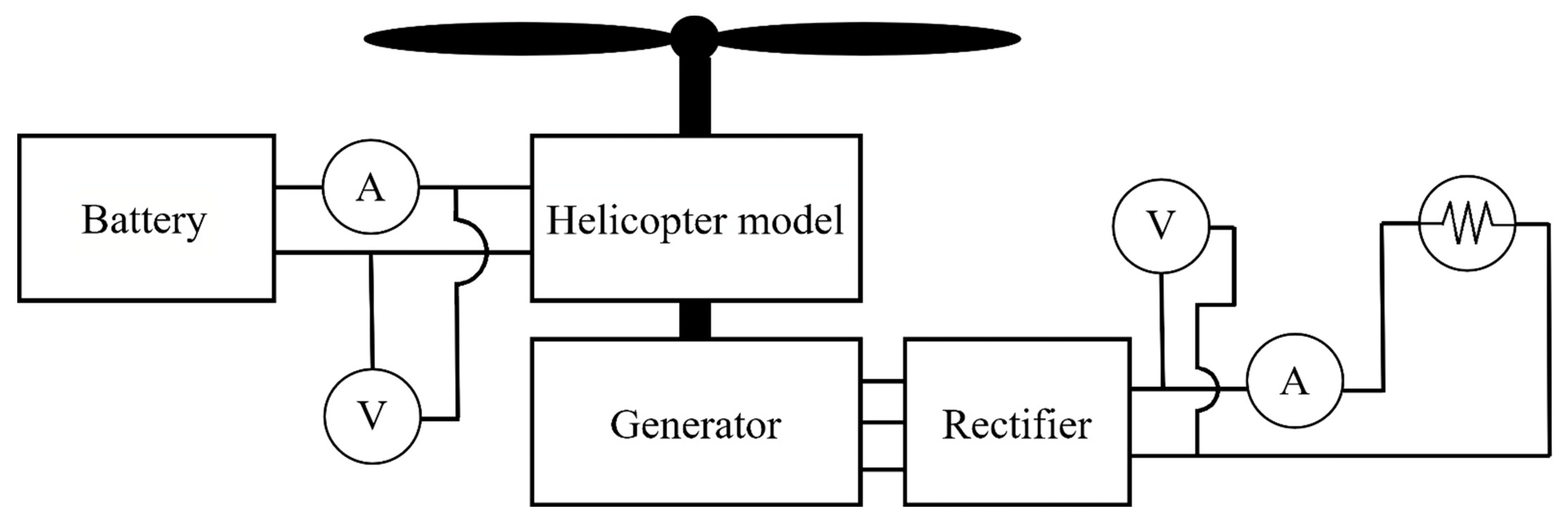
2.2. Experimental Approach
2.2.1. Experimental Model
2.2.2. Experimental Method
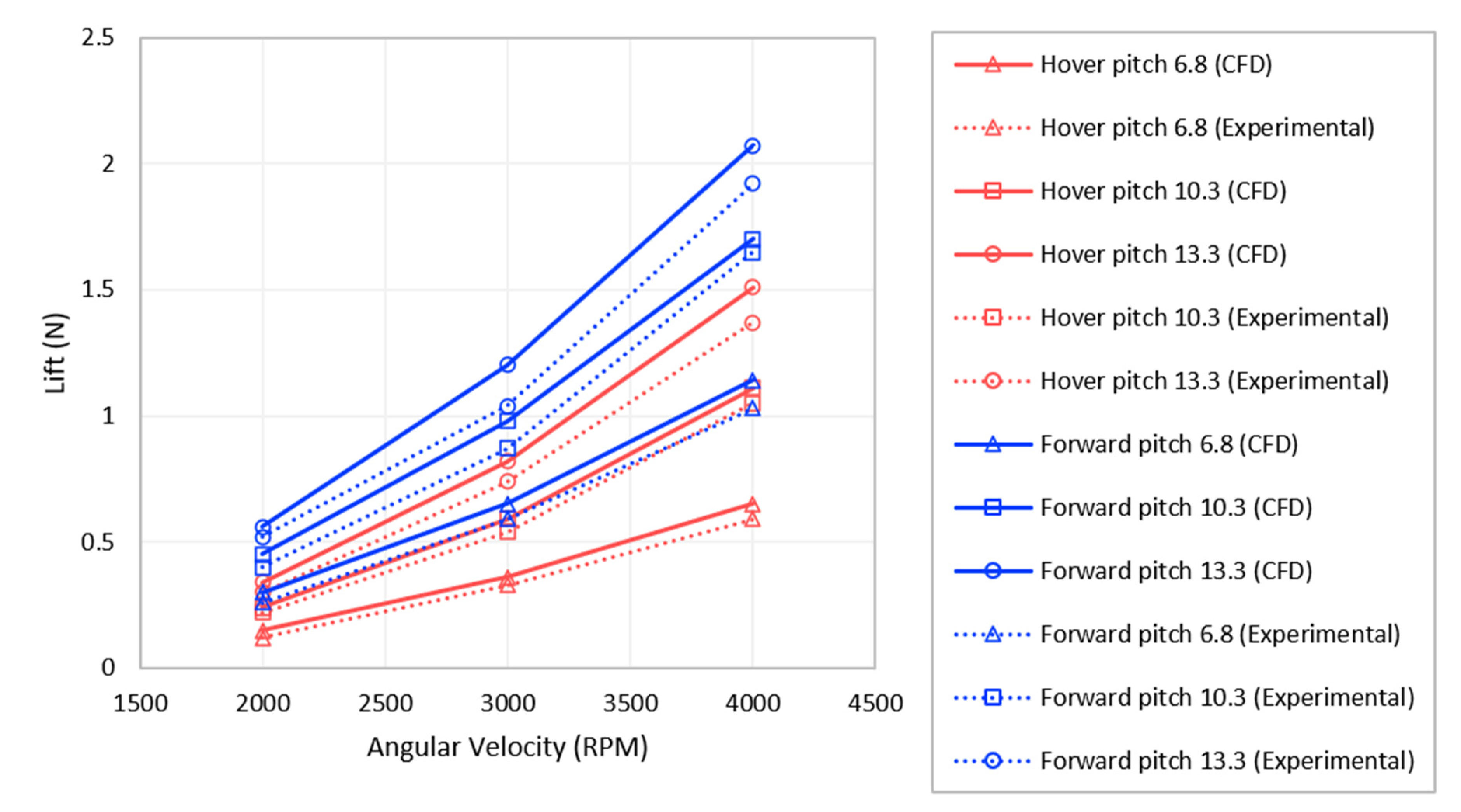
3. Validation of the Numerical Approach and Experimental Approach
4. Results and Discussion
4.1. Numerical Approach
4.2. Experimental Approach
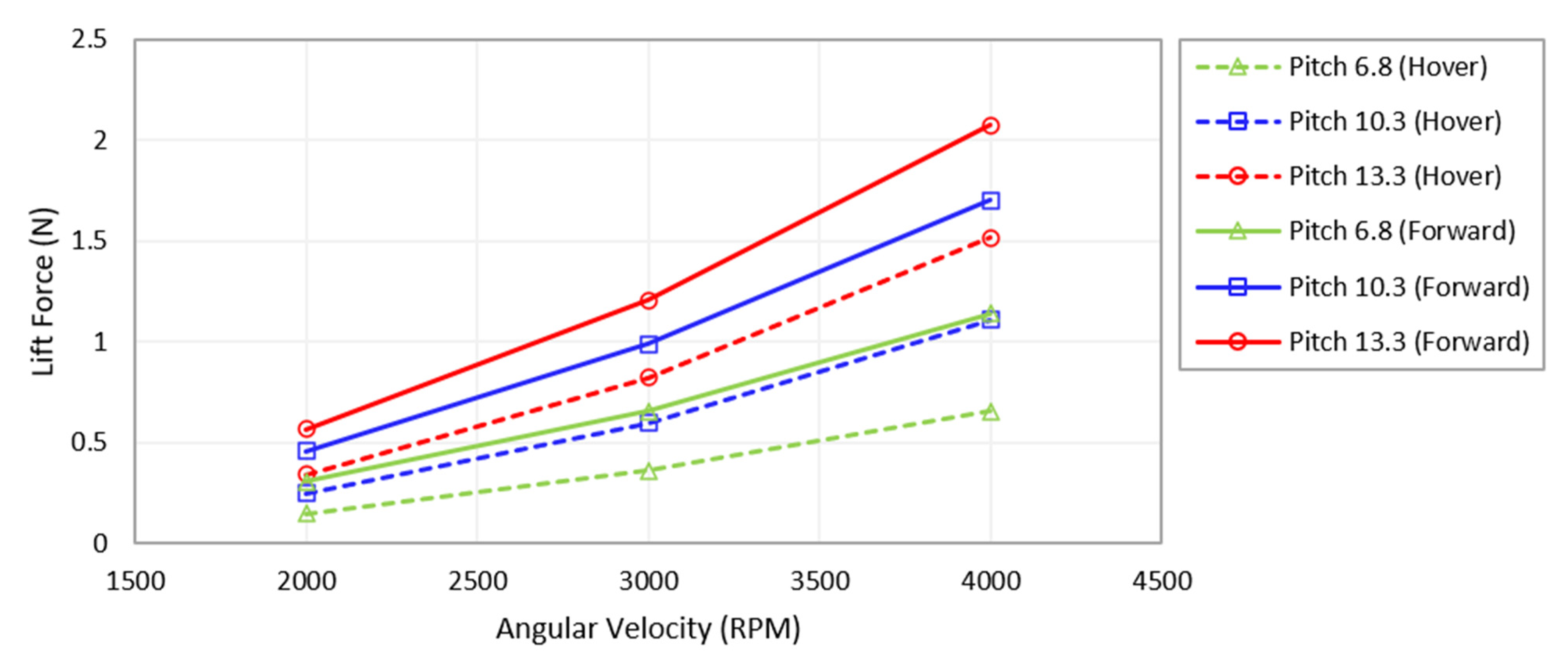
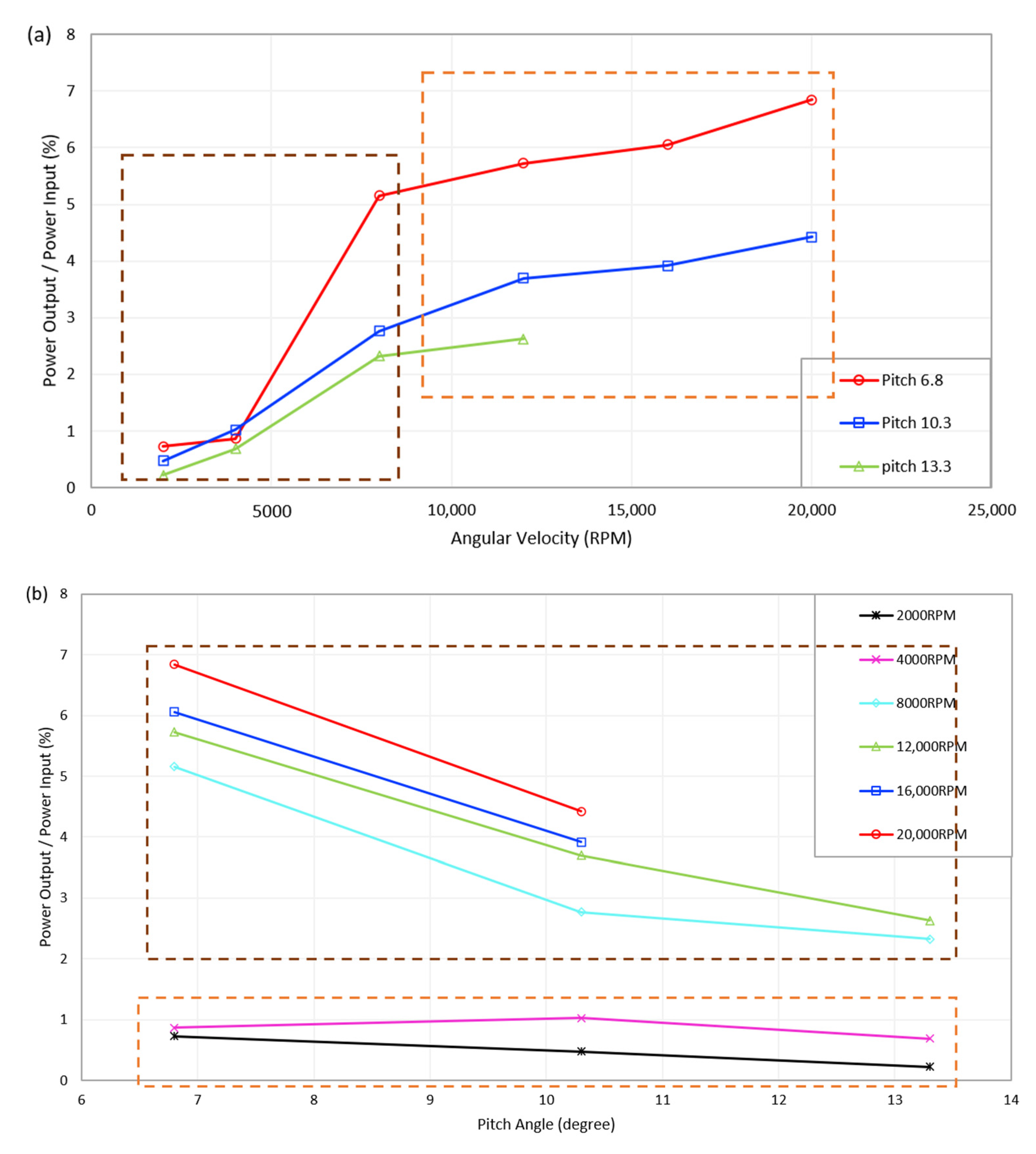
4.3. Hover Flight Condition
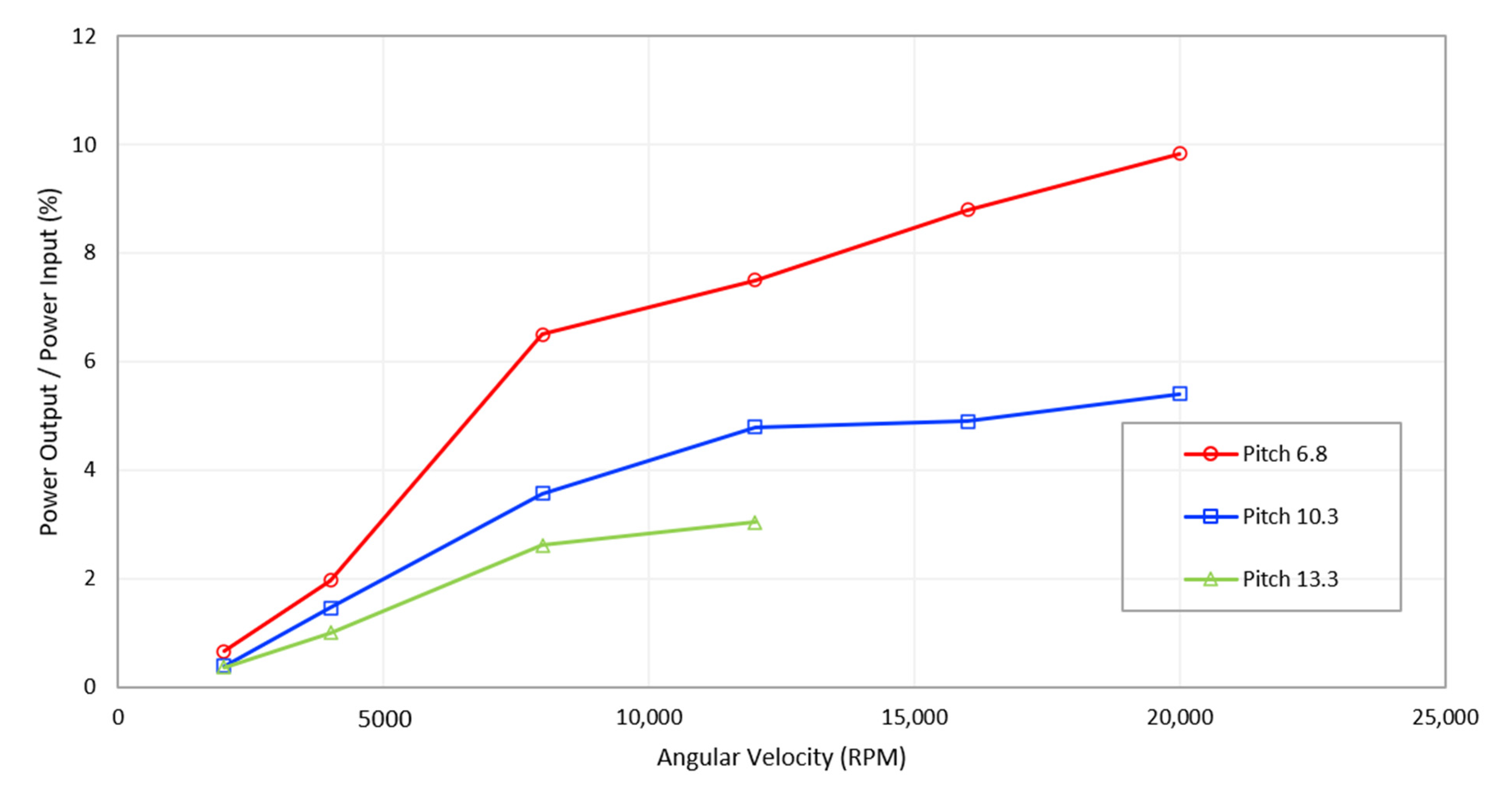
4.4. Forward Flight Condition
5. Conclusions
- Our estimations indicated that the rotor lift produced during forward flight surpassed that generated during hover flight, as determined using the numerical approach. These findings are in close alignment with the wind tunnel experimental data, thus validating the application of these methodologies in assessing helicopter performance.
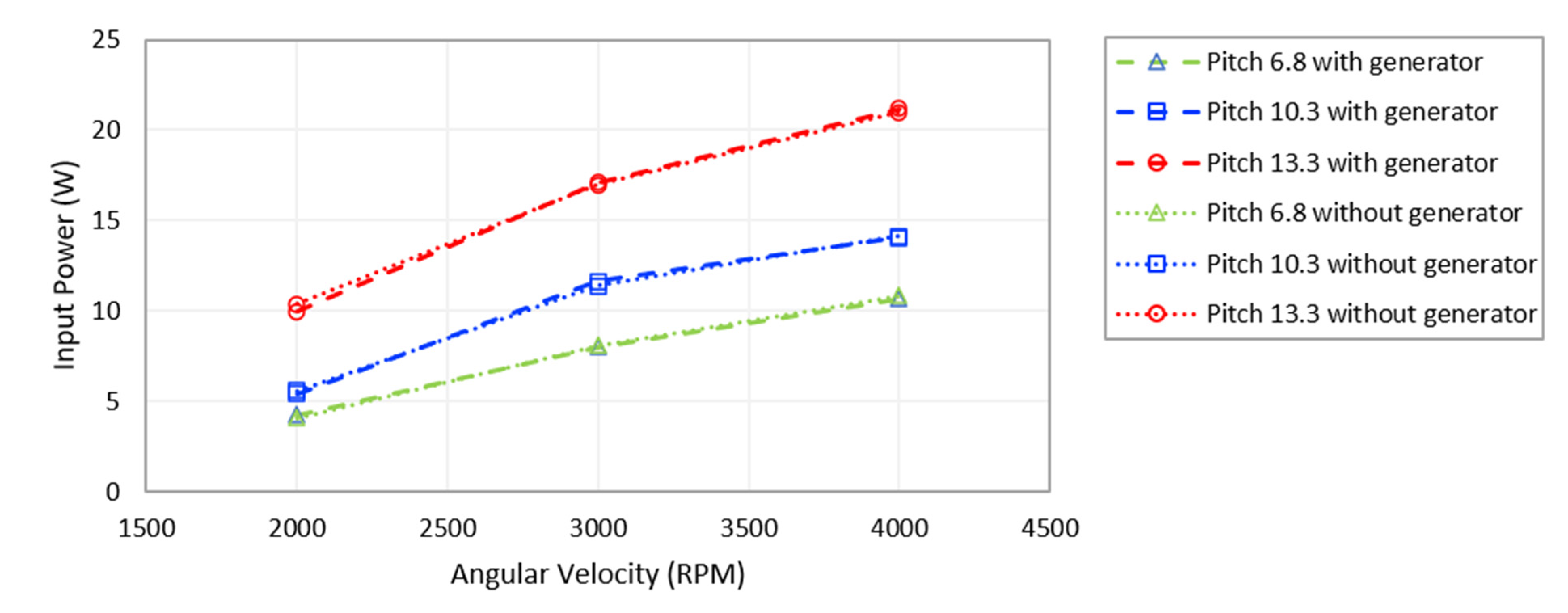
- By adjusting the main rotor angular velocity and pitch angle, the percentage of excess power can reach up to 6.84% in hover conditions and 9.83% in forward flight conditions.
- Based on the results of the hover and forward flight experiments, it can be deduced that the maximum value for the excess power percentage, attributed to the helicopter UAV’s safety design, is 6.84%, and that attributed to the helicopter UAV’s aerodynamics is 2.99%.
- This study supports the concept that helicopter performance can be enhanced by harnessing the excess power generated during flight operations. When this excess energy is harnessed, it can contribute significantly to the overall performance and efficiency of the UAV, potentially extending its flight duration or accommodating additional payload capacity.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Leishman, G.J. Principles of Helicopter Aerodynamics with CD Extra; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Padfield, G.D.J.I. Helicopter Flight Dynamics: The Theory and Application of Flying Qualities and Simulation Modeling; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 2007. [Google Scholar]
- Sikorsky, I.A. Aerodynamic parameters selection in helicopter design. J. Am. Helicopter Soc. 1960, 5, 41–60. [Google Scholar] [CrossRef]
- Pavel, M.D.; van Holten, T. Rotary Wing Vehicles. Encycl. Aerosp. Eng. 2010. [Google Scholar] [CrossRef]
- Filippone, A. Flight Performance of Fixed and Rotary Wing Aircraft; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Conlisk, A.T. Modern helicopter aerodynamics. Annu. Rev. Fluid Mech. 1997, 29, 515–567. [Google Scholar] [CrossRef]
- Seddon, J.M.; Newman, S. Basic Helicopter Aerodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Rotaru, C.; Todorov, M. Helicopter flight physics. Flight Phys.-Model. Tech. Technol. 2018, 10, 1948. [Google Scholar]
- Mistry, M.; Gandhi, F.J. Helicopter performance improvement with variable rotor radius and RPM. J. Am. Helicopter Soc. 2014, 59, 17–35. [Google Scholar] [CrossRef]
- Han, D.; Pastrikakis, V.; Barakos, G.N. Helicopter performance improvement by variable rotor speed and variable blade twist. Aerosp. Sci. Technol. 2016, 54, 164–173. [Google Scholar] [CrossRef]
- Han, D.; Wang, J.; Smith, E.C.; Lesieutre, G.A. Transient loads control of a variable speed rotor during lagwise resonance crossing. AIAA J. 2013, 51, 20–29. [Google Scholar] [CrossRef]
- Fenny, C. Mechanism for varying the diameter of rotors using compound differential rotary transmissions. In Annual Forum Proceedings-American Helicopter Society; American Helicopter Society, Inc.: Fairfax, VA, USA, 2005; p. 1359. [Google Scholar]
- Berry, B.; Chopra, I. Wind tunnel testing for performance and vibratory loads of a variable-speed mach-scale rotor. In Proceedings of the American Helicopter Society 67th Annual Forum, Virginia Beach, VA, USA, 3–5 May 2011. [Google Scholar]
- Han, D.; Smith, E.C. Lagwise dynamic analysis of a variable speed rotor. Aerosp. Sci. Technol. 2013, 29, 277–286. [Google Scholar] [CrossRef]
- Datta, A.; Yeo, H.; Norman, T.R. Experimental investigation and fundamental understanding of a slowed UH-60A rotor at high advance ratios. In Proceedings of the AHS 67th Annual Forum and Technology Display, Virtual, 6–8 October 2020. [Google Scholar]
- Kang, H.; Saberi, H.; Gandhi, F. Dynamic blade shape for improved helicopter rotor performance. J. Am. Helicopter Soc. 2010, 55, 32008-32008. [Google Scholar] [CrossRef]
- Brouwers, E.; Zientek, T.; Centolanza, L. Twist Effects on Rotor Performance, Loads and Vibrations. In Proceedings of the 71st Annual Forum of the American Helicopter Society, Beach, VA, USA, 5–7 May 2015. [Google Scholar]
- Chen, P.C.; Chopra, I. Hover testing of smart rotor with induced-strain actuation of blade twist. AIAA J. 1997, 35, 6–16. [Google Scholar] [CrossRef]
- Cheng, R.P.; Celi, R.J. Optimum two-per-revolution inputs for improved rotor performance. J. Aircr. 2005, 42, 1409–1417. [Google Scholar] [CrossRef]
- Thakkar, D.; Ganguli, R. Use of single crystal and soft piezoceramics for alleviation of flow separation induced vibration in a smart helicopter rotor. Smart Mater. Struct. 2006, 15, 331. [Google Scholar] [CrossRef]
- Thakkar, D.; Ganguli, R.J. Induced shear actuation of helicopter rotor blade for active twist control. Thin-Walled Struct. 2007, 45, 111–121. [Google Scholar] [CrossRef]
- Jain, R.; Yeo, H.; Chopra, I. Computational fluid dynamics—Computational structural dynamics analysis of active control of helicopter rotor for performance improvement. J. Am. Helicopter Soc. 2010, 55, 42004. [Google Scholar] [CrossRef]
- Thiemeier, J.; Oehrle, C.; Frey, F.; Keßler, M.; Krämer, E. Aerodynamics and flight mechanics analysis of Airbus Helicopters’ compound helicopter RACER in hover under crosswind conditions. CEAS Aeronaut. J. 2019, 11, 49–66. [Google Scholar] [CrossRef]
- Cerny, M.; Breitsamter, C.J.A. A comparison of isolated and ducted fixed-pitch propellers under non-axial inflow conditions. Aerospace 2020, 7, 112. [Google Scholar] [CrossRef]
- Carreno Ruiz, M.; Scanavino, M.; D’Ambrosio, D.; Guglieri, G.; Vilardi, A. Experimental and numerical analysis of multicopter rotor aerodynamics. In Proceedings of the AIAA Aviation 2021 Forum, Virtual Event, 2–6 August 2021; p. 2539. [Google Scholar]
- Doerffer, P.; Szulc, O. Numerical simulation of model helicopter rotor in hover. Sci. Bull. Acad. Comput. Cent. Gdan. 2008, 12, 227–236. [Google Scholar]
- Wilcox, D.C. Multiscale model for turbulent flows. AIAA J. 1988, 26, 1311–1320. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Velte, C.M.; Mikkelsen, R.F.; Sørensen, J.N.; Kaloyanov, T.; Gaunaa, M. Closed loop control of a flap exposed to harmonic aerodynamic actuation. In In Proceedings of the Torque 2012, The science of making torque from wind, Oldenburg, Germany, 9–11 October 2012. [Google Scholar]
- Maeda, T.; Kamada, Y.; Murata, J.; Suzuki, D.; Kaga, N.; Kagisaki, Y. LDV measurement of boundary layer on rotating blade surface in wind tunnel. J. Phys. Conf. Ser. 2014, 555 , 012057. [Google Scholar]
- Beaty, H.W.; Santoso, S. Handbook of Electric Power Calculations; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Hasan, I.; Mukesh, R.; Krishnan, P.R.; Srinath, R.; Babu, D.P.; Gurmu, N.L. Wind Tunnel Testing and Validation of Helicopter Rotor Blades Using Additive Manufacturing. Adv. Mater. Sci. Eng. 2022, 2022, 4052208. [Google Scholar] [CrossRef]
- Federal Aviation Administration, Airman Testing Branch. In Rotorcraft Flying Handbook; FAA-H-8083-21A. 2019; U.S. Department of Transportation: Washington, DC, USA, 2000.
- Prouty, R.W. Helicopter Performance, Stability, and Control; Krieger Publishing: Marlaba, FL, USA, 1995. [Google Scholar]
- Fox, R.W.; McDonald, A.T.; Mitchell, J.W. Fox and McDonald’s Introduction to Fluid Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Howell, R.; Qin, N.; Edwards, J.; Durrani, N. Wind tunnel and numerical study of a small vertical axis wind turbine. Renew. Energy 2010, 35, 412–422. [Google Scholar] [CrossRef]
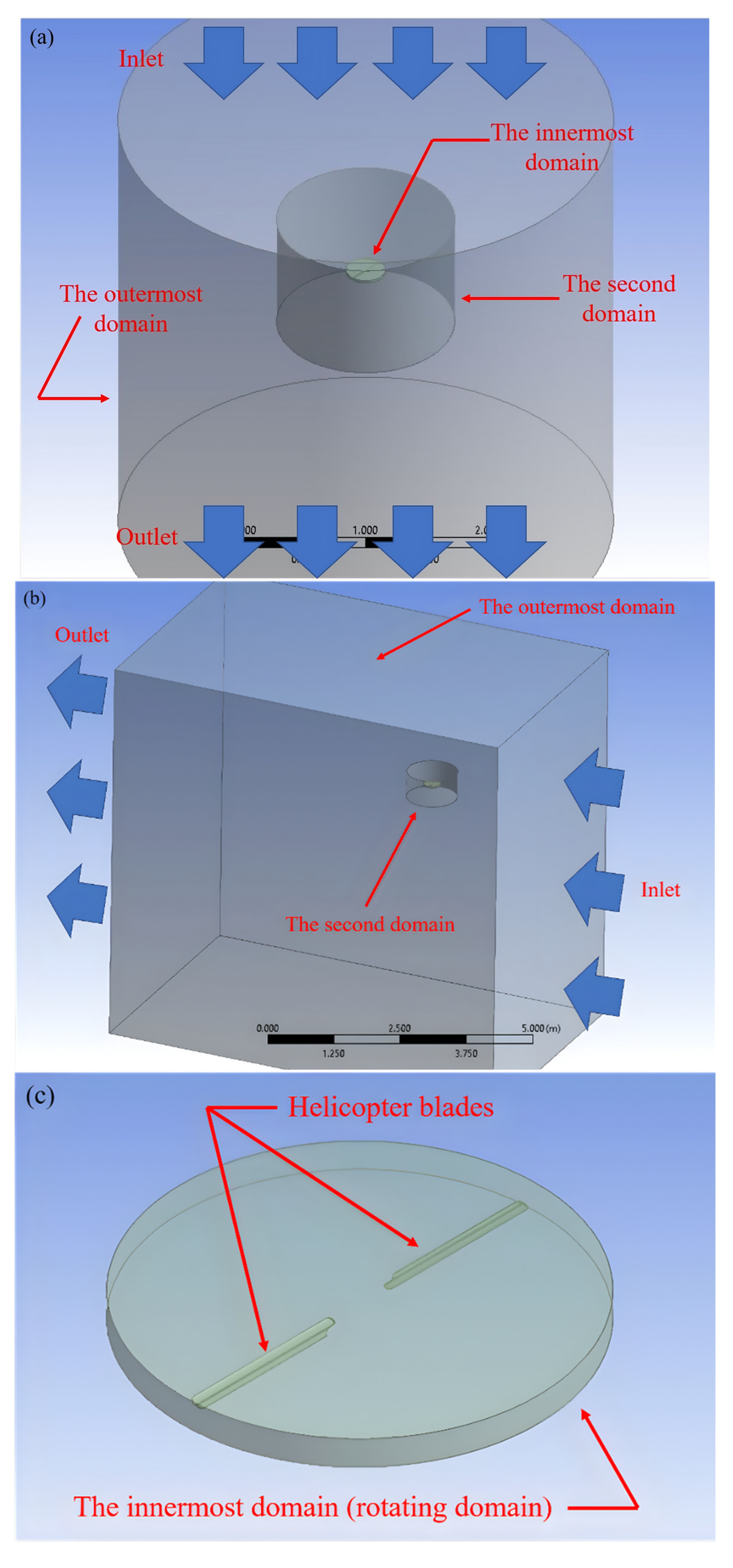
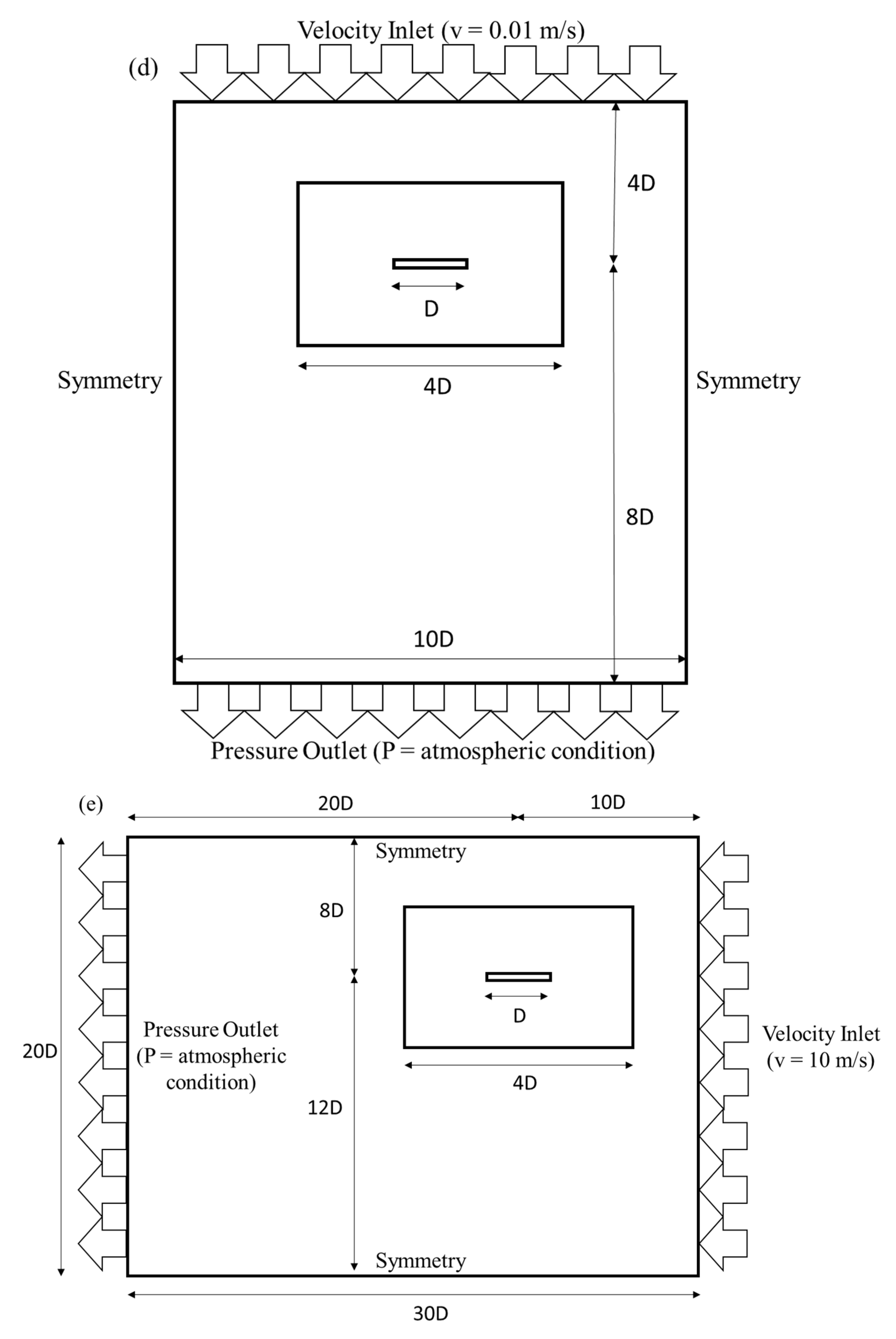
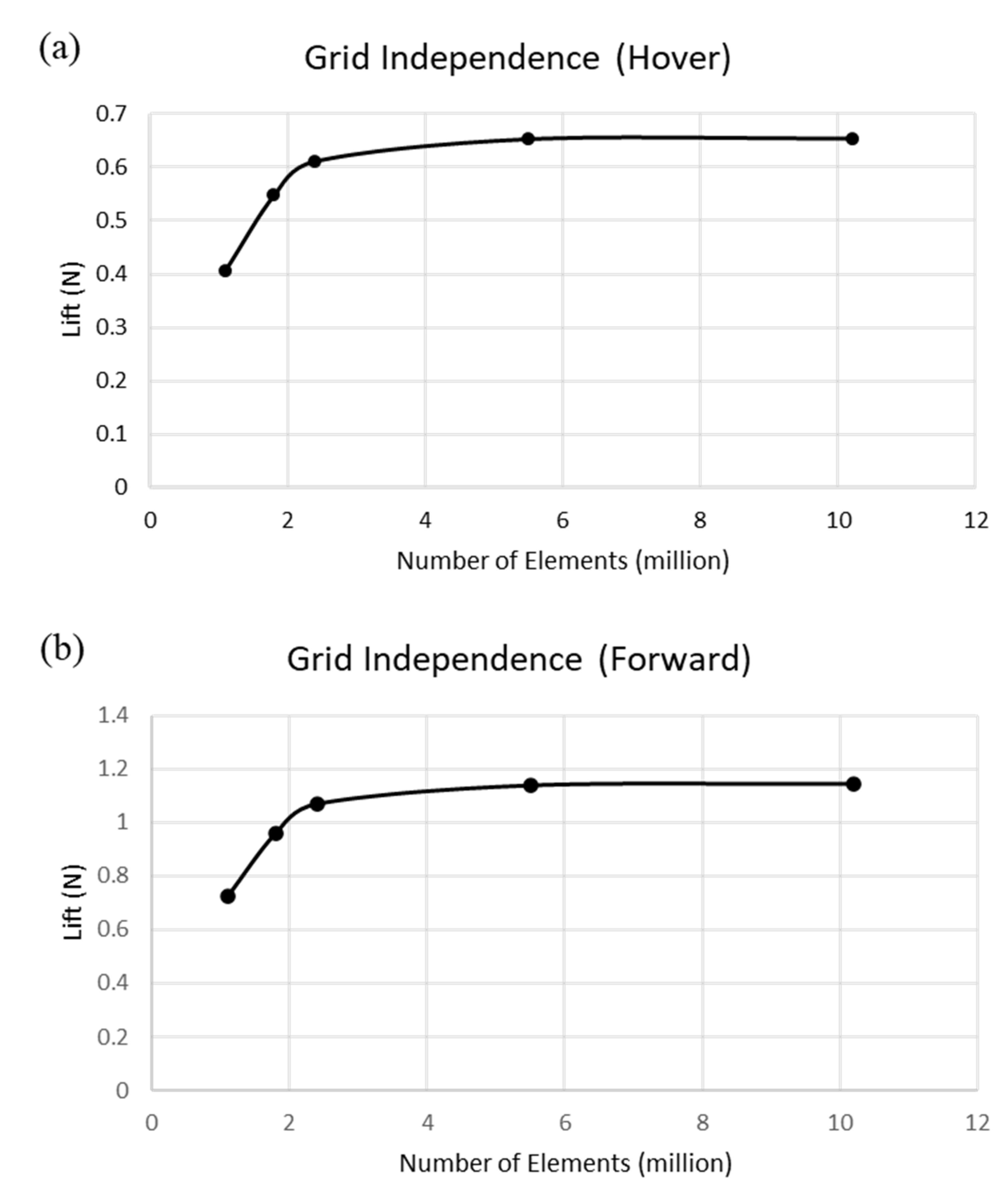





| Main Rotor Parameter | |
|---|---|
| Main rotor radius | 135.5 mm |
| Blade chord length | 18.8 mm |
| Number of blades | 2 |
| Blade twist | none |
| The Rotating Domain | |
| Number of elements on innermost domain | 1.6 million |
| Number of inflation layers | 10 |
| The Static Domain | |
| Number of elements on second domain | 1.9 million |
| Number of elements on outermost domain of hover condition | 5.3 million |
| Number of elements on outermost domain of forward condition | 5.57 million |
| Mesh Quality | |
| Minimum orthogonal quality of hover condition | 9.07 × 10−2 |
| Minimum orthogonal quality of forward condition | 8.35 × 10−2 |
| Maximum skewness of hover condition | 8.54 × 10−1 |
| Maximum skewness of forward condition | 9.16 × 10−1 |
| Battery, Motor Parameter | |
| Battery | 2S LiPo 7.4 V |
| Motor | Align RCM-BL150M rated at 9000 kv |
| Generator parameter | |
| KV value | 1500KV |
| Number of silicon steel sheet slots | 12 |
| Number of magnet poles | 14 |
| Parameter | Uncertainty |
|---|---|
| Temperature | 0.5% |
| Current | 1.5% |
| Voltage | 1.5% |
| Cases | Rotor Speed | ||
|---|---|---|---|
| Pitch 6.8 | 2000 RPM | 3000 RPM | 4000 RPM |
| Forward (with generator) | 18 min 30 s | 6 min 50 s | 5 min 15 s |
| Forward (non-generator) | 18 min 41 s | 6 min 54 s | 5 min 20 s |
| Pitch 10.3 | 2000 RPM | 3000 RPM | 4000 RPM |
| Forward (with generator) | 13 min 55 s | 4 min 50 s | 2 min 57 s |
| Forward (non-generator) | 13 min 55 s | 4 min 53 s | 2 min 57 s |
| Pitch 13.3 | 2000 RPM | 3000 RPM | 4000 RPM |
| Forward (with generator) | 5 min 40 s | 2 min 10 s | 57 s |
| Forward (non-generator) | 5 min 42 s | 2 min 17 s | 1 min 2 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kodchaniphaphong, C.; Pukrushpan, J.-t.; Klumpol, C. Investigating and Analyzing the Potential for Regenerating Excess Energy in a Helicopter UAV. Drones 2023, 7, 643. https://doi.org/10.3390/drones7100643
Kodchaniphaphong C, Pukrushpan J-t, Klumpol C. Investigating and Analyzing the Potential for Regenerating Excess Energy in a Helicopter UAV. Drones. 2023; 7(10):643. https://doi.org/10.3390/drones7100643
Chicago/Turabian StyleKodchaniphaphong, Chindanai, Jay-tawee Pukrushpan, and Chaiwat Klumpol. 2023. "Investigating and Analyzing the Potential for Regenerating Excess Energy in a Helicopter UAV" Drones 7, no. 10: 643. https://doi.org/10.3390/drones7100643
APA StyleKodchaniphaphong, C., Pukrushpan, J.-t., & Klumpol, C. (2023). Investigating and Analyzing the Potential for Regenerating Excess Energy in a Helicopter UAV. Drones, 7(10), 643. https://doi.org/10.3390/drones7100643





