Scheduling Drones for Ship Emission Detection from Multiple Stations
Abstract
1. Introduction
2. Related Studies
2.1. Emission Control Area (ECA)
2.2. Drone-Scheduling Problem
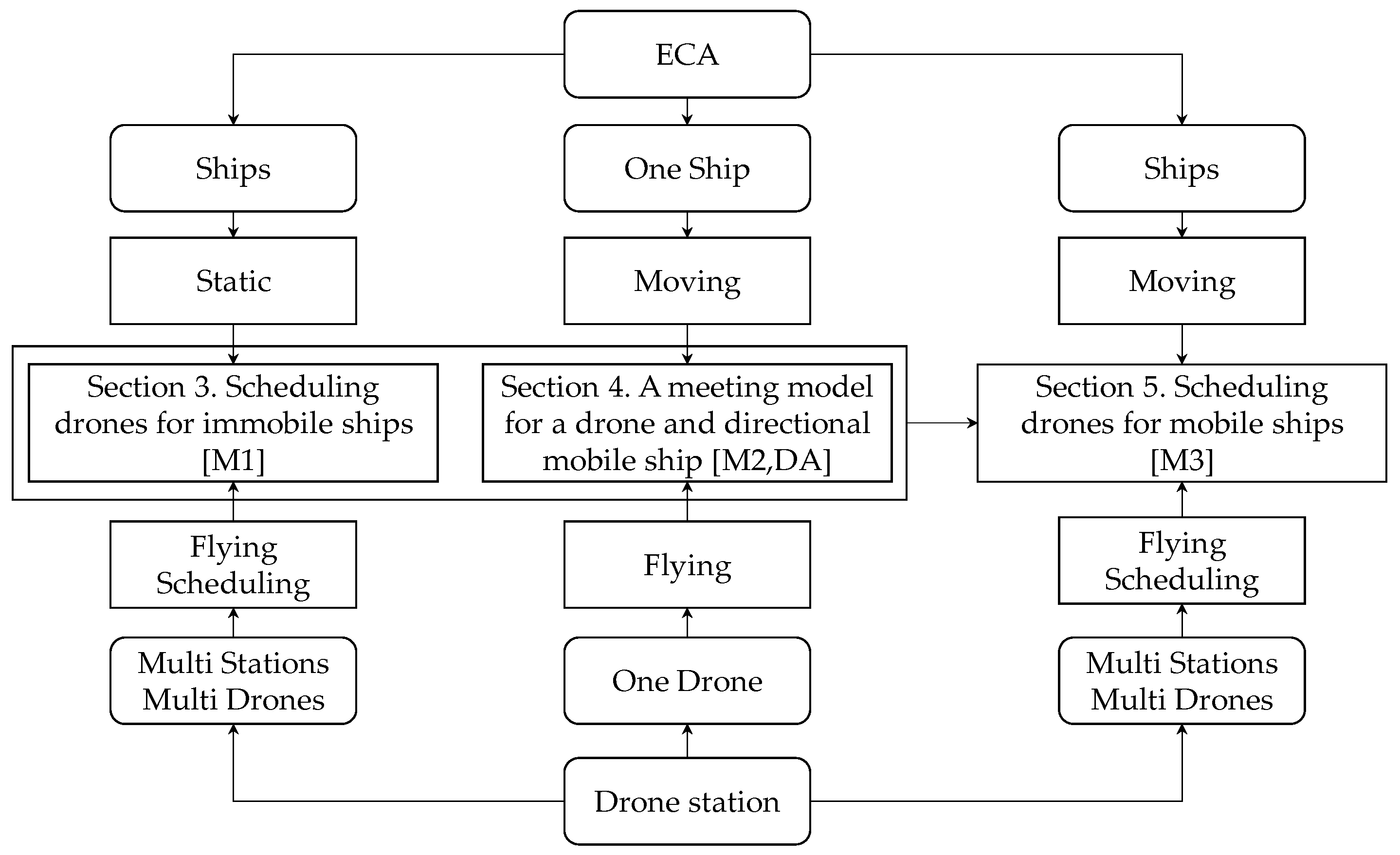
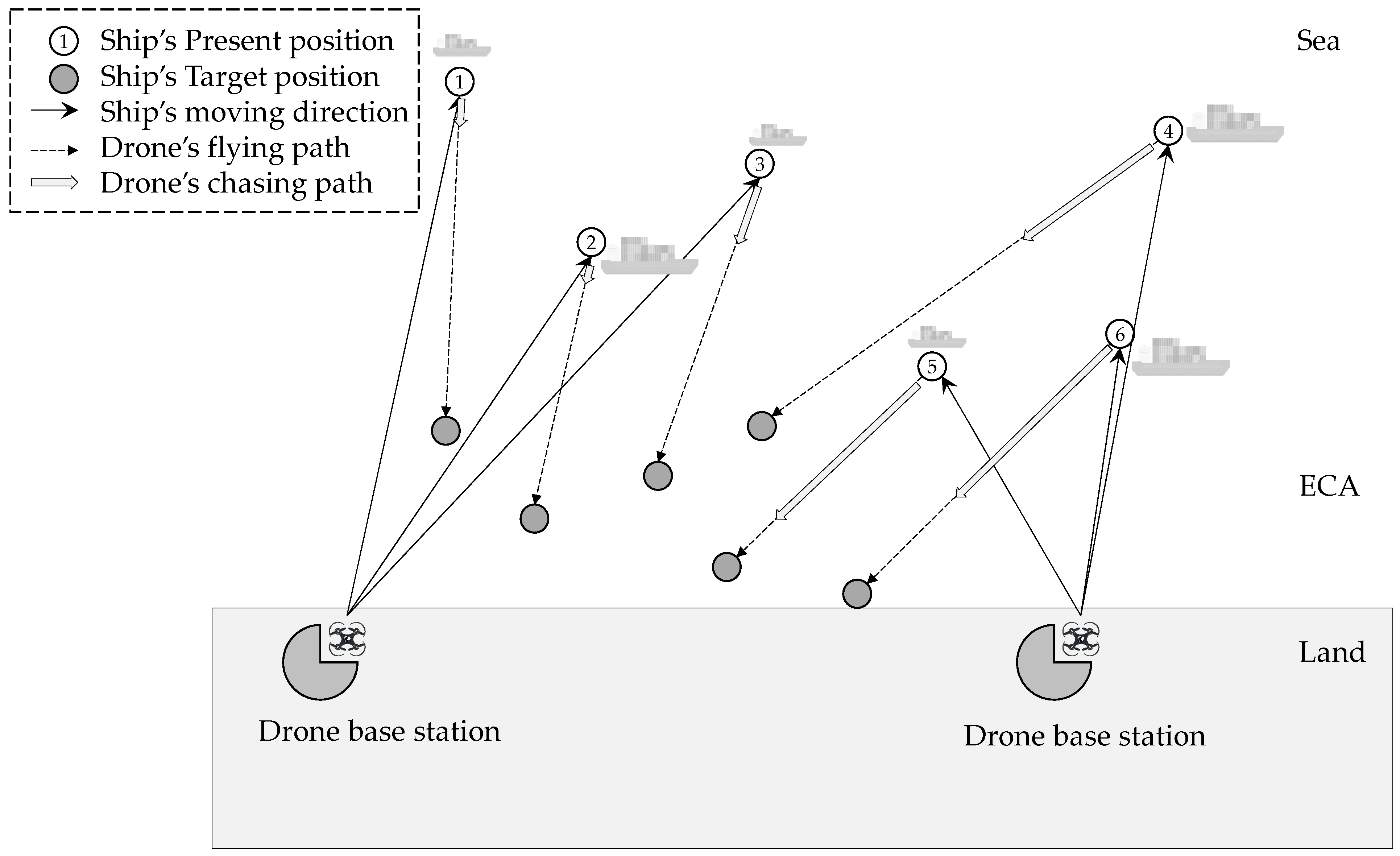
3. Scheduling Drones for Immobile Ships
3.1. Problem Statement
3.2. Formulation
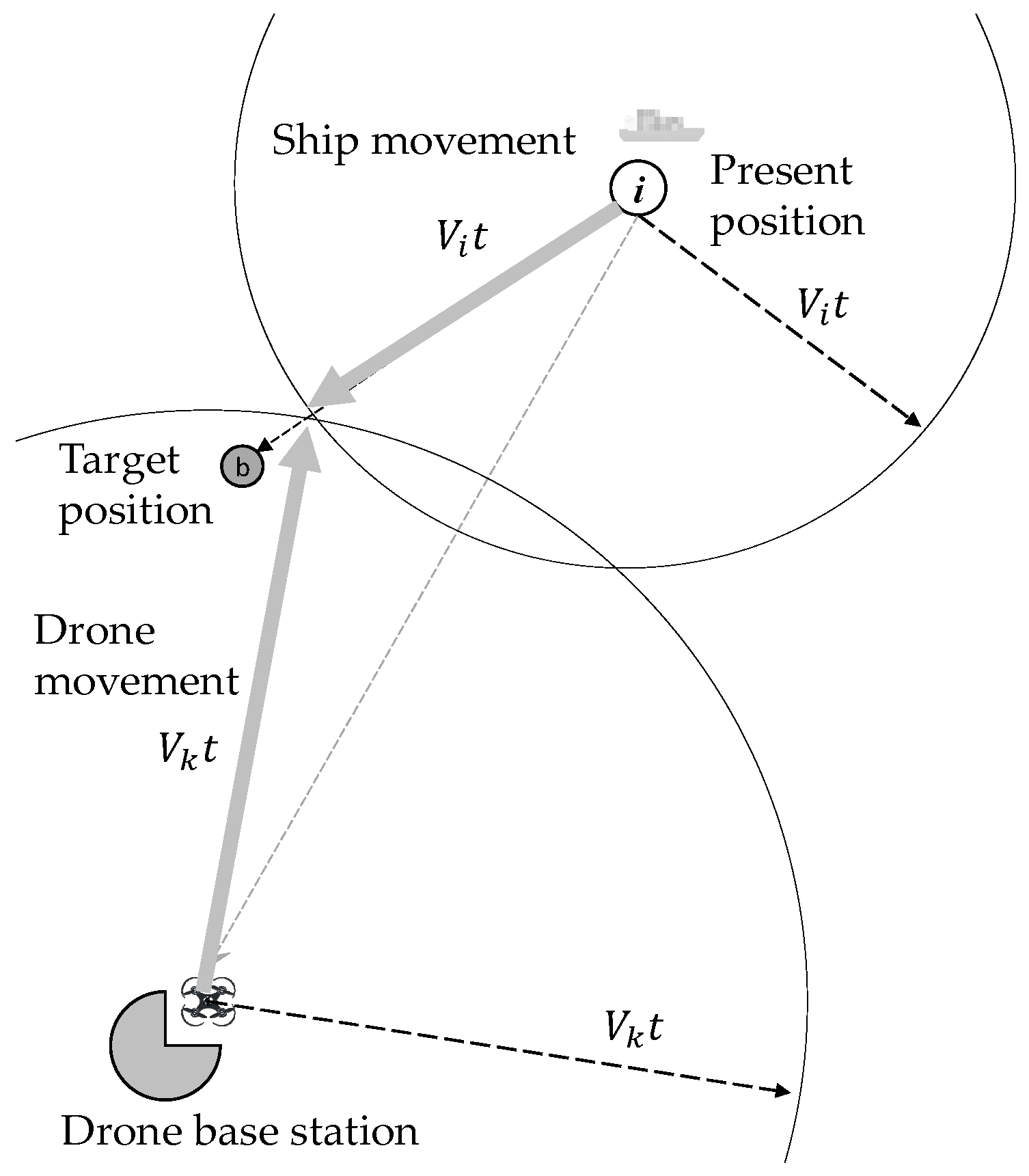
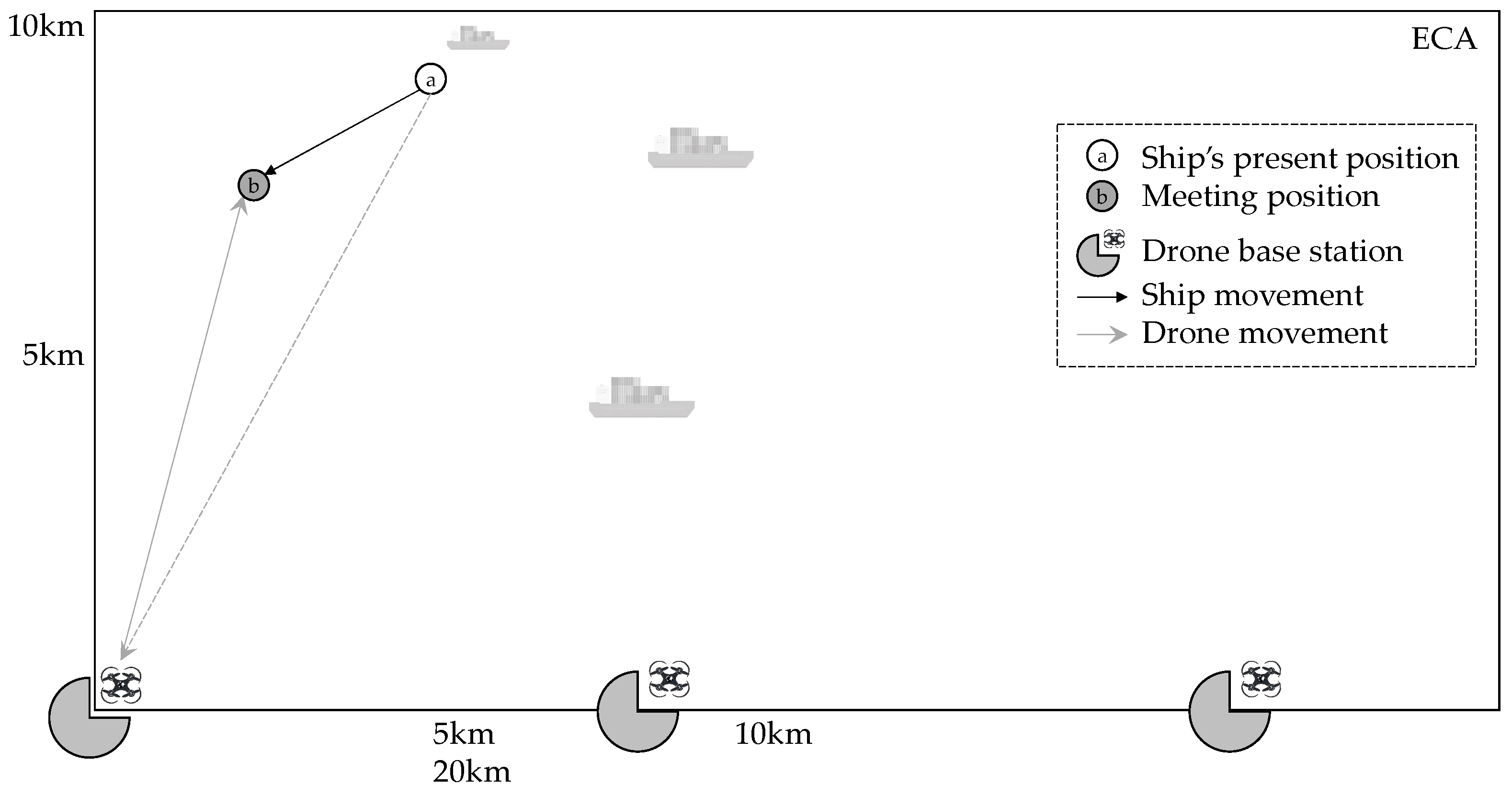
4. A Meeting Model for a Drone and Directional Mobile Ship
4.1. Formulation
4.2. Solution Algorithm
| Algorithm 1 | Dichotomy algorithm (DA) |
| Input | ship ’s position; |
| ship ’s target position; the drone base position; : ship ’s speed; : The speed of the drone. | |
| Output | : the position and time. |
| Variable | : the lower and upper bounds of the intersection position of the drone and ship; |
| : the moment at which the ship begins to travel to the intersection point; : tolerance. | |
| Steps | |
| Step 1 | Initialize and . |
| ; ; . | |
| Step 2 | Compute |
| . | |
| Step 3 | While : |
| Step 3.1 | If : |
| Step 3.2 | Else: |
| End if | |
| Step 3.3 | Update . |
| . | |
| Step 3.4 | Update |
| . | |
| Step 4 | Return |
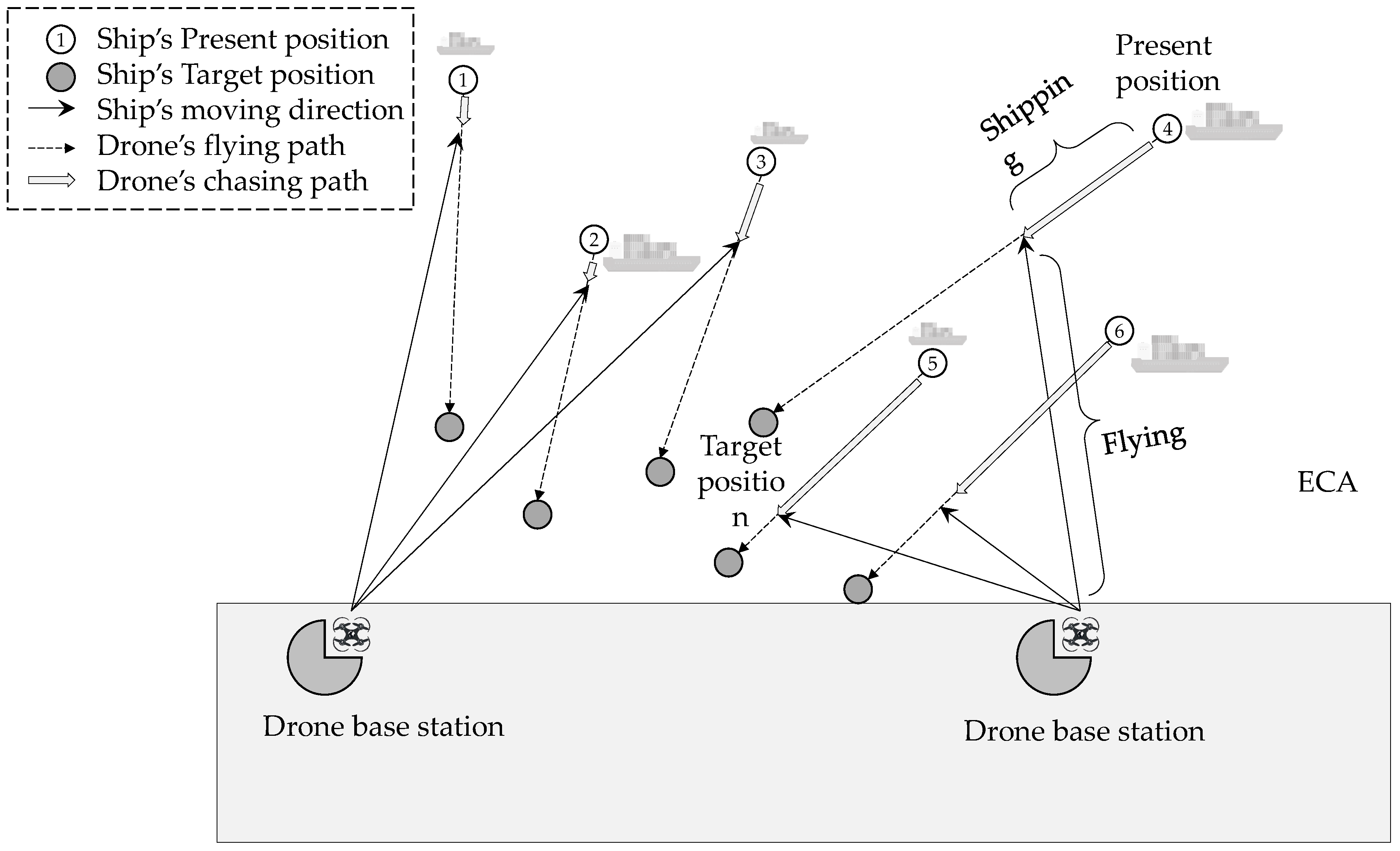
5. Scheduling Drones for Mobile Ships
5.1. Problem Statement
5.2. Formulation
6. Numerical Experiments
6.1. Parameter Estimation
6.2. Dataset Generation
6.3. Experimental Results
6.3.1. Demonstration of [M1] and [M3]
6.3.2. Comparing [M1] and [M3]
6.3.3. Sensitivity Analysis of Speeds via Solving [M3]
6.4. Discussion and Managerial Implications
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J.H.; Duru, O.; Law, A.W.K. Assessment of atmospheric pollutant emissions with maritime energy strategies using bayesian simulations and time series forecasting. Environ. Pollut. 2021, 270, 116068. [Google Scholar] [CrossRef]
- Bacalja, B.; Krcum, M.; Sliskovic, M. A Line Ship Emissions while Manoeuvring and Hotelling-A Case Study of Port Split. J. Mar. Sci. Eng. 2020, 8, 953. [Google Scholar] [CrossRef]
- Fan, L.X.; Gu, B.M.; Luo, M.F. A cost-benefit analysis of fuel-switching vs. hybrid scrubber installation: A container route through the Chinese SECA case. Transp. Policy 2020, 99, 336–344. [Google Scholar] [CrossRef]
- Huang, L.; Wen, Y.Q.; Zhang, Y.M.; Zhou, C.H.; Zhang, F.; Yang, T.T. Dynamic calculation of ship exhaust emissions based on real-time AIS data. Transp. Res. Part D-Transp. Environ. 2020, 80, 102277. [Google Scholar] [CrossRef]
- Anand, A.; Wei, P.; Gali, N.K.; Sun, L.; Yang, F.H.; Westerdahl, D.; Zhang, Q.; Deng, Z.Q.; Wang, Y.; Liu, D.G.; et al. Protocol development for real-time ship fuel sulfur content determination using drone based plume sniffing microsensor system. Sci. Total Environ. 2020, 744, 140885. [Google Scholar] [CrossRef]
- Tovar, B.; Tichavska, M. Environmental cost and eco-efficiency from vessel emissions under diverse SOx regulatory frameworks: A special focus on passenger port hubs. Transp. Res. Part D-Transp. Environ. 2019, 69, 1–12. [Google Scholar] [CrossRef]
- Sun, Y.L.; Yang, L.X.; Zheng, J.F. Emission control areas: More or fewer? Transp. Res. Part D-Transp. Environ. 2020, 84, 102349. [Google Scholar] [CrossRef]
- Chang, Y.T.; Park, H.; Lee, S.; Kim, E. Have Emission Control Areas (ECAs) harmed port efficiency in Europe? Transp. Res. Part D-Transp. Environ. 2018, 58, 39–53. [Google Scholar] [CrossRef]
- Zhen, L.; Li, M.; Hu, Z.; Lv, W.Y.; Zhao, X. The effects of emission control area regulations on cruise shipping. Transp. Res. Part D-Transp. Environ. 2018, 62, 47–63. [Google Scholar] [CrossRef]
- Chen, L.Y.; Yip, T.L.; Mou, J.M. Provision of Emission Control Area and the impact on shipping route choice and ship emissions. Transp. Res. Part D-Transp. Environ. 2018, 58, 280–291. [Google Scholar] [CrossRef]
- Carr, E.W.; Corbett, J.J. Ship Compliance in Emission Control Areas: Technology Costs and Policy Instruments. Environ. Sci. Technol. 2015, 49, 9584–9591. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.H.; Hao, S.F.; Ma, D.F.; Wang, D.H.; Jin, S.; Qu, F.Z. Scheduling decision model of liner shipping considering emission control areas regulations. Appl. Ocean. Res. 2021, 106, 102416. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, X.Q.; Xue, H.L.; Li, J.; Gong, Y. An evolutionary game model analysis on emission control areas in China. Mar. Policy 2020, 118, 104010. [Google Scholar] [CrossRef]
- Cariou, P.; Cheaitou, A.; Larbi, R.; Hamdan, S. Liner shipping network design with emission control areas: A genetic algorithm-based approach. Transp. Res. Part D-Transp. Environ. 2018, 63, 604–621. [Google Scholar] [CrossRef]
- Abioye, O.F.; Dulebenets, M.A.; Pasha, J.; Kavoosi, M. A Vessel Schedule Recovery Problem at the Liner Shipping Route with Emission Control Areas. Energies 2019, 12, 2380. [Google Scholar] [CrossRef]
- Tian, X.C.; Yan, R.; Qi, J.W.; Zhuge, D.; Wang, H. A Bi-Level Programming Model for China’s Marine Domestic Emission Control Area Design. Sustainability 2022, 14, 3562. [Google Scholar] [CrossRef]
- Dong, G.; Lee, P.T.W. Environmental effects of emission control areas and reduced speed zones on container ship operation. J. Clean. Prod. 2020, 274, 122582. [Google Scholar] [CrossRef]
- Ma, W.H.; Lu, T.F.; Ma, D.F.; Wang, D.H.; Qu, F.Z. Ship route and speed multi-objective optimization considering weather conditions and emission control area regulations. Marit. Policy Manag. 2021, 48, 1053–1068. [Google Scholar] [CrossRef]
- Li, L.Y.; Pan, Y.; Gao, S.X.; Yang, W.G. An innovative model to design extreme emission control areas (ECAs) by considering ship?s evasion strategy. Ocean. Coast. Manag. 2022, 227, 106289. [Google Scholar] [CrossRef]
- Sheng, D.; Meng, Q.; Li, Z.C. Optimal vessel speed and fleet size for industrial shipping services under the emission control area regulation. Transp. Res. Part C-Emerg. Technol. 2019, 105, 37–53. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, H.Y.; Wan, Z. Evaluation on the effectiveness of ship emission control area policy: Heterogeneity detection with the regression discontinuity method. Environ. Impact Assess. Rev. 2022, 94, 106747. [Google Scholar] [CrossRef]
- Wang, X.; Pang, Y.; Wang, H.; Shen, C.Q.; Wang, X. Emission Control in River Network System of the Taihu Basin for Water Quality Assurance of Water Environmentally Sensitive Areas. Sustainability 2017, 9, 301. [Google Scholar] [CrossRef]
- Cui, H.; Notteboom, T. Modelling emission control taxes in port areas and port privatization levels in port competition and co-operation sub-games. Transp. Res. Part D-Transp. Environ. 2017, 56, 110–128. [Google Scholar] [CrossRef]
- Wan, Z.; Zhou, X.J.; Zhang, Q.; Chen, J.H. Do ship emission control areas in China reduce sulfur dioxide concentrations in local air? A study on causal effect using the difference-in-difference model. Mar. Pollut. Bull. 2019, 149, 110506. [Google Scholar] [CrossRef]
- Kuzniar, M.; Pawlak, M.; Orkisz, M. Comparison of Pollutants Emission for Hybrid Aircraft with Traditional and Multi-Propeller Distributed Propulsion. Sustainability 2022, 14, 15076. [Google Scholar] [CrossRef]
- Yi, W.; Sutrisna, M. Drone scheduling for construction site surveillance. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 3–13. [Google Scholar] [CrossRef]
- Hassija, V.; Saxena, V.; Chamola, V. Scheduling drone charging for multi-drone network based on consensus time-stamp and game theory. Comput. Commun. 2020, 149, 51–61. [Google Scholar] [CrossRef]
- Torabbeigi, M.; Lim, G.J.; Kim, S.J. Drone Delivery Scheduling Optimization Considering Payload-induced Battery Consumption Rates. J. Intell. Robot. Syst. 2020, 97, 471–487. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Matheuristic algorithms for the parallel drone scheduling traveling salesman problem. Ann. Oper. Res. 2020, 289, 211–226. [Google Scholar] [CrossRef]
- Chowdhery, A.; Jamieson, K. Aerial Channel Prediction and User Scheduling in Mobile Drone Hotspots. IEEE-Acm Trans. Netw. 2018, 26, 2679–2692. [Google Scholar] [CrossRef]
- Torabbeigi, M.; Lim, G.J.; Ahmadian, N.; Kim, S.J. An Optimization Approach to Minimize the Expected Loss of Demand Considering Drone Failures in Drone Delivery Scheduling. J. Intell. Robot. Syst. 2021, 102, 22. [Google Scholar] [CrossRef]
- Kim, S.J.; Lim, G.J.; Cho, J. Drone flight scheduling under uncertainty on battery duration and air temperature. Comput. Ind. Eng. 2018, 117, 291–302. [Google Scholar] [CrossRef]
- Kim, S.J.; Lim, G.J. A Hybrid Battery Charging Approach for Drone-Aided Border Surveillance Scheduling. Drones 2018, 2, 38. [Google Scholar] [CrossRef]
- Park, H.J.; Mirjalili, R.; Cote, M.J.; Lim, G.J. Scheduling Diagnostic Testing Kit Deliveries with the Mothership and Drone Routing Problem. J. Intell. Robot. Syst. 2022, 105, 38. [Google Scholar] [CrossRef] [PubMed]
- Torky, M.; El-Dosuky, M.; Goda, E.; Snasel, V.; Hassanien, A.E. Scheduling and Securing Drone Charging System Using Particle Swarm Optimization and Blockchain Technology. Drones 2022, 6, 237. [Google Scholar] [CrossRef]
- Gentili, M.; Mirchandani, P.B.; Agnetis, A.; Ghelichi, Z. Locating platforms and scheduling a fleet of drones for emergency delivery of perishable items. Comput. Ind. Eng. 2022, 168, 108057. [Google Scholar] [CrossRef]
- Jung, H.; Kim, J. Drone scheduling model for delivering small parcels to remote islands considering wind direction and speed. Comput. Ind. Eng. 2022, 163, 107784. [Google Scholar] [CrossRef]
- Salama, M.R.; Srinivas, S. Collaborative truck multi-drone routing and scheduling problem: Package delivery with flexible launch and recovery sites. Transp. Res. Part E-Logist. Transp. Rev. 2022, 164, 102788. [Google Scholar] [CrossRef]
- Su, Y.; Wang, S.J.; Cheng, Q.N.; Qiu, Y.H. Buffer evaluation model and scheduling strategy for video streaming services in 5G-powered drone using machine learning. Eurasip J. Image Video Process. 2021, 2021, 29. [Google Scholar] [CrossRef]
- Liu, C.; Chen, H.P.; Li, X.P.; Liu, Z.Y. A scheduling decision support model for minimizing the number of drones with dynamic package arrivals and personalized deadlines. Expert Syst. Appl. 2021, 167, 114157. [Google Scholar] [CrossRef]
- Asadi, A.; Pinkley, S.N. A Monotone Approximate Dynamic Programming Approach for the Stochastic Scheduling, Allocation, and Inventory Replenishment Problem: Applications to Drone and Electric Vehicle Battery Swap Stations. Transp. Sci. 2022, 56, 1085–1110. [Google Scholar] [CrossRef]
- Krichen, M.; Adoni, W.Y.H.; Mihoub, A.; Alzahrani, M.Y.; Nahhal, T. Security Challenges for Drone Communications: Possible Threats, Attacks and Countermeasures. In Proceedings of the 2nd International Conference of Smart Systems and Emerging Technologies (SMARTTECH), Riyadh, Saudi Arabia, 9–11 May 2022; pp. 184–189. [Google Scholar]
- Bunse, C.; Plotz, S. Security Analysis of Drone Communication Protocols. In Engineering Secure Software and Systems. ESSoS 2018. Lecture Notes in Computer Science; Payer, M., Rashid, A., Such, J., Eds.; Springer: Cham, Switzerland, 2018; Volume 10953. [Google Scholar]
- Yang, H.; Yuan, J.; Li, C.; Zhao, G.; Sun, Z.; Yao, Q.; Bao, B.; Vasilakos, A.V.; Zhang, J. BrainIoT: Brain-Like Productive Services Provisioning With Federated Learning in Industrial IoT. IEEE Internet Things J. 2022, 9, 2014–2024. [Google Scholar] [CrossRef]
- Li, C.; Yang, H.; Sun, Z.; Yao, Q.; Bao, B.; Zhang, J.; Vasilakos, A.V. Federated Hierarchical Trust-Based Interaction Scheme for Cross-Domain Industrial IoT. IEEE Internet Things J. 2023, 10, 447–457. [Google Scholar] [CrossRef]

| Study | Research Problem | Method | Region/Port |
|---|---|---|---|
| [7] | An ECA location problem minimizes the impact of sulfur emissions on human health. | MILP | China + Africa |
| [8] | Impacts of ECA regulations on port efficiency. | DEA | EU + North America |
| [9] | Reduction in fuel costs by rescheduling voyage plans, speeds, and sailing patterns. | MILP + Tabu | - |
| [10] | The impacts of ECAs on global shipping; route-choosing behavior of liner shipping through ECAs. | A | Mediterranean Sea |
| [11] | Impacts of Panama Canal Authority pollution tax on emissions from ships transiting the Panama Canal. | A | Panama Canal |
| [12] | Rescheduling of ports-of-call sequences, ship routes, and speed to minimize total sailing costs. | NLP + GA | North America |
| [13] | Coordination of ECA programs to align conflict interests between governments and shipping companies. | EGT | China |
| [14] | The trade-off between cost and emission (CO2 and SOx) reduction considering ECAs. | MILP + GA | - |
| [15] | Green vessel schedule recovery strategies, including vessel sailing speed adjustment and port skipping. | NLP | - |
| [16] | Assessment of the effect of China’s ECA policy and determination of the optimal ECA width. | BLP | China |
| [17] | Examination of dual environmental effects of ECAs on liner service markets. | A | Shanghai + Persian Gulf |
| [18] | The undertaking of route and speed optimization to simultaneously reduce sailing cost and time, considering ECA regulations and weather conditions. | MOP + TOPSIS | US Coast |
| [19] | ECA boundary design and emission reduction assessment. | NLP | North America |
| [20] | Optimization of vessel speeds and ship fleet sizes considering ECAs. | NLP | |
| [21] | Investigation of potentially varying effectiveness of ECA policies in port cities located in a specific region. | A | China |
| [22] | A total emission control method with an emphasis on environmentally sensitive water areas. | A | Yangtze Delta |
| [23] | Impacts of emission tax on vessel and port operations for emission control in port areas. | GT | - |
| [24] | Impacts of ECAs on reduction in SO2 concentrations. | A | China |
| Study | Research Problem | Methods | Scenario |
|---|---|---|---|
| [26] | The flying speed of the drone is optimized while ensuring that it completes the route within a specific time and without depleting its battery. | NLP + DP | Surveillance |
| [27] | Energy trading between the drones and charging station. | GT | Delivery |
| [28] | A parcel delivery system using drones. | MILP + H | Delivery |
| [29] | Parallel drone-scheduling-oriented traveling salesman problem; a set of customers requiring a delivery is split between a truck and a fleet of drones. | MILP + H | Delivery |
| [30] | Drone mobility in the lateral or vertical path leads to a time-selective and frequency-selective wireless channel for a low-altitude drone. | A | Communication |
| [31] | A drone-based delivery-scheduling method considering drone failures to minimize the expected loss of demand. | SA | Delivery |
| [32] | Drone flight scheduling under uncertainty of battery duration and air temperature. | ML | - |
| [33] | A hybrid battery-charging approach with dynamic wireless charging systems. | NLP | - |
| [34] | A drone-based diagnostic testing kit delivery-scheduling problem with one truck and multiple drones. | H | Emergency delivery |
| [35] | Authentication of drones and verification of their charging transactions with charging stations. | PSO + GT | - |
| [36] | Delivery of perishable items to remote areas accessible only by helicopters or drones. | A | Emergency delivery |
| [37] | A drone-scheduling problem regarding the delivery of small parcels to remote islands considering wind direction and speed. | RO | Island delivery |
| [38] | Coordinating a truck and multiple heterogeneous drones for last-mile package deliveries. | SA + VNS VNS | Delivery |
| [39] | 5G-powered drone video transmission. | ML | Video streaming |
| [40] | On-time delivery of packages. | MILP GA + PSO | Warehouse |
| [41] | Deriving actions at a battery swap station when explicitly considering the uncertain arrival of swap demand, battery degradation, and replacement. | DP | Delivery |
| I | Xi/km | Yi/km | Vi(m/s) | I | Xi/km | Yi/km | Vi(m/s) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 9 | 8 | 7 | 4 | 6 | 11 | 10 | 12 | 7 | 4 | 5 |
| 2 | 4 | 4 | 9 | 5 | 8 | 12 | 8 | 1 | 7 | 4 | 9 |
| 3 | 15 | 14 | 7 | 4 | 6 | 13 | 4 | 4 | 8 | 4 | 7 |
| 4 | 0 | 17 | 8 | 5 | 7 | 14 | 19 | 18 | 7 | 6 | 5 |
| 5 | 17 | 19 | 9 | 6 | 5 | 15 | 16 | 13 | 7 | 6 | 8 |
| 6 | 16 | 13 | 7 | 6 | 6 | 16 | 4 | 11 | 7 | 5 | 8 |
| 7 | 17 | 5 | 8 | 5 | 6 | 17 | 15 | 10 | 9 | 5 | 6 |
| 8 | 8 | 13 | 7 | 6 | 5 | 18 | 11 | 9 | 7 | 4 | 7 |
| 9 | 9 | 19 | 9 | 6 | 7 | 19 | 11 | 15 | 9 | 4 | 6 |
| 10 | 0 | 13 | 7 | 4 | 8 | 20 | 1 | 18 | 9 | 6 | 5 |
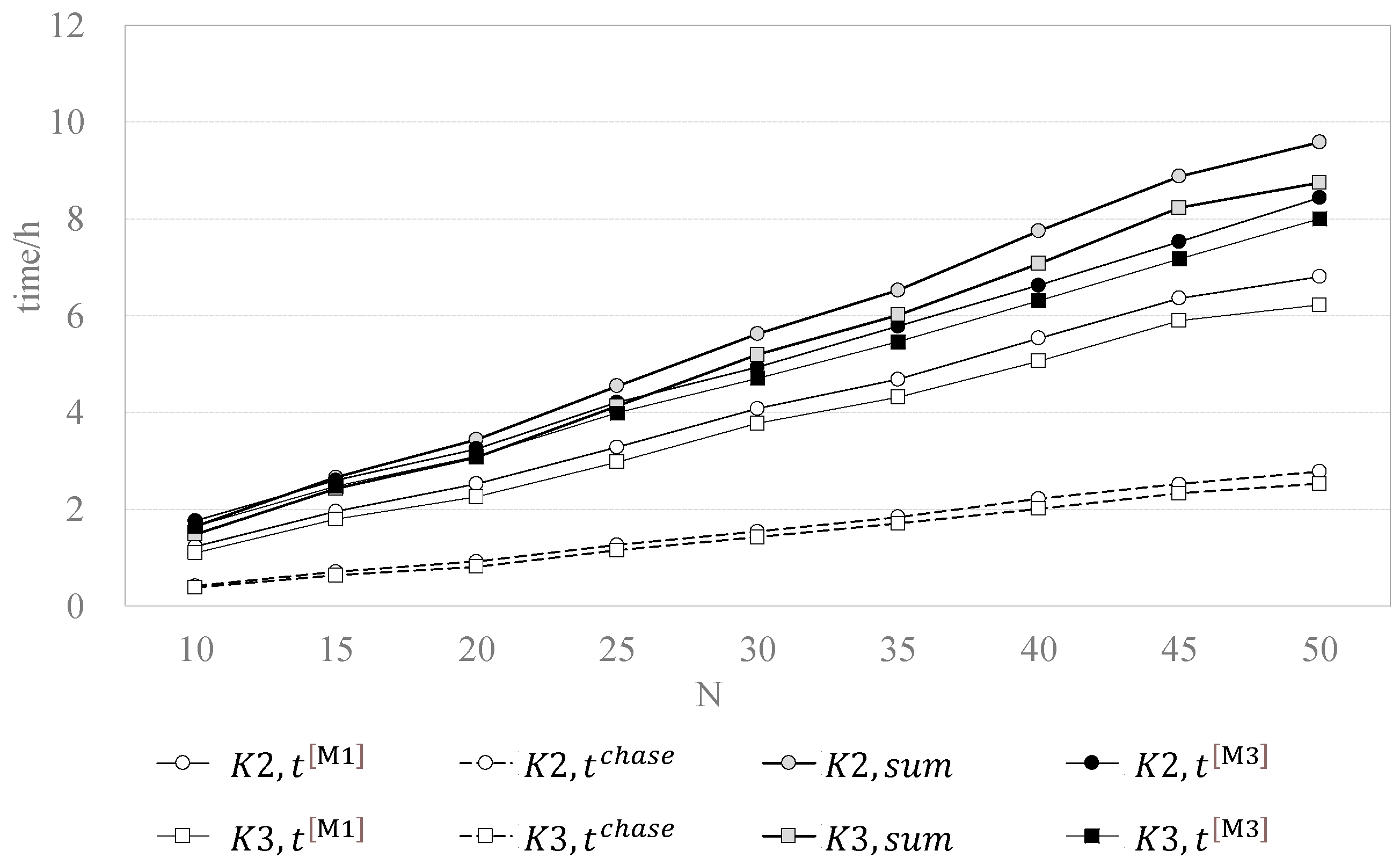
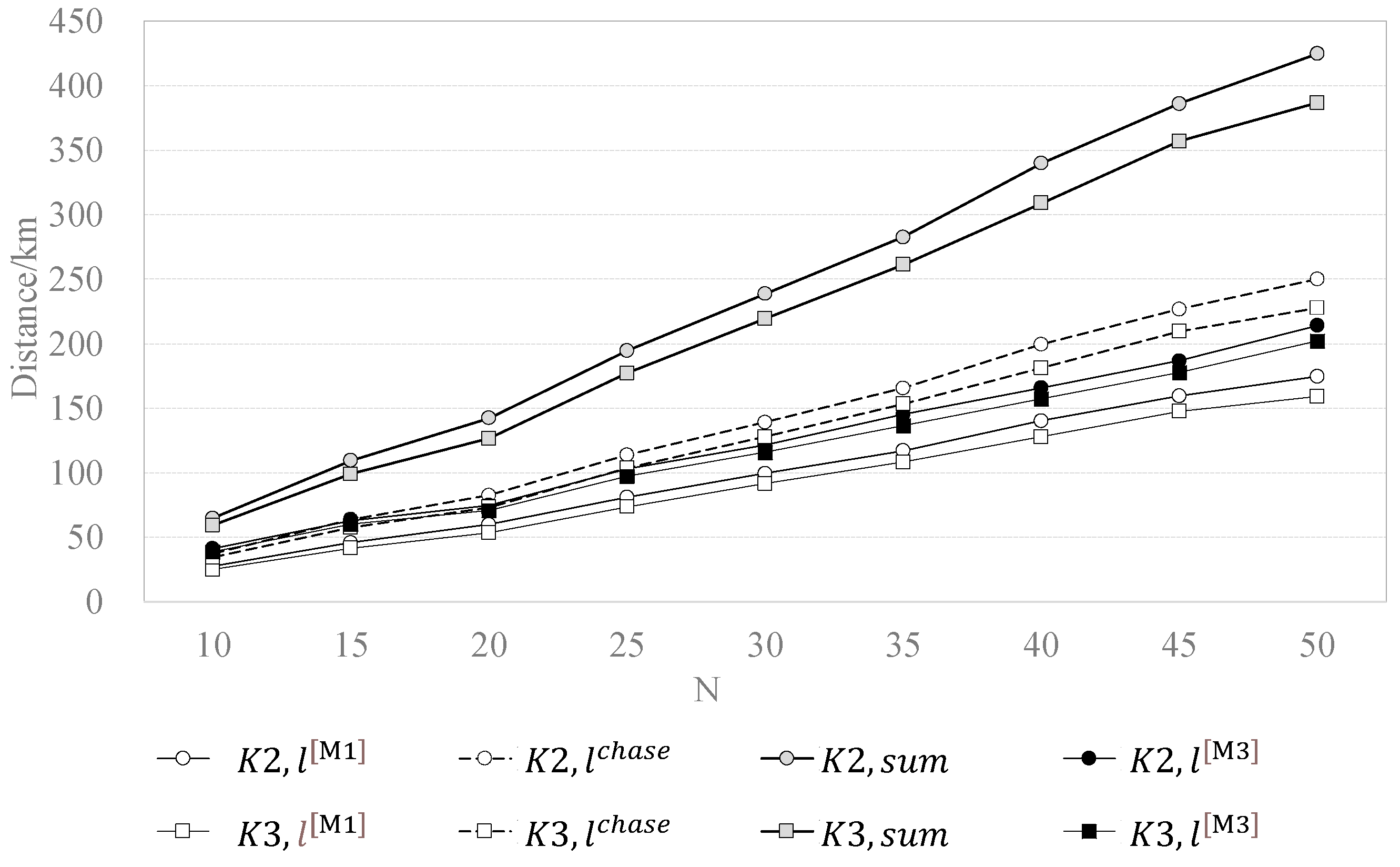
| Solving | t[M ]/h | tchase/h | Sum/h | l[M ]/km | lchase/km | Sum/km |
|---|---|---|---|---|---|---|
| [M1] | 2.524 | 0.856 | 3.381 | 56.886 | 77.069 | 133.955 |
| [M3] | 1.991 | 0 | 1.991 | 46.227 | 0 | 46.227 |
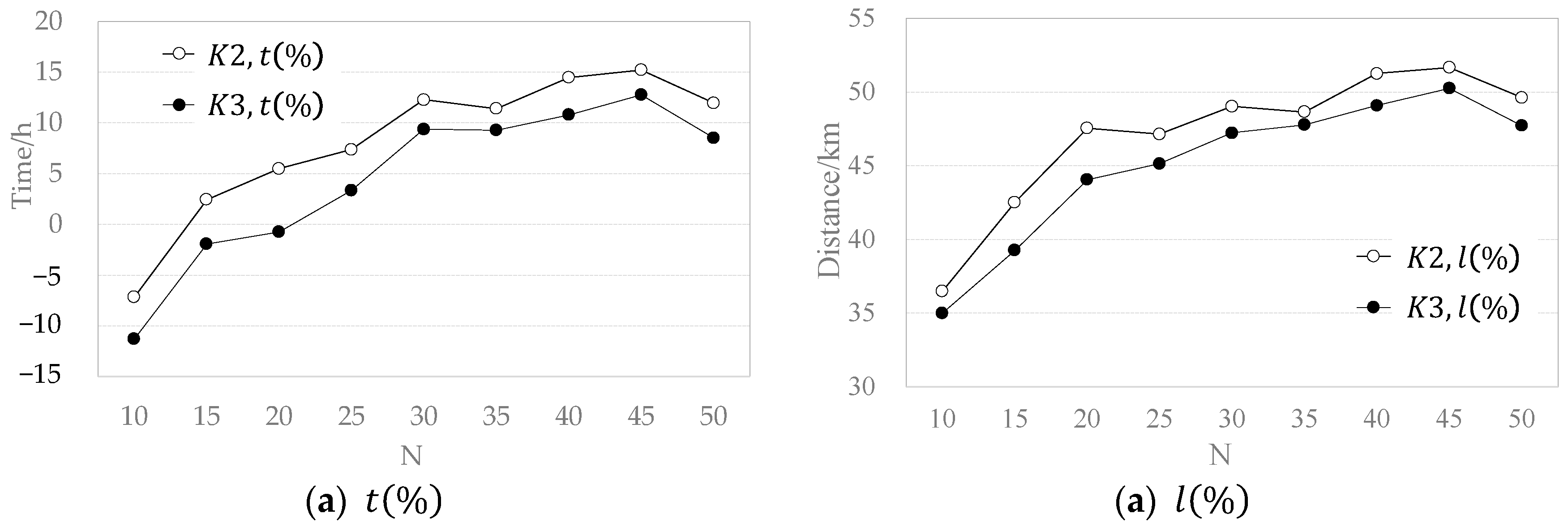
| K | N | t[M1] | tchase | Sum | l[M1] | lchase | Sum | t[M3] | l[M3] | t(%) | l(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| h | h | h | km | km | km | h | km | % | % | ||
| 2 | 10 | 1.23 | 0.42 | 1.65 | 27.40 | 37.36 | 64.75 | 6.35 | 41.12 | −7.17 | 36.50 |
| 2 | 15 | 1.95 | 0.71 | 2.66 | 45.69 | 63.79 | 109.48 | 9.35 | 62.93 | 2.45 | 42.52 |
| 2 | 20 | 2.52 | 0.92 | 3.44 | 59.84 | 82.49 | 142.33 | 11.70 | 74.65 | 5.51 | 47.55 |
| 2 | 25 | 3.29 | 1.26 | 4.55 | 80.87 | 113.68 | 194.55 | 15.16 | 102.85 | 7.39 | 47.14 |
| 2 | 30 | 4.08 | 1.55 | 5.63 | 99.41 | 139.11 | 238.52 | 17.77 | 121.58 | 12.31 | 49.03 |
| 2 | 35 | 4.69 | 1.84 | 6.53 | 117.02 | 165.52 | 282.54 | 20.81 | 145.07 | 11.41 | 48.65 |
| 2 | 40 | 5.53 | 2.22 | 7.75 | 140.28 | 199.49 | 339.77 | 23.86 | 165.62 | 14.49 | 51.26 |
| 2 | 45 | 6.36 | 2.52 | 8.88 | 159.38 | 226.60 | 385.97 | 27.10 | 186.57 | 15.22 | 51.66 |
| 2 | 50 | 6.81 | 2.78 | 9.58 | 174.55 | 250.12 | 424.67 | 30.38 | 213.94 | 11.97 | 49.62 |
| 3 | 10 | 1.10 | 0.38 | 1.48 | 25.02 | 34.38 | 59.40 | 5.93 | 38.61 | −11.31 | 35.01 |
| 3 | 15 | 1.79 | 0.64 | 2.43 | 41.41 | 57.54 | 98.94 | 8.92 | 60.09 | −1.93 | 39.27 |
| 3 | 20 | 2.26 | 0.81 | 3.07 | 53.27 | 73.23 | 126.50 | 11.14 | 70.76 | −0.75 | 44.06 |
| 3 | 25 | 2.98 | 1.15 | 4.13 | 73.60 | 103.59 | 177.18 | 14.37 | 97.19 | 3.35 | 45.15 |
| 3 | 30 | 3.78 | 1.42 | 5.20 | 91.52 | 127.81 | 219.34 | 16.96 | 115.73 | 9.40 | 47.23 |
| 3 | 35 | 4.32 | 1.70 | 6.02 | 108.13 | 153.17 | 261.30 | 19.65 | 136.45 | 9.29 | 47.78 |
| 3 | 40 | 5.06 | 2.01 | 7.07 | 127.64 | 181.11 | 308.76 | 22.72 | 157.18 | 10.80 | 49.09 |
| 3 | 45 | 5.90 | 2.33 | 8.23 | 147.50 | 209.50 | 357.01 | 25.83 | 177.60 | 12.78 | 50.25 |
| 3 | 50 | 6.22 | 2.53 | 8.75 | 159.05 | 227.62 | 386.67 | 28.82 | 202.15 | 8.52 | 47.72 |
| K | N | t[M3]/h | l[M3]/km | ||||
|---|---|---|---|---|---|---|---|
| −5% | Vi/100% | 5% | −5% | Vi/100% | 5% | ||
| 2 | 10 | −0.73 | 1.76 | 0.71 | 4.28 | 41.12 | −4.22 |
| 2 | 15 | −0.43 | 2.60 | 0.46 | 4.57 | 62.93 | −4.77 |
| 2 | 20 | −0.63 | 3.25 | 0.61 | 4.37 | 74.65 | −4.32 |
| 2 | 25 | −0.62 | 4.21 | 0.60 | 4.41 | 102.85 | −4.37 |
| 2 | 30 | −0.76 | 4.94 | 0.74 | 4.26 | 121.58 | −4.21 |
| 2 | 35 | −0.60 | 5.78 | 0.58 | 4.41 | 145.07 | −4.37 |
| 2 | 40 | −0.57 | 6.63 | 0.55 | 4.44 | 165.62 | −4.40 |
| 2 | 45 | −0.65 | 7.53 | 0.63 | 4.35 | 186.57 | −4.30 |
| 2 | 50 | −0.71 | 8.44 | 0.69 | 4.30 | 213.94 | −4.25 |
| 3 | 10 | −0.67 | 1.65 | 0.65 | 4.36 | 38.61 | −4.31 |
| 3 | 15 | −0.56 | 2.48 | 0.61 | 4.41 | 60.09 | −4.41 |
| 3 | 20 | −0.68 | 3.09 | 0.69 | 4.43 | 70.76 | −4.22 |
| 3 | 25 | −0.67 | 3.99 | 0.68 | 4.35 | 97.19 | −4.12 |
| 3 | 30 | −0.79 | 4.71 | 0.79 | 4.23 | 115.73 | −4.14 |
| 3 | 35 | −0.67 | 5.46 | 0.68 | 4.24 | 136.45 | −4.26 |
| 3 | 40 | −0.62 | 6.31 | 0.60 | 4.39 | 157.18 | −4.35 |
| 3 | 45 | −0.68 | 7.18 | 0.68 | 4.28 | 177.60 | −4.24 |
| 3 | 50 | −0.74 | 8.01 | 0.72 | 4.28 | 202.15 | −4.17 |
| K | N | t[M3]/h | l[M3]/km | ||||
|---|---|---|---|---|---|---|---|
| −5% | Vk/100% | 5% | −5% | Vk/100% | 5% | ||
| 2 | 10 | −0.73 | 1.76 | 0.71 | 4.28 | 41.12 | −4.22 |
| 2 | 15 | −0.43 | 2.60 | 0.46 | 4.57 | 62.93 | −4.77 |
| 2 | 20 | −0.63 | 3.25 | 0.61 | 4.37 | 74.65 | −4.32 |
| 2 | 25 | −0.62 | 4.21 | 0.60 | 4.41 | 102.85 | −4.37 |
| 2 | 30 | −0.76 | 4.94 | 0.74 | 4.26 | 121.58 | −4.21 |
| 2 | 35 | −0.60 | 5.78 | 0.58 | 4.41 | 145.07 | −4.37 |
| 2 | 40 | −0.57 | 6.63 | 0.55 | 4.44 | 165.62 | −4.40 |
| 2 | 45 | −0.65 | 7.53 | 0.63 | 4.35 | 186.57 | −4.30 |
| 2 | 50 | −0.71 | 8.44 | 0.69 | 4.30 | 213.94 | −4.25 |
| 3 | 10 | −0.67 | 1.65 | 0.65 | 4.36 | 38.61 | −4.31 |
| 3 | 15 | −0.56 | 2.48 | 0.61 | 4.41 | 60.09 | −4.41 |
| 3 | 20 | −0.68 | 3.09 | 0.69 | 4.43 | 70.76 | −4.22 |
| 3 | 25 | −0.67 | 3.99 | 0.68 | 4.35 | 97.19 | −4.12 |
| 3 | 30 | −0.79 | 4.71 | 0.79 | 4.23 | 115.73 | −4.14 |
| 3 | 35 | −0.67 | 5.46 | 0.68 | 4.24 | 136.45 | −4.26 |
| 3 | 40 | −0.62 | 6.31 | 0.60 | 4.39 | 157.18 | −4.35 |
| 3 | 45 | −0.68 | 7.18 | 0.68 | 4.28 | 177.60 | −4.24 |
| 3 | 50 | −0.74 | 8.01 | 0.72 | 4.28 | 202.15 | −4.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.-H.; Liu, T.-C.; Tian, X.-D. Scheduling Drones for Ship Emission Detection from Multiple Stations. Drones 2023, 7, 158. https://doi.org/10.3390/drones7030158
Hu Z-H, Liu T-C, Tian X-D. Scheduling Drones for Ship Emission Detection from Multiple Stations. Drones. 2023; 7(3):158. https://doi.org/10.3390/drones7030158
Chicago/Turabian StyleHu, Zhi-Hua, Tian-Ci Liu, and Xi-Dan Tian. 2023. "Scheduling Drones for Ship Emission Detection from Multiple Stations" Drones 7, no. 3: 158. https://doi.org/10.3390/drones7030158
APA StyleHu, Z.-H., Liu, T.-C., & Tian, X.-D. (2023). Scheduling Drones for Ship Emission Detection from Multiple Stations. Drones, 7(3), 158. https://doi.org/10.3390/drones7030158







