Control Algorithms, Kalman Estimation and Near Actual Simulation for UAVs: State of Art Perspective
Abstract
1. Introduction
1.1. Objective and Contents
1.2. Paper Organization
2. Relevant Studies
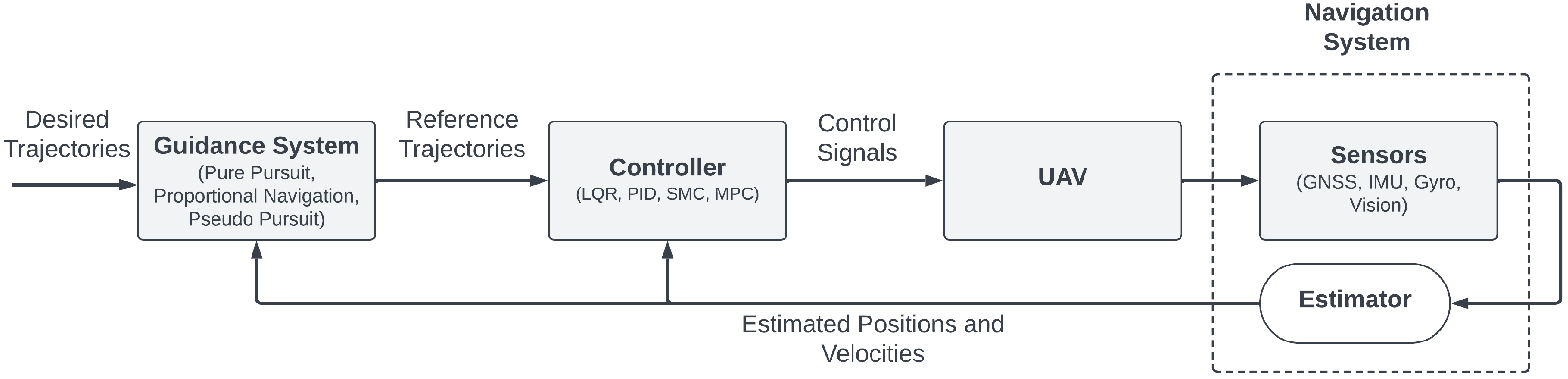
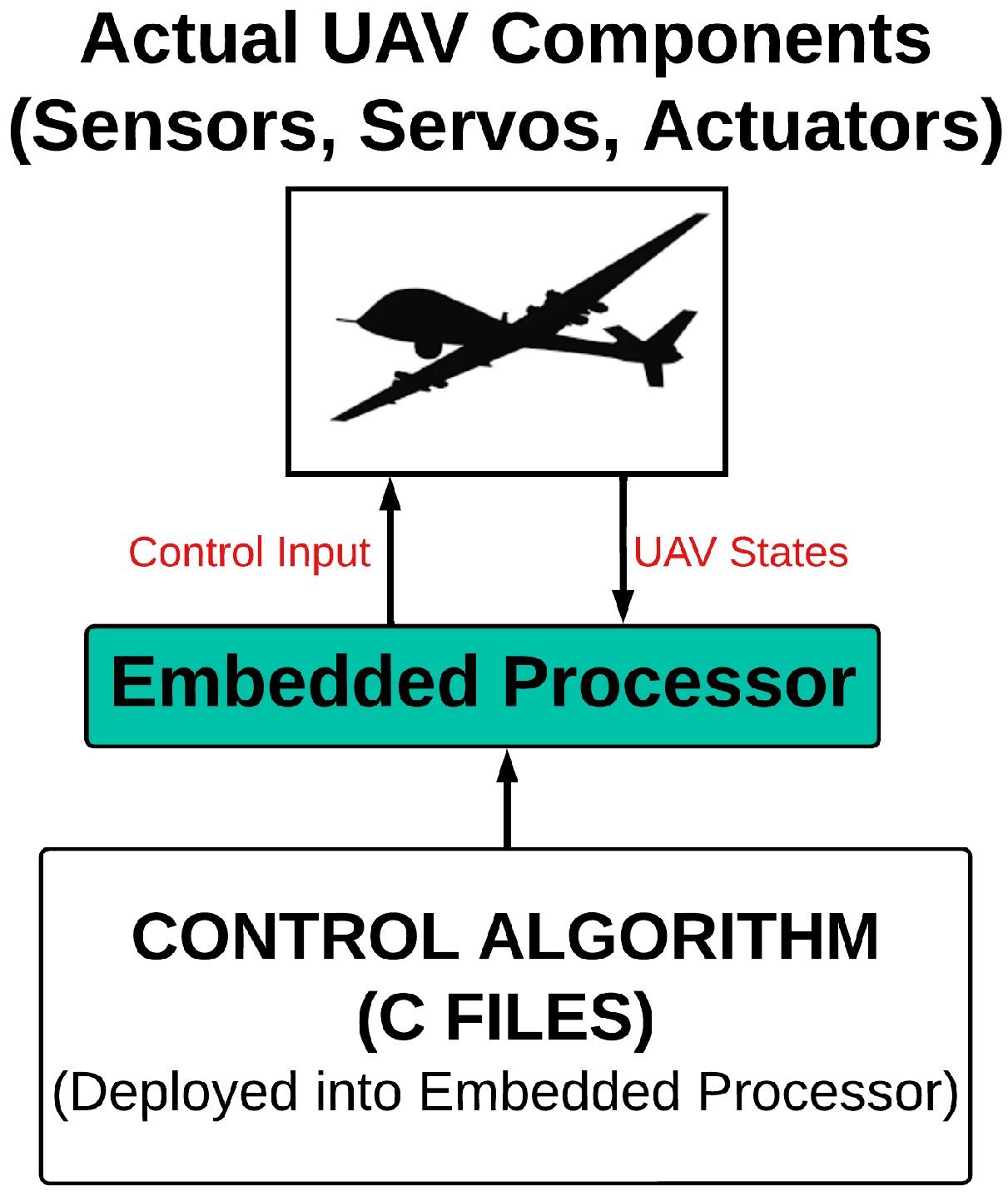
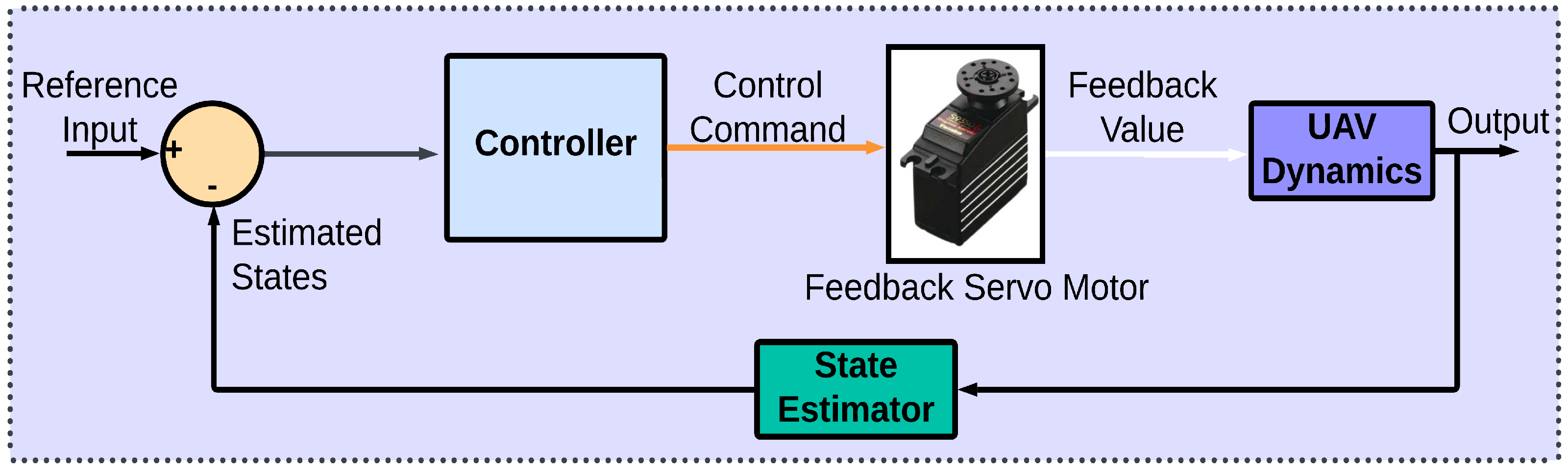
3. UAV Dynamic Modeling and Control Architecture
3.1. Flight Control Algorithms
4. Exploration of State Estimation Techniques
5. Simulation and User Adaptation Techniques
5.1. Realistic Simulation Techniques
5.2. User Adaptation Techniques
6. Existing Challenges and Way Forward
Future Work Directions
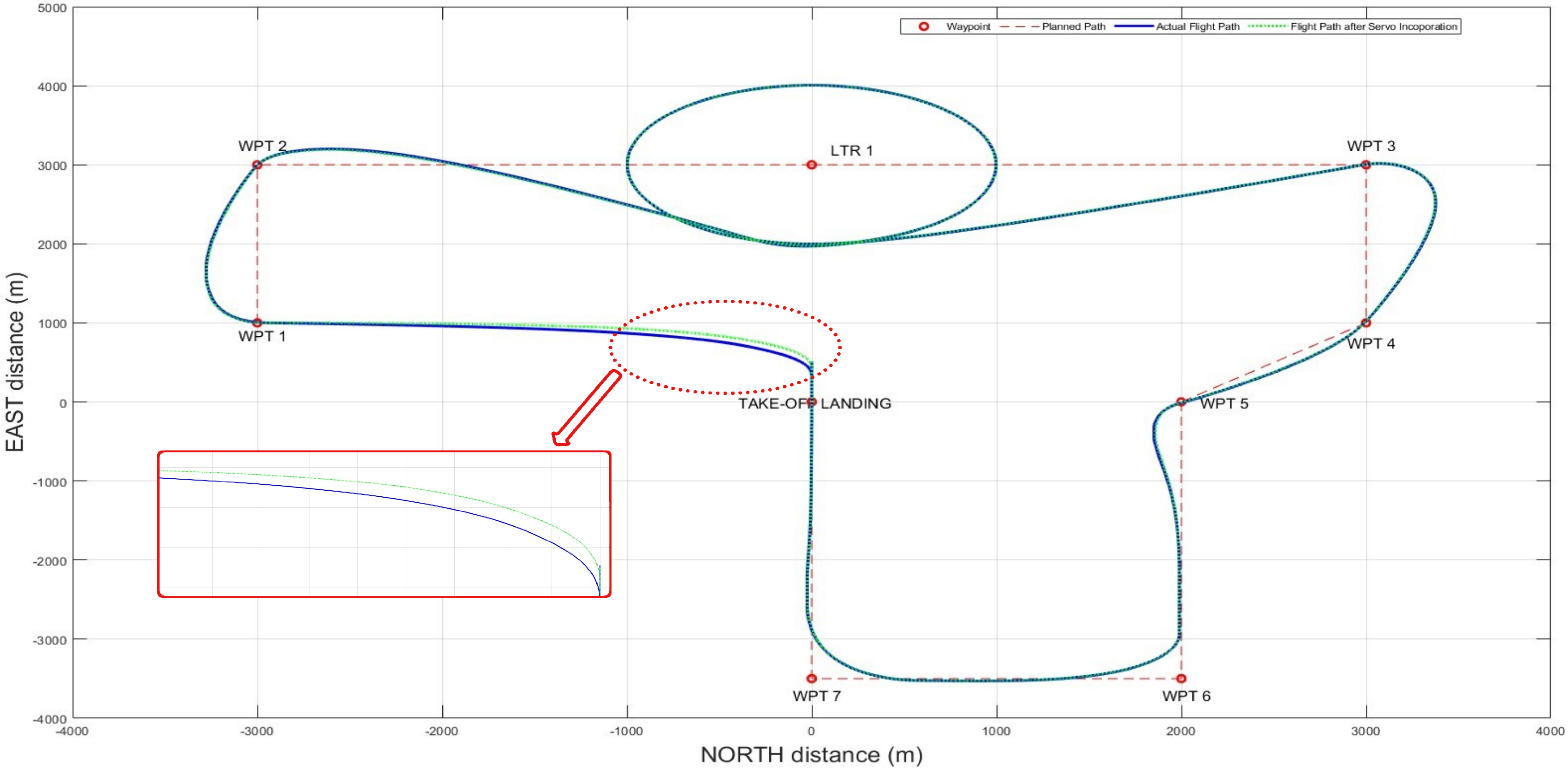
Illustration for Further Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mir, I.; Gul, F.; Eisa, S.; Maqsood, A.; Mir, S. Contraction analysis of dynamic soaring. In Proceedings of the American Institute of Aeronautics and Astronautics Science and Technology (AIAA SCITECH), San Diego, CA, USA, 3–7 January 2022; p. 0881. [Google Scholar]
- Mir, I.; Gul, F.; Eisa, S.; Taha, H.E.; Mir, S. On the stability of dynamic soaring: Floquet-based investigation. In Proceedings of the American Institute of Aeronautics and Astronautics Science and Technology (AIAA SCITECH), San Diego, CA, USA, 3–7 January 2022; p. 0882. [Google Scholar]
- Mir, I.; Maqsood, A.; Eisa, S.A.; Taha, H.; Akhtar, S. Optimal morphing–Augmented dynamic soaring maneuvers for unmanned air vehicle capable of span and sweep morphologies. Aerosp. Sci. Technol. 2018, 79, 17–36. [Google Scholar] [CrossRef]
- Mir, I.; Taha, H.; Eisa, S.A.; Maqsood, A. A controllability perspective of dynamic soaring. Nonlinear Dyn. 2018, 94, 2347–2362. [Google Scholar] [CrossRef]
- Mir, I.; Maqsood, A.; Akhtar, S. Optimization of dynamic soaring maneuvers to enhance endurance of a versatile UAV. Inst. Phys. Conf. Ser. Mater. Sci. Eng. 2017, 211, 012010. [Google Scholar] [CrossRef]
- Paucar, C.; Morales, L.; Pinto, K.; Sánchez, M.; Rodríguez, R.; Gutierrez, M.; Palacios, L. Use of drones for surveillance and reconnaissance of military areas. In Proceedings of the International Conference of Research Applied to Defense and Security, Salinas, Ecuador, 18–20 April 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 119–132. [Google Scholar] [CrossRef]
- van Lieshout, M.; Friedewald, M. Drones–dull, dirty or dangerous?: The social construction of privacy and security technologies. In Socially Responsible Innovation in Security; Routledge: Oxfordshire, UK, 2018; pp. 25–43. [Google Scholar] [CrossRef]
- Li, H.; Savkin, A.V. Wireless sensor network based navigation of micro flying robots in the industrial internet of things. IEEE Trans. Ind. Inform. 2018, 14, 3524–3533. [Google Scholar] [CrossRef]
- Mir, I.; Eisa, S.A.; Taha, H.; Maqsood, A.; Akhtar, S.; Islam, T.U. A stability perspective of bioinspired unmanned aerial vehicles performing optimal dynamic soaring. Bioinspiration Biomim. 2021, 16, 066010. [Google Scholar] [CrossRef]
- Savkin, A.V.; Huang, H. A method for optimized deployment of a network of surveillance aerial drones. IEEE Syst. J. 2019, 13, 4474–4477. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V. An algorithm of reactive collision free 3-D deployment of networked unmanned aerial vehicles for surveillance and monitoring. IEEE Trans. Ind. Inform. 2019, 16, 132–140. [Google Scholar] [CrossRef]
- Madridano, Á.; Al-Kaff, A.; Martín, D.; de la Escalera, A. Trajectory planning for multi-robot systems: Methods and applications. Expert Syst. Appl. 2021, 173, 114660. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V. Towards the internet of flying robots: A survey. Sensors 2018, 18, 4038. [Google Scholar] [CrossRef]
- Pajares, G. Overview and current status of remote sensing applications based on unmanned aerial vehicles (UAVs). Photogramm. Eng. Remote Sens. 2015, 81, 281–330. [Google Scholar] [CrossRef]
- Chen, Y.; Rosolia, U.; Ames, A.D. Decentralized Task and Path Planning for Multi-Robot Systems. IEEE Robot. Autom. Lett. 2021, 6, 4337–4344. [Google Scholar] [CrossRef]
- Manchester, Z.; Peck, M. Stochastic space exploration with microscale spacecraft. In Proceedings of the American Institute of Aeronautics and Astronautics Science and Technology (AIAA) Guidance Navigation, and Control, Portland, OR, USA, 8–11 August 2011; p. 6648. [Google Scholar]
- Louali, R.; Gacem, H.; Elouardi, A.; Bouaziz, S. Implementation of an UAV Guidance, Navigation and Control System based on the CAN data bus: Validation using a Hardware In the Loop Simulation. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 1418–1423. [Google Scholar]
- Jin, X.B.; Robert Jeremiah, R.J.; Su, T.L.; Bai, Y.T.; Kong, J.L. The new trend of state estimation: From model-driven to hybrid-driven methods. Sensors 2021, 21, 2085. [Google Scholar] [CrossRef]
- Khamseh, H.B.; Janabi-Sharifi, F.; Abdessameud, A. Aerial manipulation—A literature survey. Robot. Auton. Syst. 2018, 107, 221–235. [Google Scholar] [CrossRef]
- Raja, M.M. Extended Kalman Filter and LQR Controller Design for Quadrotor UAVs. Master’s Thesis, Wright State University, Dayton, OH, USA, 2017. [Google Scholar]
- Carnes, T. A Low Cost Implementation of Autonomous Takeoff and Landing for a Fixed Wing UAV. Master’s Thesis, Virginia Commonwealth University, Richmond, VA, USA, 2014. [Google Scholar]
- Kurnaz, S.; Çetin, O. Autonomous navigation and landing tasks for fixed wing small unmanned aerial vehicles. Acta Polytech. Hung. 2010, 7, 87–102. [Google Scholar]
- Mir, I.; Eisa, S.A.; Maqsood, A. Review of dynamic soaring: Technical aspects, nonlinear modeling perspectives and future directions. Nonlinear Dyn. 2018, 94, 3117–3144. [Google Scholar] [CrossRef]
- Mir, I.; Maqsood, A.; Akhtar, S. Biologically inspired dynamic soaring maneuvers for an unmanned air vehicle capable of sweep morphing. Int. J. Aeronaut. Space Sci. 2018, 19, 1006–1016. [Google Scholar] [CrossRef]
- Mir, I.; Maqsood, A.; Akhtar, S. Dynamic modeling & stability analysis of a generic UAV in glide phase. In Proceedings of the Materials science, Engineering and Chemistry (MATEC Web of Conferences). Engineering Design Process (EDP) Sciences, Sibiu, Romania, 7–9 June 2017; Volume 114, p. 01007. [Google Scholar]
- Wadood, A.; Anavatti, S.; Hassanein, O. Robust controller design for an autonomous underwater vehicle. In Proceedings of the 2017 Ninth International Conference on Advanced Computational Intelligence (ICACI), Doha, Qatar, 4–6 February 2017; pp. 237–244. [Google Scholar]
- Gul, F.; Rahiman, W.; Alhady, S.N.; Ali, A.; Mir, I.; Jalil, A. Meta-heuristic approach for solving multi-objective path planning for autonomous guided robot using PSO–GWO optimization algorithm with evolution ary programming. J. Ambient. Intell. Humaniz. Comput. 2020, 12, 7873–7890. [Google Scholar] [CrossRef]
- Gul, F.; Mir, I.; Rahiman, W.; Islam, T.U. Novel Implementation of Multi-Robot Space Exploration Utilizing Coordinated Multi-Robot Exploration and Frequency Modified Whale Optimization Algorithm. IEEE Access 2021, 9, 22774–22787. [Google Scholar] [CrossRef]
- Gul, F.; Mir, I.; Abualigah, L.; Sumari, P.; Forestiero, A. A Consolidated Review of Path Planning and Optimization Techniques: Technical Perspectives and Future Directions. Electronics 2021, 10, 2250. [Google Scholar] [CrossRef]
- Das, P.; Behera, H.; Panigrahi, B. Intelligent-based multi-robot path planning inspired by improved classical Q-learning and improved particle swarm optimization with perturbed velocity. Eng. Sci. Technol. Int. J. 2016, 19, 651–669. [Google Scholar] [CrossRef]
- Gul, F.; Rahiman, W.; Nazli Alhady, S.S. A comprehensive study for robot navigation techniques. Cogent Eng. 2019, 6, 1632046. [Google Scholar] [CrossRef]
- Gul, F.; Mir, I.; Abualigah, L.; Sumari, P. Multi-Robot Space Exploration: An Augmented Arithmetic Approach. IEEE Access 2021, 9, 107738–107750. [Google Scholar] [CrossRef]
- Gul, F.; Mir, S.; Mir, I. Coordinated Multi-Robot Exploration: Hybrid Stochastic Optimization Approach. In Proceedings of the American Institute of Aeronautics and Astronautics Science and Technology (AIAA SCITECH Forum), San Diego, CA, USA, 3–7 January 2022; p. 1414. [Google Scholar]
- Gul, F.; Mir, S.; Mir, I. Multi Robot Space Exploration: A Modified Frequency Whale Optimization Approach. In Proceedings of the American Institute of Aeronautics and Astronautics Science and Technology (AIAA SCITECH Forum), San Diego, CA, USA, 3–7 January 2022; p. 1416. [Google Scholar]
- Szczepanski, R.; Bereit, A.; Tarczewski, T. Efficient Local Path Planning Algorithm Using Artificial Potential Field Supported by Augmented Reality. Energies 2021, 14, 6642. [Google Scholar] [CrossRef]
- Szczepanski, R.; Tarczewski, T. Global path planning for mobile robot based on Artificial Bee Colony and Dijkstra’s algorithms. In Proceedings of the 2021 IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 25–29 April 2021; pp. 724–730. [Google Scholar]
- Kaviyarasu, A.; Saravanakumar, A.; Logavenkatesh, M. Software in Loop Simulation based Waypoint Navigation for Fixed Wing UAV. Def. Sci. J. 2021, 71, 448–455. [Google Scholar] [CrossRef]
- ud Din, A.F.; Mir, I.; Gul, F.; Mir, S.; Saeed, N.; Althobaiti, T.; Abbas, S.M.; Abualigah, L. Deep Reinforcement Learning for integrated non-linear control of autonomous UAVs. Processes 2022, 10, 1307. [Google Scholar] [CrossRef]
- Vidal Morató, J.; Gomáriz Castro, S.; Manuel Lázaro, A. Autonomous Underwater Vehicle control. Instrum. Viewp. 2005, 4, 10. [Google Scholar]
- Dadkhah, N.; Mettler, B. Survey of motion planning literature in the presence of uncertainty: Considerations for UAV guidance. J. Intell. Robot. Syst. 2012, 65, 233–246. [Google Scholar] [CrossRef]
- Puri, A. A Survey of Unmanned Aerial Vehicles (UAV) for Traffic Surveillance; Department of Computer Science and Engineering, University of South Florida: Tampa, FL, USA, 2005; pp. 1–29. [Google Scholar]
- Ollero, A.; Merino, L. Control and perception techniques for aerial robotics. Annu. Rev. Control 2004, 28, 167–178. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.M.; Li, Y. A survey of autonomous control for UAV. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009; Volume 2, pp. 267–271. [Google Scholar]
- Emami, S.A.; Castaldi, P.; Banazadeh, A. Neural network-based flight control systems: Present and future. Annu. Rev. Control. 2022, 53, 97–137. [Google Scholar] [CrossRef]
- Budiyono, A. Recent advances in control and instrumentation of unmanned aerial vehicles. In Proceedings of the Conference on Instrumentation and Control, Bandung, Indonesia, 19 February 2007; pp. 19–20. [Google Scholar]
- Chao, H.; Cao, Y.; Chen, Y. Autopilots for small unmanned aerial vehicles: A survey. Int. J. Control. Autom. Syst. 2010, 8, 36–44. [Google Scholar] [CrossRef]
- Gautam, A.; Sujit, P.; Saripalli, S. A survey of autonomous landing techniques for UAVs. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 1210–1218. [Google Scholar]
- Nguyen, H.T.; Quyen, T.V.; Nguyen, C.V.; Le, A.M.; Tran, H.T.; Nguyen, M.T. Control algorithms for UAVs: A comprehensive survey. EAI Endorsed Trans. Ind. Networks Intell. Syst. 2020, 7, e5. [Google Scholar] [CrossRef]
- Gu, W.; Valavanis, K.P.; Rutherford, M.J.; Rizzo, A. UAV model-based flight control with artificial neural networks: A survey. J. Intell. Robot. Syst. 2020, 100, 1469–1491. [Google Scholar] [CrossRef]
- Michailidis, M.G.; Rutherford, M.J.; Valavanis, K.P. A survey of controller designs for new generation UAVs: The challenge of uncertain aerodynamic parameters. Int. J. Control Autom. Syst. 2020, 18, 801–816. [Google Scholar] [CrossRef]
- Zuo, Z.; Liu, C.; Han, Q.L.; Song, J. Unmanned aerial vehicles: Control methods and future challenges. IEEE/CAA J. Autom. Sin. 2022, 9, 601–614. [Google Scholar] [CrossRef]
- Chandar, E.A.S. A Review on Longitudinal Control Law Design for a Small Fixed-Wing UAV. Int. Res. J. Eng. Technol. (IRJET) 2022, 9, 197–202. [Google Scholar]
- Goerzen, C.; Kong, Z.; Mettler, B. A survey of motion planning algorithms from the perspective of autonomous UAV guidance. J. Intell. Robot. Syst. 2010, 57, 65–100. [Google Scholar] [CrossRef]
- Quan, L.; Han, L.; Zhou, B.; Shen, S.; Gao, F. Survey of UAV motion planning. IET Cyber-Syst. Robot. 2020, 2, 14–21. [Google Scholar] [CrossRef]
- Israr, A.; Ali, Z.A.; Alkhammash, E.H.; Jussila, J.J. Optimization methods applied to motion planning of unmanned aerial vehicles: A review. Drones 2022, 6, 126. [Google Scholar] [CrossRef]
- Iqbal, M.M.; Ali, Z.A.; Khan, R.; Shafiq, M. Motion Planning of UAV Swarm: Recent Challenges and Approaches. In Aeronautics-New Advances; IntechOpen: Vienna, Austria, 2022. [Google Scholar] [CrossRef]
- Adams, S.M.; Friedland, C.J. A survey of unmanned aerial vehicle (UAV) usage for imagery collection in disaster research and management. In Proceedings of the 9th International Workshop on Remote Sensing for Disaster Response, Stanford, CA, USA, 15–16 September 2011; Volume 8, pp. 1–8. [Google Scholar]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Cai, G.; Dias, J.; Seneviratne, L. A survey of small-scale unmanned aerial vehicles: Recent advances and future development trends. Unmanned Syst. 2014, 2, 175–199. [Google Scholar] [CrossRef]
- Menouar, H.; Guvenc, I.; Akkaya, K.; Uluagac, A.S.; Kadri, A.; Tuncer, A. UAV-enabled intelligent transportation systems for the smart city: Applications and challenges. IEEE Commun. Mag. 2017, 55, 22–28. [Google Scholar] [CrossRef]
- Srivastava, S.; Narayan, S.; Mittal, S. A survey of deep learning techniques for vehicle detection from UAV images. J. Syst. Archit. 2021, 117, 102152. [Google Scholar] [CrossRef]
- Albaker, B.; Rahim, N. A survey of collision avoidance approaches for unmanned aerial vehicles. In Proceedings of the 2009 International Conference for Technical Postgraduates (TECHPOS), Kuala Lumpur, Malaysia, 14–15 December 2009; pp. 1–7. [Google Scholar]
- Pham, H.; Smolka, S.A.; Stoller, S.D.; Phan, D.; Yang, J. A survey on unmanned aerial vehicle collision avoidance systems. arXiv 2015, arXiv:1508.07723. [Google Scholar]
- Lu, Y.; Xue, Z.; Xia, G.S.; Zhang, L. A survey on vision-based UAV navigation. Geo-Spat. Inf. Sci. 2018, 21, 21–32. [Google Scholar] [CrossRef]
- Elmokadem, T.; Savkin, A.V. Towards fully autonomous UAVs: A survey. Sensors 2021, 21, 6223. [Google Scholar] [CrossRef] [PubMed]
- Santoso, F.; Garratt, M.A.; Anavatti, S.G. State-of-the-art integrated guidance and control systems in unmanned vehicles: A review. IEEE Syst. J. 2020, 15, 3312–3323. [Google Scholar] [CrossRef]
- Chai, R.; Tsourdos, A.; Savvaris, A.; Chai, S.; Xia, Y.; Chen, C.P. Review of advanced guidance and control algorithms for space/aerospace vehicles. Prog. Aerosp. Sci. 2021, 122, 100696. [Google Scholar] [CrossRef]
- Emer, N.; Özbek, N. A survey on Kalman Filtering for Unmanned Aerial Vehicles: Recent Trends, Applications, and Challenges. In Proceedings of the International Conference on Engineering Technologies (ICENTE’20), Konya, Turkey, 19–21 November 2020. [Google Scholar]
- Vaigandla, K.K.; Thatipamula, S.; Karne, R.K. Investigation on Unmanned Aerial Vehicle (UAV): An Overview. IRO J. Sustain. Wirel. Syst. 2022, 4, 130–148. [Google Scholar] [CrossRef]
- Ebeid, E.; Skriver, M.; Jin, J. A survey on open-source flight control platforms of unmanned aerial vehicle. In Proceedings of the 2017 Euromicro Conference on Digital System Design (DSD), Vienna, Austria, 30 August–1 September 2017; pp. 396–402. [Google Scholar]
- Sachs, G.; Traugott, J.; Nesterova, A.P.; Dell’Omo, G.; Kümmeth, F.; Heidrich, W.; Vyssotski, A.L.; Bonadonna, F. Flying at no mechanical energy cost: Disclosing the secret of wandering albatrosses. PLoS ONE 2012, 7, e41449. [Google Scholar] [CrossRef]
- Zhao, Y.J. Optimal patterns of glider dynamic soaring. Optim. Control. Appl. Methods 2004, 25, 67–89. [Google Scholar] [CrossRef]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Stevens, B.L.; Lewis, F.L.; Johnson, E.N. Aircraft Control and Simulation: Dynamics, Controls Design, and Autonomous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Din, A.F.U.; Mir, I.; Gul, F.; Nasar, A.; Rustom, M.; Abualigah, L. Reinforced Learning-Based Robust Control Design for Unmanned Aerial Vehicle. Arab. J. Sci. Eng. 2022, 48, 1221–1236. [Google Scholar] [CrossRef]
- Szczepanski, R.; Tarczewski, T.; Grzesiak, L.M. Adaptive state feedback speed controller for PMSM based on Artificial Bee Colony algorithm. Appl. Soft Comput. 2019, 83, 105644. [Google Scholar] [CrossRef]
- Mir, I.; Maqsood, A.; Taha, H.E.; Eisa, S.A. Soaring Energetics for a Nature Inspired Unmanned Aerial Vehicle. In Proceedings of the American Institute of Aeronautics and Astronautics Science and Technology (AIAA SCITECH Forum), San Diego, CA, USA, 7–11 January 2019; p. 1622. [Google Scholar]
- Chen, K. The design of longitudinal autonomous landing control for a fixed wing Unmanned Aerial vehicle. In Proceedings of the 2021 4th World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMEIM), Shanghai, China, 12–14 November 2021; pp. 120–127. [Google Scholar]
- Poksawat, P.; Wang, L.; Mohamed, A. Gain scheduled attitude control of fixed-wing UAV with automatic controller tuning. IEEE Trans. Control. Syst. Technol. 2017, 26, 1192–1203. [Google Scholar] [CrossRef]
- Jetley, P.; Sujit, P.; Saripalli, S. Safe landing of fixed wing UAVs. In Proceedings of the 2017 47th Annual IEEE/IFIP International Conference on Dependable Systems and Networks Workshops (DSN-W), Denver, CO, USA, 26–29 June 2017; pp. 2–9. [Google Scholar]
- Santoso, F.; Liu, M.; Egan, G. Linear quadratic optimal control synthesis for a uav. In Proceedings of the 12th Australian International Aerospace Congress AIAC12, Melbourne, Australia, 19–22 March 2007. [Google Scholar]
- Manjarrez, H.; Davila, J.; Lozano, R. Low level control architecture for automatic takeoff and landing of fixed wing UAV. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 6737–6742. [Google Scholar]
- Lesprier, J.; Biannic, J.M.; Roos, C. Nonlinear structured H∞ controllers for parameter-dependent uncertain systems with application to aircraft landing. In Proceedings of the 2014 IEEE Conference on Control Applications (CCA), Juan Les Antibes, France, 8–10 October 2014; pp. 433–438. [Google Scholar]
- Qayyum, N.; Bhatti, A.I.; Liaquat, M. Landing control of unmanned aerial vehicle using continuous model predictive control. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 1804–1808. [Google Scholar]
- Lungu, M. Backstepping and dynamic inversion control techniques for automatic landing of fixed wing unmanned aerial vehicles. Aerosp. Sci. Technol. 2022, 120, 107261. [Google Scholar] [CrossRef]
- Zhu, G.; Qi, J.; Wu, C. Landing control of fixed-wing uav based on adrc. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 8020–8025. [Google Scholar]
- Nho, K.; Agarwal, R.K. Automatic landing system design using fuzzy logic. J. Guid. Control Dyn. 2000, 23, 298–304. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, X. Autonomous landing control of fixed-wing uavs: From theory to field experiment. J. Intell. Robot. Syst. 2017, 88, 619–634. [Google Scholar] [CrossRef]
- Jantawong, J.; Deelertpaiboon, C. Automatic landing control based on GPS for fixed-wing aircraft. In Proceedings of the 2018 15th International Conference on Electrical Engineering/Electronics Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Rai, Thailand, 18–21 July 2018; pp. 313–316. [Google Scholar]
- Mathisen, S.; Gryte, K.; Gros, S.; Johansen, T.A. Precision deep-stall landing of fixed-wing UAVs using nonlinear model predictive control. J. Intell. Robot. Syst. 2021, 101, 1–15. [Google Scholar] [CrossRef]
- Hsiao, F.B.; Chan, W.L.; Lai, Y.C.; Tseng, L.C.; Hsieh, S.Y.; Tenn, H.K. Landing longitudinal control system design for a fixed wing UAV. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; p. 868. [Google Scholar] [CrossRef]
- Prach, A.; Gürsoy, G.; Yavrucuk, L. Nonlinear Controller for a Fixed-Wing Aircraft Landing. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 2897–2902. [Google Scholar]
- Rao, D.V.; Go, T.H. Automatic landing system design using sliding mode control. Aerosp. Sci. Technol. 2014, 32, 180–187. [Google Scholar]
- de Sousa Pereira, J.J.V. Automatic Landing Control Design for Unmanned Aerial Vehicles. Master’s Thesis, Universidade do Porto, Porto, Portugal, 2016. Available online: https://repositorio-aberto.up.pt/bitstream/10216/85551/2/146173.pdf (accessed on 20 May 2023).
- Daibing, Z.; Xun, W.; Weiwei, K. Autonomous control of running takeoff and landing for a fixed-wing unmanned aerial vehicle. In Proceedings of the 2012 12th International Conference on Control Automation Robotics & Vision (ICARCV), Guangzhou, China, 5–7 December 2012; pp. 990–994. [Google Scholar]
- Carnes, T.W.; Bakker, T.M.; Klenke, R.H. A fully parameterizable implementation of autonomous take-off and landing for a fixed wing UAV. In Proceedings of the American Institute of Aeronautics and Astronautics Science and Technology Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 5–9 January 2015; p. 0603. [Google Scholar]
- Lai, Y.C.; Chan, K.C.; Liu, Y.C.; Hsiao, F.B. Development of an automatic landing system based on adaptive fuzzy logic control for fixed-wing unmanned aerial vehicles. J. Aeronaut. Astronaut. Aviat. 2016, 48, 183–194. [Google Scholar]
- Zheng, Z.; Jin, Z.; Sun, L.; Zhu, M. Adaptive sliding mode relative motion control for autonomous carrier landing of fixed-wing unmanned aerial vehicles. IEEE Access 2017, 5, 5556–5565. [Google Scholar] [CrossRef]
- Mahmood, A.; Bhatti, A.I.; Siddique, B.A. Landing of Aircraft Using Integral State Feedback Sliding Mode Control. In Proceedings of the 2019 International Conference on Electrical Communication and Computer Engineering (ICECCE), Swat, Pakistan, 24–25 July 2019; pp. 1–6. [Google Scholar]
- Mathisen, S.H.; Fossen, T.I.; Johansen, T.A. Non-linear model predictive control for guidance of a fixed-wing UAV in precision deep stall landing. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 356–365. [Google Scholar]
- Ishioka, S.; Uchiyama, K.; Masuda, K. Landing System Using Extended Dynamic Window Approach For Fixed-Wing UAV. In Proceedings of the 32nd Congress of the International Council of the Aeronautical Sciences, Shanghai, China, 6–10 September 2021. [Google Scholar]
- Xu, J.; Keshmiri, S. Dubins-Based Autolanding Procedure for Fixed-Wing UAS. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 146–154. [Google Scholar]
- Cho, A.; Kim, J.; Lee, S.; Kim, B.; Park, N.; Kim, D.; Kee, C. Fully automatic taxiing, takeoff and landing of a UAV based on a single-antenna GNSS receiver. IFAC Proc. Vol. 2008, 41, 4719–4724. [Google Scholar] [CrossRef]
- Yoon, S.H.; Kim, Y.D.; Park, S.H. Constrained adaptive backstepping controller design for aircraft landing in wind disturbance and actuator stuck. Int. J. Aeronaut. Space Sci. 2012, 13, 74–89. [Google Scholar] [CrossRef]
- Lungu, M. Auto-landing of fixed wing unmanned aerial vehicles using the backstepping control. ISA Trans. 2019, 95, 194–210. [Google Scholar] [CrossRef] [PubMed]
- Lungu, M. Backstepping and dynamic inversion combined controller for auto-landing of fixed wing UAVs. Aerosp. Sci. Technol. 2020, 96, 105526. [Google Scholar] [CrossRef]
- prasad B, B.; Pradeep, S. Automatic landing system design using feedback linearization method. In Proceedings of the AIAA infotech@ Aerospace 2007 Conference and Exhibit, Rohnert Park, CA, USA, 7–10 May 2007; p. 2733. [Google Scholar]
- You, D.I.; Jung, Y.D.; Cho, S.W.; Shin, H.M.; Lee, S.H.; Shim, D.H. A guidance and control law design for precision automatic take-off and landing of fixed-wing UAVs. In Proceedings of the American Institute of Aeronautics and Astronautics Science and Technology Guidance Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012; p. 4674. [Google Scholar]
- Chunlei, D.; Qingbo, G.; Qing, F. High performance L 1 adaptive take-off and landing controller design for fixed-wing UAV. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 3091–3096. [Google Scholar]
- Hajiyev, C.; Vural, S.Y. LQR controller with Kalman estimator applied to UAV longitudinal dynamics. Positioning 2013, 4, 36–41. [Google Scholar] [CrossRef]
- Homayouni Amlashi, A.; Mojed Gharamaleki, R.; Hamidi Nejad, M.H.; Mirzaei, M. Design of estimator-based nonlinear dynamic inversion controller and nonlinear regulator for robust trajectory tracking with aerial vehicles. Int. J. Dyn. Control 2018, 6, 707–725. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Khodarahmi, M.; Maihami, V. A Review on Kalman Filter Models. Arch. Comput. Methods Eng. 2022, 30, 727–747. [Google Scholar] [CrossRef]
- Borup, K.T.; Stovner, B.N.; Fossen, T.I.; Johansen, T.A. Kalman filters for air data system bias correction for a fixed-wing UAV. IEEE Trans. Control Syst. Technol. 2019, 28, 2164–2176. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Liu, X.; Guo, Y.; Zhang, W. Model-Free Integrated Navigation of Small Fixed-Wing UAVs Full State Estimation in Wind Disturbance. IEEE Sens. J. 2022, 22, 2771–2781. [Google Scholar] [CrossRef]
- Lie, F.A.P.; Gebre-Egziabher, D. Synthetic air data system. J. Aircr. 2013, 50, 1234–1249. [Google Scholar] [CrossRef]
- Warsi, F.A.; Hazry, D.; Ahmed, S.F.; Joyo, M.K.; Tanveer, M.H.; Kamarudin, H.; Razlan, Z.M. Yaw, Pitch and Roll controller design for fixed-wing UAV under uncertainty and perturbed condition. In Proceedings of the 2014 IEEE 10th International Colloquium on Signal Processing and Its Applications, Kuala Lumpur, Malaysia, 7–9 March 2014; pp. 151–156. [Google Scholar]
- Pettersson, M. Extended Kalman Filter for Robust UAV Attitude Estimation. Master’s Thesis, Department of Electrical Engineering Linköping University, Linkoping, Sweden, 2015; p. 86. [Google Scholar]
- Magnusson, T. State Estimation of Uav Using Extended Kalman Filter. Master’s Thesis, Department of Electrical Engineering Automatic Control, The Institute of Technology, Linköping University, Linkoping, Sweden, 2013; p. 76. [Google Scholar]
- Hervas, J.R.; Reyhanoglu, M.; Tang, H.; Kayacan, E. Nonlinear control of fixed-wing UAVs in presence of stochastic winds. Commun. Nonlinear Sci. Numer. Simul. 2016, 33, 57–69. [Google Scholar] [CrossRef]
- Yin, X.; Peng, X.; Zhang, G.; Che, B.; Tang, M. Research on Attitude Control System Design and Flight Experiments of Small-scale Unmanned Aerial Vehicle. In Proceedings of the 2022 34th Chinese Control and Decision Conference (CCDC), Hefei, China, 15–17 August 2022; pp. 5866–5871. [Google Scholar]
- Xiaoqian, T.; Feicheng, Z.; Zhengbing, T.; Hongying, W. Nonlinear Extended Kalman Filter for Attitude Estimation of the Fixed-Wing UAV. Int. J. Opt. 2022, 2022, 7883851. [Google Scholar] [CrossRef]
- Yu, Y.j.; Zhang, X.; Khan, M.S.A. Attitude heading reference algorithm based on transformed cubature Kalman filter. Meas. Control 2020, 53, 1446–1453. [Google Scholar] [CrossRef]
- De Marina, H.G.; Espinosa, F.; Santos, C. Adaptive UAV attitude estimation employing unscented Kalman filter, FOAM and low-cost MEMS sensors. Sensors 2012, 12, 9566–9585. [Google Scholar] [CrossRef]
- De Marina, H.G.; Pereda, F.J.; Giron-Sierra, J.M.; Espinosa, F. UAV attitude estimation using unscented Kalman filter and TRIAD. IEEE Trans. Ind. Electron. 2011, 59, 4465–4474. [Google Scholar] [CrossRef]
- Burchett, B.T. Feedback linearization guidance for approach and landing of reusable launch vehicles. In Proceedings of the Proceedings of the 2005, American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 2093–2097. [Google Scholar]
- Yang, J.; Thomas, A.G.; Singh, S.; Baldi, S.; Wang, X. A semi-physical platform for guidance and formations of fixed-wing unmanned aerial vehicles. Sensors 2020, 20, 1136. [Google Scholar] [CrossRef]
- Prabowo, Y.A.; Trilaksono, B.R.; Triputra, F.R. Hardware in-the-loop simulation for visual servoing of fixed wing UAV. In Proceedings of the 2015 international conference on electrical engineering and informatics (ICEEI), Denpasar, Indonesia, 10–11 August 2015; pp. 247–252. [Google Scholar]
- Ülker, H.; Baykara, C.; Özsoy, C. PIL simulations of an FWUAV under windy conditions. Aircr. Eng. Aerosp. Technol. 2018, 90, 461–470. [Google Scholar] [CrossRef]
- Santos, M.H.; Oliveira, N.M.; D’Amore, R. From Control Requirements to PIL Test: Development of a Structure to Autopilot Implementation. IEEE Access 2021, 9, 154788–154803. [Google Scholar] [CrossRef]
- Bacic, M. On hardware-in-the-loop simulation. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 3194–3198. [Google Scholar]
- Johnson, E.N.; Fontaine, S. Use of flight simulation to complement flight testing of low-cost UAVs. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Montreal, QC, Canada, 6–9 August 2001. [Google Scholar]
- Sorton, E.; Hammaker, S. Simulated flight testing of an autonomous unmanned aerial vehicle using flightgear. In Proceedings of the Infotech@ Aerospace, Arlington, VA, USA, 26–29 September 2005; p. 7083. [Google Scholar]
- Bulka, E.; Nahon, M. Autonomous fixed-wing aerobatics: From theory to flight. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 6573–6580. [Google Scholar]
- Arif, A.; Sasongko, R.; Stepen. Numerical Simulation Platform for a Generic Aircraft Flight Dynamic Simulation. In Proceedings of the International Conference on Aviation Technology and Management 2018 (ICATeM 2018), Kuala Lumpur, Malaysia, 12–14 September 2018. [Google Scholar]
- Ribeiro, L.R.; Oliveira, N.M.F. UAV autopilot controllers test platform using Matlab/Simulink and X-Plane. In Proceedings of the 2010 IEEE Frontiers in Education Conference (FIE), Arlington, VA, USA, 27–30 October 2010. Session: S2H. [Google Scholar]
- Nugroho, L. Comparison of classical and modern landing control system for a small unmanned aerial vehicle. In Proceedings of the 2014 International Conference on Computer, Control, Informatics and Its Applications (IC3INA), Bandung, Indonesia, 21–23 October 2014; pp. 187–192. [Google Scholar]
- Priyambodo, T.K.; Majid, A. Modeling and simulation of the UX-6 fixed-wing Unmanned Aerial Vehicle. J. Control Autom. Electr. Syst. 2021, 32, 1344–1355. [Google Scholar] [CrossRef]
- Zhang, J.; Geng, Q.; Fei, Q. UAV flight control system modeling and simulation based on FlightGear. In Proceedings of the International Conference on Automatic Control and Artificial Intelligence (ACAI 2012), Xiamen, China, 3–5 March 2012; pp. 2231–2234. [Google Scholar]






| Reference | Research Focus |
|---|---|
| [45,46,47,48,49,50,51,52] | Control algorithms |
| [53,54,55,56] | Motion planning techniques algorithms |
| [57,58,59,60,61] | Applications of UAV |
| [62,63] | Collision avoidance strategies |
| [64,65] | Navigation techniques |
| [66,67] | Guidance and Control algorithms |
| [68] | Kalman Filtering Techniques |
| [69] | 6G UAV communication |
| [70] | Open-source Hardware and Software Flight Control Platforms |
| Flight Phase | Control Technique | Reference |
|---|---|---|
| Landing | PID | [78,88,89,90,91,92,93,94,95,96] |
| Fuzzy Logic | [97] | |
| Sliding Mode Control | [93,98,99] | |
| Model Predictive Control | [84,90,100] | |
| LQR | [80,94,101,102,103] | |
| Backstepping | [104,105,106] | |
| Feedback Linearization | [101,105,106,107] | |
| Adaptive Controller | [108,109] | |
| ADRC | [86,88] | |
| Take-off | LQR | [103] |
| ADRC | [86] | |
| LQG | [81] | |
| PID | [95,96] | |
| Adaptive Controller | [108,109] | |
| Cruise | LQR | [110] |
| Feedback Linearization | [111] |
| Control Algorithms | Advantages | Disadvantages |
|---|---|---|
| PID | Easy to implement and tune | Sensitive to noise and disturbances |
| LQR | Provides optimal control solutions, engineering friendly, guarantees stability margins | Full state feedback is required, requires an accurate model of the system |
| Handle uncertainties and disturbances | Require accurate model of the system, computationally expensive, tuning is very time-consuming | |
| Gain Scheduling | Handle non-linear systems effectively, coverage of a wide range of operating conditions and flight envelops is possible | Stability issues if the transition between gains is not smooth, slow and laborious design process |
| Adaptive Control | Can handle uncertain and time-varying systems, can handle disturbances and unmodeled system dynamics | Computationally expensive, good knowledge of system dynamics is needed, tuning of parameters requires expertise |
| Backstepping | Excellent tracking performance and disturbance rejection capabilities, can handle under-actuated systems effectively | Computationally expensive, requires an accurate mathematical model of the system |
| Model Predictive Control | Can handle systems with constraints on inputs and states, can handle multivariable control problems with multiple objectives | Performance depends heavily on the accuracy of the prediction model. |
| Feedback Linearization | Handle non-linear systems effectively, good tracking performance and disturbance rejection capability | Require accurate mathematical model of the system, computationally expensive |
| Sliding Mode Control | Can handle uncertainties and disturbances effectively, good tracking performance, disturbance rejection capability, does not require an accurate model of the plant | Chattering effect |
| Features | FlightGear | X-Plane |
|---|---|---|
| Product Price and availability | Open source software (Free) | Paid software (USD 59.99) |
| Operating System | Linux, Windows, and MAC | Linux, Windows, and MAC |
| Aircraft Catalogue | Vast selection of user-contributed aircraft models are available for free download | Compared to FlightGear, they have lesser airplanes available by default, a large collection of payware aircraft from independent developers are available |
| Flight dynamics model | Use JBSim model | Based on blade element theory |
| Co-simulation | Easy integration with MATLAB/Simulink, batch file generation is required | Easy integration with MATLAB/Simulink |
| Scenery Quality | High-quality graphics, use of OpenGL rendering engine, less detailed and realistic view than X-Plane, highly customizable | High-quality graphics, use of HDR and PBR rendering for realistic weather and detailed texture, excellent depiction of world and aircraft |
| Customization | Highly customizable | Less customizable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tahir, M.A.; Mir, I.; Islam, T.U. Control Algorithms, Kalman Estimation and Near Actual Simulation for UAVs: State of Art Perspective. Drones 2023, 7, 339. https://doi.org/10.3390/drones7060339
Tahir MA, Mir I, Islam TU. Control Algorithms, Kalman Estimation and Near Actual Simulation for UAVs: State of Art Perspective. Drones. 2023; 7(6):339. https://doi.org/10.3390/drones7060339
Chicago/Turabian StyleTahir, Muhammad Amir, Imran Mir, and Tauqeer Ul Islam. 2023. "Control Algorithms, Kalman Estimation and Near Actual Simulation for UAVs: State of Art Perspective" Drones 7, no. 6: 339. https://doi.org/10.3390/drones7060339
APA StyleTahir, M. A., Mir, I., & Islam, T. U. (2023). Control Algorithms, Kalman Estimation and Near Actual Simulation for UAVs: State of Art Perspective. Drones, 7(6), 339. https://doi.org/10.3390/drones7060339






