Iterative Trajectory Planning and Resource Allocation for UAV-Assisted Emergency Communication with User Dynamics
Abstract
1. Introduction
1.1. Related Works
1.2. Our Contributions
- UAV-assisted communication model with the dynamic environment. For emergency cases, few researchers test their algorithm with dynamic users. We have established an A2G communication model with moving ground users, where the energy consumption and assistance communication quality are jointly optimized.
- Dynamic bandwidth allocation. For resource allocation in UAV-assisted communication, few researchers focus on bandwidth, due to its high complexity. Our work tackles dynamic bandwidth allocation, providing an algorithm for real UAV planning.
- Designed iterative algorithm. For the NP-hard optimization problem of UAV planning in emergency communication, we leverage the idea of subtask iterative algorithm and work out an effective iterative scheduling algorithm of trajectory and resource.
- Simulation analysis. Experiments are implemented to evaluate the effectiveness of the proposed optimization algorithm, which achieves obvious performance compared with non-optimized and several other methods and can maintain the performance in different environments.
- The A2G communication model, user moving strategy, and mathematical optimization model are established in Section 2.
- The iterative scheduling algorithm for trajectory and resource (ISATR) is elaborated on in Section 3.
- In Section 4, the results and performance are discussed, with comparisons in different environments.
- Section 5 concludes the paper.
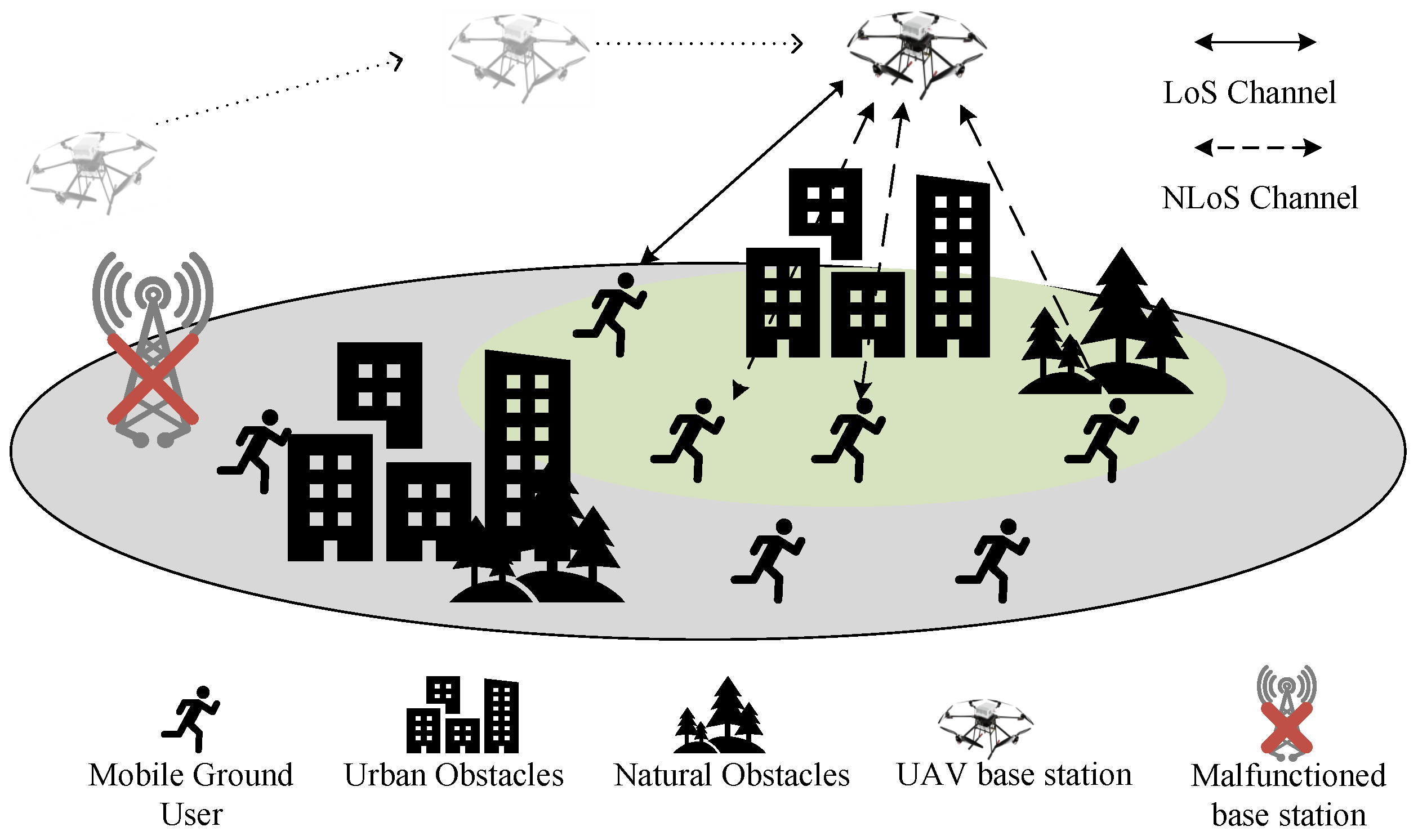
2. Modeling of UAV-Assisted Communication
2.1. UAV Air-to-Ground Channel Model
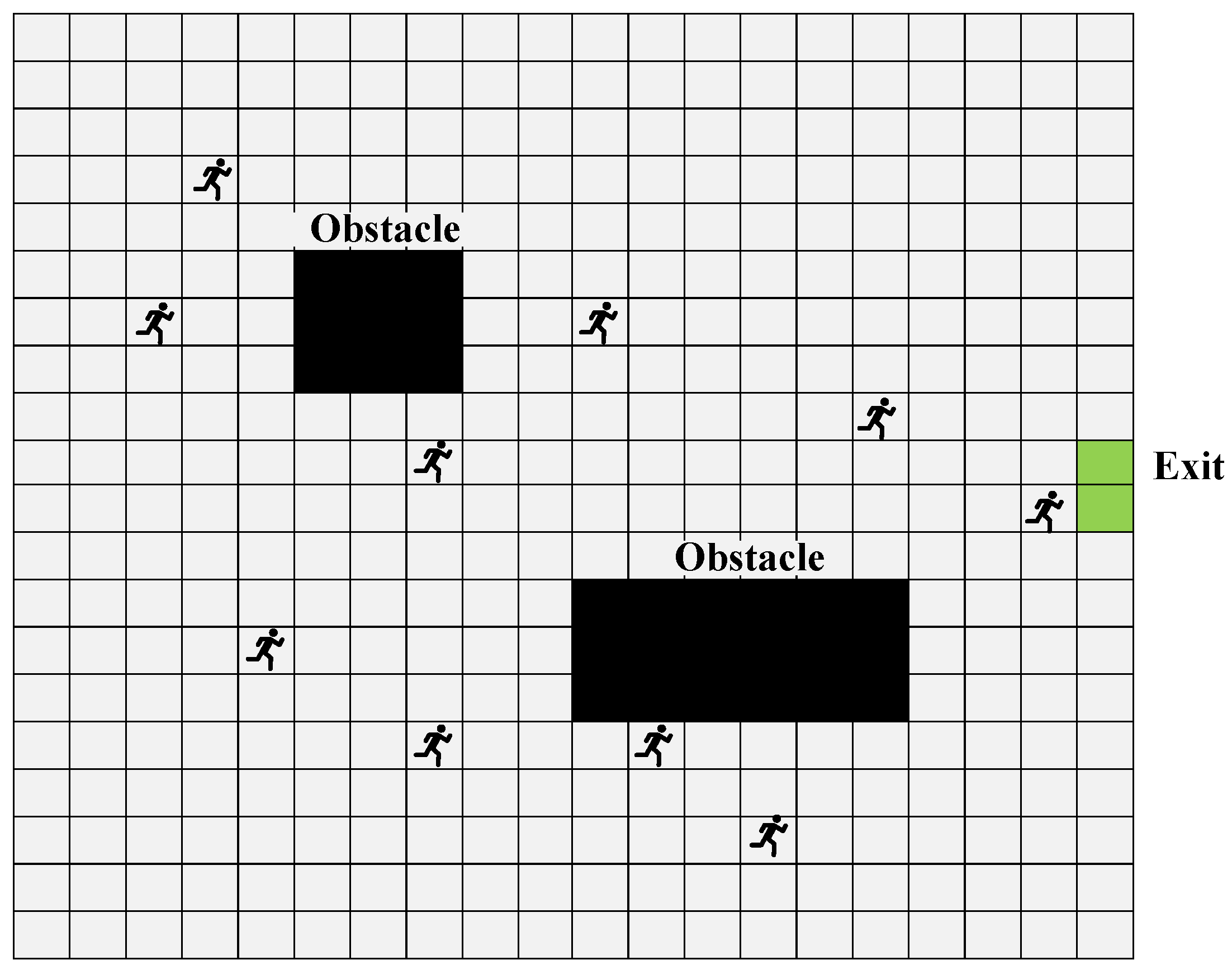
2.2. User Trajectory Prediction Model
2.3. Optimization Mathematical Model
3. Iterative Scheduling Algorithm for Throughput Optimization
3.1. Algorithm Architecture of ISATR
| Algorithm 1: Block coordinate descent algorithm |
 |
| Algorithm 2: ISATR (Iterative Scheduling Algorithm of Trajectory and Resource) |
 |
3.2. UAV Trajectory Subtask Optimization
3.3. Transmission Power Subtask Optimization
3.4. Communication Bandwidth Allocation Subtask Optimization
4. Numerical Results and Analysis
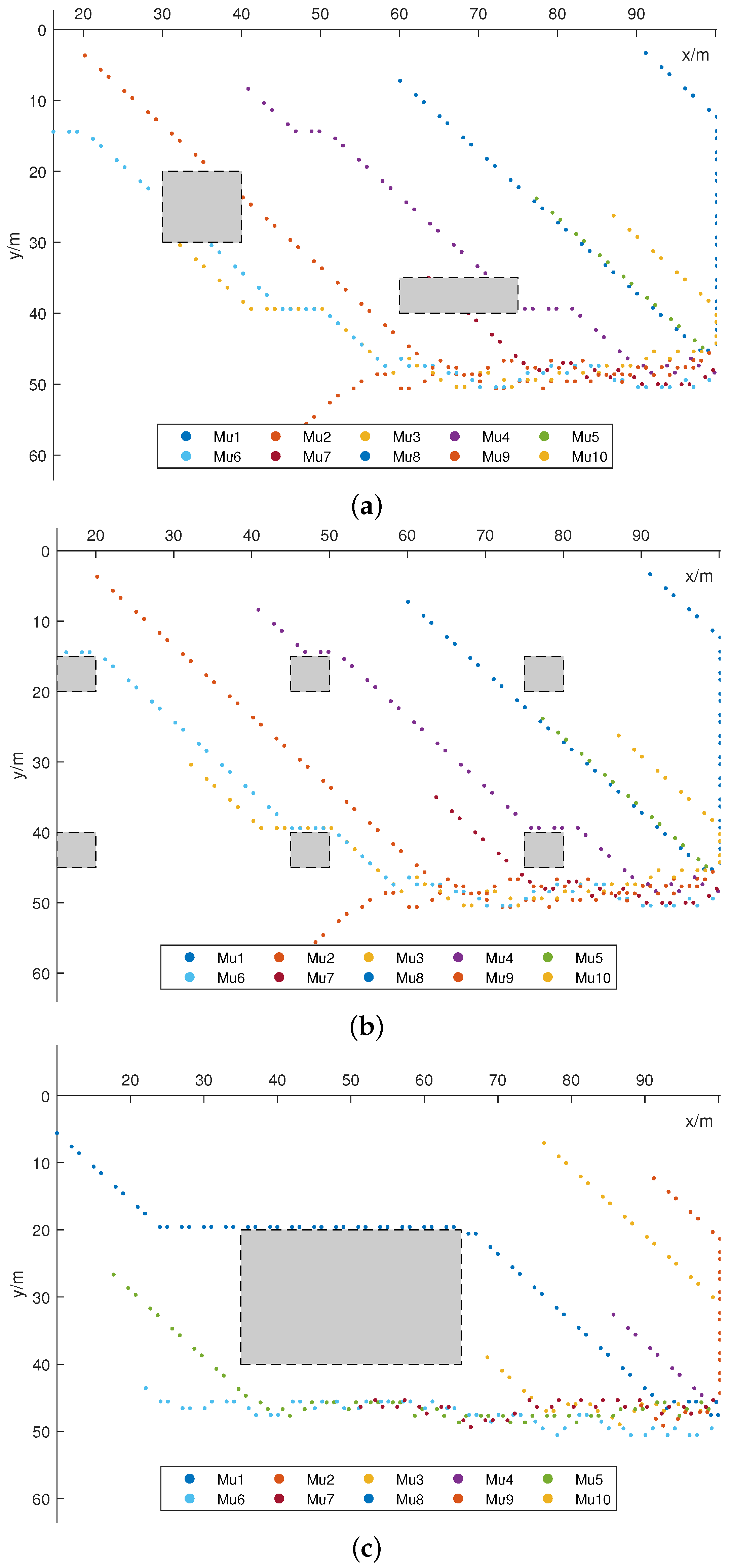
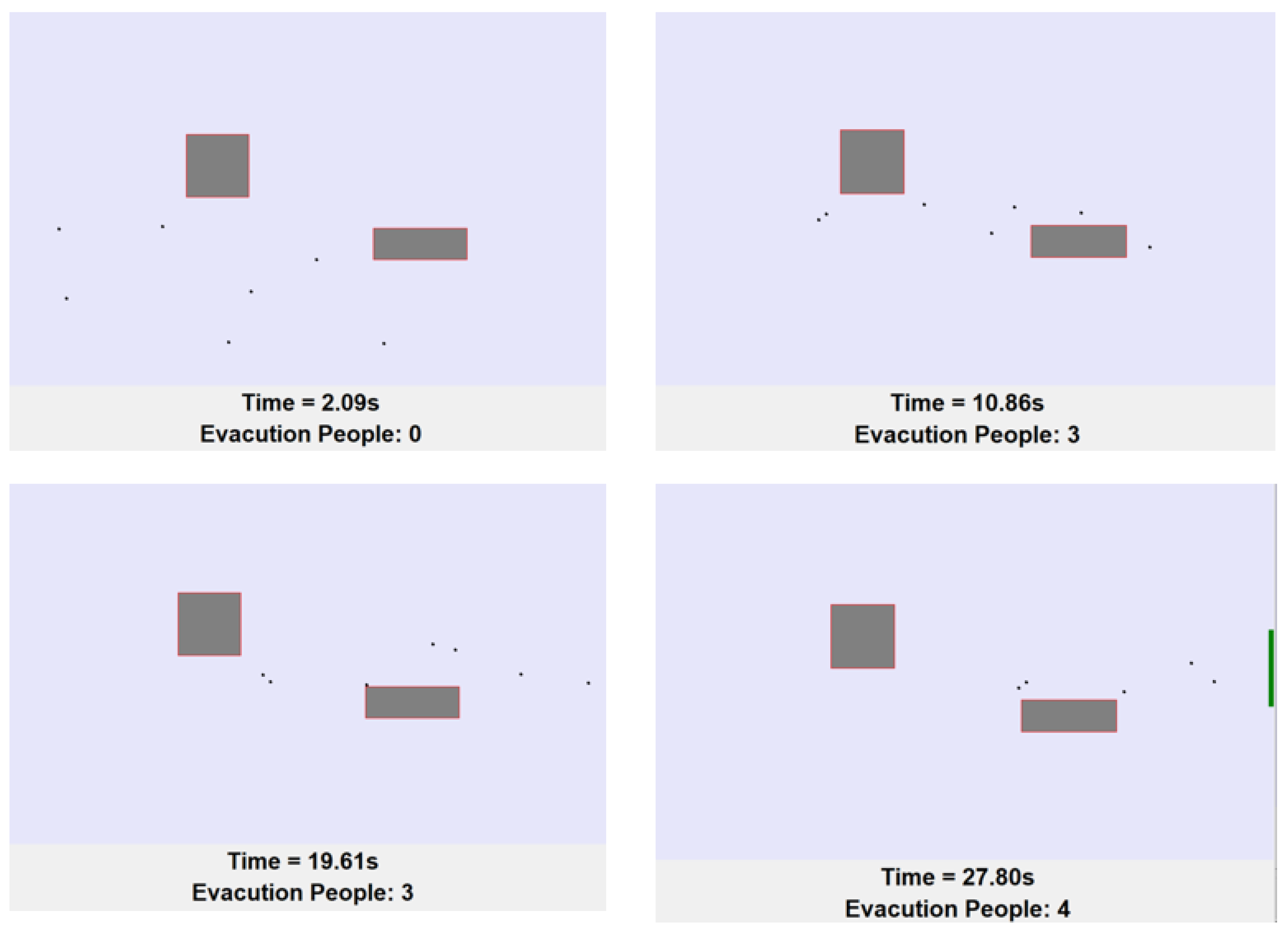
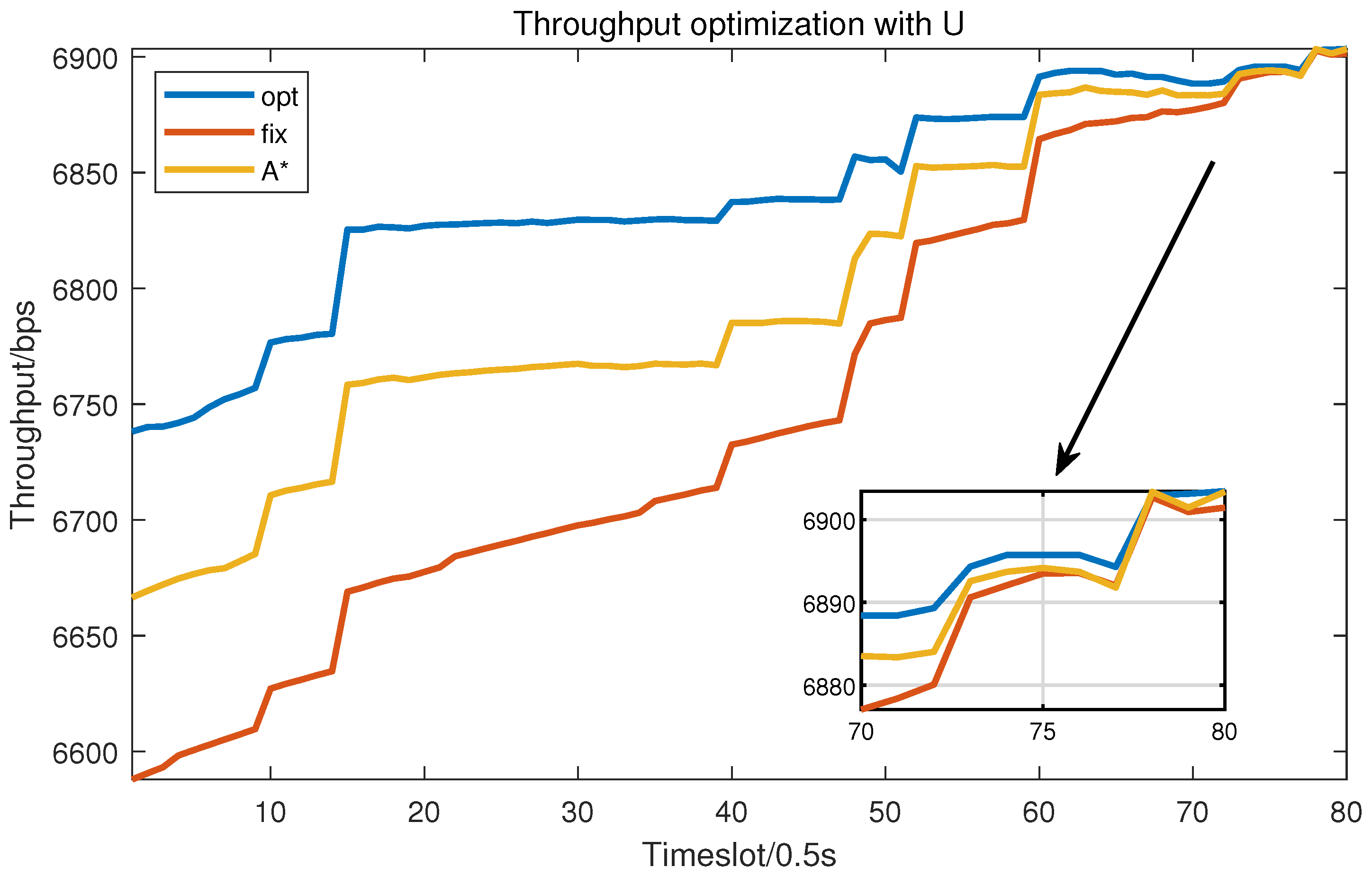
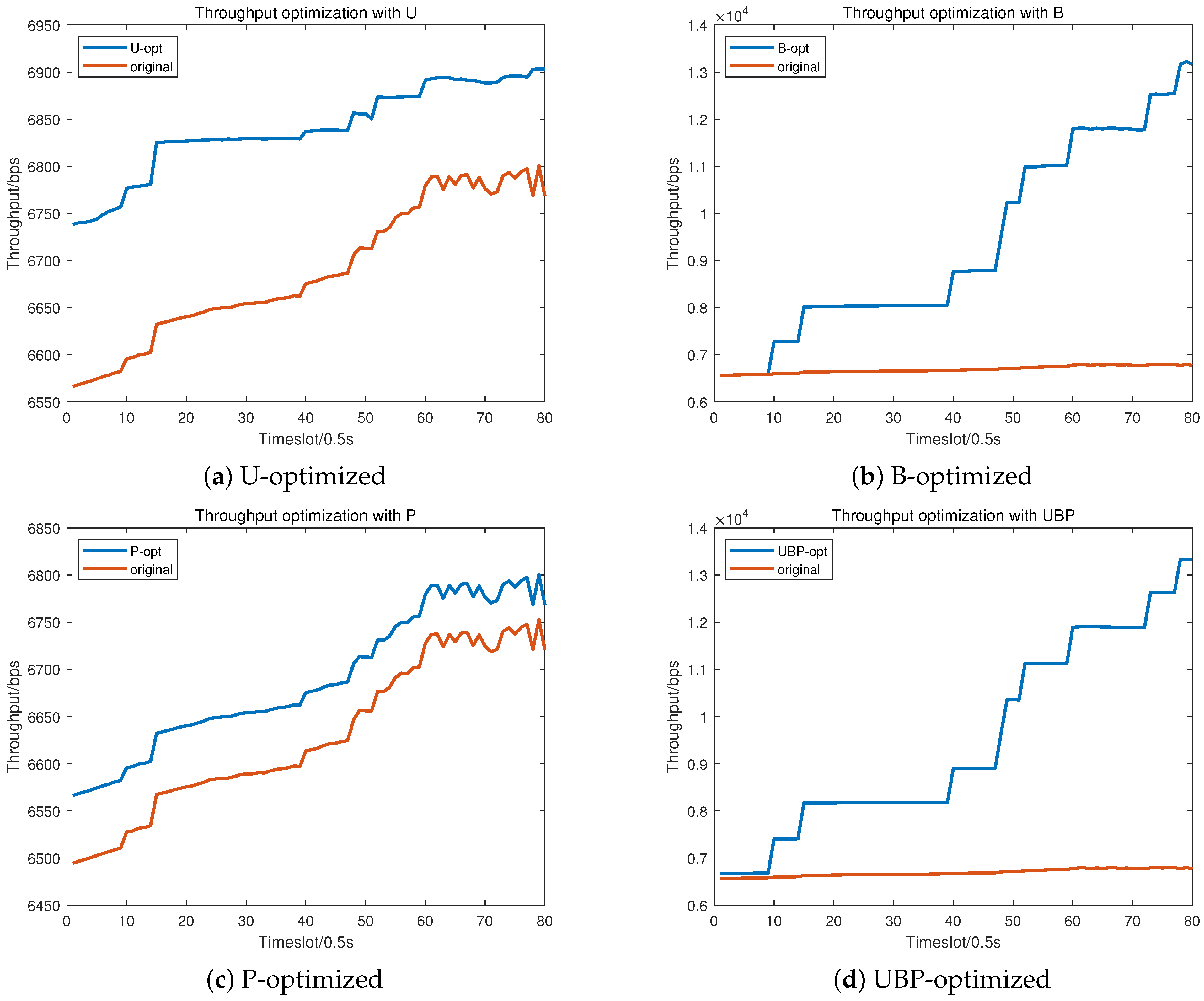
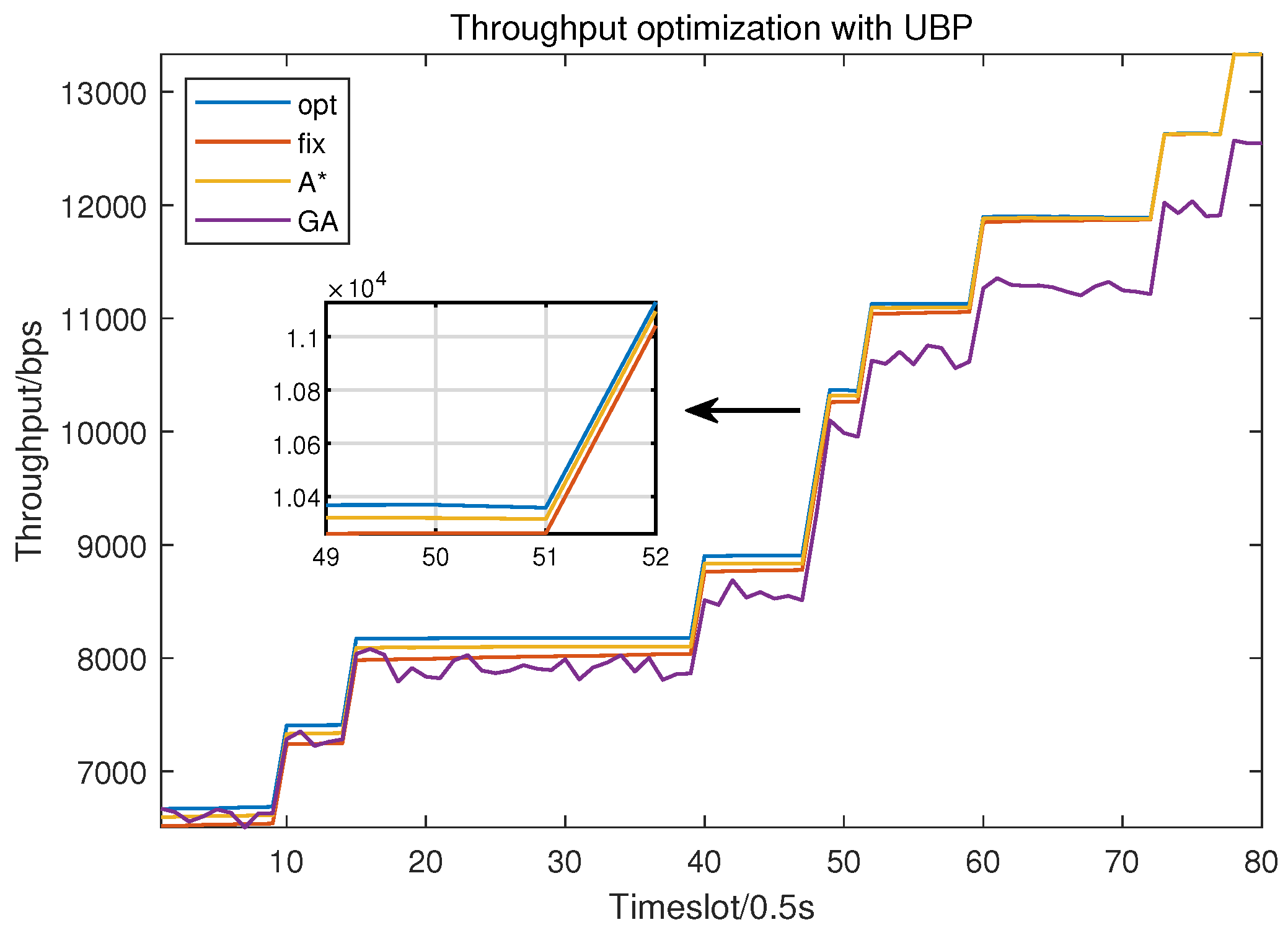
4.1. Evaluation of UAV Trajectory planning
4.2. Evaluation of Resource Allocation
4.3. Evaluation of Trajectory and Resource Joint Optimization
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Kim, H.; Ben-Othman, J. A Collision-Free Surveillance System Using Smart UAVs in Multi Domain IoT. IEEE Commun. Lett. 2018, 22, 2587–2590. [Google Scholar] [CrossRef]
- Hasan, K.M.; Suhaili, W.S.; Shah Newaz, S.H.; Ahsan, M.S. Development of an Aircraft Type Portable Autonomous Drone for Agricultural Applications. In Proceedings of the 2020 International Conference on Computer Science and Its Application in Agriculture (ICOSICA), Bogor, Indonesia, 16–17 September 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Alsawy, A.; Hicks, A.; Moss, D.; Mckeever, S. An Image Processing Based Classifier to Support Safe Dropping for Delivery-by-Drone. In Proceedings of the 2022 IEEE 5th International Conference on Image Processing Applications and Systems (IPAS), Genova, Italy, 5–7 December 2022; Volume 5, pp. 1–5. [Google Scholar] [CrossRef]
- Alrayes, F.S.; Alzahrani, J.S.; Alissa, K.A.; Alharbi, A.; Alshahrani, H.; Elfaki, M.A.; Yafoz, A.; Mohamed, A.; Hilal, A.M. Dwarf Mongoose Optimization-Based Secure Clustering with Routing Technique in Internet of Drones. Drones 2022, 6, 247. [Google Scholar] [CrossRef]
- Samir, M.; Sharafeddine, S.; Assi, C.M.; Nguyen, T.M.; Ghrayeb, A. UAV Trajectory Planning for Data Collection from Time-Constrained IoT Devices. IEEE Trans. Wirel. Commun. 2020, 19, 34–46. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, C.; Pan, M. Multiobjective UAV Path Planning for Emergency Information Collection and Transmission. IEEE Internet Things J. 2020, 7, 6993–7009. [Google Scholar] [CrossRef]
- Xu, J.; Ota, K.; Dong, M. Big Data on the Fly: UAV-Mounted Mobile Edge Computing for Disaster Management. IEEE Trans. Netw. Sci. Eng. 2020, 7, 2620–2630. [Google Scholar] [CrossRef]
- Jeong, S.; Simeone, O.; Kang, J. Mobile Edge Computing via a UAV-Mounted Cloudlet: Optimization of Bit Allocation and Path Planning. IEEE Trans. Veh. Technol. 2018, 67, 2049–2063. [Google Scholar] [CrossRef]
- Asad, M.; Aidaros, O.A.; Beg, R.; Dhahri, M.A.; Neyadi, S.A.; Hussein, M. Development of autonomous drone for gas sensing application. In Proceedings of the 2017 International Conference on Electrical and Computing Technologies and Applications (ICECTA), Ras Al Khaimah, United Arab Emirates, 21–23 November 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, C.; Ju, B.; Wu, Y.; Lin, X.; Xiong, N.; Xu, G.; Li, H.; Liang, X. UAV Autonomous Target Search Based on Deep Reinforcement Learning in Complex Disaster Scene. IEEE Access 2019, 7, 117227–117245. [Google Scholar] [CrossRef]
- Abeygunawaradana, P.; Gamage, N.; De Alwis, L.; Ashan, S.; Nilanka, C.; Godamune, P. E-Medic—Autonomous Drone for Healthcare System. In Proceedings of the 2021 International Conference on Computing, Communication, and Intelligent Systems (ICCCIS), Greater Noida, India, 19–20 February 2021; pp. 994–999. [Google Scholar] [CrossRef]
- Bitar, A.; Jamal, A.; Sultan, H.; Alkandari, N.; El-Abd, M. Medical Drones System for Amusement Parks. In Proceedings of the 2017 IEEE/ACS 14th International Conference on Computer Systems and Applications (AICCSA), Hammamet, Tunisia, 30 October–3 November 2017; pp. 19–20, ISSN 2161-5330. [Google Scholar] [CrossRef]
- Besada, J.A.; Bernardos, A.M.; Bergesio, L.; Vaquero, D.; Campaña, I.; Casar, J.R. Drones-as-a-service: A management architecture to provide mission planning, resource brokerage and operation support for fleets of drones. In Proceedings of the 2019 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Kyoto, Japan, 11–15 March 2019; pp. 931–936. [Google Scholar] [CrossRef]
- Yan, C.; Fu, L.; Zhang, J.; Wang, J. A Comprehensive Survey on UAV Communication Channel Modeling. IEEE Access 2019, 7, 107769–107792. [Google Scholar] [CrossRef]
- Khawaja, W.; Guvenc, I.; Matolak, D.W.; Fiebig, U.C.; Schneckenburger, N. A Survey of Air-to-Ground Propagation Channel Modeling for Unmanned Aerial Vehicles. IEEE Commun. Surv. Tutorials 2019, 21, 2361–2391. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Shvetsov, A.V.; Shvetsova, S.V.; Hawbani, A.; Guizani, M.; Alhartomi, M.A.; Ma, O. Blockchain-Empowered Security and Energy Efficiency of Drone Swarm Consensus for Environment Exploration. IEEE Trans. Green Commun. Netw. 2023, 7, 328–338. [Google Scholar] [CrossRef]
- Srivastava, K.; Pandey, P.C.; Sharma, J.K. An Approach for Route Optimization in Applications of Precision Agriculture Using UAVs. Drones 2020, 4, 58. [Google Scholar] [CrossRef]
- Luan, Q.; Cui, H.; Zhang, L.; Lv, Z. A Hierarchical Hybrid Subtask Scheduling Algorithm in UAV-Assisted MEC Emergency Network. IEEE Internet Things J. 2022, 9, 12737–12753. [Google Scholar] [CrossRef]
- Cabreira, T.M.; Brisolara, L.B.; Ferreira, P.R., Jr. Survey on Coverage Path Planning with Unmanned Aerial Vehicles. Drones 2019, 3, 4. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Kandeepan, S.; Jamalipour, A. Modeling air-to-ground path loss for low altitude platforms in urban environments. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 2898–2904, ISSN 1930-529X. [Google Scholar] [CrossRef]
- Lyu, Y.; Wang, W.; Sun, Y.; Yue, H.; Chai, J. Low-Altitude UAV Air-to-Ground Multilink Channel Modeling and Analysis at 2.4 and 5.9 GHz. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 2135–2139. [Google Scholar] [CrossRef]
- Goddemeier, N.; Daniel, K.; Wietfeld, C. Role-Based Connectivity Management with Realistic Air-to-Ground Channels for Cooperative UAVs. IEEE J. Sel. Areas Commun. 2012, 30, 951–963. [Google Scholar] [CrossRef]
- Ge, C.; Zhai, D.; Jiang, Y.; Zhang, R.; Yang, X.; Li, B.; Tang, X. Pathloss and Airframe Shadowing Loss of Air-to-Ground UAV Channel in the Airport Area at UHF- and L-Band. IEEE Trans. Veh. Technol. 2023, 72, 8094–8098. [Google Scholar] [CrossRef]
- Li, H.; Ding, L.; Wang, Y.; Wang, Z. Air-to-Ground Channel Modeling and Performance Analysis for Cellular-Connected UAV Swarm. IEEE Commun. Lett. 2023, 27, 2172–2176. [Google Scholar] [CrossRef]
- Wang, S.; Lim, T.H.; Choo, H. Path Loss Analysis Considering Atmospheric Refractivity and Precipitation for Air-to-Ground Radar. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 1968–1972. [Google Scholar] [CrossRef]
- Cui, Z.; Guan, K.; Oestges, C.; Briso-Rodríguez, C.; Ai, B.; Zhong, Z. Cluster-Based Characterization and Modeling for UAV Air-to-Ground Time-Varying Channels. IEEE Trans. Veh. Technol. 2022, 71, 6872–6883. [Google Scholar] [CrossRef]
- Wan, Y.; Zhong, Y.; Ma, A.; Zhang, L. An Accurate UAV 3-D Path Planning Method for Disaster Emergency Response Based on an Improved Multiobjective Swarm Intelligence Algorithm. IEEE Trans. Cybern. 2023, 53, 2658–2671. [Google Scholar] [CrossRef]
- Wang, X.; Pan, J.; Yang, Q.; Kong, L.; Snášel, V.; Chu, S. Modified Mayfly Algorithm for UAV Path Planning. Drones 2022, 6, 134. [Google Scholar] [CrossRef]
- Zheng, L.; Tian, Y.; Wang, H.; Hong, C.; Li, B. Path Planning of Autonomous Mobile Robots Based on an Improved Slime Mould Algorithm. Drones 2023, 7, 257. [Google Scholar] [CrossRef]
- Shen, Y.; Zhu, Y.; Kang, H.; Sun, X.; Chen, Q.; Wang, D. UAV Path Planning Based on Multi-Stage Constraint Optimization. Drones 2021, 5, 144. [Google Scholar] [CrossRef]
- Wang, B.; Sun, Y.; Sun, Z.; Nguyen, L.D.; Duong, T.Q. UAV-Assisted Emergency Communications in Social IoT: A Dynamic Hypergraph Coloring Approach. IEEE Internet Things J. 2020, 7, 7663–7677. [Google Scholar] [CrossRef]
- Prasad, N.L.; Ramkumar, B. 3-D Deployment and Trajectory Planning for Relay Based UAV Assisted Cooperative Communication for Emergency Scenarios Using Dijkstra’s Algorithm. IEEE Trans. Veh. Technol. 2023, 72, 5049–5063. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.; Zhang, R. Cellular-Enabled UAV Communication: A Connectivity-Constrained Trajectory Optimization Perspective. IEEE Trans. Commun. 2019, 67, 2580–2604. [Google Scholar] [CrossRef]
- Jayaweera, H.; Hanoun, S. Path Planning of Unmanned Aerial Vehicles (UAVs) in Windy Environments. Drones 2022, 6, 101. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Y.; Ye, F.; Geng, X.; Zhou, Z.; Shi, T. A Hybrid Human-in-the-Loop Deep Reinforcement Learning Method for UAV Motion Planning for Long Trajectories with Unpredictable Obstacles. Drones 2023, 7, 311. [Google Scholar] [CrossRef]
- Gubán, M.; Udvaros, J. A Path Planning Model with a Genetic Algorithm for Stock Inventory Using a Swarm of Drones. Drones 2022, 6, 364. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, X.; Zhuang, Z.; Xu, H.; Sharma, V.; Han, Z. Q-Learning Aided Intelligent Routing With Maximum Utility in Cognitive UAV Swarm for Emergency Communications. IEEE Trans. Veh. Technol. 2023, 72, 3707–3723. [Google Scholar] [CrossRef]
- Zhang, T.; Lei, J.; Liu, Y.; Feng, C.; Nallanathan, A. Trajectory Optimization for UAV Emergency Communication With Limited User Equipment Energy: A Safe-DQN Approach. IEEE Trans. Green Commun. Netw. 2021, 5, 1236–1247. [Google Scholar] [CrossRef]
- Qie, H.; Shi, D.; Shen, T.; Xu, X.; Li, Y.; Wang, L. Joint Optimization of Multi-UAV Target Assignment and Path Planning Based on Multi-Agent Reinforcement Learning. IEEE Access 2019, 7, 146264–146272. [Google Scholar] [CrossRef]
- Wang, F.; Xu, X.; Chen, M.; Nzige, J.; Chong, F. Simulation Research on Fire Evacuation of Large Public Buildings Based on Building Information Modeling. Complex Syst. Model. Simul. 2021, 1, 122–130. [Google Scholar] [CrossRef]
- Hou, Z.; Sun, Y.; Cai, M. 3D Visualization of Forest Fire Spread Model Based on Cellular Automata. In Proceedings of the 2023 8th International Conference on Computer and Communication Systems (ICCCS), Guangzhou, China, 21–23 April 2023; pp. 880–883. [Google Scholar] [CrossRef]
- Ye, Z.; Yin, Y.; Zong, X.; Wang, M. An Optimization Model for Evacuation Based on Cellular Automata and Ant Colony Algorithm. In Proceedings of the 2014 Seventh International Symposium on Computational Intelligence and Design, Hangzhou, China, 13–14 December 2014; Volume 1, pp. 7–10. [Google Scholar] [CrossRef]






| Variable | Definition |
|---|---|
| m | Mass of UAV |
| UAV location at nth time slot | |
| Flight direction of UAV at nth time slot | |
| Flight velocity of UAV at nth time slot | |
| Maximum flight speed of UAV | |
| ith user’s location at nth time slot | |
| Transmission power of UAV at nth time slot | |
| Upper bound of transmission power | |
| Bandwidth allocated to ith user at nth time slot | |
| Total bandwidth for A2G communication at time slot i | |
| UAV communication power consumption with ith user at nth time slot | |
| UAV flight energy consumption in nth time slot | |
| Upper bound of total energy consumption | |
| Throughput for communication with user i | |
| R | Total throughput of A2G communication |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, Y.; Luo, Y.; Zhang, H.; Zhang, X.; Ding, W. Iterative Trajectory Planning and Resource Allocation for UAV-Assisted Emergency Communication with User Dynamics. Drones 2024, 8, 149. https://doi.org/10.3390/drones8040149
Zhang Z, Wang Y, Luo Y, Zhang H, Zhang X, Ding W. Iterative Trajectory Planning and Resource Allocation for UAV-Assisted Emergency Communication with User Dynamics. Drones. 2024; 8(4):149. https://doi.org/10.3390/drones8040149
Chicago/Turabian StyleZhang, Zhilan, Yufeng Wang, Yizhe Luo, Hang Zhang, Xiaorong Zhang, and Wenrui Ding. 2024. "Iterative Trajectory Planning and Resource Allocation for UAV-Assisted Emergency Communication with User Dynamics" Drones 8, no. 4: 149. https://doi.org/10.3390/drones8040149
APA StyleZhang, Z., Wang, Y., Luo, Y., Zhang, H., Zhang, X., & Ding, W. (2024). Iterative Trajectory Planning and Resource Allocation for UAV-Assisted Emergency Communication with User Dynamics. Drones, 8(4), 149. https://doi.org/10.3390/drones8040149






