Tendon-Driven Continuum Robots for Aerial Manipulation—A Survey of Fabrication Methods
Abstract
:1. Introduction
1.1. Overview of Aerial Manipulation Systems
1.2. Overview of Continuum Arm Aerial Manipulation System (CAAMS)
1.3. Overview of CRs
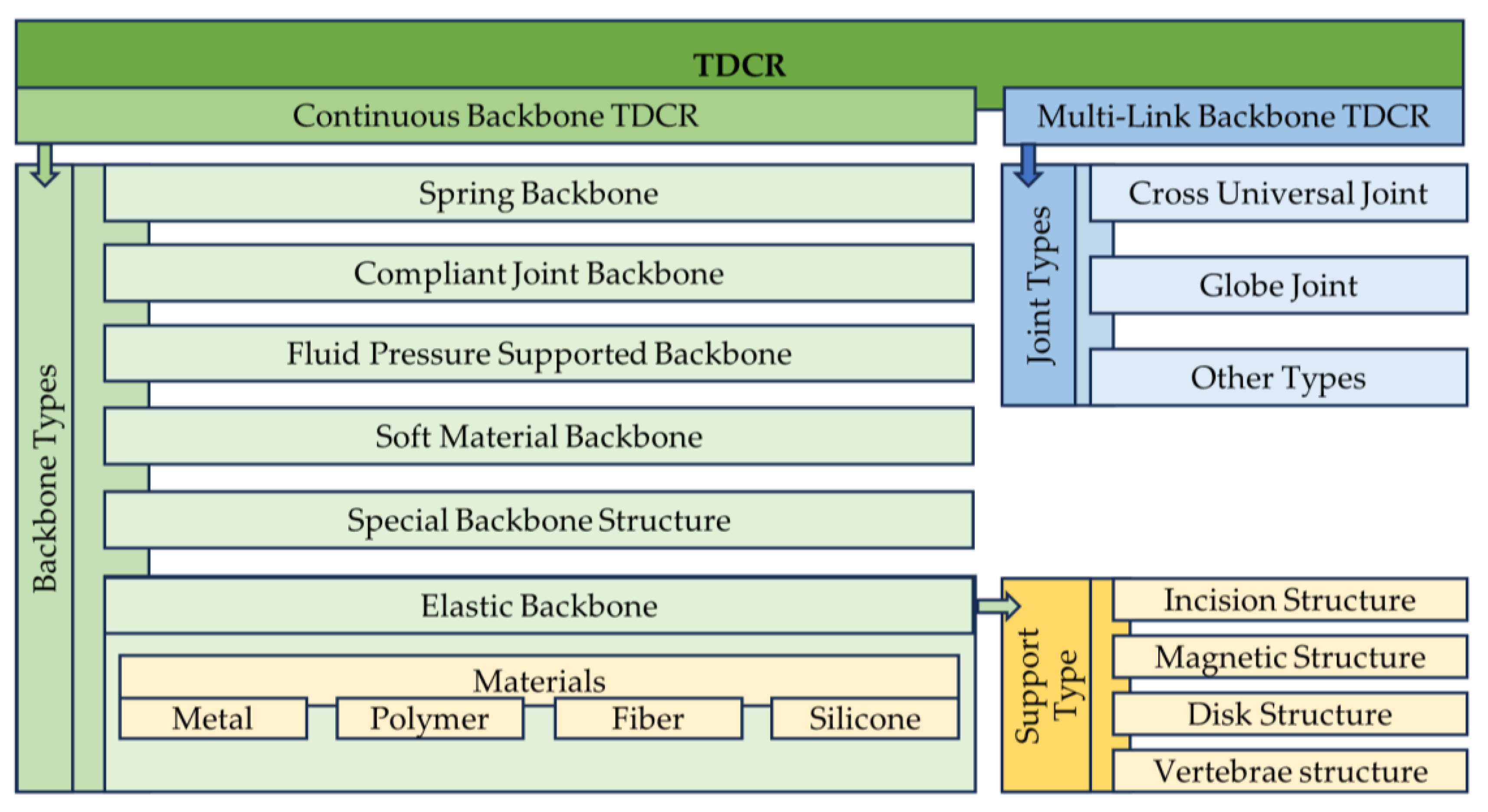
1.4. Categories of CRs
1.5. Previous Literature Surveys on CRs
1.6. Contribution of This Work
- Providing a summary of existing works on CAAMSs and our perspectives on the research horizon;
- Summarising the literature of prototyping materials and methodologies of continuous backbone TDCRs/multi-link backbone TDCRs/manipulators (hereafter, the term ‘flexible manipulators’ will be used to refer both the types together) under a well-structured classification. We study the aspects of flexible manipulators through the following categories: (1) multi-link backbone TDCRs, (2) preparation of TDCR backbone, (3) fabrication of TDCR support structure, (4) tendons, (5) stiffness tuning, and (6) errors and calibration in the TDCR synthesis. This classification provides a systematic approach to understanding various aspects of flexible manipulators and their fabrication;
- Our perspectives on different aspects of flexible manipulator components and fabrication towards aerial manipulation using drones.
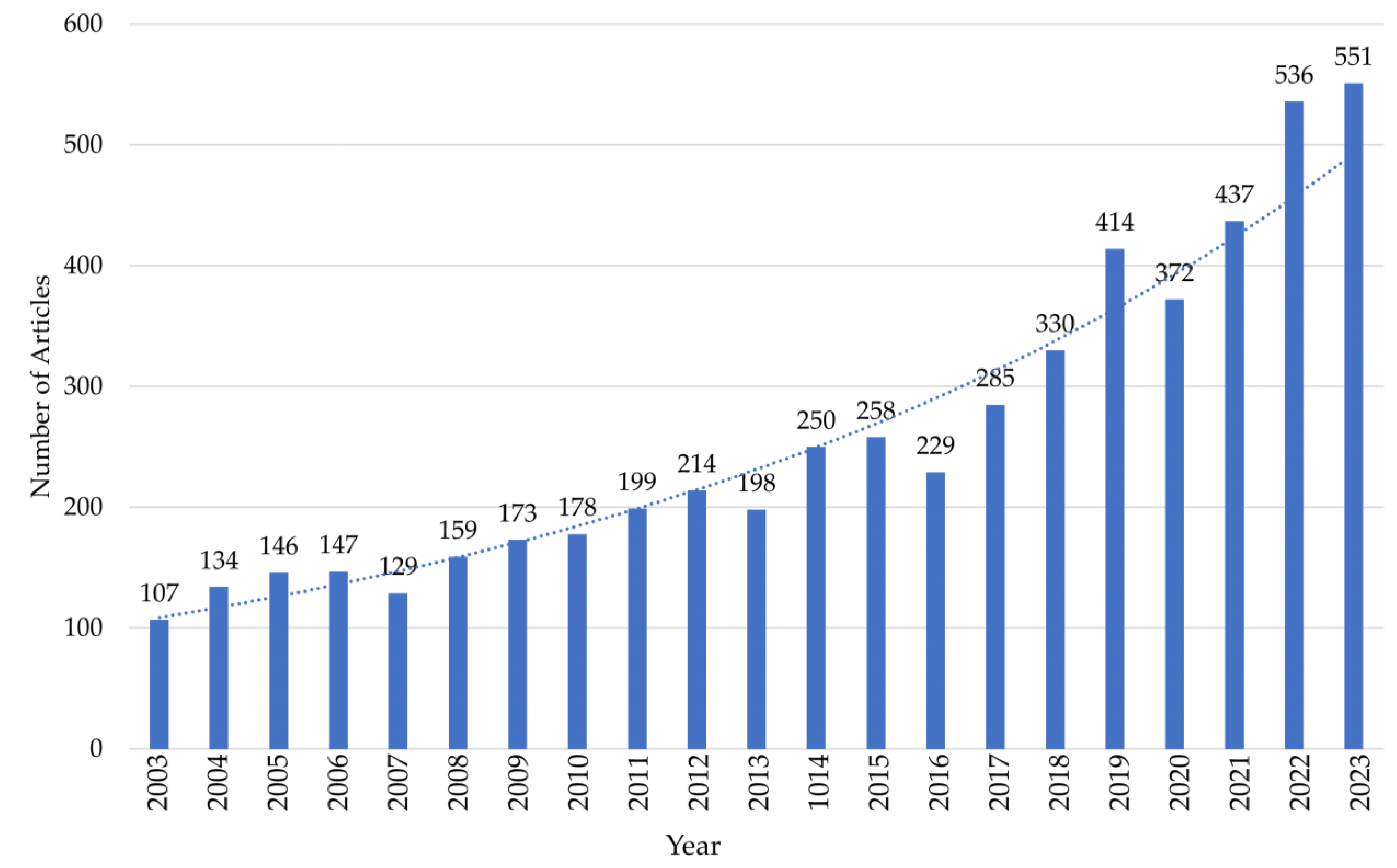
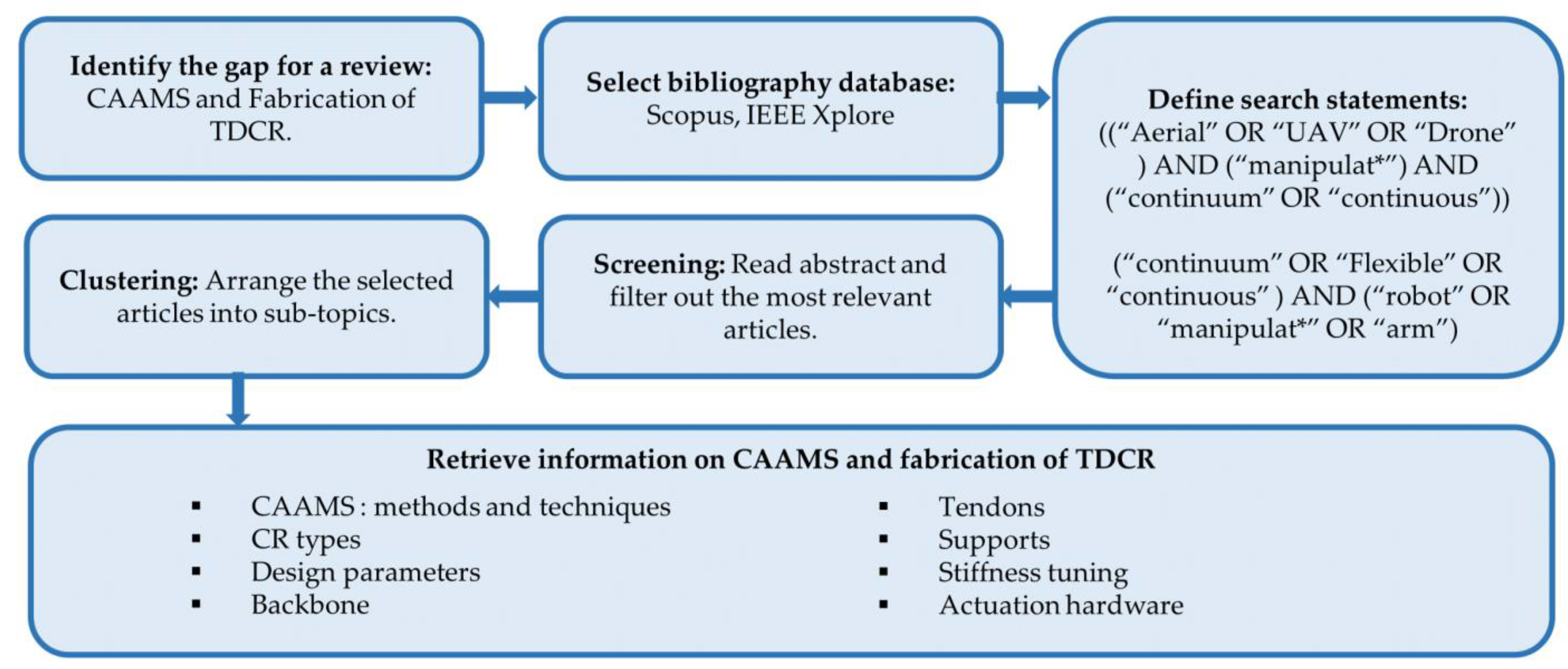
1.7. Review Methodology
2. Continuum Arm Aerial Manipulation Systems (CAAMS)
2.1. Perspectives on CAAMS Research
3. Elements of a TDCR
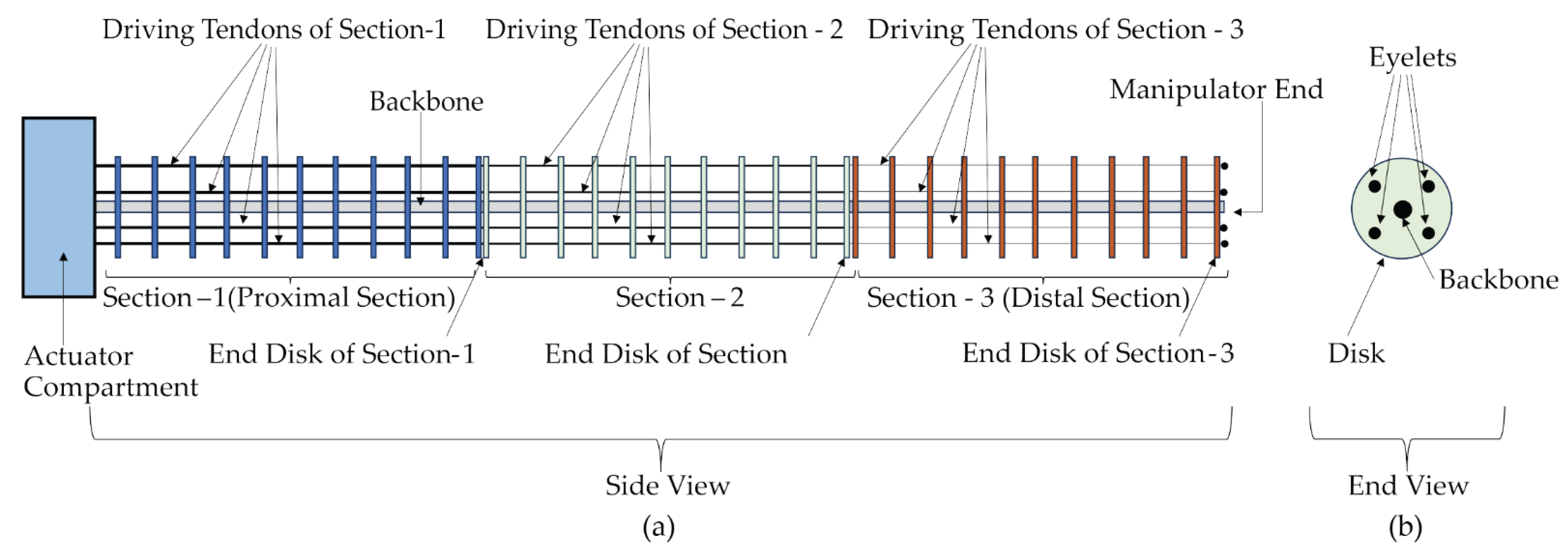
General Design of Typical TDCRs
4. Fabrication of TDCR
4.1. Preparation of Multi-Link Backbone TDCR Structure
4.1.1. Cross-Universal Joint
Vertebrae Profile
Tubular Profile
4.1.2. Globe Joint
4.1.3. Perspectives on Multi-Link Backbone TDCR Designs
4.2. Preparation of TDCR Backbone
4.2.1. Spring Backbone
4.2.2. Elastic Backbone
Metal Alloy Backbone: Fixed Length
Metal Alloy Backbone: Variable Length
- Expandability of the CM;
- Controllability of the individual sections for their lengths if it is a multi-section CM;
- Limit of the diameter of the CM;
- Means of control on bending (extrinsic tendon actuation/intrinsic actuation);
- Adjustability of section stiffness.
4.2.3. Compliant Joint Backbone and Soft Material Backbone
4.2.4. Perspectives on TDCR Backbone Preparation
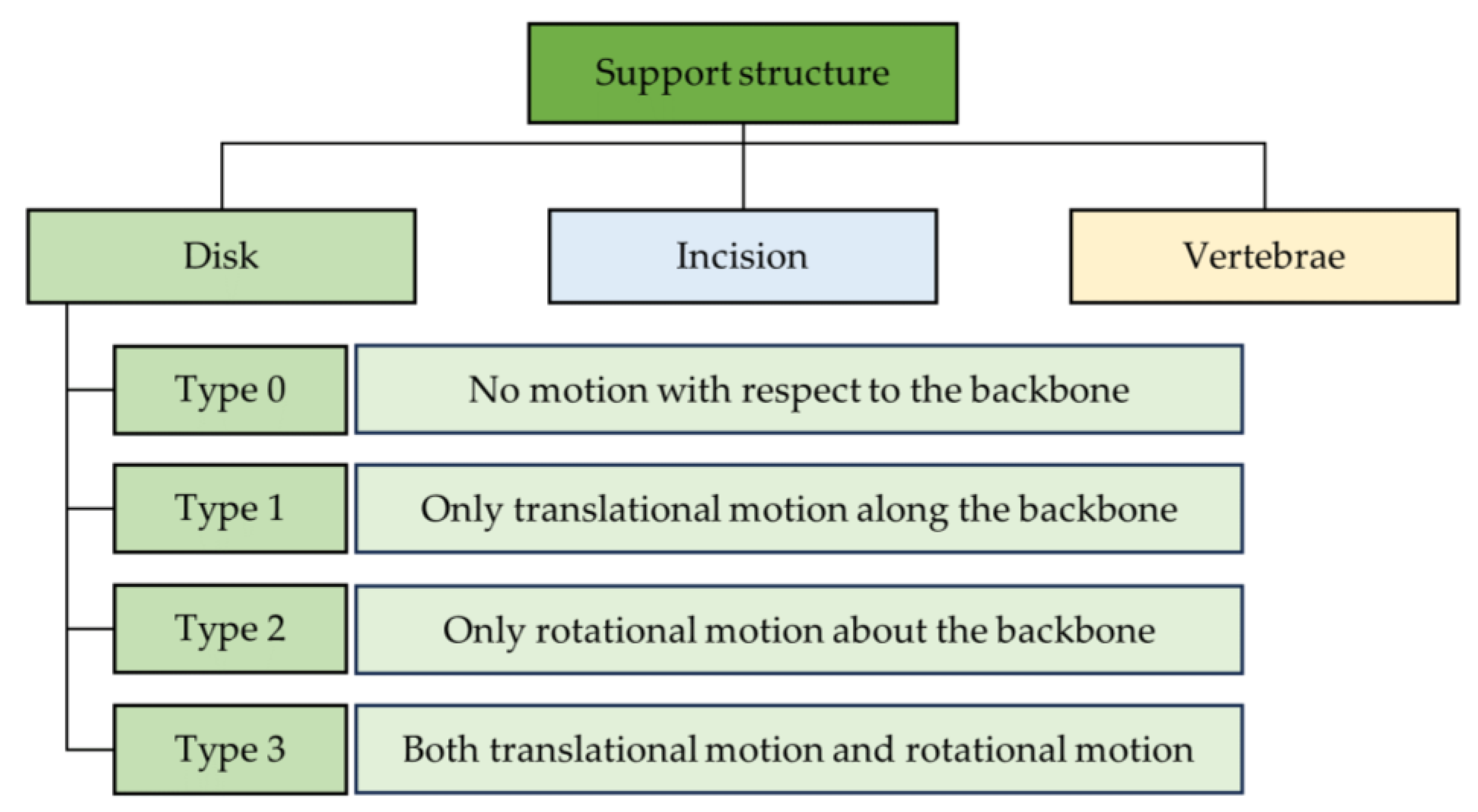
4.3. Fabrication of TDCR Support Structure
Perspectives on TDCR Support Structure
4.4. Preparation and Methods of Tendons
4.4.1. Tendon Pairs
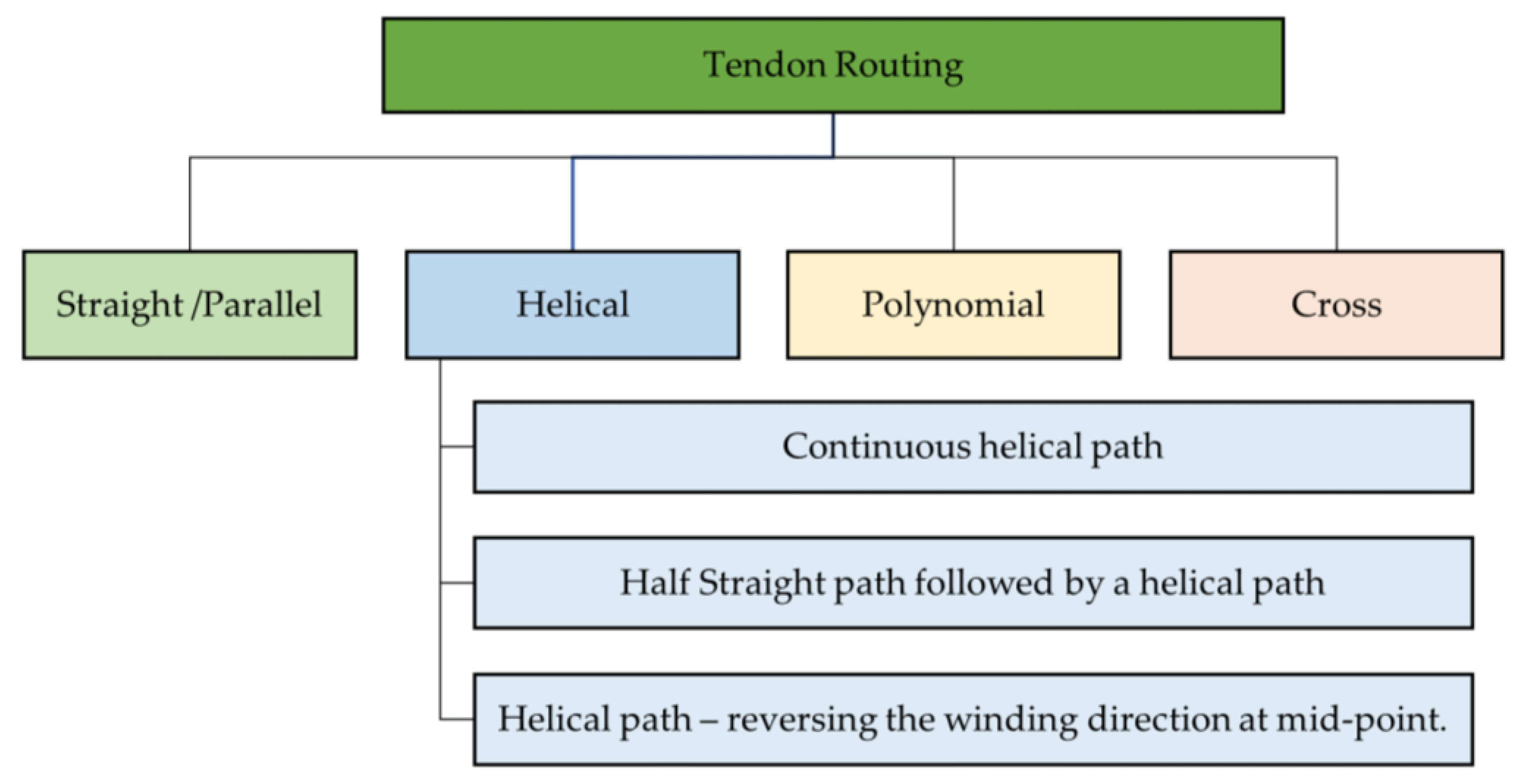
4.4.2. Tendon Routing Methods
- Continuous helix or partial helix;
- Direction of helix (single/mixed);
- Eyelet height;
- Number of turns;
- Initial routing angle and ending angle;
- Helix angle;
- Backbone length;
- Method of routing.
4.4.3. Selection of Tendons
4.4.4. Avoiding Friction
4.4.5. Actuator Reduction Techniques along Side of Tendon Configuration
Technique 1: Driving an Antagonistic Tendon Pair
Technique 2: Cross-Tendon Routing
Technique 3: Using Locking Mechanism
Technique 4: Helical Tendon Routing
4.4.6. Perspectives on Tendons
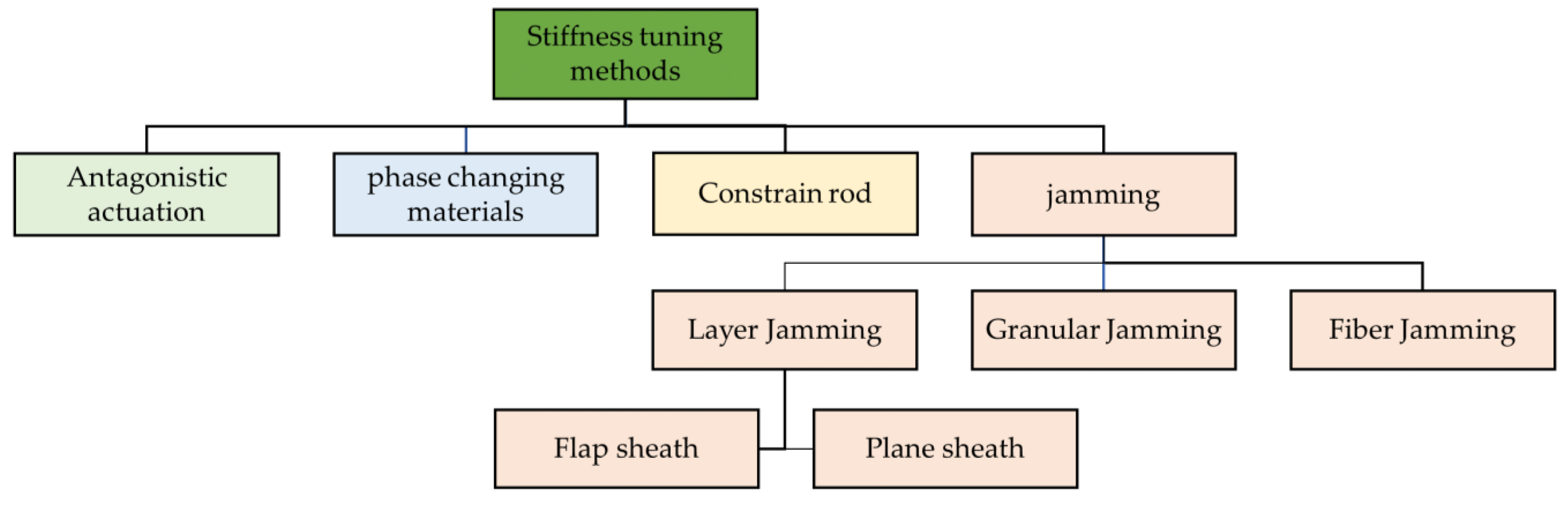
4.5. Stiffness Tuning
| Ref. | Stiffness Direction | Method | Material Used | Remarks | External/Internal to the CM Body | Application |
|---|---|---|---|---|---|---|
| [196] | Transverse | Rods as driving means |
|
| ||
| [150] | Transverse | Curvature-constraining rod |
|
| ||
| [197] | Transverse | Curvature-constraining rod |
|
| MIS instruments | |
| [157] | Transverse and axial directions | Layer jamming |
|
| External surface that only packs the backbone while tendons are lying outside. | Space |
| [193] | Layer jamming and Grannular jamming |
|
| External surface | Medical | |
| [146] | Transverse and axial directions | Layer jamming sheath, vacuum pressure-driven |
|
| External surface | MIS |
| [194] | Transverse | Granular jamming |
|
| Internal jamming. Only packs the backbone spring. | N/A |
| [198] | Transverse | Granular + layer jamming (hybrid) |
|
| External surface | MIS |
| [199] | Granular jamming, layer jamming, hybrid jamming |
|
| Comparative study | ||
| [191] | Transverse | SMA |
|
| Internal |
4.5.1. Jamming-Based Stiffness Tuning
- Layer jamming provides a fast response for both activation and deactivation;
- Hybrid approaches are the best for resistant force-oriented functions;
- Granular jamming using deformable granules is the slowest in response to activation and deactivation.
4.5.2. Curvature-Constraining Rod-Based Stiffness Tuning
4.5.3. Thermomechanical Effects-Based Stiffness Tuning
4.5.4. Perspectives on Stiffness Tuning
4.6. Common Causes of Errors and Calibration
4.6.1. Errors
4.6.2. Calibration
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nooralishahi, P.; Ibarra-Castanedo, C.; Deane, S.; López, F.; Pant, S.; Genest, M.; Avdelidis, N.P.; Maldague, X.P.V. Drone-Based Non-Destructive Inspection of Industrial Sites: A Review and Case Studies. Drones 2021, 5, 106. [Google Scholar] [CrossRef]
- Messina, G.; Modica, G. Applications of UAV Thermal Imagery in Precision Agriculture: State of the Art and Future Research Outlook. Remote Sens. 2020, 12, 1491. [Google Scholar] [CrossRef]
- Kim, J.; Kim, S.; Ju, C.; Son, H.I. Unmanned Aerial Vehicles in Agriculture: A Review of Perspective of Platform, Control, and Applications. IEEE Access 2019, 7, 105100–105115. [Google Scholar] [CrossRef]
- Daud, S.M.S.M.; Yusof, M.Y.P.M.; Heo, C.C.; Khoo, L.S.; Singh, M.K.C.; Mahmood, M.S.; Nawawi, H. Applications of drone in disaster management: A scoping review. Sci. Justice 2022, 62, 30–42. [Google Scholar] [CrossRef] [PubMed]
- Asadzadeh, S.; de Oliveira, W.J.; de Souza Filho, C.R. UAV-based remote sensing for the petroleum industry and environmental monitoring: State-of-the-art and perspectives. J. Pet. Sci. Eng. 2022, 208, 109633. [Google Scholar] [CrossRef]
- Ding, L.; Zhu, G.; Li, Y.; Wang, Y. Cable-Driven Unmanned Aerial Manipulator Systems for Water Sampling: Design, Modeling, and Control. Drones 2023, 7, 450. [Google Scholar] [CrossRef]
- Villa, T.F.; Gonzalez, F.; Miljievic, B.; Ristovski, Z.D.; Morawska, L. An Overview of Small Unmanned Aerial Vehicles for Air Quality Measurements: Present Applications and Future Prospectives. Sensors 2016, 16, 1072. [Google Scholar] [CrossRef] [PubMed]
- Abbas, N.; Abbas, Z.; Liu, X.; Khan, S.S.; Foster, E.D.; Larkin, S. A Survey: Future Smart Cities Based on Advance Control of Unmanned Aerial Vehicles (UAVs). Appl. Sci. 2023, 13, 9881. [Google Scholar] [CrossRef]
- Mohsan, S.A.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the Unmanned Aerial Vehicles (UAVs): A Comprehensive Review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Galvez-Serna, J.; Vanegas, F.; Brar, S.; Sandino, J.; Flannery, D.; Gonzalez, F. UAV4PE: An Open-Source Framework to Plan UAV Autonomous Missions for Planetary Exploration. Drones 2022, 6, 391. [Google Scholar] [CrossRef]
- Serna, J.G.; Vanegas, F.; Gonzalez, F.; Flannery, D. A Review of Current Approaches for UAV Autonomous Mission Planning for Mars Biosignatures Detection. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–15. [Google Scholar] [CrossRef]
- Holness, C.; Matthews, T.; Satchell, K.; Swindell, E.C. Remote sensing archeological sites through Unmanned Aerial Vehicle (UAV) imaging. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6695–6698. [Google Scholar] [CrossRef]
- Bonyan Khamseh, H.; Janabi-Sharifi, F.; Abdessameud, A. Aerial manipulation—A literature survey. Robot. Auton. Syst. 2018, 107, 221–235. [Google Scholar] [CrossRef]
- Ollero, A.; Tognon, M.; Suarez, A.; Lee, D.; Franchi, A. Past, Present, and Future of Aerial Robotic Manipulators. IEEE Trans. Robot. 2022, 38, 626–645. [Google Scholar] [CrossRef]
- Mellinger, D.; Lindsey, Q.; Shomin, M.; Kumar, V. Design, modeling, estimation and control for aerial grasping and manipulation. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 2668–2673. [Google Scholar] [CrossRef]
- Ng, M.; Vanegas, F.; Morton, K.; Sandino, J.; Gonzalez, F. Design and Flight Test of an Aerial Manipulator for Applications in GPS-Denied Environments. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems, ICUAS 2022, Dubrovnik, Croatia, 21–24 June 2022; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2022; pp. 20–29. [Google Scholar] [CrossRef]
- Trujillo, M.Á.; Martínez-de Dios, J.R.; Martín, C.; Viguria, A.; Ollero, A. Novel Aerial Manipulator for Accurate and Robust Industrial NDT Contact Inspection: A New Tool for the Oil and Gas Inspection Industry. Sensors 2019, 19, 1305. [Google Scholar] [CrossRef] [PubMed]
- AlAkhras, A.; Sattar, I.H.; Alvi, M.; Qanbar, M.W.; Jaradat, M.A.; Alkaddour, M. The Design of a Lightweight Cable Aerial Manipulator with a CoG Compensation Mechanism for Construction Inspection Purposes. Appl. Sci. 2022, 12, 1173. [Google Scholar] [CrossRef]
- Zaman, A.; Seo, J. Design and Control of Autonomous Flying Excavator. Machines 2023, 12, 23. [Google Scholar] [CrossRef]
- Heredia, G.; Jimenez-Cano, A.E.; Sanchez, I.; Llorente, D.; Vega, V.; Braga, J.; Acosta, J.A.; Ollero, A. Control of a multirotor outdoor aerial manipulator. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 3417–3422. [Google Scholar]
- Suarez, A.; Jimenez-Cano, A.E.; Vega, V.M.; Heredia, G.; Rodriguez-Castaño, A.; Ollero, A. Design of a lightweight dual arm system for aerial manipulation. Mechatronics 2018, 50, 30–44. [Google Scholar] [CrossRef]
- Suarez, A.; Heredia, G.; Ollero, A. Design of an Anthropomorphic, Compliant, and Lightweight Dual Arm for Aerial Manipulation. IEEE Access 2018, 6, 29173–29189. [Google Scholar] [CrossRef]
- Zhang, K.; Chermprayong, P.; Xiao, F.; Tzoumanikas, D.; Dams, B.; Kay, S.; Kocer, B.B.; Burns, A.; Orr, L.; Alhinai, T.; et al. Aerial additive manufacturing with multiple autonomous robots. Nature 2022, 609, 709–717. [Google Scholar] [CrossRef] [PubMed]
- Chermprayong, P.; Zhang, K.; Xiao, F.; Kovac, M. An Integrated Delta Manipulator for Aerial Repair: A New Aerial Robotic System. IEEE Robot. Autom. Mag. 2019, 26, 54–66. [Google Scholar] [CrossRef]
- Estevez, J.; Garate, G.; Lopez-Guede, J.M.; Larrea, M. Review of Aerial Transportation of Suspended-Cable Payloads with Quadrotors. Drones 2024, 8, 35. [Google Scholar] [CrossRef]
- Caballero, A.; Suarez, A.; Real, F.; Vega, V.M.; Bejar, M.; Rodriguez-Castaño, A.; Ollero, A. First Experimental Results on Motion Planning for Transportation in Aerial Long-Reach Manipulators with Two Arms. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 8471–8477. [Google Scholar]
- Sanchez-Cuevas, P.J.; Gonzalez-Morgado, A.; Cortes, N.; Gayango, D.B.; Jimenez-Cano, A.E.; Ollero, A.; Heredia, G. Fully-Actuated Aerial Manipulator for Infrastructure Contact Inspection: Design, Modeling, Localization, and Control. Sensors 2020, 20, 4708. [Google Scholar] [CrossRef]
- Nicotra, M.M.; Naldi, R.; Garone, E. Taut Cable Control of a Tethered UAV. IFAC Proc. Vol. 2014, 47, 3190–3195. [Google Scholar] [CrossRef]
- Boukoberine, M.N.; Zhou, Z.; Benbouzid, M. A critical review on unmanned aerial vehicles power supply and energy management: Solutions, strategies, and prospects. Appl. Energy 2019, 255, 113823. [Google Scholar] [CrossRef]
- Robla-Gómez, S.; Becerra, V.M.; Llata, J.R.; González-Sarabia, E.; Torre-Ferrero, C.; Pérez-Oria, J. Working Together: A Review on Safe Human-Robot Collaboration in Industrial Environments. IEEE Access 2017, 5, 26754–26773. [Google Scholar] [CrossRef]
- Jalali, A.; Janabi-Sharifi, F. Aerial Continuum Manipulation: A New Platform for Compliant Aerial Manipulation. Front. Robot. AI 2022, 9, 903877. [Google Scholar] [CrossRef] [PubMed]
- Cataldi, E.; Muscio, G.; Trujillo, M.A.; Rodriguez, Y.; Pierri, F.; Antonelli, G.; Caccavale, F.; Viguria, A.; Chiaverini, S.; Ollero, A. Impedance Control of an aerial-manipulator: Preliminary results. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 3848–3853. [Google Scholar]
- Suarez, A.; Perez, M.; Heredia, G.; Ollero, A. Cartesian Aerial Manipulator with Compliant Arm. Appl. Sci. 2021, 11, 1001. [Google Scholar] [CrossRef]
- Forte, F.; Naldi, R.; Macchelli, A.; Marconi, L. Impedance control of an aerial manipulator. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 3839–3844. [Google Scholar] [CrossRef]
- Suarez, A.; Soria, P.R.; Heredia, G.; Arrue, B.C.; Ollero, A. Anthropomorphic, compliant and lightweight dual arm system for aerial manipulation. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 992–997. [Google Scholar] [CrossRef]
- Yüksel, B.; Mahboubi, S.; Secchi, C.; Bülthoff, H.H.; Franchi, A. Design, identification and experimental testing of a light-weight flexible-joint arm for aerial physical interaction. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 870–876. [Google Scholar] [CrossRef]
- Suarez, A.; Heredia, G.; Ollero, A. Lightweight compliant arm for aerial manipulation. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1627–1632. [Google Scholar] [CrossRef]
- Samadikhoshkho, Z.; Ghorbani, S.; Janabi-Sharifi, F. Coupled dynamic modeling and control of aerial continuum manipulation systems. Appl. Sci. 2021, 11, 9108. [Google Scholar] [CrossRef]
- Peng, R.; Wang, Z.; Lu, P. AeCoM: An Aerial Continuum Manipulator With IMU-Based Kinematic Modeling and Tendon-Slacking Prevention. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4740–4752. [Google Scholar] [CrossRef]
- Chien, J.L.; Leong, C.; Liu, J.; Foong, S. Design and control of an aerial-ground tethered tendon-driven continuum robot with hybrid routing. Robot. Auton. Syst. 2023, 161, 104344. [Google Scholar] [CrossRef]
- Samadi Khoshkho, M.; Samadikhoshkho, Z.; Lipsett, M.G. Distilled neural state-dependent Riccati equation feedback controller for dynamic control of a cable-driven continuum robot. Int. J. Adv. Robot. Syst. 2023, 20, 17298806231174737. [Google Scholar] [CrossRef]
- Ghorbani, S.; Samadikhoshkho, Z.; Janabi–Sharifi, F. Dual-arm aerial continuum manipulation systems: Modeling, pre-grasp planning, and control. Nonlinear Dyn. 2023, 111, 7339–7355. [Google Scholar] [CrossRef]
- Ghorbani, S.; Janabi-Sharifi, F. Extended Kalman Filter State Estimation for Aerial Continuum Manipulation Systems. IEEE Sens. Lett. 2022, 6, 7002704. [Google Scholar] [CrossRef]
- Chien, J.L.; Clarissa, L.T.L.; Liu, J.; Low, J.; Foong, S. Kinematic model predictive control for a novel tethered aerial cable-driven continuum robot. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, AIM, Delft, The Netherlands, 12–16 July 2021; Institute of Electrical and Electronics Engineers Inc.: Delft, The Netherlands, 2021; pp. 1348–1354. [Google Scholar] [CrossRef]
- Samadikhoshkho, Z.; Ghorbani, S.; Janabi-Sharifi, F. Modeling and Control of Aerial Continuum Manipulation Systems: A Flying Continuum Robot Paradigm. IEEE Access 2020, 8, 176883–176894. [Google Scholar] [CrossRef]
- Szasz, R.; Allenspach, M.; Han, M.; Tognon, M.; Katzschmann, R.K. Modeling and Control of an Omnidirectional Micro Aerial Vehicle Equipped with a Soft Robotic Arm. In Proceedings of the 2022 IEEE 5th International Conference on Soft Robotics, RoboSoft, Edinburgh, UK, 4–8 April 2022; Institute of Electrical and Electronics Engineers Inc.: Edinburgh, UK, 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Hashemi, S.H.; Janabi-Sharifi, F.; Jalali, A. Robust Global stabilization of aerial continuum manipulation systems via hybrid feedback. ISA Trans. 2023, 138, 160–167. [Google Scholar] [CrossRef] [PubMed]
- Samadikhoshkho, Z.; Ghorbani, S.; Janabi-Sharifi, F. Vision-based reduced-order adaptive control of aerial continuum manipulation systems. Aerosp. Sci. Technol. 2022, 121, 107322. [Google Scholar] [CrossRef]
- Merz, M.; Pedro, D.; Skliros, V.; Bergenhem, C.; Himanka, M.; Houge, T.; Matos-Carvalho, J.P.; Lundkvist, H.; Cürüklü, B.; Hamrén, R.; et al. Autonomous UAS-Based Agriculture Applications: General Overview and Relevant European Case Studies. Drones 2022, 6, 128. [Google Scholar] [CrossRef]
- Hassler, S.C.; Baysal-Gurel, F. Unmanned Aircraft System (UAS) Technology and Applications in Agriculture. Agronomy 2019, 9, 618. [Google Scholar] [CrossRef]
- Choi, H.-W.; Kim, H.-J.; Kim, S.-K.; Na, W.S. An Overview of Drone Applications in the Construction Industry. Drones 2023, 7, 515. [Google Scholar] [CrossRef]
- Koparan, C.; Koc, A.B.; Privette, C.V.; Sawyer, C.B.; Sharp, J.L. Evaluation of a UAV-Assisted Autonomous Water Sampling. Water 2018, 10, 655. [Google Scholar] [CrossRef]
- Morton, K.; Toro, L.F.G.; McFadyen, A. Search and Retrieve with a Fully Autonomous Aerial Manipulator. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Walker, I.D.; Choset, H.; Chirikjian, G.S. Snake-Like and Continuum Robots. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 481–498. [Google Scholar] [CrossRef]
- Chirikjian, G.S. Snakelike and Continuum Robots: A Review of Reviews. In Encyclopedia of Robotics; Ang, M.H., Khatib, O., Siciliano, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–14. [Google Scholar] [CrossRef]
- Roth, B.; Rastegar, J.; Scheinman, V. On the Design of Computer Controlled Manipulators. In On Theory and Practice of Robots and Manipulators: Volume I; Serafini, P., Guazzelli, E., Schrefler, B., Pfeiffer, F., Rammerstorfer, F.G., Eds.; Springer: Vienna, Austria, 1974; pp. 93–113. [Google Scholar] [CrossRef]
- Anderson, V.C.; Horn, R.C. TENSOR ARM MANIPULATOR. 1968, US3497083A, 24 February 1970. Available online: https://patents.google.com/patent/US3497083A/en#patentCitations (accessed on 25 November 2023).
- Burgner-Kahrs, J.; Rucker, D.C.; Choset, H. Continuum Robots for Medical Applications: A Survey. IEEE Trans. Robot. 2015, 31, 1261–1280. [Google Scholar] [CrossRef]
- Robinson, G.; Davies, J.B.C. Continuum robots—A state of the art. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No.99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 4, pp. 2849–2854. [Google Scholar] [CrossRef]
- Walker, I.D. Continuous Backbone “Continuum” Robot Manipulators. ISRN Robot. 2013, 2013, 726506. [Google Scholar] [CrossRef]
- Mitros, Z.; Sadati, S.M.H.; Henry, R.; Da Cruz, L.; Bergeles, C. From Theoretical Work to Clinical Translation: Progress in Concentric Tube Robots. Annu. Rev. Control Robot. Auton. Syst. 2022, 5, 335–359. [Google Scholar] [CrossRef]
- Cao, Y.; Shi, Y.; Hong, W.; Dai, P.; Sun, X.; Yu, H.; Xie, L. Continuum robots for endoscopic sinus surgery: Recent advances, challenges, and prospects. Int. J. Med. Robot. Comput. Assist. Surg. 2023, 19, e2471. [Google Scholar] [CrossRef] [PubMed]
- Kolachalama, S.; Lakshmanan, S. Continuum robots for manipulation applications: A survey. J. Robot. 2020, 2020, 4187048. [Google Scholar] [CrossRef]
- Russo, M.; Sadati, S.M.H.; Dong, X.; Mohammad, A.; Walker, I.D.; Bergeles, C.; Xu, K.; Axinte, D.A. Continuum Robots: An Overview. Adv. Intell. Syst. 2023, 5, 2200367. [Google Scholar] [CrossRef]
- Blumenschein, L.H.; Coad, M.M.; Haggerty, D.A.; Okamura, A.M.; Hawkes, E.W. Design, Modeling, Control, and Application of Everting Vine Robots. Front. Robot. AI 2020, 7, 548266. [Google Scholar] [CrossRef] [PubMed]
- Angrisani, L.; Grazioso, S.; Gironimo, G.D.; Panariello, D.; Tedesco, A. On the use of soft continuum robots for remote measurement tasks in constrained environments: A brief overview of applications. In Proceedings of the 2019 IEEE International Symposium on Measurements and Networking, M and N, Catania, Italy, 8–10 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Alfalahi, H.; Renda, F.; Stefanini, C. Concentric Tube Robots for Minimally Invasive Surgery: Current Applications and Future Opportunities. IEEE Trans. Med. Robot. Bionics 2020, 2, 410–424. [Google Scholar] [CrossRef]
- Nwafor, C.J.; Girerd, C.; Laurent, G.J.; Morimoto, T.K.; Rabenorosoa, K. Design and Fabrication of Concentric Tube Robots: A Survey. IEEE Trans. Robot. 2023, 39, 2510–2528. [Google Scholar] [CrossRef]
- Tang, D.; Cheng, C.; Xiao, L.; Tang, C.; Lv, X.; Wang, G. A Review on Wire-Driven Flexible Robot Manipulators. Recent Pat. Eng. 2023, 17, 37–57. [Google Scholar] [CrossRef]
- Li, S.; Hao, G. Current trends and prospects in compliant continuum robots: A survey. Actuators 2021, 10, 145. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, H.; Cao, Y.; Cui, Y.; Zhang, L. Magnetically Actuated Continuum Medical Robots: A Review. Adv. Intell. Syst. 2023, 5, 2200416. [Google Scholar] [CrossRef]
- Du, X.; Liu, Y.; Yu, J. Magnetically driven robots for clinical treatment. In Robotics for Cell Manipulation and Characterization; Academic Press: Cambridge, MA, USA, 2023; pp. 173–199. [Google Scholar] [CrossRef]
- Walker, I.D. Robot strings: Long, thin continuum robots. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 2–9 March 2013; pp. 1–12. [Google Scholar] [CrossRef]
- Seetohul, J.; Shafiee, M. Snake Robots for Surgical Applications: A Review. Robotics 2022, 11, 57. [Google Scholar] [CrossRef]
- Yang, X.; Zheng, L.; Lü, D.; Wang, J.; Wang, S.; Su, H.; Wang, Z.; Ren, L. The snake-inspired robots: A review. Assem. Autom. 2022, 42, 567–583. [Google Scholar] [CrossRef]
- Walker, I.D. Biologically inspired vine-like and tendril-like robots. In Proceedings of the 2015 Science and Information Conference, London, UK, 28–30 July 2015; Institute of Electrical and Electronics Engineers Inc.: London, UK, 2015; pp. 714–720. [Google Scholar] [CrossRef]
- Wooten, M.B.; Walker, I.D. Circumnutation: From plants to robots. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer International Publishing: Cham, Switzerland, 2016; Volume 9825, pp. 1–11. [Google Scholar] [CrossRef]
- Seleem, I.A.; El-Hussieny, H.; Ishii, H. Recent Developments of Actuation Mechanisms for Continuum Robots: A Review. Int. J. Control Autom. Syst. 2023, 21, 1592–1609. [Google Scholar] [CrossRef] [PubMed]
- Pagoli, A.; Chapelle, F.; Corrales-Ramon, J.A.; Mezouar, Y.; Lapusta, Y. Review of soft fluidic actuators: Classification and materials modeling analysis. Smart Mater. Struct. 2022, 31, 013001. [Google Scholar] [CrossRef]
- Dou, W.; Zhong, G.; Cao, J.; Shi, Z.; Peng, B.; Jiang, L. Soft Robotic Manipulators: Designs, Actuation, Stiffness Tuning, and Sensing. Adv. Mater. Technol. 2021, 6, 2100018. [Google Scholar] [CrossRef]
- Zhang, J.; Fang, Q.; Xiang, P.; Sun, D.; Xue, Y.; Jin, R.; Qiu, K.; Xiong, R.; Wang, Y.; Lu, H. A Survey on Design, Actuation, Modeling, and Control of Continuum Robot. Cyborg Bionic Syst. 2022, 2022, 9754697. [Google Scholar] [CrossRef]
- Simaan, N.; Yasin, R.M.; Wang, L. Medical Technologies and Challenges of Robot-Assisted Minimally Invasive Intervention and Diagnostics. Annu. Rev. Control Robot. Auton. Syst. 2018, 1, 465–490. [Google Scholar] [CrossRef]
- Walker, I.D.; Clemson University. Use of continuum robots for remote inspection operations. In Proceedings of the 2017 Computing Conference, London, UK, 18–20 July 2017; pp. 1382–1385. [Google Scholar] [CrossRef]
- Kim, J.; De Mathelin, M.; Ikuta, K.; Kwon, D.S. Advancement of Flexible Robot Technologies for Endoluminal Surgeries. Proc. IEEE 2022, 110, 909–931. [Google Scholar] [CrossRef]
- Da Veiga, T.; Chandler, J.H.; Lloyd, P.; Pittiglio, G.; Wilkinson, N.J.; Hoshiar, A.K.; Harris, R.A.; Valdastri, P. Challenges of continuum robots in clinical context: A review. Prog. Biomed. Eng. 2020, 2, 032003. [Google Scholar] [CrossRef]
- Chikhaoui, M.T.; Burgner-Kahrs, J. Control of continuum robots for medical applications: State of the art. In Proceedings of the ACTUATOR 2018, 16th International Conference on New Actuators, Bremen, Germany, 25-27 June 2018; pp. 1–11. [Google Scholar]
- Hu, X.; Chen, A.; Luo, Y.; Zhang, C.; Zhang, E. Steerable catheters for minimally invasive surgery: A review and future directions. Comput. Assist. Surg. 2018, 23, 21–41. [Google Scholar] [CrossRef]
- Gu, X.; Ren, H. A Survey of Transoral Robotic Mechanisms: Distal Dexterity, Variable Stiffness, and Triangulation. Cyborg Bionic Syst. 2023, 4, 0007. [Google Scholar] [CrossRef] [PubMed]
- Chirikjian, G.S. Conformational Modeling of Continuum Structures in Robotics and Structural Biology: A Review. Adv. Robot. 2015, 29, 817–829. [Google Scholar] [CrossRef] [PubMed]
- Webster Iii, R.J.; Jones, B.A. Design and kinematic modeling of constant curvature continuum robots: A review. Int. J. Robot. Res. 2010, 29, 1661–1683. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Zhang, H.; Liang, J.; Zang, H.; Li, H.; Wang, R. Design of compliant mechanisms using continuum topology optimization: A review. Mech. Mach. Theory 2020, 143, 103622. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Ghayesh, M.H.; Chin, R.; Amabili, M. Hyperelastic structures: A review on the mechanics and biomechanics. Int. J. Non-Linear Mech. 2023, 148, 104275. [Google Scholar] [CrossRef]
- Shamilyan, O.; Kabin, I.; Dyka, Z.; Sudakov, O.; Cherninskyi, A.; Brzozowski, M.; Langendoerfer, P. Intelligence and Motion Models of Continuum Robots: An Overview. IEEE Access 2023, 11, 60988–61003. [Google Scholar] [CrossRef]
- Sadati, S.M.H.; Naghibi, S.E.; Shiva, A.; Walker, I.D.; Althoefer, K.; Nanayakkara, T. Mechanics of Continuum Manipulators, a Comparative Study of Five Methods with Experiments. In Towards Autonomous Robotic Systems. TAROS 2017; Gao, Y., Fallah, S., Jin, Y., Lekakou, C., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10454. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Ghayesh, M.H.; Chin, R.; Amabili, M. A review on the nonlinear dynamics of hyperelastic structures. Nonlinear Dyn. 2022, 110, 963–994. [Google Scholar] [CrossRef]
- Saab, W.; Rone, W.S.; Ben-Tzvi, P. Robotic tails: A state-of-the-art review. Robotica 2018, 36, 1263–1277. [Google Scholar] [CrossRef]
- Armanini, C.; Boyer, F.; Mathew, A.T.; Duriez, C.; Renda, F. Soft Robots Modeling: A Structured Overview. IEEE Trans. Robot. 2023, 39, 1728–1748. [Google Scholar] [CrossRef]
- Pore, A.; Li, Z.; Dall’Alba, D.; Hernansanz, A.; De Momi, E.; Menciassi, A.; Casals Gelpi, A.; Dankelman, J.; Fiorini, P.; Poorten, E.V. Autonomous Navigation for Robot-Assisted Intraluminal and Endovascular Procedures: A Systematic Review. IEEE Trans. Robot. 2023, 39, 2529–2548. [Google Scholar] [CrossRef]
- George Thuruthel, T.; Ansari, Y.; Falotico, E.; Laschi, C. Control Strategies for Soft Robotic Manipulators: A Survey. Soft Robot. 2018, 5, 149–163. [Google Scholar] [CrossRef] [PubMed]
- Della Santina, C.; Duriez, C.; Rus, D. Model-Based Control of Soft Robots: A Survey of the State of the Art and Open Challenges. IEEE Control Syst. 2023, 43, 30–65. [Google Scholar] [CrossRef]
- Xu, F.; Wang, H. Soft Robotics: Morphology and Morphology-inspired Motion Strategy. IEEE/CAA J. Autom. Sin. 2021, 8, 1500–1522. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Kwok, K.W. A Survey for Machine Learning-Based Control of Continuum Robots. Front. Robot. AI 2021, 8, 730330. [Google Scholar] [CrossRef] [PubMed]
- Nazari, A.A.; Zareinia, K.; Janabi-Sharifi, F. Visual servoing of continuum robots: Methods, challenges, and prospects. Int. J. Med. Robot. Comput. Assist. Surg. 2022, 18, e2384. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Ren, L.; Chen, Y.; Niu, S.; Han, Z.; Ren, L. Bio-Inspired Soft Grippers Based on Impactive Gripping. Adv. Sci. 2021, 8, 2002017. [Google Scholar] [CrossRef] [PubMed]
- Mehrkish, A.; Janabi-Sharifi, F. A comprehensive grasp taxonomy of continuum robots. Robot. Auton. Syst. 2021, 145, 103860. [Google Scholar] [CrossRef]
- Russo, M.; Gautreau, E.; Bonnet, X.; Laribi, M.A. Continuum Robots: From Conventional to Customized Performance Indicators. Biomimetics 2023, 8, 147. [Google Scholar] [CrossRef]
- Sahu, S.K.; Sozer, C.; Rosa, B.; Tamadon, I.; Renaud, P.; Menciassi, A. Shape Reconstruction Processes for Interventional Application Devices: State of the Art, Progress, and Future Directions. Front. Robot. AI 2021, 8, 758411. [Google Scholar] [CrossRef]
- Shi, C.; Luo, X.; Qi, P.; Li, T.; Song, S.; Najdovski, Z.; Fukuda, T.; Ren, H. Shape sensing techniques for continuum robots in minimally invasive surgery: A survey. IEEE Trans. Biomed. Eng. 2017, 64, 1665–1678. [Google Scholar] [CrossRef] [PubMed]
- Howard, D.; Connor, J.O.; Letchford, J.; Joseph, T.; Lin, S.; Baldwin, S.; Delaney, G. A Comprehensive Dataset of Grains for Granular Jamming in Soft Robotics: Grip Strength and Shock Absorption. In Proceedings of the 2023 IEEE International Conference on Soft Robotics (RoboSoft), Singapore, 3–7 April 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Aktaş, B.; Narang, Y.S.; Vasios, N.; Bertoldi, K.; Howe, R.D. A Modeling Framework for Jamming Structures. Adv. Funct. Mater. 2021, 31, 2007554. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Chen, Y. Principles and methods for stiffness modulation in soft robot design and development. Bio-Des. Manuf. 2018, 1, 14–25. [Google Scholar] [CrossRef]
- Mahvash, M.; Dupont, P.E. Stiffness control of surgical continuum manipulators. IEEE Trans. Robot. 2011, 27, 334–345. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Peyron, Q.; Kim, J.; Burgner-Kahrs, J. Design of lightweight and extensible tendon-driven continuum robots using origami patterns. In Proceedings of the 2021 IEEE 4th International Conference on Soft Robotics, New Haven, CT, USA, 12–16 April 2021; Institute of Electrical and Electronics Engineers Inc.: New Haven, CT, USA, 2021; pp. 308–314. [Google Scholar] [CrossRef]
- Zhang, K.; Qiu, C.; Dai, J.S. An extensible continuum robot with integrated origami parallel modules. J. Mech. Robot. 2016, 8, 031010. [Google Scholar] [CrossRef]
- Hassan, T.; Cianchetti, M.; Mazzolai, B.; Laschi, C.; Dario, P. Active-Braid, a Bioinspired Continuum Manipulator. IEEE Robot. Autom. Lett. 2017, 2, 2104–2110. [Google Scholar] [CrossRef]
- Yeshmukhametov, A.; Koganezawa, K.; Yamamoto, Y. Design and Kinematics of Cable-Driven Continuum Robot Arm with Universal Joint Backbone. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 2444–2449. [Google Scholar] [CrossRef]
- Mousa, A.; Khoo, S.; Norton, M. Robust Control of Tendon Driven Continuum Robots. In Proceedings of the 2018 15th International Workshop on Variable Structure Systems (VSS), Graz, Austria, 9–11 July 2018; pp. 49–54. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, G.; Jafarnejadsani, H.; Wang, L. A Modular Continuum Manipulator for Aerial Manipulation and Perching. In Proceedings of the ASME 2022 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Volume 7: 46th Mechanisms and Robotics Conference (MR), St. Louis, MI, USA, 14–17 August 2022. V007T07A014. ASME. [Google Scholar] [CrossRef]
- Hughes, J.; Culha, U.; Giardina, F.; Guenther, F.; Rosendo, A.; Iida, F. Soft Manipulators and Grippers: A Review. Front. Robot. AI 2016, 3, 69. [Google Scholar] [CrossRef]
- Zhang, B.; Xie, Y.; Zhou, J.; Wang, K.; Zhang, Z. State-of-the-art robotic grippers, grasping and control strategies, as well as their applications in agricultural robots: A review. Comput. Electron. Agric. 2020, 177, 105694. [Google Scholar] [CrossRef]
- Starke, J.; Amanov, E.; Chikhaoui, M.T.; Burgner-Kahrs, J. On the merits of helical tendon routing in continuum robots. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Vancouver, BC, Canada, 24–28 September 2017; Institute of Electrical and Electronics Engineers Inc.: Vancouver, BC, Canada, 2017; pp. 6470–6476. [Google Scholar] [CrossRef]
- Rucker, D.C.; Webster, R.J., III. Statics and Dynamics of Continuum Robots With General Tendon Routing and External Loading. IEEE Trans. Robot. 2011, 27, 1033–1044. [Google Scholar] [CrossRef]
- Anzhu, G.; Hao, L.; Yuanyuan, Z.; Zhenda, Y.; Zhidong, W.; Hongyi, L. A cross-helical tendons actuated dexterous continuum manipulator. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 2012–2017. [Google Scholar] [CrossRef]
- Li, C.; Rahn, C.D. Design of Continuous Backbone, Cable-Driven Robots. J. Mech. Des. 2002, 124, 265–271. [Google Scholar] [CrossRef]
- Tonapi, M.M.; Godage, I.S.; Vijaykumar, A.M.; Walker, I.D. A novel continuum robotic cable aimed at applications in space. Adv. Robot. 2015, 29, 861–875. [Google Scholar] [CrossRef]
- Amanov, E.; Nguyen, T.D.; Burgner-Kahrs, J. Tendon-driven continuum robots with extensible sections—A model-based evaluation of path-following motions. Int. J. Robot. Res. 2021, 40, 7–23. [Google Scholar] [CrossRef]
- Briot, S.; Goldsztejn, A. Singularity Conditions for Continuum Parallel Robots. IEEE Trans. Robot. 2022, 38, 507–525. [Google Scholar] [CrossRef]
- Shihora, N.; Simaan, N. Geometric Insights into Kinematically-Singular Configurations of Planar Continuum Robots. In Advances in Robot Kinematics 2022; Altuzarra, O., Kecskeméthy, A., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 237–247. [Google Scholar]
- Mayer, A.; Sawodny, O. Singularity and Workspace Analysis for Modular Continuum Robots. In Proceedings of the 2018 IEEE Conference on Control Technology and Applications (CCTA), Copenhagen, Denmark, 21–24 August 2018; pp. 280–285. [Google Scholar] [CrossRef]
- Gravagne, I.A.; Walker, I.D. Manipulability and force ellipsoids for continuum robot manipulators. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the Next Millennium (Cat. No.01CH37180), Maui, HI, USA, 29 October–3 November 2001; Volume 1, pp. 304–311. [Google Scholar] [CrossRef]
- Jones, B.A.; Walker, I.D. Limiting-case Analysis of Continuum Trunk Kinematics. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 1363–1368. [Google Scholar] [CrossRef]
- Zaccaria, F.; Idá, E.; Briot, S. Singularity Conditions of Concentric Tube Robots. In Advances in Mechanism and Machine Science; Okada, M., Ed.; Springer Nature: Cham, Switzerland, 2023; pp. 376–385. [Google Scholar]
- Lilge, S.; Wen, K.; Burgner-Kahrs, J. Singularity analysis of 3-DOF planar parallel continuum robots with constant curvature links. Front. Robot. AI 2023, 9, 1082185. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Wang, X.; Zhang, Z.; Zhu, P.; Cheng, S.S.; Samuel Au, K.W. Design and Experimental Validation of a Novel Hybrid Continuum Robot With Enhanced Dexterity and Manipulability in Confined Space. IEEE/ASME Trans. Mechatron. 2023, 28, 1826–1835. [Google Scholar] [CrossRef]
- Wang, M.; Palmer, D.; Dong, X.; Alatorre, D.; Axinte, D.; Norton, A. Design and Development of a Slender Dual-Structure Continuum Robot for In-Situ Aeroengine Repair. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; Institute of Electrical and Electronics Engineers Inc.: Madrid, Spain, 2018; pp. 5648–5653. [Google Scholar] [CrossRef]
- Li, G.; Yu, J.; Dong, D.; Pan, J.; Wu, H.; Cao, S.; Pei, X.; Huang, X.; Yi, J. Systematic Design of a 3-DOF Dual-Segment Continuum Robot for In Situ Maintenance in Nuclear Power Plants. Machines 2022, 10, 596. [Google Scholar] [CrossRef]
- Yeshmukhametov, A.; Koganezawa, K.; Yamamoto, Y.; Buribayev, Z.; Mukhtar, Z.; Amirgaliyev, Y. Development of Continuum Robot Arm and Gripper for Harvesting Cherry Tomatoes. Appl. Sci. 2022, 12, 6922. [Google Scholar] [CrossRef]
- Walker, I.D.; Hannan, M.W. A novel ‘elephant’s trunk’ robot. In Proceedings of the 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (Cat. No.99TH8399), Atlanta, GA, USA, 19–23 September 1999; pp. 410–415. [Google Scholar] [CrossRef]
- Harsono, E.; Yang, J.; Bhattacharya, S.; Yu, H. Design and analysis of a novel hybrid-driven continuum robot with variable stiffness. Mech. Mach. Theory 2022, 177, 105067. [Google Scholar] [CrossRef]
- Gautreau, E.; Sandoval, J.; Bonnet, X.; Arsicault, M.; Zeghloul, S.; Laribi, M.A. A New Bio-Inspired Hybrid Cable-Driven Robot (HCDR) to Design More Realistic Snakebots. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 2134–2140. [Google Scholar] [CrossRef]
- Lei, F.; Yi, S.; Liu, S.; Liao, J.; Guo, Z.; Wang, Z.; Yan, T.; Dang, R.; Su, B. Design and Modeling of a Cable-driven Continuum Robot Considering Large Load. In Proceedings of the 2023 International Conference on Advanced Robotics and Mechatronics (ICARM), Sanya, China, 8–10 July 2023; pp. 581–586. [Google Scholar] [CrossRef]
- Liu, N.; Abdelaziz, M.E.M.K.; Shen, M.; Yang, G.Z. Design and kinematics characterization of a laser-profiled continuum manipulator for the guidance of bronchoscopic instruments. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 25–31. [Google Scholar] [CrossRef]
- Gao, A.; Liu, N.; Shen, M.; Abdelaziz, M.E.M.K.; Temelkuran, B.; Yang, G.Z. Laser-Profiled Continuum Robot with Integrated Tension Sensing for Simultaneous Shape and Tip Force Estimation. Soft Robot. 2020, 7, 421–443. [Google Scholar] [CrossRef]
- Na, Y.M.; Lee, H.S.; Park, J.K. Fabrication and experiment of an automatic continuum robot system using image recognition. J. Mech. Robot. 2020, 12, 011017. [Google Scholar] [CrossRef]
- Shen, D.; Zhang, Q.; Han, Y.; Tu, C.; Wang, X. Design and Development of a Continuum Robot with Switching-Stiffness. Soft Robot. 2023, 10, 1015–1027. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Liu, D.; Ye, L. A Novel Continuum Robot With Stiffness Variation Capability Using Layer Jamming: Design, Modeling, and Validation. IEEE Access 2022, 10, 130253–130263. [Google Scholar] [CrossRef]
- Li, L.; Jin, T.; Tian, Y.; Yang, F.; Xi, F. Design and Analysis of a Square-Shaped Continuum Robot with Better Grasping Ability. IEEE Access 2019, 7, 57151–57162. [Google Scholar] [CrossRef]
- Ma, N.; Monk, S.; Cheneler, D. Modelling and Analysis of the Spital Branched Flexure-Hinge Adjustable-Stiffness Continuum Robot. Robotics 2022, 11, 97. [Google Scholar] [CrossRef]
- Mehling, J.S.; Diftler, M.A.; Chu, M.; Valvo, M. A Minimally Invasive Tendril Robot for In-Space Inspection. In Proceedings of the First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, BioRob 2006, Pisa, Italy, 20–22 February 2006; pp. 690–695. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, W.; Zhang, Z.; Zhu, X.; Xu, K. Continuum Manipulator with Redundant Backbones and Constrained Bending Curvature for Continuously Variable Stiffness. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7492–7499. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Burgner-Kahrs, J. A tendon-driven continuum robot with extensible sections. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; Institute of Electrical and Electronics Engineers Inc.: Hamburg, Germany, 2015; pp. 2130–2135. [Google Scholar] [CrossRef]
- Wooten, M.B.; Walker, I.D. Vine-inspired continuum tendril robots and circumnutations. Robotics 2018, 7, 58. [Google Scholar] [CrossRef]
- Case, J.C.; White, E.L.; Sunspiral, V.; Kramer-Bottiglio, R. Reducing Actuator Requirements in Continuum Robots through Optimized Cable Routing. Soft Robot. 2018, 5, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Remirez, A.A.; Webster, R.J. A new continuum robot with crossed elastic strips: Extensible sections with only one actuator per section. In Proceedings of the ASME 2015 Dynamic Systems and Control Conference, DSCC 2015, Columbus, OH, USA, 28–30 October 2015; American Society of Mechanical Engineers: Columbus, OH, USA, 2015; Volume 3. [Google Scholar] [CrossRef]
- Visentin, F.; Mishra, A.K.; Naselli, G.A.; Mazzolai, B. Simplified Sensing and Control of a Plant-Inspired Cable Driven Manipulator. In Proceedings of the 2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), Seoul, Republic of Korea, 14–18 April 2019; pp. 422–427. [Google Scholar] [CrossRef]
- Su, B.; Tang, J.; Kuang, S.; Jin, M.; Wu, H.; Liu, L.; Liu, H.; Wang, J.; Sun, H.; Lam, L.; et al. Extensible and Compressible Continuum Robot: A Preliminary Result. In Proceedings of the WRC SARA 2019-World Robot Conference Symposium on Advanced Robotics and Automation 2019, Beijing, China, 21–22 August 2019; Institute of Electrical and Electronics Engineers Inc.: Beijing, China, 2019; pp. 44–49. [Google Scholar] [CrossRef]
- Santiago, J.L.C.; Walker, I.D.; Godage, I.S. Continuum robots for space applications based on layer-jamming scales with stiffening capability. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 7–14 March 2015; IEEE Computer Society: Big Sky, MT, USA, 2015. [Google Scholar] [CrossRef]
- Xing, Z.; Wang, P.; Cao, G.; Liu, Y.; He, Z.; Zhao, J. A Novel Design of a Contractible, Tubular Continuum Manipulator. In Proceedings of the 2021 6th IEEE International Conference on Advanced Robotics and Mechatronics (ICARM), Chongqing, China, 3–5 July 2021; pp. 335–339. [Google Scholar] [CrossRef]
- Simaan, N.; Kai, X.; Wei, W.; Kapoor, A.; Kazanzides, P.; Taylor, R.; Flint, P. Design and Integration of a Telerobotic System for Minimally Invasive Surgery of the Throat. Int. J. Robot. Res. 2009, 28, 1134–1153. [Google Scholar] [CrossRef] [PubMed]
- Qi, P.; Qiu, C.; Liu, H.; Dai, J.S.; Seneviratne, L.D.; Althoefer, K. A Novel Continuum Manipulator Design Using Serially Connected Double-Layer Planar Springs. IEEE/ASME Trans. Mechatron. 2016, 21, 1281–1292. [Google Scholar] [CrossRef]
- Amouri, A.; Cherfia, A.; Belkhiri, A.; Merabti, H. Bio-inspired a novel dual-cross-module sections cable-driven continuum robot: Design, kinematics modeling and workspace analysis. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 265. [Google Scholar] [CrossRef]
- Grassmann, R.M.; Rao, P.; Peyron, Q.; Burgner-Kahrs, J. FAS—A Fully Actuated Segment for Tendon-Driven Continuum Robots. Front. Robot. AI 2022, 9, 873446. [Google Scholar] [CrossRef]
- Kang, B.; Kojcev, R.; Sinibaldi, E. The First Interlaced Continuum Robot, Devised to Intrinsically Follow the Leader. PLoS ONE 2016, 11, e0150278. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Zhao, Q.-J.; Wang, L. A Lightweight Modular Continuum Manipulator with IMU-based Force Estimation. arXiv 2022, arXiv:2211.11874. [Google Scholar]
- Wu, Z.; Li, Q.; Zhao, J.; Gao, J.; Xu, K. Design of a Modular Continuum-Articulated Laparoscopic Robotic Tool with Decoupled Kinematics. IEEE Robot. Autom. Lett. 2019, 4, 3545–3552. [Google Scholar] [CrossRef]
- Pogue, C.; Rao, P.; Peyron, Q.; Kim, J.; Burgner-Kahrs, J.; Diller, E. Multiple Curvatures in a Tendon-Driven Continuum Robot Using a Novel Magnetic Locking Mechanism. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Kyoto, Japan, 23–27 October 2022; Institute of Electrical and Electronics Engineers Inc.: Kyoto, Japan, 2022; pp. 472–479. [Google Scholar] [CrossRef]
- Amanov, E.; Granna, J.; Burgner-Kahrs, J. Toward improving path following motion: Hybrid continuum robot design. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; Institute of Electrical and Electronics Engineers Inc.: Singapore, 2017; pp. 4666–4672. [Google Scholar] [CrossRef]
- Chikhaoui, M.T.; Lilge, S.; Kleinschmidt, S.; Burgner-Kahrs, J. Comparison of Modeling Approaches for a Tendon Actuated Continuum Robot With Three Extensible Segments. In IEEE Robotics and Automation Letters; IEEE: Piscateville, NJ, USA, 2019; Volume 4, pp. 989–996. [Google Scholar] [CrossRef]
- Blessing, M.; Walker, I.D. Novel Continuum Robots with Variable-Length Sections. IFAC Proc. Vol. 2004, 37, 55–60. [Google Scholar] [CrossRef]
- Qi, P.; Qiu, C.; Liu, H.; Dai, J.S.; Seneviratne, L.; Althoefer, K. A novel continuum-style robot with multilayer compliant modules. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; Institute of Electrical and Electronics Engineers Inc.: Chicago, IL, USA, 2014; pp. 3175–3180. [Google Scholar] [CrossRef]
- Barrientos-Diez, J.; Russo, M.; Dong, X.; Axinte, D.; Kell, J. Asymmetric Continuum Robots. IEEE Robot. Autom. Lett. 2023, 8, 1279–1286. [Google Scholar] [CrossRef]
- Dong, X.; Raffles, M.; Cobos-Guzman, S.; Axinte, D.; Kell, J. A novel continuum robot using twin-Pivot compliant joints: Design, modeling, and validation. J. Mech. Robot. 2016, 8, 021010. [Google Scholar] [CrossRef]
- Dong, X.; Axinte, D.; Palmer, D.; Cobos, S.; Raffles, M.; Rabani, A.; Kell, J. Development of a slender continuum robotic system for on-wing inspection/repair of gas turbine engines. Robot. Comput.-Integr. Manuf. 2017, 44, 218–229. [Google Scholar] [CrossRef]
- Clark, A.B.; Mathivannan, V.; Rojas, N. A Continuum Manipulator for Open-Source Surgical Robotics Research and Shared Development. IEEE Trans. Med. Robot. Bionics 2021, 3, 277–280. [Google Scholar] [CrossRef]
- Sun, Y.; Lueth, T.C. Design of 3D-Printed Continuum Robots Using Topology Optimized Compliant Joints. In Proceedings of the 2023 IEEE International Conference on Soft Robotics, RoboSoft 2023, Singapore, 3–7 April 2023; Institute of Electrical and Electronics Engineers Inc.: Singapore, 2023. [Google Scholar] [CrossRef]
- Sun, Y.; Lueth, T.C. Enhancing Torsional Stiffness of Continuum Robots Using 3-D Topology Optimized Flexure Joints. IEEE/ASME Trans. Mechatron. 2023, 28, 1844–1852. [Google Scholar] [CrossRef]
- Dong, X.; Palmer, D.; Axinte, D.; Kell, J. In-situ repair/maintenance with a continuum robotic machine tool in confined space. J. Manuf. Process. 2019, 38, 313–318. [Google Scholar] [CrossRef]
- Cianchetti, M.; Follador, M.; Mazzolai, B.; Dario, P.; Laschi, C. Design and development of a soft robotic octopus arm exploiting embodied intelligence. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 5271–5276. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Lueth, T.C. Optimization of Stress Distribution in Tendon-Driven Continuum Robots Using Fish-Tail-Inspired Method. IEEE Robot. Autom. Lett. 2022, 7, 3380–3387. [Google Scholar] [CrossRef]
- Zhou, P.; Yao, J.; Zhang, S.; Wei, C.; Zhang, H.; Qi, S. A bioinspired fishbone continuum robot with rigid-flexible-soft coupling structure. Bioinspiration Biomim. 2022, 17, 066012. [Google Scholar] [CrossRef]
- Janabi-Sharifi, F.; Jalali, A.; Walker, I.D. Cosserat Rod-Based Dynamic Modeling of Tendon-Driven Continuum Robots: A Tutorial. IEEE Access 2021, 9, 68703–68719. [Google Scholar] [CrossRef]
- David, B.C.; Milne, C.F.; Christopher, R.C.; Michael, R.Z.; Salisbury, J.K. Mechanics Modeling of Tendon-Driven Continuum Manipulators. IEEE Trans. Robot. 2008, 24, 1262–1273. [Google Scholar] [CrossRef]
- Marzi, C.; Buck, F.; Mathis-Ullrich, F. Continuum robot actuation by a single motor per antagonistic tendon pair: Workspace and repeatability analysis. At-Automatisierungstechnik 2023, 71, 528–536. [Google Scholar] [CrossRef]
- Lin, J.; Zhou, Z.H. Design and Implementation of a Cable-Driven Dexterous Continuum Manipulators in Confined Space Usage. In Proceedings of the 2022 International Conference on Electrical, Computer and Energy Technologies (ICECET), Prague, Czech Republic, 20–22 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Yoshikawa, D.; Shimizu, M.; Umedachi, T. A single motor-driven continuum robot that can be designed to deform into a complex shape with curvature distribution. ROBOMECH J. 2023, 10, 18. [Google Scholar] [CrossRef]
- Yang, C.; Geng, S.; Walker, I.; Branson, D.T.; Liu, J.; Dai, J.S.; Kang, R. Geometric constraint-based modeling and analysis of a novel continuum robot with Shape Memory Alloy initiated variable stiffness. Int. J. Robot. Res. 2020, 39, 1620–1634. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, R.; Haggerty, D.A.; Naclerio, N.D.; Hawkes, E.W. A Dexterous Tip-extending Robot with Variable-length Shape-locking. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 9035–9041. [Google Scholar] [CrossRef]
- Bishop, C.; Russo, M.; Dong, X.; Axinte, D. A Novel Underactuated Continuum Robot With Shape Memory Alloy Clutches. IEEE/ASME Trans. Mechatron. 2022, 27, 5339–5350. [Google Scholar] [CrossRef]
- Sun, C.; Chen, L.; Liu, J.; Dai, J.S.; Kang, R. A hybrid continuum robot based on pneumatic muscles with embedded elastic rods. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 318–328. [Google Scholar] [CrossRef]
- Zuo, S.; Yamanaka, N.; Sato, I.; Masamune, K.; Liao, H.; Matsumiya, K.; Dohi, T. MRI-Compatible Rigid and Flexible Outer Sheath Device with Pneumatic Locking Mechanism for Minimally Invasive Surgery. In Medical Imaging and Augmented Reality; Dohi, T., Sakuma, I., Liao, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 210–219. [Google Scholar]
- Wang, P.; Guo, S.; Wang, X.; Wu, Y. Design and Analysis of a Novel Variable Stiffness Continuum Robot With Built-in Winding-Styled Ropes. IEEE Robot. Autom. Lett. 2022, 7, 6375–6382. [Google Scholar] [CrossRef]
- Jeon, H.; Le, Q.N.; Jeong, S.; Jang, S.; Jung, H.; Chang, H.; Pandya, H.J.; Kim, Y. Towards a Snake-Like Flexible Robot With Variable Stiffness Using an SMA Spring-Based Friction Change Mechanism. IEEE Robot. Autom. Lett. 2022, 7, 6582–6589. [Google Scholar] [CrossRef]
- Langer, M.; Amanov, E.; Burgner-Kahrs, J. Stiffening sheaths for continuum robots. Soft Robot. 2018, 5, 291–303. [Google Scholar] [CrossRef] [PubMed]
- Wockenfuß, W.R.; Brandt, V.; Weisheit, L.; Drossel, W.G. Design, Modeling and Validation of a Tendon-Driven Soft Continuum Robot for Planar Motion Based on Variable Stiffness Structures. IEEE Robot. Autom. Lett. 2022, 7, 3985–3991. [Google Scholar] [CrossRef]
- Jalali, A.; Janabi-Sharifi, F. Dynamic Manipulation and Stiffness Modulation of Cooperative Continuum Robots: Theory and Experiment. J. Mech. Robot. 2024, 16, 121001. [Google Scholar] [CrossRef]
- Xu, K.; Fu, M.; Zhao, J. An experimental kinestatic comparison between continuum manipulators with structural variations. In Proceedings of the IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; Institute of Electrical and Electronics Engineers Inc.: Hong Kong, China, 2014; pp. 3258–3264. [Google Scholar] [CrossRef]
- Li, Z.; Ren, H.; Chiu, P.W.Y.; Du, R.; Yu, H. A novel constrained wire-driven flexible mechanism and its kinematic analysis. Mech. Mach. Theory 2016, 95, 59–75. [Google Scholar] [CrossRef]
- Amanov, E.; Nguyen, T.D.; Markmann, S.; Imkamp, F.; Burgner-Kahrs, J. Toward a Flexible Variable Stiffness Endoport for Single-Site Partial Nephrectomy. Ann. Biomed. Eng. 2018, 46, 1498–1510. [Google Scholar] [CrossRef] [PubMed]
- Clark, A.B.; Rojas, N. Assessing the Performance of Variable Stiffness Continuum Structures of Large Diameter. IEEE Robot. Autom. Lett. 2019, 4, 2455–2462. [Google Scholar] [CrossRef]
- He, B.; Xu, S.; Wang, Z. Research on Stiffness of Multibackbone Continuum Robot Based on Screw Theory and Euler-Bernoulli Beam. Math. Probl. Eng. 2018, 2018, 6910468. [Google Scholar] [CrossRef]









| Work | Main Contribution | Prototype Made? | DCPM/CPM | Modelling Method |
|---|---|---|---|---|
| [45] | Modelling and control simulation | No | DPM | CRT |
| [38] | Modelling and control simulation | No | CPM | E-L |
| [42] | Modelling a CAAMS with dual arm, pre-grasp planning and control | No | CPM | E-L |
| [43] | Development of EKF utilizing DNN for state estimation of dual arm CAAMS | No | CPM | E-L |
| [118] | Prototyped a CM and experimentally tested its kinematic, static and stiffness properties | Yes | N/A | CRT |
| [39] |
| Yes | CPM | N/A |
| Design Parameter | Equation | Reference |
|---|---|---|
| Non-dimensional load capacity (w) | Where: : Applied tip load of a segment : Length of the segment at its natural position : Young’s modulus of the backbone : Second moment of area of the backbone | Li and Rahn [124] |
| Non-dimensional eyelet height (h) | Where: : eyelet height : Length of the segment | Li and Rahn [124] |
| Minimum length of a section of a variable length CM made by concentric tubes as backbone. | Amanov et. al. [126] | |
| Maximum curvature of a section of a variable length CM made by concentric tubes as backbone. | : Section length in neutral condition d: Spacer disk diameter : Minimum length of a section Where : Maximum recoverable strain of the backbone material : The largest tube diameter of the respective backbone section | Amanov et. al. [126] |
| Slenderness | Tonapi et al. [125] |
| Design | Advantages | Limitations | Length Varying Mechanism | Ref. |
|---|---|---|---|---|
| Magnetic repulsion supported floating disks with CT backbone. |
|
| Variable length backbone on which the support disks are free floating. The concentric tubes are driven by a carriage mechanism. | [151] |
| Spring-loaded backbones with floating disks. |
|
| Pulling/releasing all the tendons parallelly by an equal amount, while letting the backbones to change the length in a synchronized manner. | [125] |
| Spring backbone (NASA’s Tendril) |
|
| A reel-drum mechanism that winds the manipulator for retraction or unwinds it for extending. | [149] |
| Fully actuated segment-based CM. |
|
| Usage of Type-3 disks allow the free movement of the backbone using a carriage mechanism. The alternating pole magnetic disks provide equidistance. | [162] |
| Work | Number of Segments | Actuators per Section | Total Numbers of Actuators | 3D/2D Operation | Type of Backbone | Technique | Targeted Function | Application Scenario | Actuator Reduction Potential |
|---|---|---|---|---|---|---|---|---|---|
| [153] | 6 | N/A | 8 | 2D | Soft | Cross-tendon | Obtaining multiple bending while having desired workspace and repeatability. | Complex path following | Six times for 2D space with three S-curves. |
| [166] | 2 | 3 | 3 | 3D | Elastic | Magnetic locking | S-curve within the arm using less number of actuators | Complex path following | |
| [185] | 2 | 1 | 1 | 2D | Elastic | Antagonistic tendon driving using a single motor, cross-tendon routing | Obtaining S-curve and distributed multiple curvatures using single motor. | Complex path following or complex shape handling in 2D | Four times for 2D space with single S-curve. |
| [183] | 2 | 2 | 4 | 3D | Elastic | Antagonistic tendon driving using a single motor | Reducing bulkiness of CM actuation system while having desired workspace and repeatability. | Surgical | Two times for 3D space with single S-curve. |
| [184] | 2 | 2 | 4 | 3D | Elastic supported with cross-universal joints | Antagonistic tendon driving using a single motor | S-curve within the arm using a lesser number of actuators | Confined space usage as an end-effector for a cable-suspended robot | Two times for 3D space with single S-curve. |
| Method of Stiffness Adjustment | Procedure |
|---|---|
| Actuation of antagonistic tendon pairs. | By providing controlled tension and displacement over the antagonistic tendon pairs in the opposite direction, the stiffness of the CM is maintained. |
| Using phase changing materials through thermomechanical effects. | When subjected to heat energy, heat-sensitive shape memory alloys (SMAs) undergo a phase change from martensite to austenite and revert when the heat energy is removed. This behaviour is harnessed in spring form, resulting in variable stiffness. |
| Curvature-constraining rod method. | The rod-constraining curvature modifies the effective length of the segment, thereby altering its stiffness. In this context, it is essential for the rod to possess higher stiffness compared to the continuum section or be rigid. |
| Jamming methods. | The variation in pressure between material surfaces influences friction, which can vary the interlocking strength of the constituent materials. This principle is employed through various material arrangements, leading to the achievement of stiffness variation. |
| No | Metric | Explanation |
|---|---|---|
| 1 | Resisting force | A measure of the stiffness as a ratio between the force experienced by the CM while bending and the deflection. |
| 2 | Positional accuracy | Ability to hold the same position when internal elements are rearranged to obtain various stiffness. |
| 3 | Bending diameter | Amount of change occuring on the diameter of the CM when it undergoes bending. |
| 4 | Deformation under external forces | Diameter change when external forces are applied, such as grasping/pushing of the CM’s body at an intermediate point. |
| 5 | Cylindrical density and | Ratio between the structure weight and the volume of the structure considering it as a cylinder for its outer dimensions. |
| Stiffening duration | Time taken to transition from flexible to rigid mode (activation time) and rigid to flexible mode (deactivation time) |
| Flap Sheath | Granule |
|---|---|
| Material (Young’s modulus) [157,193] | Rigid/deformable [109,199] |
| Coefficient of friction [146] | Coefficient of friction [193,199] |
| Number of layers wrapped [146] | Size [193] |
| Inclination angle [146,193] | Low density [194] |
| Distance between rows of holes [146,193] | Fast stiffness changing [194] |
| Flap width [146,193] | High stiffness ratio [194] |
| Flap length [146,193] | Shape [109] |
| Flap thickness [146,193] | |
| Flap count [193] | |
| Contact area [193] | |
| Weaving method of flaps [146] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uthayasooriyan, A.; Vanegas, F.; Jalali, A.; Digumarti, K.M.; Janabi-Sharifi, F.; Gonzalez, F. Tendon-Driven Continuum Robots for Aerial Manipulation—A Survey of Fabrication Methods. Drones 2024, 8, 269. https://doi.org/10.3390/drones8060269
Uthayasooriyan A, Vanegas F, Jalali A, Digumarti KM, Janabi-Sharifi F, Gonzalez F. Tendon-Driven Continuum Robots for Aerial Manipulation—A Survey of Fabrication Methods. Drones. 2024; 8(6):269. https://doi.org/10.3390/drones8060269
Chicago/Turabian StyleUthayasooriyan, Anuraj, Fernando Vanegas, Amir Jalali, Krishna Manaswi Digumarti, Farrokh Janabi-Sharifi, and Felipe Gonzalez. 2024. "Tendon-Driven Continuum Robots for Aerial Manipulation—A Survey of Fabrication Methods" Drones 8, no. 6: 269. https://doi.org/10.3390/drones8060269
APA StyleUthayasooriyan, A., Vanegas, F., Jalali, A., Digumarti, K. M., Janabi-Sharifi, F., & Gonzalez, F. (2024). Tendon-Driven Continuum Robots for Aerial Manipulation—A Survey of Fabrication Methods. Drones, 8(6), 269. https://doi.org/10.3390/drones8060269








