Performance Analysis of Distributed Reconfigurable-Intelligent-Surface-Assisted Air–Ground Fusion Networks with Non-Ideal Environments

Abstract

This paper investigates the impact of non-ideal environmental factors, including hardware impairments, random user distributions, and imperfect channel conditions, on the performance of distributed reconfigurable intelligent surface (RIS)-assisted air–ground fusion networks. Using an unmanned aerial vehicle (UAV) as an aerial base station, performance metrics such as the outage probability, ergodic rate, and energy efficiency are analyzed with Nakagami-m fading channels. To highlight the superiority of RIS-assisted air–ground networks, comparisons are made with point-to-point links, amplify-and-forward (AF) relay scenarios, conventional centralized RIS deployment, and fusion networks without hardware impairments. Monte Carlo simulations are employed to validate theoretical analyses, demonstrating that in non-ideal environmental conditions, distributed RIS-assisted air–ground fusion networks outperform benchmark scenarios. This model offers some insights into the improvement of wireless communication networks in emerging smart cities.

1. Introduction

Mobile communication networks play a crucial role in facilitating global enterprise digital transformation, driving economic development, and fostering industrial technological advancements. The gradual acceleration of 5G (Fifth Generation) mobile network deployment is revealing its transformative impact on society and production, while the foundational technologies of 6G (Sixth Generation) mobile networks are being systematically unveiled as planned. The envisioned deployment of 6G networks emphasizes ubiquitous coverage, intelligent connectivity across all entities, and holographic connections, thereby imposing heightened demands on network coverage depth, universal access capabilities, high-frequency transmission capacities, air interface speeds, end-to-end latencies, and device connectivity [1,2]. However, wireless signal propagation inherently embodies stochastic characteristics, and wireless environments remain unpredictable. Since the advent of communication systems, phenomena in the wireless channel environment, such as path loss and multipath fading, have been addressed primarily through passive, adaptive methods. Especially in high-frequency bands, signal propagation and penetration losses are significant, rendering networks susceptible to obstruction effects and coverage blind spots, thereby impeding the realization of ubiquitous wireless connectivity. Therefore, the ability to dynamically reconfigure wireless channel environments as required will emerge as a core challenge for the next generation of mobile communication networks.

Reconfigurable intelligent Surfaces (RISs) have attracted considerable attention for their ability to flexibly manipulate the electromagnetic characteristics of channel environments, transitioning from passive adaptation to active controllability [3]. Consisting of multiple electromagnetic units, RISs can dynamically adjust the phase and amplitude of reflected signals by transmitting control signals through a controller. Moreover, as metamaterials, RISs offer cost-effectiveness, simplicity, and ease of deployment, positioning them as an emerging paradigm in 6G-enabling technologies [4]. The existing research on single-RIS-assisted wireless communication systems has reached a mature stage [5]. Studies on RIS-assisted multiple-input multiple-output (MIMO) systems [6], RIS-assisted orthogonal frequency division multiplexing (OFDM) systems [7], and RIS-assisted non-orthogonal multiple access (NOMA) systems have collectively demonstrated significant enhancements in system performance [8,9,10]. With the comprehensive coverage of urban wireless networks, the imminent deployment of numerous RISs in cities is on the horizon, thereby intensifying the focus on distributed, RIS-assisted, wireless communication networks. Ref. [11] investigates the deployment issues of a distributed RIS in scenarios where obstacles hinder signal propagation along certain RIS reflection paths. Distributed RIS deployment allows for placement at multiple locations to ensure that the majority of RIS reflection paths reach the receiver effectively. Additionally, it enables the selection of the optimal RIS from multiple options for communication purposes [12]. Ref. [13] compares the system performance of a distributed RIS with a centralized RIS. Simulation results indicate that the ergodic rate of the distributed RIS surpasses that of centralized RIS systems with the same number of reflecting elements. Ref. [14] models the positions of the distributed RIS based on a Gamma distribution, and simulation outcomes validated significant enhancements in system outage performance and transmission rates in distributed RIS-assisted communication scenarios.

Relying solely on terrestrial network communication is limited by terrain features and fails to deliver ubiquitous connectivity. To address this, 6G networks integrate ground and non-ground networks to ensure global coverage and connect regions beyond the reach of traditional ground networks [15,16]. Similarly, the inflexible network topology of ground base stations and coverage blind spots pose fresh challenges with the increasing number of devices, necessitating enhancements in network capacity, performance, and ubiquitous connectivity [17,18,19]. Air–ground fusion networks bridge coverage gaps in ground networks, enhancing network capacity, serving edge users, extending signal coverage, and surmounting non-line-of-sight transmission challenges. Extensive research has been conducted on unmanned aerial vehicle (UAV) communication models, leveraging the flexibility of UAV deployment and reliable line-of-sight links [20,21]. In the context of RIS-assisted UAV communication networks, exploiting the characteristics of RIS-reflected signals enables the establishment of novel signal transmission paths. This strategy introduces line-of-sight links to enhance the transmission performance of UAV communication. It can also enhance the communication quality of legitimate communication links while mitigating eavesdropping communication links to ensure secure communication. Furthermore, it greatly simplifies channel modeling for UAV communication, thus reducing algorithmic complexity [22,23].

The aforementioned studies were predominantly carried out under idealized conditions for specific parameters. However, in the context of future urban wireless communication networks facing heightened transmission pressures and complex transmission environments, numerous non-ideal factors can affect communication quality. In practical, wireless communication systems, hardware impairments (HIs) resulting from the non-ideal physical characteristics of components (e.g., IQ imbalance and phase noise) degrade system performance. Ref. [24] explores the non-ideal hardware conditions, highlighting potential impairments that transceivers may encounter. These impairments encompass phenomena such as phase noise, in-phase and quadrature imbalances, as well as distortions arising from the nonlinearity of components like amplifiers, mixers, and converters [25,26]. Despite some studies proposing remedies for these issues, the stochastic and time-varying nature of hardware characteristics results in parameter inaccuracies, culminating in residual hardware impairments [27]. Moreover, limited studies quantify the impact of user mobility on performance [28]. Stochastic geometry can be employed to compute the randomness of network topology [29]. Refs. [30,31] assume that the user distribution adheres to a binomial point process (BPP) and evaluate the influence of user position changes on system performance. Existing works predominantly focus on perfect channel state information (CSI). However, in practical applications, it is difficult to obtain accurate CSI due to the influence of physical channel estimation errors, feedback delays, and quantization errors. In Refs. [32,33], performance analyses and design optimizations of RIS-assisted NOMA networks with unknown CSI were undertaken to compensate for performance loss, which results from imperfect channels, by increasing the number of RISs or reflection units.

Drawing from the aforementioned issues, this paper considers non-ideal environmental factors, such as hardware impairments, imperfect channels, and random users on the distributed RIS-assisted UAV communication networks. The specific contributions are summarized as follows:

• A distributed RIS-assisted air–ground fusion network model (referred as k²_RIS) is proposed. This model utilizes a UAV as an aerial base station, and deploys RISs on multiple buildings to establish a distributed RIS-assisted UAV communication link. To quantify the impact of user positions on the outage probability, ergodic rate, and energy efficiency, the model integrates stochastic geometry to capture the random nature of network topology, assuming that the user distribution follows a binomial distribution (BBP) and analyzing the impact of random users on system performance.
• Addressing the realistic challenges anticipated in future air–ground fusion networks, non-ideal factors such as hardware impairments and imperfect channels are proposed. In response to the high-intensity and high-saturation hardware operations in future urban networks, hardware impairments are considered for all nodes except the RIS, accounting for potential hardware impairments in user devices and UAV base stations. Additionally, a UAV base station hovering in the air may be influenced by aerial airflow, causing the UAV to experience slight distance oscillations. Hence, the impact of imperfect channels on the model is taken into account. These non-ideal factors are designed to address real-world issues in UAV communication networks, enhancing the applicability to practical scenarios.
• The performance metrics of the outage probability, ergodic rate, and energy efficiency with non-ideal environments with Nakagami-m fading channels in distributed RIS-assisted air–ground fusion networks are analyzed. To emphasize the superior characteristics of distributed RIS-assisted air–ground networks, point-to-point (P2P) link systems between users, AF relaying, conventional centralized RIS deployment, and distributed RIS air–ground fusion networks without hardware impairments are employed as benchmarks. Under non-ideal environmental conditions, the distributed RIS-assisted air–ground fusion network exhibits superior system performance compared to the benchmark scenarios. Simulation experiments were conducted to validate the proposed solution and theoretical analysis.

In Section 2, the distributed RIS-assisted air–ground fusion network is discussed. In Section 3, the analytical results are evaluated to quantify the performance attained. The numerical results in Section 4 verify the accuracy of our analysis, which is followed by conclusions in Section 5. The main symbols defined in this paper are listed in

Table 1. Main Notation.

Notation	Definition
N	Number of RISs
Ln	Number of RIS reflecting elements
h0, hn, gn	The channel gains for the UAV-USER, UAV-RIS, RIS-USER
d1, d2,n, d3,n	The distance for UAV-USER, UAV-RIS, RIS-USER
Λ	Path loss exponent
N0	Gaussian white noise
Ne1	Noise caused by imperfect channels in UAV-USER links
Ne2	Noise caused by imperfect channels in UAV-RIS links
k2	HI level
r0, R	The inner and outer parameters of the annulus
m	The shape parameter indicating the severity of fading
Ω	The extended parameter of the distribution

.

2. System Model for Distributed RIS-Assisted Air–Ground Fusion Network

The system model of the distributed RIS-assisted air–ground fusion network, illustrated in Figure 1, consists of a UAV base station, a random user, and RISs that constitute the downlink transmission system. The RISs are installed on high-rise structures, while the UAV maneuvers to specified locations as required. The system includes N RISs, each composed of L_n reflecting elements. The channel gains for the RIS-UAV, RIS-USER, and UAV-USER links are denoted as h_n, g_n, and h₀, respectively, with the assumption that all channels follow the Nakagami-m distribution. The center location of the user’s movement zone is assumed to be r_u, with coordinates (x₀, y₀), and the distances for the UAV-USER, UAV-RIS, and RIS-USER are d₁, d_2,n, and d_3,n, respectively. Note that distances d₁ and d_3,n are stochastic, indicating the random spatial distribution of users within a defined region. To avoid potential singularities that may arise due to close proximity, a minimum distance of r₀ is enforced, ensuring that r₀ remains greater than or equal to 1 m [34]. The UAV transmit power attenuation resulting from the UAV-to-user communication path, facilitated by RIS reflection, follows the product distance law [35]:

$$D_n={\left(d_{2,n}{d}_{3,n}\right)}^{-\Lambda }$$

(1)

where Λ is the path loss exponent.

2.1. Signal Model

Based on the analysis of the system model scenario, it is apparent that hardware impairments are present at the transmission nodes of both the UAV base station and the USER equipment. Moreover, the UAV’s hovering process may be influenced by external factors such as airflow, potentially causing fluctuations in channel conditions. Consequently, the communication link between the UAV and the user is named the direct link (UAV-USER), and the signal received by the user is formulated as follows:

$$y_1={\tilde{h}}_0{d_1}^{-\Lambda }(x_s+{ϵ}_u)+{ϵ}_s+N_0+N_{e1},$$

(2)

the noise in the direct link consists of ϵ_u and ϵ_s, where ϵ_u is the distortion noise induced by the HI at the UAV. Similarly, the received signal at the user in the HI system is distorted by the noise term ϵ_s, N₀ is Gaussian white noise, $N_0\sim CN(0,{\sigma }_0^2)$, σ₀² denotes the variance of additive white Gaussian noise at user, N_e1 is noise caused by imperfect channels, and $N_{e1}={\sigma }_e^2{P}_U\sqrt{h_0{d}_1^{-\Lambda }}$ [29], where σ_e² represent estimation errors.

In the case of hardware damage and imperfect channels, the UAV communicates with the user through RIS reflection as a cascaded link (UAV-RIS-USER), and the signal received by the user is formulated as follows:

$$y_{2,n}=(D_n{\displaystyle \sum _{l=1}^{L_n}{\tilde{h}}_{nl}{\tilde{\beta }}_{nl}{\tilde{g}}_{nl})(x_s+{ϵ}_u)+{ϵ}_s+N_0+N_{e2}},$$

(3)

where ${\tilde{h}}_0=h_0{e}^{(-j{\varnothing }_0)}$, ${\tilde{h}}_{nl}=h_{nl}{e}^{-j{\theta }_{nl}}$, and ${\tilde{g}}_{nl}=g_{nl}{e}^{-j{\vartheta }_{nl}}$ and $\left(h_0,{\varnothing }_0\right)$, $\left(h_{nl},{\theta }_{nl}\right)$, and $\left(g_{nl},{\vartheta }_{nl}\right)$ represent the amplitudes and phases of ${\tilde{h}}_0$, ${\tilde{h}}_{nl}$, and ${\tilde{g}}_{nl}$, respectively. The phase shift matrix of the RIS is given by $\widetilde{{\Theta }_n}=diag\left({\tilde{\beta }}_{n1}\cdots {\tilde{\beta }}_{nl}\cdots {\tilde{\beta }}_{nLn}\right)=diag\left({\beta }_{n1}{e}^{j{\alpha }_{n1}}\cdots {\beta }_{nl}{e}^{j{\alpha }_{nl}}\cdots {\beta }_{nLn}{e}^{j{\alpha }_{nLn}}\right)$, (α_nLn, β_nLn) denotes the amplitude and phase of the L_n-th reflective unit in the N-th RIS, N_e2 denotes the noise induced by imperfect channels, and $N_{e2}={\sigma }_e^2{P}_U\sqrt{h_{nl}{d}_{2,n}^{-\Lambda }}$ [29]. Consequently, the signals received by the user from the direct link and cascaded link can be reformulated as:

$$y_1=h_0{d_1}^{-\Lambda }{e}^{-j{\varnothing }_0}\left(x_s+{ϵ}_u\right)+{ϵ}_s+N_0+N_{e1},$$

(4)

$$\begin{array}{ll}{y}_{2,n}& =\left(D_n{\displaystyle \sum _{l=1}^{L_n}{h}_{nl}{e}^{-j{\theta }_{nl}}{\beta }_{nl}{e}^{j{\alpha }_{nl}}{g}_{nl}{e}^{-j{\vartheta }_{nl}}}\right)\left(x_s+{ϵ}_u\right)+{ϵ}_s+N_0+N_{e2}\\ & =\left(D_n{\displaystyle \sum _{l=1}^{L_n}{h}_{nl}{\beta }_{nl}{g}_{nl}}{e}^{j\left({\alpha }_{nl}-{\theta }_{nl}-{\vartheta }_{nl}\right)}\right)\left(x_s+{ϵ}_u\right)+{ϵ}_s+N_0+N_{e2}\end{array},$$

(5)

where $a_{nl}-{\theta }_{nl}-{\vartheta }_{nl}$ denotes the phase error. To significantly enhance the performance of the distributed RIS-assisted air–ground fusion network system with non-ideal environments (k²_RIS), it is imperative to minimize the phase error. Given that the RIS comprises numerous unit surfaces, their phases can be adjusted via microcontrollers. Specifically, these unit surfaces have the capability to independently manipulate the phase of reflected signals. Due to hardware constraints, the actual phase of the RIS is typically presented discretely. Consequently, the number of phases depends upon the phase resolution, with phase values spanning from 0 to 2π, and $R_n\triangleq 2^{(b_n)}$ represents the phase resolution, where b_n signifies the quantity of quantization bits in the N-th RIS. Consequently, viable phase values can be selected from the set $S=\left\{0,\frac{2\pi }{R_n},\frac{4\pi }{R_n},\cdots ,\frac{2\pi \left(R_n-1\right)}{R_n}\right\}$. Moreover, armed with knowledge of the channel state information [31], the RIS controller can ascertain the optimal phase to ensure that $a_{nl}-{\theta }_{nl}-{\vartheta }_{nl}$, and the signal expression received by the user in the UAV-RIS-USER link is:

$$y_{2,n}=\left(D_n{\displaystyle \sum _{l=1}^{L_n}{h}_{nl}{\beta }_{nl}{g}_{nl}}\right)\left(x_s+{ϵ}_u\right)+{ϵ}_s+N_0+N_{e2}.$$

(6)

2.2. Signal-to-Interference Plus-Noise Ratio Model

The received signal at the user can be delineated into three types: The first type comprises pristine signals transmitted through direct and cascaded links, the second type consists of distorted noise stemming from hardware malfunctions, and the third type is Gaussian white noise and distortions induced by suboptimal channel conditions resulting from the stationary position of the UAV. In conclusion, the signal-to-interference plus-noise ratio (SINR) for the dual links are expressed as:

$${\gamma }_1=\frac{{\left(h_0{d_1}^{-\Lambda }\right)}^2{P}_U}{{\left(h_0{d_1}^{-\Lambda }\right)}^2{k}^2{P}_U+N_0+N_{e1}};$$

(7)

$${\gamma }_{2,n}=\frac{{\left(D_n{\displaystyle \sum _{l=1}^{L_n}{h}_{nl}{\beta }_{nl}{g}_{nl}}\right)}^2{P}_U}{{\left(D_n{\displaystyle \sum _{l=1}^{L_n}{h}_{nl}{\beta }_{nl}{g}_{nl}}\right)}^2{k}^2{P}_U+N_0+N_{e2}},$$

(8)

in this context, γ₁ denotes the SINR at the user of the direct link, while γ_2,n signifies the SINR at the user of the cascaded link. k² denotes the HI level [24].

3. Performance Analysis of Distributed RIS-Assisted Air–Ground Fusion Networks with Non-Ideal Environments

This section incorporates the non-ideal factors examined in this study, that is, imperfect channels and hardware impairments. To address user variability, we propose a scheme that involves a randomized user distribution. Furthermore, this paper evaluates the outage probability, ergodic rate, and energy efficiency of the system under non-ideal conditions.

3.1. User Distribution

In this paper, it is assumed that the random distances of the user follow the BPP distribution. Assuming that the random user appearance area is a disk with radii 0 < r₀ < R, where r₀ and R are the inner and outer parameters of the annulus, the probability density function (PDF) of the user distance, denoted by r, is expressed as follows:

$$f_d\left(r\right)=\frac{2r}{R^2-r_0^2}.$$

(9)

3.2. Outage Probability

The outage probability of users is defined as:

$$P_{th}=P\left\{{\gamma }_u\le {\gamma }_{th}\right\}.$$

(10)

The outage probability is assessed in two distinct stages. Initially, the focus is on the analysis of the direct link’s outage probability. Secondly, based on the calculation method of the outage probability of the direct link, we analyze the outage probability of the cascaded link.

3.2.1. The Outage Probability of the Direct Link

Theorem 1. 

Assuming that the UAV communicates directly with the user, the outage probability expression is determined as:

$$\begin{array}{ll}{P}_{th1}=& \frac{{\Theta }_1{{\Xi }_1}^{\alpha }{R_1}^{2m_{h_0}\Lambda +2}}{m_{h_0}\left(2m_{h_0}\Lambda +2\right)}{}_{2}F_2\left(m_{h_0},m_{h_0}+\frac{1}{2\Lambda };m_{h_0}+1,m_{h_0}+\frac{1}{2\Lambda }+1;-{\Xi }_1{R_1}^{2\Lambda }\right)\\ & -\frac{{\Theta }_1{{\Xi }_1}^{m_{h_0}}{r_0}^{2m_{h_0}\Lambda +2}}{m_{h_0}\left(2m_{h_0}\Lambda +2\right)}{}_{2}F_2\left(m_{h_0},m_{h_0}+\frac{1}{2\Lambda };m_{h_0}+1,m_{h_0}+\frac{1}{2\Lambda }+1;-\Xi r_0^{2\Lambda }\right)\end{array},$$

(11)

where m_h0 represents the shape parameter indicating the severity of fading, ${\Xi }_1=\frac{m}{\Omega }\frac{\left(N_0+N_e\right){\gamma }_{th}}{P_U\left(1-k^2{\gamma }_{th}\right)}$, and  ${\Theta }_1=\frac{2}{\Gamma \left(m\right)\left(R_1^2-r_0^2\right)}$.

Proof of Theorem 1. 

In accordance with Equation (7), the outage probability of the direct link is given by:

$$\begin{array}{ll}{P}_{th}& =P\left\{{\gamma }_u\le {\gamma }_{th}\right\}=P\left\{\frac{{\left(h_0{d_1}^{-\Lambda }\right)}^2{P}_U}{{\left(h_0{d_1}^{-\Lambda }\right)}^2{k}^2{P}_1+N_0+N_{e1}}\le {\gamma }_{th}\right\}\\ & =P\left\{{\left(h_o{d}_1^{-\Lambda }\right)}^2{P}_U\left(1-k^2{\gamma }_{th}\right)\le \left(N_0+N_{e1}\right){\gamma }_{th}\right\}\end{array},$$

(12)

at this point, it is necessary to discuss the relationship between $1-k^2{\gamma }_{th}$ and 0. When $1-k^2{\gamma }_{th}<0$, it follows ${\left(h_o{d}_1^{-\Lambda }\right)}^2{P}_U\left(1-k^2{\gamma }_{th}\right)<0$; thus, ${\left(h_o{d}_1^{-\Lambda }\right)}^2{P}_U\left(1-k^2{\gamma }_{th}\right)\le \left(N_0+N_{e1}\right){\gamma }_{th}$ always holds true. When $1-k^2{\gamma }_{th}\ge 0$, Equation (11) is rewritten as:

$$\begin{array}{ll}{P}_{th1}& =P\left\{{\gamma }_1\le {\gamma }_{th}\right\}==P\left\{{\left(h_o{d}_1^{-\Lambda }\right)}^2\le \frac{\left(N_0+N_{e1}\right){\gamma }_{th}}{P_U\left(1-k^2{\gamma }_{th}\right)}\right\}\\ & =P\left\{h_o{d}_1^{-\Lambda }\le \sqrt{\frac{\left(N_0+N_{e1}\right){\gamma }_{th}}{P_U\left(1-k^2{\gamma }_{th}\right)}}\right\}=P\left\{h_o\le \sqrt{\frac{\left(N_0+N_{e1}\right){\gamma }_{th}}{P_U\left(1-k^2{\gamma }_{th}\right)}}{d}_1^{\Lambda }\right\}\end{array}.$$

(13)

Since h₀ is a random variable following a Nakagami-m distribution, its probability density function (PDF) and cumulative distribution function (CDF) are parameterized by m and Ω, thus yielding $h_o\sim \left(m_{h_0},{\Omega }_{h_0}\right)$; then, it has:

$$f_{h_0}\left(m_{h_0};{\Omega }_{h_0}\right)=\frac{2{m_{h_0}}^{m_{h_0}}}{\Gamma \left(m_{h_0}\right){{\Omega }_{h_0}}^{m_{h_0}}}{x}^{2m_{h_0}-1}{e}^{-\frac{m_{h_0}}{{\Omega }_{h_0}}{x}^2};$$

(14)

$$F_{h_0}\left(m_{h_0};{\Omega }_{h_0}\right)=\frac{\gamma \left(m_{h_0},\frac{m_{h_0}}{{\Omega }_{h_0}}{x}^2\right)}{\Gamma \left(m_{h_0}\right)},$$

(15)

where m represents the shape parameter indicating the severity of fading, Ω is the extended parameter of the distribution, and $\Omega =E\left[X^2\right]$ corresponds to the average channel gain. Substituting the CDF of h₀ into Equation (13), it can be rewritten as:

$$P_{th1}=\frac{2}{\Gamma \left(m_{h_0}\right)\left({R_1}^2-r_0^2\right)}{\displaystyle \underset{r_0}{\overset{R1}{\int }}\gamma \left(m_{h_0},\frac{m_{h_0}}{{\Omega }_{h_0}}\frac{\left(N_0+N_e\right){\gamma }_{th}}{P_U\left(1-k^2{\gamma }_{th}\right)}{r^2}^{\Lambda }\right)rdr}.$$

(16)

After further algebraic manipulation, i.e., $x=\Xi r^{2\Lambda }$, it can be obtained as follows:

$$P_{th1}={\Theta }_1{\displaystyle \underset{r_0}{\overset{R}{\int }}{\rm Y}\left(m_{h_0},{\Xi }_1{r}^{2\Lambda }\right)rdr}\stackrel{x=\Xi r^{2\Lambda }}{\to }{\Theta }_1{\Xi }_1^{-\frac{1}{2\Lambda }}{\displaystyle {\int }_{{\Xi }_1{r}^{2\Lambda }}^{{\Xi }_1{R_1}^{2\Lambda }}{\rm Y}\left(m_{h_0},{\Xi }_{1}x\right)x^{\frac{1}{2\Lambda }}dx},$$

(17)

where ${\Xi }_1=\frac{m}{\Omega }\frac{\left(N_0+N_e\right){\gamma }_{th}}{P_U\left(1-k^2{\gamma }_{th}\right)}$, and ${\Theta }_1=\frac{2}{\Gamma \left(m\right)\left(R_1^2-r_0^2\right)}$.

Based on [28], the outage probability can be simplified as:

$$\begin{array}{ll}{P}_{th1}=& \frac{{\Theta }_1{{\Xi }_1}^{\alpha }{R_1}^{2m_{h_0}\Lambda +2}}{m_{h_0}\left(2m_{h_0}\sigma +2\right)}{}_{2}F_2\left(m_{h_0},m_{h_0}+\frac{1}{2\Lambda };m_{h_0}+1,m_{h_0}+\frac{1}{2\Lambda }+1;-{\Xi }_1{R_1}^{2\Lambda }\right)\\ & -\frac{{\Theta }_1{{\Xi }_1}^{m_{h_0}}{r_0}^{2m_{h_0}\Lambda +2}}{m_{h_0}\left(2m_{h_0}\Lambda +2\right)}{}_{2}F_2\left(m_{h_0},m_{h_0}+\frac{1}{2\Lambda };m_{h_0}+1,m_{h_0}+\frac{1}{2\Lambda }+1;-\Xi r_0^{2\Lambda }\right)\end{array}.$$

(18)

The proof is now complete. □

3.2.2. The Outage Probability of the Cascaded Link

Theorem 2. 

Assuming that the UAV communicates with the user through RIS reflection, the outage probability expression is determined as:

$$\begin{array}{ll}{P}_{th2,n}=& \frac{{\Theta }_2{\Xi }_2^{L_n{\alpha }_{U_{nl}}}{R_{2,n}}^{L_n{\alpha }_{U_{nl}}\Lambda +2}}{L_n{\alpha }_{U_{nl}}\left(L_n{\alpha }_{U_{nl}}\Lambda +2\right)}\\ & \begin{array}{c}\\ \\ \end{array}\times {}_{2}F_2\left(L_n{\alpha }_{U_{nl}},L_n{\alpha }_{U_{nl}}+\frac{1}{\Lambda };L_n{\alpha }_{U_{nl}}+1,L_n{\alpha }_{U_{nl}}+\frac{1}{\Lambda }+1;-\Xi {R_{2,n}}^{\Lambda }\right)\\ & \begin{array}{c}\\ \end{array}-\frac{{\Theta }_2{\Xi }_2^{L_n{\alpha }_{U_{nl}}}{r_0}^{L_n{\alpha }_{U_{nl}}\Lambda +2}}{L_n{\alpha }_{U_{nl}}\left(L_n{\alpha }_{U_{nl}}\Lambda +2\right)}\\ & \begin{array}{c}\\ \end{array}\times {}_{2}F_2\left(L_n{\alpha }_{U_{nl}},L_n{\alpha }_{U_{nl}}+\frac{1}{\Lambda };L_n{\alpha }_{U_{nl}}+1,L_n{\alpha }_{U_{nl}}+\frac{1}{\Lambda }+1;-\Xi r_0^{\Lambda }\right)\end{array},$$

(19)

where the distribution of U_nl can be approximated by the Gamma distribution, which is characterized by two parameters, α_Unl and β_Unl, ${\Xi }_2={\beta }_{U_{nl}}\sqrt{\frac{\left(N_0+N_{e2}\right){\gamma }_{th}}{P_U\left(1-k^2{\gamma }_{th}\right)}}{d}_{2,n}^{\Lambda }$, ${\Theta }_2=\frac{2}{\Gamma \left(L_n{\alpha }_{U_{nl}}\right)\left({R_{2,n}}^2-r_0^2\right)}$.

Proof of Theorem 2. 

Similarly, the outage probability of the cascaded link is given by:

$$P_{th2}=P\left\{{\gamma }_{2,n}\le {\gamma }_{th}\right\}=P\left\{T_n\le \sqrt{\frac{\left(N_0+N_{e2}\right){\gamma }_{th}}{P_U\left(1-k^2{\gamma }_{th}\right)}}{\left(d_{2,n}{d}_{3,n}\right)}^{\Lambda }\right\}.$$

(20)

Consider random variables h_nl and g_nl that conform to Nakagami-m distributions. Characterized by its probability density function (PDF) and cumulative distribution function (CDF) parameterized by m and Ω, identified as $h_{nl}\sim \left(m_{h_{nl}},{\Omega }_{h_{nl}}\right),g_{nl}\sim \left(m_{g_{nl}},{\Omega }_{g_{nl}}\right)$, $U_{nl}=h_{nl}{\beta }_{nl}{g}_{nl}$ in reference to [36]. The PDF of $U_{nl}$ can be expressed as:

$$f_{U_{nl}}\left(z\right)=\frac{1}{{\beta }_{nl}}{\displaystyle {\int }_0^{\infty }\frac{1}{x}}{f}_{h_{nl}}\left(\frac{z}{{\beta }_{nl}x}\right)f_{g_{nl}}\left(x\right)dx.$$

(21)

Since both channels follow the Nakagami-m distribution, substituting the PDF of h_nl, g_nl into (21), the formula can be rewritten as:

$$\begin{array}{ll}{f}_{U_{nl}}\left(z\right)=& \frac{4}{\Gamma \left(m_{h_{nl}}\right)\Gamma \left(m_{g_{nl}}\right)}{\left(\frac{m_{h_{nl}}}{{{\beta }_{nl}}^2{\Omega }_{h_{nl}}}\right)}^{m_{h_{nl}}}{\left(\frac{m_{g_{nl}}}{{\Omega }_{g_{nl}}}\right)}^{m_{g_{nl}}}{z}^{2m_{h_{nl}}-1}\\ & \begin{array}{c}\\ \end{array}\times {\displaystyle {\int }_0^{\infty }{x}^{2m_{g_{nl}}-2m_{h_{nl}}-1}}{e}^{\left(-\frac{z^2{m}_{h_{nl}}}{{{\beta }_{nl}}^2{\Omega }_{h_{nl}}}-\frac{m_{g_{nl}}}{{\Omega }_{g_{nl}}}{x}^2\right)}dx\end{array}.$$

(22)

By simplifying Formula (22) using formula Equation (3.478.4) from ref. [37], we obtain:

$$f_{U_{nl}}\left(z\right)=\frac{4{\rho }_{nl}^{m_{h_{nl}}}}{\Gamma \left(m_{h_{nl}}\right)\Gamma \left(m_{g_{nl}}\right)}{z}^{m_{g_{nl}}+m_{h_{nl}}-1}{{\rm K}}_{m_{g_{nl}}-m_{h_{nl}}}\left(2{\rho }_{nl}z\right),$$

(23)

where ${\rho }_{nl}=\sqrt{\frac{m_{h_{nl}}{m}_{g_{nl}}}{{{\beta }_{nl}}^2{\Omega }_{h_{nl}}{\Omega }_{g_{nl}}}}$.

Therefore, the z-th moment of U_nl can be obtained [38]:

$${\mu }_{U_{nl}}\left(k\right)=\mathsf{{\rm E}}\left\{{U_{nl}}^k\right\}={\displaystyle {\int }_0^{\infty }{z}^k{f}_{U_{nl}}\left(z\right)}dz.$$

(24)

Furthermore, according to Equation (6.561.16) of ref. [37], Formula (24) can be rewritten as:

$${\mu }_{U_{nl}}\left(k\right)={\rho }_{nl}^{-k}\frac{\Gamma \left(m_{h_{nl}}+\frac{k}{2}\right)\Gamma \left(m_{g_{nl}}+\frac{k}{2}\right)}{\Gamma \left(m_{h_{nl}}\right)\Gamma \left(m_{g_{nl}}\right)}.$$

(25)

As described in [38] (p. 239), the flexibility of the framework is enhanced when the distribution and statistical characteristics are identical. Let $U_{nl}=h_{nl}{\beta }_{nl}{g}_{nl}$, $T_n={\displaystyle \sum _{l=1}^{L_n}{h}_{nl}{\beta }_{nl}{g}_{nl}}$, so $U_{nl}\sim Gamma\left({\alpha }_{U_{nl}},{\beta }_{U_{nl}}\right)$; then, we have:

$${\alpha }_{U_{nl}}=\frac{\mathsf{{\rm E}}{\left[U_{nl}\right]}^2}{Var\left[U_{nl}\right]}=\frac{{\left[{\mu }_{U_{nl}}\left(1\right)\right]}^2}{{\mu }_{U_{nl}}\left(2\right)-{\left[{\mu }_{U_{nl}}\left(1\right)\right]}^2};$$

(26)

$${\beta }_{U_{nl}}=\frac{\mathsf{{\rm E}}\left[U_{nl}\right]}{Var\left[U_{nl}\right]}=\frac{{\mu }_{U_{nl}}\left(1\right)}{{\mu }_{U_{nl}}\left(2\right)-{\left[{\mu }_{U_{nl}}\left(1\right)\right]}^2}.$$

(27)

Furthermore, since $U_{nl}\sim Gamma\left({\alpha }_{U_{nl}},{\beta }_{U_{nl}}\right)$, the CDF and PDF of U_nl can be expressed as:

$$f_{U_{nl}}\left(y;{\alpha }_{U_{nl}};{\beta }_{U_{nl}}\right)=\frac{{{\beta }_{U_{nl}}}^{{\alpha }_{U_{nl}}}}{\Gamma \left({\alpha }_{U_{nl}}\right)}{y}^{{\alpha }_{U_{nl}}-1}{e}^{-{\beta }_{U_{nl}}y};$$

(28)

$$F_{U_{nl}}\left(y;{\alpha }_{U_{nl}};{\beta }_{U_{nl}}\right)=\frac{\gamma \left({\alpha }_{U_{nl}},{\beta }_{U_{nl}}y\right)}{\Gamma \left({\alpha }_{U_{nl}}\right)}.$$

(29)

$T_n={\displaystyle \sum _{l=1}^{L_n}{h}_{nl}{\beta }_{nl}{g}_{nl}}$ can be approximated by $T_n\sim Gamma\left(L_n{\alpha }_{U_{nl}},{\beta }_{U_{nl}}\right)$, and its PDF and CDF can be obtained as:

$$f_{T_n}(z)=\left(z;L_n{\alpha }_{U_{nl}};{\beta }_{U_{nl}}\right);$$

(30)

$$F_{T_n}\left(z;L_n{\alpha }_{U_{nl}};{\beta }_{U_{nl}}\right)=\frac{\gamma \left(L_n{\alpha }_{U_{nl}},{\beta }_{U_{nl}}z\right)}{\Gamma \left(L_n{\alpha }_{U_{nl}}\right)}.$$

(31)

By incorporating the PDF of the user distance into the above inference, the outage probability of the cascaded link can be written as:

$$P_{th2}=\frac{2}{\Gamma \left(L_n{\alpha }_{U_{nl}}\right)\left({R_{2,n}}^2-r_0^2\right)}{\displaystyle \underset{r_0}{\overset{R_{2,n}}{\int }}\gamma \left(L_n{\alpha }_{U_{nl}},{\beta }_{U_{nl}}\sqrt{\frac{\left(N_0+N_{e2}\right){\gamma }_{th}}{P_{2,n}\left(1-k^2{\gamma }_{th}\right)}}{d}_{2,n}^{\Lambda }{r}^{\Lambda }\right)rdr}.$$

(32)

After further algebraic manipulation, $x={\Xi }_2{r}^{\Lambda }$, while letting ${\Xi }_2={\beta }_{U_{nl}}\sqrt{\frac{\left(N_0+N_{e2}\right){\gamma }_{th}}{P_U\left(1-k^2{\gamma }_{th}\right)}}{d}_{2,n}^{\Lambda },{\Theta }_2=\frac{2}{\Gamma \left(L_n{\alpha }_{U_{nl}}\right)\left({R_{2,n}}^2-r_0^2\right)}$, it can be substituted as:

$$\begin{array}{ll}{P}_{2,n}& ={\Theta }_2{\displaystyle \underset{r_0}{\overset{R_{2,n}}{\int }}\gamma \left(L_n{\alpha }_{U_{nl}},{\Xi }_2{r}^{\Lambda }\right)rdr}\\ & \stackrel{x={\Xi }_2{r}^{\Lambda }}{\to }{\Theta }_2{{\Xi }_2}^{-\frac{1}{\Lambda }}{\displaystyle {\int }_{{\Xi }_2{r}^{\Lambda }}^{{\Xi }_2{R_{2,n}}^{\Lambda }}\gamma \left(L_n{\alpha }_{U_{nl}},{\Xi }_{2}x\right)x^{\frac{1}{\Lambda }}dx}\end{array}.$$

(33)

Based on [28], the outage probability of the cascaded link can be simplified as:

$$\begin{array}{ll}{P}_{th2,n}=& \frac{{\Theta }_2{\Xi }_2^{L_n{\alpha }_{U_{nl}}}{R_{2,n}}^{L_n{\alpha }_{U_{nl}}\Lambda +2}}{L_n{\alpha }_{U_{nl}}\left(L_n{\alpha }_{U_{nl}}\Lambda +2\right)}\\ & \begin{array}{c}\\ \end{array}\times {}_{2}F_2\left(L_n{\alpha }_{U_{nl}},L_n{\alpha }_{U_{nl}}+\frac{1}{\Lambda };L_n{\alpha }_{U_{nl}}+1,L_n{\alpha }_{U_{nl}}+\frac{1}{\Lambda }+1;-\Xi {R_{2,n}}^{\Lambda }\right)\\ & \begin{array}{c}\\ \end{array}-\frac{{\Theta }_2{\Xi }_2^{L_n{\alpha }_{U_{nl}}}{r_0}^{L_n{\alpha }_{U_{nl}}\Lambda +2}}{L_n{\alpha }_{U_{nl}}\left(L_n{\alpha }_{U_{nl}}\Lambda +2\right)}\\ & \begin{array}{c}\\ \end{array}\times {}_{2}F_2\left(L_n{\alpha }_{U_{nl}},L_n{\alpha }_{U_{nl}}+\frac{1}{\Lambda };L_n{\alpha }_{U_{nl}}+1,L_n{\alpha }_{U_{nl}}+\frac{1}{\Lambda }+1;-\Xi r_0^{\Lambda }\right)\end{array}.$$

(34)

Based on the above process, the outage probabilities of the direct link and the cascaded link are derived. In the user communication process, a distributed RIS provides multiple paths for communication. If the signal encounters obstruction, as long as there exists at least one viable path for transmission, the user can receive the signal. Therefore, the outage occurs when all signal paths are interrupted. Thus, the system outage probability is calculated as:

$$\begin{array}{ll}{P}_{th}& =P_{th1}{P}_{th2,1}\cdots P_{th2,n}\\ & =\left(\begin{array}{l}\frac{{\Theta }_1{{\Xi }_1}^{\alpha }{R_1}^{2m_{h_0}\Lambda +2}}{m_{h_0}\left(2m_{h_0}\Lambda +2\right)}{}_{2}F_2\left(m_{h_0},m_{h_0}+\frac{1}{2\Lambda };m_{h_0}+1,m_{h_0}+\frac{1}{2\Lambda }+1;-{\Xi }_1{R_1}^{2\Lambda }\right)\\ -\frac{{\Theta }_1{{\Xi }_1}^{m_{h_0}}{r_0}^{2m_{h_0}\Lambda +2}}{m_{h_0}\left(2m_{h_0}\Lambda +2\right)}{}_{2}F_2\left(m_{h_0},m_{h_0}+\frac{1}{2\Lambda };m_{h_0}+1,m_{h_0}+\frac{1}{2\Lambda }+1;-\Xi r_0^{2\Lambda }\right)\end{array}\right)\\ & \times \cdots \times \left(\begin{array}{l}\frac{{\Theta }_2{\Xi }_2^{L_n{\alpha }_{U_{nl}}}{R_{2,n}}^{L_n{\alpha }_{U_{nl}}\Lambda +2}}{L_n{\alpha }_{U_{nl}}\left(L_n{\alpha }_{U_{nl}}\Lambda +2\right)}\\ \times {}_{2}F_2\left(L_n{\alpha }_{U_{nl}},L_n{\alpha }_{U_{nl}}+\frac{1}{\Lambda };L_n{\alpha }_{U_{nl}}+1,L_n{\alpha }_{U_{nl}}+\frac{1}{\Lambda }+1;-\Xi {R_{2,n}}^{\Lambda }\right)\\ -\frac{{\Theta }_2{\Xi }_2^{L_n{\alpha }_{U_{nl}}}{r_0}^{L_n{\alpha }_{U_{nl}}\Lambda +2}}{L_n{\alpha }_{U_{nl}}\left(L_n{\alpha }_{U_{nl}}\Lambda +2\right)}\\ \times {}_{2}F_2\left(L_n{\alpha }_{U_{nl}},L_n{\alpha }_{U_{nl}}+\frac{1}{\Lambda };L_n{\alpha }_{U_{nl}}+1,L_n{\alpha }_{U_{nl}}+\frac{1}{\Lambda }+1;-\Xi r_0^{\Lambda }\right)\end{array}\right)\end{array}.$$

(35)

The proof is now complete. □

3.3. Ergodic Rate

The ergodic rate of the user’s direct link is given by:

$$\overline{R}=\mathsf{{\rm E}}\left\{{\log }_2\left(1+\gamma \right)\right\}={\displaystyle {\int }_0^{\infty }{\log }_2\left(1+x\right)f_{\gamma }\left(x\right)dx},$$

(36)

where f_γ is the PDF of γ.

3.3.1. The Ergodic Rate of the Direct Link

Theorem 3. 

Assuming that the UAV communicates directly with the user, the ergodic rate expression is determined as:

$$\begin{array}{ll}{\overline{R}}_1=& \frac{2}{\left(R_1^2-r_0^2\right)}\frac{1}{\ln 2\Gamma \left(m_{h_0}\right)}\pi \frac{\sqrt{1-u_1^2}}{2k^2+1+u_1}\\ & \times \left[\begin{array}{l}\frac{{R_1}^2}{2\Gamma (m_{h_0})}{G_1^2}_2^0(y{R_1}^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}\end{array})-\frac{y^{-\frac{1}{\Lambda }}}{2\Gamma (m_{h_0})}{G_1^2}_2^0(y{R}^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}+\frac{1}{\Lambda }\end{array})\\ -\frac{{r_0}^2}{2\Gamma (m_{h_0})}{G_1^2}_2^0(y{r}_0^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}\end{array})+\frac{y^{-\frac{1}{\Lambda }}}{2\Gamma (m_{h_0})}{G_1^2}_2^0(y{r}_0^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}+\frac{1}{\Lambda }\end{array})\end{array}\right]\end{array},$$

(37)

where $u_i=\cos \left(\frac{\left(2i-1\right)\pi }{2N}\right)$, and $y=\frac{m_{h_0}}{{\Omega }_{h_0}}\frac{\left(N_0+N_e\right)\left(1+u_1\right)}{P_U{k}^2\left(1-u_1\right)}$.

Proof of Theorem 3. 

Formula (36) is further computed as:

$${\overline{R}}_1=\frac{1}{\ln 2}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1-F_{{\gamma }_1}}{1+x}}dx,$$

(38)

where F_γ1 is the CDF of γ₁.

By utilizing Equation (8.356.3) from ref. [37], i.e., $\Gamma \left(\alpha ,x\right)+\gamma \left(\alpha ,x\right)=\Gamma \left(\alpha \right)$ and Equation (14), the calculation of Formula (38) is written as:

$${\overline{R}}_1=\frac{1}{\ln 2}{\displaystyle \underset{0}{\overset{\frac{1}{k^2}}{\int }}\frac{1}{1+x}}\frac{\Gamma \left(m_{h_0},\frac{m_{h_0}}{{\Omega }_{h_0}}\frac{\left(N_0+N_e\right)x}{P_U\left(1-k^{2}x\right)}{d_1}^{2\Lambda }\right)}{\Gamma \left(m_{h_0}\right)}dx.$$

(39)

Formula (39) can be simplified using Chebyshev parameters:

$$\begin{array}{ll}{\overline{R}}_1& =\frac{1}{\ln 2\Gamma \left(m_{h_0}\right)}\frac{\pi }{2k^2}\frac{\sqrt{1-u_1^2}}{1+\frac{1+u_1}{2k^2}}\Gamma \left(m_{h_0},\frac{m_{h_0}}{{\Omega }_{h_0}}{d_1}^{2\Lambda }\frac{\left(N_0+N_e\right)\frac{1+u_1}{2k^2}}{P_U\left(1-k^2\frac{1+u_1}{2k^2}\right)}\right)\\ & =\frac{1}{\ln 2\Gamma \left(m_{h_0}\right)}\pi \frac{\sqrt{1-u_1^2}}{2k^2+1+u_1}\Gamma \left(m_{h_0},\frac{m_{h_0}}{{\Omega }_{h_0}}{d}_1^{2\Lambda }\frac{\left(N_0+N_e\right)\left(1+u_1\right)}{P_U{k}^2\left(1-u_1\right)}\right)\end{array},$$

(40)

where $u_i=\cos \left(\frac{\left(2i-1\right)\pi }{2N}\right)$, N is the Chebyshev parameter and also the number of RISs.

Let $y=\frac{m_{h_0}}{{\Omega }_{h_0}}\frac{\left(N_0+N_e\right)\left(1+u_1\right)}{P_U{k}^2\left(1-u_1\right)}$. The direct link traversal factor can be simplified as:

$${\overline{R}}_1=\frac{2}{\left(R_1^2-r_0^2\right)}\frac{1}{\ln 2\Gamma \left(m_{h_0}\right)}\pi \frac{\sqrt{1-u_1^2}}{2k^2+1+u_1}{\displaystyle {\int }_{r_0}^{R_1}\Gamma \left(m_{h_0},y{r}^{2\Lambda }\right)}rdr.$$

(41)

By utilizing the upper incomplete gamma function, we can derive:

$$\begin{array}{l}{\overline{R}}_1\underset{\_}{\underset{\_}{j=y{r}^{2\Lambda }}}\frac{y^{-\frac{1}{\Lambda }}}{2\sigma \Gamma (m_{h_0})}{{\displaystyle \underset{y{r}_0^{2\Lambda }}{\overset{y{R_1}^{2\Lambda }}{\int }}\Gamma (m_{h_0},j)j}}^{\frac{1}{\Lambda }}dj\\ =\frac{2}{\left(R_1^2-r_0^2\right)}(\frac{1}{2\Gamma (m_{h_0})}{R_1}^2\Gamma (m_{h_0},y{R_1}^{2\Lambda })-\frac{1}{2\Gamma (m_{h_0})}{y}^{-\frac{1}{\Lambda }}\Gamma (m_{h_0}+\frac{2}{2\Lambda },y{R_1}^{2\Lambda }),\\ -\frac{1}{2\Gamma (m_{h_0})}{r_0}^2\Gamma (m_{h_0},y{r}_0^{2\Lambda })+\frac{1}{2\Gamma (m_{h_0})}{y}^{-\frac{1}{\Lambda }}\Gamma (m_{h_0}+\frac{2}{2\Lambda },y{r}_0^{2\Lambda }))\end{array}$$

(42)

Through the above analysis, we have obtained a manageable ergodic rate, which can convert the upper incomplete gamma function to the Meijer-G function:

$$\Gamma (m_{h_0},y{R_1}^{2\Lambda })={G_1^2}_2^0(y{R_1}^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}\end{array}).$$

(43)

Subsequently, the ergodic rate of the direct link is:

$$\begin{array}{ll}{\overline{R}}_1=& \frac{2}{\left(R_1^2-r_0^2\right)}\frac{1}{\ln 2\Gamma \left(m_{h_0}\right)}\pi \frac{\sqrt{1-u_1^2}}{2k^2+1+u_1}\\ & \begin{array}{c}\\ \end{array}\times \left[\begin{array}{l}\frac{{R_1}^2}{2\Gamma (m_{h_0})}{G_1^2}_2^0(y{R_1}^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}\end{array})-\frac{y^{-\frac{1}{\Lambda }}}{2\Gamma (m_{h_0})}{G_1^2}_2^0(y{R}^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}+\frac{1}{\Lambda }\end{array})\\ -\frac{{r_0}^2}{2\Gamma (m_{h_0})}{G_1^2}_2^0(y{r}_0^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}\end{array})+\frac{y^{-\frac{1}{\Lambda }}}{2\Gamma (m_{h_0})}{G_1^2}_2^0(y{r}_0^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}+\frac{1}{\Lambda }\end{array})\end{array}\right]\end{array}.$$

(44)

The proof is now complete. □

3.3.2. The Ergodic Rate of the Cascaded Link

Theorem 4. 

Assuming that the UAV communicates with the user through RIS reflection, the user’s ergodic rate expression is determined as:

$$\begin{array}{ll}{\overline{R}}_{2,n}=& \frac{2}{\left(R_1^2-r_0^2\right)}\frac{1}{\ln 2\Gamma \left(L_n{\alpha }_{U_{nl}}\right)}\frac{\pi }{M}{\displaystyle \sum _{i=1}^M\frac{\sqrt{1-u_i^2}}{2k^2+1+u_i}}\\ & \begin{array}{c}\\ \end{array}\times \left[\begin{array}{l}\frac{{R_{2,n}}^2}{2}{G_1^2}_2^0(y_2{R_{2,n}}^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}\end{array})\\ -\frac{y_2^{-\frac{2}{\Lambda }}}{2}{G_1^2}_2^0(y_2{R_{2,n}}^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}+\frac{2}{\Lambda }\end{array})\\ -\frac{{r_0}^2}{2}{G_1^2}_2^0(y_2{r}_0^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}\end{array})\\ +\frac{y_2^{-\frac{2}{\Lambda }}}{2}{G_1^2}_2^0(y_2{r}_0^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}+\frac{2}{\Lambda }\end{array})\end{array}\right]\end{array},$$

(45)

where $y_2={\beta }_{U_{nl}}{d_{2,n}}^{\Lambda }\sqrt{\frac{\left(N_0+N_e\right)\left(1+u_i\right)}{P_U{k}^2\left(1-u_i\right)}}$.

Proof of Theorem 4. 

Through the solution method of the direct link, we can similarly obtain the ergodic rate of the cascaded link:

$${\overline{R}}_{2,n}=\frac{1}{\ln 2}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1-F_{{\gamma }_{2,n}}}{1+x}}dx,$$

(46)

where Fγ_2,n is the CDF of γ_2,n.

By utilizing Equation (8.356.3) from ref. [37] for $\Gamma \left(\alpha ,x\right)+\gamma \left(\alpha ,x\right)=\Gamma \left(\alpha \right)$ and Equation (29), we can obtain:

$${\overline{R}}_{2,n}=\frac{1}{\ln 2}{\displaystyle \underset{0}{\overset{\frac{1}{k^2}}{\int }}\frac{1}{1+x}}\frac{\Gamma \left(L_n{\alpha }_{U_{nl}},{\beta }_{U_{nl}}\sqrt{\frac{\left(N_0+N_e\right)x}{P_{2,n}\left(1-k^{2}x\right)}}{\left(d_2{d}_{3,n}\right)}^{\Lambda }\right)}{\Gamma \left(L_n{\alpha }_{U_{nl}}\right)}dx.$$

(47)

Formula (47) can be simplified using Chebyshev parameters:

$$\begin{array}{lll}{\overline{R}}_{2,n}& =& \frac{1}{\ln 2\Gamma \left(L_n{\alpha }_{U_{nl}}\right)}\frac{\pi }{2M{k}^2}{\displaystyle \sum _{i=1}^M\frac{\sqrt{1-u_i^2}}{1+\frac{1+u_i}{2k^2}}}\\ & & \begin{array}{c}\\ \end{array}\times \Gamma \left(L_n{\alpha }_{U_{nl}},{\beta }_{U_{nl}}{\left(d_{2,n}{d}_{3,n}\right)}^{\Lambda }\sqrt{\frac{\left(N_0+N_e\right)\frac{1+u_i}{2k^2}}{P_{2,n}\left(1-k^2\frac{1+u_i}{2k^2}\right)}}\right)\\ & =& \frac{1}{\ln 2\Gamma \left(L_n{\alpha }_{U_{nl}}\right)}\frac{\pi }{M}{\displaystyle \sum _{i=1}^M\frac{\sqrt{1-u_i^2}}{2k^2+1+u_i}}\\ & & \begin{array}{c}\\ \end{array}\times \Gamma \left(L_n{\alpha }_{U_{nl}},{\beta }_{U_{nl}}{\left(d_{2,n}{d}_{3,n}\right)}^{\Lambda }\sqrt{\frac{\left(N_0+N_e\right)\left(1+u_i\right)}{P_{2,n}{k}^2\left(1-u_i\right)}}\right)\end{array},$$

(48)

where $u_i=\cos \left(\frac{\left(2i-1\right)\pi }{2N}\right)$, and N is the Chebyshev parameter and also the number of RISs.

Let $y_2={\beta }_{U_{nl}}{d_{2,n}}^{\Lambda }\sqrt{\frac{\left(N_0+N_e\right)\left(1+u_i\right)}{P_U{k}^2\left(1-u_i\right)}}$. The traversal coefficient of the cascaded link can be simplified as:

$$\begin{array}{l}{\overline{R}}_{2,n}\underset{\_}{\underset{\_}{j=y{r}^{\Lambda }}}\frac{2}{\left(R_1^2-r_0^2\right)}\frac{1}{\ln 2\Gamma \left(L_n{\alpha }_{U_{nl}}\right)}\frac{\pi }{2M{k}^2}\\ \begin{array}{c}\\ \end{array}\times {\displaystyle \sum _{i=1}^M\frac{\sqrt{1-u_i^2}}{1+\frac{1+u_i}{2k^2}}}{\displaystyle \underset{y_2{r}_0^{\Lambda }}{\overset{y_2{R}_{2,n}^{\Lambda }}{\int }}\Gamma (L_n{\alpha }_{U_{nl}},j)}{j}^{\frac{2}{\Lambda }}dj\\ =\frac{2}{\left(R_1^2-r_0^2\right)}\frac{1}{\ln 2\Gamma \left(L_n{\alpha }_{U_{nl}}\right)}\frac{\pi }{2M{k}^2}\\ \begin{array}{c}\\ \end{array}\times \left(\begin{array}{l}\frac{1}{2}{R}_{2,n}^2\Gamma (L_n{\alpha }_{U_{nl}},y_2{R}_{2,n}^{\Lambda })-\frac{1}{2}{y}_2^{\frac{2}{\Lambda }}\Gamma (L_n{\alpha }_{U_{nl}}+\frac{2}{\Lambda },y_2{R}_{2,n}^{\Lambda })\\ -\frac{1}{2}{r}_0^2\Gamma (L_n{\alpha }_{U_{nl}},y_2{r}_0^{\Lambda })+\frac{1}{2}{y}_2^{\frac{2}{\Lambda }}\Gamma (L_n{\alpha }_{U_{nl}}+\frac{2}{\Lambda },y_2{r}_0^{\Lambda })\end{array}\right)\end{array}.$$

(49)

Through the above analysis, we have obtained the manageable ergodic rate, which can convert the upper incomplete gamma function to the Meijer-G function:

$$\Gamma (\alpha L_n{\alpha }_{U_{nl}},y_2{R_{2,n}}^{\Lambda })={G_1^2}_2^0(y_2{R_{2,n}}^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}\end{array}).$$

(50)

Subsequently, the ergodic rate of the cascaded link is:

$$\begin{array}{ll}{\overline{R}}_{2,n}=& \frac{2}{\left(R_1^2-r_0^2\right)}\frac{1}{\ln 2\Gamma \left(L_n{\alpha }_{U_{nl}}\right)}\frac{\pi }{M}{\displaystyle \sum _{i=1}^M\frac{\sqrt{1-u_i^2}}{2k^2+1+u_i}}\\ & \begin{array}{c}\\ \end{array}\times \left[\begin{array}{l}\frac{{R_{2,n}}^2}{2}{G_1^2}_2^0(y_2{R_{2,n}}^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}\end{array})\\ -\frac{y_2^{-\frac{2}{\Lambda }}}{2}{G_1^2}_2^0(y_2{R_{2,n}}^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}+\frac{2}{\Lambda }\end{array})\\ -\frac{{r_0}^2}{2}{G_1^2}_2^0(y_2{r}_0^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}\end{array})\\ +\frac{y_2^{-\frac{2}{\Lambda }}}{2}{G_1^2}_2^0(y_2{r}_0^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}+\frac{2}{\Lambda }\end{array})\end{array}\right]\end{array}.$$

(51)

According to the system model, the ergodic rate can be superimposed. The UAV base station can communicate through RIS reflections to each link of the user, so the ergodic rate should be the sum of all link rates.

$$\begin{array}{lll}\overline{R}& =& {\overline{R}}_1+{\overline{R}}_{2,1}+\cdots +{\overline{R}}_{2,n}\\ & =& \frac{2}{\left(R_1^2-r_0^2\right)}\frac{1}{\ln 2\Gamma \left(m_{h_0}\right)}\pi \frac{\sqrt{1-u_1^2}}{2k^2+1+u_1}\\ & & \begin{array}{c}\\ \end{array}\times \left[\begin{array}{l}\frac{{R_1}^2}{2\Gamma (m_{h_0})}{G_1^2}_2^0(y{R_1}^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}\end{array})-\frac{y^{-\frac{1}{\Lambda }}}{2\Gamma (m_{h_0})}{G_1^2}_2^0(y{R}^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}+\frac{1}{\Lambda }\end{array})\\ -\frac{{r_0}^2}{2\Gamma (m_{h_0})}{G_1^2}_2^0(y{r}_0^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}\end{array})+\frac{y^{-\frac{1}{\Lambda }}}{2\Gamma (m_{h_0})}{G_1^2}_2^0(y{r}_0^{2\Lambda }|\begin{array}{cc}1& \\ 0& m_{h_0}+\frac{1}{\Lambda }\end{array})\end{array}\right]\\ & & \begin{array}{c}\\ \end{array}+\cdots +\frac{2}{\left(R_1^2-r_0^2\right)}\frac{1}{\ln 2\Gamma \left(L_n{\alpha }_{U_{nl}}\right)}\frac{\pi }{M}{\displaystyle \sum _{i=1}^M\frac{\sqrt{1-u_i^2}}{2k^2+1+u_i}}\\ & & \begin{array}{c}\\ \end{array}\times \left[\begin{array}{l}\frac{{R_{2,n}}^2}{2}{G_1^2}_2^0(y_2{R_{2,n}}^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}\end{array})\\ -\frac{y_2^{-\frac{2}{\Lambda }}}{2}{G_1^2}_2^0(y_2{R_{2,n}}^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}+\frac{2}{\Lambda }\end{array})\\ -\frac{{r_0}^2}{2}{G_1^2}_2^0(y_2{r}_0^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}\end{array})\\ +\frac{y_2^{-\frac{2}{\Lambda }}}{2}{G_1^2}_2^0(y_2{r}_0^{\Lambda }|\begin{array}{cc}1& \\ 0& L_n{\alpha }_{U_{nl}}+\frac{2}{\Lambda }\end{array})\end{array}\right]\end{array}.$$

(52)

The proof is now complete. □

3.4. Energy Efficiency

The energy consumed in the model mainly includes the energy consumption of the UAV base station, the reflection phase angle of each RIS reflection unit, and the energy consumption of the communication device. The energy consumption metric can be modeled as:

$$P_e=P_U+NL{P}_{RIS}+P_1,$$

(53)

where P_U is the transmission power of the UAV base station, P_RIS is the power consumption of each RIS element, and P₁ is the power consumption of the user. From Formulas (48) and (49), the energy efficiency can be deduced as:

$$EE=\frac{\overline{R}}{P_e}=\frac{{\overline{R}}_1+{\overline{R}}_{2,1}+\cdots +{\overline{R}}_{2,n}}{P_U+NL{P}_{RIS}+P_1}.$$

(54)

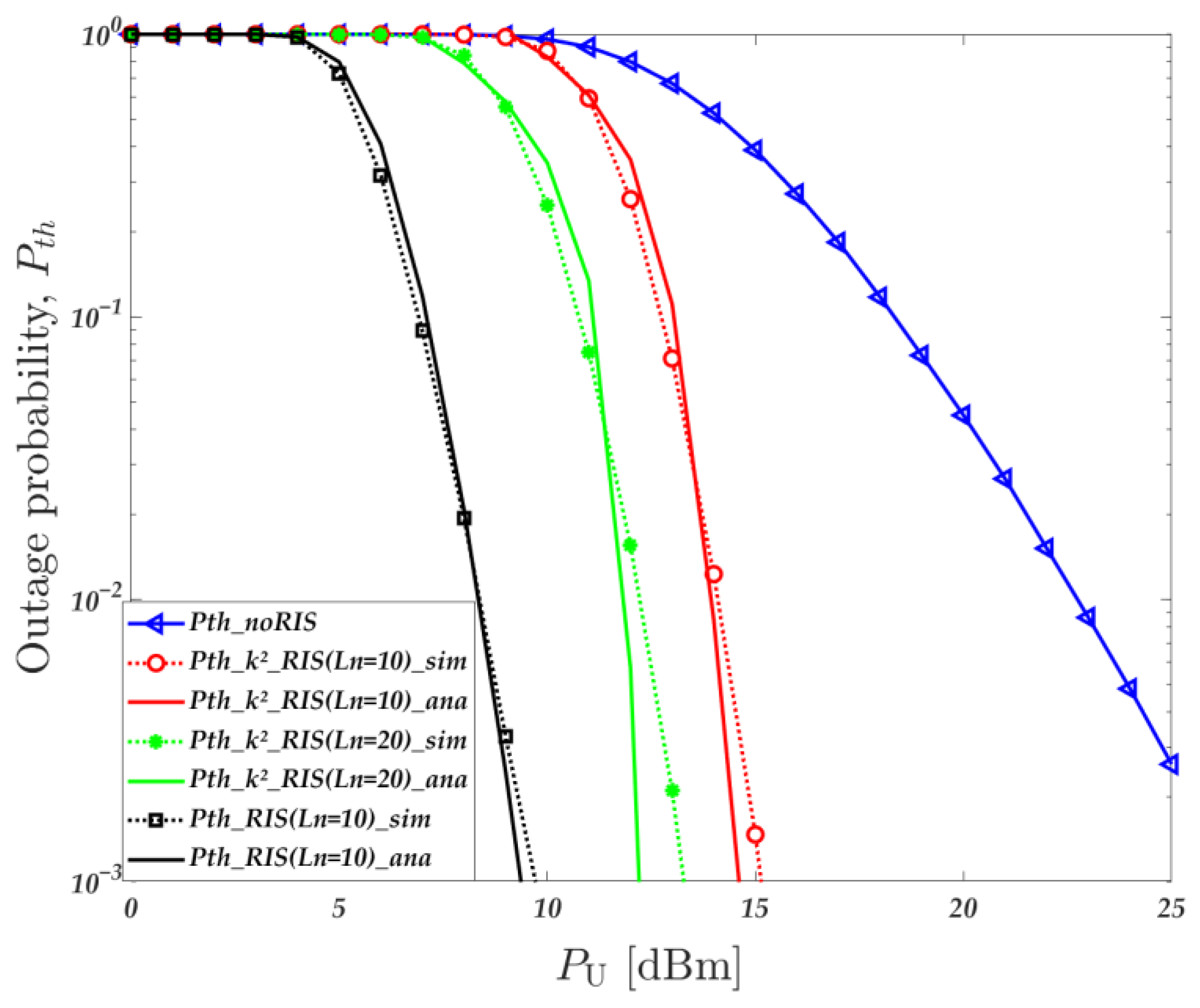
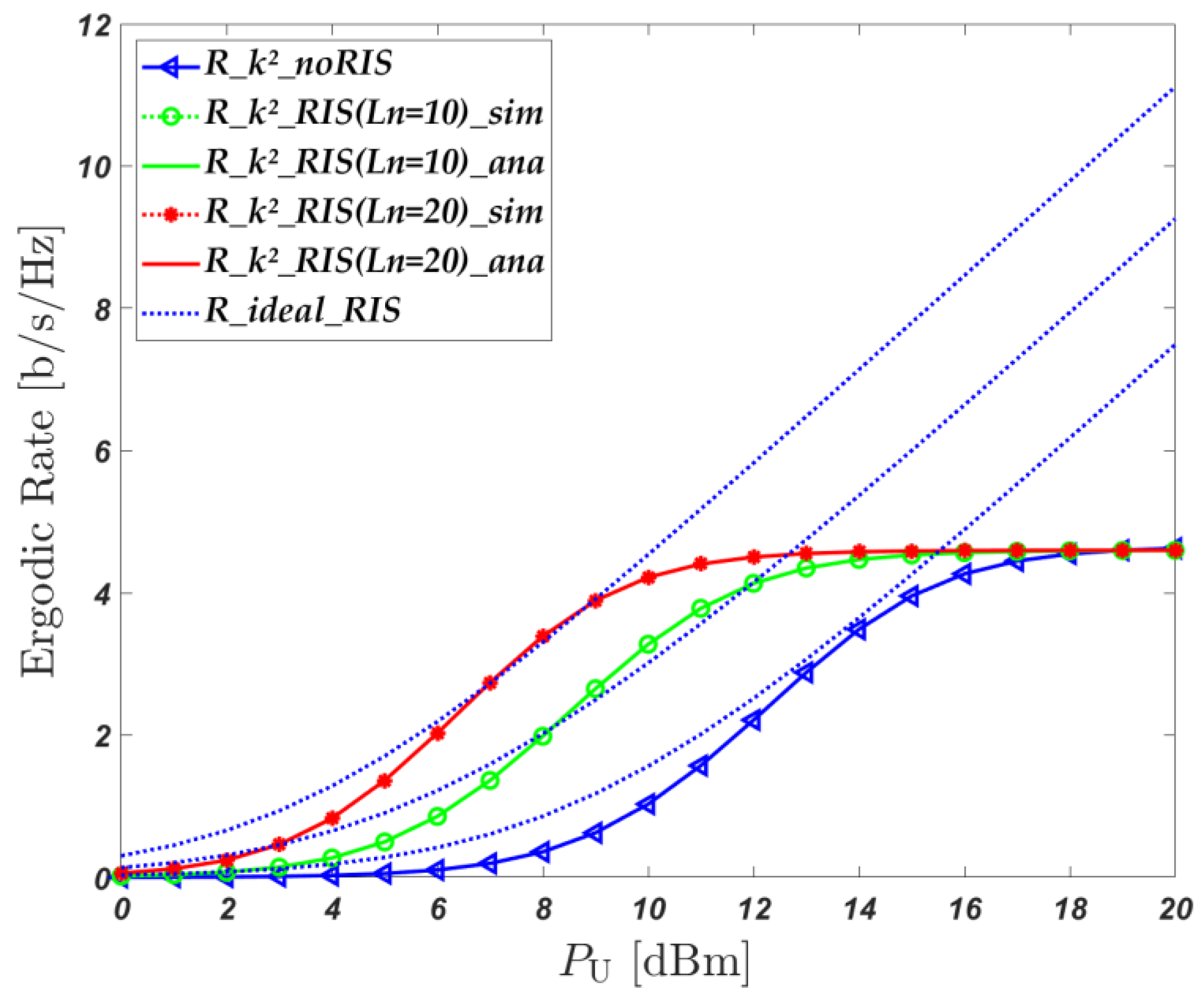
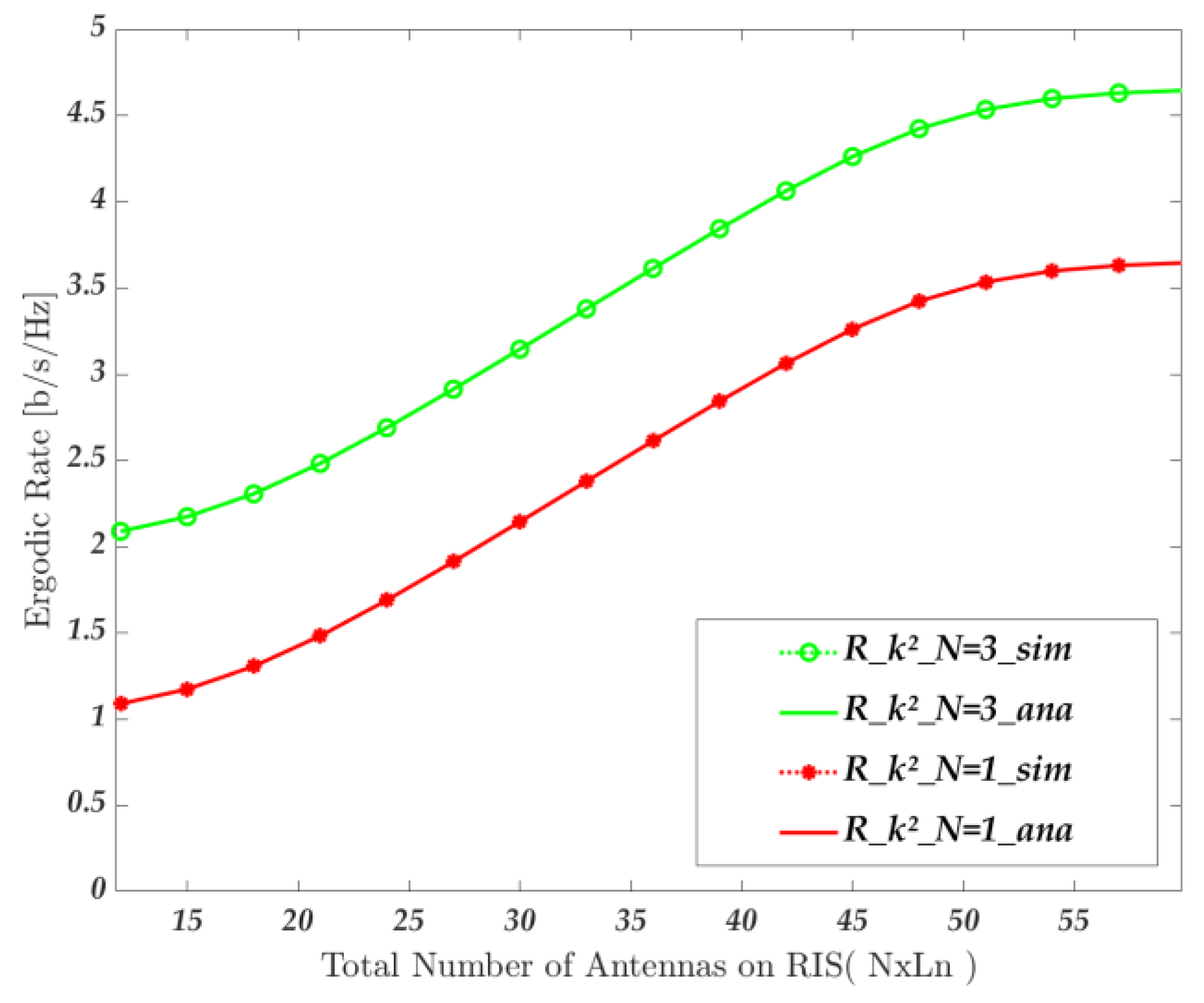
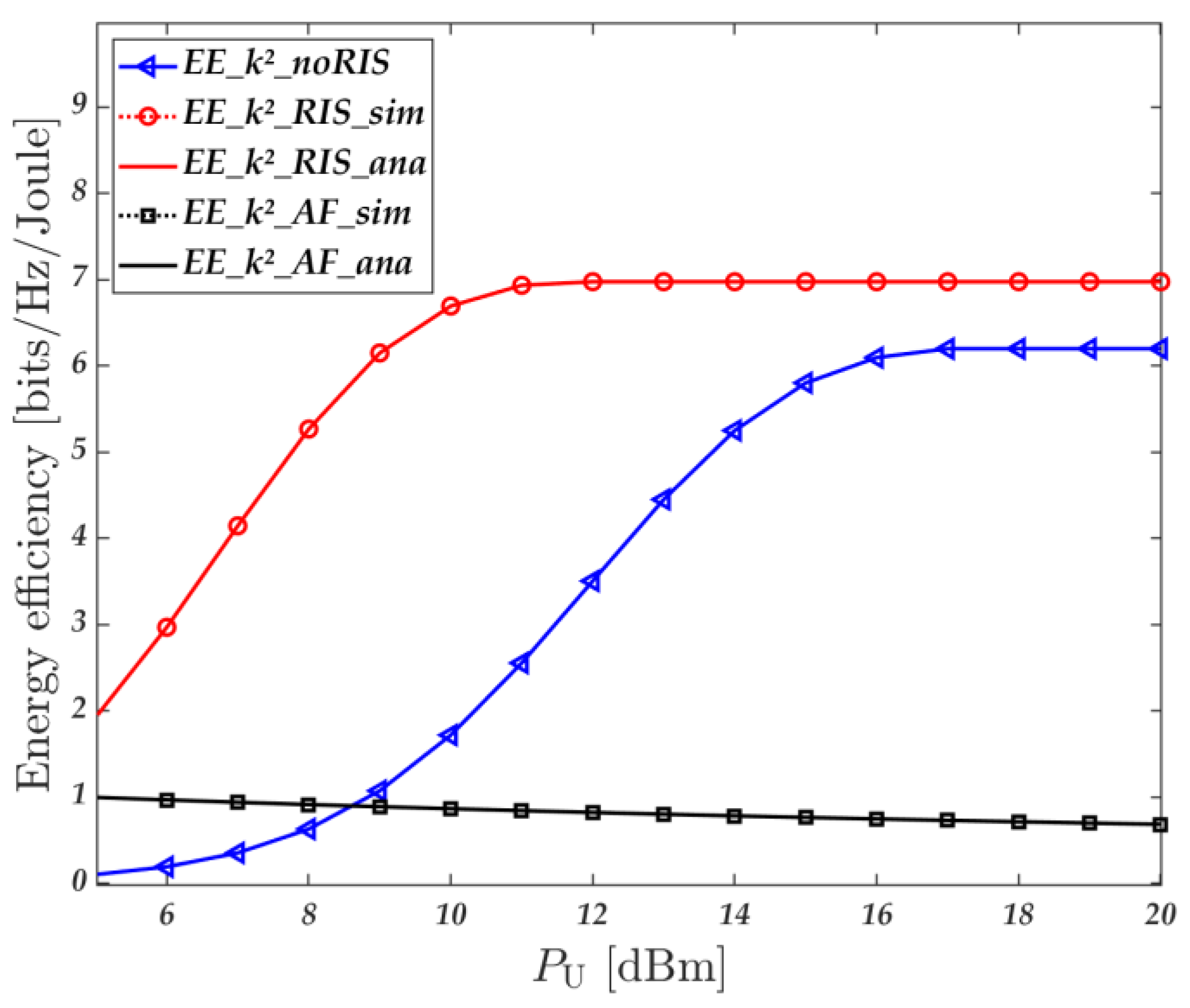
4. Simulation Results

This section verifies the correctness of the theoretical derivation through simulation, and the outage probability, ergodic rate, and energy efficiency of distributed RIS-assisted air–ground fusion networks in non-ideal environments are analyzed. This paper discusses the following four schemes, where scheme 1 is the proposed scheme for a distributed RIS-assisted air–ground fusion network with non-ideal factors, and schemes 2–4 are benchmark schemes:

• Communication scheme of distributed RIS-assisted air–ground fusion network considering non-ideal factors as discussed in this paper. This scheme is named k²_RIS;
• Direct link communication scheme from the UAV base station to user. This scheme is named k²_noRIS [24];
• Ideal conditions scheme not considering non-ideal environments (hardware damage, imperfect channels, and random user. This scheme is named ideal _RIS [14];
• Communication scheme using AF relay but with hardware impairments for the UAV base station and user. This scheme is named AF_ k² [39].

It is assumed that all channels follow the Nakagami-m distribution. The simulation platform is established using MATLAB 2021a software. The transmission bandwidth D is set to 100 MHz [14], and the power of additive white Gaussian noise is set to −174 + 10log₁₀D dBm [28]. The path loss exponent Λ is 3 [28], and the power attenuation at the reference distance is set to −30 dBm. The random radius R and r₀ are set to 10 m and 1 m, respectively. Assuming that there are 3 RISs (N = 3), with the RIS position coordinates being (21 m, 12 m), (51 m, 36 m), and (80 m, 40 m), respectively, the center position of randomly distributed users is (90 m, 10 m), and the UAV position is (0, 100 m). The power consumption of each RIS element is 1 dBm, and the power consumption of the user is 10 dBm [28]. The main simulation parameters are summarized in

Table 2. Simulation parameters.

Simulation Parameters	Value
Path loss exponent	3
The number of RISs	N = 3
The power consumption of the user	P1 = 10 dBm
The power consumption of RIS element	PRIS = 1 dBm
The radius of disc	R = 10 m r0 = 1 m
Bandwidth	100 MHz

.

Figure 2 illustrates the relationship between outage probability and transmit power of the UAV across three scenarios: k²_noRIS, k²_RIS, and ideal _RIS. In these scenarios, we consider that each RIS unit L_n = {10, 20}, with a hardware impairment factor of k² = 0.01. The alignment between the simulation curve and the theoretical approximation curve, as shown in Figure 2, validates the accuracy of our theoretical derivation. Simulation results demonstrate that employing the RIS results in a lower outage probability compared to scenarios without RIS (k²_noRIS), primarily due to the introduction of cascaded links in communication, thus reducing the likelihood of communication outage. Furthermore, the outage probability is impacted by the quantity of RIS units, with a decrease in outage probability correlating with an increase in RIS units. A comparison between the outage probabilities of k²_RIS (L_n = {10, 20}) and ideal_ RIS (L_n = 10) indicates that adding additional RIS units does not fully offset the impact of hardware impairment on outage probability. Notably, hardware impairment heightens the risk of communication outage, underscoring the necessity of accounting for real-world, non-ideal environments in our analysis.

Figure 3 depicts the correlation between the ergodic rate and transmit power of UAV fluctuation in three settings: k²_noRIS, k²_RIS, and ideal _RIS. In these configurations, we consider that each RIS unit L_n = {10, 20}, with a hardware impairment factor of k² = 0.04. Analysis of Figure 3 reveals that at lower power levels, the ergodic rate of k²_RIS exceeds that of k²_noRIS as the UAV transmit power increases, showcasing the system’s ability to boost the rate with RIS assistance. Simultaneously, the ergodic rate of k²_RIS (L_n = 20) is higher than that of k²_RIS (L_n = 10), which proves that the more RIS units there are, the faster the ergodic rate. However, with the increase in the UAV transmit power, system metrics afflicted by hardware impairment tend to converge, due to hardware damage constraining the upper limit of the ergodic rate. Prior to convergence, under identical circumstances, the curves of k²_RIS and ideal _RIS (L_n = 10) exhibit similarity, suggesting the minimal impact of hardware impairment at lower UAV transmit power levels. Consequently, in practical scenarios with hardware impairment, the UAV base station can effectively operate at lower UAV transmit power levels.

In Figure 4, the correlation between hardware impairment k², parameter m, and UAV transmit power fluctuation is illustrated, assuming a fixed number of 10 RIS units. The simulation outcomes reveal an inverse relationship between hardware impairment and the ergodic rate’s upper threshold. Specifically, as hardware impairment diminishes, the upper limit of the ergodic rate escalates, a consequence of the impairment’s influence on the rate. Simultaneously, an increase in the parameter m at reduced UAV transmit power levels precipitates a contraction of the ergodic rate. This is primarily due to the fact that when the channel conditions deteriorate, the ergodic rate experiences a significant decrease. Therefore, it can be concluded that the upper limit of the traversal rate is related to hardware damage.

Figure 5 shows the correlation between the ergodic rate and the number of RIS units, considering the presence of hardware impairment. The study compares the ergodic rate of the centralized RIS (N = 1), where all units are centralized into a single RIS, with that of distributed RIS (N = 3). Simulation results demonstrate that the ergodic rate of the distributed RIS outperforms that of the centralized RIS as the number of units increases. These findings emphasize the importance of considering distributed RIS configurations in practical implementations.

Figure 6 illustrates the correlation between the UAV transmit power variation and energy efficiency in three scenarios: k²_noRIS, k²_RIS, and AF_ k². The analysis assumes the presence of assuming a fixed number of 10 RIS units and a fixed value of k² = 0.05. The simulation results clearly indicate that the energy efficiency of k²_RIS surpasses that of k²_noRIS and AF_ k², attributed to the enhanced transmission rate facilitated by RIS. Furthermore, as k²_noRIS and k²_RIS approach their peaks, a convergence in energy efficiency is observed. This convergence results from the optimization of the UAV transmit power, preventing a decline in energy efficiency. The findings from Figure 6 highlight the potential of distributed RIS-assisted UAV communication in improving energy efficiency, emphasizing the importance of selecting the optimal transmit power level of the UAV to maintain the system energy efficiency.

5. Conclusions

This paper delves into an analysis of the outage probability, ergodic rate, and energy efficiency of distributed RIS-assisted air–ground fusion networks, taking into account non-ideal environmental factors such as hardware impairment, imperfect channels, and random users. Closed-form solutions pertinent to the system performance metrics are derived, utilizing the k²_RIS model as a foundation. An initial comparison between the k²_RIS and k²_noRIS systems demonstrates that RISs can reduce outage probability and enhance the ergodic rate and energy efficiency of air–ground fusion networks. Subsequent comparison with the ideal _RIS system highlights the significant impact of non-ideal factors on the network, emphasizing the necessity of considering these factors. Furthermore, based on the k²_RIS system, differences are distinguished between distributed and centralized RISs. Experimental results indicate that, with a constant number of RIS reflecting units, the energy efficiency of distributed RISs surpasses that of the centralized RIS. A final comparison of the energy efficiency of k²_RIS and AF_ k² confirms the superior energy efficiency of RIS-assisted networks over AF relay-assisted air–ground fusion networks. Therefore, the proposed distributed RIS-assisted network addresses potential challenges in future wireless communication networks and provides a valuable reference for the practical application of future air–ground fusion networks. In our future research, we will combine a simultaneously transmitting and reflecting reconfigurable intelligent surface (STAR-RIS) and integrated sensing and communication to enhance the overall performance and adaptability of the network, thereby enabling us to delve deeper into the study of RIS-assisted air–ground integrated networks.