Adaptive Path Guidance Law for a Small Fixed-Wing UAS with Bounded Bank Angle
Abstract
:1. Introduction
- Derivation of a robust path-following guidance law, supported by theoretical proof and experimental validation.
- Low-level autopilot command generation incorporating the approximated roll closed-loop system where the modeling uncertainty is handled through parameter adaptation.
2. Materials and Method
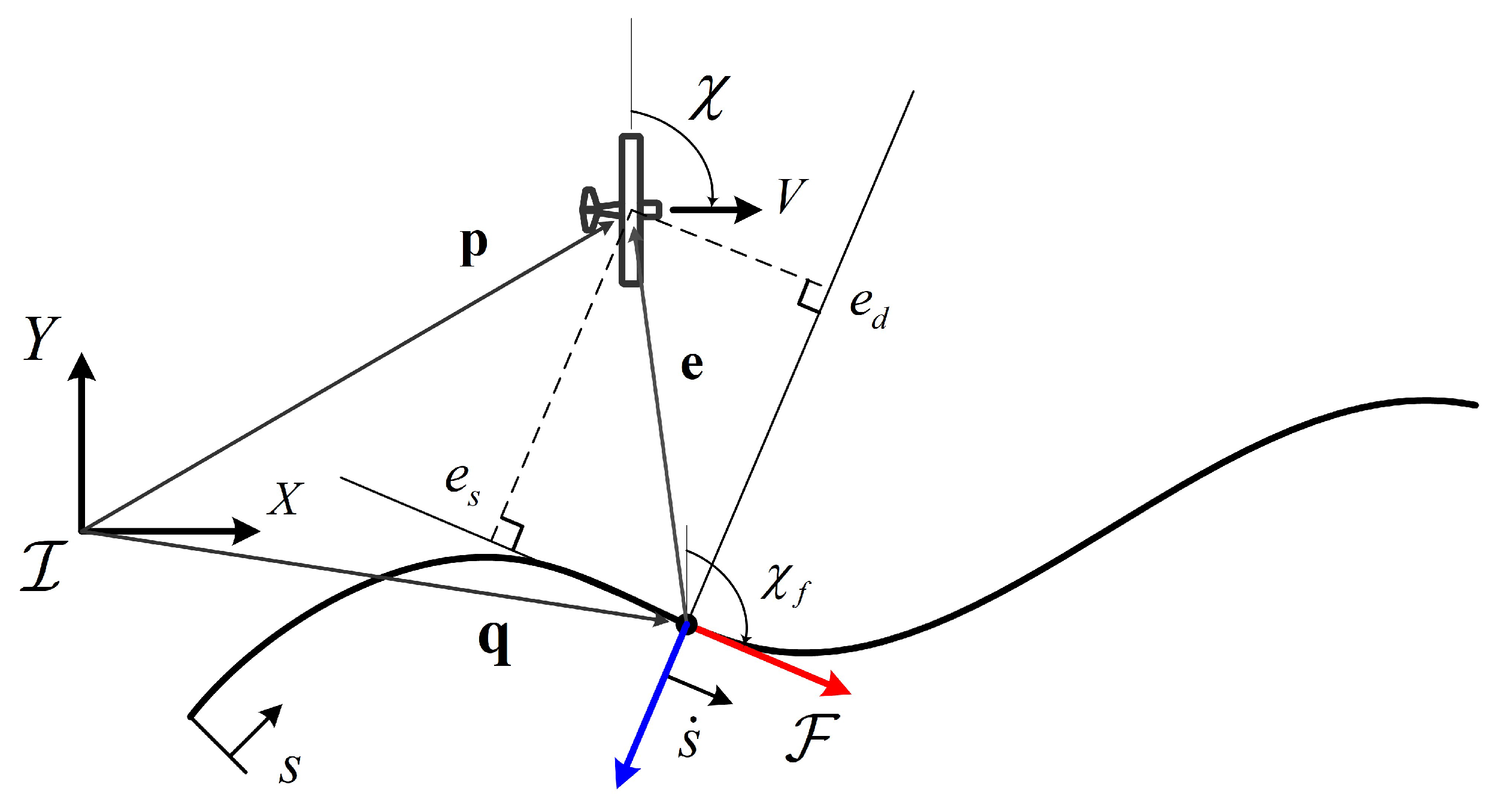
2.1. System Model
2.2. Nonlinear Guidance Control Law
2.2.1. Kinematic Control Law
2.2.2. Backstepping Design for Lateral Control
2.2.3. Adaptive Parameter Estimation
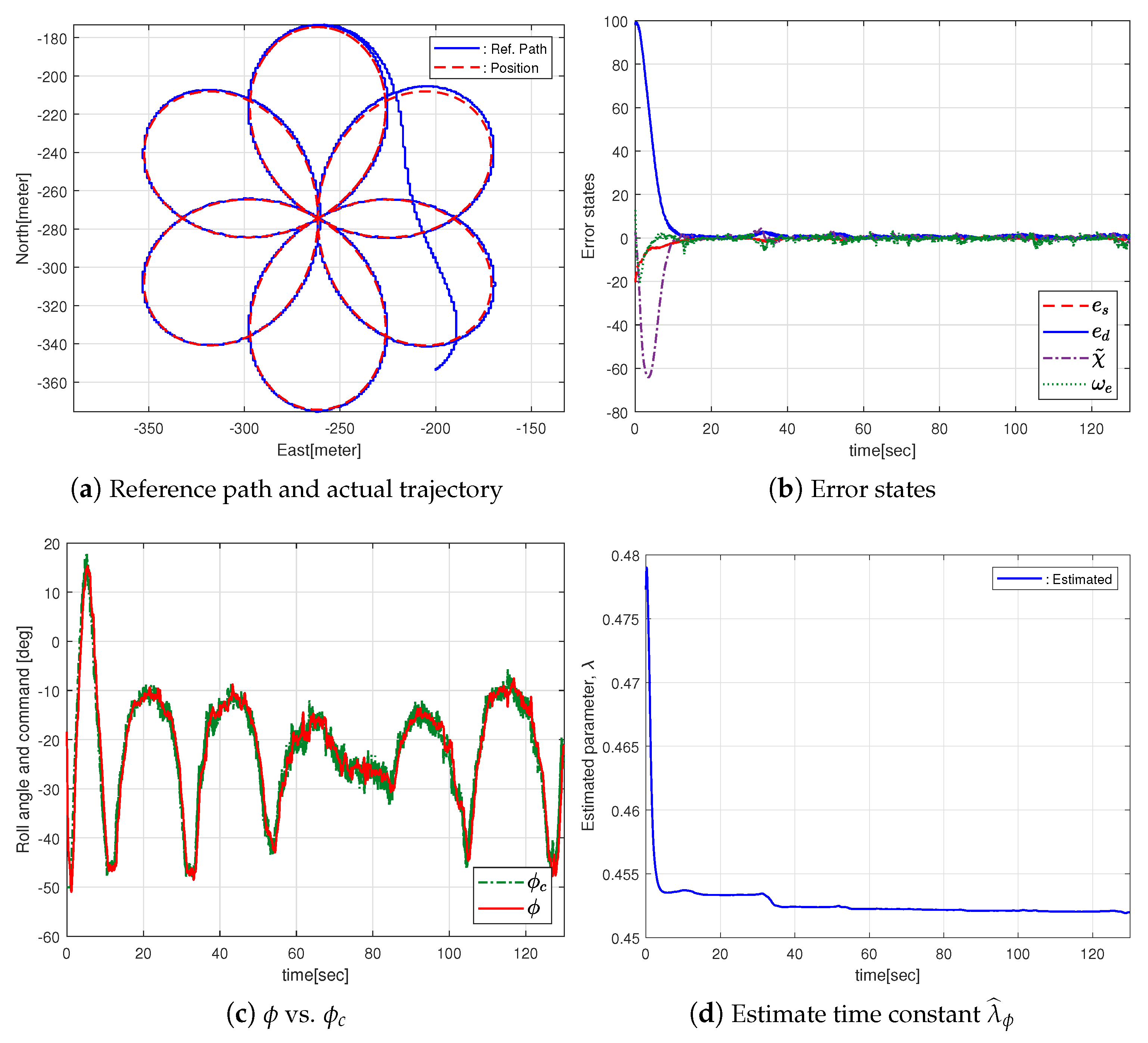
3. Results
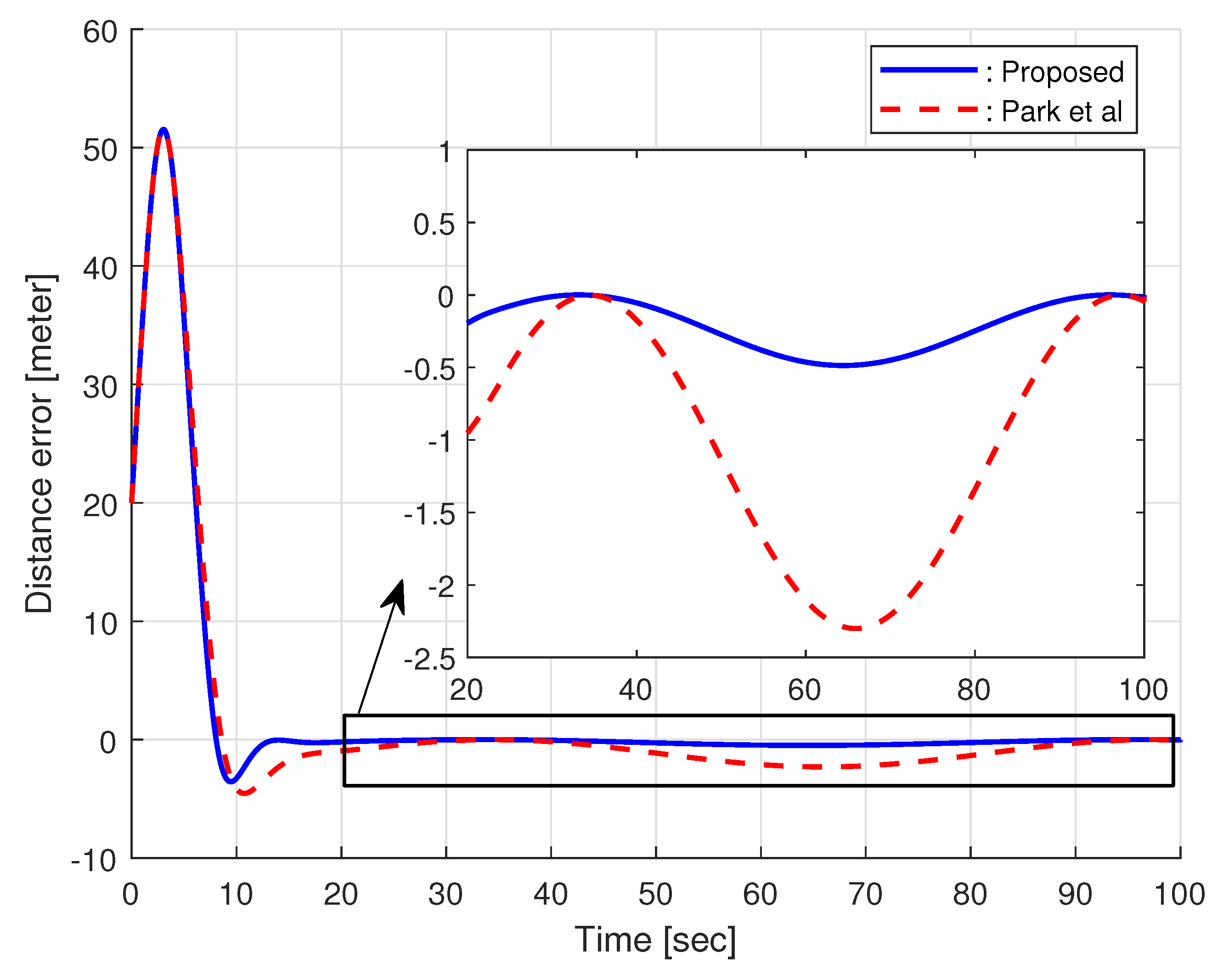
3.1. Performance Comparison via Numerical Simulation
3.2. Performance Validation via HILS
3.2.1. HILS Environment
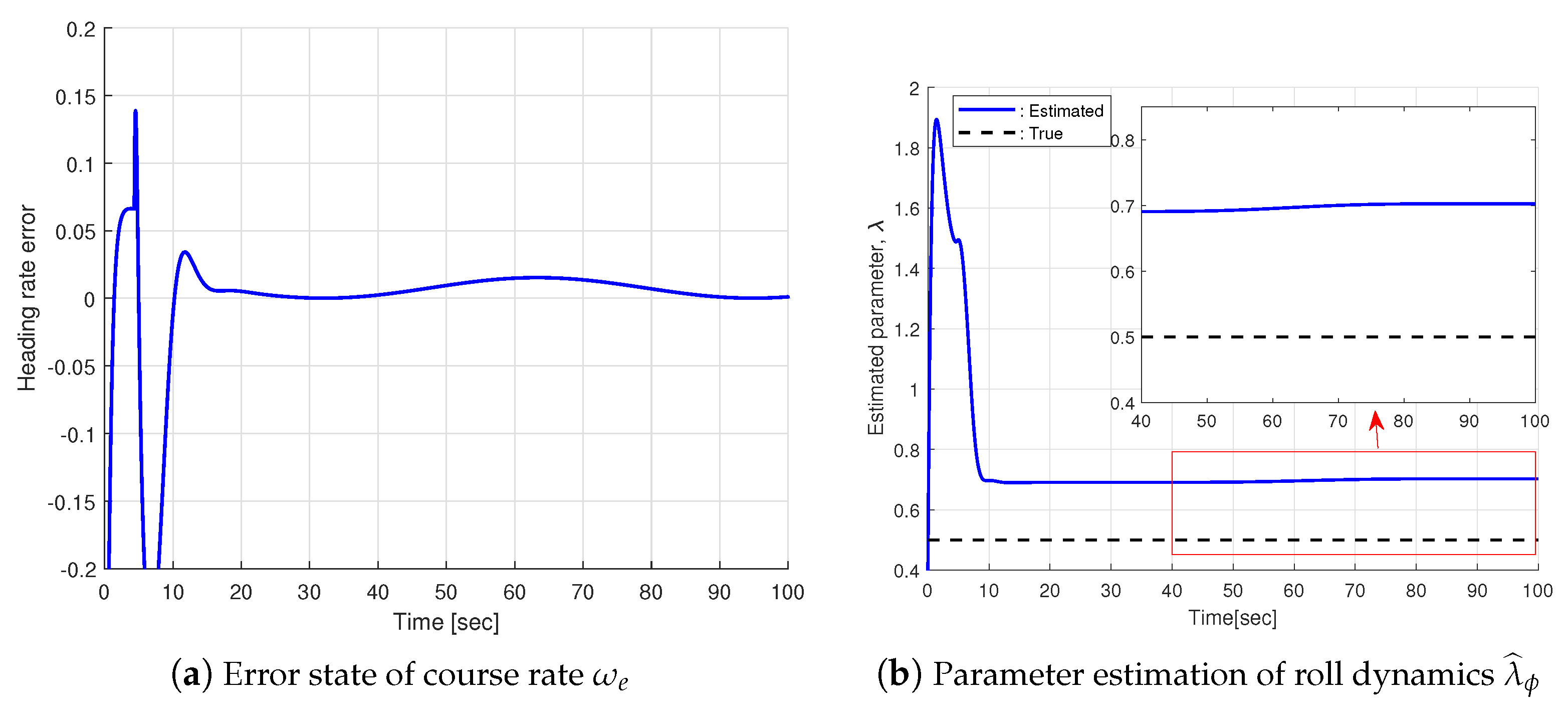
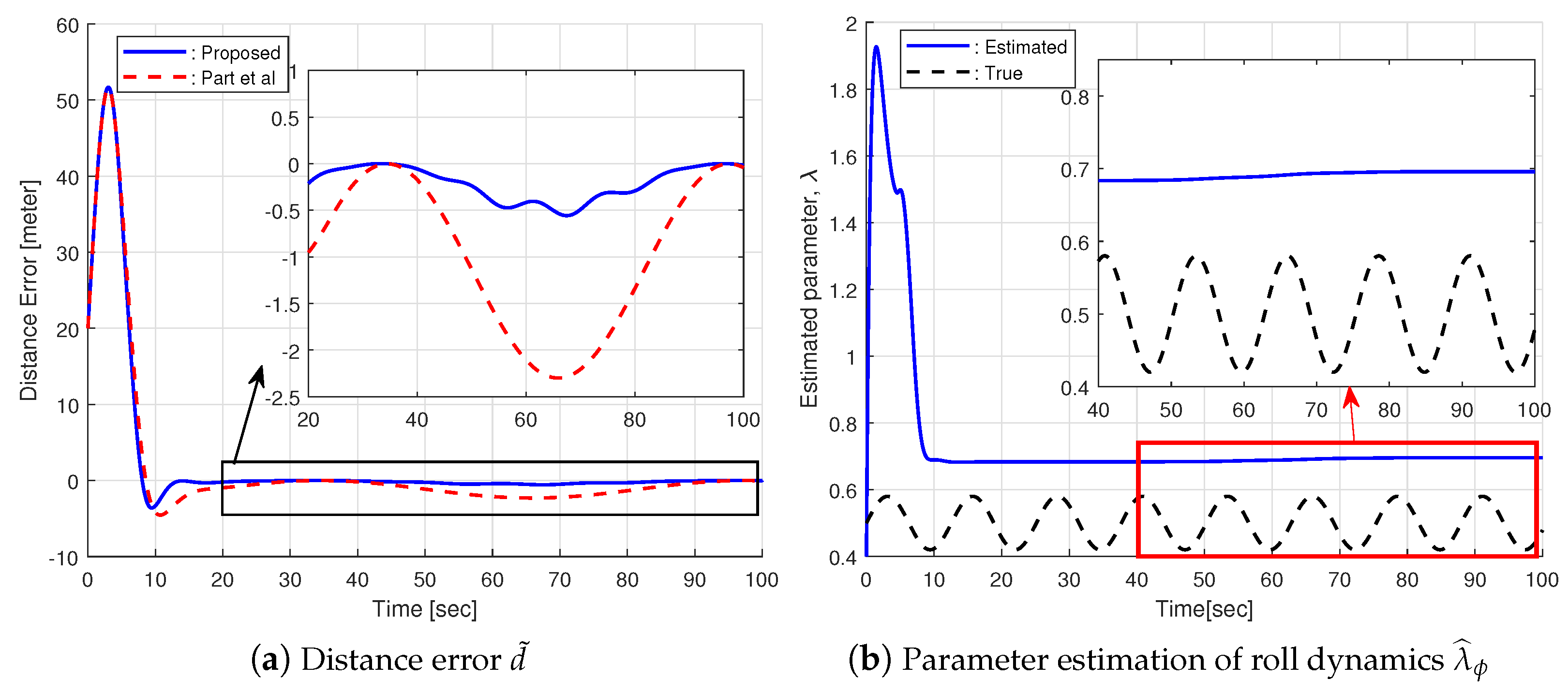
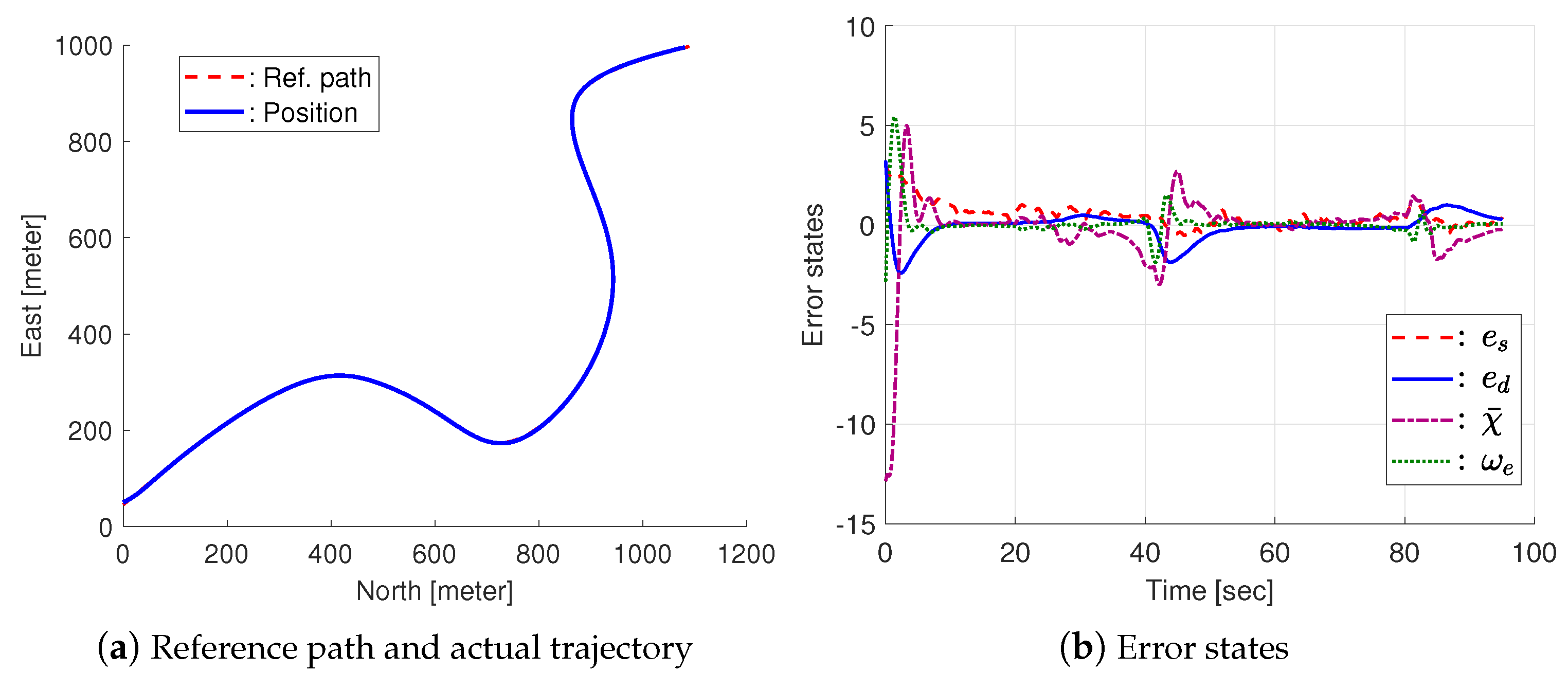
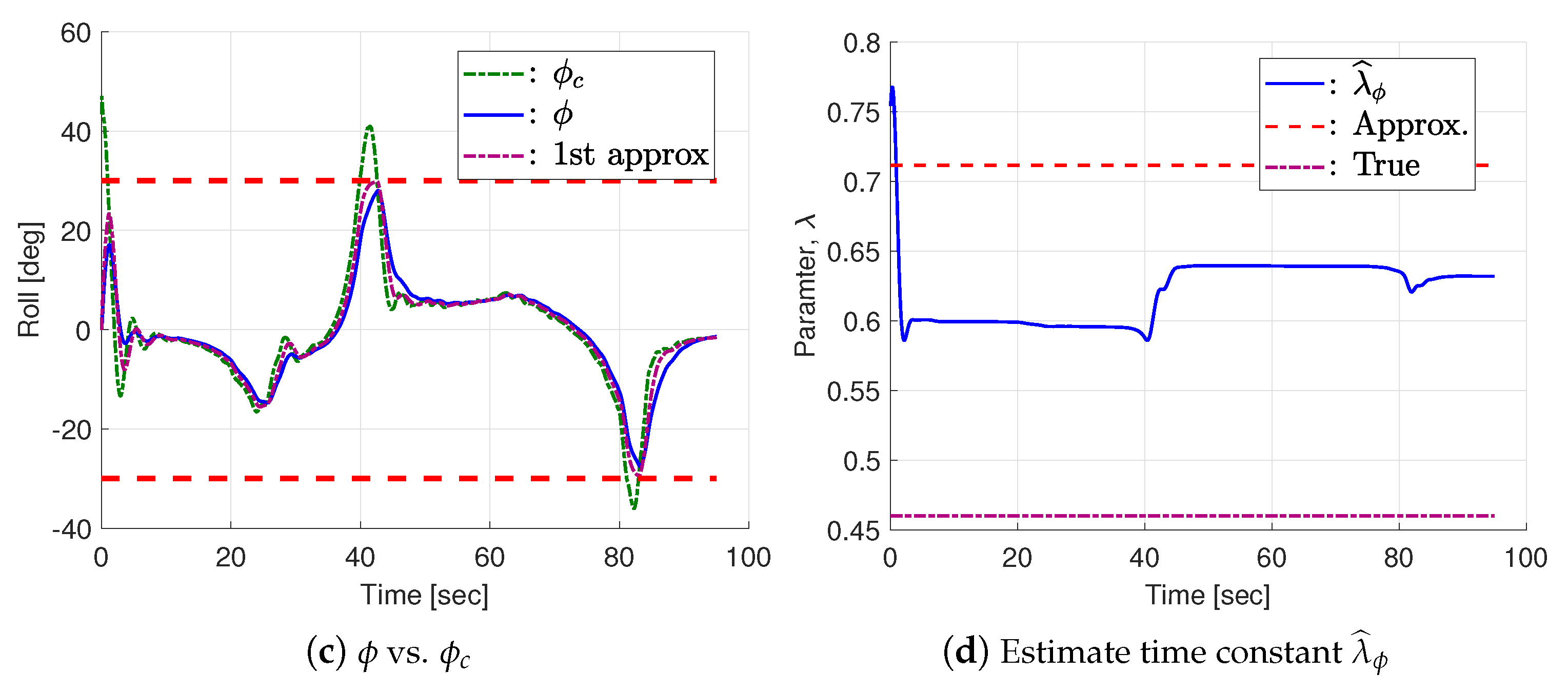
3.2.2. HILS Results
3.2.3. Modified Path-Following Control Strategy for Bounded Control Input
3.3. Performance Validation via Flight Test
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Invernizzi, D.; Giurato, M.; Gattazzo, P.; Lovera, M. Comparison of Control Methods for Trajectory Tracking in Fully Actuated Unmanned Aerial Vehicles. IEEE Trans. Control Syst. Technol. 2020, 29, 1147–1160. [Google Scholar] [CrossRef]
- Willis, J.B.; Beard, R.W. Nonlinear trajectory tracking control for winged eVTOL UAVs. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–25 May 2021; pp. 1687–1692. [Google Scholar]
- Chen, H.; Cong, Y.; Wang, X.; Xu, X.; Shen, L. Coordinated path-following control of fixed-wing unmanned aerial vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 2540–2554. [Google Scholar] [CrossRef]
- Park, S. Rendezvous Guidance on Circular Path for Fixed-Wing UAV. Int. J. Aeronaut. Space Sci. 2021, 22, 129–139. [Google Scholar] [CrossRef]
- Soetanto, D.; Lapierre, L.; Pascoal, A. Adaptive, non-singular Path-following Control of Dynamic Wheeled Robots. In Proceedings of the 42nd IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 9–12 December 20023; pp. 1765–1770. [Google Scholar]
- Liang, X.; Qu, X.; Hou, Y.; Zhang, J. Three-dimensional Path Following Control of Underactuated Autonomous Underwater Vehicle based on Damping Backstepping. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417724179. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y. Guidance-Based Path Following of an Underactuated Ship Based on Event-Triggered Sliding Mode Control. J. Mar. Sci. Eng. 2022, 10, 1780. [Google Scholar] [CrossRef]
- Miao, J.; Sun, X.; Chen, Q.; Zhang, H.; Liu, W.; Wang, Y. Robust Path-Following Control for AUV under Multiple Uncertainties and Input Saturation. Drones 2023, 7, 665. [Google Scholar] [CrossRef]
- Stephan, J.; Pfeifle, O.; Notter, S.; Pinchetti, F.; Fichter, W. Precise Tracking of Extended Three-Dimensional Dubins Paths for Fixed-wing Aircraft. J. Guid. Control Dyn. 2020, 43, 2399–2405. [Google Scholar] [CrossRef]
- Park, S.; Deyst, J.; How, J.P. Performance and Lyapunov Stability of a Nonlinear Path-Following Guidance Method. J. Guid. Control Dyn. 2007, 30, 1718–1728. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Trajectory Tracking for Unmanned Air Vehicles with Velocity and Heading Rate Constraints. IEEE Trans. Control Syst. Technol. 2004, 12, 706–716. [Google Scholar] [CrossRef]
- Nelson, D.R.; Barber, D.B.; McLain, T.W.; Beard, R.W. Vector Field Path Following for Small Unmanned Air Vehicles. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 5788–5794. [Google Scholar]
- Zhang, Z.; He, C.; Chen, H.; Zhang, Y.; Wang, H.; Cai, Y.; Lu, T. Small Fixed-Wing Unmanned Aerial Vehicle Path Following Under Low Altitude Wind Shear Disturbance. IEEE Trans. Intell. Transp. Syst. 2024, 25, 13991–14003. [Google Scholar] [CrossRef]
- Shivam, A.; Ratnoo, A. Arcsine Vector Field for Path Following Guidance. J. Guid. Control Dyn. 2023, 46, 2409–2420. [Google Scholar] [CrossRef]
- Shivam, A.; Ratnoo, A. Vector Field for Following Elliptic Paths. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Wilhelm, J.P.; Clem, G. Vector Field UAV Guidance for Path Following and Obstacle Avoidance with Minimal Deviation. J. Guid. Control Dyn. 2019, 42, 1848–1856. [Google Scholar] [CrossRef]
- Song, Y.; Yong, K.; Wang, X. Disturbance Interval Observer-Based Robust Constrained Control for Unmanned Aerial Vehicle Path Following. Drones 2023, 7, 90. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, G.; Li, J.; Chang, Z.; Yan, Q. Path-Following Control of Small Fixed-Wing UAVs under Wind Disturbance. Drones 2023, 7, 253. [Google Scholar] [CrossRef]
- Zhao, C.; Guo, L.; Yan, Q.; Chang, Z.; Chen, P. Path Tracking Control of Fixed-Wing Unmanned Aerial Vehicle Based on Modified Supertwisting Algorithm. Int. J. Aerosp. Eng. 2024, 2024, 5941107. [Google Scholar] [CrossRef]
- Kumar, S.; Sinha, A.; Kumar, S.R. Robust Path-following Guidance for an Autonomous Vehicle in the Presence of Wind. Aerosp. Sci. Technol. 2024, 150, 109225. [Google Scholar] [CrossRef]
- Nian, X.H.; Zhou, W.X.; Li, S.L.; Wu, H.Y. 2-D Path Following for Fixed Wing UAV using Global Fast Terminal Sliding Mode Control. ISA Trans. 2023, 136, 162–172. [Google Scholar] [CrossRef]
- Reinhardt, D.; Gros, S.; Johansen, T.A. Fixed-Wing UAV Path-Following Control via NMPC on the Lowest Level. In Proceedings of the 2023 IEEE Conference on Control Technology and Applications (CCTA), Bridgetown, Barbados, 16–18 August 2023; pp. 451–458. [Google Scholar]
- Lapierre, L.; Soetanto, D.; Pascoal, A. Nonlinear Path Following with Applications to the Control of Autonomous Underwater Vehicles. In Proceedings of the 42nd IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003; Volume 2, pp. 1256–1261. [Google Scholar]
- Kaminer, I.; Pascoal, A.; Yakimenko, O. Nonlinear Path Following Control of Fully Actuated Marine Vehicles with Parameter Uncertainty. In Proceedings of the 16th IFAC World Congress, Prague, Czech Republic, 3–8 July 2005; pp. 25–30. [Google Scholar]
- Lapierre, L.; Soetanto, D. Nonlinear Path-Following Control of an AUV. Ocean Eng. 2007, 34, 1734–1744. [Google Scholar] [CrossRef]
- Jung, D. Hierarchical Path Planning and Control of a Small Fixed-Wing UAS: Theory and Experimental Validation. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2007. Available online: http://hdl.handle.net/1853/19781 (accessed on 2 November 2024).
- Miao, J.; Wang, S.; Zhao, Z.; Li, Y. Nonlinear Path Following Control of the Underactuated AUV via Reduced-order LESOs and NTD. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016. [Google Scholar]
- Micaelli, A.; Samson, C. Trajectory Tracking for Unicycle-Type and Two-Steering-Wheels Mobile Robots. Ph.D. Thesis, INRIA, Chesnay, France, 1993. [Google Scholar]
- Spooner, J.T.; Maggiore, M.; Ordóñez, R.; Passino, K.M. Stable Adaptive Control and Estimation for Nonlinear Systems; John Wiley & Sons, Inc.: New York, NY, USA, 1999; ISBN 9780471415455. [Google Scholar]
- Gearhart, W.B.; Schulz, H.S. The function sin x/x. Coll. Math. J. 1990, 21, 90–99. [Google Scholar]
- Ardupilot. L1 Controller. Available online: https://github.com/ArduPilot/ardupilot/tree/master/libraries/AP_L1_Control (accessed on 4 October 2024).
- Kang, D.; Kim, S.; Jung, D. Real-time Validation of Formation Control for Fixed-wing UAVs using Multi Hardware-in-the-loop Simulation. In Proceedings of the 2019 IEEE 15th International Conference on Control and Automation (ICCA), Ediburgh, UK, 16–19 July 2019; pp. 590–595. [Google Scholar]
- Jung, D.; Tsiotras, P. On-Line Path Generation for Unmanned Aerial Vehicles Using B-Spline Path Templates. J. Guid. Control Dyn. 2013, 36, 1642–1653. [Google Scholar] [CrossRef]
- Kim, S.; Cho, H.; Jung, D. Evaluation of Cooperative Guidance for Formation Flight of Fixed-wing UAVs using Mesh Network. In Proceedings of the 2020 IEEE International Conference on Unmanned Aircraft System (ICUAS), Athens, Greece, 1–4 September 2020. [Google Scholar]

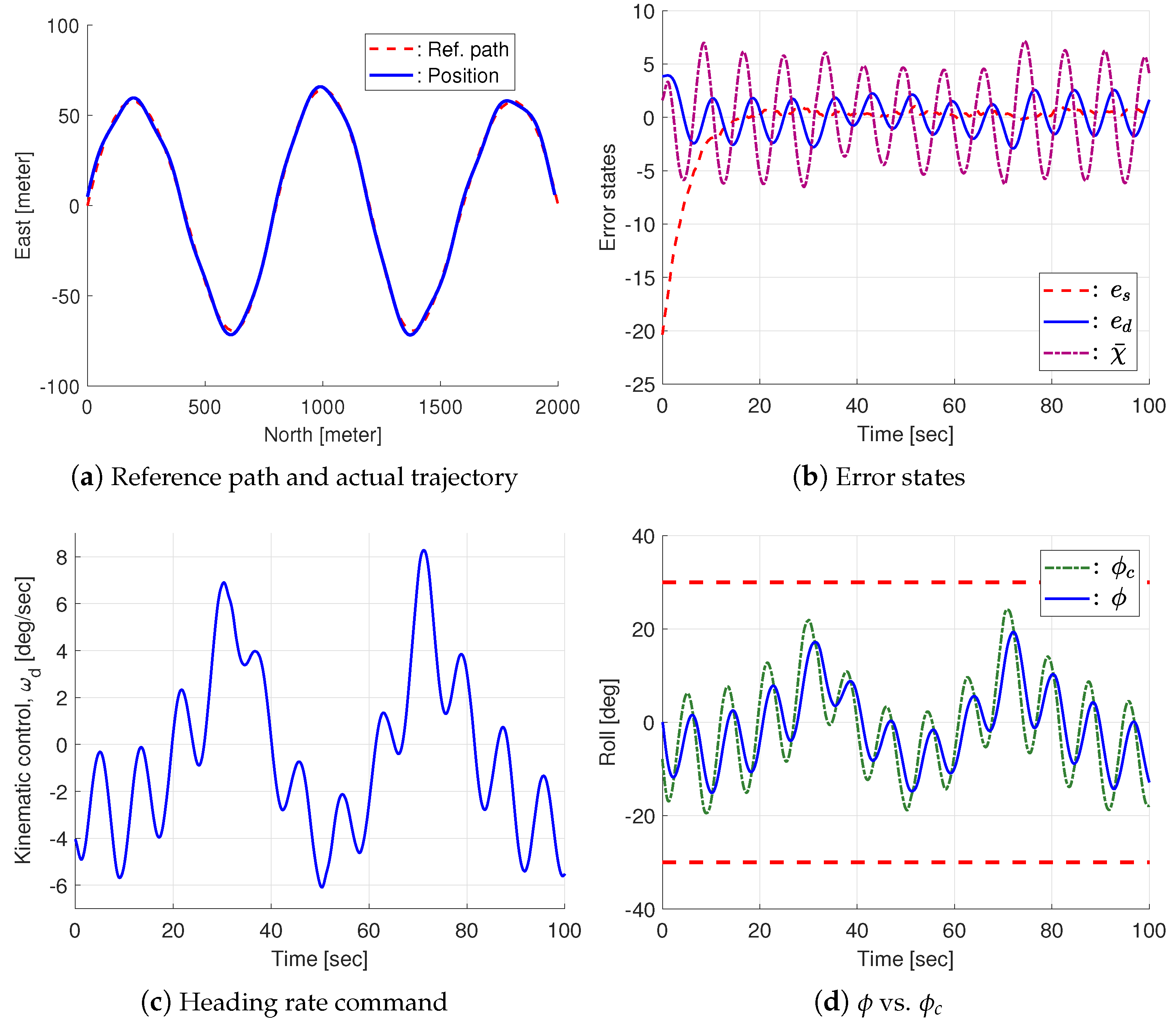
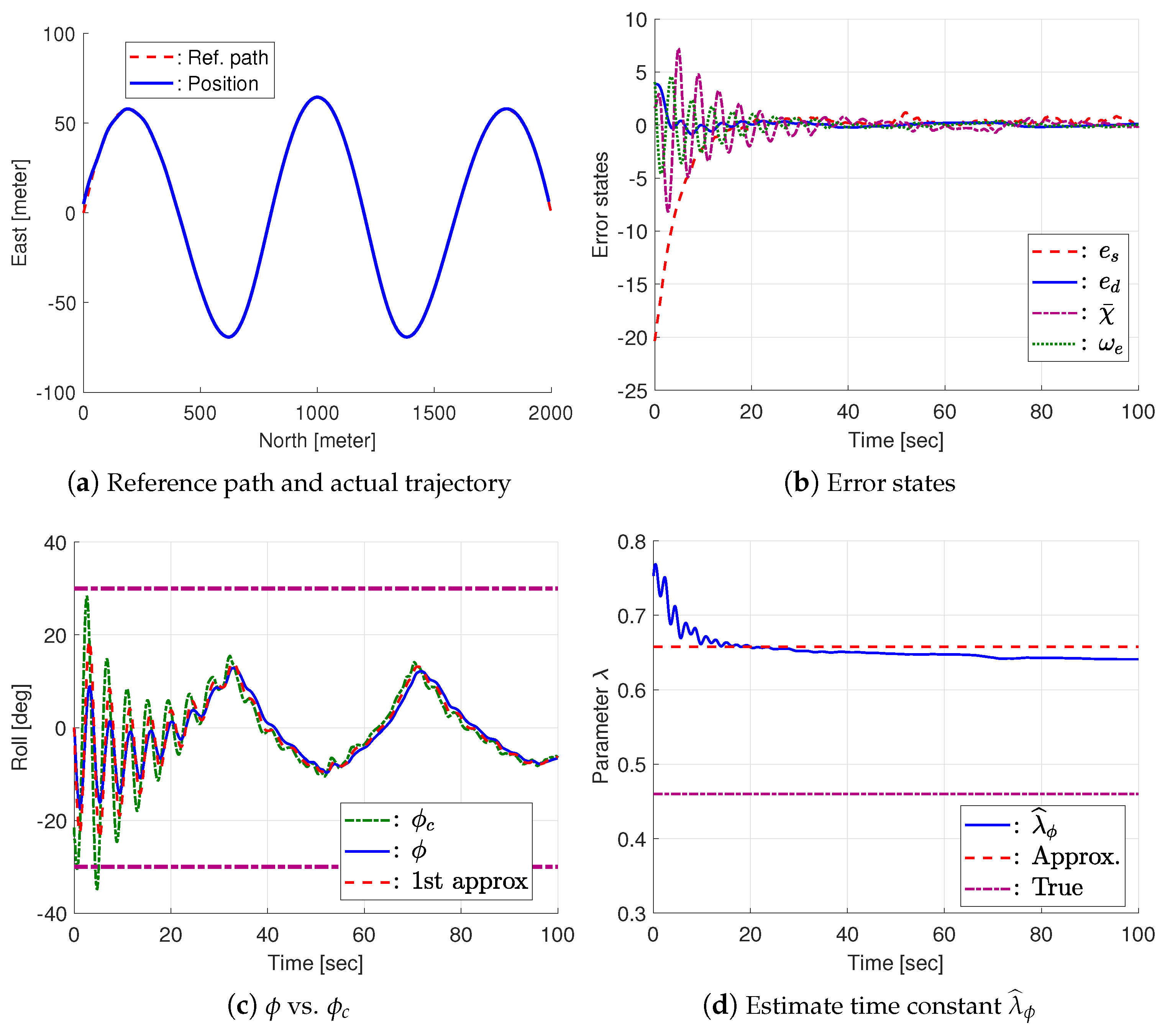


| V = 20 [m/s] | k = 0.01 | = 0.2 | = 0.005 | |
| = 2.0 | = 0.1 | = 4000 | = 0.05 | = |
| Skywalker Eve-2000 | |
|---|---|
| Wingspan/Length | 2240/1270 mm |
| Total weight | 4.6 kg (including battery) |
| Cruise speed | 15–22 m/s |
| Propulsion system | Twin-prop BLDC motor |
| Battery | 6 cells 10,000 mAh |
| Flight control system | Cupido FCC (in-house) |
| V = 15 [m/s] | k = 0.02 | = 0.8 | = 0.001 | |
| = 3.9 | = 0.05 | = 1000 | = 0.05 | = |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Jung, D. Adaptive Path Guidance Law for a Small Fixed-Wing UAS with Bounded Bank Angle. Drones 2025, 9, 180. https://doi.org/10.3390/drones9030180
Kim S, Jung D. Adaptive Path Guidance Law for a Small Fixed-Wing UAS with Bounded Bank Angle. Drones. 2025; 9(3):180. https://doi.org/10.3390/drones9030180
Chicago/Turabian StyleKim, Suhyeon, and Dongwon Jung. 2025. "Adaptive Path Guidance Law for a Small Fixed-Wing UAS with Bounded Bank Angle" Drones 9, no. 3: 180. https://doi.org/10.3390/drones9030180
APA StyleKim, S., & Jung, D. (2025). Adaptive Path Guidance Law for a Small Fixed-Wing UAS with Bounded Bank Angle. Drones, 9(3), 180. https://doi.org/10.3390/drones9030180









