Digital Low-Altitude Airspace Unmanned Aerial Vehicle Path Planning and Operational Capacity Assessment in Urban Risk Environments
Abstract
1. Introduction
1.1. Related Prior Work
| Type | Paper | Method and Study | Core Contribution |
|---|---|---|---|
| Digital grid airspace | Mohamed Salleh et al. [9] | AirMatrix | Propose the implementation of AirMatrix three-dimensional airway network for the quantitative analysis of airspace capacity and throughput. |
| Xu et al. [10] | GeoSOT | Introduce the hierarchical coding mechanism of grid partitioning for GeoSOT. | |
| Tang et al. [11] | GeoSOT | Research on Dynamic Geographical Fence Establishment Based on GeoSOT. | |
| Shi et al. [12] | GeoSOT | Carry out flight conflict detection based on GeoSOT. | |
| Risk assessment | Martin et al. [13] | Mid-Air Collision Risk, Ground Impact Risk | A set of procedures for managing the risk assessment of UAVs in both mid-air collision risk and ground impact risk. |
| Civil Aviation Administration of China (CAAC) [14] | Mid-Air Collision Risk, Ground Impact Risk | Provide ground impact risk and mid-air collision risk assessment services for CAAC, operation responsible persons of specific types of unmanned aircraft to be operated, service providers of air traffic management and other relevant third parties. | |
| Shao et al. [15] | Mid-Air Collision Risk, Ground Impact Risk | Conduct risk assessment of mid-air collision risk and ground impact risk for UAV logistics delivery scenarios. | |
| Banerjee et al. [16] | Mid-Air Collision Risk, Third-Party Risk | It elaborated on the possibility of risk associated with obstacle collision and took into account the influence of abnormal conditions introduced by component failures, reduced controllability, and environmental interference. | |
| Pang et al. [17] | Mid-Air Collision Risk, Ground Impact Risk, Third-Party Risk, Risk Maps | Risk is quantified by using risk maps. The risk assessment model includes risk of death, property loss and noise impact. | |
| Primatesta et al. [18] | Ground Impact Risk, Risk Maps | Employ risk maps to define the ground risks associated with unmanned aircraft accidents. | |
| UAV path planning | AVGC et al. [19] | Traditional A* | Path planning algorithm based on sampling search. |
| Zhang et al. [3] | Weighted A* | Set the risk as the weight to solve the problem of setting up the logistics distribution routes for the “last mile”. | |
| Zhang et al. [20] | Weighted A* | Establish a risk-based urban airspace environment model, and plan UAVs with low operational risks, low noise levels, and low transportation costs. | |
| Jung et al. [21] | Path Smoothing | The problem of generating smooth reference paths was raised under the condition that a finite discrete set of local optimal path families was given. | |
| Wang et al. [28] | Path Smoothing | An improved A* algorithm based on the optimization of key point selection and smooth path generation is proposed. The A* algorithm is combined with Bezier curves to process the smoothness of the generated path. | |
| Airspace capacity assessment | Bulusu et al. [29] | Simulation Analysis | Estimate flight capacity through the assessment of flight conflicts among unmanned aerial vehicles operating in the airspace. |
| Starita et al. [24] | Simulation Analysis | Take into account a large number of traffic scenarios to consider the uncertainties of traffic and capacity supply. | |
| Cho et al. [25] | Topological Analysis | The topology method of setting up access-restricted and exit-restricted geographic fences is adopted for conducting airspace capacity assessment. | |
| Vascik et al. [26] | Modeling Optimization | A method of integer programming is proposed to analyze and estimate the capacity of vertical take-off and landing airports. | |
| Zhou et al. [27] | Modeling Optimization | Introduce the traffic dynamics model and solve the capacity of the UAV in both stable and unstable states. |
1.2. Our Contributions
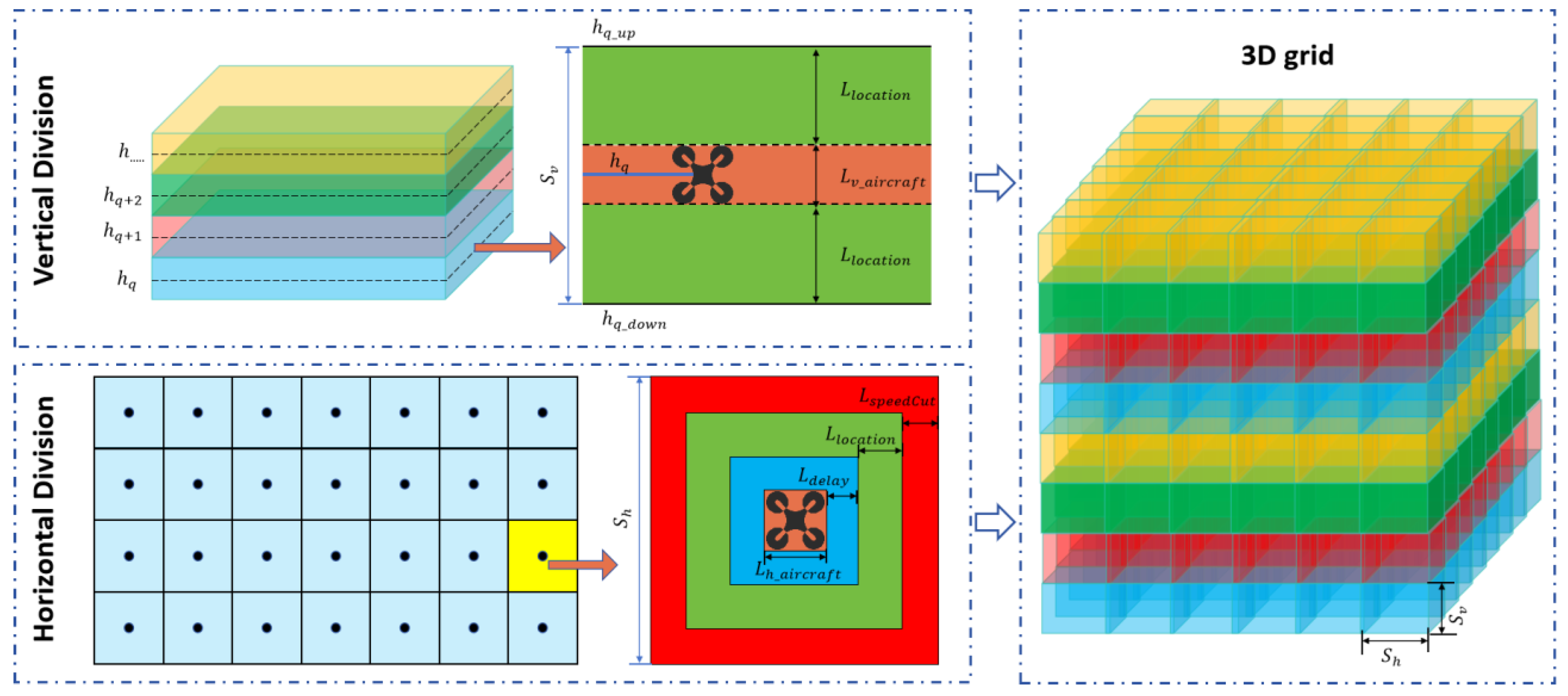
2. Airspace Grid-Based Modeling
2.1. Vertical–Horizontal Grid Partitioning
2.1.1. Vertical Partitioning
2.1.2. Horizontal Partitioning
2.2. Classification and Configuration of “Management-Operation” Grids
2.2.1. Management-Scale Grids
2.2.2. Operation-Scale Grids
- (1)
- Determination of Vertical Grid Scale
- (2)
- Determination of Horizontal Grid Scale
3. Discrete Quantitative Risk Assessment Model for Urban Low-Altitude Airspace Grids
3.1. Mid-Air Collision Risk
3.2. Ground Impact Risk
3.3. Third-Party Risk
3.4. UAV Turning Risk
3.5. Comprehensive Risk
4. Parallelogram-Based Turning Point Optimization Path Planning Method
4.1. UAV Path Planning Model
4.1.1. Objective Function
4.1.2. Constraints
- (1)
- Flight Range Constraint
- (2)
- Turning Angle Constraint
- (3)
- Maximum Take-Off Weight Constraint
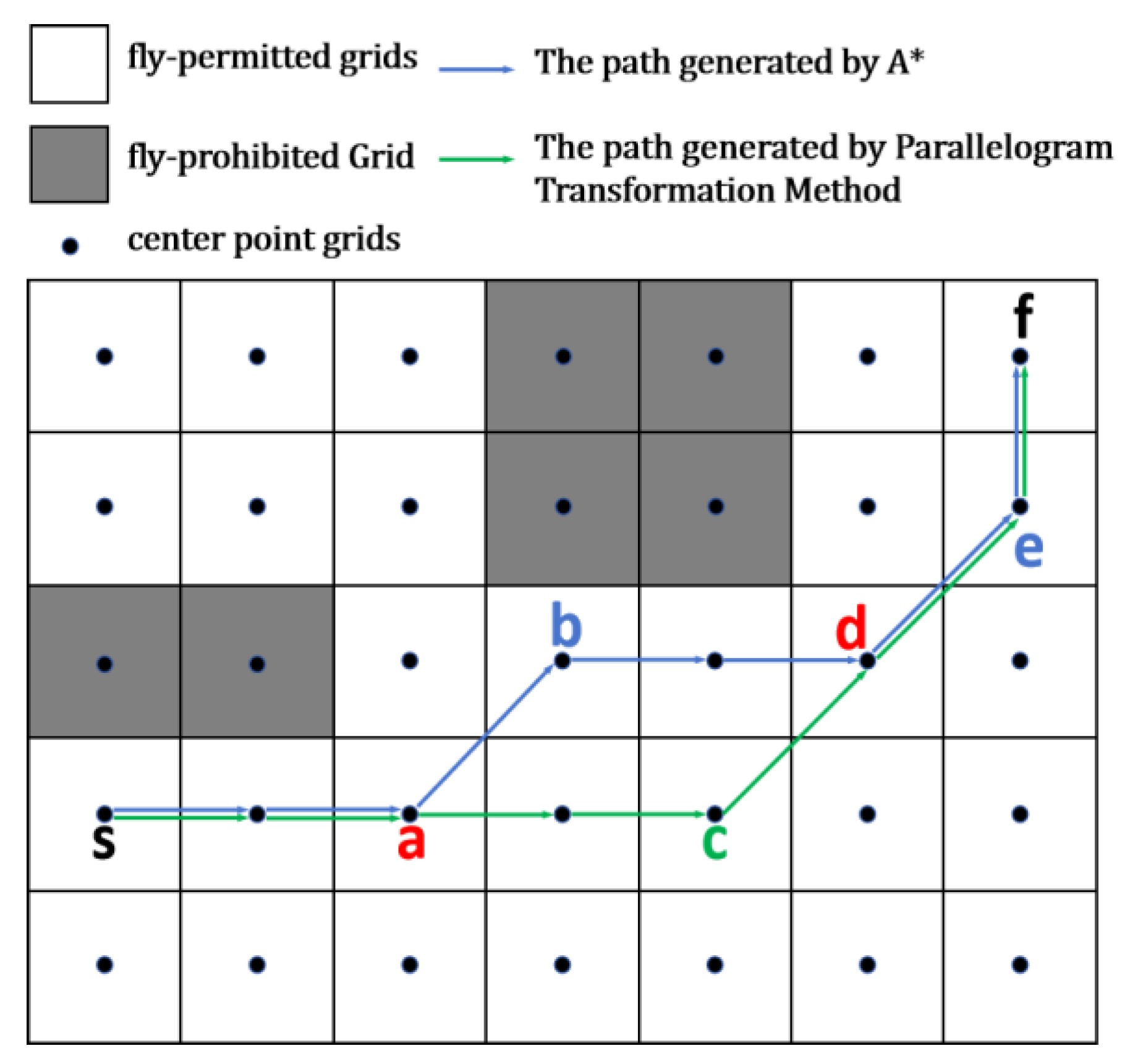
4.2. Parallel-A* Algorithm
4.2.1. Initial Path Planning Based on Weight-A*
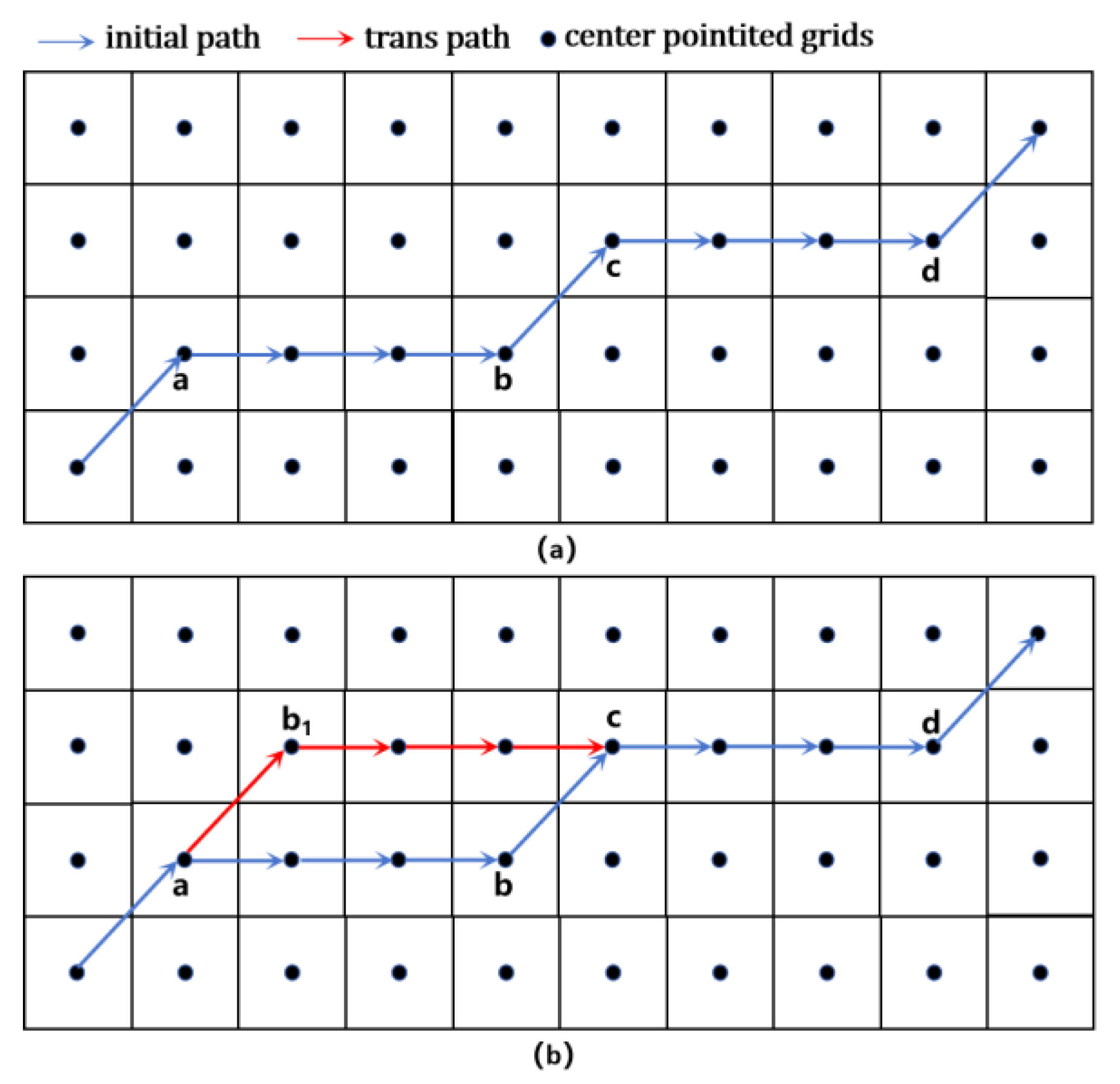
4.2.2. Parallelogram-Based Turning Point Optimization
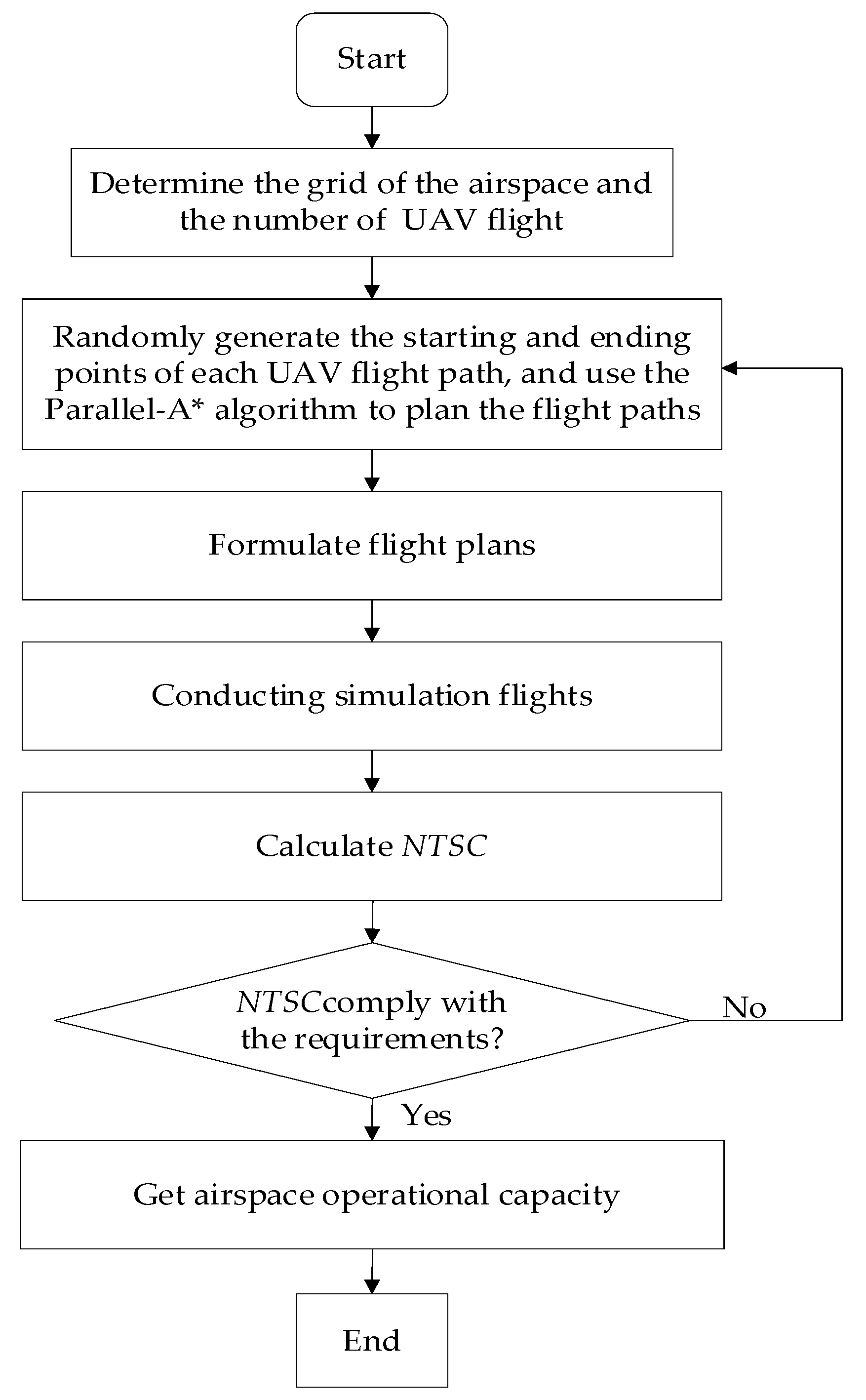
5. Airspace Capacity Assessment Method
5.1. Airspace Operational Capacity Assessment Model
5.2. Conflict Simulation Model
6. Experimental Analysis
6.1. Parameter Configuration
6.2. Risk Analysis
6.2.1. Basic Information Distribution Maps
6.2.2. Environmental Risk Maps
6.3. Path Planning Analysis
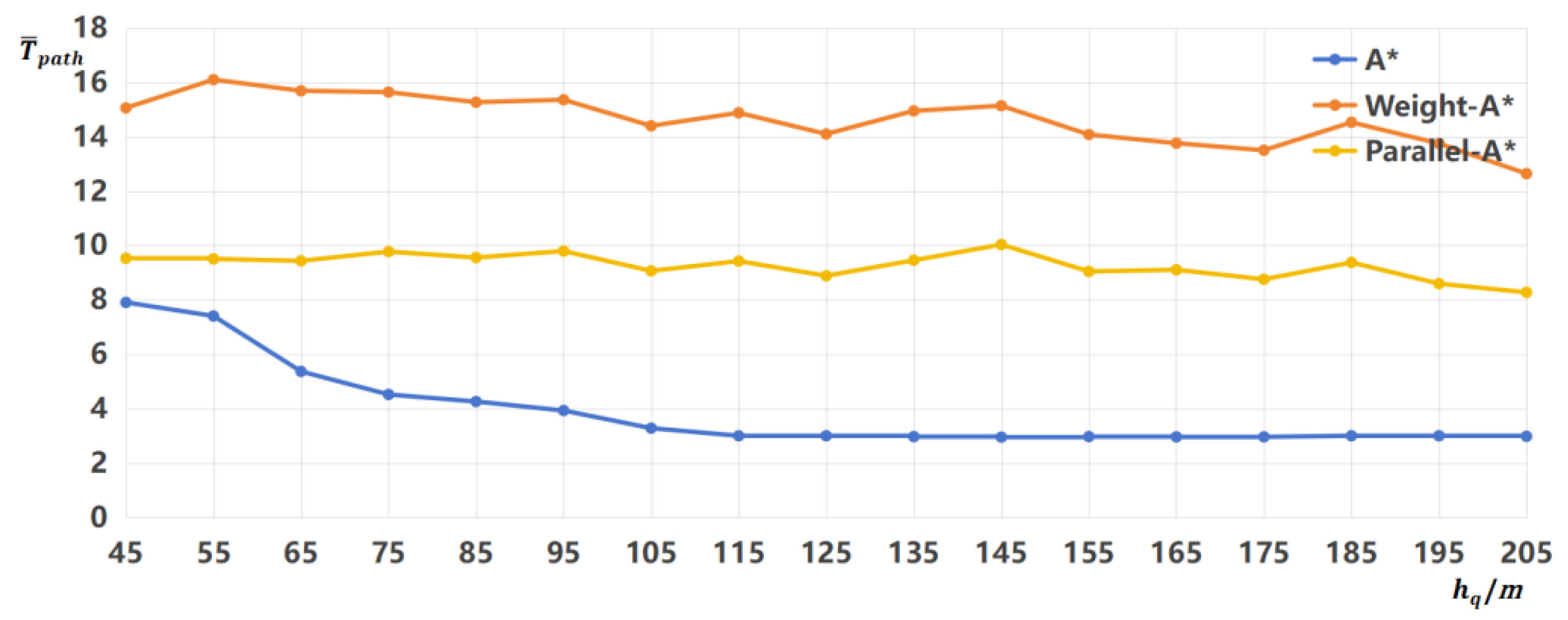
6.3.1. Parameter Analysis
6.3.2. Algorithm Comparison
6.4. Analysis of Low-Altitude Airspace Operational Capacity
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| UAM | Urban Air Mobility |
| CAAC | Civil Aviation Administration of China |
References
- Wu, K.; Lan, J.; Lu, S.; Wu, C.; Liu, B.; Lu, Z. Integrative Path Planning for Multi-Rotor Logistics UAVs Considering UAV Dynamics, Energy Efficiency, and Obstacle Avoidance. Drones 2025, 9, 93. [Google Scholar] [CrossRef]
- Farrag, T.A.; Askr, H.; Elhosseini, M.A.; Hassanien, A.E.; Farag, M.A. Intelligent Parcel Delivery Scheduling Using Truck-Drones to Cut down Time and Cost. Drones 2024, 8, 477. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Feng, D.; Du, S.; Zhong, G.; Deng, C.; Zhou, J. A Logistics UAV Parcel-Receiving Station and Public Air-Route Planning Method Based on Bi-Layer Optimization. Appl. Sci. 2023, 13, 1842. [Google Scholar] [CrossRef]
- Callewaert, N.; Pareyn, I.; Acke, T.; Desplinter, B.; Van de Pitte, K.; Van Vooren, J.; De Meyer, M.; Seeldraeyers, E.; Peeters, F.; De Meyer, S.F.; et al. Limited Impact of Drone Transport of Blood on Platelet Activation. Drones 2024, 8, 752. [Google Scholar] [CrossRef]
- Tang, P.; Li, J.; Sun, H. A Review of Electric UAV Visual Detection and Navigation Technologies for Emergency Rescue Missions. Sustainability 2024, 16, 2105. [Google Scholar] [CrossRef]
- Zhou, Y.; Jin, Z.; Shi, H.; Shi, L.; Lu, N.; Dong, M. Enhanced Emergency Communication Services for Post-Disaster Rescue: Multi-IRS Assisted Air-Ground Integrated Data Collection. IEEE T Netw. Sci. Eng. 2024, 11, 4651–4664. [Google Scholar] [CrossRef]
- Tan, Y.; Yi, W.; Chen, P.; Zou, Y. An adaptive crack inspection method for building surface based on BIM, UAV and edge computing. Autom. Constr. 2024, 157, 105161. [Google Scholar] [CrossRef]
- Aela, P.; Chi, H.; Fares, A.; Zayed, T.; Kim, M. UAV-based studies in railway infrastructure monitoring. Autom. Constr. 2024, 167, 105714. [Google Scholar] [CrossRef]
- Mohamed Salleh, M.F.B.; Wanchao, C.; Wang, Z.; Huang, S.; Tan, D.Y.; Huang, T.; Low, K.H. Preliminary concept of adaptive urban airspace management for unmanned aircraft operations. In Proceedings of the 2018 AIAA Information Systems-AIAA Infotech@ Aerospace, Kissimmee, FL, USA, 8–12 January 2018; p. 2260. [Google Scholar]
- Xu, X.Y.; Wan, L.J.; Chen, P.; Dai, J.B.; Cai, M. An Airspace Raster Representation Method Based on GeoSOT Grid. J. Air Force Eng. Univ. (Nat. Sci. Ed.) 2021, 22, 15–22. [Google Scholar]
- Tang, X.M.; Gu, J.W.; Zheng, P.C.; Li, T. A Method for Unmanned Aerial Vehicle (UAV) Dynamic Geographic Fence Planning Based on Spatial Gridization. China Patent 202010909173.0A, 2020. [Google Scholar]
- Shi, H.F.; Wang, Z.Y.; Zheng, Y.; Xu, Y.B. Refined Management System of Airspace Resources Based on BeiDou Grid Location Code. J. Civ. Aviat. 2022, 6, 44–47. [Google Scholar]
- Martin, T.; Huang, Z.F.; McFadyen, A. Airspace risk management for UAVs a framework for optimising detector performance standards and airspace traffic using JARUS SORA. In Proceedings of the 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; pp. 1516–1525. [Google Scholar]
- CAAC Management Regulations for Trial Operation of Specific Types of UAVs. Available online: https://www.caac.gov.cn/XXGK/XXGK/GFXWJ/201902/t20190201_194511.html (accessed on 1 February 2019).
- Shao, P. Risk assessment for UAS logistic delivery under UAS traffic management environment. Aerospace 2020, 7, 140. [Google Scholar] [CrossRef]
- Banerjee, P.; Gorospe, G.; Ancel, E. 3D representation of UAV-obstacle collision risk under off-nominal conditions. In Proceedings of the IEEE Conference on Aerospace, Big Sky, MT, USA, 6–13 March 2021; pp. 1–7. [Google Scholar]
- Pang, B.; Hu, X.; Dai, W.; Low, K.H. UAV path optimization with an integrated cost assessment model considering third-party risks in metropolitan environments. Reliab. Eng. Syst. Safe 2022, 222, 108399. [Google Scholar] [CrossRef]
- Primatesta, S.; Rizzo, A.; la Cour-Harbo, A. Ground Risk Map for Unmanned Aircraft in Urban Environments. J. Intell. Robot. Syst. 2020, 97, 489–509. [Google Scholar] [CrossRef]
- Harrelson, A.V.G.C. Computing the Shortest Path: A* Search Meets Graph Theory. Proc. Soda 2005, 2005. [Google Scholar] [CrossRef]
- Zhang, H.H.; Zhang, L.D.; Liu, H.; Gang, H. Track Planning Model for Logistics Unmanned Aerial Vehicle in Urban Low-altitude Airspace. J. Transp. Syst. Eng. Inf. Technol. 2022, 22, 256–264. [Google Scholar]
- Jung, D.; Tsiotras, P. On-line path generation for unmanned aerial vehicles using B-spline path templates. J. Guid. Control Dyn. 2013, 36, 1642–1653. [Google Scholar] [CrossRef]
- Damilano, L.; Guglieri, G.; Quagliotti, F.; Sale, I.; Lunghi, A. Ground control station embedded mission planning for UAS. J. Intell. Robot. Syst. 2013, 69, 241–256. [Google Scholar] [CrossRef]
- Bulusu, V.; Sengupta, R.; Liu, Z. Unmanned aviation: To be free or not to be free? In Proceedings of the 7th International Conference on Research in Air Transportation, Philadelphia, PA, USA, 20–24 June 2016. [Google Scholar]
- Starita, S.; Strauss, A.K.; Fei, X.; Jovanović, R.; Ivanov, N.; Pavlović, G.; Fichert, F. Air traffic control capacity planning under demand and capacity provision uncertainty. Transp. Sci. 2020, 54, 882–896. [Google Scholar] [CrossRef]
- Cho, J.; Yoon, Y. How to assess the capacity of urban airspace: A topological approach using keep-in and keep-out geofence. Transp. Res. Part C Emerg. Technol. 2018, 92, 137–149. [Google Scholar] [CrossRef]
- Vascik, P.D.; Hansman, R.J. Development of vertiport capacity envelopes and analysis of their sensitivity to topological and operational factors. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 526. [Google Scholar]
- Zhou, J.; Jin, L.; Wang, X.; Sun, D. Resilient uav traffic congestion control using fluid queuing models. IEEE T Intell. Transp. 2020, 22, 7561–7572. [Google Scholar] [CrossRef]
- Wang, Y.L.; Zhang, S.; Wu, Y.J. Path Planning Algorithm Based on Improved A* Smoothness. Comput. Appl. Softw. 2025, 42, 258–263. [Google Scholar]
- Bulusu, V.; Polishchuk, V.; Sengupta, R.; Sedov, L. Capacity estimation for low altitude airspace. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017; p. 4266. [Google Scholar]
- Jin, A.; Cheng, C.Q. Spatial Data Coding Method Based on Global Subdivision Grid. J. Geomat. Sci. Technol. 2013, 30, 284–287. [Google Scholar]
- Interim Regulation on the Administration of the Flight of Unmanned Aircraft; The State Council of the People’s Republic of China, Central Military Commission of the People’s Republic of China: Beijing, China, 2024.
- Park, S.; Lee, M.C.; Kim, J. Trajectory Planning with Collision Avoidance for Redundant Robots Using Jacobian and Artificial Potential Field-based Real-time Inverse Kinematics. Int. J. Control Autom. Syst. 2020, 18, 2095–2107. [Google Scholar] [CrossRef]
- Xinhui, R.; Caixia, C. Construction and application of third-party risk model for unmanned aerial vehicle operation in urban environment. China Saf. Sci. J. 2021, 31, 15–20. [Google Scholar]
- Zhou, R.J. Research on UAV Path Planning. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2023. [Google Scholar]
- Zhang, Q.Q.; Xu, W.W.; Zhang, H.H.; Zou, Y.Y.; Chen, Y.T. Path planning for logistics UAV in complex low-altitude airspace. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 1275–1286. [Google Scholar]
- Baganoff, F.K.; Maeda, Y.; Morris, M.; Bautz, M.W.; Townsley, A.L.K. Chandra X-Ray Spectroscopic Imaging of Sgr A* and the Central Parsec of the Galaxy. 2001. Available online: https://ui.adsabs.harvard.edu/abs/2003ApJ...591..891B/exportcitation (accessed on 8 February 2001).
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Huttunen, M. The u-space concept. Air Space Law 2019, 44, 69–89. [Google Scholar] [CrossRef]



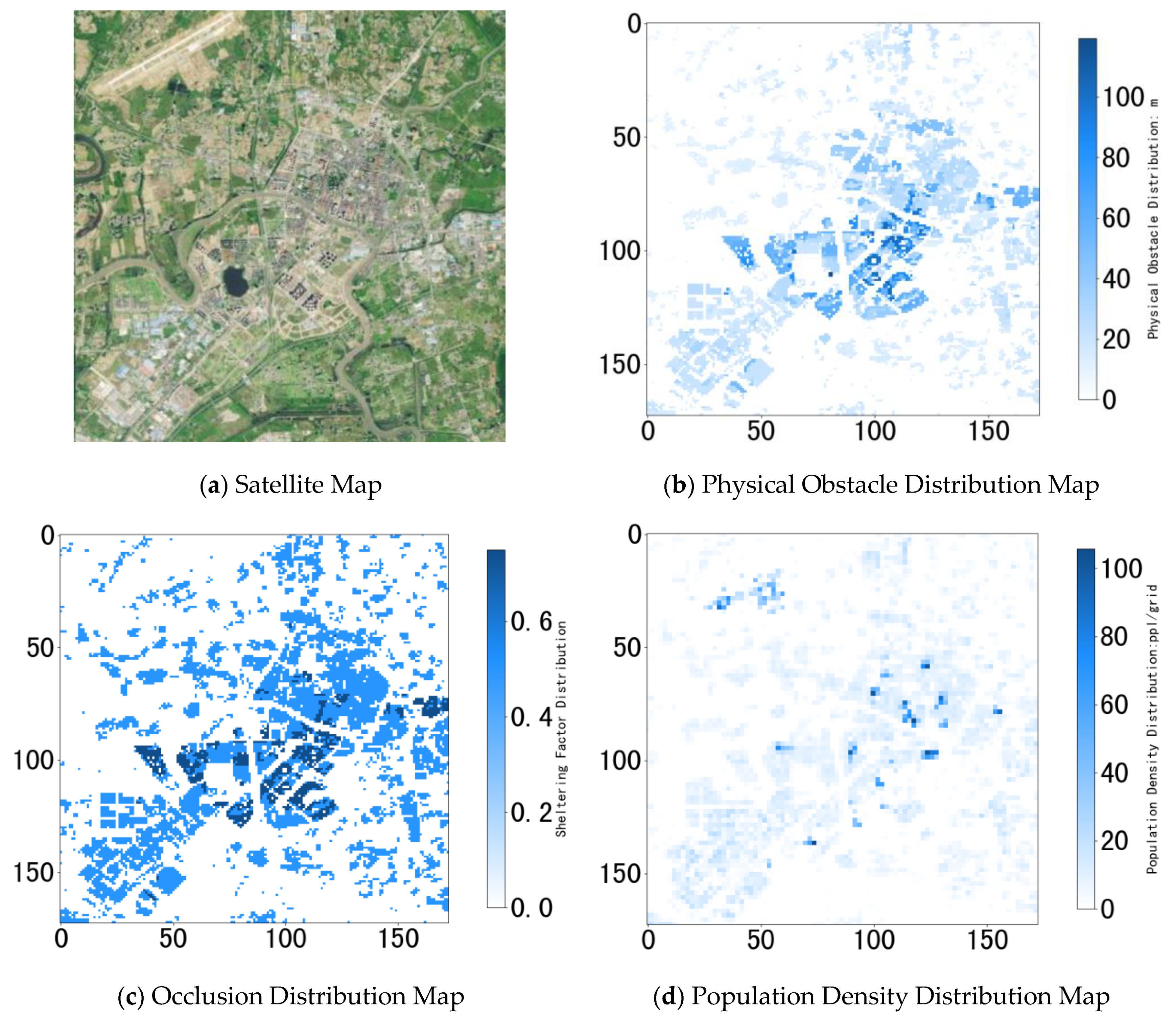
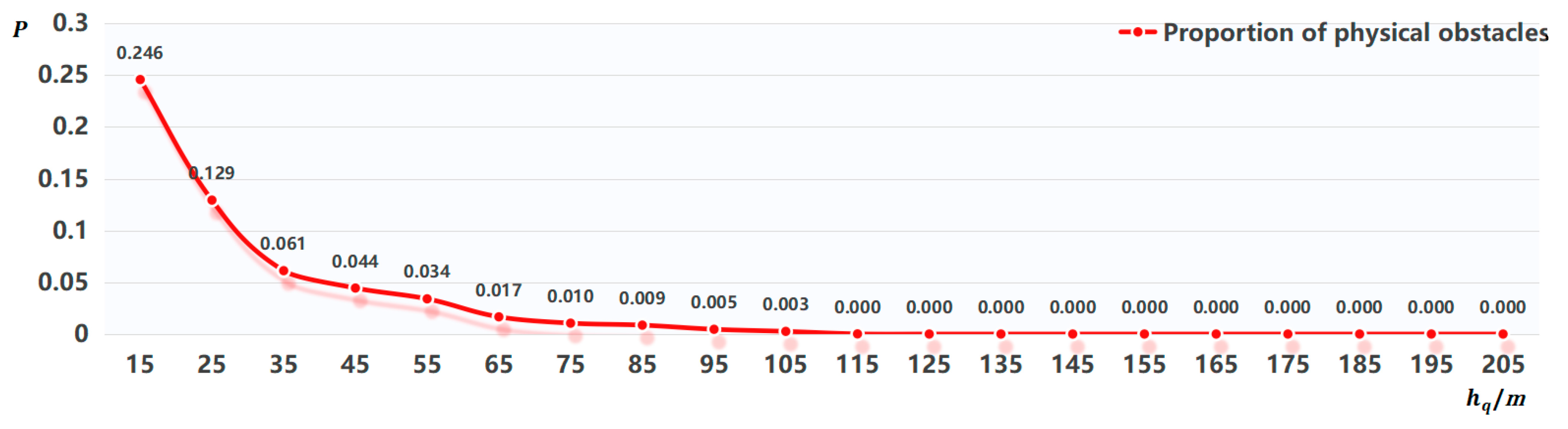
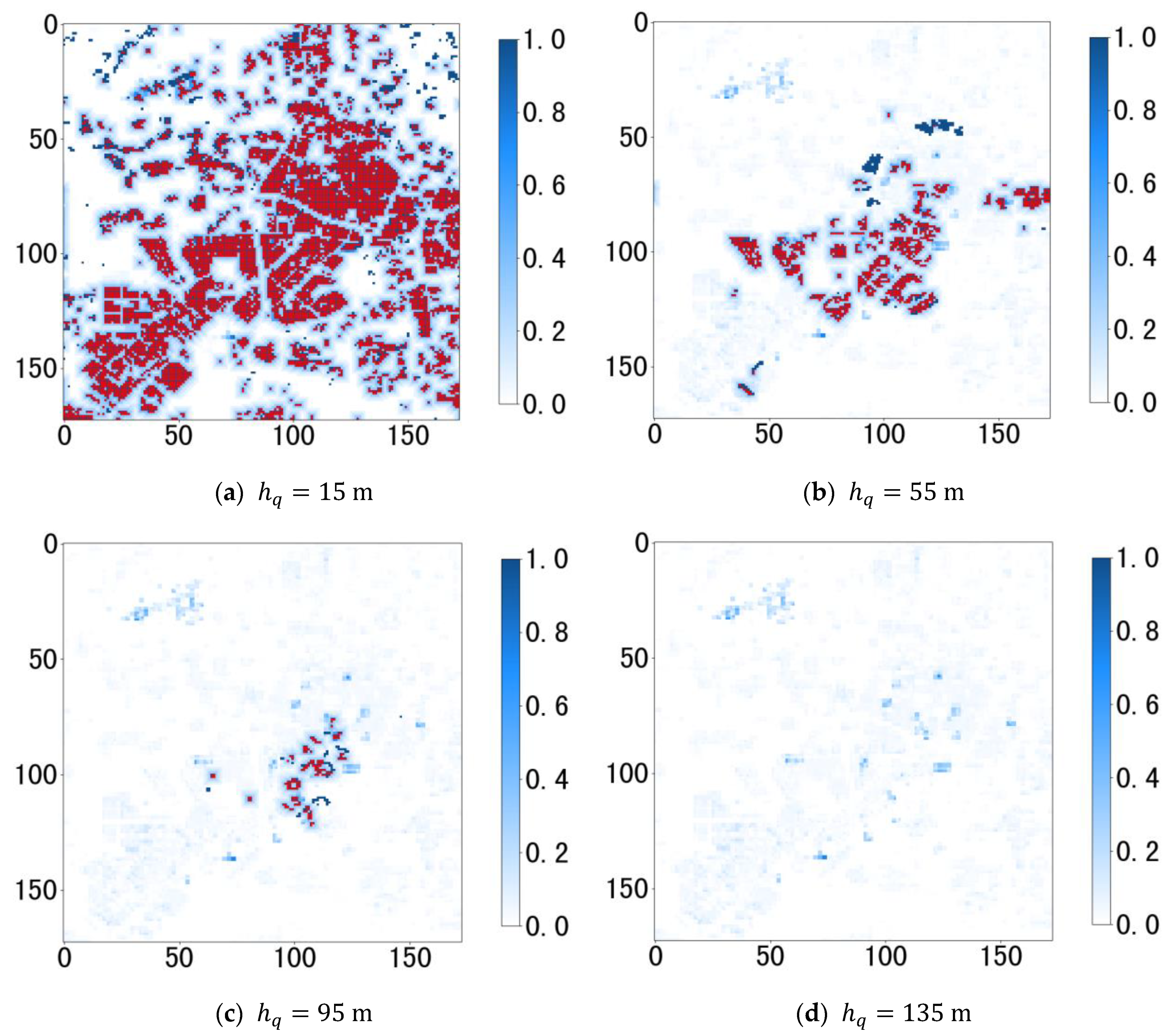


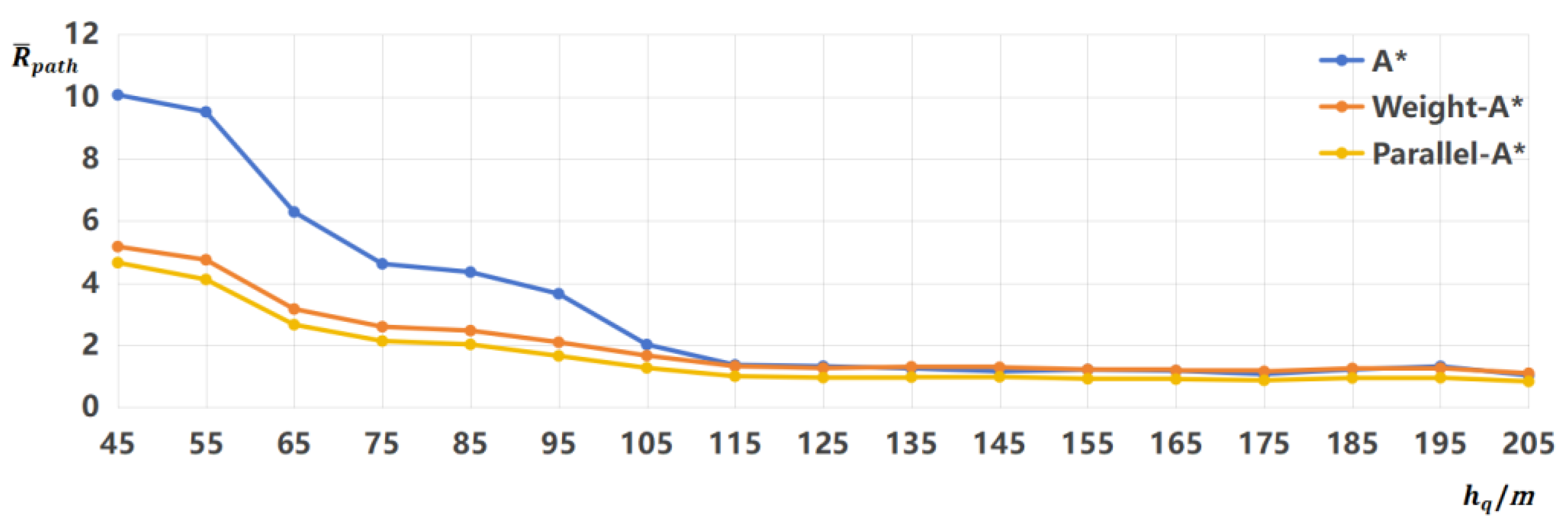

| Level | Grid Size | Scale | Level | Grid Size | Scale |
|---|---|---|---|---|---|
| 0 | 512° | 17 | 16″ | 512 m | |
| 1 | 256° | 18 | 8″ | 256 m | |
| 2 | 128° | 19 | 4″ | 128 m | |
| 3 | 64° | 20 | 2″ | 64 m | |
| 4 | 32° | 21 | 1″ | 32 m | |
| 5 | 16° | 22 | 1/2″ | 16 m | |
| 6 | 8° | 1024 km | 23 | 1/4″ | 8 m |
| 7 | 4° | 512 km | 24 | 1/8″ | 4 m |
| 8 | 2° | 256 km | 25 | 1/16″ | 2 m |
| 9 | 1° | 128 km | 26 | 1/32″ | 1 m |
| 10 | 32′ | 64 km | 27 | 1/64″ | 0.5 m |
| 11 | 16′ | 32 km | 28 | 1/128″ | 25 cm |
| 12 | 8′ | 16 km | 29 | 1/256″ | 12.5 cm |
| 13 | 4′ | 8 km | 30 | 1/512″ | 6.2 cm |
| 14 | 2′ | 4 km | 31 | 1/1024″ | 3.1 cm |
| 15 | 1′ | 2 km | 32 | 1/2048″ | 1.5 cm |
| 16 | 32″ | 1 km |
| Values | Classification |
|---|---|
| 0.00 | No obstacles |
| 0.25 | Sparse trees |
| 0.50 | Vehicles and low-rise buildings |
| 0.75 | High buildings |
| 1.00 | Industrial buildings |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 6 | |||
| / | 4 | 110 | |
| / | 1.225 | /m | 100 |
| 0.3 | 3 | ||
| 0.1 | /km | ||
| 180 |
| Model | Wingspan/m | / | / | Maximum Wind Resistance Level/Grade | ||||
|---|---|---|---|---|---|---|---|---|
| 45.82 | 64 | 8.43 |
| Computational Results | Performance Ratio Compared with Path 1 | |||
| Path 1 | 2.42 | 3.51 | 100% | 0% |
| Path 2 | 1.51 | 7.66 | 38%↓ | 118%↑ |
| Path 3 | 1.32 | 8.53 | 45%↓ | 143%↑ |
| Path 4 | 1.20 | 9.60 | 50%↓ | 173%↑ |
| Algorithm | Comprehensive Risk (Mean ± SD) | Number of Turning Points (Mean ± SD) |
|---|---|---|
| Weight-A* | ||
| Parallel-A* | ||
| A* | ||
| ANOVA Results (F-value/p-value) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, O.; Zhang, H.; Tang, W.; Wang, F.; Feng, D.; Zhong, G. Digital Low-Altitude Airspace Unmanned Aerial Vehicle Path Planning and Operational Capacity Assessment in Urban Risk Environments. Drones 2025, 9, 320. https://doi.org/10.3390/drones9050320
Feng O, Zhang H, Tang W, Wang F, Feng D, Zhong G. Digital Low-Altitude Airspace Unmanned Aerial Vehicle Path Planning and Operational Capacity Assessment in Urban Risk Environments. Drones. 2025; 9(5):320. https://doi.org/10.3390/drones9050320
Chicago/Turabian StyleFeng, Ouge, Honghai Zhang, Weibin Tang, Fei Wang, Dikun Feng, and Gang Zhong. 2025. "Digital Low-Altitude Airspace Unmanned Aerial Vehicle Path Planning and Operational Capacity Assessment in Urban Risk Environments" Drones 9, no. 5: 320. https://doi.org/10.3390/drones9050320
APA StyleFeng, O., Zhang, H., Tang, W., Wang, F., Feng, D., & Zhong, G. (2025). Digital Low-Altitude Airspace Unmanned Aerial Vehicle Path Planning and Operational Capacity Assessment in Urban Risk Environments. Drones, 9(5), 320. https://doi.org/10.3390/drones9050320








