Thermal Intra-Layer Interaction of Discretized Fractal Exposure Strategies in Non-Isothermal Powder Bed Fusion of Polypropylene
Abstract
1. Introduction
2. State of the Art
2.1. Thermal Processing Conditions in Powder Bed Fusion Processes
2.2. Process-Structure-Property Interdependencies of Non-Isothermal Additive Processing
2.3. Crystallization Characteristics of Polypropylene under Non-Isothermal Processing Conditions
2.4. Interaction of Processing Parameters and Thermal Process Characteristics
3. Materials and Methods
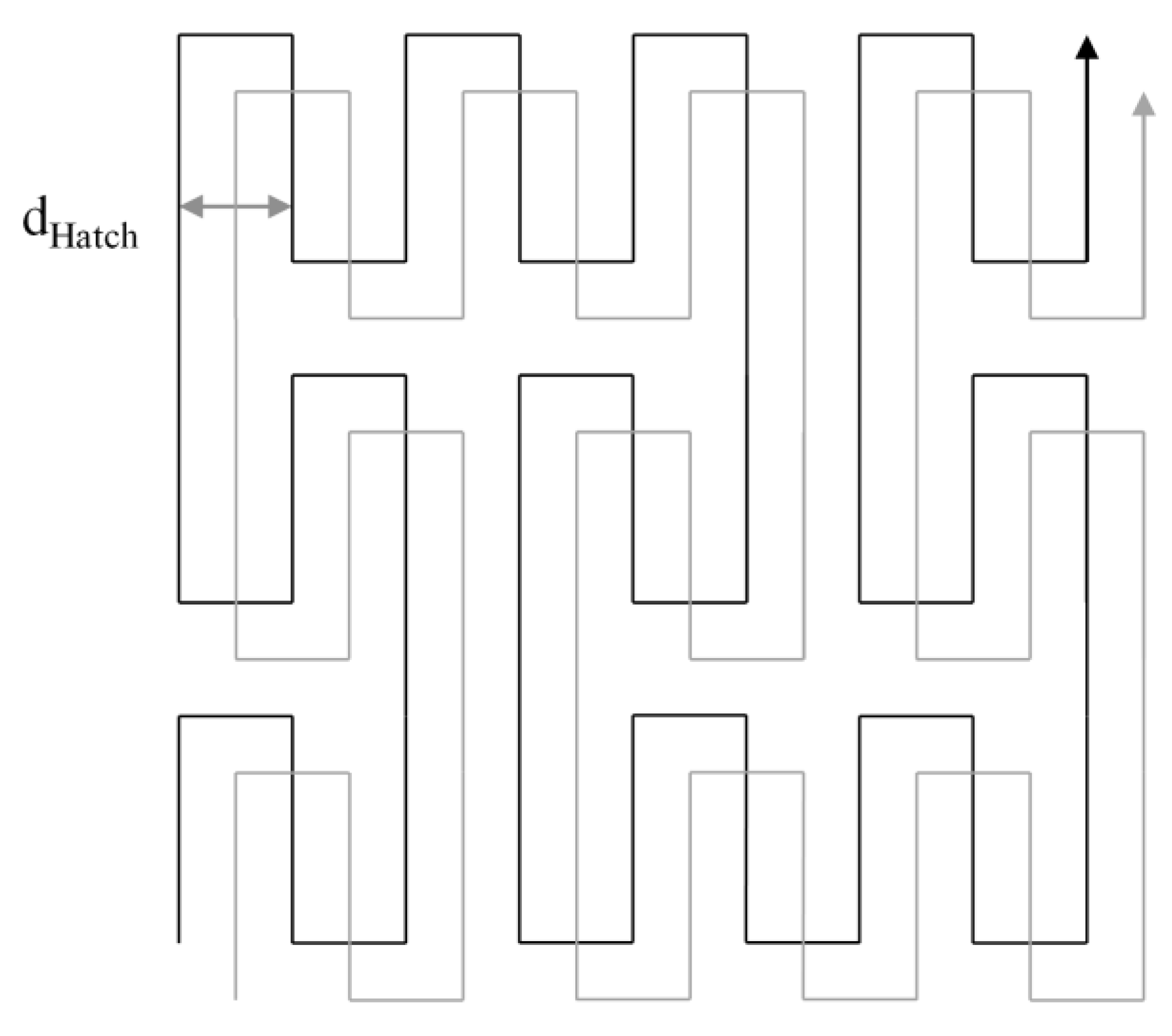
3.1. Implementation of Discretized Exposure Strategies
3.2. Exposure Implementation and Applied Materials
3.3. Design of Experiments
3.4. Thermographic In Situ Investigations
3.5. Topological and Thermal Part Characterizations
4. Results and Discussion
4.1. Spatial Exposure Discretization
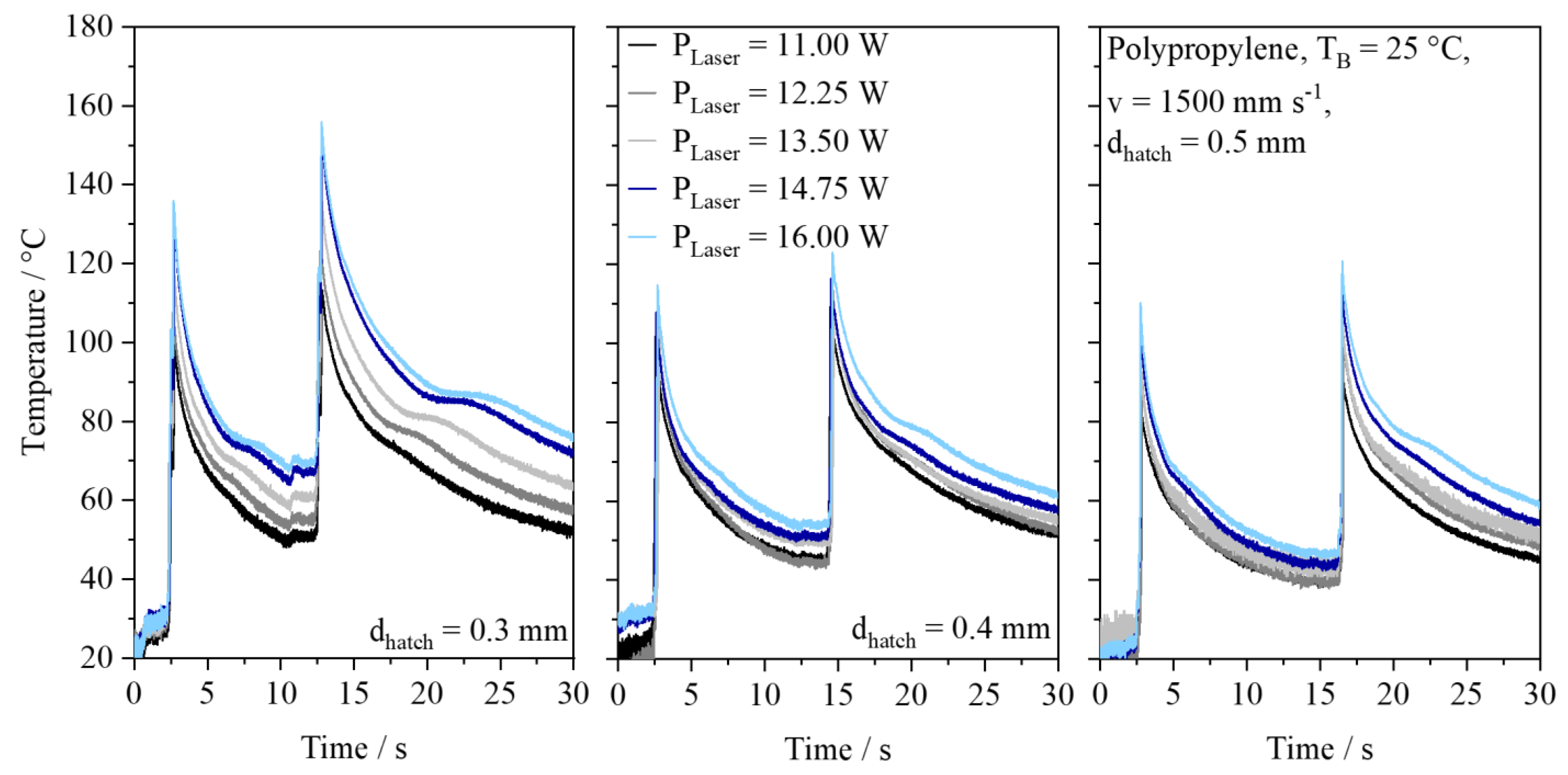
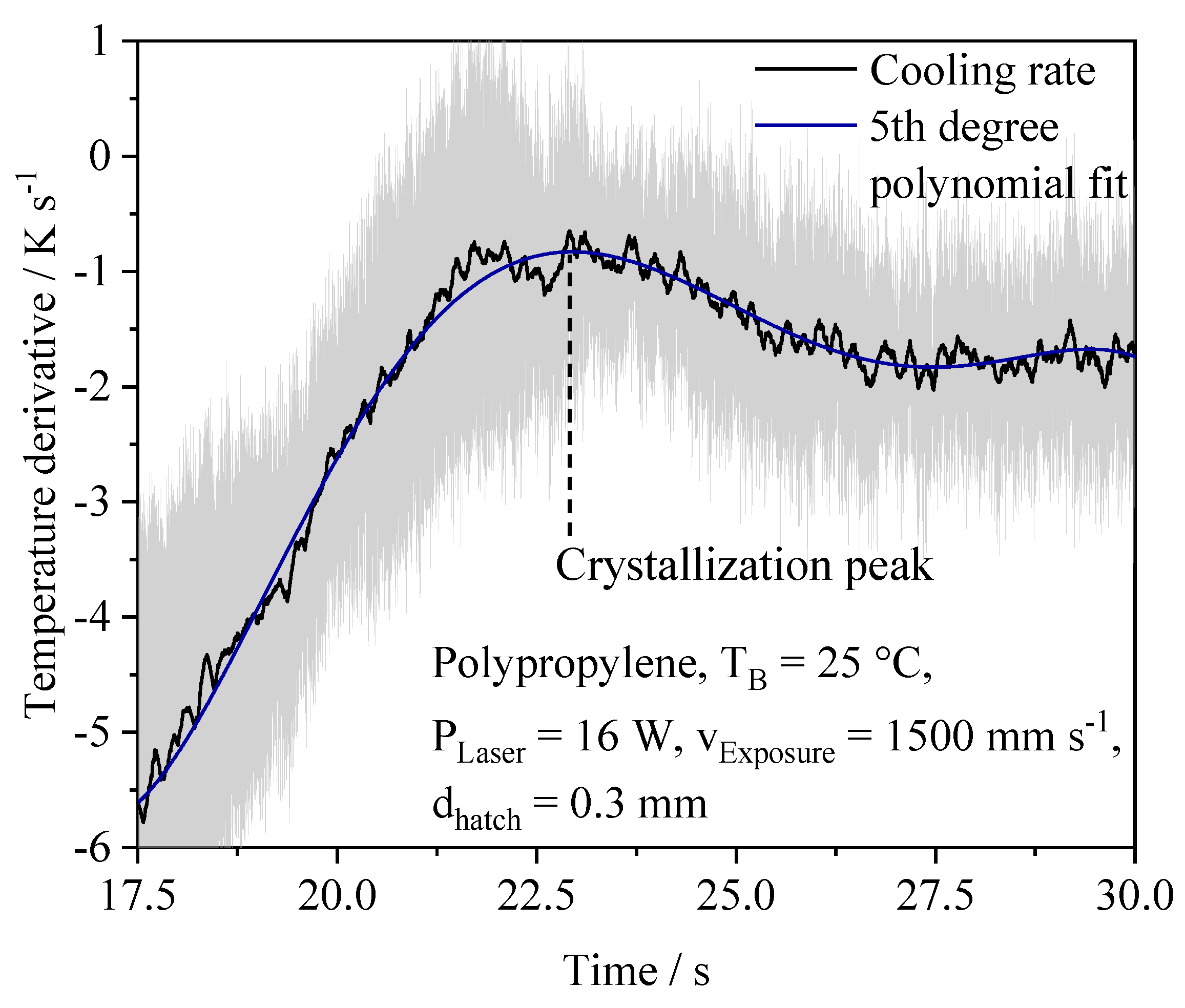
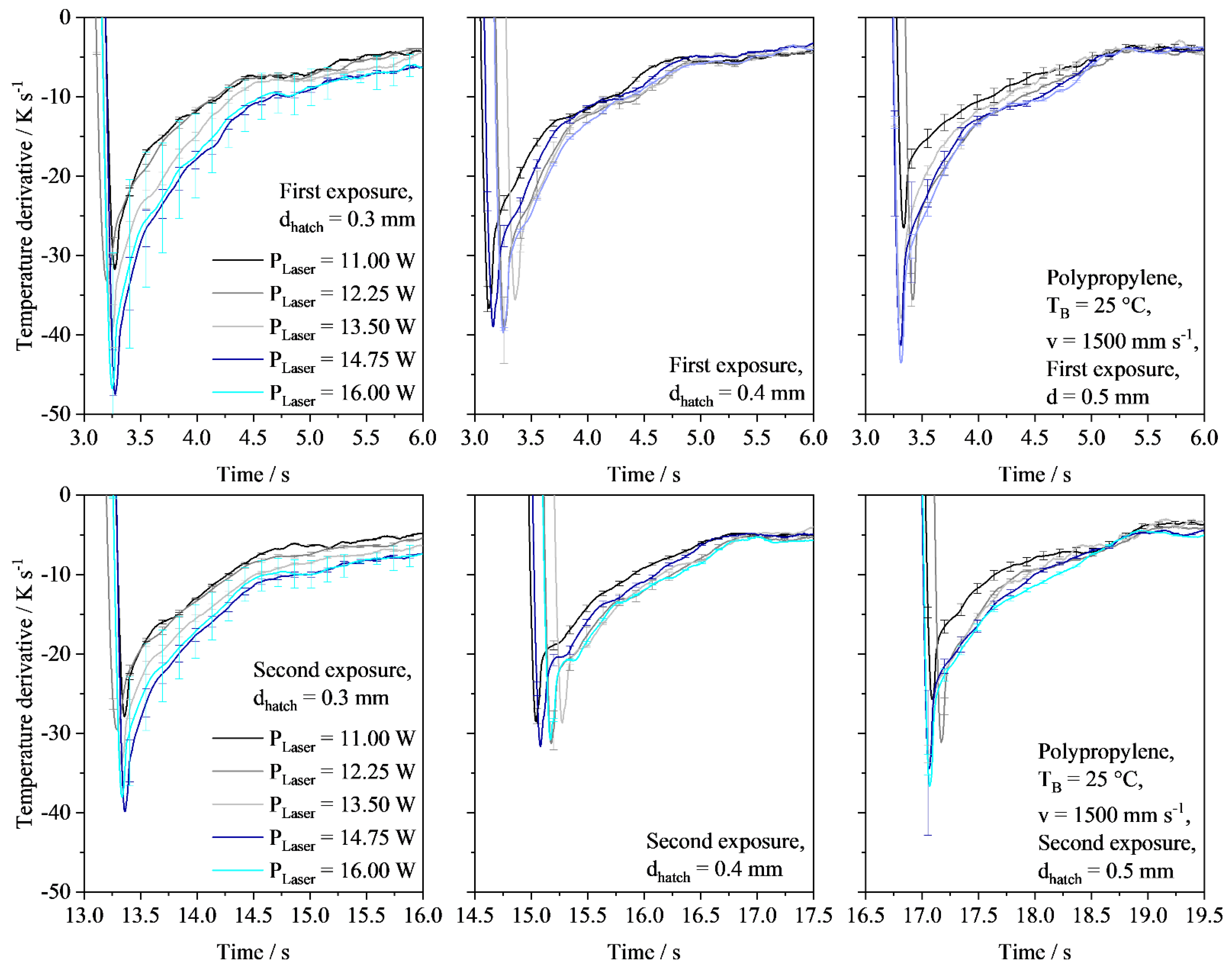
4.2. Process-Dependent Thermal Vector–Vector Interaction
4.3. Process-Dependent Thermal Part Properties
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paolucci, F.; van Mook, M.J.H.; Govaert, L.E.; Peters, G.W.M. Influence of post-condensation on the crystallization kinetics of PA12: From virgin to reused powder. Polymer 2019, 175, 161–170. [Google Scholar] [CrossRef]
- Wudy, K.; Drummer, D. Aging effects of polyamide 12 in selective laser sintering: Molecular weight distribution and thermal properties. Addit. Manuf. 2019, 25, 1–9. [Google Scholar] [CrossRef]
- Schlicht, S.; Cholewa, S.; Drummer, D. Process-Structure-Property Interdependencies in Non-Isothermal Powder Bed Fusion of Polyamide 12. J. Manuf. Mater. Process. 2023, 7, 33. [Google Scholar] [CrossRef]
- Li, Y.; Gu, D. Thermal behavior during selective laser melting of commercially pure titanium powder: Numerical simulation and experimental study. Addit. Manuf. 2014, 1–4, 99–109. [Google Scholar] [CrossRef]
- Shi, Q.; Gu, D.; Xia, M.; Cao, S.; Rong, T. Effects of laser processing parameters on thermal behavior and melting/solidification mechanism during selective laser melting of TiC/Inconel 718 composites. Opt. Laser Technol. 2016, 84, 9–22. [Google Scholar] [CrossRef]
- Schlicht, S.; Greiner, S.; Drummer, D. Low Temperature Powder Bed Fusion of Polymers by Means of Fractal Quasi-Simultaneous Exposure Strategies. Polymers 2022, 14, 1428. [Google Scholar] [CrossRef] [PubMed]
- Niino, T.; Haraguchi, H.; Itagaki, Y.; Iguchi, S.; Hagiwara, M. Feasibility study on plastic laser sintering without powder bed preheating. In Proceedings of the 22nd Annual International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, SFF, Austin, TX, USA, 8–10 August 2011; 2011; 2011, pp. 17–29. [Google Scholar]
- Niino, T.; Haraguchi, H.; Itagaki, Y.; Hara, K.; Morita, S. Microstructural observation and mechanical property evaluation of plastic parts obtained by preheat free laser sintering. In Proceedings of the 2012 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 6–8 August 2012; University of Texas at Austin: Austin, TX, USA, 2012; pp. 617–628. [Google Scholar]
- Kigure, T.; Yamauchi, Y.; Niino, T. Relationship between powder bed temperature and microstructure of laser sintered PA12 parts. In Proceedings of the 2019 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 12–14 August 2019; University of Texas at Austin: Austin, TX, USA. [Google Scholar]
- Zhang, D.; Zhang, P.; Liu, Z.; Feng, Z.; Wang, C.; Guo, Y. Thermofluid field of molten pool and its effects during selective laser melting (SLM) of Inconel 718 alloy. Addit. Manuf. 2018, 21, 567–578. [Google Scholar] [CrossRef]
- Greiner, S.; Wudy, K.; Wörz, A.; Drummer, D. Thermographic investigation of laser-induced temperature fields in selective laser beam melting of polymers. Opt. Laser Technol. 2019, 109, 569–576. [Google Scholar] [CrossRef]
- Drummer, D.; Greiner, S.; Zhao, M.; Wudy, K. A novel approach for understanding laser sintering of polymers. Addit. Manuf. 2019, 27, 379–388. [Google Scholar] [CrossRef]
- Soldner, D.; Greiner, S.; Burkhardt, C.; Drummer, D.; Steinmann, P.; Mergheim, J. Numerical and experimental investigation of the isothermal assumption in selective laser sintering of PA12. Addit. Manuf. 2020, 37, 101676. [Google Scholar] [CrossRef]
- Soldner, D.; Steinmann, P.; Mergheim, J. Modeling crystallization kinetics for selective laser sintering of polyamide 12. GAMM-Mitteilungen 2021, 44, e202100011. [Google Scholar] [CrossRef]
- Bian, P.; Shao, X.; Du, J. Finite Element Analysis of Thermal Stress and Thermal Deformation in Typical Part during SLM. Appl. Sci. 2019, 9, 2231. [Google Scholar] [CrossRef]
- Soe, S.P. Quantitative analysis on SLS part curling using EOS P700 machine. J. Mater. Process. Technol. 2012, 212, 2433–2442. [Google Scholar] [CrossRef]
- Verbelen, L.; Dadbakhsh, S.; Van den Eynde, M.; Kruth, J.-P.; Goderis, B.; Van Puyvelde, P. Characterization of polyamide powders for determination of laser sintering processability. Eur. Polym. J. 2016, 75, 163–174. [Google Scholar] [CrossRef]
- Santis, F.D.; Pantani, R.; Speranza, V.; Titomanlio, G. Analysis of Shrinkage Development of a Semicrystalline Polymer during Injection Molding. Ind. Eng. Chem. Res. 2010, 49, 2469–2476. [Google Scholar] [CrossRef]
- Wegner, A.; Witt, G. Process monitoring in laser sintering using thermal imaging. In Proceedings of the 2011 International Solid Freeform Fabrication Symposium, University of Texas at Austin, Austin, TX, USA, 8–10 August 2011. [Google Scholar]
- Jain, P.K.; Pandey, P.M.; Rao, P.V.M. Effect of delay time on part strength in selective laser sintering. Int. J. Adv. Manuf. Technol. 2008, 43, 117. [Google Scholar] [CrossRef]
- Drexler, M.; Lexow, M.; Drummer, D. Selective Laser Melting of Polymer Powder—Part Mechanics as Function of Exposure Speed. Phys. Procedia 2015, 78, 328–336. [Google Scholar] [CrossRef]
- Sindinger, S.-L.; Kralovec, C.; Tasch, D.; Schagerl, M. Thickness dependent anisotropy of mechanical properties and inhomogeneous porosity characteristics in laser-sintered polyamide 12 specimens. Addit. Manuf. 2020, 33, 101141. [Google Scholar] [CrossRef]
- Pavan, M.; Faes, M.; Strobbe, D.; Van Hooreweder, B.; Craeghs, T.; Moens, D.; Dewulf, W. On the influence of inter-layer time and energy density on selected critical-to-quality properties of PA12 parts produced via laser sintering. Polym. Test. 2017, 61, 386–395. [Google Scholar] [CrossRef]
- Schlicht, S.; Jaksch, A.; Drummer, D. Inline Quality Control through Optical Deep Learning-Based Porosity Determination for Powder Bed Fusion of Polymers. Polymers 2022, 14, 885. [Google Scholar] [CrossRef]
- Paolucci, F.; Baeten, D.; Roozemond, P.C.; Goderis, B.; Peters, G.W.M. Quantification of isothermal crystallization of polyamide 12: Modelling of crystallization kinetics and phase composition. Polymer 2018, 155, 187–198. [Google Scholar] [CrossRef]
- Lv, Y.; Thomas, W.; Chalk, R.; Hewitt, A.; Singamneni, S. Experimental Evaluation of Polyphenylsulfone (PPSF) Powders as Fire-Retardant Materials for Processing by Selective Laser Sintering. Polymers 2021, 13, 2704. [Google Scholar] [CrossRef] [PubMed]
- Chatham, C.A.; Long, T.E.; Williams, C.B. Powder bed fusion of poly(phenylene sulfide) at bed temperatures significantly below melting. Addit. Manuf. 2019, 28, 506–516. [Google Scholar] [CrossRef]
- Mubarak, Y.; Harkin-Jones, E.M.A.; Martin, P.J.; Ahmad, M. Modeling of non-isothermal crystallization kinetics of isotactic polypropylene. Polymer 2001, 42, 3171–3182. [Google Scholar] [CrossRef]
- Piccarolo, S.; Saiu, M.; Brucato, V.; Titomanlio, G. Crystallization of polymer melts under fast cooling. II. High-purity iPP. J. Appl. Polym. Sci. 1992, 46, 625–634. [Google Scholar] [CrossRef]
- Caldas, V.; Brown, G.R.; Nohr, R.S.; MacDonald, J.G.; Raboin, L.E. The structure of the mesomorphic phase of quenched isotactic polypropylene. Polymer 1994, 35, 899–907. [Google Scholar] [CrossRef]
- Schael, G.W. A study of the morphology and physical properties of polypropylene films. J. Appl. Polym. Sci. 1966, 10, 901–915. [Google Scholar] [CrossRef]
- Kapur, S.; Rogers, C.E. Aging of quenched polypropylene. J. Polym. Sci. Polym. Phys. Ed. 1972, 10, 2107–2124. [Google Scholar] [CrossRef]
- Gezovich, D.M.; Geil, P.H. Morphology of quenched polypropylene. Polym. Eng. Sci. 1968, 8, 202–209. [Google Scholar] [CrossRef]
- De Rosa, C.; Auriemma, F.; Di Girolamo, R.; de Ballesteros, O.R. Crystallization of the mesomorphic form and control of the molecular structure for tailoring the mechanical properties of isotactic polypropylene. J. Polym. Sci. Part B Polym. Phys. 2014, 52, 677–699. [Google Scholar] [CrossRef]
- De Rosa, C.; Di Girolamo, R.; De Ballesteros, O.R.; Pepe, M.; Tarallo, O.; Malafronte, A. Morphology and Mechanical Properties of the Mesomorphic Form of Isotactic Polypropylene in Stereodefective Polypropylene. Macromolecules 2013, 46, 5202–5214. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Y.Q.; Su, X.B.; Chen, Y.H. Study on energy input and its influences on single-track, multi-track, and multi-layer in SLM. Int. J. Adv. Manuf. Technol. 2012, 58, 1189–1199. [Google Scholar] [CrossRef]
- Li, Z.; Xu, R.; Zhang, Z.; Kucukkoc, I. The influence of scan length on fabricating thin-walled components in selective laser melting. Int. J. Mach. Tools Manuf. 2018, 126, 1–12. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, S.; Gan, Y.; Huang, T.; Yang, C.; Junjie, L.; Lin, J. Study on the microstructure, mechanical property and residual stress of SLM Inconel-718 alloy manufactured by differing island scanning strategy. Opt. Laser Technol. 2015, 75, 197–206. [Google Scholar] [CrossRef]
- Parry, L.; Ashcroft, I.A.; Wildman, R.D. Understanding the effect of laser scan strategy on residual stress in selective laser melting through thermo-mechanical simulation. Addit. Manuf. 2016, 12, 1–15. [Google Scholar] [CrossRef]
- Catchpole-Smith, S.; Aboulkhair, N.; Parry, L.; Tuck, C.; Ashcroft, I.A.; Clare, A. Fractal scan strategies for selective laser melting of ‘unweldable’ nickel superalloys. Addit. Manuf. 2017, 15, 113–122. [Google Scholar] [CrossRef]
- Greiner, S.; Schlicht, S.; Drummer, D. Temperature field homogenization by fractal exposure strategies in laser sintering of polymers. In Proceedings of the 17th Rapid.Tech 3D Conference, Erfurt, Germany, 22–23 June 2021; Carl Hanser Verlag GmbH & Co. KG: Munich, Germany, 2021; pp. 188–197, ISBN 978-3-446-47171-9. [Google Scholar]
- Bader, M.; Bungartz, H.-J.; Mehl, M. Space-Filling Curves. In Encyclopedia of Parallel Computing; Padua, D., Ed.; Springer: Boston, MA, USA, 2011; pp. 1862–1867. ISBN 978-0-387-09766-4. [Google Scholar]
- Peano, G. Sur une courbe, qui remplit toute une aire plane. Math. Ann. 1890, 36, 157–160. [Google Scholar] [CrossRef]
- DIN EN ISO 1628-3:2010-10; Kunststoffe—Bestimmung der Viskosität von Polymeren in verdünnter Lösung durch ein Kapillarviskosimeter—Teil 3: Polyethylen und Polypropylen. Beuth Verlag GmbH: Berlin, Germany, 2010. [CrossRef]
- Shen, F.; Zhu, W.; Zhou, K.; Ke, L.-L. Modeling the temperature, crystallization, and residual stress for selective laser sintering of polymeric powder. Acta Mech. 2021, 232, 3635–3653. [Google Scholar] [CrossRef]
- Osmanlic, F.; Wudy, K.; Laumer, T.; Schmidt, M.; Drummer, D.; Körner, C. Modeling of Laser Beam Absorption in a Polymer Powder Bed. Polymers 2018, 10, 784. [Google Scholar] [CrossRef]
- Mileva, D.; Wang, J.; Gahleitner, M.; Jariyavidyanont, K.; Androsch, R. New Insights into Crystallization of Heterophasic Isotactic Polypropylene by Fast Scanning Chip Calorimetry. Polymers 2020, 12, 1683. [Google Scholar] [CrossRef]



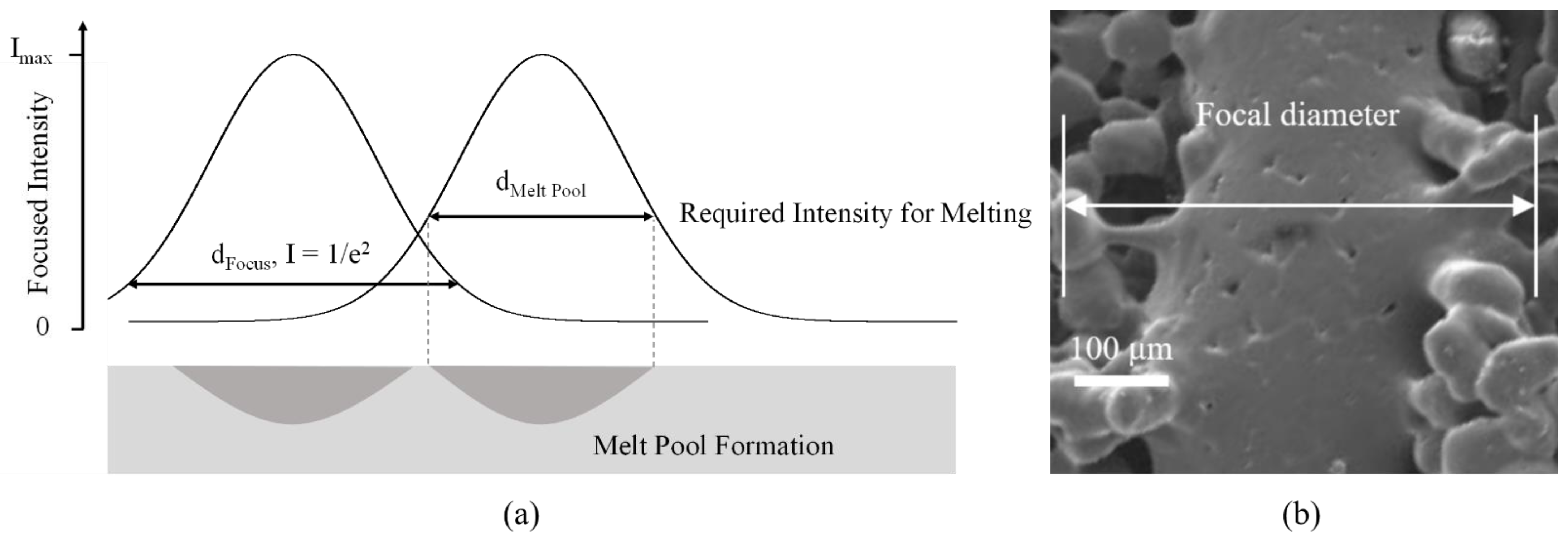
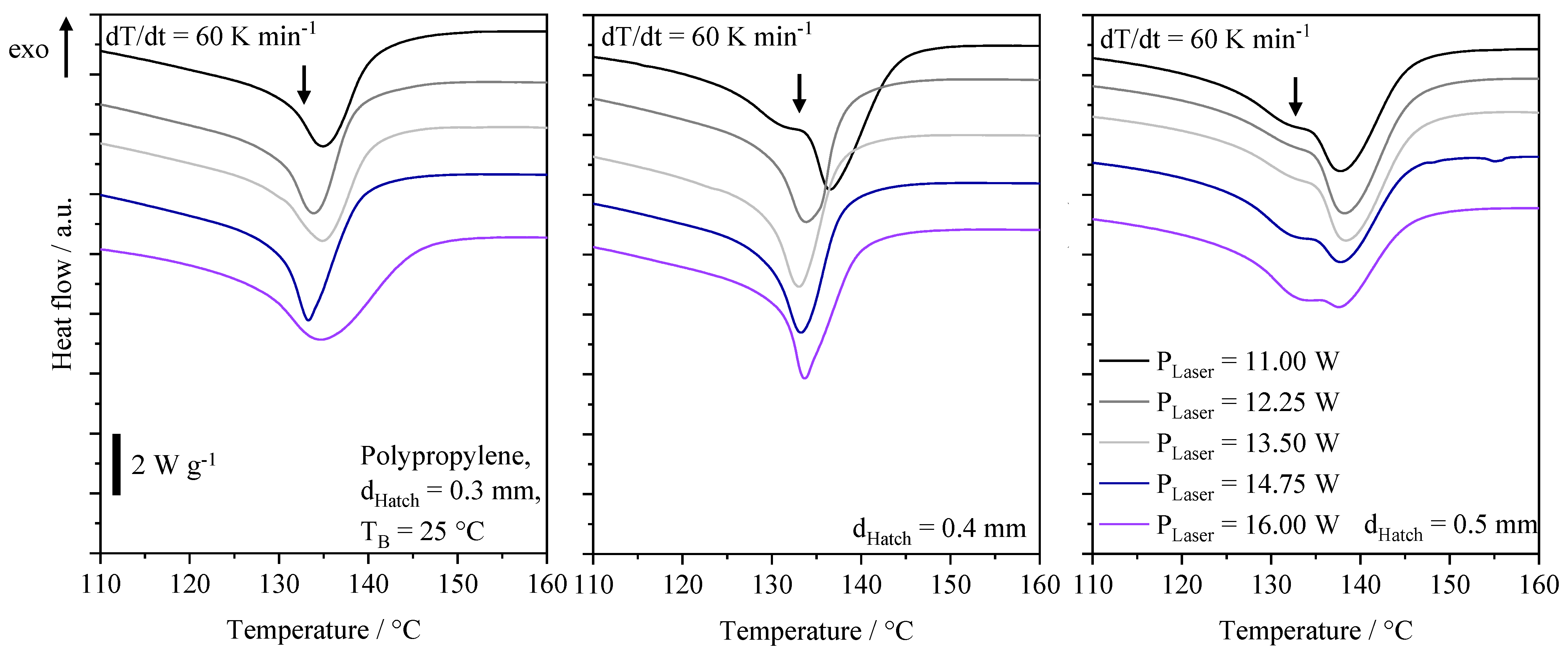
| Parameter Set/- | Hatch Distance/mm | Laser Power/W | Part Edge Length/mm |
|---|---|---|---|
| 1 | 0.3 | 11.00 | 22.5 |
| 2 | 12.25 | ||
| 3 | 13.50 | ||
| 4 | 14.75 | ||
| 5 | 16.00 | ||
| 6 | 0.4 | 11.00 | 30 |
| 7 | 12.25 | ||
| 8 | 13.50 | ||
| 9 | 14.75 | ||
| 10 | 16.00 | ||
| 11 | 0.5 | 11.00 | 37.5 |
| 12 | 12.25 | ||
| 13 | 13.50 | ||
| 14 | 14.75 | ||
| 15 | 16.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schlicht, S.; Drummer, D. Thermal Intra-Layer Interaction of Discretized Fractal Exposure Strategies in Non-Isothermal Powder Bed Fusion of Polypropylene. J. Manuf. Mater. Process. 2023, 7, 63. https://doi.org/10.3390/jmmp7020063
Schlicht S, Drummer D. Thermal Intra-Layer Interaction of Discretized Fractal Exposure Strategies in Non-Isothermal Powder Bed Fusion of Polypropylene. Journal of Manufacturing and Materials Processing. 2023; 7(2):63. https://doi.org/10.3390/jmmp7020063
Chicago/Turabian StyleSchlicht, Samuel, and Dietmar Drummer. 2023. "Thermal Intra-Layer Interaction of Discretized Fractal Exposure Strategies in Non-Isothermal Powder Bed Fusion of Polypropylene" Journal of Manufacturing and Materials Processing 7, no. 2: 63. https://doi.org/10.3390/jmmp7020063
APA StyleSchlicht, S., & Drummer, D. (2023). Thermal Intra-Layer Interaction of Discretized Fractal Exposure Strategies in Non-Isothermal Powder Bed Fusion of Polypropylene. Journal of Manufacturing and Materials Processing, 7(2), 63. https://doi.org/10.3390/jmmp7020063






