Next Article in Journal
Weldability of 316L Parts Produced by Metal Additive Manufacturing
Next Article in Special Issue
Theoretical Analysis of Rolling Force during Cold Rolling with Roll Crossing and Shifting System
Previous Article in Journal
Experimental Investigation on the Cutting of Additively Manufactured Ti6Al4V with Wire-EDM and the Analytical Modelling of Cutting Speed and Surface Roughness
Previous Article in Special Issue
An Experimental and Numerical Study on Aluminum Alloy Tailor Heat Treated Blanks
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMMP
Volume 7
Issue 2
10.3390/jmmp7020070
jmmp-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Numerical Investigation of Step Size Effect on Formability of 2024-T3 Aluminum in Incremental Forming

by
Tyler J. Grimm
1,
Filipe Colombini
2 and
Ihab Ragai
3,*
1
International Center for Automotive Research, Clemson University, Greenville, SC 29607, USA
2
Faculty of Engineering, Rosenheim Technical University of Applied Sciences, 83024 Rosenheim, Germany
3
School of Engineering, The Behrend College, Penn State University, Erie, PA 16563, USA
*
Author to whom correspondence should be addressed.
J. Manuf. Mater. Process. 2023, 7(2), 70; https://doi.org/10.3390/jmmp7020070
Submission received: 21 February 2023 / Revised: 14 March 2023 / Accepted: 17 March 2023 / Published: 19 March 2023
(This article belongs to the Special Issue Advances in Material Forming)
Browse Figures
Versions Notes

Abstract

:
Incremental forming (IF) is an advanced manufacturing process in which a forming tool locally deforms sheet material into a desired geometry through successive passes at incremental depths. An inherent benefit to the IF process is its formability improvement over conventional stamping; however, further enhancements will enable the forming of increasingly complex geometries. To progress the IF process towards heavy industrial use, the modeling of such processes must be further developed. Single point incremental forming (SPIF) of AA2024-T3 was modeled herein utilizing explicit formulations. The model geometry featured a nominally rectangular-shaped clamping region. A friction factor was experimentally determined and utilized within the model, which is a novel addition to this work. Formability was determined and forming limit diagrams were composed. It was found that the present model shows greater formability and underestimates plastic strain compared to experimental testing. The generation of forming limit diagrams for this material processed by IF is also a novel addition to this field.

1. Introduction

Incremental forming is a sheet material forming process capable of forming complex geometries without dedicated dies. Forming is typically achieved using a hemispherical tool that traces along the contours of the final geometry while incrementally increasing in depth. The elimination of forming dies makes this process ideal for low- to medium-volume industries. The use of incremental forming in the industry is currently stifled by several limitations, including spring back and degraded surface finishes.

1.1. Formability

The formability of an incremental forming process is typically characterized as the maximum wall angle and depth which can be formed prior to the failure of the material. The effects of toolpath parameters on formability are summarized in Table 1.
Many modifications to the incremental forming process have been investigated for their effectiveness in increasing formability. One such method is to incorporate the addition of heat or energy to the workpiece throughout forming. This induces thermal softening which enables greater elongation. An additional benefit is observed as a reduction in forming force. While incremental forming inherently requires significantly lower forming forces relative to stamping, this additional force reduction further improves the process. Heat assistance can be achieved by traditional heating methods, by passing an electric current through the forming tool to the workpiece, which is known as electrically-assisted incremental forming [7,8,9,10,11,12,13,14,15,16,17,18], laser-assisted IF [19,20,21,22], induction-assisted IF [23], and high tool rotation [24].
Other methods used tool modifications to improve formability, which includes the use of a free-spinning roller ball as a forming tool [1,25,26], vibration-assisted IF [27,28,29,30,31,32,33,34], flat-end tooling [35], and axially offset rotating tooling [36,37]. These methods are not as effective as heat-assisted forming. However, they offer some efficiency improvement since they do not require additional energy input during the forming process. Additionally, toolpath modifications have also shown an increase in formability, which includes the use of a multi-pass toolpath [38,39,40,41,42,43]. This method forms a complete geometry by initially forming several shapes by increasing the wall angle. This method can be used to form the inner dimensions of the geometry, which typically remain untouched with traditional toolpaths. This process allows material thinning to be more evenly dispersed. Other toolpath modifications which resulted in formability improvements include a wavy toolpath design [44] and a radially travelling toolpath [45].
While a significant amount of research has gone into formability improvements in IF, it is important to note that an increase in formability is experienced using IF compared to conventional stamping. This has been attributed to the local deformation mode inherent to the IF process, which causes stretching, rather than conventional forming, at the tool-workpiece interface [3]. Additionally, hydrostatic pressure from elastic deformation surrounding the local plastic deformation enables even greater formability [46].
Forming limit diagrams (FLDs) for several materials formed using the IF process has been experimentally developed [47,48,49,50,51,52,53,54]. Generally, testing is conducted on pyramid or cone shapes with various wall angles; however, other studies included several geometries. From this, the effect of geometry on formability was discovered [47]. This study investigated complex geometries which resulted in negative strains; however, the trend of this type of strain is not explicitly reported. General IF forming limit curves are distinctly different from conventional forming limit curves as they display a negative slope, whereas conventional curves form a V-shape [55].
The step size, tool size, and feed rate effect on the formability of incrementally formed annealed and pre-aged AA-2024 was previously reported by Hussain et al. [56]. This effect was determined experimentally through the Design of Experiments adapted from previous works [57]. The following equation was produced based on their experimental findings:
θ m a x = 73.44 − 1.01 r + 0.003 f − 8.04 p − 0.00008 r f + 1.2 r p + 0.0003 f p
where θ m a x is the maximum angle which can be formed without producing fracture, r is the tool radius (mm), f is the feed rate (mm/min), and p is the step size (mm). Adapting this equation to the experimental parameters discussed herein produces the results shown in Table 2. This equation predicts that an increase in step size will decrease formability when using the feed rate and tool radius utilized herein. It should be noted that the 0.9° increase calculated with this equation is relatively small. In fact, it is likely to be within the standard deviation of test results.

1.2. IF Modeling

The development of forming limit diagrams is essential for the industrialization of a forming process. Such a diagram enables engineers to design processes/geometries which do not result in fracture without the need for extensive experimental testing. However, there are challenges to developing forming limit diagrams with an incremental forming process. Many of the experimentally developed forming limit diagrams found in the literature are coupled with numerical analyses. Nguyen et al. used a modified maximum force criterion to predict failure in incrementally formed cold-rolled steel [53]. Huang et al. performed analyses on straight-line tests experimentally and numerically. This simplified test method produced similar forming limit curves to others determined with more complex methods [52]. Eyckens et al. confirmed their numerical analysis results with digital image correlation (DIC) measurements. It was discovered that increasing through-thickness nodes does not improve accuracy and that accurate friction modeling will most likely contribute to a more accurate model [51]. Bambach used a generalized sine law in the IF modeling of truncated pyramid shapes with various wall angles. Several limitations of this type of model are listed in this research; however, its accuracy is greater than the traditional sine law results. Kurra et al. formed various funnel shapes, analyzing the thickness of the formed material at several depths of forming [58]. This study, conducted on steel, was moderately successful in predicting the thickness variation of this material, with a maximum percent error of 15.84%. Experimental formability was presented in the work; however, the formability predicted through simulation is absent. Ghazanfari et al. [59] were able to improve the accuracy of their simulation by including through-thickness shear.
Altair® Radioss®, a powerful FEA tool for highly nonlinear dynamic problems was used for the models presented in this work. The models utilized herein investigate the ability of numerical simulations to predict failure and strain for moderately scaled parts (>200 mm) and thin material (≈0.5 mm). This presents a distinction from previous modeling attempts found throughout literature which generally formed small geometries with thicker material [60,61,62,63,64]. The geometry will also be formed in a nominally shaped clamping fixture. Much of the previous work on incremental forming utilized clamping fixtures that closely match the periphery of the desired geometry. This helps to eliminate some elastic deformations during the initial stages of forming. However, the use of dedicated fixturing limits the freeform nature of this process and should be avoided. Furthermore, this study is unique in its numerical characterization of the step size effect on formability.

2. Methodology

The formability of a single-point incremental forming (SPIF) process was investigated experimentally and numerically. The goal of this work was to capture the effect of step size on sheet formability and to develop a method for numerically generating forming limit diagrams in IF, which results in a significant reduction in experimental time and cost The SPIF process uses a single hemispherical forming tool to locally deform sheet material. The tool travels along the contours of the desired geometry at incremental depths. A HAAS TM3 CNC milling machine was used for the experiments and is shown in Figure 1. This process does not require any dedicated fixturing.
The material utilized in this study was 2024-T3 aluminum of 0.50 mm thickness. The blank was 279.4 mm × 279.4 mm and the clamping fixture had inner dimensions of 254 mm × 254 mm. The forming tool was a 9.5 mm diameter hemispherical rod constructed from H13 tool steel. PTFE lubricant was used during forming. A helical toolpath was used for simulation and experiments. The feed rate for the experimental tests was set to 3810 mm/min and 50,000 mm/min for modeling. Feed rate scaling was used in order to reduce computational time. It was ensured that this scaling did not significantly alter the kinetic energy applied to the system, as it is much smaller than the total internal energy. This controlled relation between energies guarantees the quasi-static condition of the simulation, which is not influenced by dynamic effects. Therefore, in the case of low strain rates as in SPIF procedures, the scaling is acceptable without any change of behavior.
The formability of the IF process was determined by forming a funnel-shaped geometry that features a wall angle that increases with depth. This method, first proposed by Hussain et al. [65], is widely used throughout literature as a comparative method of determining formability. When utilizing this method, the geometry is formed until the fracture is detected. The depth at which fracture occurs is recorded. The wall angle at which the part failed can then be calculated using this value. The geometry used throughout testing can be seen in Figure 2. This metric was used in both simulation and experiment to quantify formability.

2.1. Modeling

One of the challenges in finding the proper material formulation for the current model was the extremely long computational time of each parameter tryout. Usually, in the scope of numerical analysis, a series of iterations are required in order to refine the model and increase accuracy. This scenario is exaggerated in the case of SPIF, where the physical phenomena involved are too complex to be modeled using implicit methods (i.e., complex frictional contacts, high strains, material non-linearities, etc.) and the process cycle is too long for an explicit approach. After weighing both methods, it was decided to utilize explicit numerical simulations since they are able to better capture the physical effects of the SPIF process [66,67,68].
The FEA model was created to mimic the experimental setup, clamping, tool distance, and dimensions are identical. The mesh used for simulation is shown in Figure 3, as well as additional dimensions of the clamping fixture. The fixture had a 254 mm square forming area with 6.35 mm-radius corners. The shape of the clamping fixture is important in the SPIF process and can have a significant influence on the final results of forming [69]. The sheet was modeled with a total of 8053, 3.5 mm × 3.5 mm elements.
In order to simulate the clamping fixture, a simplified mesh was created for the fixture. Contact between the fixture and sheet was established. The nodes from the bottom mesh are constrained in all degrees of freedom, while for the top mesh, a displacement is imposed on the fixture until the aluminum sheet is pressed between the supports and fixed by friction.

2.1.1. Material Formulation

The material within the model was defined using Hill’s Criteria with Tabulated Yield Curve. This material formulation considers anisotropic properties, which are apparent in the tested material. Typical mechanical properties for this alloy are summarized in Table 3. The values related to the yield curve and anisotropic properties were obtained from the literature [70]. The strain rate influence was neglected considering the relatively slow speeds employed on the experimental IF procedure. This material formulation was assigned to shell orthotropic elements with 5 integration points through the thickness. 2D shell elements offer a computational advantage over 3D brick elements and reduce the computation time. An improved under-integrated formulation with hourglass stabilization was also used.

2.1.2. Toolpath Generation

The toolpath was translated to the FE model using an imposed displacement function. When using this feature, it is possible to dictate the displacement of an exact node over a period of time. The toolpath generated is in the form of a database with X, Y and Z coordinate points. These data are then used to translate the center node of the tool tip along the path, which will result in generating the desired shape, as shown in Figure 4.

2.1.3. Friction Analysis

Accurate friction determination in numerical IF simulations is critical to its overall success. Due to the type of deformation inherent to this process, friction affects several factors of forming, such as formability and spring back. This is apparent in tests that significantly reduce tool friction, such as the utilization of a roller ball as a forming tool [1,25,26]. While the importance of this factor is well known, other works fail to provide justification for the friction coefficient used in simulations. Therefore, supplemental testing which mimicked the conditions experienced during formability testing was conducted. When making comparisons between SPIF simulation and experiment, the experimental friction factor should always be determined for use in the simulation on a case-by-case basis. This value will obviously change depending on the individual test conditions. Studies that made such comparisons but failed to use the experimentally determined friction factor cannot provide any definitive conclusions.
Truncated pyramid shapes were formed experimentally using similar conditions to the study (tool, lubricant, feed rate, material, etc.). Force measurements were used to determine a friction coefficient using the following equation:
μ = F x 2 + F y 2 F z
A plot of the friction coefficient throughout an example test can be seen in Figure 5. The early stages of forming produce an unsteady friction coefficient. This is due to purely elastic forming. Once the tool reaches a certain depth, the friction coefficient remains cyclical but is stable. The average friction coefficient from this stable region was 0.37. This value was used in the simulation.

2.2. Strain Measurement

When observing numerical results, a difference in strain was found depending on the location in relation to the shape of the clamping fixture. Therefore, the strain was measured along the XZ plane and through a plane that passes through the Z axis and is 45° from the XZ plane. These planes can be seen in Figure 6 and the approximate locations of these measurements can be seen as (a) and (b), respectively. These measurements were taken at opposite edges to where the failure occurred and parallel to the roll direction of the material.
Prior to conducting the forming experiments, the blank surface which was not contacted by the forming tool (opposite/bottom surface) was etched with a circular pattern. Existing literature has shown this method of marking to be appropriate, as it does not significantly compromise the strength of the material, as is seen in other works which utilized deep etches that created stress concentrations across the material [48,55]. The diameter of these circles was measured after forming to determine the major and minor strain.
A numerical simulation of the funnel geometry was completed until the depth at which experimental failure occurred. Once this depth was reached, the forming tool and clamping fixture was removed and a simulation of spring back took place. The maximum strain was then located along the planes shown in Figure 6. Similarly, the maximum strain was found in experimental tests by measuring the displacement of the circles along these planes. Deformation was measured using a microscope fitted with a digital readout. In areas where the maximum strain was located across a bend (i.e., the circle did not lie in one plane), the deformation was approximated by acquiring a measurement in the center of the circle. The length between these three points was then calculated and designated as the total deformation.
Major and minor strains were measured as axial and hoop strains, respectively. Examples of the orientations of strains can be seen in Figure 7. Due to the type of geometry utilized in this analysis, this was determined to provide a more effective measurement system than Cartesian coordinates. Other works have used this form of designation as well [48,51].
In the numerical simulation, thinning of the material is calculated using the strains on each element and applying the basic formulas of tension and compression. The thinning data from the simulation was taken as a percentage of thickness reduction. The data was selected at the exact location as in the experiments, providing a baseline for comparison.
With a known strain state of each element, it is possible to determine when the rupture takes place. Hence, it is possible to state that at a specific strain condition, the material in reality would have failed. Since the depth of failure is not known before the simulation is run, the model was set to follow the toolpath regardless of the strain limits of the material. Once the simulation run time ends, the built-in FLD tool was utilized to find the depth at which the first element ruptured. This point is analogous to the rupture location on the experiment and will be called the “Depth of failure” as shown in Figure 8.

2.3. Thickness Measurement

Since spring back distortions take place after the sheet is unclamped, it is impractical to set the test sample at a standard bench and measure its thickness. Therefore, an alternative method is proposed and the measurements are performed on five specifically defined positions across the wall profile, points 1 to 5, as shown in Figure 9.
In order to compare the thickness for both experiments and finite element simulation, these measurement points were selected to coincide with the element centroid. In the current case, where an element of 3.5 × 3.5 mm is used, it is not possible to measure thickness values within 1 mm of distance, as the values would be similar. For this reason, the points selected to perform the measurements are spaced at a distance of 3.5 mm.
Points 1 to 5 are referenced by their height from the undeformed horizontal plane. For each of these five locations, five additional points, across the circumference, for each location were selected at the same depth of the sheet. To reduce the deviation of the measurement, two values were taken for the same point. For example, for the test of 0.381 mm step size, 50 different measurements, on five different points across the height, taken twice on five different locations around the curved part, shown as points (a), (b), etc. in Figure 9.
Once all the data were collected, the standard deviation was calculated and a confidence interval with α = 5% on a normal distribution was created. These values were compared to their corresponding locations obtained from the model as shown in Figure 10.

3. Results

3.1. Formability

The maximum forming angles determined both experimentally and numerically can be found in Figure 11. No significant trend could be established from the obtained data. At the smallest simulated step size of 0.127 mm, a formability of 50.06° was realized. The formability at the largest step size of 1.143 mm was found to be 52.73°. The maximum formability was realized at a step size of 0.864 mm. This indicates a possible parabolic trend. However, the difference between results is minimal.
These formability results can also be presented as a function of the failure depth, as shown in Figure 12, the results constitute a possible parabolic trend. It is apparent with the increase in the step size, may correlate to an increase in formability; however, only up to a certain threshold, a step size of 0.8636 mm in the present study, and then correlates to a general decrease.
These results are contradictory to other published works, which cite a decrease in formability as the step size is increased [4,5,6]. This is also contradictory to the works of Hussain et al., who experimentally determined the relationship between formability and step size for a similar material [56]. Interestingly, the formability values predicted from the empirical formula derived in [56] are much greater than what is observed herein. As shown in Table 2, study [56] predicts formability of about 60°. However, the material investigated in the aforementioned work and the present research were not identical. Furthermore, testing parameters such as the clamping area and lubricant used were not fully disclosed within other works. This provides good evidence that these are critical factors in the incremental forming process. Therefore, these works cannot be directly compared. It is necessary that future works in this field fully disclose all critical test conditions.
There is a clear difference between experimental and simulation results. Experiments resulted in approximately 12∼16% lower formability relative to simulation. This effect is further discussed in the following sections.

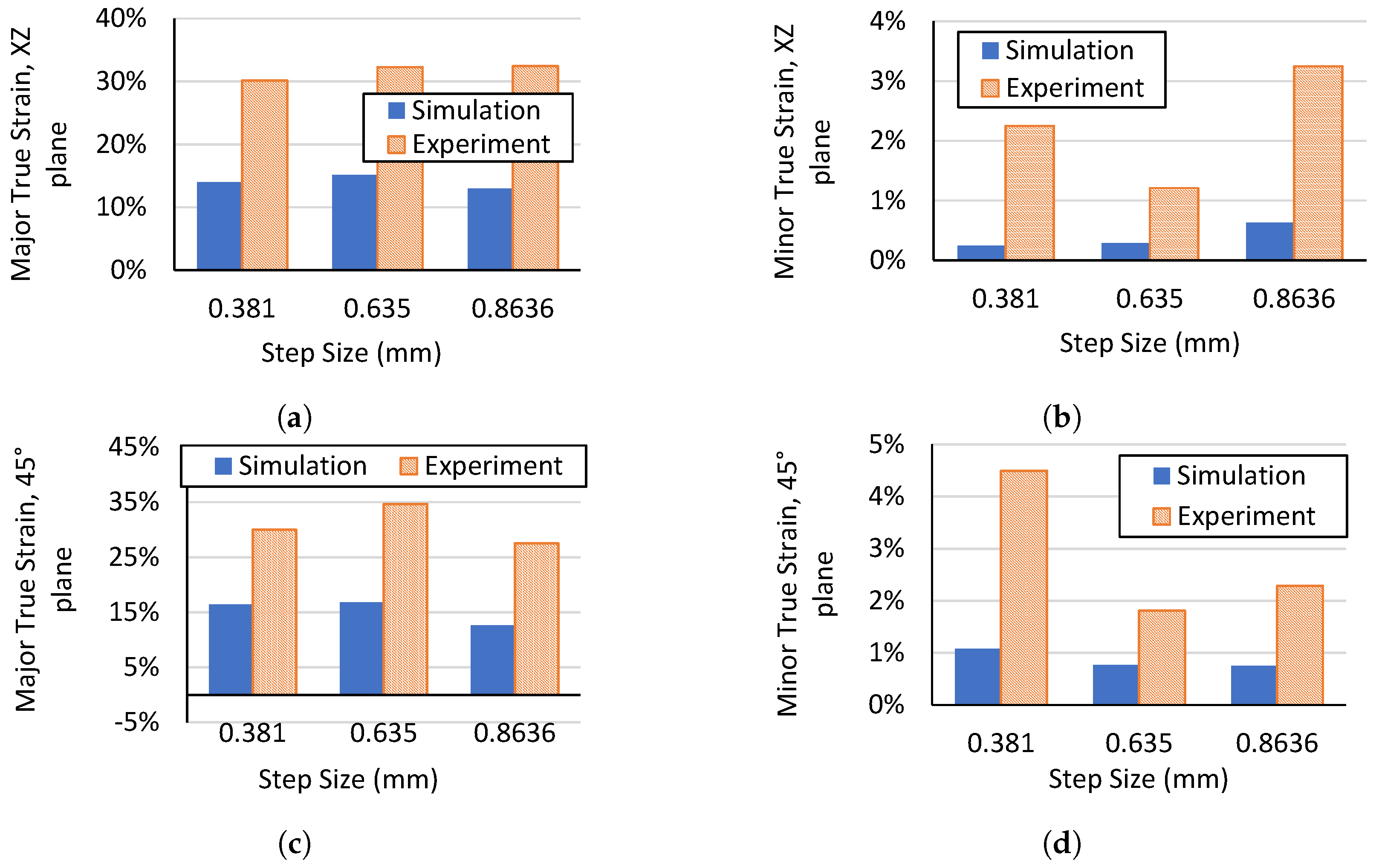
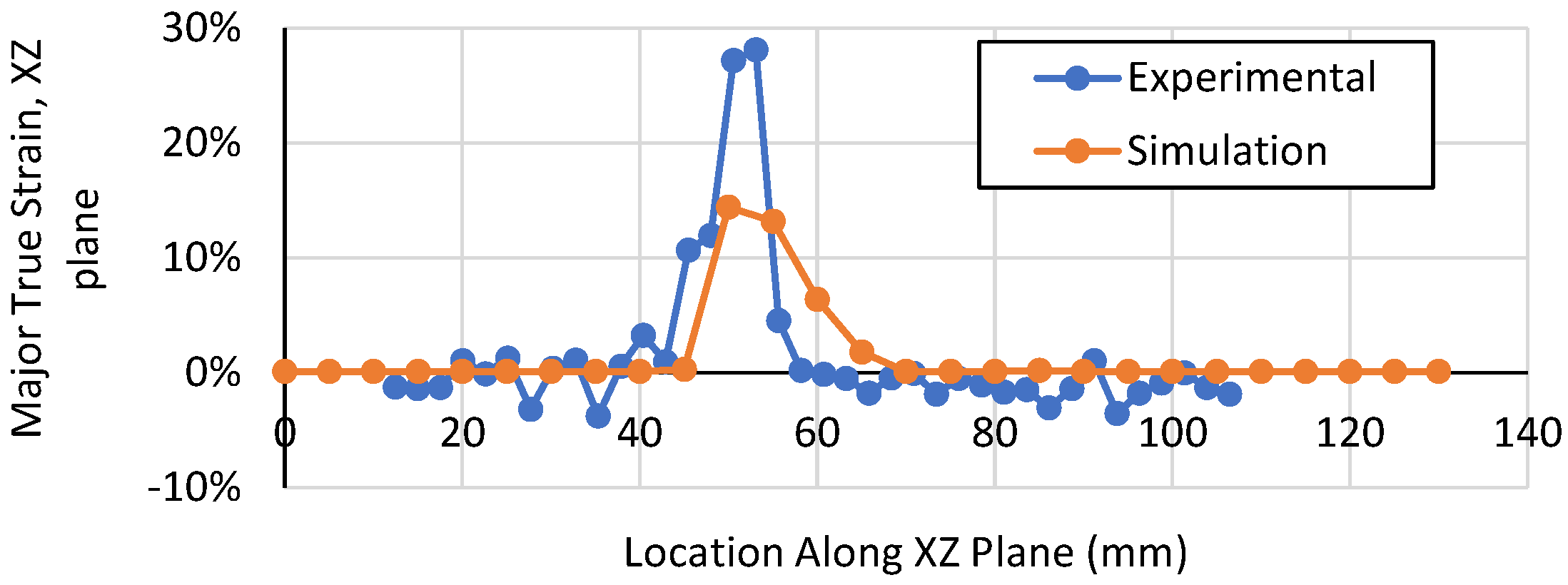
3.2. Maximum Strain

The resulting strain located at the points of interest previously described, (a) and (b) in Figure 6 and Figure 7, can be seen in Figure 13. Simulation results formed a slight trend that showed an increase in step size may correlate to a decrease in major strain and an increase in minor strain. However, it should be noted that the intermediate step size experienced a slight increase in major strain, forming a slightly parabolic trend. Though not definitive, this data shows that step size variation can be used to alter the type of deformation that occurs during forming (e.g., biaxial or uniaxial).
Further analysis of the experiment and simulation reveals that overall, strain predictions within the system were underestimated in simulation results (i.e., the simulation predicts greater formability over experiments). This correlates with the error observed in formability. It can be seen in Figure 11 that formability was predicted to be greater than was experienced in experimental testing. These two factors are correlated in that failure is predicted based on strain. Therefore, the slight error seen in formability testing is most likely the result of an error in strain simulation. In order to further assess the manner of the strain in these tests, the strain was measured along the XZ plane in the experimental and numerical tests for the 0.381 mm step size. This comparison can be seen in Figure 14. These results show that the strained region in experimental tests experienced higher strain closer to the edge of the sheet than is observed in the simulations. Additionally, the strained region appears to be elongated in the simulations, causing the strain to reach deeper into the center of the workpiece than in the experimental test.

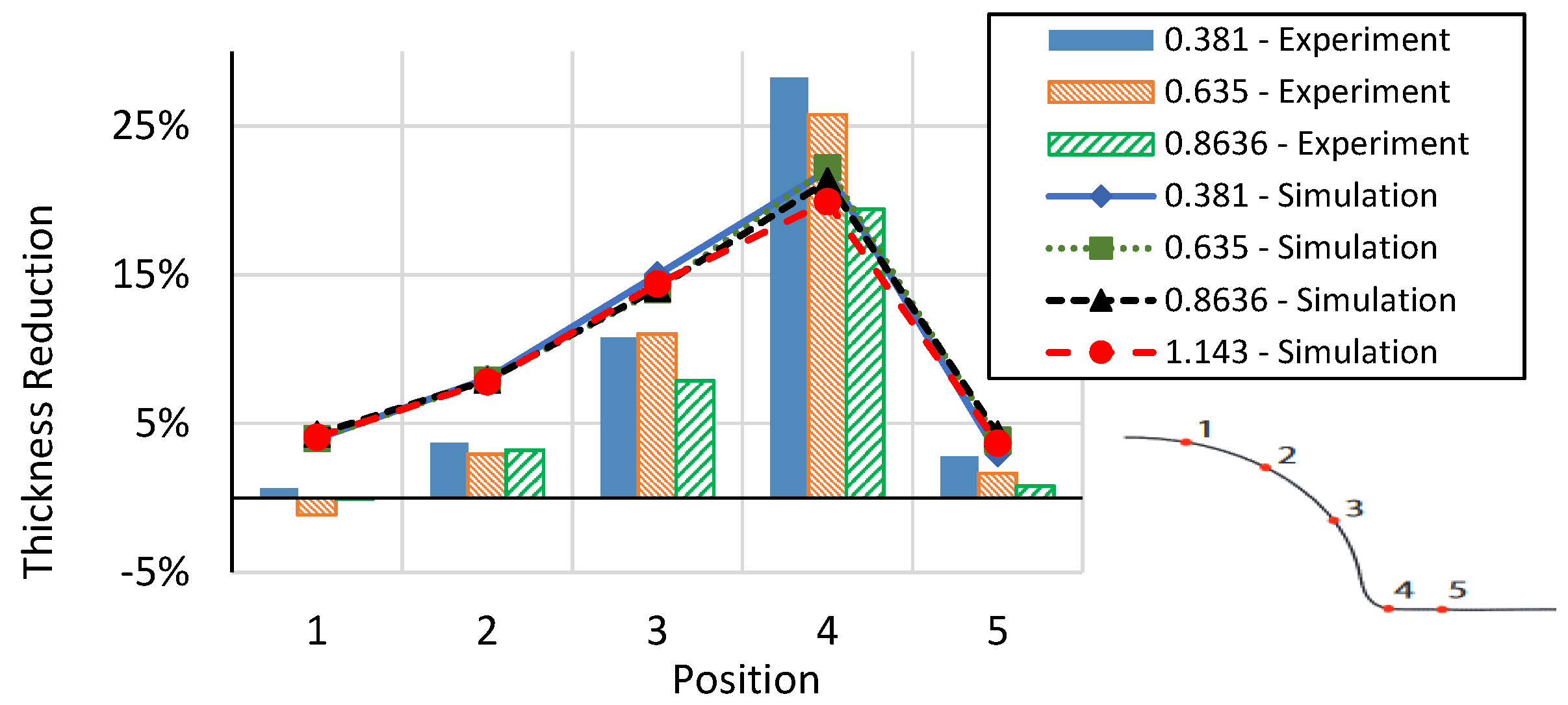
3.3. Thickness Reduction

The thickness reduction of experimental and simulation results was measured at various depths. The results of this testing can be seen in Figure 15. A trend is formed across all tests which reveals an increase in thickness reduction as depth is increased until the central portion of the workpiece is reached. This region is not formed by the forming tool and is therefore similar to the initial material thickness. A distinguishable trend between step sizes can be seen, especially at position 4. At this location, larger step sizes resulted in less thinning. This trend is similar in both experimental and simulation results. It is worth mentioning that the simulations are underestimating the thinning of the sheet. The percentage of thickness reduction results shows that the larger step size results in less material thinning; therefore, failure takes place at a later stage, producing greater formability.

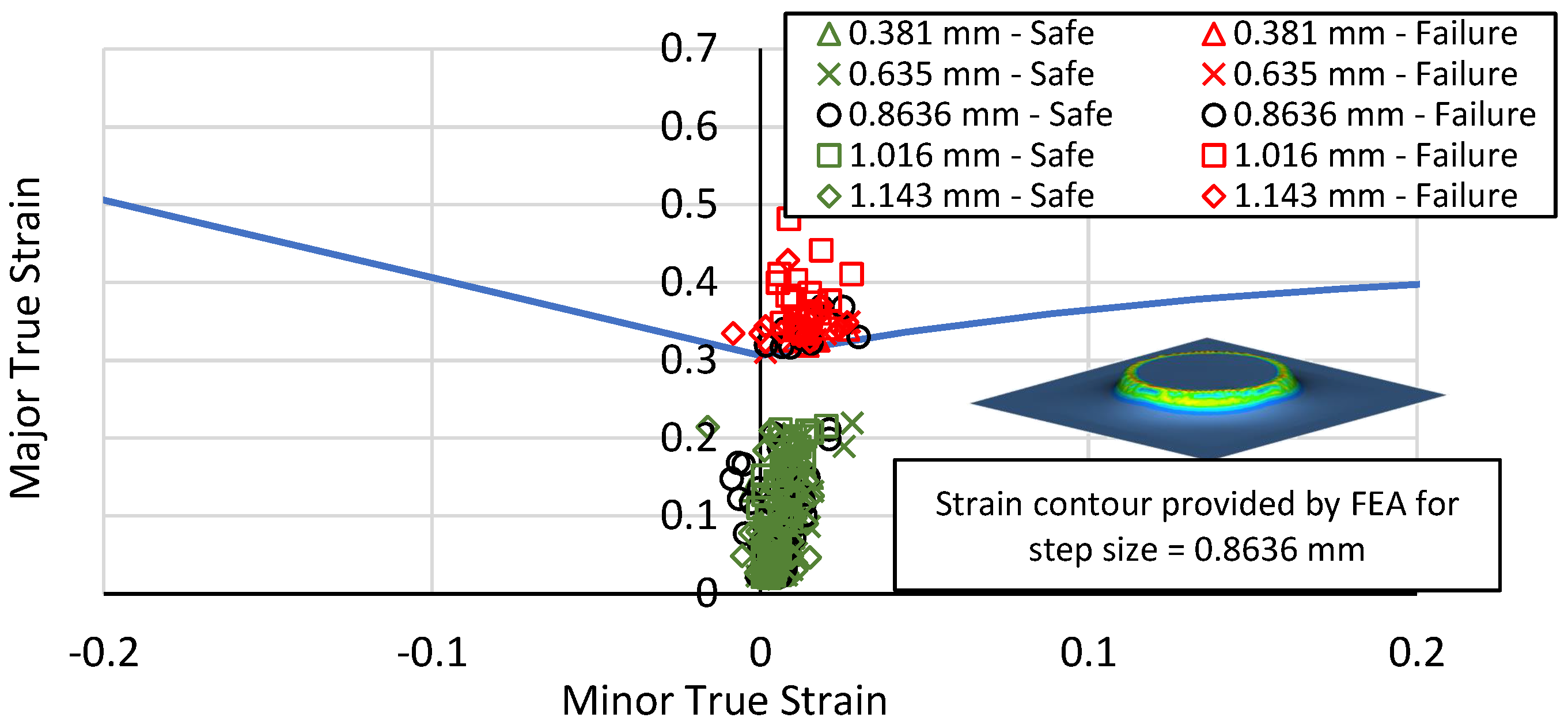
3.4. Forming Limit Diagram

The forming limit diagram (FLD) derived from IF simulations is shown in Figure 16. Since only one geometry was used in simulations, one forming limit curve (FLC) was produced for all runs. Similar to formability results, the FLDs displayed a general trend of enhanced formability with the increase of step size up until a threshold value, 0.8636 mm in the case presented herein, then a gradual decrease is observed. It is worth noting that the gap in the FLD between the “safe” and “failure” locations represents a 10% marginal zone.

4. Conclusions

A model was developed for simulating a SPIF process of 2024-T3 aluminum using Hill’s Criteria with Tabulated (nonlinear) Yield Curve material definition with properties derived from [70]. Friction values utilized in the simulation were experimentally determined. Funnel shapes were formed to assess various factors of this process at varying step sizes. The numerical model presented in this work, regardless of the limited number of experiments and simulation runs, allows for evaluating formability and failure in the SPIF process and providing fair predictions. It was found that the simulation overestimated formability. Generally, the models are in agreement with the experimental results within 12% to 16%. Additionally, no significant trend was observed over the range of step sizes investigated. However, it seems that there is a threshold of step size; when exceeded, formability starts to decrease slightly. Finally, comparisons between this study and similar literature provide further evidence that the clamping fixture geometry can significantly affect results. This comparison, as well as the discussions of step size effect and simulation methodology, are novel additions to this work.

Author Contributions

Conceptualization, I.R., F.C. and T.J.G.; methodology, T.J.G., F.C. and I.R.; validation, I.R., F.C. and T.J.G.; formal analysis, F.C., T.J.G. and I.R.; writing—original draft preparation, T.J.G., F.C. and I.R.; writing—review and editing, T.J.G. and I.R.; supervision, I.R.; project administration, I.R.; funding acquisition, I.R. and F.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by the Bavarian State Ministry of Science and the Arts, in cooperation with Rosenheim Technical University of Applied Sciences, Germany and Penn State University, The Behrend College, USA.

Data Availability Statement

All data generated or analysed during this study are included in this published article.

Acknowledgments

The authors would like to thank Glenn Craig for assisting in the fabrication of fixtures used within this research.

Conflicts of Interest

The authors declare no conflict of interest. Additionally, the funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Kim, Y.H.; Park, J.J. Effect of process parameters on formability in incremental forming of sheet metal. J. Mater. Process. Technol. 2002, 130, 42–46. [Google Scholar] [CrossRef]
  2. Strano, M.; Sorrentino, L.; Carrino, L. Some issues about tools and friction in the negative dieless incremental forming process. In Proceedings of the Conference Metal Forming 2004, Krakow, Poland, 19–22 September 2004; pp. 345–350. [Google Scholar]
  3. Micari, F.; Ambrogio, G. A common shape for conducting incremental forming tests. In Proceedings of the 1st Incremental Forming Workshop, Saarbrücken, Germany, 9 June 2004; Volume 9. [Google Scholar]
  4. Micari, F. Single point incremental forming: Recent results. In Proceedings of the Seminar on Incremental Forming, Cambridge, UK, 22 October 2004; Volume 22. [Google Scholar]
  5. Hirt, G.; Junk, S.; Witulski, N. Incremental sheet forming: Quality evaluation and process simulation. In Proceedings of the 7th ICTP International Conference on Technology of Plasticity, Yokohama, Japan, 27 October–1 November 2002; pp. 925–930. [Google Scholar]
  6. Hagan, E.; Jeswiet, J. Analysis of surface roughness for parts formed by computer numerical controlled incremental forming. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2004, 218, 1307–1312. [Google Scholar] [CrossRef]
  7. Fan, G.; Gao, L. Numerical simulation and experimental investigation to improve the dimensional accuracy in electric hot incremental forming of Ti-6Al-4V titanium sheet. Int. J. Adv. Manuf. Technol. 2014, 72, 1133–1141. [Google Scholar] [CrossRef]
  8. Honarpisheh, M.; Abdolhoseini, M.J.; Amini, S. Experimental and numerical investigation of the hot incremental forming of Ti-6Al-4V sheet using electrical current. Int. J. Adv. Manuf. Technol. 2016, 83, 2027–2037. [Google Scholar] [CrossRef]
  9. Fan, G.; Gao, L. Mechanical property of Ti-6Al-4V sheet in one-sided electric hot incremental forming. Int. J. Adv. Manuf. Technol. 2014, 72, 989–994. [Google Scholar] [CrossRef]
  10. Ambrogio, G.; Filice, L.; Gagliardi, F. Formability of lightweight alloys by hot incremental sheet forming. Mater. Des. 2012, 34, 501–508. [Google Scholar] [CrossRef]
  11. Fan, G.; Sun, F.; Meng, X.; Gao, L.; Tong, G. Electric hot incremental forming of Ti-6Al-4V titanium sheet. Int. J. Adv. Manuf. Technol. 2010, 49, 941–947. [Google Scholar] [CrossRef]
  12. Fan, G.; Gao, L.; Hussain, G.; Wu, Z. Electric hot incremental forming: A novel technique. Int. J. Mach. Tools Manuf. 2008, 48, 1688–1692. [Google Scholar] [CrossRef]
  13. Adams, D.; Jeswiet, J. Single-point incremental forming of 6061-T6 using electrically assisted forming methods. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 228, 757–764. [Google Scholar] [CrossRef]
  14. Xu, D.; Lu, B.; Cao, T.; Chen, J.; Long, H.; Cao, J. A comparative study on process potentials for frictional stir-and electric hot-assisted incremental sheet forming. Procedia Eng. 2014, 81, 2324–2329. [Google Scholar] [CrossRef] [Green Version]
  15. Shi, X.; Gao, L.; Khalatbari, H.; Xu, Y.; Wang, H. Electric hot incremental forming of low carbon steel sheet: Accuracy improvement. Int. J. Adv. Manuf. Technol. 2013, 68, 241–247. [Google Scholar] [CrossRef]
  16. Adams, D.W. Improvements on Single Point Incremental Forming Through Electrically Assisted Forming, Contact Area Prediction and Tool Development. Ph.D. Thesis, Queens University, Kingston, ON, Canada, 2013. [Google Scholar]
  17. Meier, H.; Magnus, C. Incremental sheet metal forming with direct resistance heating using two moving tools. In Key Engineering Materials; Trans Tech Publications Ltd.: Zürich, Switzerland, 2013; Volume 554, pp. 1362–1367. [Google Scholar]
  18. Grimm, T.J.; Ragai, I.; Roth, J.T. The Effects of Polarity and Current Path in Electrically Assisted Single Point Incremental Forming of 2024-T3 Aluminum. In Proceedings of the International Manufacturing Science and Engineering Conference, Los Angeles, CA, USA, 4–8 June 2017; Volume 1. Processes:V001T02A063. [Google Scholar] [CrossRef]
  19. Duflou, J.R.; Callebaut, B.; Verbert, J.; De Baerdemaeker, H. Laser assisted incremental forming: Formability and accuracy improvement. CIRP Ann.-Manuf. Technol. 2007, 56, 273–276. [Google Scholar] [CrossRef]
  20. Göttmann, A.; Diettrich, J.; Bergweiler, G.; Bambach, M.; Hirt, G.; Loosen, P.; Poprawe, R. Laser-assisted asymmetric incremental sheet forming of titanium sheet metal parts. Prod. Eng. 2011, 5, 263–271. [Google Scholar] [CrossRef]
  21. Taleb Araghi, B.; Göttmann, A.; Bergweiler, G.; Saeed-Akbari, A.; Bültmann, J.; Zettler, J.; Bambach, M.; Hirt, G. Investigation on incremental sheet forming combined with laser heating and stretch forming for the production of lightweight structures. In Key Engineering Materials; Trans Tech Publications Ltd.: Zürich, Switzerland, 2011; Volume 473, pp. 919–928. [Google Scholar]
  22. Mohammadi, A.; Vanhove, H.; Van Bael, A.; Duflou, J.R. Towards accuracy improvement in single point incremental forming of shallow parts formed under laser assisted conditions. Int. J. Mater. Form. 2016, 9, 339–351. [Google Scholar] [CrossRef]
  23. Al-Obaidi, A.; Kräusel, V.; Landgrebe, D. Hot single-point incremental forming assisted by induction heating. Int. J. Adv. Manuf. Technol. 2016, 82, 1163–1171. [Google Scholar] [CrossRef]
  24. Palumbo, G.; Brandizzi, M. Experimental investigations on the single point incremental forming of a titanium alloy component combining static heating with high tool rotation speed. Mater. Des. 2012, 40, 43–51. [Google Scholar] [CrossRef]
  25. Li, Y.; Liu, Z.; Daniel, W.J.T.; Meehan, P.A. Simulation and experimental observations of effect of different contact interfaces on the incremental sheet forming process. Mater. Manuf. Process. 2014, 29, 121–128. [Google Scholar] [CrossRef]
  26. Lu, B.; Fang, Y.; Xu, D.K.; Chen, J.; Ou, H.; Moser, N.H.; Cao, J. Mechanism investigation of friction-related effects in single point incremental forming using a developed oblique roller-ball tool. Int. J. Mach. Tools Manuf. 2014, 85, 14–29. [Google Scholar] [CrossRef]
  27. Vihtonen, L.; Puzik, A.; Katajarinne, T. Comparing two robot assisted incremental forming methods: Incremental forming by pressing and incremental hammering. Int. J. Mater. Form. 2008, 1, 1207–1210. [Google Scholar] [CrossRef]
  28. Schafer, T.; Schraft, R.D. Incremental sheet metal forming by industrial robots. Rapid Prototyp. J. 2005, 11, 278–286. [Google Scholar] [CrossRef]
  29. Puzik, A. Incremental sheet forming with a robot system for an industrial application. In Manufacturing Systems and Technologies for the New Frontier; Springer: Berlin/Heidelberg, Germany, 2008; pp. 421–424. [Google Scholar]
  30. Meier, H.; Buff, B.; Laurischkat, R.; Smukala, V. Increasing the part accuracy in dieless robot-based incremental sheet metal forming. CIRP Ann. 2009, 58, 233–238. [Google Scholar] [CrossRef]
  31. Kreimeier, D.; Buff, B.; Magnus, C.; Smukala, V.; Zhu, J. Robot-based incremental sheet metal forming–increasing the geometrical accuracy of complex parts. In Key Engineering Materials; Trans Tech Publications Ltd.: Zürich, Switzerland, 2011; Volume 473, pp. 853–860. [Google Scholar]
  32. Amini, S.; Gollo, A.H.; Paktinat, H. An investigation of conventional and ultrasonic-assisted incremental forming of annealed AA1050 sheet. Int. J. Adv. Manuf. Technol. 2017, 90, 1569–1578. [Google Scholar] [CrossRef]
  33. Vahdati, M.; Mahdavinejad, R.; Amini, S. Investigation of the ultrasonic vibration effect in incremental sheet metal forming process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 971–982. [Google Scholar] [CrossRef]
  34. Cai, G.P.; Xing, C.W.; Jiang, Z.H.; Zhang, Z.K. Sheet Single point vibration incremental forming process simulation and analysis of process parameters. In Advanced Materials Research; Trans Tech Publications Ltd.: Zürich, Switzerland, 2012; Volume 430, pp. 74–78. [Google Scholar]
  35. Ziran, X.; Gao, L.; Hussain, G.; Cui, Z. The performance of flat end and hemispherical end tools in single-point incremental forming. Int. J. Adv. Manuf. Technol. 2010, 46, 1113–1118. [Google Scholar] [CrossRef]
  36. Grimm, T.J.; Ragai, I.; Roth, J.T. A Novel Modification to the Incremental Forming Process, Part 1: Multi-directional Tooling. Procedia Manuf. 2017, 10, 510–519. [Google Scholar] [CrossRef]
  37. Grimm, T.J.; Ragai, I.; Roth, J.T. A Novel Modification to the Incremental Forming Process, Part 2: Validation of the Multi-directional Tooling Method. Procedia Manuf. 2017, 10, 520–530. [Google Scholar] [CrossRef]
  38. Young, D.; Jeswiet, J. Wall thickness variations in single-point incremental forming. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2004, 218, 1453–1459. [Google Scholar] [CrossRef]
  39. Kim, T.J.; Yang, D.Y. Improvement of formability for the incremental sheet metal forming process. Int. J. Mech. Sci. 2000, 42, 1271–1286. [Google Scholar] [CrossRef]
  40. Liu, Z.; Daniel, W.J.T.; Li, Y.; Liu, S.; Meehan, P.A. Multi-pass deformation design for incremental sheet forming: Analytical modeling, finite element analysis and experimental validation. J. Mater. Process. Technol. 2014, 214, 620–634. [Google Scholar] [CrossRef] [Green Version]
  41. Malhotra, R.; Bhattacharya, A.; Kumar, A.; Reddy, N.V.; Cao, J. A new methodology for multi-pass single point incremental forming with mixed toolpaths. CIRP Ann.-Manuf. Technol. 2011, 60, 323–326. [Google Scholar] [CrossRef]
  42. Duflou, J.R.; Verbert, J.; Belkassem, B.; Gu, J.; Sol, H.; Henrard, C.; Habraken, A.M. Process window enhancement for single point incremental forming through multi-step toolpaths. CIRP Ann.-Manuf. Technol. 2008, 57, 253–256. [Google Scholar] [CrossRef] [Green Version]
  43. Verbert, J.; Belkassem, B.; Henrard, C.; Habraken, A.M.; Gu, J.; Sol, H.; Lauwers, B.; Duflou, J.R. Multi-Step toolpath approach to overcome forming limitations in single point incremental forming. Int. J. Mater. Form. 2008, 1, 1203–1206. [Google Scholar] [CrossRef] [Green Version]
  44. Grimm, T.J.; Ragai, I.; Roth, J.T. Utilization of Wavy Toolpath in Single-Point Incremental Forming. In Proceedings of the ASME 2018 International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018. [Google Scholar]
  45. Grimm, T.J.; Mears, L. Investigation of a radial toolpath in single point incremental forming. Procedia Manuf. 2020, 48, 215–222. [Google Scholar] [CrossRef]
  46. Hirt, G.; Junk, S.; Bambach, M.; Chouvalova, I. Process limits and material behaviour in incremental sheet forming with CNC-tools. In Materials Science Forum; Trans Tech Publications Ltd.: Zurich-Uetikon, Switzerland, 2003; Volume 426, pp. 3825–3830. [Google Scholar]
  47. Jeswiet, J.; Young, D. Forming limit diagrams for single-point incremental forming of aluminium sheet. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2005, 219, 359–364. [Google Scholar] [CrossRef]
  48. Filice, L.; Fratini, L.; Micari, F. Analysis of material formability in incremental forming. CIRP Ann.-Manuf. Technol. 2002, 51, 199–202. [Google Scholar] [CrossRef]
  49. Silva, M.B.; Skjødt, M.; Atkins, A.G.; Bay, N.; Martins, P.A.F. Single-point incremental forming and formability—Failure diagrams. J. Strain Anal. Eng. Des. 2008, 43, 15–35. [Google Scholar] [CrossRef]
  50. Ham, M.; Jeswiet, J. Forming limit curves in single point incremental forming. CIRP Ann.-Manuf. Technol. 2007, 56, 277–280. [Google Scholar] [CrossRef]
  51. Eyckens, P.; Belkassem, B.; Henrard, C.; Gu, J.; Sol, H.; Habraken, A.M.; Duflou, J.R.; Van Bael, A.; Van Houtte, P. Strain evolution in the single point incremental forming process: Digital image correlation measurement and finite element prediction. Int. J. Mater. Form. 2011, 4, 55–71. [Google Scholar] [CrossRef]
  52. Huang, Y.; Wang, Y.J.; Cao, J.; Li, M. Prediction of forming limit in single point incremental forming with the ductile fracture criterion. In Proceedings of the ASME 2007 International Manufacturing Science and Engineering Conference, Atlanta, GA, USA, 15–18 October 2007; American Society of Mechanical Engineers: New York, NY, USA, 2007; pp. 929–934. [Google Scholar]
  53. Nguyen, D.T.; Kim, Y.S. A numerical study on establishing the forming limit curve and indicating the formability of complex shape in incremental sheet forming process. Int. J. Precis. Eng. Manuf. 2013, 14, 2087–2093. [Google Scholar] [CrossRef]
  54. Arshad, S. A Study of Forming Parameters, Forming Limits and Part Accuracy of Aluminium 2024, 6061 and 7475 Alloys. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2012. [Google Scholar]
  55. Jeswiet, J.; Micari, F.; Hirt, G.; Bramley, A.; Duflou, J.; Allwood, J. Asymmetric single point incremental forming of sheet metal. CIRP Ann.-Manuf. Technol. 2005, 54, 88–114. [Google Scholar] [CrossRef]
  56. Hussain, G.; Gao, L.; Hayat, N.; Dar, N.U. The formability of annealed and pre-aged AA-2024 sheets in single-point incremental forming. Int. J. Adv. Manuf. Technol. 2010, 46, 543–549. [Google Scholar] [CrossRef]
  57. Ham, M.; Jeswiet, J. Single point incremental forming and the forming criteria for AA3003. CIRP Ann.-Manuf. Technol. 2006, 55, 241–244. [Google Scholar] [CrossRef]
  58. Kurra, S.; Regalla, S.P. Experimental and numerical studies on formability of extra-deep drawing steel in incremental sheet metal forming. J. Mater. Res. Technol. 2014, 3, 158–171. [Google Scholar] [CrossRef] [Green Version]
  59. Ghazanfari, A.; Soleimani, S.S.; Keshavarzzadeh, M.; Habibi, M.; Assempuor, A.; Hashemi, R. Prediction of FLD for sheet metal by considering through-thickness shear stresses. Mech. Based Des. Struct. Mach. 2020, 48, 755–772. [Google Scholar] [CrossRef]
  60. Khan, M.S.; Coenen, F.; Dixon, C.; El-Salhi, S.; Penalva, M.; Rivero, A. An intelligent process model: Predicting springback in single point incremental forming. Int. J. Adv. Manuf. Technol. 2015, 76, 2071–2082. [Google Scholar] [CrossRef] [Green Version]
  61. Arfa, H.; Bahloul, R.; BelHadjSalah, H. Finite element modelling and experimental investigation of single point incremental forming process of aluminum sheets: Influence of process parameters on punch force monitoring and on mechanical and geometrical quality of parts. Int. J. Mater. Form. 2013, 6, 483–510. [Google Scholar] [CrossRef]
  62. He, S.; Van Bael, A.; Van Houtte, P.; Duflou, J.R.; Szekeres, A.; Henrard, C.; Habraken, A.M. Finite element modeling of incremental forming of aluminum sheets. In Advanced Materials Research; Trans Tech Publications Ltd.: Zürich, Switzerland, 2005; Volume 6, pp. 525–532. [Google Scholar]
  63. Salem, E.; Shin, J.; Nath, M.; Banu, M.; Taub, A.I. Investigation of thickness variation in single point incremental forming. Procedia Manuf. 2016, 5, 828–837. [Google Scholar] [CrossRef] [Green Version]
  64. Senthil, R.; Gnanavelbabu, A. Numerical analysis on formability of AZ61A magnesium alloy by incremental forming. Procedia Eng. 2014, 97, 1975–1982. [Google Scholar] [CrossRef] [Green Version]
  65. Hussain, G.; Gao, L.; Hayat, N.; Ziran, X. A new formability indicator in single point incremental forming. J. Mater. Process. Technol. 2009, 209, 4237–4242. [Google Scholar] [CrossRef]
  66. Benedetti, M.; Fontanari, V.; Monelli, B.; Tassan, M. Single-point incremental forming of sheet metals: Experimental study and numerical simulation. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 301–312. [Google Scholar] [CrossRef]
  67. Esmaeilpour, R.; Pourboghrat, F.; Kim, H.; Park, T. Finite Element Analysis of Single Point Incremental Forming (SPIF) of Aluminum 7075 Using Different Types of Toolpath. IOP Conf. Ser. Mater. Sci. Eng. 2019, 521, 012012. [Google Scholar] [CrossRef]
  68. Li, Q.M.; Yi, Z.W.; Liu, Y.Q.; Tang, X.F.; Jiang, W.; Li, H.J. Explicit Analysis of Sheet Metal Forming Processes Using Solid-Shell Elements. Metals 2022, 12, 52. [Google Scholar] [CrossRef]
  69. Grimm, T.J.; Mears, L. Numerical Determination of Unconstrained Area Effect on Springback in Incremental Forming of 5052-H32 Aluminum. In Proceedings of the ASME 2019 International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, USA, 11–14 November 2019; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2019. [Google Scholar]
  70. Rice, R.C.; Jackson, J.L.; Bakuckas, J.; Thompson, S. Metallic Materials Properties Development and Standardization (MMPDS), Scientific Report DOT/FAA/AR-MMPDS-01; U.S. Department of Transportation—Federal Aviation Administration—Office of Aviation Research: Washington, DC, USA.
  71. Kaufman, J.G. Properties of Aluminum Alloys: Tensile, Creep, and Fatigue Data at High and Low Temperatures; ASM International: Almere, The Netherlands, 1999. [Google Scholar]
  72. Bauccio, M. ASM Metals Reference Book; ASM International: Almere, The Netherlands, 1993. [Google Scholar]
  73. ASM International Handbook Committee. Properties and selection: Nonferrous alloys and special-purpose materials. ASM Int. 1992, 2, 1143–1144. [Google Scholar]
Jmmp 07 00070 g001 550
Figure 1. HAAS TM3 milling machine used for incremental forming.
Figure 1. HAAS TM3 milling machine used for incremental forming.
Jmmp 07 00070 g001
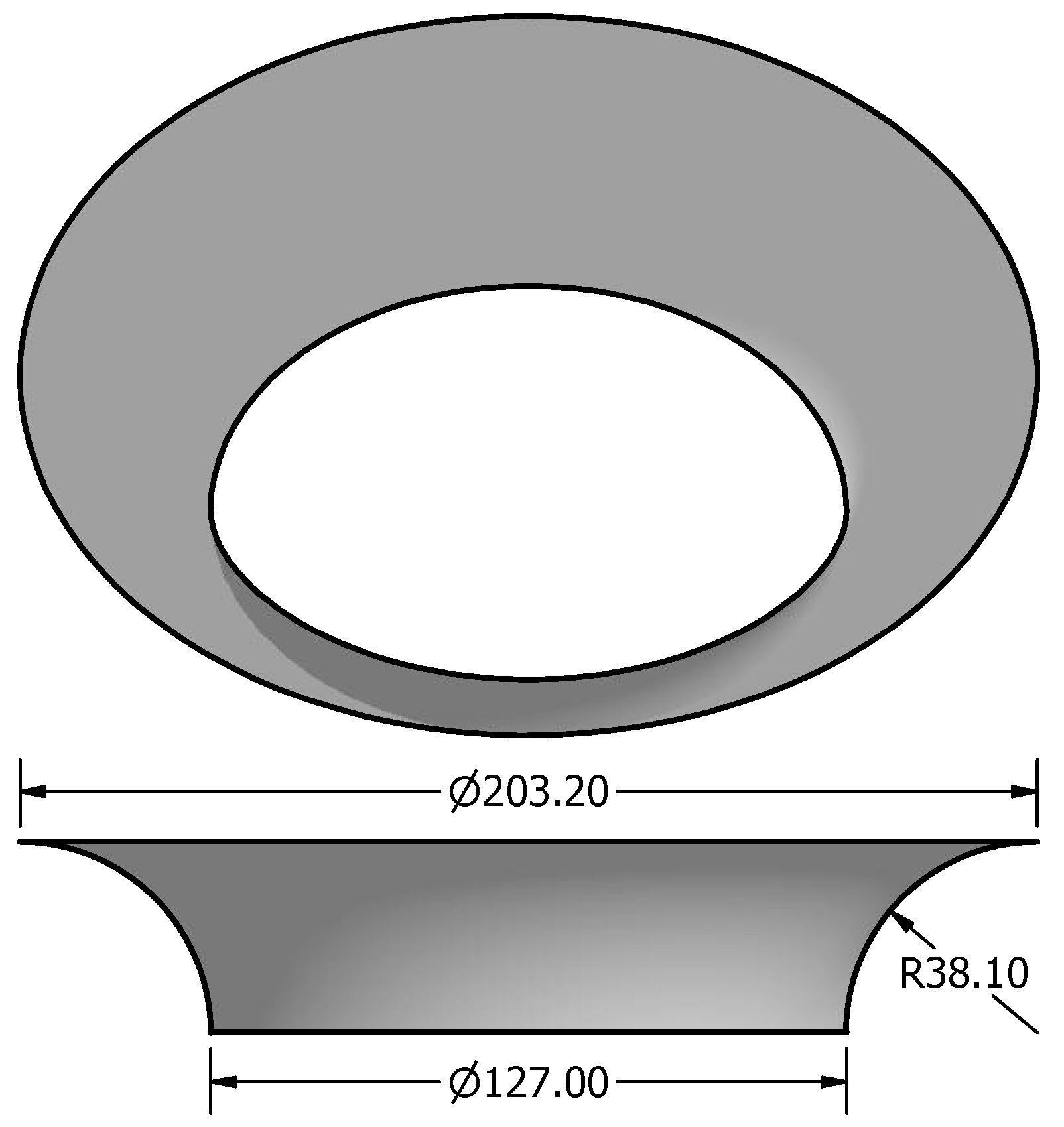
Jmmp 07 00070 g002 550
Figure 2. Geometry used to analyze formability; dimensions in mm.
Figure 2. Geometry used to analyze formability; dimensions in mm.
Jmmp 07 00070 g002
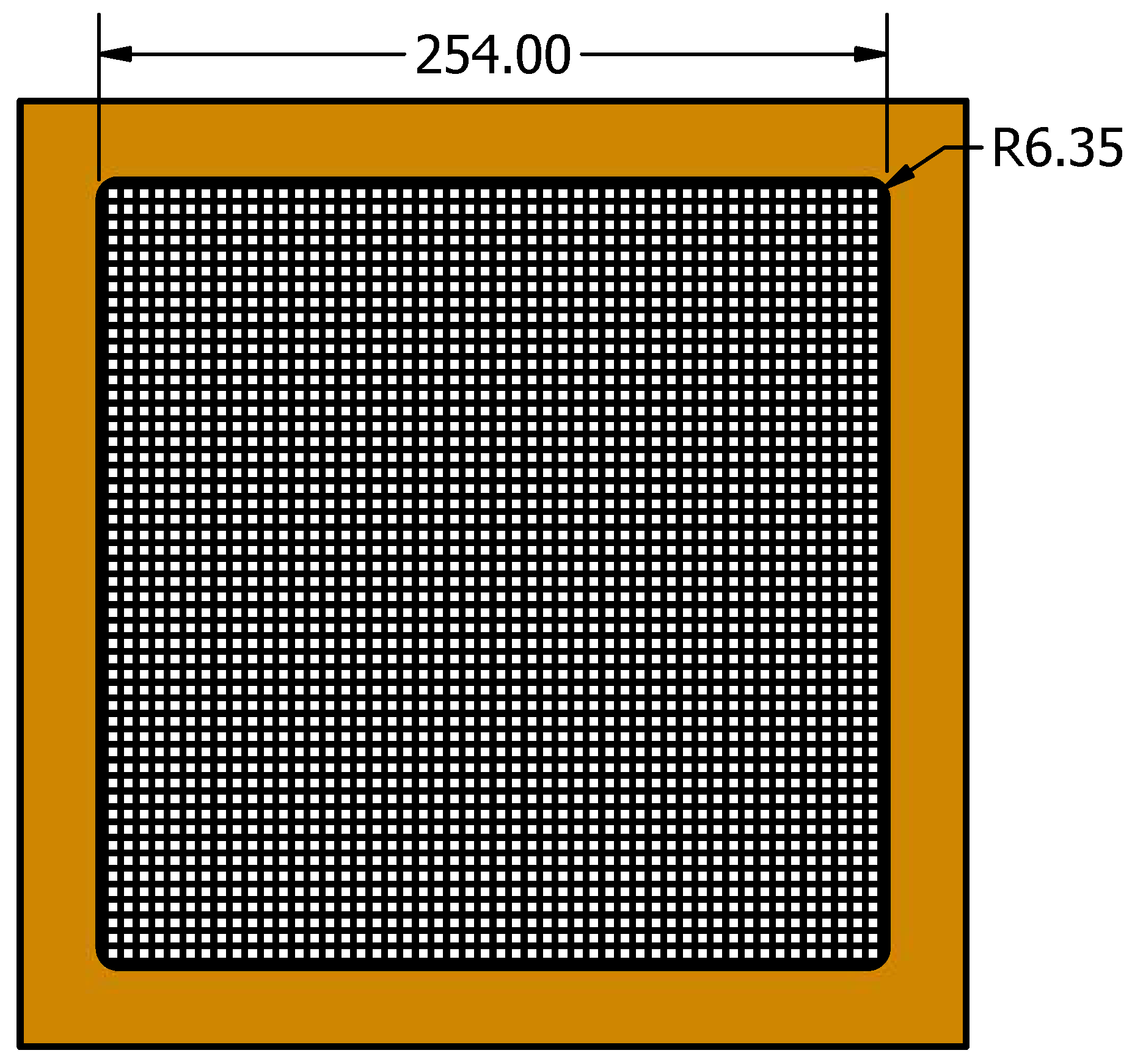
Jmmp 07 00070 g003 550
Figure 3. Mesh and dimensions (mm) of the frame and sheet used throughout testing.
Figure 3. Mesh and dimensions (mm) of the frame and sheet used throughout testing.
Jmmp 07 00070 g003
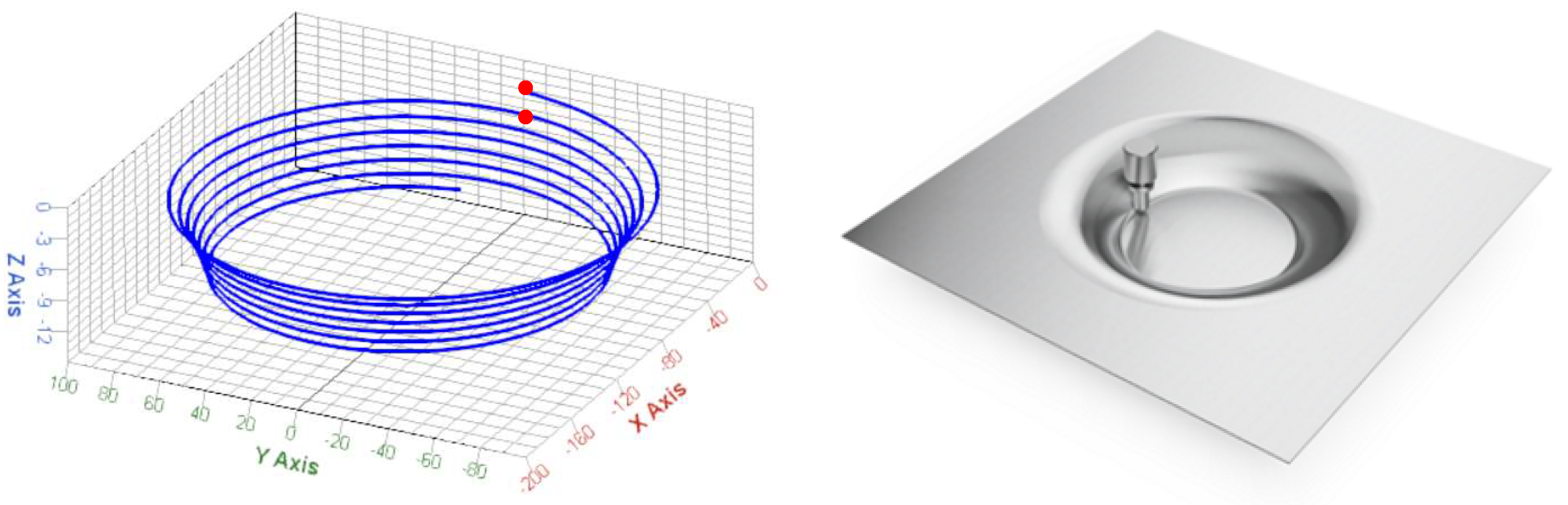
Jmmp 07 00070 g004 550
Figure 4. Toolpath and formed shape illustrations.
Figure 4. Toolpath and formed shape illustrations.
Jmmp 07 00070 g004
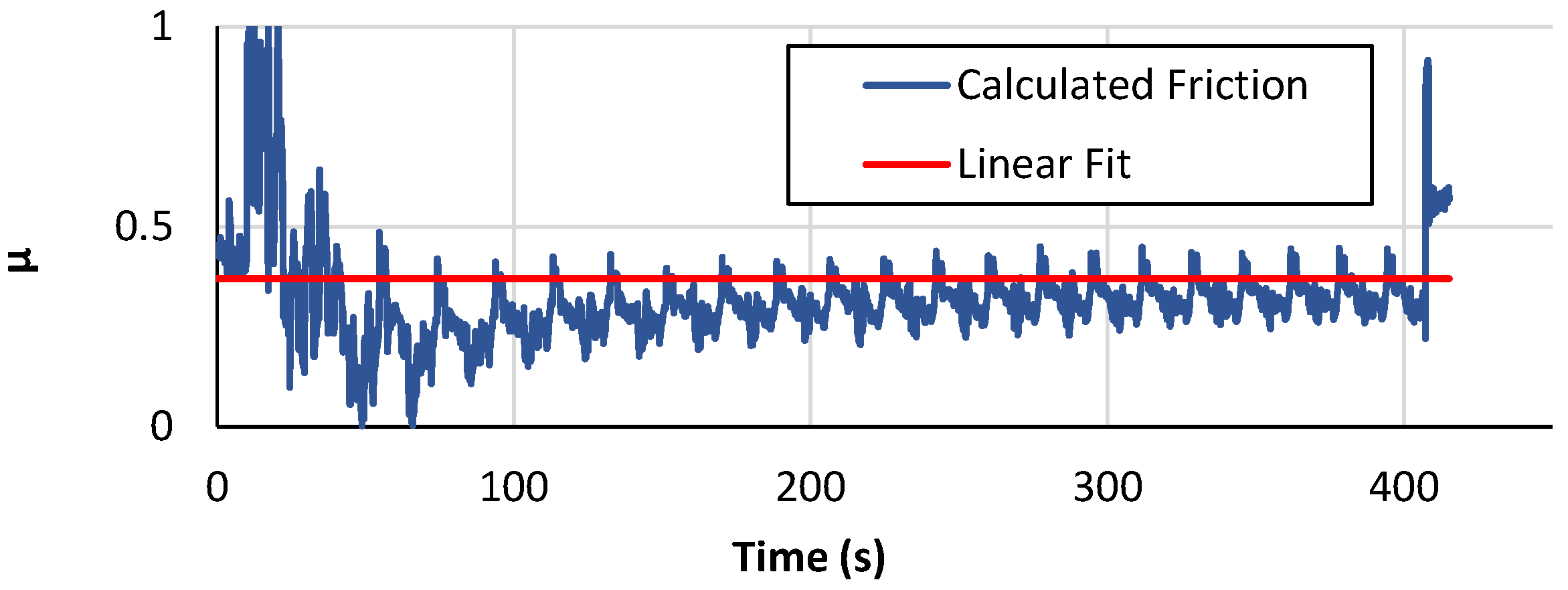
Jmmp 07 00070 g005 550
Figure 5. Experimental friction coefficient for an example test.
Figure 5. Experimental friction coefficient for an example test.
Jmmp 07 00070 g005
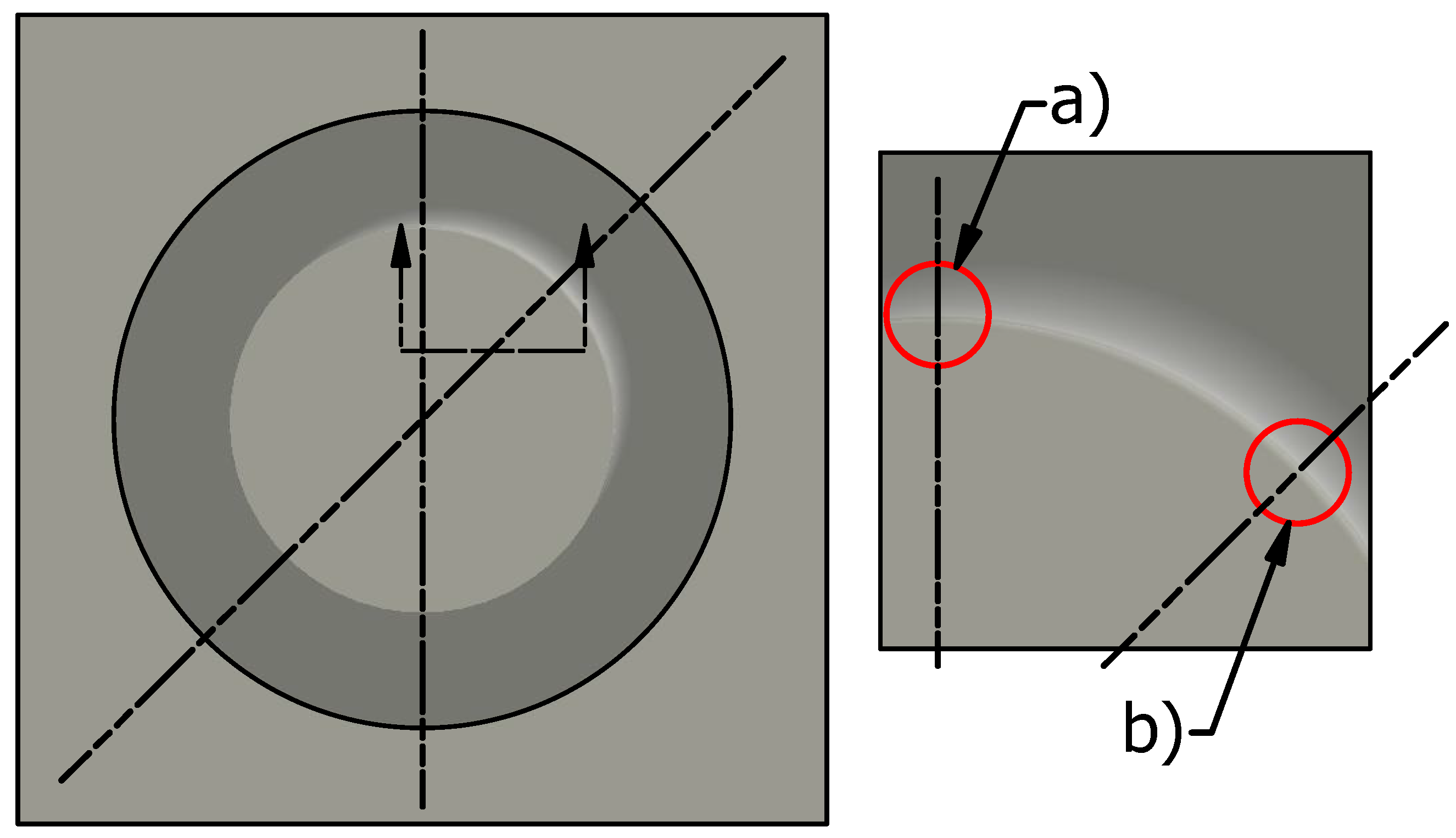
Jmmp 07 00070 g006 550
Figure 6. Approximate locations of strain measurement: (a) point on XZ plane and point (b) 45° from XZ plane.
Figure 6. Approximate locations of strain measurement: (a) point on XZ plane and point (b) 45° from XZ plane.
Jmmp 07 00070 g006
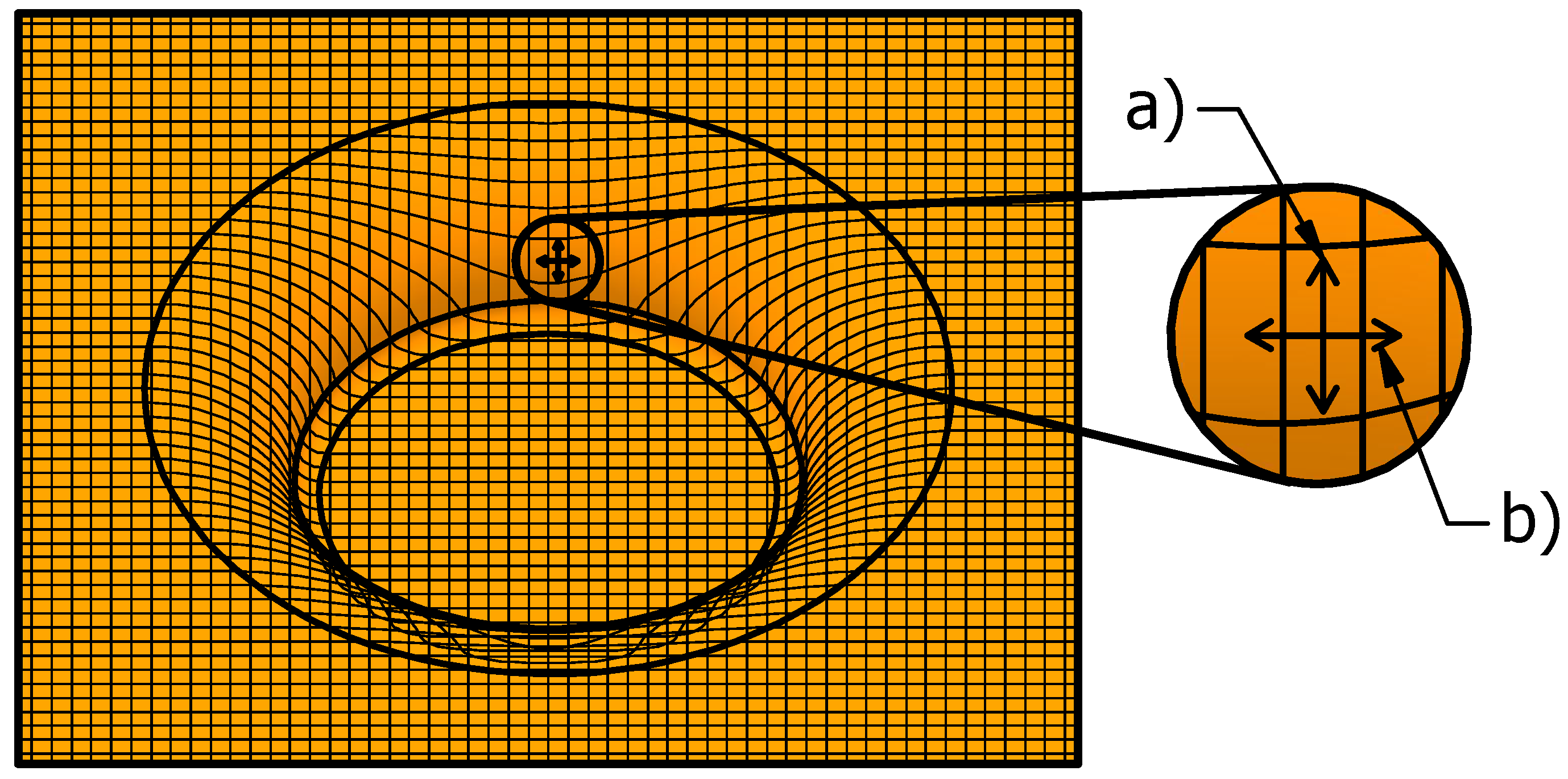
Jmmp 07 00070 g007 550
Figure 7. Strain designations—(a) Major (axial) strain and (b) Minor (hoop) strain.
Figure 7. Strain designations—(a) Major (axial) strain and (b) Minor (hoop) strain.
Jmmp 07 00070 g007
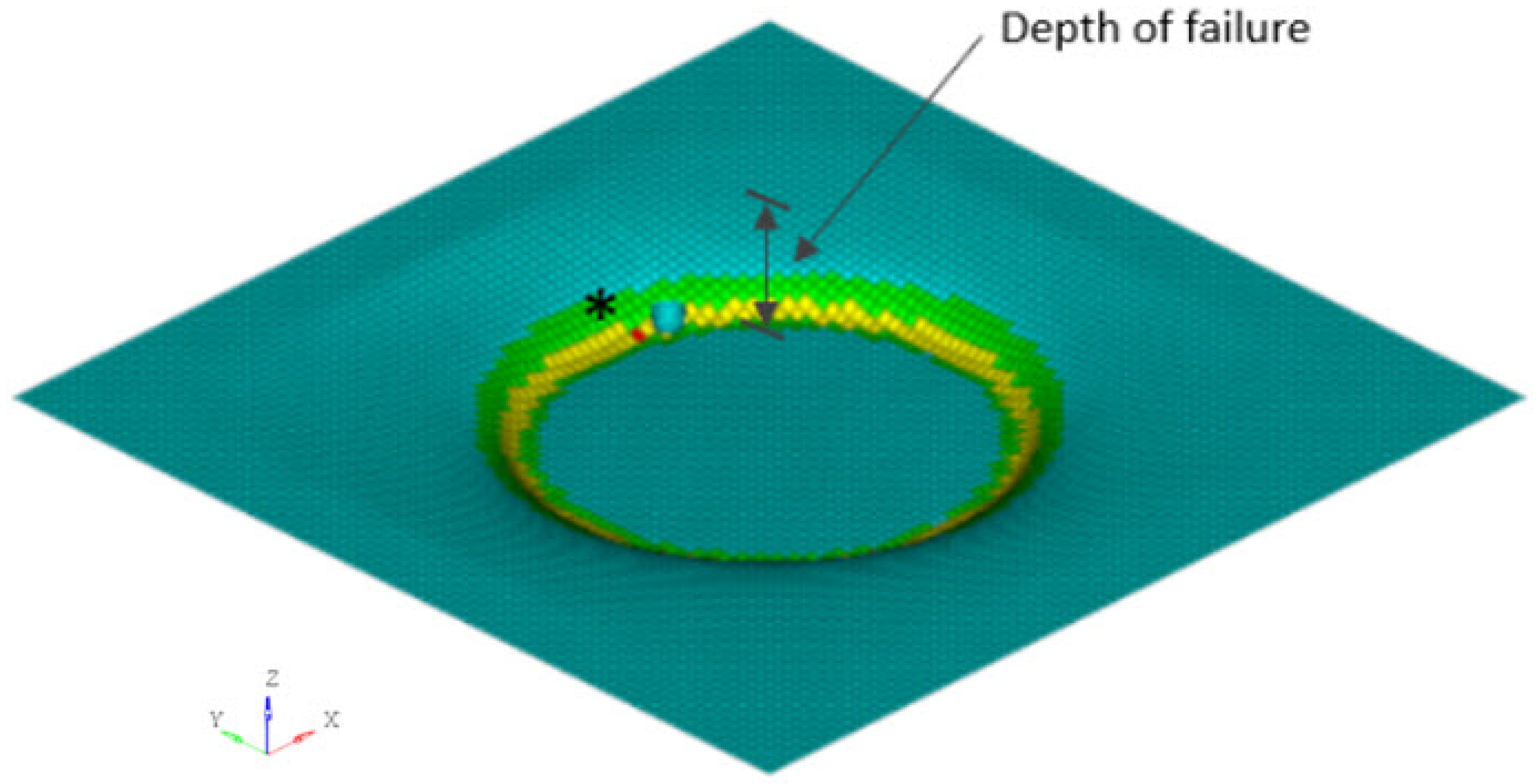
Jmmp 07 00070 g008 550
Figure 8. Defining the depth of failure in simulation.
Figure 8. Defining the depth of failure in simulation.
Jmmp 07 00070 g008
Jmmp 07 00070 g009 550
Figure 9. Thickness measurement over section cut of the sheet.
Figure 9. Thickness measurement over section cut of the sheet.
Jmmp 07 00070 g009
Jmmp 07 00070 g010 550
Figure 10. Elemental and experiment thickness measurement positions.
Figure 10. Elemental and experiment thickness measurement positions.
Jmmp 07 00070 g010
Jmmp 07 00070 g011 550
Figure 11. Resulting formability of experimental testing and simulations.
Figure 11. Resulting formability of experimental testing and simulations.
Jmmp 07 00070 g011
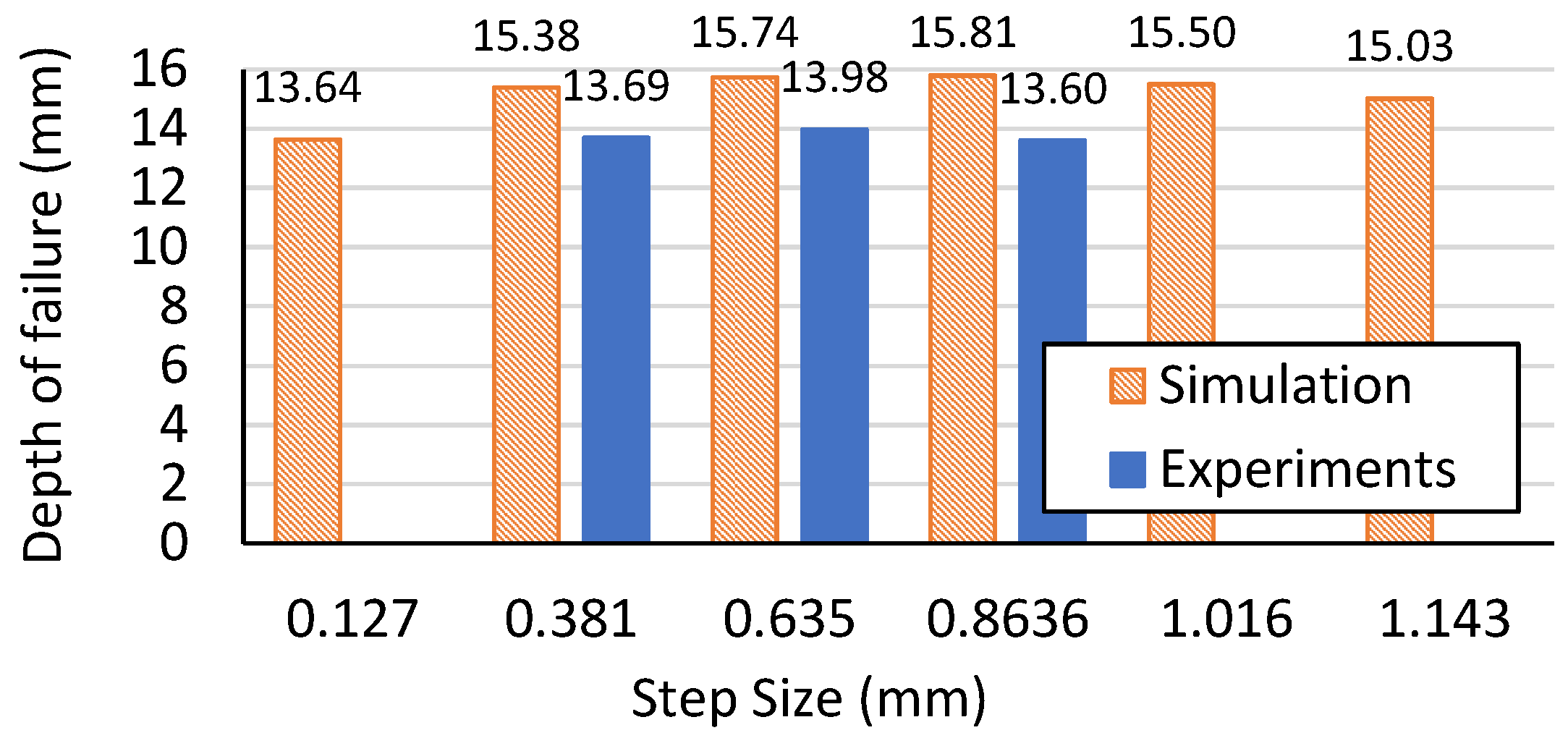
Jmmp 07 00070 g012 550
Figure 12. Resulting failure depth of experimental testing and simulation.
Figure 12. Resulting failure depth of experimental testing and simulation.
Jmmp 07 00070 g012
Jmmp 07 00070 g013 550
Figure 13. (a) Major true strain located along the XZ, (b) minor true strain located along the XZ plane, (c) Major true strain located along the 45° plane, and (d) minor true strain located along the 45° plane.
Figure 13. (a) Major true strain located along the XZ, (b) minor true strain located along the XZ plane, (c) Major true strain located along the 45° plane, and (d) minor true strain located along the 45° plane.
Jmmp 07 00070 g013
Jmmp 07 00070 g014 550
Figure 14. Strain measured along the XZ plane.
Figure 14. Strain measured along the XZ plane.
Jmmp 07 00070 g014
Jmmp 07 00070 g015 550
Figure 15. Thickness measured along the XZ plane.
Figure 15. Thickness measured along the XZ plane.
Jmmp 07 00070 g015
Jmmp 07 00070 g016 550
Figure 16. Forming limit diagram of numerical simulations.
Figure 16. Forming limit diagram of numerical simulations.
Jmmp 07 00070 g016
Table
Table 1. A summary of the effects of process parameters on formability.
Table 1. A summary of the effects of process parameters on formability.
Feed rate ↓ [1]Formability ↑
Tool size ↑ [1]
Friction ↓ [1,2]
Tool rotation ↑ [3]
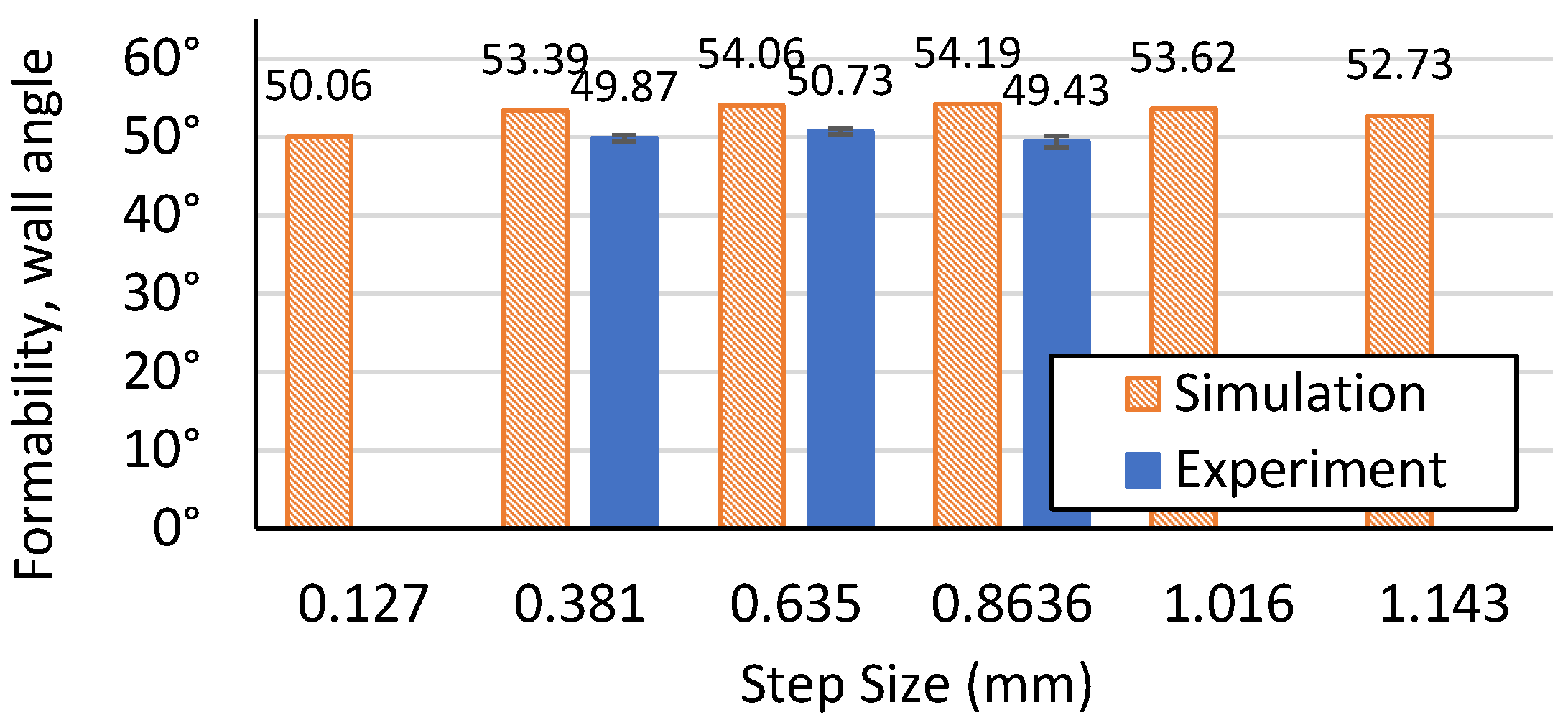
Step size ↓ [4,5,6]
Table
Table 2. Derived results from [56].
Table 2. Derived results from [56].
Step Size (mm)Feed Rate (mm/min)Tool Radius (mm)Formability
0.38138104.762567.9°
0.63567.6°
0.863667.3°
1.14367.0°
Table
Table 3. Material properties used in the simulation.
Table 3. Material properties used in the simulation.
Ultimate tensile strength483 MPa [71]
Tensile yield strength345 MPa [71]
Percent elongation18% [72]
Modulus of elasticity73.1 GPa [73]
Lankford parameters, r 00 , r 45 , r 90 0.75, 1.05, 0.682
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Grimm, T.J.; Colombini, F.; Ragai, I. Numerical Investigation of Step Size Effect on Formability of 2024-T3 Aluminum in Incremental Forming. J. Manuf. Mater. Process. 2023, 7, 70. https://doi.org/10.3390/jmmp7020070

AMA Style

Grimm TJ, Colombini F, Ragai I. Numerical Investigation of Step Size Effect on Formability of 2024-T3 Aluminum in Incremental Forming. Journal of Manufacturing and Materials Processing. 2023; 7(2):70. https://doi.org/10.3390/jmmp7020070

Chicago/Turabian Style

Grimm, Tyler J., Filipe Colombini, and Ihab Ragai. 2023. "Numerical Investigation of Step Size Effect on Formability of 2024-T3 Aluminum in Incremental Forming" Journal of Manufacturing and Materials Processing 7, no. 2: 70. https://doi.org/10.3390/jmmp7020070

APA Style

Grimm, T. J., Colombini, F., & Ragai, I. (2023). Numerical Investigation of Step Size Effect on Formability of 2024-T3 Aluminum in Incremental Forming. Journal of Manufacturing and Materials Processing, 7(2), 70. https://doi.org/10.3390/jmmp7020070

Article Metrics

Back to TopTop