A Ray Tracing Model for Electron Optical Imaging in Electron Beam Powder Bed Fusion
Abstract
:1. Introduction
2. Materials and Methods
2.1. ELO Ray Tracing Model
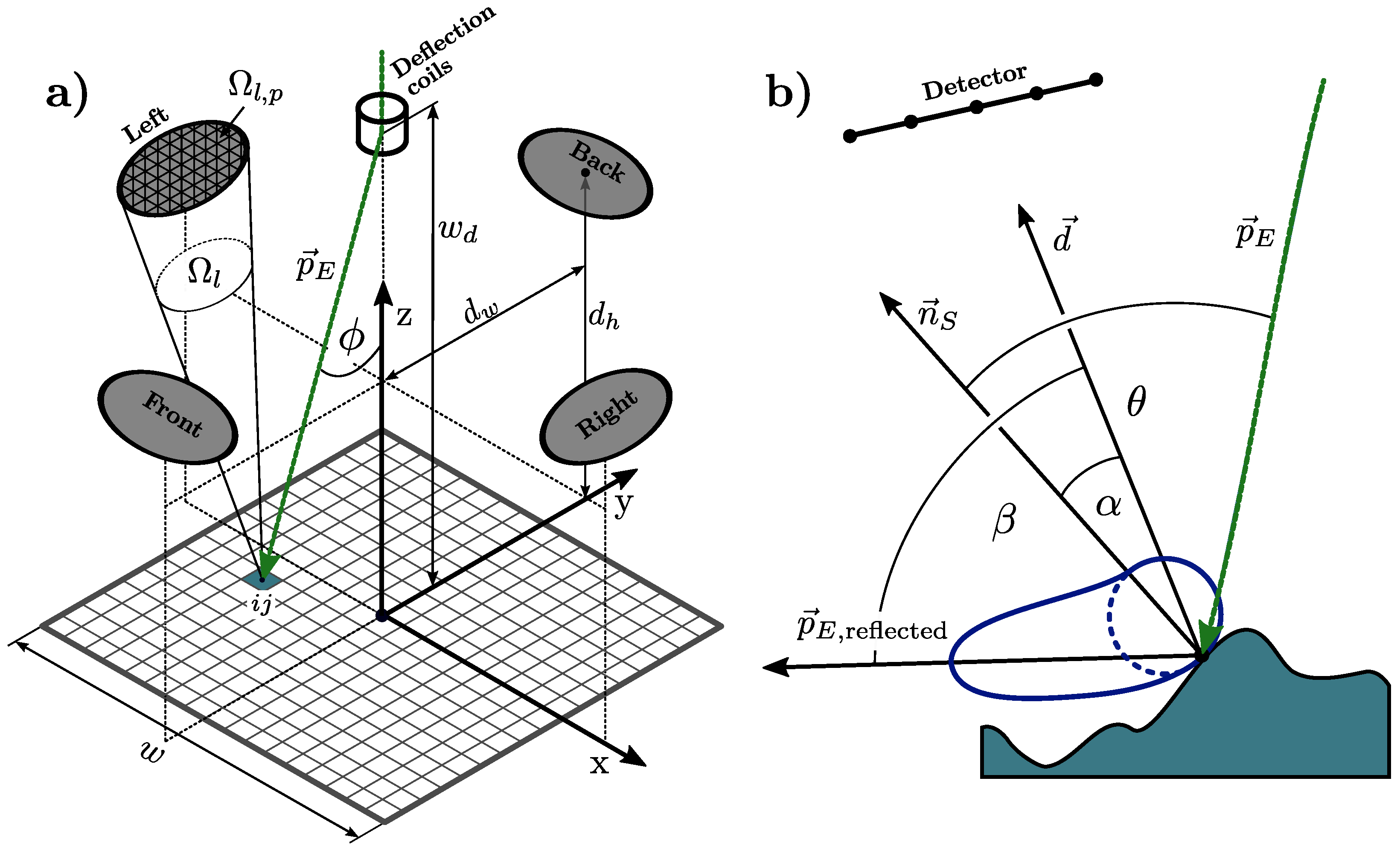
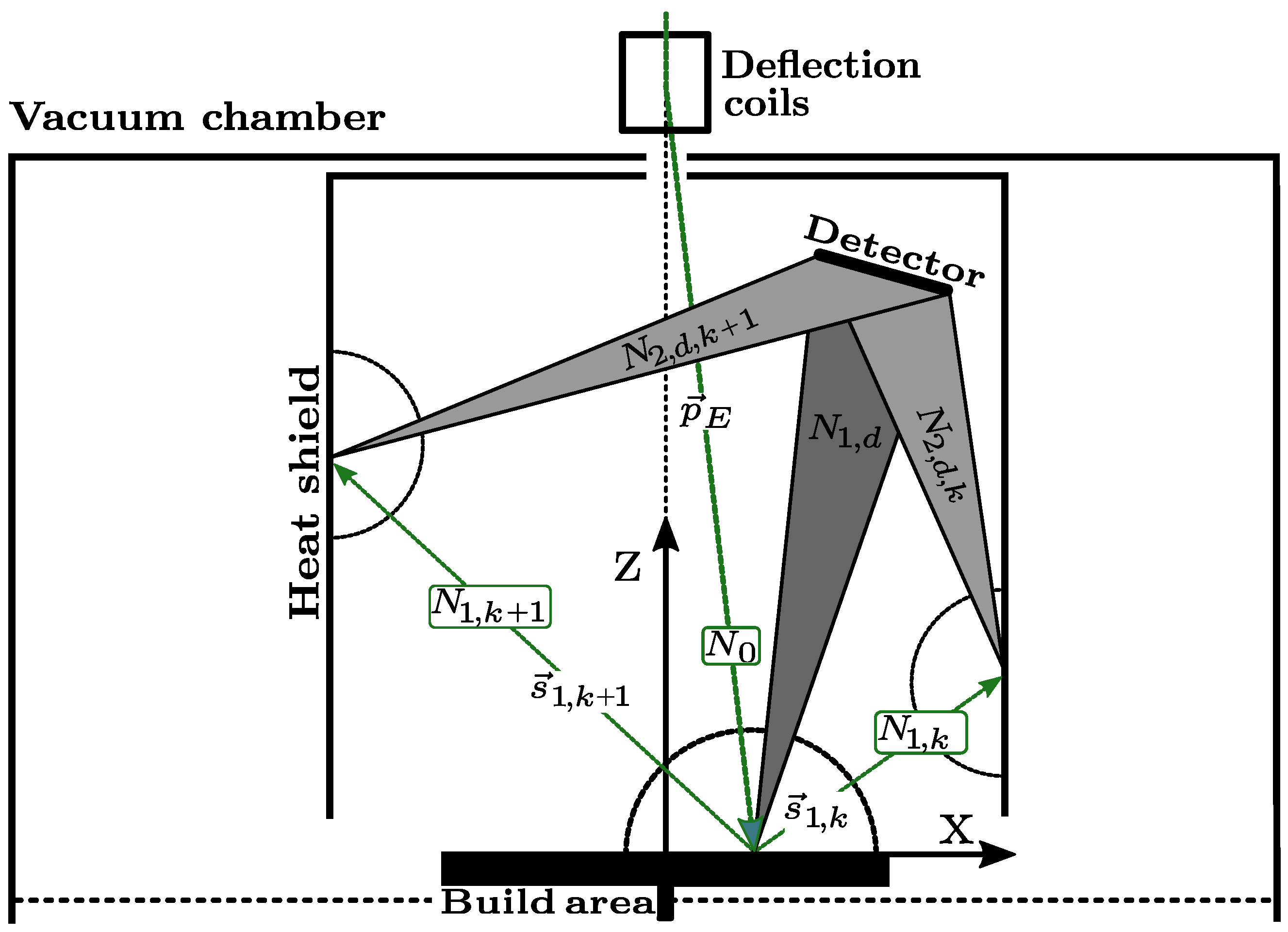
2.1.1. Model Definition
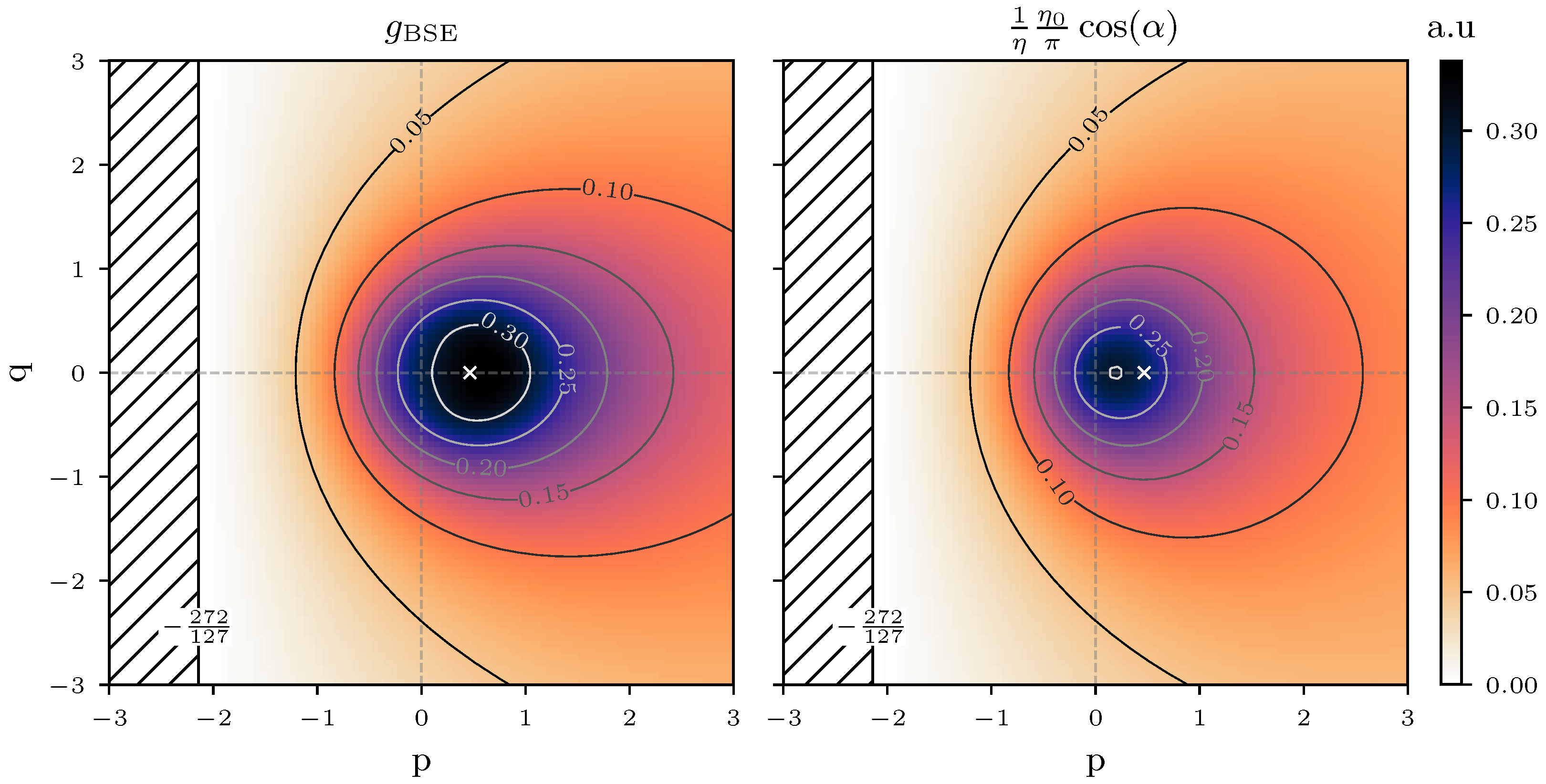
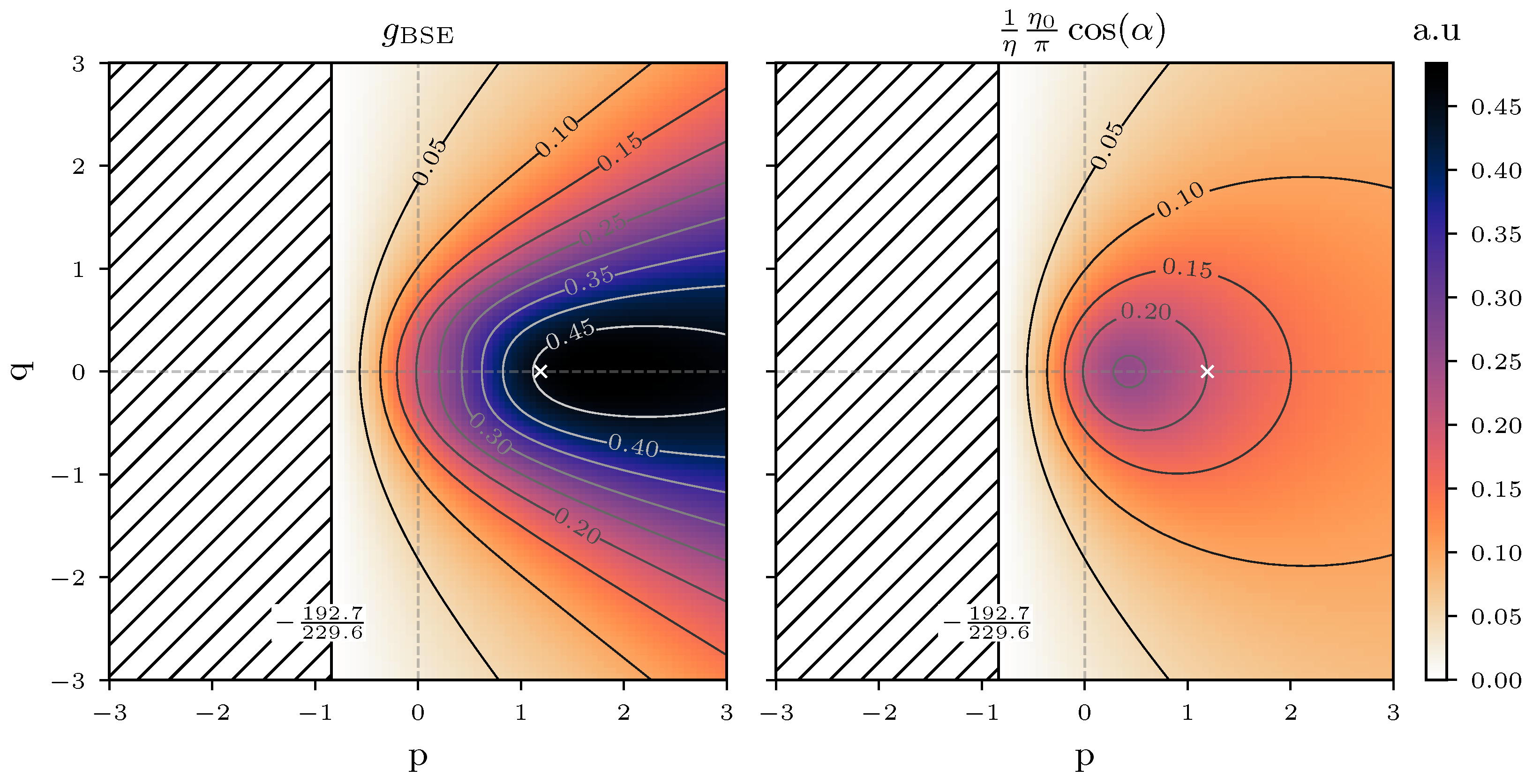
2.1.2. Back Scattered Electrons (BSE) Coefficient
2.1.3. Scattering Function
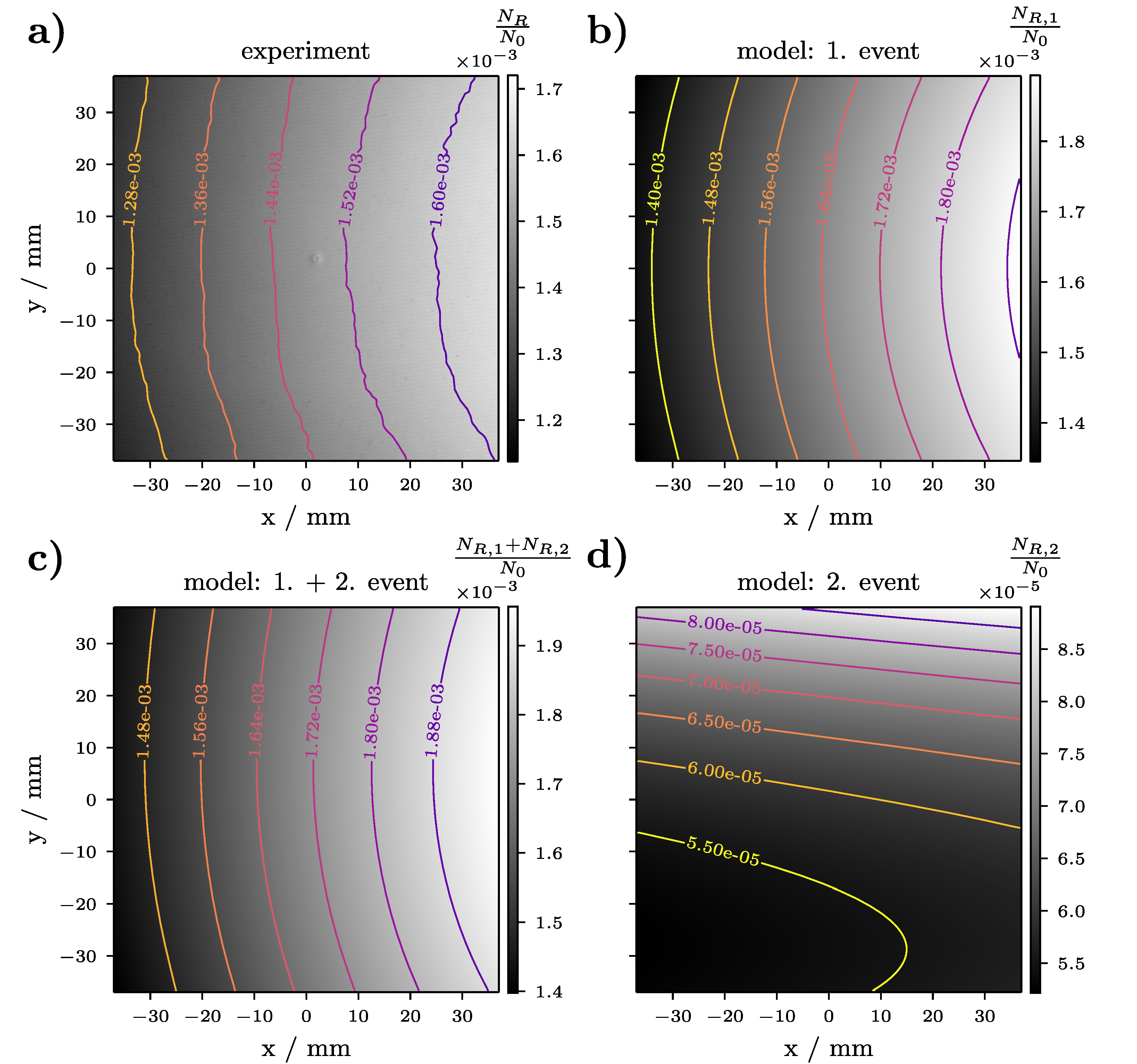
2.1.4. Surface Tilt and Solid Angle (STSA) Contrast Correction, Normalised Difference Images and Surface Gradient
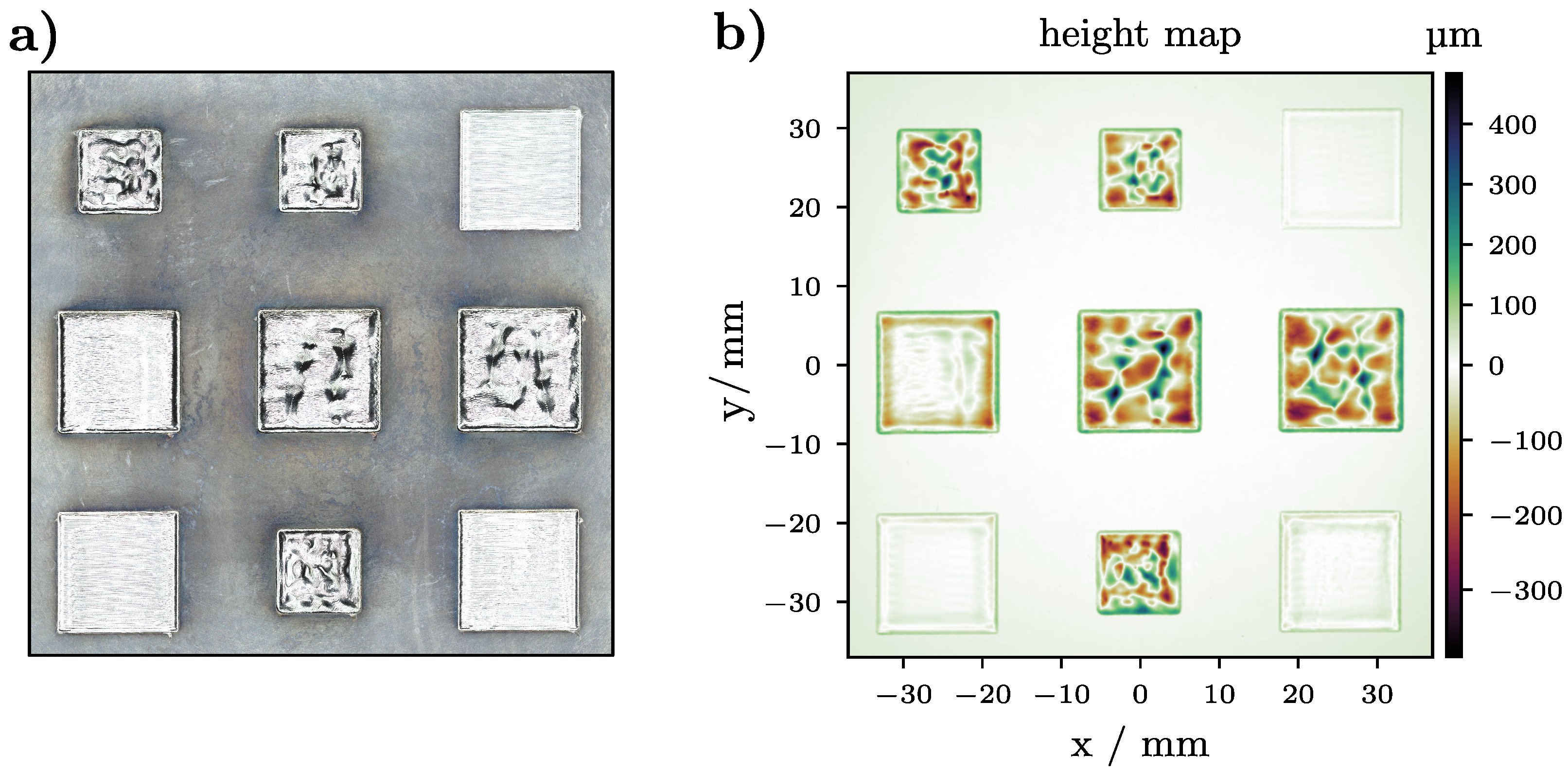
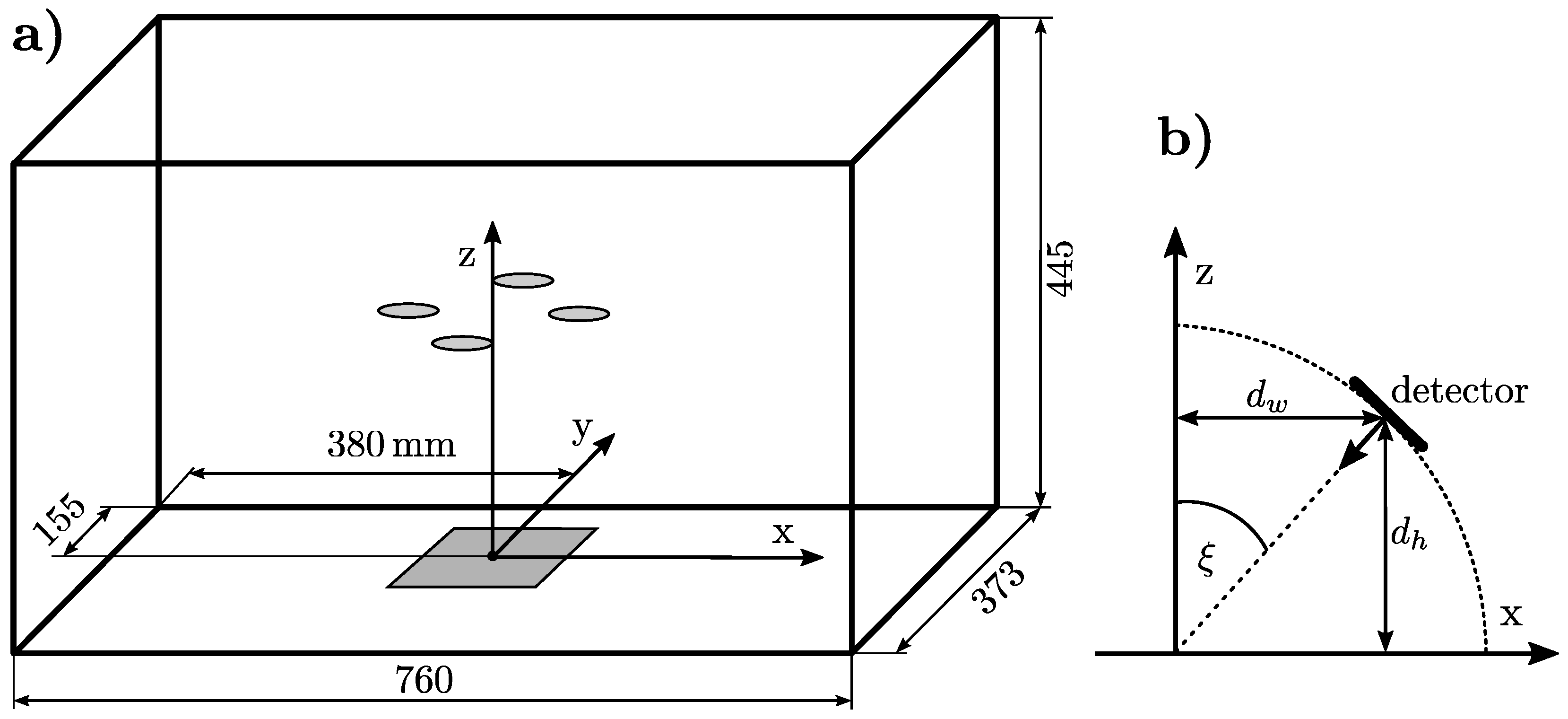
2.2. Validation Experiments
2.3. Software
2.4. Simulations
Validation
3. Results
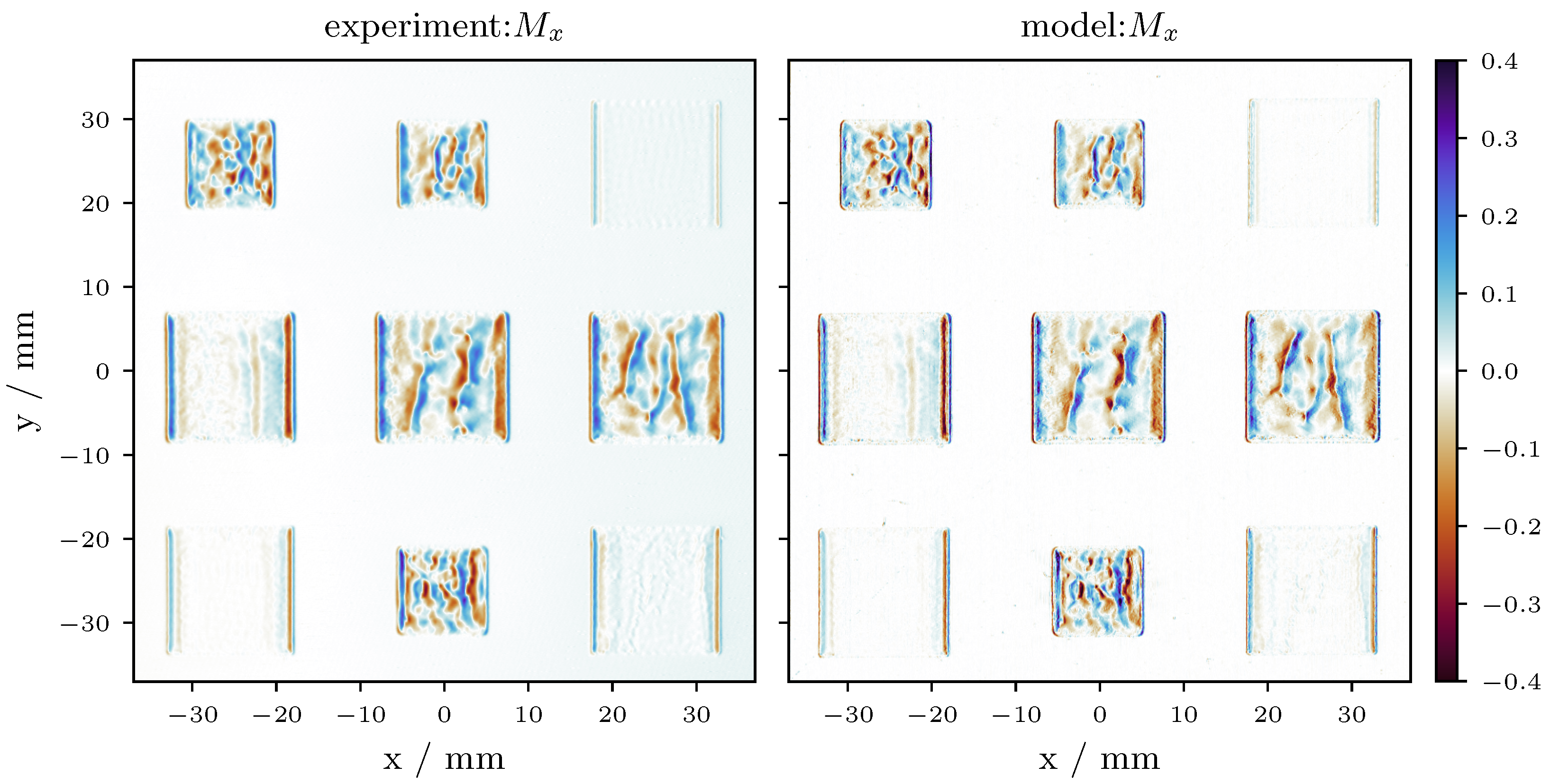
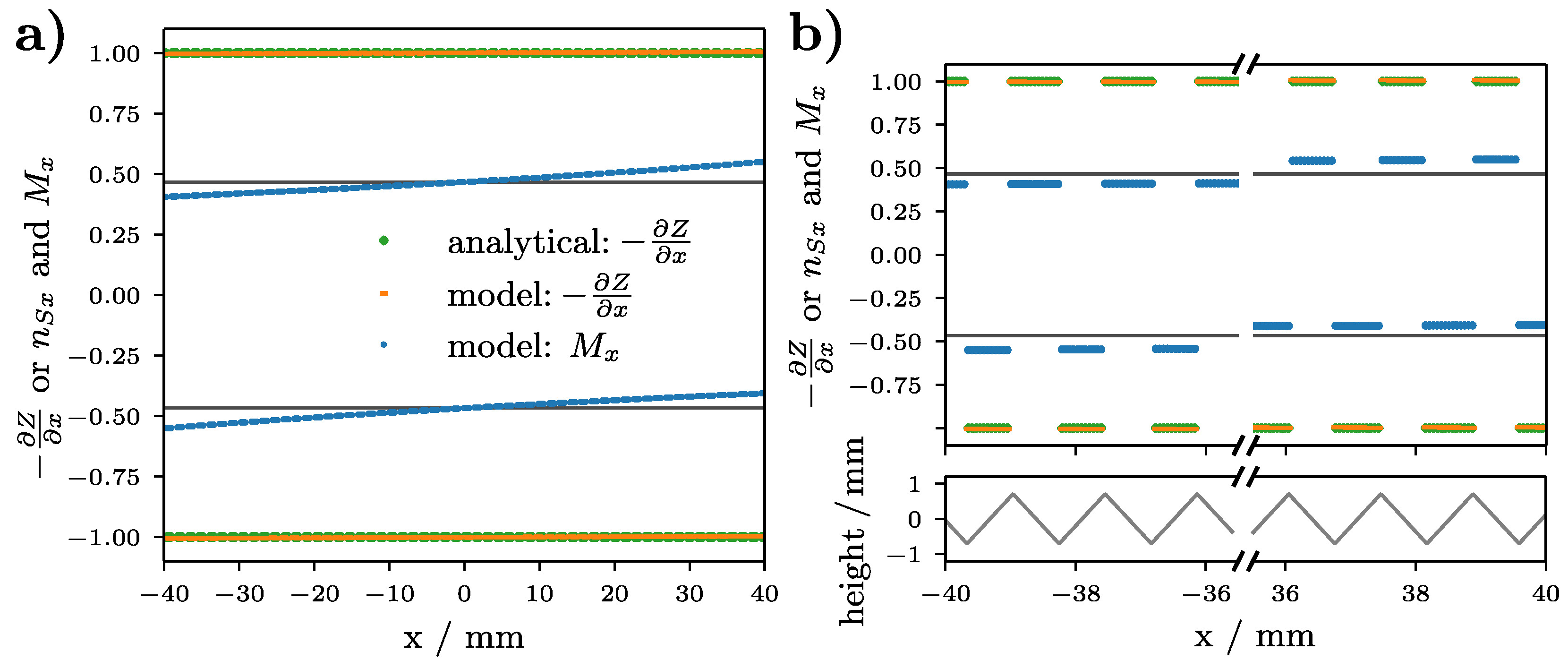
3.1. Validation: STSA Contrast
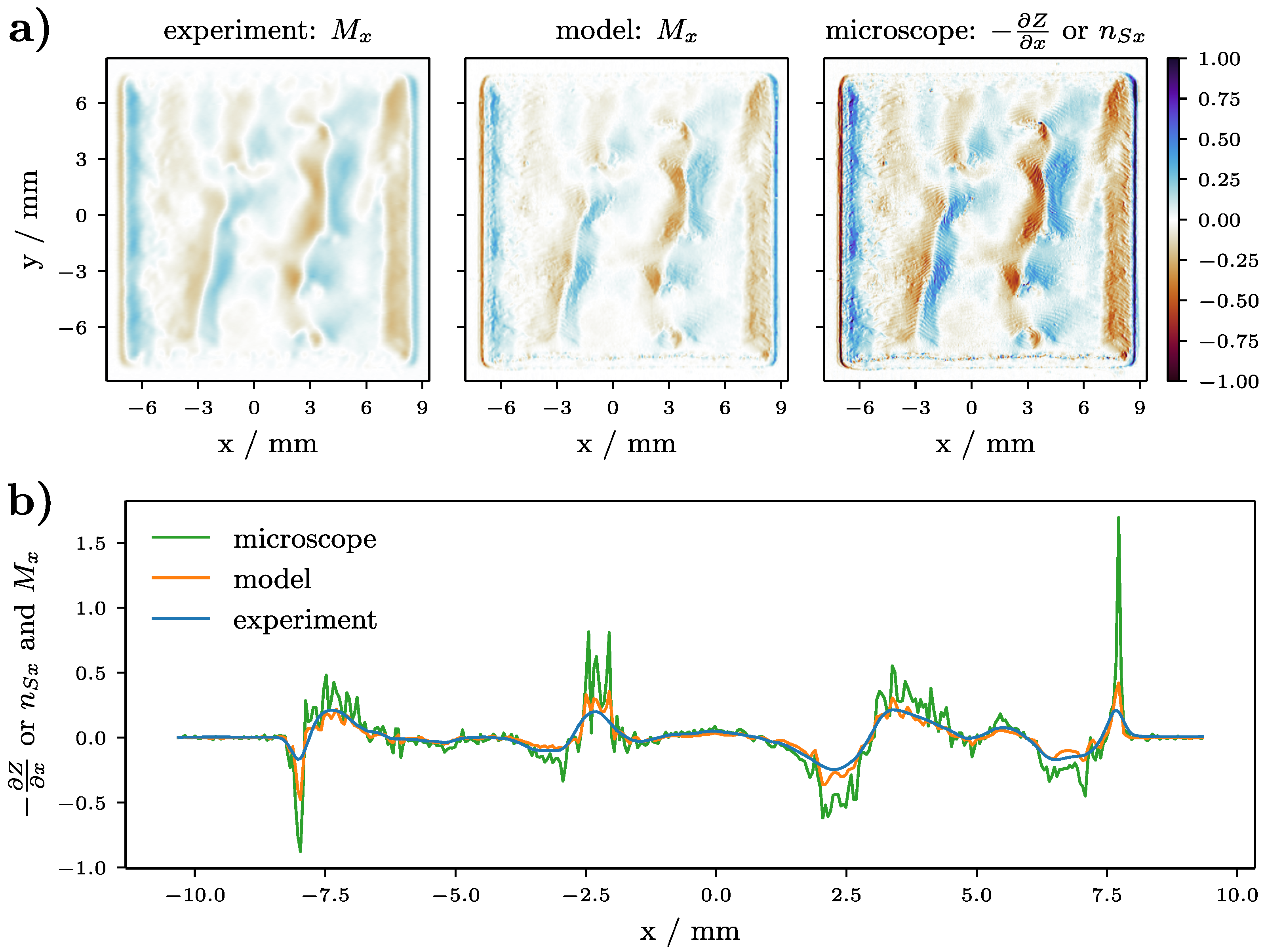
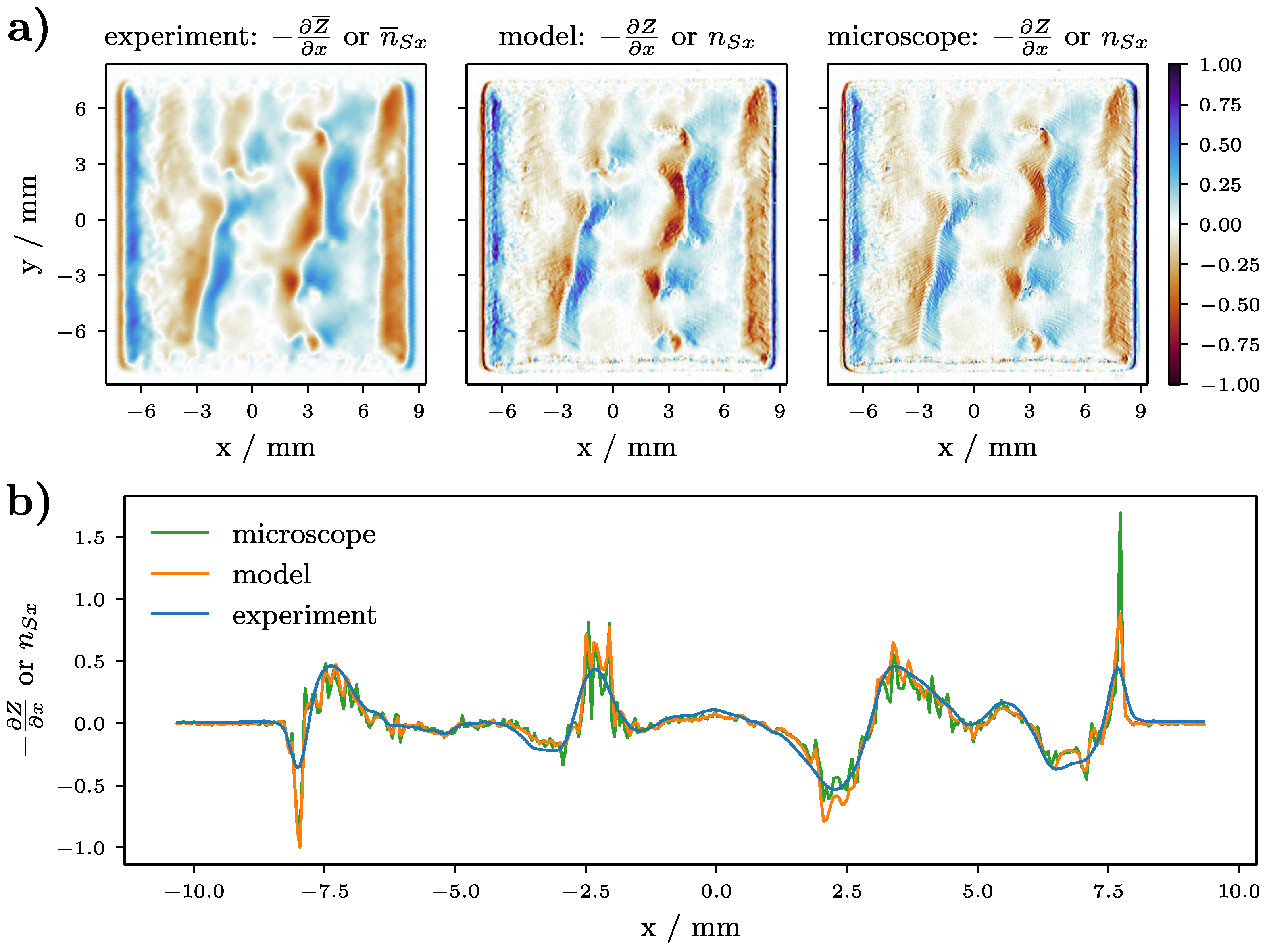
3.2. Validation: Melt Plate
4. Discussion
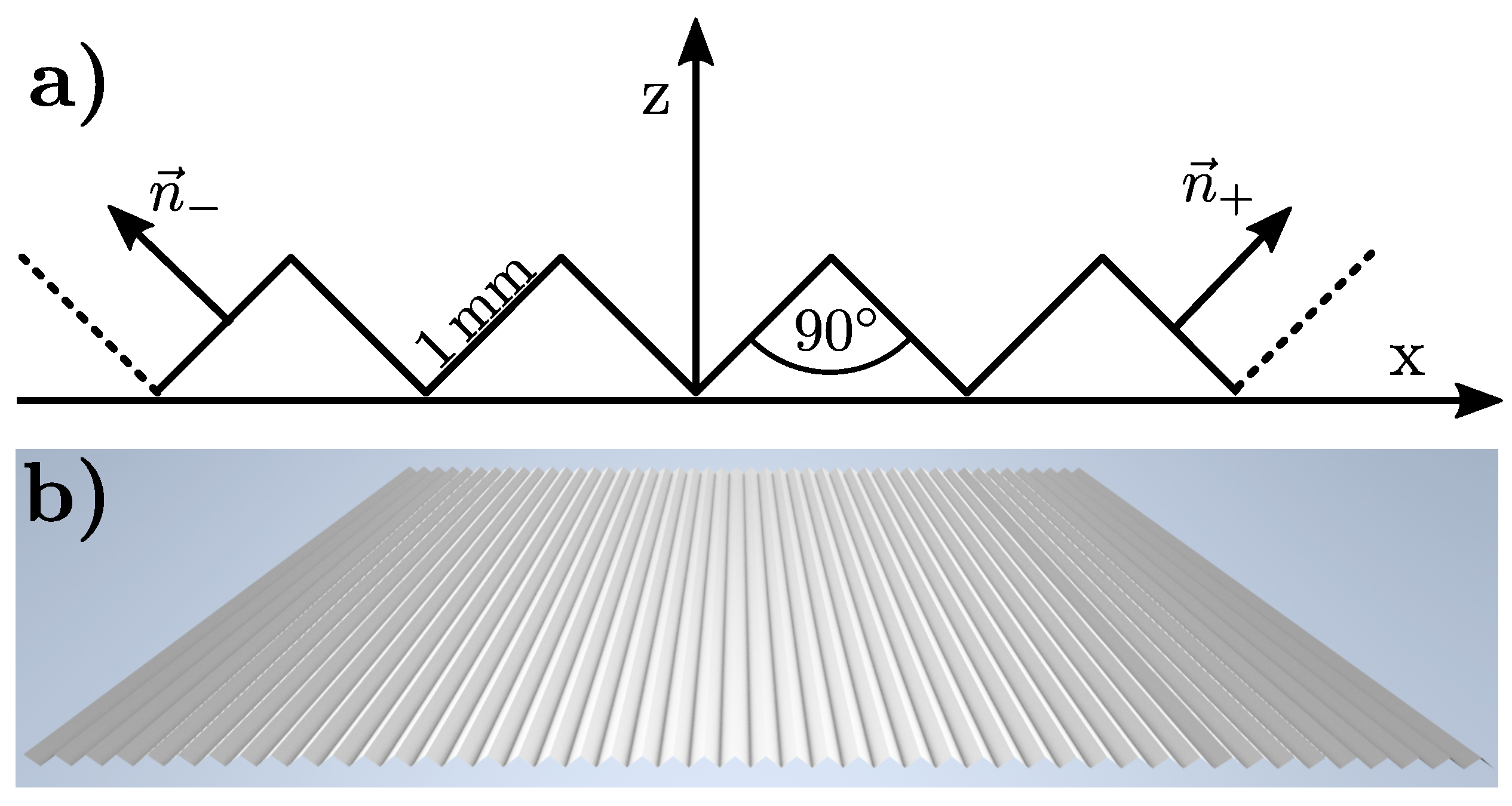
4.1. Distortion Effects in Gradient Computation
4.2. Correct Gradient Computation
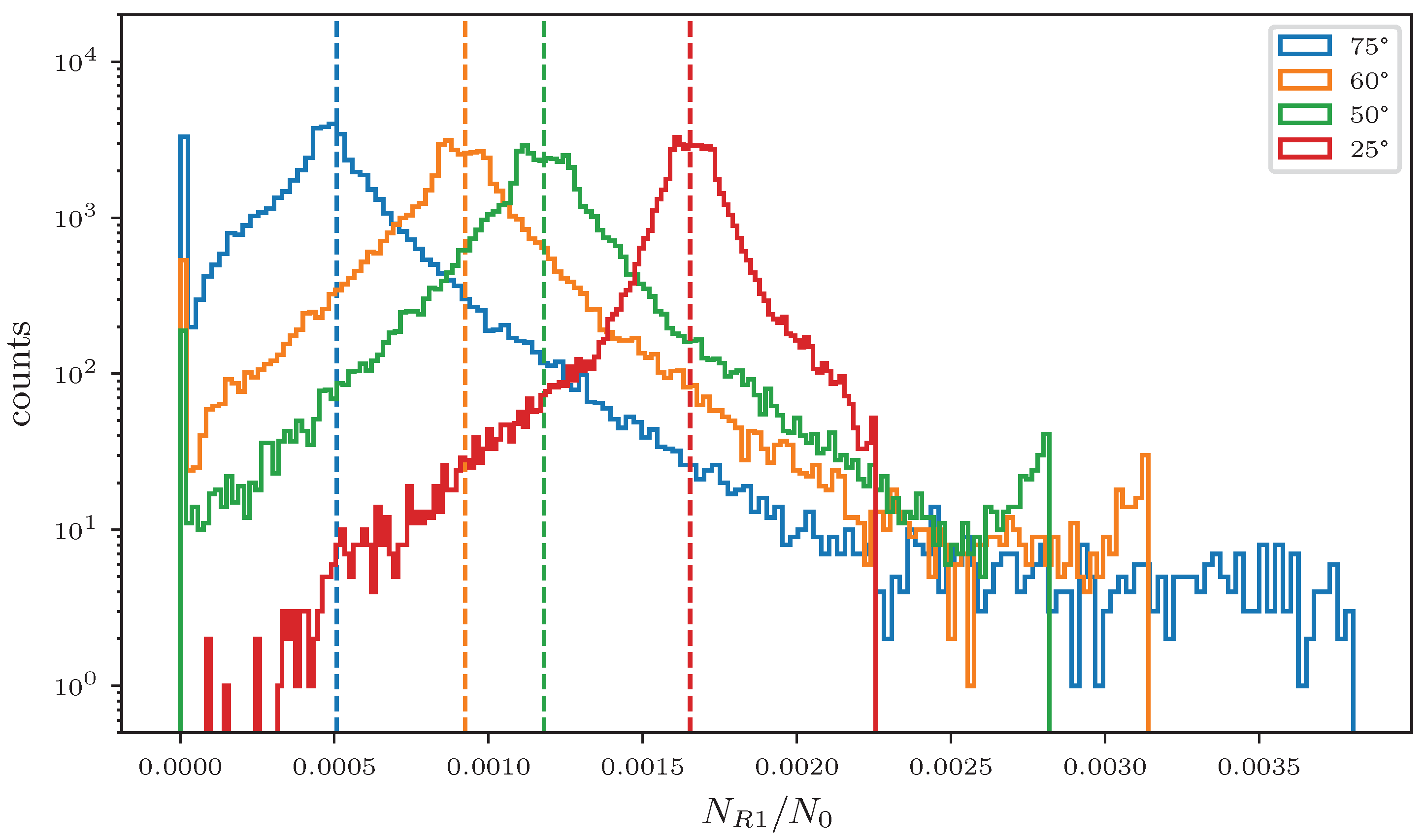
4.3. Scattering Function, Detector Positioning and Masking
4.4. Masking and Contrast in PBF-EB
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Integrals over Solid Angles
Appendix B. Treatment of SE
References
- Ramirez, D.; Murr, L.; Li, S.; Tian, Y.; Martinez, E.; Martinez, J.; Machado, B.; Gaytan, S.; Medina, F.; Wicker, R. Open-Cellular Copper Structures Fabricated by Additive Manufacturing Using Electron Beam Melting. Mater. Sci. Eng. A 2011, 528, 5379–5386. [Google Scholar] [CrossRef]
- Blachowicz, T.; Ehrmann, G.; Ehrmann, A. Metal Additive Manufacturing for Satellites and Rockets. Appl. Sci. 2021, 11, 12036. [Google Scholar] [CrossRef]
- Kiener, L.; Saudan, H.; Cosandier, F.; Perruchoud, G.; Spanoudakis, P. Innovative Concept of Compliant Mechanisms Made by Additive Manufacturing. MATEC Web Conf. 2019, 304, 07002. [Google Scholar] [CrossRef]
- Leach, R.K.; Carmignato, S. (Eds.) Precision Additive Metal Manufacturing, 1st ed.; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Pobel, C.R.; Arnold, C.; Osmanlic, F.; Fu, Z.; Körner, C. Immediate Development of Processing Windows for Selective Electron Beam Melting Using Layerwise Monitoring via Backscattered Electron Detection. Mater. Lett. 2019, 249, 70–72. [Google Scholar] [CrossRef]
- Arnold, C.; Pobel, C.; Osmanlic, F.; Körner, C. Layerwise Monitoring of Electron Beam Melting via Backscatter Electron Detection. Rapid Prototyp. J. 2018, 24, 1401–1406. [Google Scholar] [CrossRef]
- Arnold, C.; Breuning, C.; Körner, C. Electron-Optical In Situ Imaging for the Assessment of Accuracy in Electron Beam Powder Bed Fusion. Materials 2021, 14, 7240. [Google Scholar] [CrossRef]
- Wong, H. Pilot Investigation of Surface-Tilt and Gas Amplification Induced Contrast during Electronic Imaging for Potential In-Situ Electron Beam Melting Monitoring. Addit. Manuf. 2020, 35, 101325. [Google Scholar] [CrossRef]
- Ledford, C.; Tung, M.; Rock, C.; Horn, T. Real Time Monitoring of Electron Emissions during Electron Beam Powder Bed Fusion for Arbitrary Geometries and Toolpaths. Addit. Manuf. 2020, 34, 101365. [Google Scholar] [CrossRef]
- Zhao, D.; Lin, F. Dual-Detector Electronic Monitoring of Electron Beam Selective Melting. J. Mater. Process. Technol. 2021, 289, 116935. [Google Scholar] [CrossRef]
- Renner, J.; Breuning, C.; Markl, M.; Körner, C. Surface Topographies from Electron Optical Images in Electron Beam Powder Bed Fusion for Process Monitoring and Control. Addit. Manuf. 2022, 60, 103172. [Google Scholar] [CrossRef]
- Joy, D.C. An Introduction to Monte Carlo Simulations. Scanning Microsc. 1991, 5, 329–337. [Google Scholar]
- Yano, F.; Nomura, S. Deconvolution of Scanning Electron Microscopy Images: Deconvolution of SEM Images. Scanning 1993, 15, 19–24. [Google Scholar] [CrossRef]
- Reimer, L.; Riepenhausen, M.; Tollkamp, C. Detector Strategy for Improvement of Image Contrast Analogous to Light Illumination: Image Contrast Analogous to Light Illumination. Scanning 1984, 6, 155–167. [Google Scholar] [CrossRef]
- Goldstein, J.I.; Newbury, D.E.; Michael, J.R.; Ritchie, N.W.; Scott, J.H.J.; Joy, D.C. Scanning Electron Microscopy and X-ray Microanalysis; Springer: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Reimer, L. Scanning Electron Microscopy; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 1998; Volume 45. [Google Scholar] [CrossRef]
- Reimer, L.; Böngeler, R.; Desai, V. Shape from Shading Using Multiple Detector Signals in Scanning Electron Microscopy. Scanning Microsc. 1987, 1, 963–973. [Google Scholar]
- Pharr, M.; Jakob, W.; Humphreys, G. Physically Based Rendering, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Darlington, E.H. Backscattering of IO-108 keV Electrons from Thick Targets. J. Phys. D Appl. Phys. 1975, 8, 10. [Google Scholar] [CrossRef]
- Herrmann, R.; Reimer, L. Backscattering Coefficient of Multicomponent Specimens. Scanning 1984, 6, 20–29. [Google Scholar] [CrossRef]
- Castaing, R. Electron Probe Microanalysis. Adv. Electron. Electron Phys. 1960, 13, 317–386. [Google Scholar]
- Darliński, A. Measurements of Angular Distribution of the Backscattered Electrons in the Energy Range of 5 to 30 keV. Phys. Status Solidi A 1981, 63, 663–668. [Google Scholar] [CrossRef]
- Niedrig, H. Physical Background of Electron Backscattering. Scanning 1978, 1, 17–34. [Google Scholar] [CrossRef]
- Berger, D.; Niedrig, H. Complete Angular Distribution of Electrons Backscattered from Tilted Multicomponent Specimens: Electron Backscattering from Compounds. Scanning 1999, 21, 187–190. [Google Scholar] [CrossRef]
- Phong, B.T. Illumination for Computer Generated Pictures. Commun. ACM 1975, 18, 311–317. [Google Scholar] [CrossRef]
- Reimer, L.; Riepenhausen, M. Detector Strategy for Secondary and Backscattered Electrons Using Multiple Detector Systems: Detector Strategy Using Multiple Detector Systems. Scanning 1985, 7, 221–238. [Google Scholar] [CrossRef]
- Lafortune, E.P.; Willems, Y.D.; Cw, R. Using the Modified Phong Reflectance Model for Physically Based Rendering; Katholieke Universiteit Leuven, Departement Computerwetenschappen: Leuven, Belgium, 1994. [Google Scholar]
- Quéau, Y.; Durou, J.D.; Aujol, J.F. Normal Integration: A Survey. J. Math. Imaging Vis. 2018, 60, 576–593. [Google Scholar] [CrossRef]
- Horn, B.; Klaus, B.; Horn, P. Robot Vision; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Zhou, Q.Y.; Park, J.; Koltun, V. Open3D: A Modern Library for 3D Data Processing. arXiv 2018, arXiv:1801.09847. [Google Scholar]
- Dawson-Haggerty. Trimesh. 2019. Available online: https://github.com/mikedh/trimesh (accessed on 31 March 2023).
- van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikit-Image: Image Processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- van der Velden, E. CMasher: Scientific Colormaps for Making Accessible, Informative and ‘cmashing’ Plots. J. Open Source Softw. 2020, 5, 2004. [Google Scholar] [CrossRef]
- Argyriou, V.; Petrou, M. Chapter 1 Photometric Stereo: An Overview. In Advances in Imaging and Electron Physics; Elsevier: Amsterdam, The Netherlands, 2009; Volume 156, pp. 1–54. [Google Scholar] [CrossRef]
- Paxton, F. Solid Angle Calculation for a Circular Disk. Rev. Sci. Instrum. 1959, 30, 254–258. [Google Scholar] [CrossRef]
- Van Oosterom, A.; Strackee, J. The Solid Angle of a Plane Triangle. IEEE Trans. Biomed. Eng. 1983, BME-30, 125–126. [Google Scholar] [CrossRef] [PubMed]

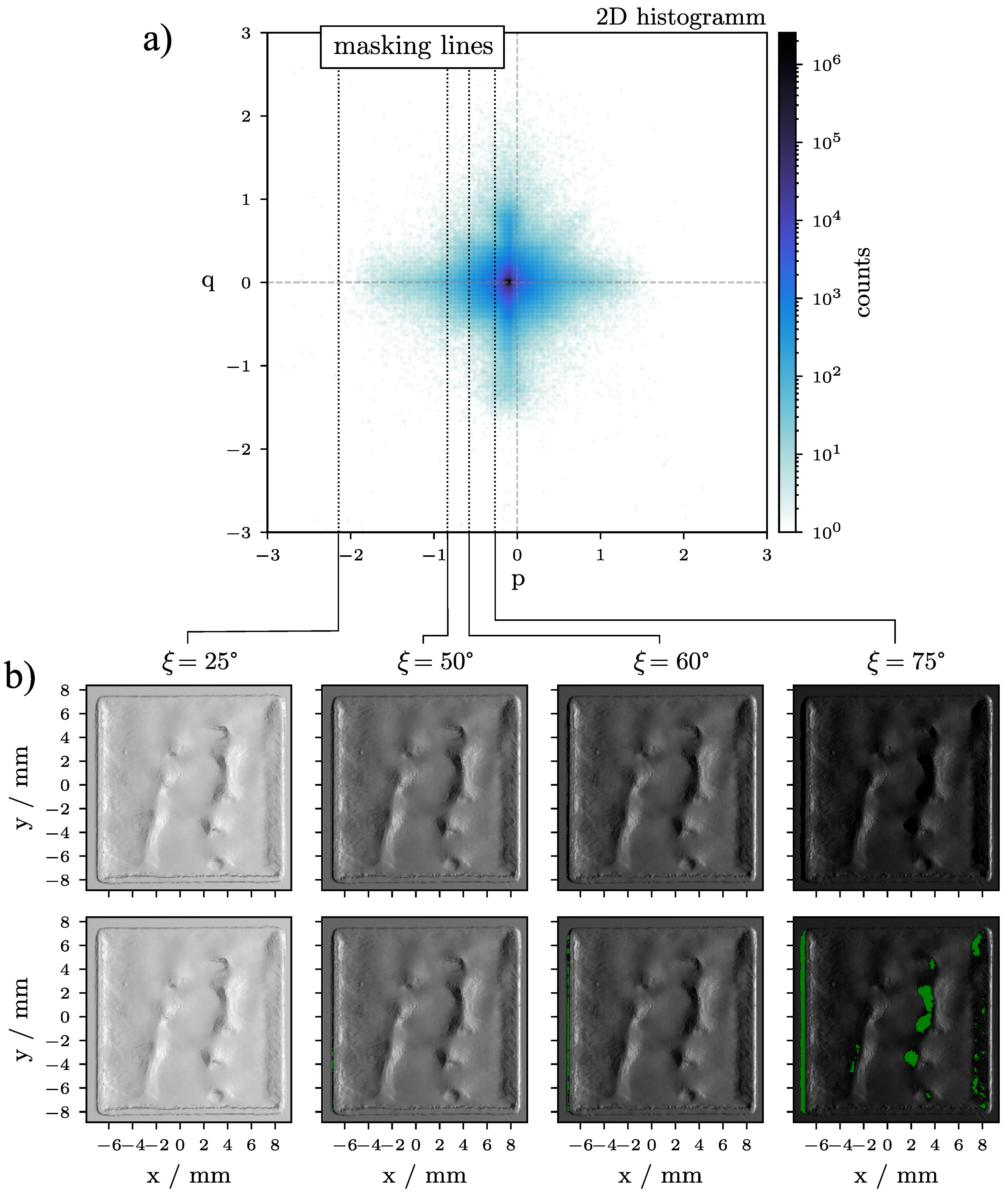
| /mm | /mm | / |
|---|---|---|
| 272.0 | 127.0 | 25.0 |
| 192.7 | 229.6 | 50.0 |
| 149.9 | 259.6 | 60.0 |
| 77.6 | 289.6 | 75.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Renner, J.; Grund, J.; Markl, M.; Körner, C. A Ray Tracing Model for Electron Optical Imaging in Electron Beam Powder Bed Fusion. J. Manuf. Mater. Process. 2023, 7, 87. https://doi.org/10.3390/jmmp7030087
Renner J, Grund J, Markl M, Körner C. A Ray Tracing Model for Electron Optical Imaging in Electron Beam Powder Bed Fusion. Journal of Manufacturing and Materials Processing. 2023; 7(3):87. https://doi.org/10.3390/jmmp7030087
Chicago/Turabian StyleRenner, Jakob, Julian Grund, Matthias Markl, and Carolin Körner. 2023. "A Ray Tracing Model for Electron Optical Imaging in Electron Beam Powder Bed Fusion" Journal of Manufacturing and Materials Processing 7, no. 3: 87. https://doi.org/10.3390/jmmp7030087
APA StyleRenner, J., Grund, J., Markl, M., & Körner, C. (2023). A Ray Tracing Model for Electron Optical Imaging in Electron Beam Powder Bed Fusion. Journal of Manufacturing and Materials Processing, 7(3), 87. https://doi.org/10.3390/jmmp7030087








