A Thermo-Structural Analysis of Die-Sinking Electrical Discharge Machining (EDM) of a Haynes-25 Super Alloy Using Deep-Learning-Based Methodologies
Abstract
:1. Introduction
2. Literature Review
Identified Research Gaps
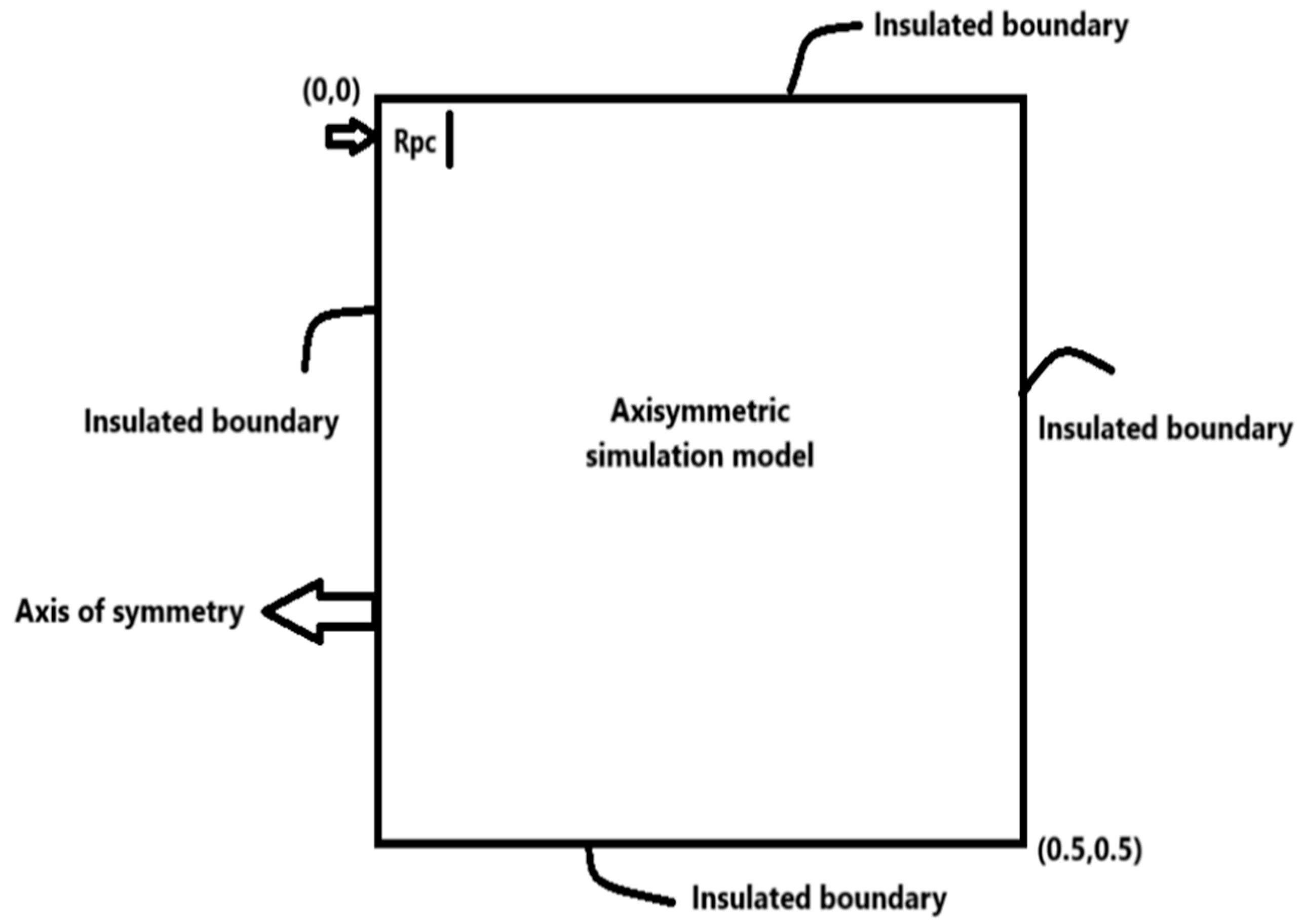
3. Methodology and Technical Specifications
3.1. Procedure Overview
3.2. Experimental Methodology
3.3. Workpiece Material Properties
3.4. Tool Material Properties
3.5. Governing Equations
3.6. Design Approach Details
3.7. Assumptions in the Proposed Model
- Both the tool and substrate materials demonstrate isotropy and homogeneity in their microstructures.
- The predominant mode of heat transfer from the plasma to the electrodes during the EDM process is conduction. Simultaneously, radiation and convection contribute significantly to the heat transfer from the plasma to the dielectric. In the present inquiry, it is postulated that conduction serves as the predominant means of heat transfer from the plasma to the electrodes.
- It is assumed that the radius of the spark produced during EDM is a function of the spark duration and discharge current.
- A Gaussian distribution is applied to the heat flux, and it is supposed that the area where the spark is applied possesses axisymmetric properties.
- The workpiece is effectively exposed to only a small portion of the applied spark energy, with the remainder being lost due to dielectric convection and radiation.
4. Results and Discussion
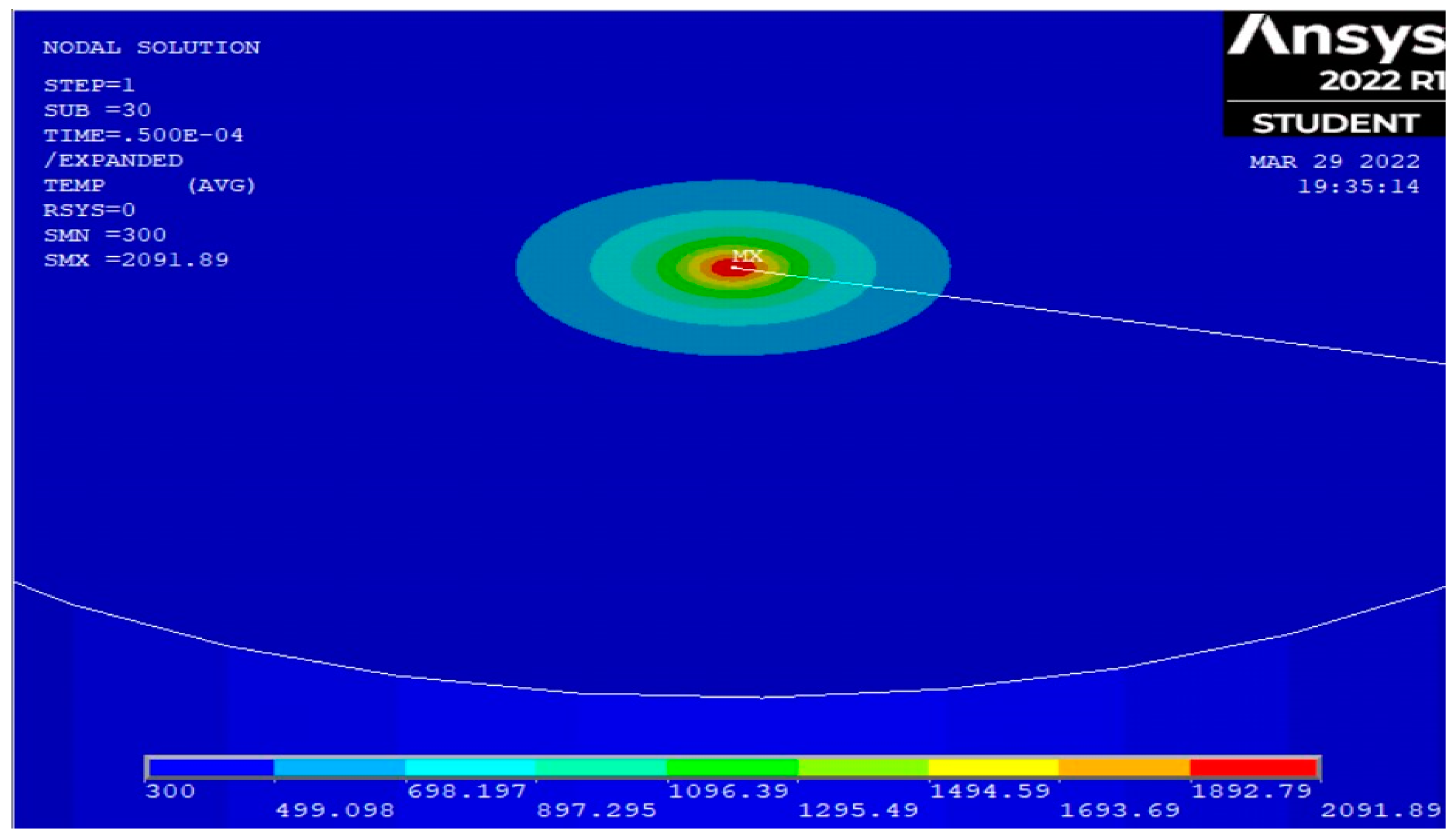
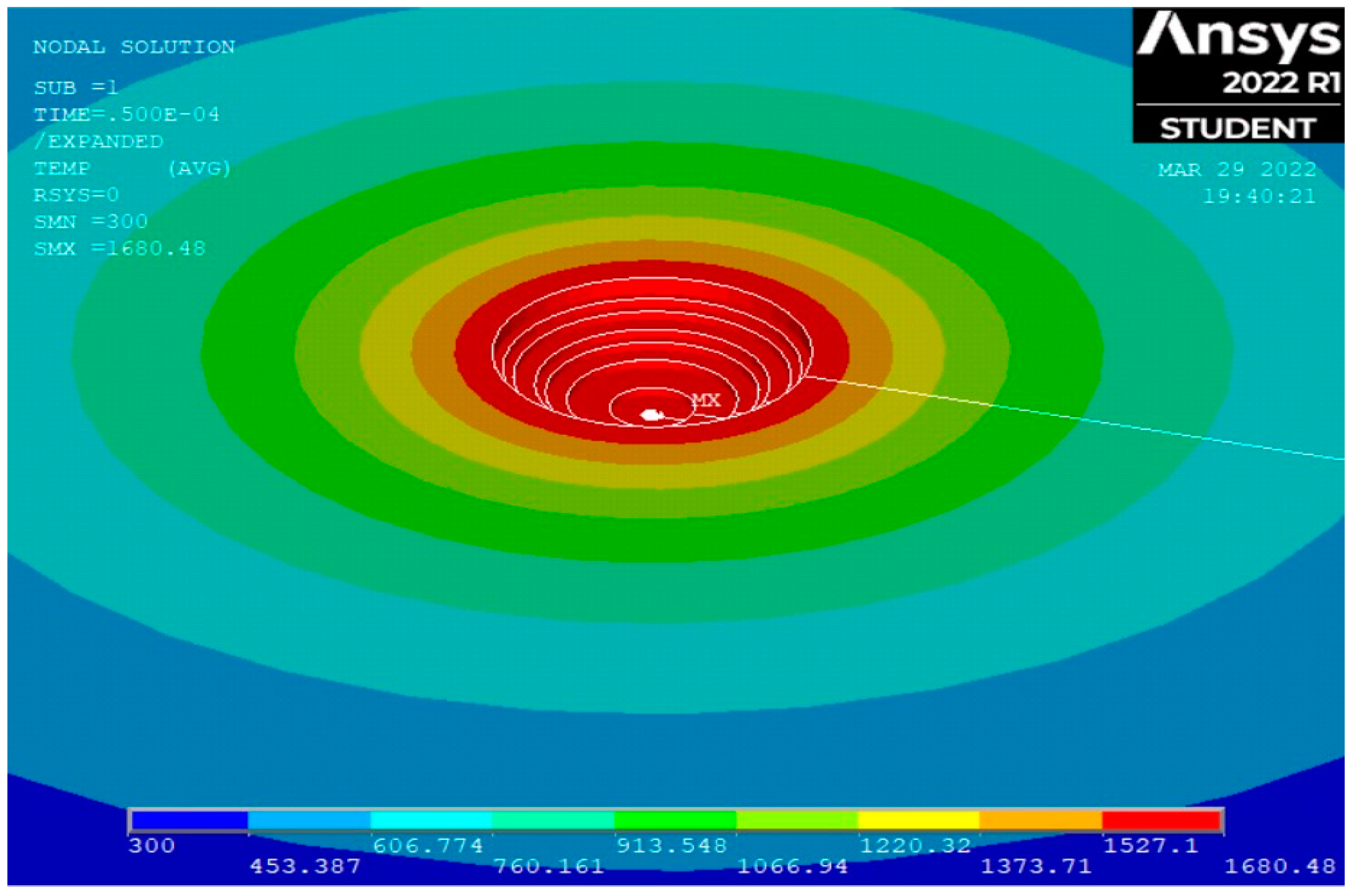
4.1. Simulation Results
4.2. Residual Stresses Occurring in the Workpiece
4.3. Experimentation
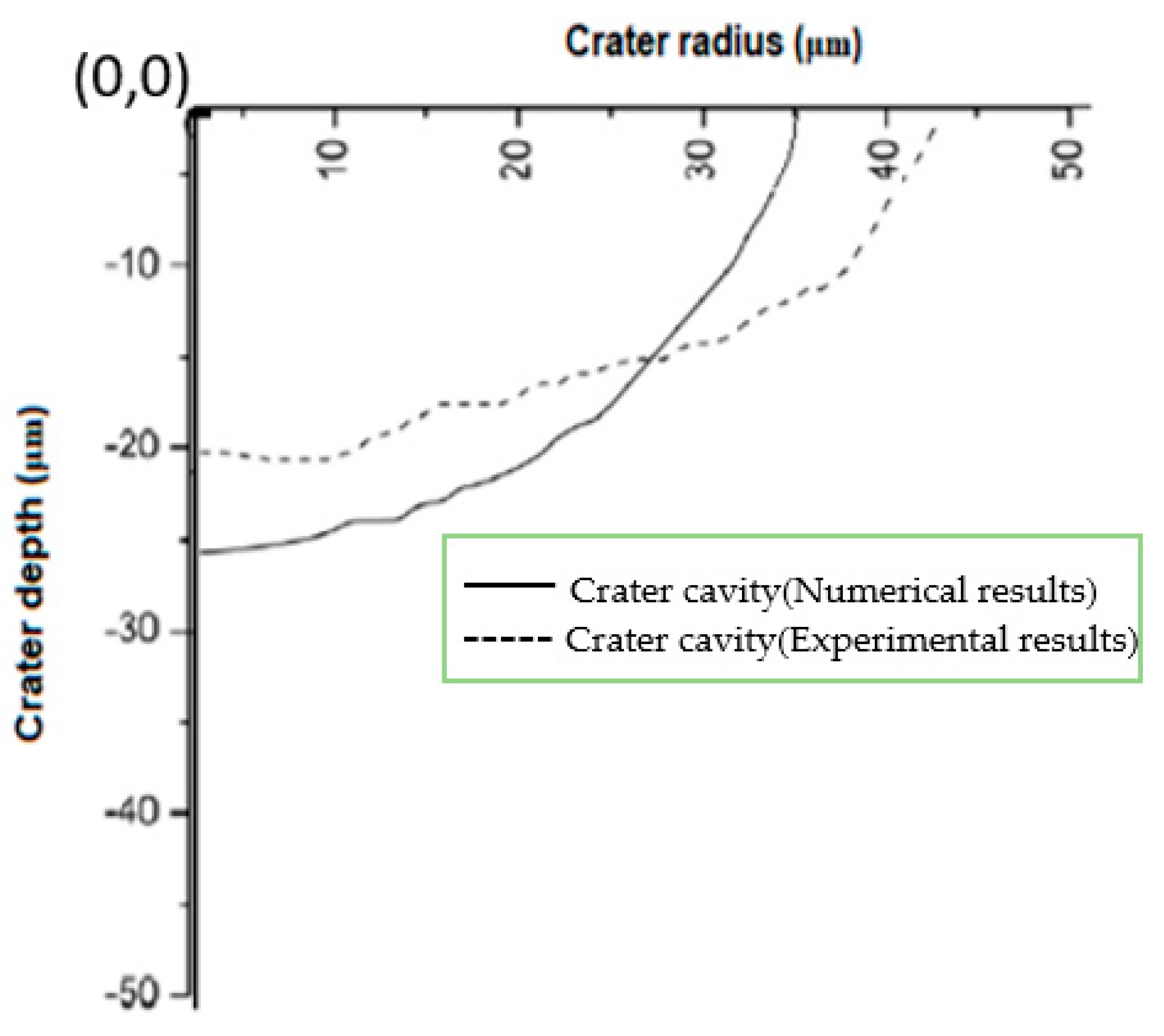
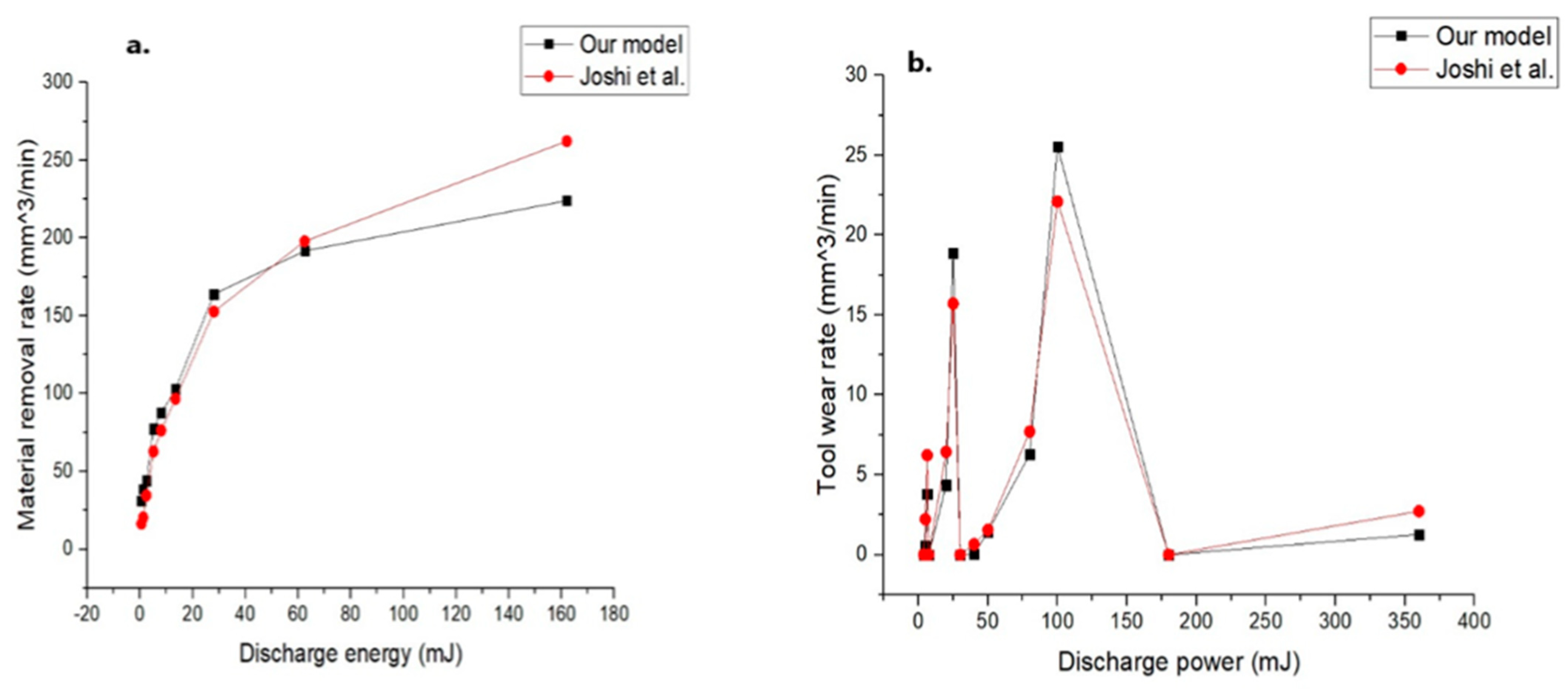
4.4. Model Validation with Experimentation
4.5. Model Validation with Prior Reputed Research Works
5. Parametric Studies on the Proposed Thermo-Structural Model
- Discharge current: 5 A, 15 A, 25 A, 35 A, 45 A;
- Spark on time (ton): 50 μs, 100 μs, 300 μs, 500 μs, 700 μs;
- Discharge voltage: 20 V, 30 V, 40 V, 50 V, 60 V;
- Duty factor: 65%, 80%, 95%.
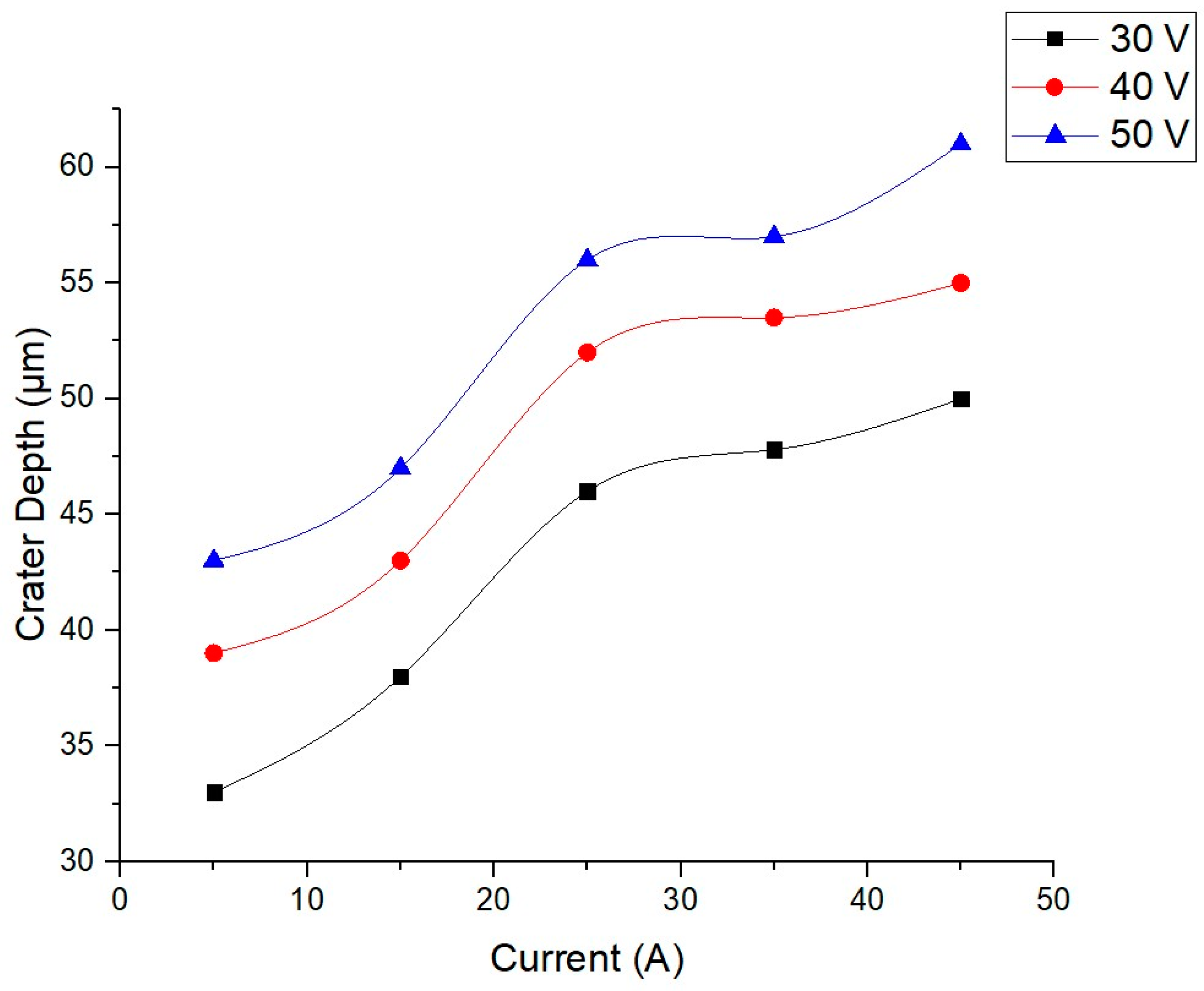
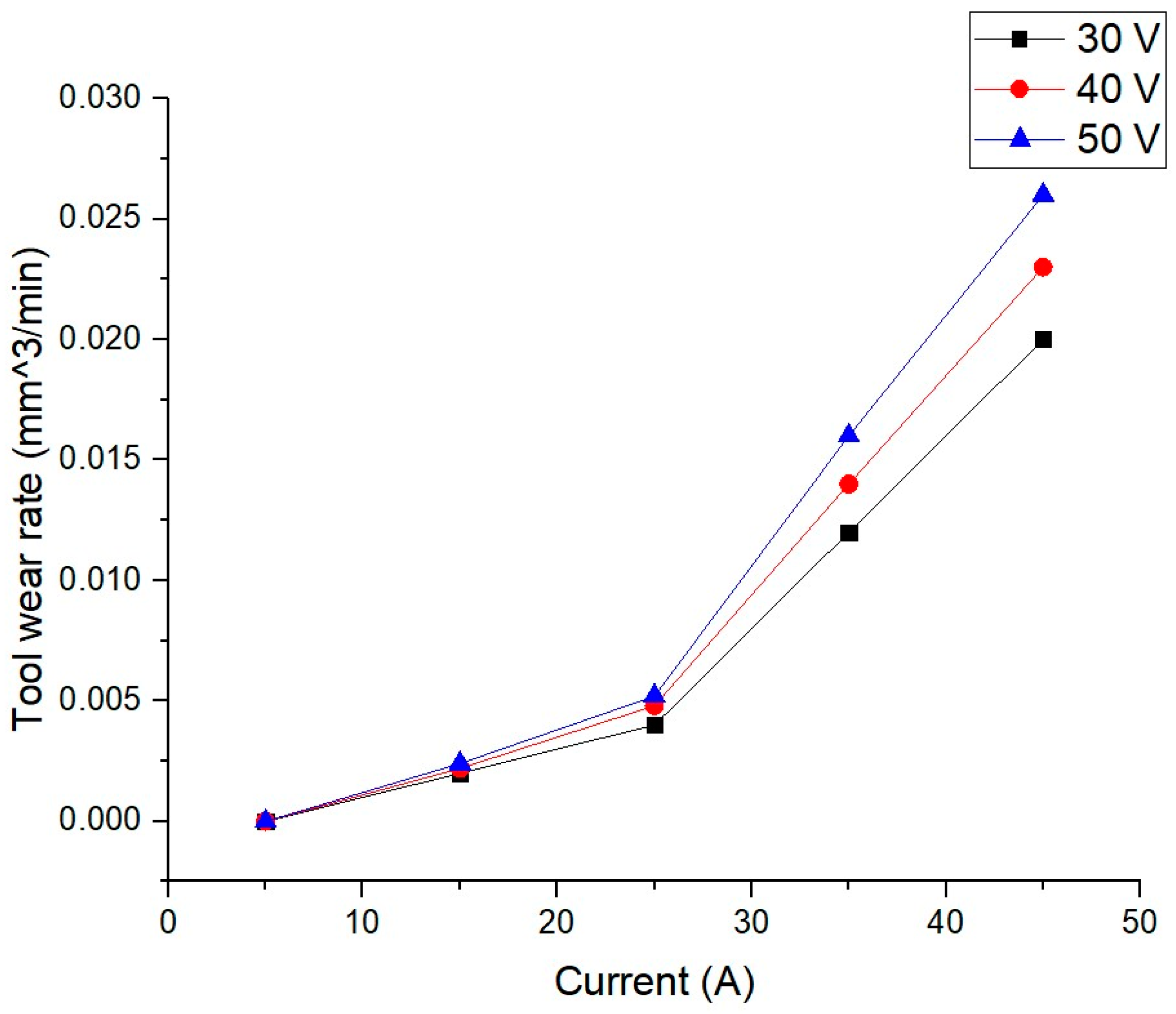
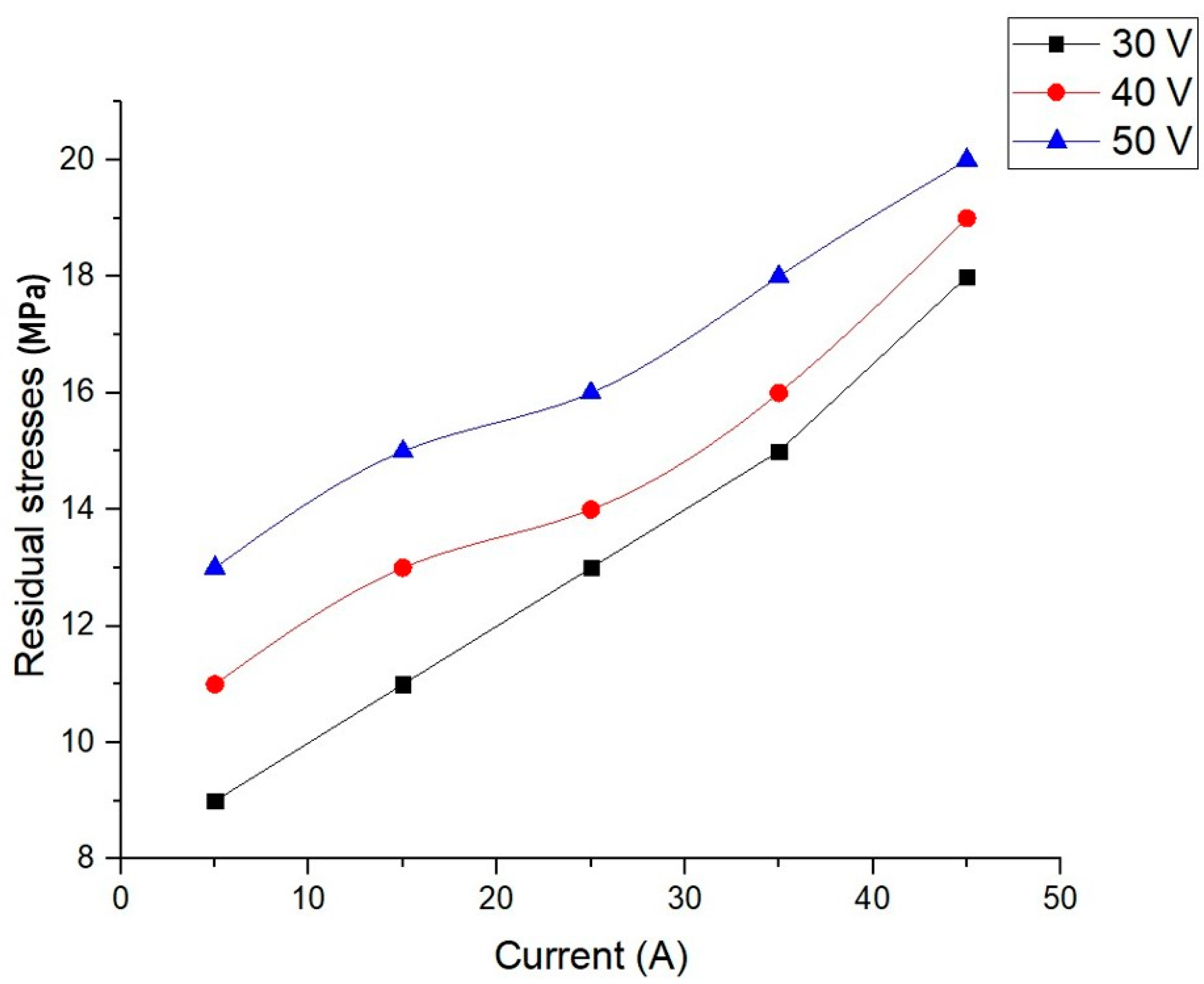
5.1. Effect of Discharge Current
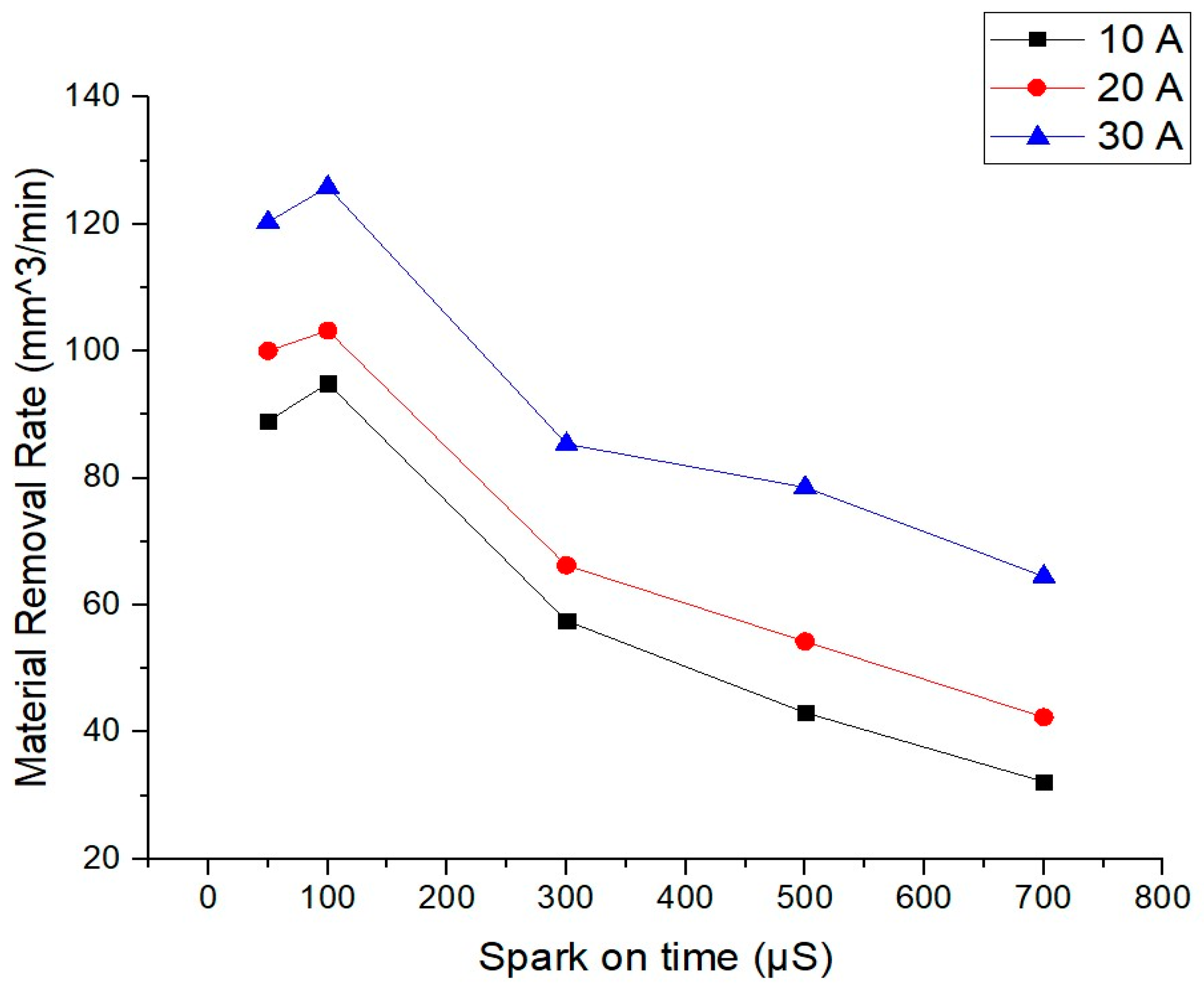
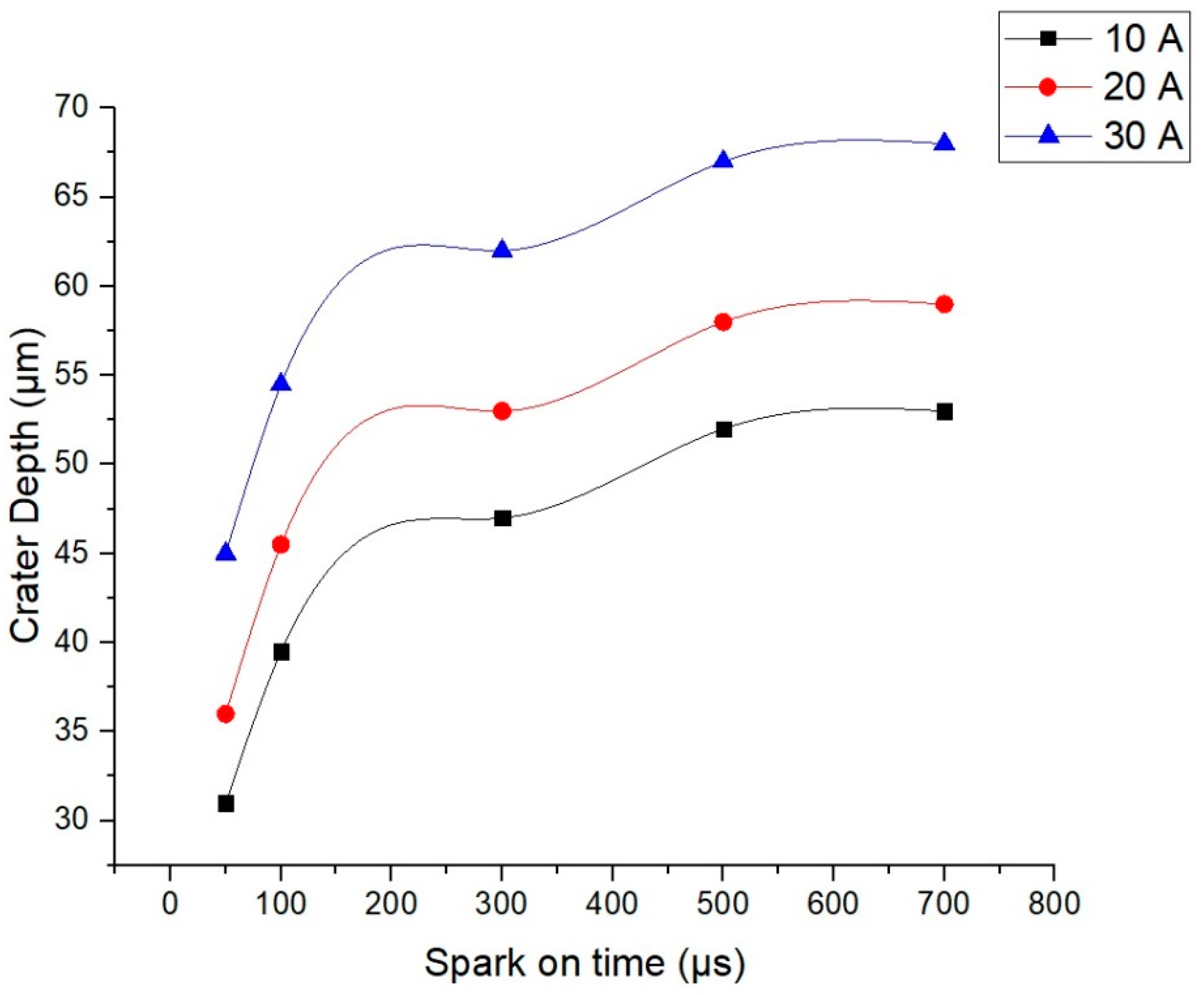
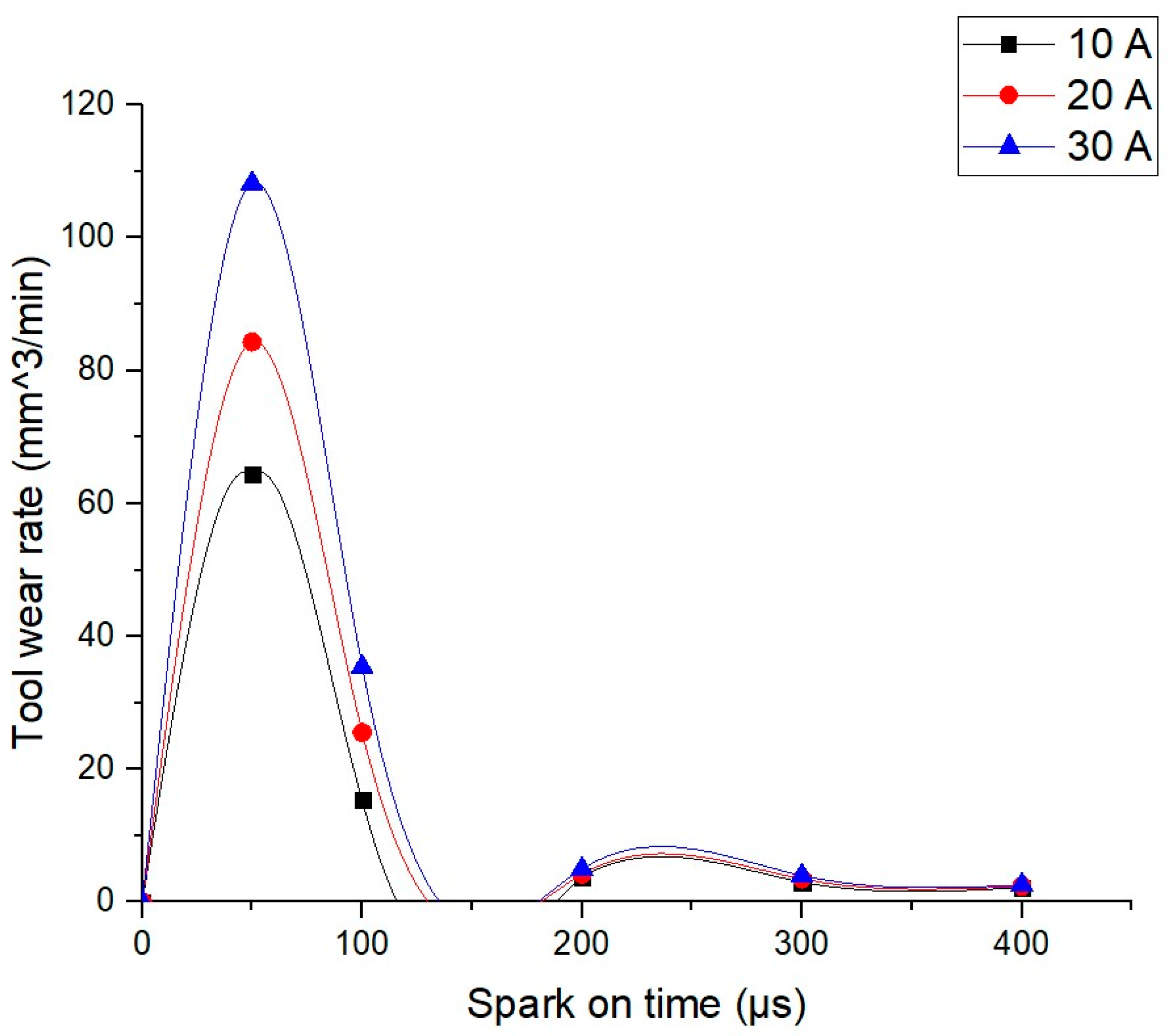
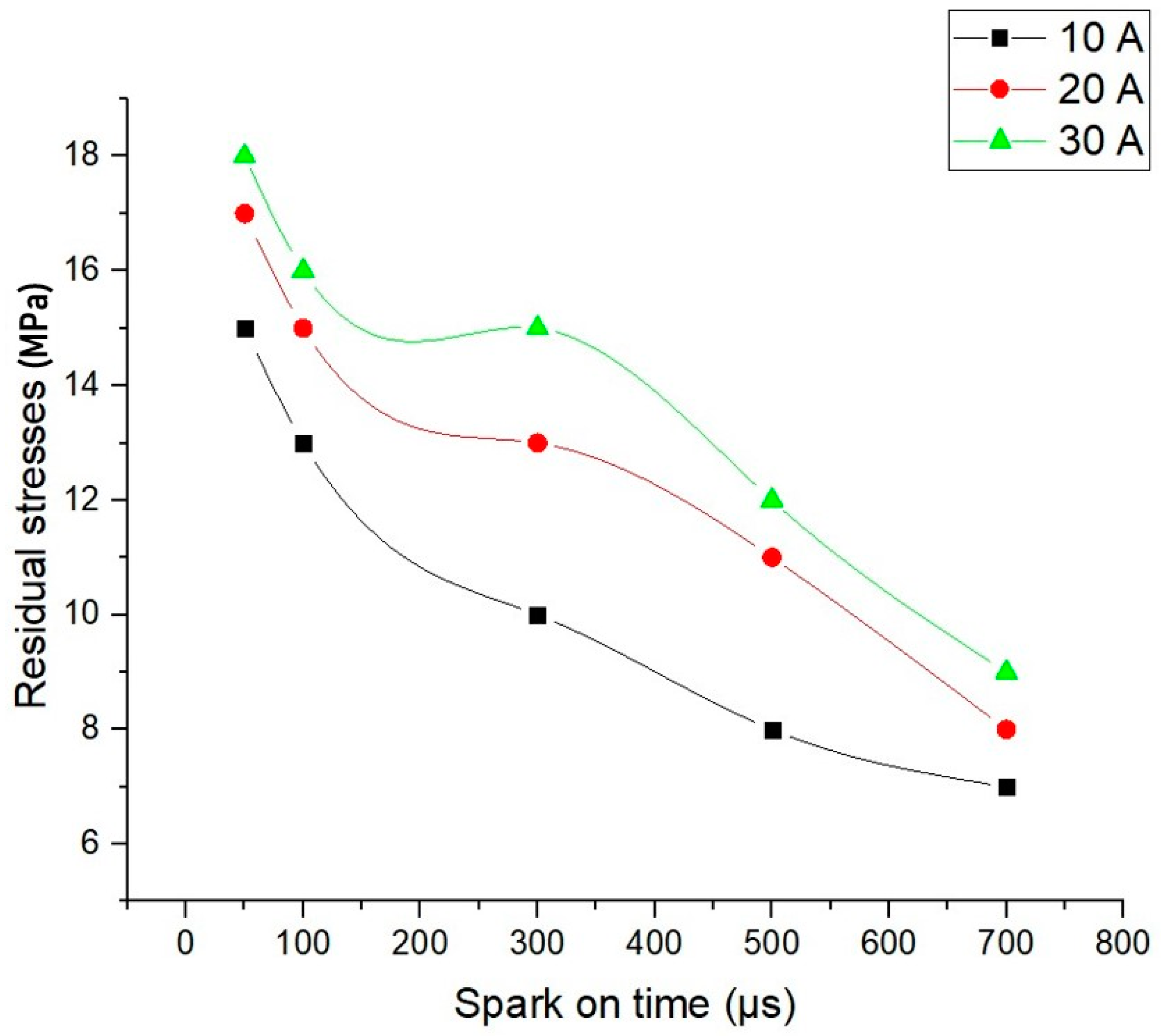
5.2. Effect of Spark-on Time
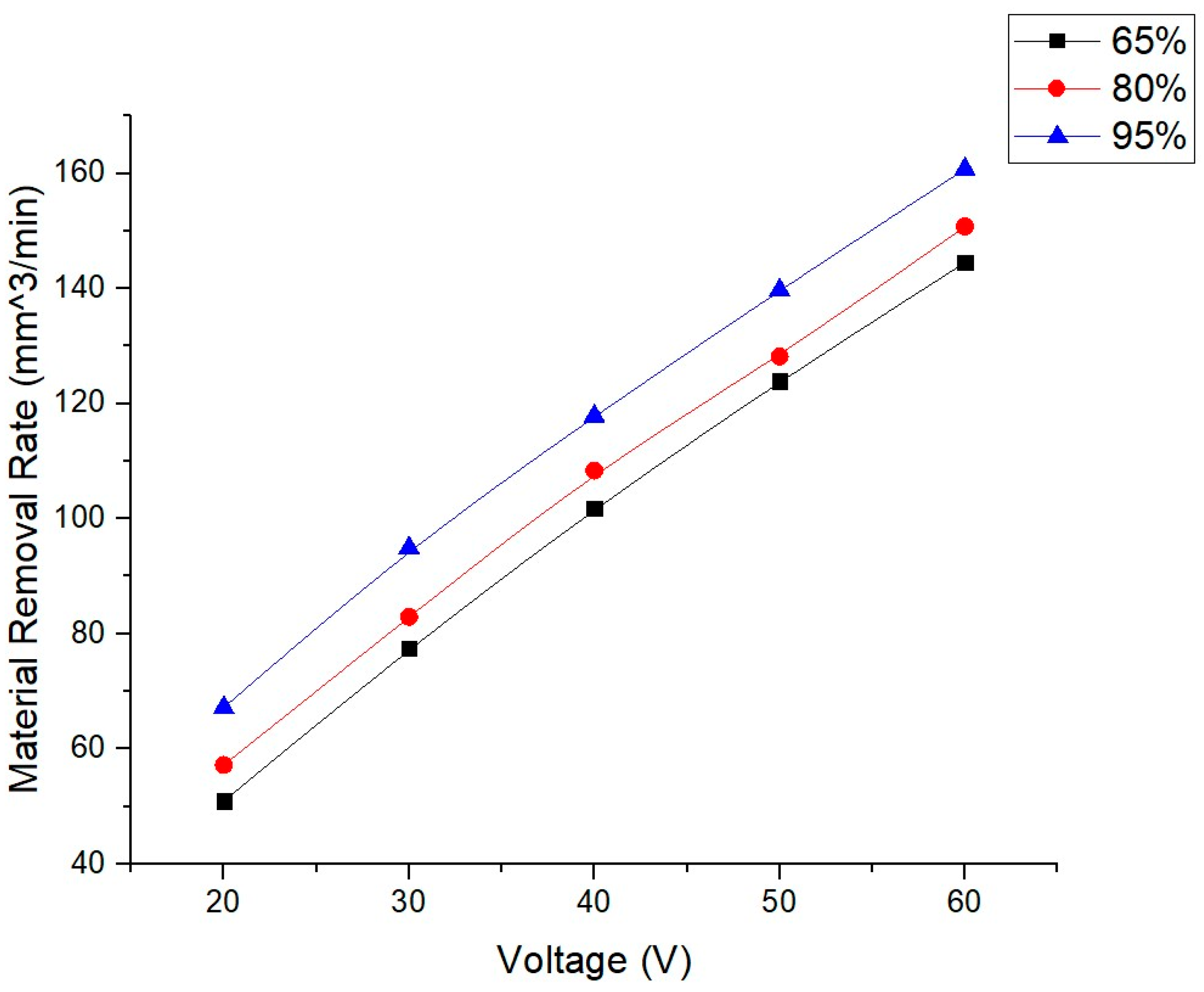
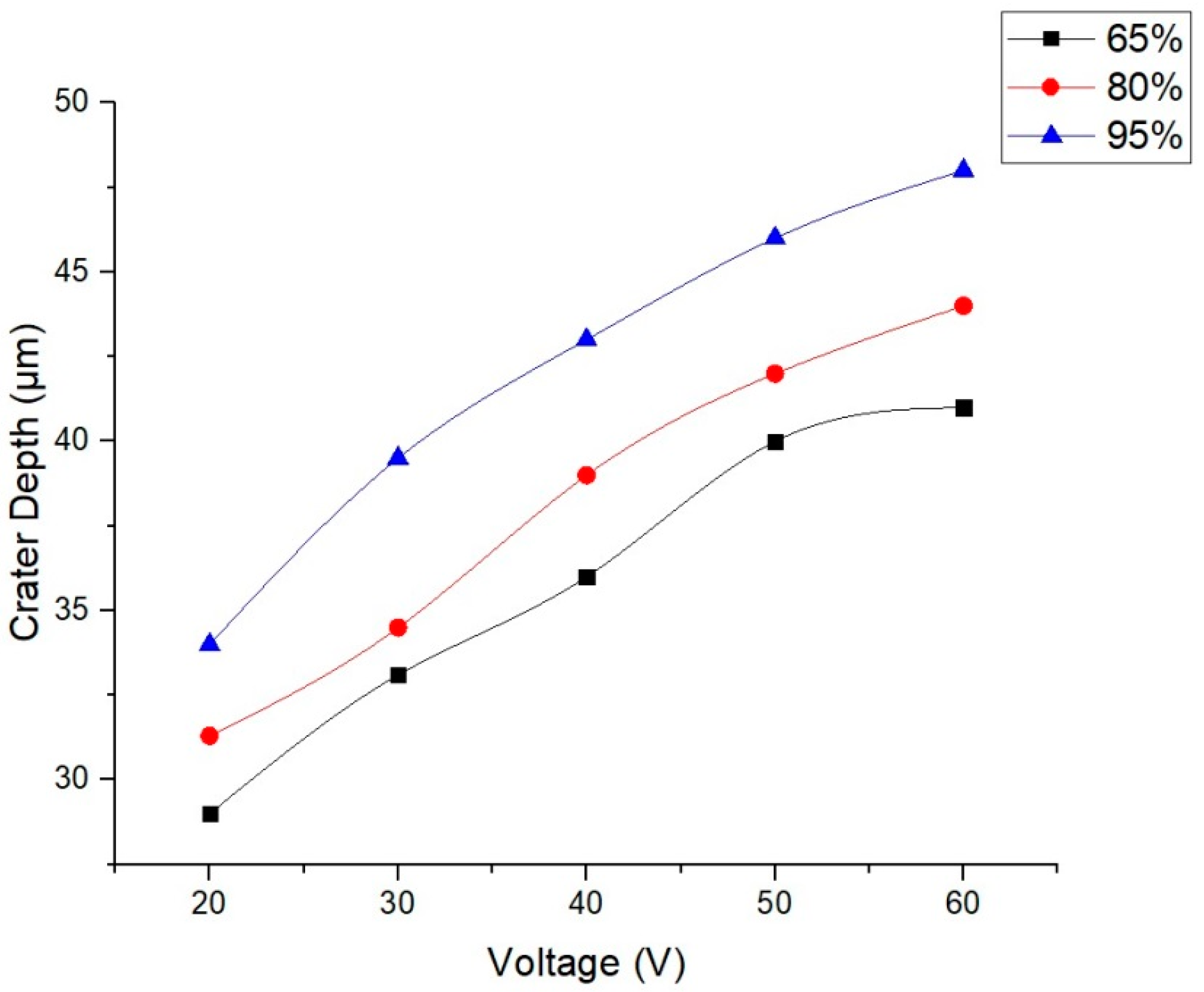
5.3. Effect of Discharge Voltage
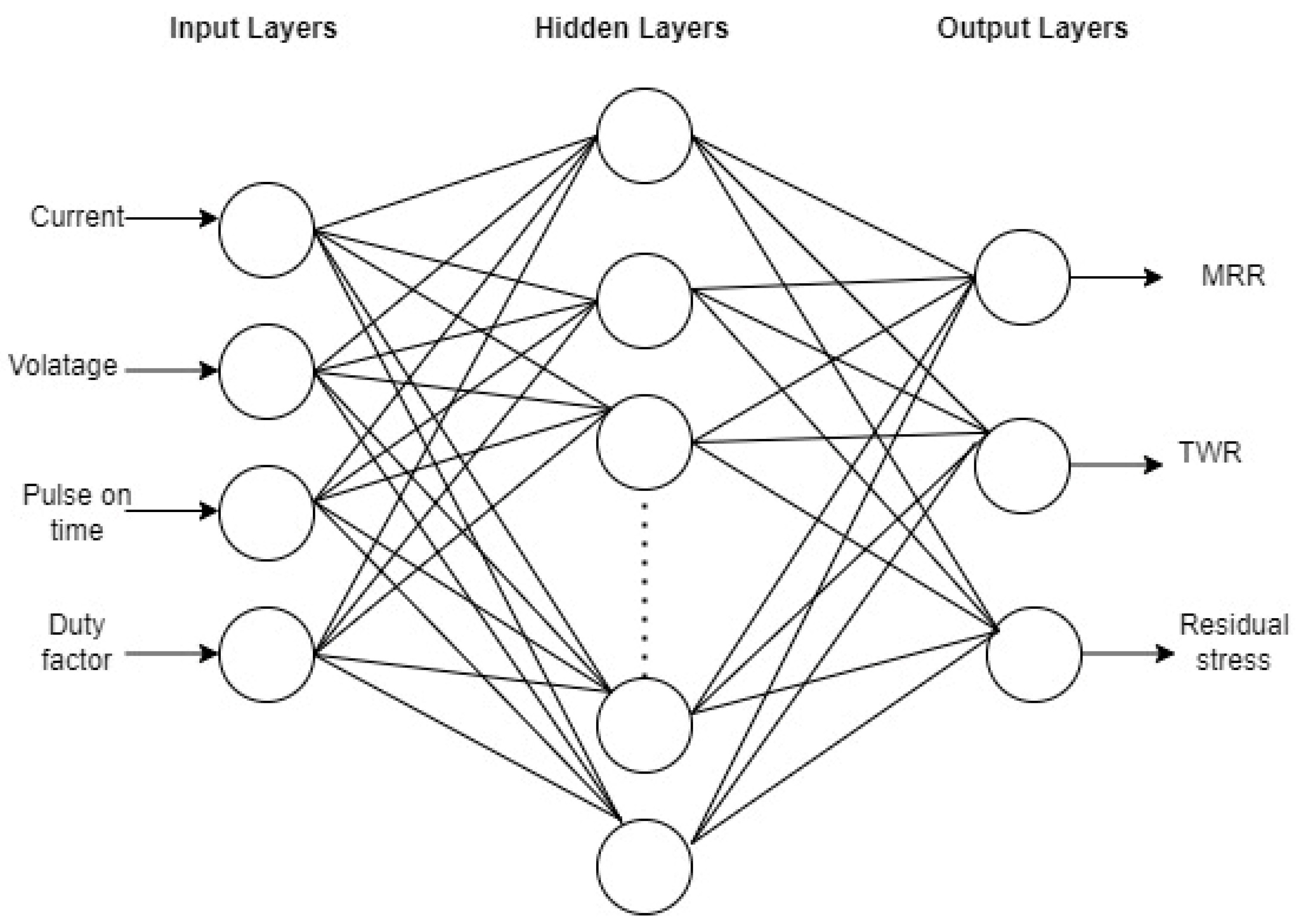
6. Prediction of EDM Simulation Responses Using Deep Neural Network
6.1. Model Selection and Training
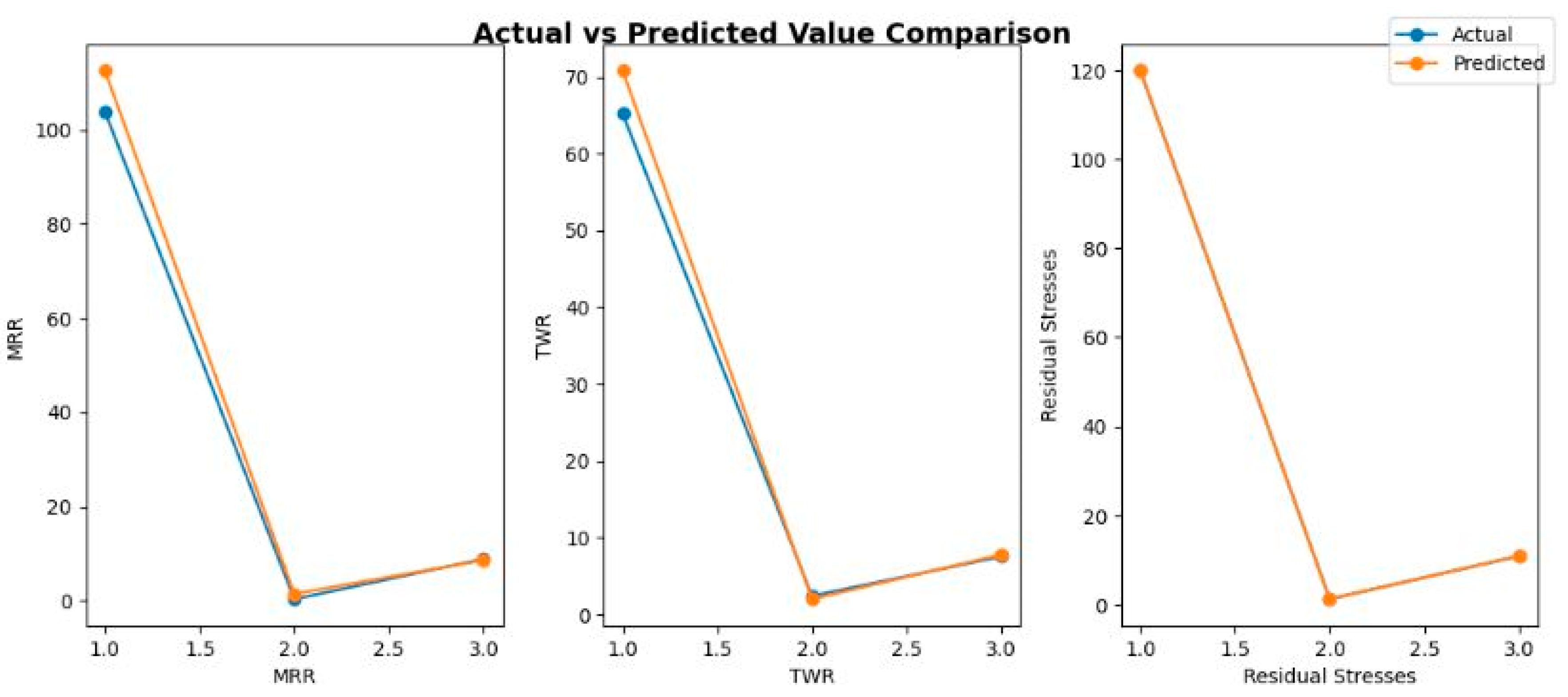
6.2. Results and Comparisons
7. Conclusions
- The discrepancy between the experimental and simulation results was reduced by expressing the spark radius as a function and adding features like latent heat and Gaussian heat flow distribution.
- Due to the large disparity in cooling rates, the workpiece experiences both tensile and compressive residual stresses during machining.
- Haynes 25 alloy workpieces should have an energy distribution factor of 5% when calculating the final heat flux in the numerical calculations to obtain the best results.
- As the discharge time increased, the MRR started falling after a certain period due to the decline in the flux density, although the crater depth and crater radius started increasing. As a result, regulating the amount of material removed with every discharge relies heavily on selecting the appropriate spark at the appropriate time.
- After a discharge time of 300 μs, the residual tension in the workpiece is found to have decreased considerably. Hence, it is recommended to have a spark-on time greater than 300 μs.
- Since the discharge voltage is directly proportional to the heat flux intensity, higher voltages can be used in surface-roughening procedures.
- By developing a deep neural network model, one can successfully predict responses and optimize outcomes in the specified setting. Its high accuracy and integration of optimization algorithms offer an efficient alternative to time-consuming and repetitive simulations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| List of Symbols | |
| Cvt | Crater volume (µm3) |
| Fc | Fraction of power reaching the cathode |
| I | Discharge current (A) |
| Kt | Thermal conductivity (W/m·K) |
| q | Heat flux at cathode surface (W/m2) |
| Rpc | Spark radius at cathode surface (µm) |
| T | Temperature variable (K) |
| Tm | Melting temperature (K) |
| t | Time variable (s) |
| ton | Spark-on time (µs) |
| toff | Discharge off-time (µs) |
| Machining time (min) | |
| V | Discharge voltage (V) |
| ρ | Density (kg/m3) |
| Abbreviations | |
| EDM | Electrical discharge machining |
| FEM | Finite element method |
| MRR | Material removal rate (mm3/min) |
| TWR | Tool wear rate (mm3/min) |
References
- Joshi, S.N.; Pande, S.S. Intelligent process modeling and optimization of die-sinking electric discharge machining. Appl. Soft Comput. 2011, 11, 2743–2755. [Google Scholar] [CrossRef]
- Mohanty, C.P.; Sahu, J.; Mahapatra, S.S. Thermal-structural analysis of electrical discharge machining process. Procedia Eng. 2013, 51, 508–513. [Google Scholar] [CrossRef]
- Joshi, S.N.; Pande, S.S. Thermo-physical modeling of die-sinking EDM process. J. Manuf. Process. 2010, 12, 45–56. [Google Scholar] [CrossRef]
- Jithin, S.; Raut, A.; Bhandarkar, U.V.; Joshi, S.S. FE modeling for single spark in EDM considering plasma flushing efficiency. Procedia Manuf. 2018, 26, 617–628. [Google Scholar] [CrossRef]
- Singh, H. Experimental study of distribution of energy during EDM process for utilization in thermal models. Int. J. Heat Mass Transf. 2012, 55, 5053–5064. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Dvivedi, A.; Pal, K. Thermal modeling of EDM process using FEA and parametric study of MRR. In AIP Conference Proceedings; AIP Publishing LLC: New York, NY, USA, 2021; Volume 2341, p. 040042. [Google Scholar]
- Patel, I.; Powar, P. FEM analysis with experimental results to study the effect of EDM parameters on MRR of AISI 1040 steel. Int. Res. J. Eng. Technol. 2018, 5, 1332. [Google Scholar]
- Kumar, S.; Das, S.; Joshi, S.N. Finite Element Modeling of Thermal Residual Stresses generated during EDM of AISI 1018 Steel. J. Inst. Eng. 2021, 103, 29–37. [Google Scholar] [CrossRef]
- Machine, P.M.E.D. Development of a Thermo-physical model of powder mixed electrical discharge machine using FEM and experimental validation. Int. J. Adv. Eng. Technol. 2014, 107, 111. [Google Scholar]
- Mohanty, C.P.; Mahapatra, S.S.; Sahu, J. Parametric optimization of electrical discharge machining process: A numerical approach. Int. J. Ind. Syst. Eng. 2016, 22, 207–244. [Google Scholar]
- Jilani, S.T.; Pandey, P.C. An analysis of surface erosion in electrical discharge machining. Wear 1983, 84, 275–284. [Google Scholar] [CrossRef]
- Halkaci, H.S.; Erden, A. Experimental investigation of surface roughness in electric discharge machining (EDM). In Proceedings of the 6th Biennial Conference on Engineering Systems Design and Analysis, Ystanbul, Turkey, 8–12 July 2002; pp. 8–11. [Google Scholar]
- Amorim, F.L.; Weingaertner, W.L. Die-sinking EDM of AISI P20 tool steel under rough machining using copper electrodes. In Proceedings of the 2o. COBEF-Congresso Brasileiro de Engenharia de Fabricação, Brasilia, Brazil, 10–12 May 2003; pp. 18–21. [Google Scholar]
- Mohanty, A.; Talla, G.; Gangopadhyay, S. Experimental investigation and analysis of EDM characteristics of Inconel 825. Mater. Manuf. Process. 2014, 29, 540–549. [Google Scholar] [CrossRef]
- Joshi, S.; Govindan, P.; Malshe, A.; Rajurkar, K. Experimental characterization of dry EDM performed in a pulsating magnetic field. CIRP Ann. 2011, 60, 239–242. [Google Scholar] [CrossRef]
- Dastagiri, M.; Kumar, A.H. Experimental Investigation of EDM Parameters on Stainless Steel&En41b. Procedia Eng. 2014, 97, 1551–1564. [Google Scholar]
- Oßwald, K.; Schneider, S.; Hensgen, L.; Klink, A.; Klocke, F. Experimental investigation of energy distribution in continuous sinking EDM. CIRP J. Manuf. Sci. Technol. 2017, 19, 36–43. [Google Scholar] [CrossRef]
- Dvivedi, A.; Kumar, P.; Singh, I. Experimental investigation and optimisation in EDM of Al 6063 SiCp metal matrix composite. Int. J. Mach. Mach. Mater. 2008, 3, 293–308. [Google Scholar]
- Prasad, A.R.; Ramji, K.; Datta, G.L. An experimental study of wire EDM on Ti-6Al-4V alloy. Procedia Mater. Sci. 2014, 5, 2567–2576. [Google Scholar] [CrossRef]
- Palanisamy, D.; Devaraju, A.; Manikandan, N.; Balasubramanian, K.; Arulkirubakaran, D. Experimental investigation and optimization of process parameters in EDM of aluminium metal matrix composites. Mater. Today Proc. 2020, 22, 525–530. [Google Scholar] [CrossRef]
- Ramakrishnan, R.; Karunamoorthy, L. Multi response optimization of wire EDM operations using robust design of experiments. Int. J. Adv. Manuf. Technol. 2006, 29, 105–112. [Google Scholar] [CrossRef]
- Somashekhar, K.P.; Panda, S.; Mathew, J.; Ramachandran, N. Numerical simulation of micro-EDM model with multi-spark. Int. J. Adv. Manuf. Technol. 2015, 76, 83–90. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Tsai, D.-M.; Chou, Y.-H. Fast and Precise Positioning in PCBs Using Deep Neural Network Regression. In IEEE Transactions on Instrumentation and Measurement; IEEE: New York, NY, USA, 2020; Volume 69, pp. 4692–4701. [Google Scholar]
- Ikai, T.; Hashigushi, K. Heat input for crater formation in EDM. In Proceedings of the International Symposium for Electro-Machining-ISEM XI, EPFL, Lausanne, Switzerland, 17–21 April 1995; pp. 163–170. [Google Scholar]
- Ming, W.; Shen, F.; Zhang, G.; Liu, G.; Du, J.; Chen, Z. Green machining: A framework for optimization of cutting parameters to minimize energy consumption and exhaust emissions during electrical discharge machining of Al 6061 and SKD 11. J. Clean. Prod. 2021, 285, 124889. [Google Scholar] [CrossRef]
- Świercz, R.; Oniszczuk-Świercz, D.; Chmielewski, T. Multi-response optimization of electrical discharge machining using the desirability function. Micromachines 2019, 10, 72. [Google Scholar] [CrossRef] [PubMed]
- Mausam, K.; Sharma, K.; Bharadwaj, G.; Singh, R.P. Multi-objective optimization design of die-sinking electric discharge machine (EDM) machining parameter for CNT-reinforced carbon fibre nanocomposite using grey relational analysis. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–8. [Google Scholar] [CrossRef]
- Mohanty, C.P.; Mahapatra, S.S.; Singh, M.R. A particle swarm approach for multi-objective optimization of electrical discharge machining process. J. Intell. Manuf. 2016, 27, 1171–1190. [Google Scholar] [CrossRef]
- Jain, A.; Kumar, C.S.; Shrivastava, Y. Fabrication and machining of fiber matrix composite through electric discharge machining: A short review. Mater. Today Proc. 2022, 51, 1233–1237. [Google Scholar] [CrossRef]
- Kirubagharan, R.; Dhanabalan, S.; Karthikeyan, T. The Effect of Electrode Size on Performance Measures of Inconel X750 using Nano-SiC Powder Mixing Electrical Discharge Machining. J. Mater. Eng. Perform. 2023, 32, 1–21. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Ming, W.; Zhang, Y.; Cao, C.; Zhang, G. A review on magnetic field assisted electrical discharge machining. J. Manuf. Process. 2021, 64, 694–722. [Google Scholar] [CrossRef]
- Boopathi, S. An extensive review on sustainable developments of dry and near-dry electrical discharge machining processes. J. Manuf. Sci. Eng. 2022, 144, 050801. [Google Scholar] [CrossRef]
- Grigoriev, S.N.; Volosova, M.A.; Okunkova, A.A.; Fedorov, S.V.; Hamdy, K.; Podrabinnik, P.A.; Pivkin, P.M.; Kozochkin, M.P.; Porvatov, A.N. Electrical discharge machining of oxide nanocomposite: Nanomodification of surface and subsurface layers. J. Manuf. Mater. Process. 2020, 4, 96. [Google Scholar] [CrossRef]
- Papazoglou, E.L.; Karmiris-Obratański, P.; Leszczyńska-Madej, B.; Markopoulos, A.P. A study on Electrical Discharge Machining of Titanium Grade2 with experimental and theoretical analysis. Sci. Rep. 2021, 11, 8971. [Google Scholar] [CrossRef]
- Prakash, V.; Kumar, P.; Singh, P.K.; Hussain, M.; Das, A.K.; Chattopadhyaya, S. Micro-electrical discharge machining of difficult-to-machine materials: A review. Proc. Inst. Mech. Eng. 2019, 233, 339–370. [Google Scholar] [CrossRef]
- Abu Qudeiri, J.E.; Saleh, A.; Ziout, A.; Mourad, A.H.I.; Abidi, M.H.; Elkaseer, A. Advanced electric discharge machining of stainless steels: Assessment of the state of the art, gaps and future prospect. Materials 2019, 12, 907. [Google Scholar] [CrossRef] [PubMed]
- Chaudhari, R.; Vora, J.J.; Patel, V.; López de Lacalle, L.N.; Parikh, D.M. Surface analysis of wire-electrical-discharge-machining-processed shape-memory alloys. Materials 2020, 13, 530. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Singh, R.P.; Trehan, R. State of the art in processing of shape memory alloys with electrical discharge machining: A review. Proc. Inst. Mech. Eng. 2021, 235, 333–366. [Google Scholar] [CrossRef]
- Bui, V.D.; Mwangi, J.W.; Meinshausen, A.K.; Mueller, A.J.; Bertrand, J.; Schubert, A. Antibacterial coating of Ti-6Al-4V surfaces using silver nano-powder mixed electrical discharge machining. Surf. Coat. Technol. 2020, 383, 125254. [Google Scholar] [CrossRef]
- Pramanik, A.; Islam, M.N.; Basak, A.K.; Dong, Y.; Littlefair, G. and Prakash, C. Optimizing dimensional accuracy of titanium alloy features produced by wire electrical discharge machining. Mater. Manuf. Process. 2019, 34, 1083–1090. [Google Scholar] [CrossRef]
- Available online: https://www.haynesintl.com/alloys/alloy-portfolio_/High-temperature-Alloys/haynes-25-alloy/typical-physical-properties (accessed on 18 January 2022).










| Properties | Values |
|---|---|
| Composition | 58% Co, 14% W, 9% Ni, 19% Cr |
| Density | 9070 kg/m3 |
| Melting point temperature | 1603 K (Solidus), 1683 K (Liquidus) |
| Modulus of elasticity | 225 GPa |
| Modulus of plasticity | 140 GPa |
| Poisson’s ratio | 0.148 |
| Thermal expansion coefficient | 1.92 × 10−5 K−1 |
| Latent heat of fusion | 266.67 J/Kg |
| Temperature (°C) | Thermal Conductivity (W/m°C) | Specific Heat (J/kg°C) |
|---|---|---|
| 25 | 10.5 | 403 |
| 100 | 12 | 424 |
| 200 | 14 | 445 |
| 300 | 15.9 | 455 |
| 400 | 17.7 | 462 |
| 500 | 19.5 | 495 |
| 600 | 21.2 | 508 |
| 700 | 22.9 | 582 |
| 800 | 24.5 | 592 |
| 900 | 26 | 596 |
| 1000 | 27.5 | 598 |
| Properties | Values |
|---|---|
| Density | 8960 kg/m3 |
| Melting point | 1380 K |
| Thermal conductivity | 401 W/(m K) |
| Specific heat | 389 J/Kg K |
| Run No. | Current (A) | Voltage (V) | Spark on Time (μs) | Duty Factor (%) | Numerical MRR (mm3/min) | Experimental MRR (mm3/min) | Numerical TWR (mm3/min) | Experimental TWR (mm3/min) | Numerical Residual Stresses (MPa) | Experimental Residual Stresses (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 30 | 200 | 80 | 65.170 | 60.646 | 2.4 | 0.149 | 7.54 | 7.14 |
| 2 | 20 | 30 | 200 | 80 | 103.833 | 98.453 | 0.32 | 0.109 | 8.86 | 7.65 |
| 3 | 10 | 50 | 200 | 80 | 104.726 | 102.826 | 0.648 | 0.982 | 8.98 | 8.15 |
| 4 | 20 | 50 | 200 | 80 | 150.221 | 145.824 | 18.340 | 15.975 | 10.69 | 9.92 |
| 5 | 15 | 40 | 100 | 70 | 122.760 | 119.905 | 13.312 | 10.149 | 8.65 | 7.53 |
| 6 | 15 | 40 | 300 | 70 | 99.640 | 94.745 | 1.235 | 0.797 | 9.95 | 8.77 |
| 7 | 15 | 40 | 100 | 90 | 122.760 | 119.904 | 13.312 | 11.075 | 8.65 | 7.63 |
| 8 | 15 | 40 | 300 | 90 | 99.640 | 95.148 | 1.254 | 0.031 | 10.89 | 9.54 |
| 9 | 10 | 40 | 200 | 70 | 89.767 | 85.181 | 2.324 | 0.609 | 8.25 | 7.76 |
| 10 | 20 | 40 | 200 | 70 | 130.146 | 127.232 | 1.599 | 0.803 | 9.79 | 8.28 |
| 11 | 10 | 40 | 200 | 90 | 84.531 | 80.234 | 1.952 | 0.325 | 8.25 | 7.32 |
| 12 | 20 | 40 | 200 | 90 | 130.507 | 123.574 | 1.599 | 1.023 | 9.78 | 8.45 |
| 13 | 15 | 30 | 100 | 80 | 104.150 | 102.24 | 0.283 | 0.114 | 7.92 | 6.96 |
| 14 | 15 | 50 | 100 | 80 | 144.021 | 138.542 | 44.908 | 39.512 | 9.48 | 8.23 |
| 15 | 15 | 50 | 300 | 80 | 119.873 | 114.36 | 1.259 | 0.214 | 10.89 | 9.58 |
| 16 | 15 | 50 | 300 | 80 | 119.873 | 110.54 | 1.227 | 0.154 | 10.89 | 9.58 |
| 17 | 10 | 40 | 100 | 80 | 94.897 | 91.696 | 1.964 | 0.478 | 8.07 | 7.23 |
| 18 | 20 | 40 | 100 | 80 | 146.524 | 142.365 | 32.204 | 30.258 | 9.12 | 8.21 |
| 19 | 10 | 40 | 300 | 80 | 79.938 | 75.357 | 3.988 | 0.211 | 9.16 | 8.56 |
| 20 | 20 | 40 | 300 | 80 | 110.980 | 108.678 | 0.228 | 0.136 | 10.56 | 9.87 |
| 21 | 15 | 30 | 200 | 70 | 91.527 | 86.21 | 4.311 | 0.211 | 8.28 | 7.23 |
| 22 | 15 | 50 | 200 | 70 | 132.556 | 127.53 | 7.686 | 5.369 | 9.96 | 8.87 |
| 23 | 15 | 30 | 200 | 90 | 92.058 | 88.57 | 2.223 | 0.114 | 8.28 | 7.52 |
| 24 | 15 | 50 | 200 | 90 | 137.974 | 132.477 | 7.686 | 4.389 | 9.96 | 8.47 |
| 25 | 15 | 40 | 200 | 80 | 114.131 | 112.69 | 1.984 | 0.425 | 8.95 | 7.85 |
| 26 | 15 | 40 | 200 | 80 | 114.131 | 114.84 | 1.984 | 0.645 | 8.95 | 7.52 |
| 27 | 15 | 40 | 200 | 80 | 114.131 | 110.69 | 1.984 | 0.411 | 8.95 | 7.82 |
| 28 | 15 | 40 | 200 | 80 | 114.131 | 108.84 | 1.984 | 0.398 | 8.95 | 7.99 |
| 29 | 15 | 40 | 200 | 80 | 114.131 | 110.19 | 1.984 | 0.469 | 8.95 | 8.05 |
| Run No. | Experimental Crater Depth (mm) | Numerical Crater Depth (mm) | Experimental Crater Radius (mm) | Numerical Crater Radius (mm) |
|---|---|---|---|---|
| 1 | 0.021 | 0.023 | 0.030 | 0.028 |
| 2 | 0.035 | 0.037 | 0.049 | 0.045 |
| 3 | 0.036 | 0.037 | 0.051 | 0.046 |
| 4 | 0.051 | 0.053 | 0.073 | 0.065 |
| 5 | 0.042 | 0.043 | 0.060 | 0.053 |
| 6 | 0.033 | 0.035 | 0.047 | 0.043 |
| 7 | 0.043 | 0.044 | 0.060 | 0.053 |
| 8 | 0.034 | 0.035 | 0.048 | 0.043 |
| 9 | 0.030 | 0.032 | 0.043 | 0.039 |
| 10 | 0.045 | 0.046 | 0.064 | 0.057 |
| 11 | 0.028 | 0.030 | 0.040 | 0.037 |
| 12 | 0.044 | 0.046 | 0.062 | 0.057 |
| 13 | 0.036 | 0.037 | 0.051 | 0.045 |
| 14 | 0.049 | 0.051 | 0.069 | 0.063 |
| 15 | 0.041 | 0.043 | 0.057 | 0.052 |
| 16 | 0.039 | 0.043 | 0.055 | 0.052 |
| 17 | 0.033 | 0.034 | 0.037 | 0.041 |
| 18 | 0.051 | 0.052 | 0.057 | 0.064 |
| 19 | 0.020 | 0.035 | 0.042 | 0.035 |
| 20 | 0.039 | 0.039 | 0.043 | 0.048 |
| 21 | 0.031 | 0.032 | 0.034 | 0.040 |
| 22 | 0.045 | 0.047 | 0.051 | 0.058 |
| 23 | 0.031 | 0.033 | 0.035 | 0.040 |
| 24 | 0.047 | 0.049 | 0.053 | 0.060 |
| 25 | 0.040 | 0.041 | 0.045 | 0.050 |
| 26 | 0.041 | 0.041 | 0.046 | 0.050 |
| 27 | 0.037 | 0.041 | 0.045 | 0.050 |
| 28 | 0.039 | 0.041 | 0.044 | 0.050 |
| 29 | 0.038 | 0.041 | 0.043 | 0.050 |
| S. No. | Current (A) | Ton (μs) | Toff (μs) | Discharge Energy (mJ) | MRR (mm3/min) |
|---|---|---|---|---|---|
| 1 | 2.34 | 5.6 | 1 | 0.327 | 30.822 |
| 2 | 2.83 | 7.5 | 1.3 | 0.53 | 31.145 |
| 3 | 3.67 | 13 | 2.4 | 1.192 | 38.467 |
| 4 | 5.3 | 18 | 2.4 | 2.385 | 44.049 |
| 5 | 8.5 | 24 | 2.4 | 5.1 | 77.436 |
| 6 | 10 | 32 | 2.4 | 8 | 87.688 |
| 7 | 12.8 | 42 | 3.2 | 13.44 | 102.79 |
| 8 | 10 | 100 | 4.2 | 25 | 151.71 |
| 9 | 20 | 56 | 3.2 | 28 | 163.87 |
| 10 | 25 | 100 | 4.2 | 62.5 | 191.78 |
| 11 | 36 | 180 | 4.2 | 162 | 224.01 |
| Optimal Parameter Settings | Actual (Values Achieved through Simulation) | Predicted (Value Achieved through Deep Neural Network Approach) | Experimental Results | |||
|---|---|---|---|---|---|---|
| Current Voltage Pulse-on time Duty factor | MRR 95.45 | MRR 95.54 | MRR 93.96 | |||
| 10 A | 50 V | 200 µs | 90% | |||
| TWR 0.24 | TWR 0.24 | TWR 0.25 | ||||
| Residual stresses 9.13 | Residual stresses 9.12 | Residual stresses 9.79 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aneesh, T.; Mohanty, C.P.; Tripathy, A.K.; Chauhan, A.S.; Gupta, M.; Annamalai, A.R. A Thermo-Structural Analysis of Die-Sinking Electrical Discharge Machining (EDM) of a Haynes-25 Super Alloy Using Deep-Learning-Based Methodologies. J. Manuf. Mater. Process. 2023, 7, 225. https://doi.org/10.3390/jmmp7060225
Aneesh T, Mohanty CP, Tripathy AK, Chauhan AS, Gupta M, Annamalai AR. A Thermo-Structural Analysis of Die-Sinking Electrical Discharge Machining (EDM) of a Haynes-25 Super Alloy Using Deep-Learning-Based Methodologies. Journal of Manufacturing and Materials Processing. 2023; 7(6):225. https://doi.org/10.3390/jmmp7060225
Chicago/Turabian StyleAneesh, T., Chinmaya Prasad Mohanty, Asis Kumar Tripathy, Alok Singh Chauhan, Manoj Gupta, and A. Raja Annamalai. 2023. "A Thermo-Structural Analysis of Die-Sinking Electrical Discharge Machining (EDM) of a Haynes-25 Super Alloy Using Deep-Learning-Based Methodologies" Journal of Manufacturing and Materials Processing 7, no. 6: 225. https://doi.org/10.3390/jmmp7060225
APA StyleAneesh, T., Mohanty, C. P., Tripathy, A. K., Chauhan, A. S., Gupta, M., & Annamalai, A. R. (2023). A Thermo-Structural Analysis of Die-Sinking Electrical Discharge Machining (EDM) of a Haynes-25 Super Alloy Using Deep-Learning-Based Methodologies. Journal of Manufacturing and Materials Processing, 7(6), 225. https://doi.org/10.3390/jmmp7060225










