Optimization of the FDM Processing Parameters on the Compressive Properties of ABS Objects for the Production of High-Heeled Shoes
Abstract
1. Introduction
2. Materials and Methods
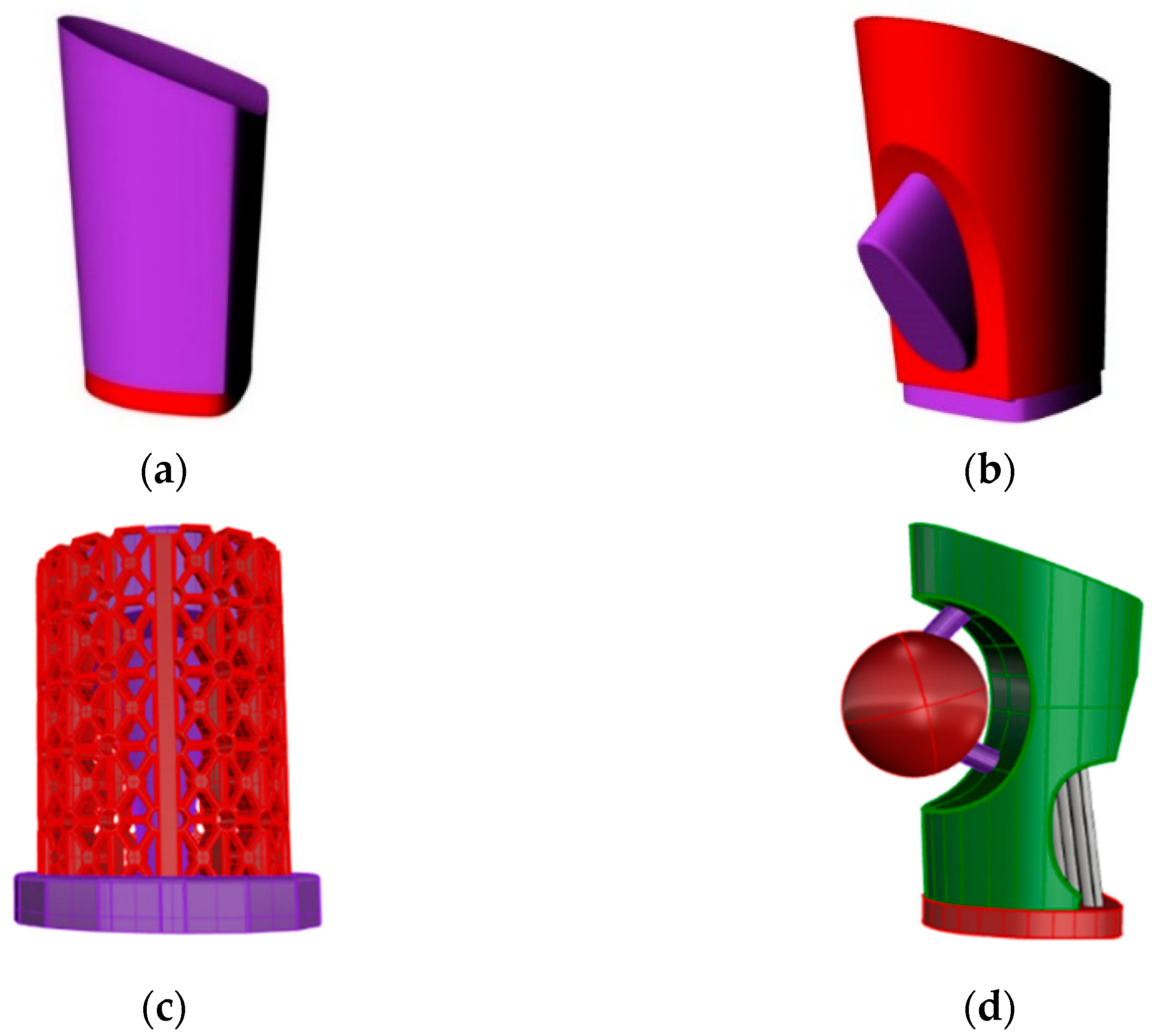
2.1. Fabrication Process
2.2. Experimental Setup
- A—layer thickness, LT = 0.10 to 0.30 mm;
- B—infill density, ID = 10 to 40%;
- C—extrusion temperature, ϑ = 205 to 255 °C.
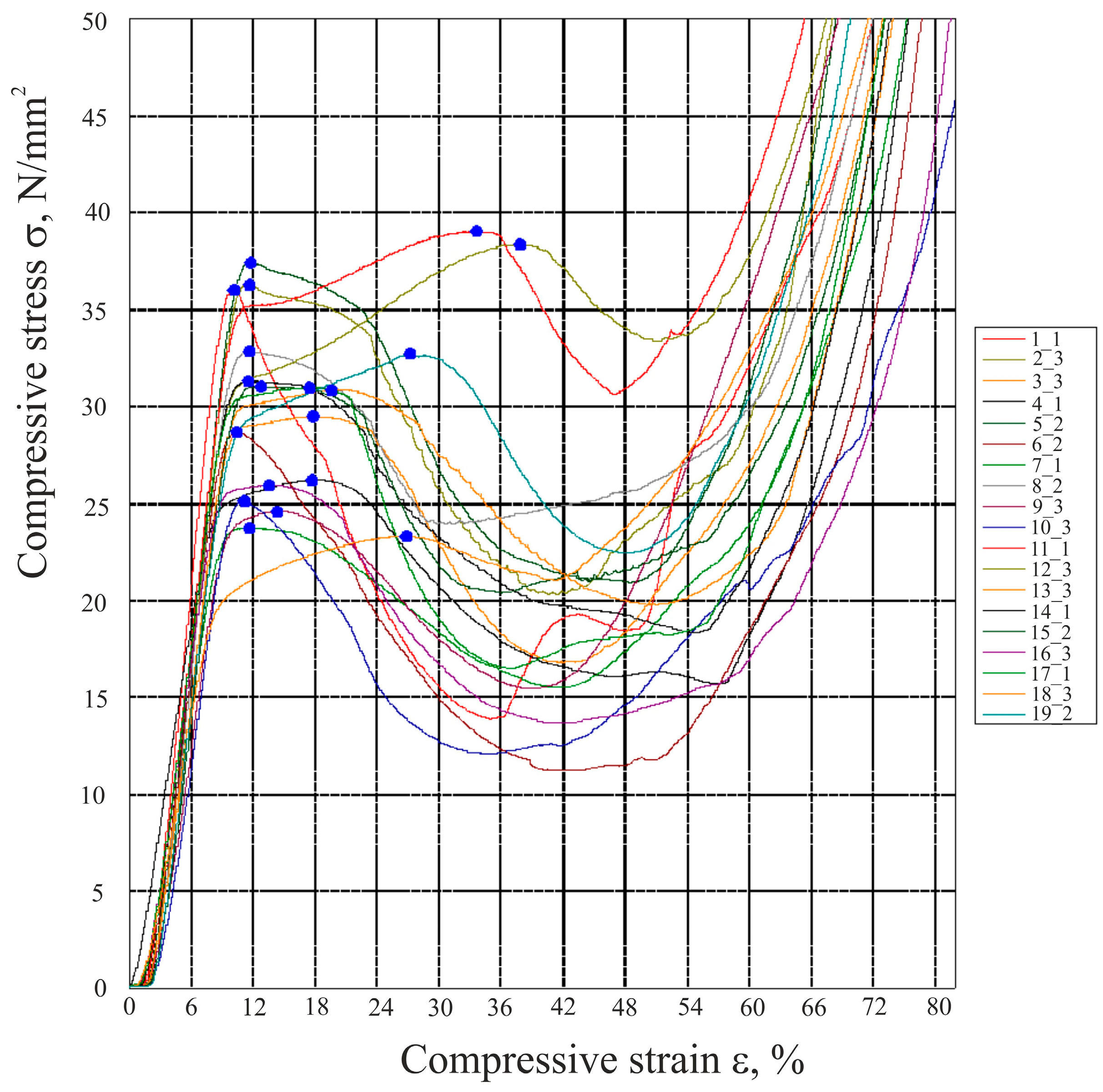
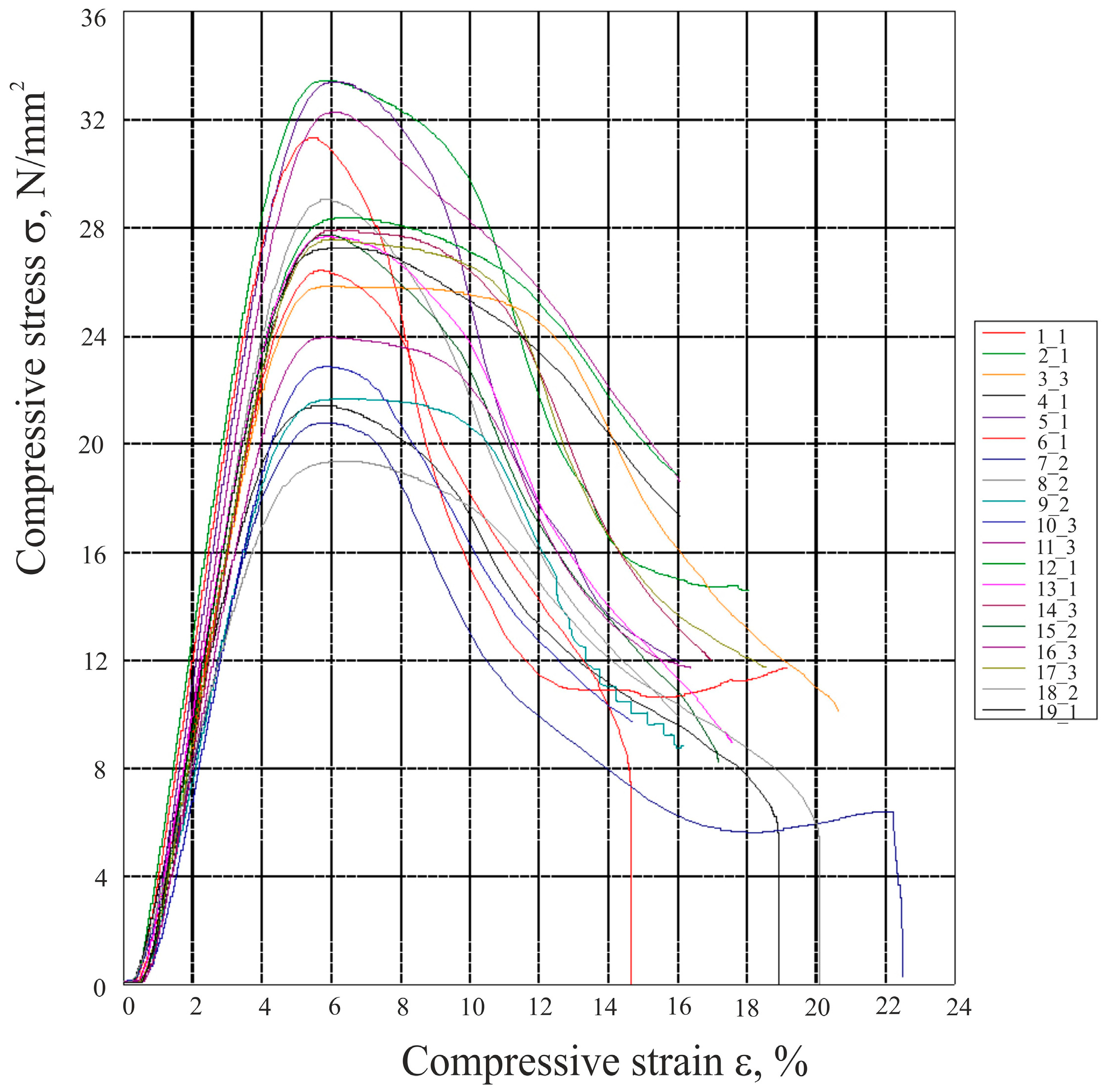
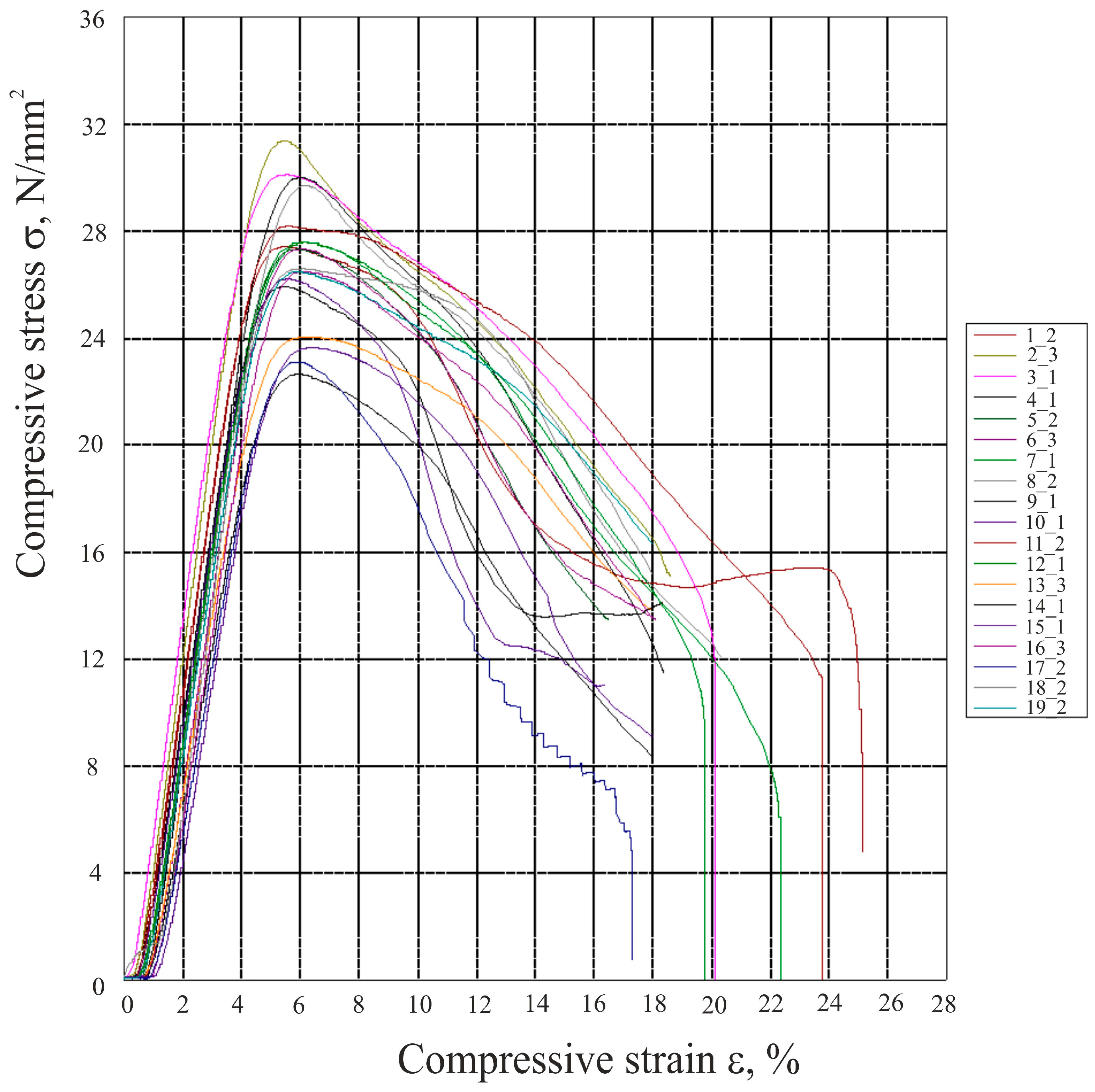
3. Results
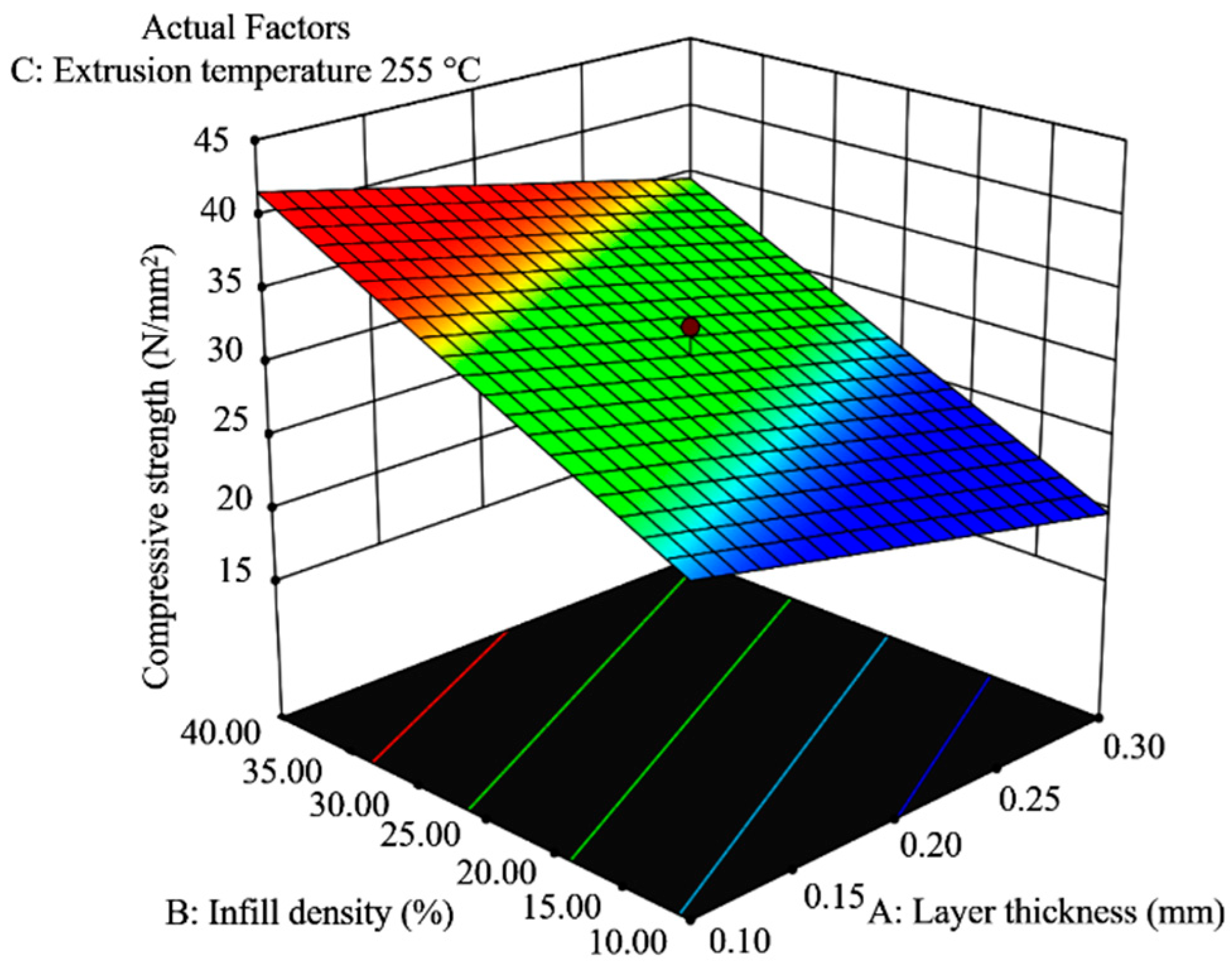
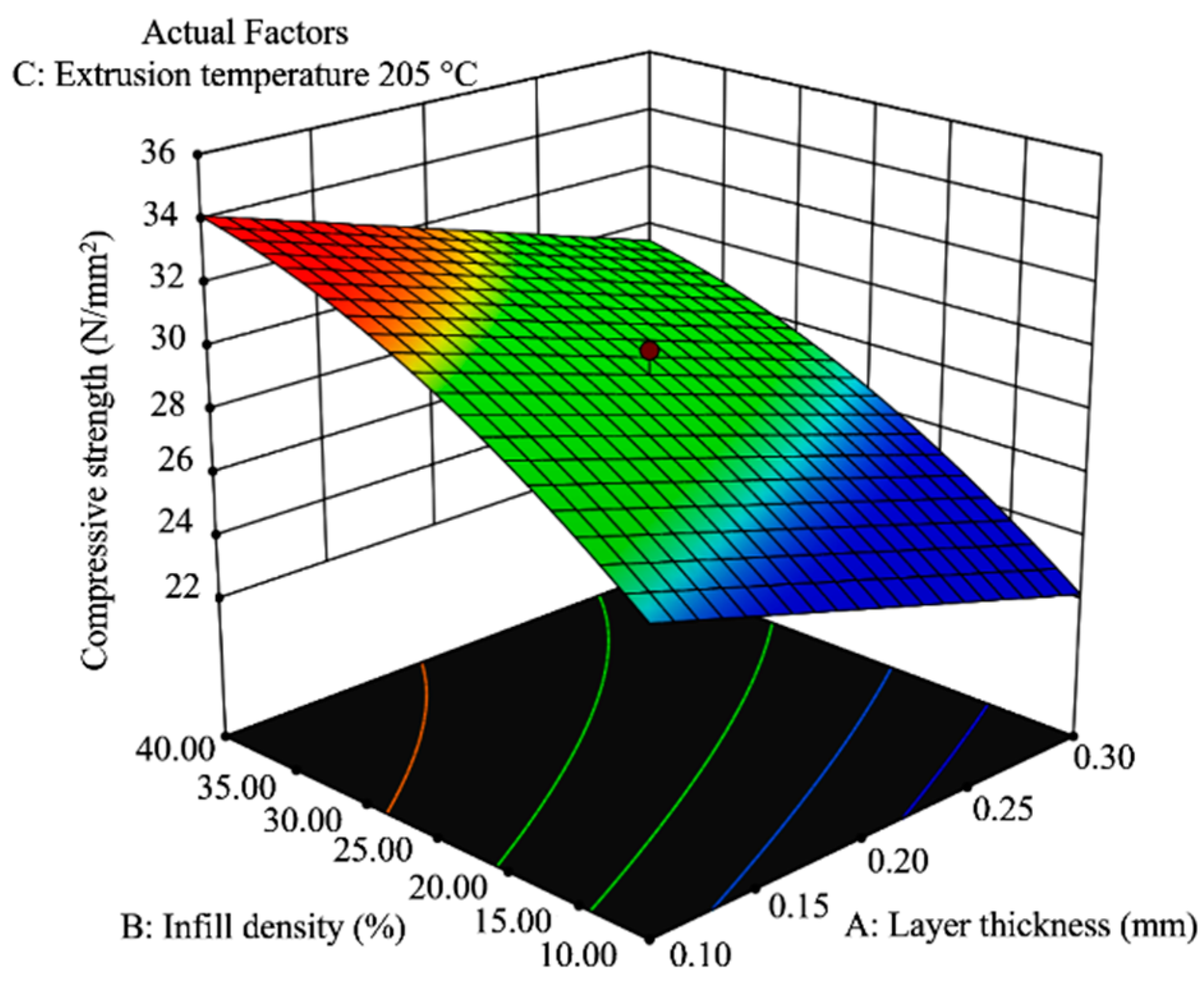
3.1. Statistical Analysis of Compressive Strength
3.1.1. Statistical Analysis of Compressive Strength—Linear Infill (L45)
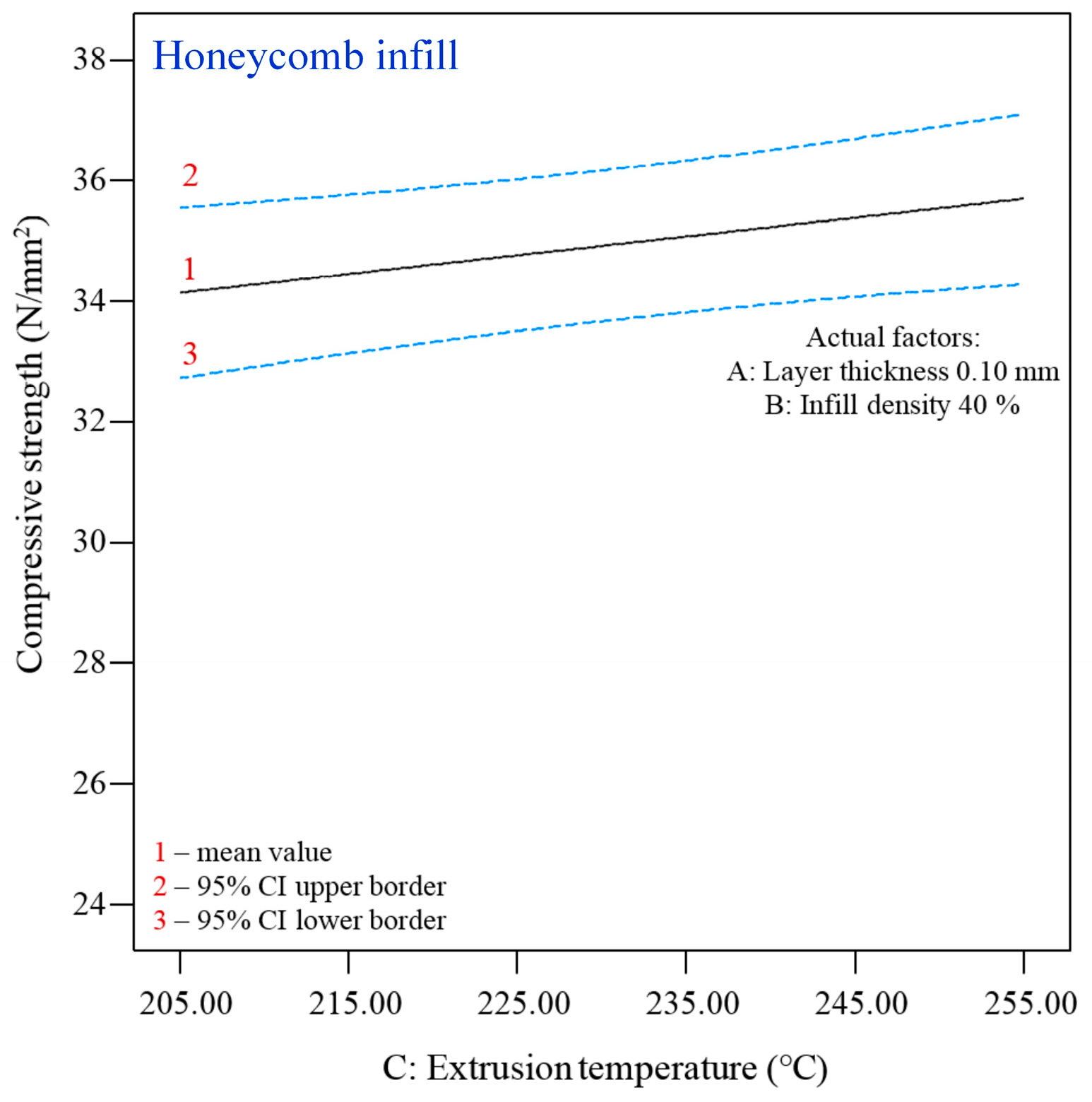
3.1.2. Statistical Analysis of Compressive Strength—Honeycomb Infill (H)
3.2. Statistical Analysis of the Compressive Modulus
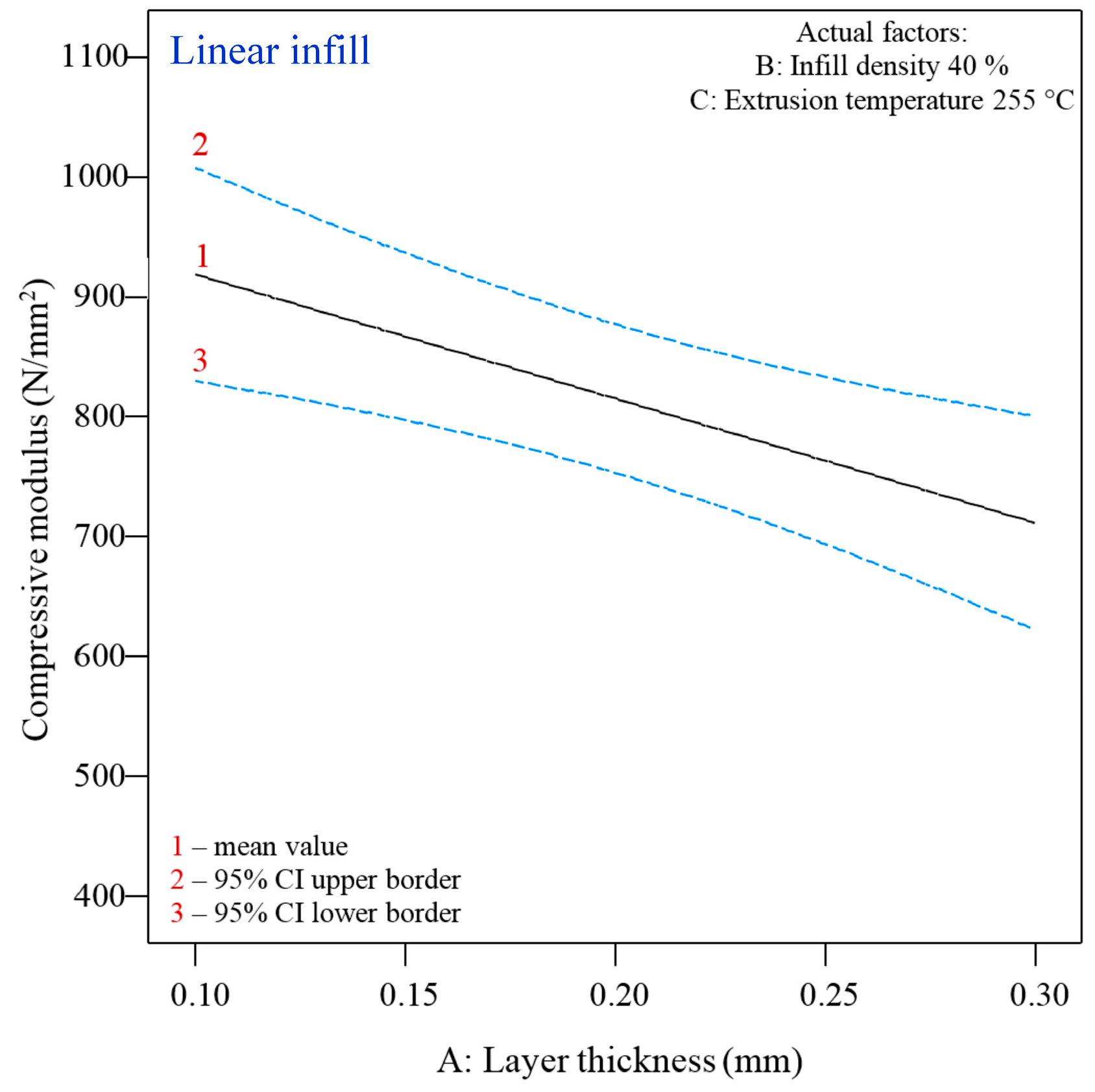
3.2.1. Statistical Analysis of the Compressive Modulus—Linear Infill (L45)
3.2.2. Statistical Analysis of the Compressive Modulus—Honeycomb Infill (H)
3.3. Statistical Model for Optimization
3.4. Practical Application
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Matias, E.; Rao, B. 3D printing: On its historical evolution and the implications for business. In Proceedings of the PICMET 2015: Management of the Technology Age, Portland International Center for Management of Engineering and Technology, Portland, OR, USA, 2–6 August 2015; pp. 551–558. [Google Scholar]
- Godec, D.; Pilipović, A.; Breški, T.; Ureña, J.; Jordá, O.; Martínez, M.; Gonzalez-Gutierrez, J.; Schuschnigg, S.; Leoben, M.; Blasco, J.R.; et al. Introduction to Additive Manufacturing. In A Guide to Additive Manufacturing; Springer Tracts in Additive Manufacturing; Springer: Cham, Switzerland, 2022; pp. 1–44. Available online: https://link.springer.com/book/10.1007/978-3-031-05863-9 (accessed on 10 May 2023).
- Rigon, D.; Ricotta, M.; Meneghetti, G. A literature survey on structural integrity of 3D printed virgin and recycled ABS and PP compounds. Sci. Procedia Struct. Integr. 2020, 28, 1655–1663. [Google Scholar]
- Bakır, A.A.; Atik, R.; Özerinç, S. Mechanical properties of thermoplastic parts produced by fused deposition modeling: A review. Rapid Prototyp. J. 2021, 27, 537–561. [Google Scholar] [CrossRef]
- Liu, W.; Liu, X.; Liu, Y.; Wang, J.; Evans, S.; Yang, M. Unpacking Additive Manufacturing Challenges and Opportunities in Moving towards Sustainability: An Exploratory Study. Sustainability 2023, 15, 3827. [Google Scholar] [CrossRef]
- Agnusdei, L.; Del Prete, A. Additive manufacturing for sustainability: A systematic literature review. Sustain. Futures 2022, 4, 100098. [Google Scholar] [CrossRef]
- Jandyal, A.; Chaturvedi, I.; Wazir, I.; Raina, A.; Haq, M.I.U. 3D printing—A review of processes, materials and applications in industry 4.0. Sustain. Oper. Comput. 2022, 3, 33–42. [Google Scholar] [CrossRef]
- Cuan-Urquizo, E.; Eduardo Barocio, E.; Tejada-Ortigoza, V.; Pipes, R.B.; Rodriguez, C.A.; Roman-Flores, A. Characterization of the Mechanical Properties of FFF Structures and Materials: A Review on the Experimental, Computational and Theoretical Approaches. Materials 2019, 12, 895. [Google Scholar] [CrossRef] [PubMed]
- Attoye, S.; Malekipur, E.; El-Mounary, H. Correlation between process parameters and mechanical properties in parts printed by the fused deposition modeling process. Mech. Addit. Adv. Manuf. 2019, 8, 35–41. [Google Scholar]
- Decuir, F.; Phelan, K.; Hollins, B. Mechanical Strength of 3-D Printed Filaments. In Proceedings of the 32nd Southern Biomedical Engineering Conference (SBEC), Shreveport, LA, USA, 11–13 March 2016. [Google Scholar] [CrossRef]
- Rankouhi, B.; Javadpour, S.; Delfanian, F.; Letcher, T. Failure Analysis and Mechanical Characterization of 3D Printed ABS With Respect to Layer Thickness and Orientation. J. Fail. Anal. Prev. 2016, 16, 467–481. [Google Scholar] [CrossRef]
- Savvakis, K.; Petousis, M.; Vairis, A.; Vidakis, N.; Bikmeye, A.T. Experimental Determination of the Tensile Strength of Fused Deposition Modeling Parts. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition IMECE2014, Montreal, QC, Canada, 14–20 November 2014; pp. 1–6. [Google Scholar]
- Kuznetsov, V.E.; Tavitov, A.G.; Urzhumtsev, O.D.; Mikhalin, M.V.; Moiseev, A.I. Hardware Factors Influencing Strength of Parts Obtained by Fused Filament Fabrication. Polymers 2019, 11, 1870. [Google Scholar] [CrossRef] [PubMed]
- Travieso-Rodriguez, J.A.; Jerez-Mesa, R.; Jordi Llumà, J.; Traver, O. Mechanical properties of 3D-printing Polylactic acid parts subjected to bending stress and fatigue testing DOE-design of experiments ANOVA—Analysis of variance. Met. Spec. Issue Adv. Plast. Deform. Technol. 2019, 12, 3859. [Google Scholar]
- Padhi, S.K.; Sahu, R.K.; Mahapatra, S.S.; Das, H. Optimization of fused deposition modeling process parameters using a fuzzy inference system coupled with Taguchi philosophy. Adv. Manuf. 2017, 5, 231–242. [Google Scholar] [CrossRef]
- Oropallo, W.; Piegl, L.A. Ten challenges in 3D printing. Eng. Comput. 2016, 32, 135–148. [Google Scholar] [CrossRef]
- Sun, Q.; Rizvi, G.M.; Bellehumeur, C.T.; Gu, P. Effect of processing conditions on the bonding quality of FDM polymer filaments. Rapid Prototyp. J. 2008, 14, 72–80. [Google Scholar] [CrossRef]
- Travieso-Rodriguez, J.A.; Jerez-Mesa, R.; Lluma, J.; Gomez-Gras, G.; Casadesus, O. Comparative study of the flexural properties of ABS, PLA and a PLA–wood composite manufactured through fused filament fabrication. Rapid Prototyp. J. 2020, 27, 81–92. [Google Scholar] [CrossRef]
- Sagias, V.D.; Giannakopoulos, K.I.; Stergiou, C. Mechanical properties of 3D printed polymer specimens. Procedia Struct. Integr. 2018, 10, 85–90. [Google Scholar] [CrossRef]
- Chaco’n, J.M.; Caminero, M.A.; Garc´ıa-Plaza, E.; Núnez, P.J. Additive manufacturing of PLA structures using fused deposition modelling: Effect of process parameters on mechanical properties and their optimal selection. Mater. Des. 2017, 24, 143–157. [Google Scholar] [CrossRef]
- Li, H.; Wang, T.; Sun, J.; Yu, Z. The effect of process parameters in fused deposition modelling on bonding degree and mechanical properties. Rapid Prototyp. J. 2018, 24, 80–92. [Google Scholar] [CrossRef]
- Zandi, M.D.; Jerez-Mesa, R.; Lluma-Fuentes, J.; Jorba-Peiro, J.; Travieso-Rodriguez, J.A. Study of the manufacturing process effects of fused filament fabrication and injection molding on tensile properties of composite PLA-wood parts. Int. J. Adv. Manuf. Technol. 2020, 108, 1725–1735. [Google Scholar] [CrossRef]
- Saniman, M.N.F.; Hashim, M.H.M.; Mohammad, K.A.; Abd Wahid, K.A.; Wan Muhamad, W.M.; Noor Mohamed, N.H. Tensile Characteristics of Low Density Infill Patterns for Mass Reduction of 3D Printed Polylactic Parts. Int. J. Automot. Mech. Eng. 2020, 17, 7927–7934. [Google Scholar] [CrossRef]
- Wu, W.; Geng, P.; Li, G.; Zhao, D.; Zhang, H.; Zhao, J. Influence of Layer Thickness and Raster Angle on the Mechanical Properties of 3D-Printed PEEK and a Comparative Mechanical Study between PEEK and ABS. Materials 2015, 8, 5834–5846. [Google Scholar] [CrossRef]
- Oudah, S.; Al-Attraqchi, H.; Nassir, N. The Effect of Process Parameters on the Compression Property of Acrylonitrile Butadiene Styrene Produced by 3D Printer. Eng. Technol. J. 2022, 40, 89–194. [Google Scholar] [CrossRef]
- Dominguez-Rodriguez, G.; Ku-Herrera, J.J.; Hernandez-Perez, A. An assessment of the effect of printing orientation, density, and filler pattern on the compressive performance of 3D printed ABS structures by fuse deposition. Int. J. Adv. Manuf. Technol. 2018, 95, 1685–1695. [Google Scholar] [CrossRef]
- Uddin, M.S.; Sidek, M.F.R.; Faizal, M.A.; Ghomashchi, R.; Pramanik, A. Evaluating Mechanical Properties and Failure Mechanisms of Fused Deposition Modeling Acrylonitrile Butadiene Styrene Parts. ASME. J. Manuf. Sci. Eng. 2017, 139, 081018. [Google Scholar] [CrossRef]
- Sood, S.; Ohdar, R.; Mahapatra, S. Parametric appraisal of mechanical property of fused deposition modelling processed parts. Mater. Des. 2010, 31, 287–295. [Google Scholar] [CrossRef]
- Vidakis, N.; Petousis, M.; Vairis, A.; Savvakis, K.; Maniadi, A. On the compressive behavior of an FDM Steward Platform part. J. Comput. Des. Eng. 2017, 4, 339–346. [Google Scholar] [CrossRef]
- Ali, H.B.; Oleiwi, J.K.; Othman, F.M. Compressive and tensile properties of ABS material as a function of 3D printing process parameters. Rev. Des Compos. Et Des Matériaux Avancés-J. Compos. Adv. Mater. 2022, 32, 117–123. [Google Scholar] [CrossRef]
- Morocho, J.; Sánchez, A.C.; Singaña, M.; Donoso, C. Efect of the flling pattern on the compression strength of 3D printed objects using acrylonitrile butadiene styrene (ABS). Key Eng. Mater. 2020, 834, 115–119. [Google Scholar] [CrossRef]
- Petousis, M.; Vidakis, N.; Mountakis, N.; Karapidakis, E.; Moutsopoulou, A. Compressive response versus power consumption of acrylonitrile butadiene styrene in material extrusion additive manufacturing: The impact of seven critical control parameters. Int. J. Adv. Manuf. Technol. 2023, 126, 1233–1245. [Google Scholar] [CrossRef]
- Banjanin, B.; Vladic, G.; Pal, M.; Balos, S.; Dramicanin, M.; Rackov, M.; Knezevic, I. Consistency analysis of mechanical properties of elements produced by FDM additive manufacturing technology. Matéria (Rio J.) 2018, 23, e12250. [Google Scholar] [CrossRef]
- Equbal, A.; Sood, K.A.; Equbal, M.I.; Badruddin, I.A.; Khan, Z.A. RSM based investigation of compressive properties of FDM fabricated part. CIRP J. Manuf. Sci. Technol. 2021, 35, 701–714. [Google Scholar] [CrossRef]
- Ligon, S.C.; Liska, R.; Stampfl, J.; Gurr, M.; Mulhaupt, R. Polymers for 3D Printing and Customized Additive Manufacturing. Chem. Rev. 2017, 117, 10212–10290. [Google Scholar] [CrossRef]
- Selvamani, S.K.; Samykano, M.; Subramaniam, S.R.; Ngui, W.K.; Kadirgama, K.; Kanagaraj, G.; Idris, M.S. 3D Printing: Overview of ABS Evolvement. In Proceedings of the 3rd International Conference on Automotive Innovation Green Energy Vehicle, Kuantan, Malaysia, 25–26 July 2018; pp. 020041-1–020041-11. [Google Scholar]
- Mazzanti, V.; Malagutti, L.; Mollica, F. FDM 3D Printing of Polymers Containing Natural Fillers: A Review of their Mechanical Properties. Polymers 2019, 11, 1094. [Google Scholar] [CrossRef]
- Chohan, J.S.; Kumar, R.; Singh, T.B.; Singh, S.; Sharma, S.; Singh, J.; Mia, M.; Pimenov, D.Y.; Chattopadhyaya, S.; Dwivedi, S.P.; et al. Taguchi S/N and TOPSIS Based Optimization of Fused Deposition Modelling and Vapor Finishing Process for Manufacturing of ABS Plastic Parts. Materials 2020, 13, 5176. [Google Scholar] [CrossRef]
- Kulich, D.M.; Gaggar, S.K.; Lowry, V.; Stepien, R. Acrylonitrile–Butadiene–Styrene Polymers. In Encyclopedia of Polymer Science and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2001; pp. 174–201. [Google Scholar]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Kutnjak-Mravlinčić, S.; Bischof, S.; Sutlović, A. Application of additive technology in footwear design. In Proceedings of the 8th Central European Conference on Fiber-Grade Polymers, Chemical Fibers and Special Textiles, Zagreb, Croatia, 16–18 September 2015; Dekanić, T., Tarbuk, A., Eds.; University of Zagreb, Faculty of Textile Technology: Zagreb, Croatia, 2015; pp. 201–206. [Google Scholar]
- Vanderploeg, A.; Lee, S.E.; Mamp, M. The application of 3D printing technology in the fashion industry. Int. J. Fash. Des. Technol. Educ. 2017, 10, 170–179. [Google Scholar] [CrossRef]
- Yap, Y.L.; Yeong, W.Y. Additive manufacture of fashion and jewellery products: A mini review. Virtual Phys. Prototyp. 2014, 9, 195–201. [Google Scholar] [CrossRef]
- Kutnjak-Mravlinčić, S.; Akalović, J.; Bischof, S. Merging footwear design and functionality. AUTEX Res. J. 2020, 20, 372–381. [Google Scholar] [CrossRef]
- Kutnjak-Mravlinčić, S.; Sutlović, A.; Glogar, M.I.; Ercegović Ražić, S.; Godec, D. Innovative Development of Batch Dyed 3D Printed Acrylonitrile/Butadiene/Styrene Objects. Molecules 2021, 26, 6637. [Google Scholar] [CrossRef]
- Thompson, M.K.; Moroni, G.; Vaneker, T.; Fadel, G.; Campbell, R.I.; Gibson, I.; Bernard, A.; Schulz, J.; Graf, P.; Ahuja, B.; et al. Design for Additive Manufacturing: Trends, Opportunities, Considerations, and Constraints. CIRP Ann. Manuf. Technol. 2016, 65, 737–760. [Google Scholar] [CrossRef]
- Rosen, D. Design for Additive Manufacturing: Past, Present, and Future Directions. J. Mech. Design. 2014, 136, 090301. [Google Scholar] [CrossRef]
- Kutnjak-Mravlinčić, S.; Godec, D.; Sutlović, A. 3D modeling and 3D printing of hollow structure in footwear industry. In Proceedings of the 9th Scientific—Professional Symposium Textile Science and Economy—Creative Mixer, Zagreb, Croatia, 25 January 2016; Glogar, M.I., Grilec, A., Eds.; University of Zagreb Faculty of Textile Technology: Zagreb, Croatia, 2016; pp. 100–103. [Google Scholar]
- Sun Lim, H. Development of 3D Printed Shoe Designs Using Traditional Muntin Patterns. Fash. Text. Res. J. 2017, 19, 134–139. [Google Scholar] [CrossRef]
- Dong, G.; Tessier, D.; Zhao, Y.F. Design of Shoe Soles Using Lattice Structures Fabricated by Additive Manufacturing. Proc. Des. Soc. Int. Conf. Eng. Des. 2019, 1, 719–728. [Google Scholar] [CrossRef]
- Kutnjak-Mravlincˇic´, S.; Pilipović, A.; Godec, D. Selection of appropriate 3D printing orientation considering actual product. In Proceedings of the RIM 2019—Development and Modernization of Production, Sarajevo, Bosnia and Herzegovina, 18–20 September 2019; Hodžić, A., Islamović, F., Mijović, B., Eds.; University of Bihac, Faculty of Engineering Sciences: Bihac, Bosnia and Herzegovina, 2019; pp. 455–460. [Google Scholar]
- García-Dominguez, A.; Claver, J.; Sebastián, M.A. Optimization Methodology for Additive Manufacturing of Customized Parts by Fused Deposition Modeling (FDM). Application to a Shoe Heel. Polymers 2020, 12, 2119. [Google Scholar] [CrossRef]
- Watkin, H. Ica & Kostika Launch 3D-Printed Exobiology Shoe Collection. Available online: https://all3dp.com/4/ica-kostika-launch-3d-printed-exobiology-shoe-collection (accessed on 31 March 2024).
- Yusuf, B. These Spring Heel Shoes Can Only Be Made with 3D Printing. Available online: https://all3dp.com/spring-heel-shoes/ (accessed on 31 May 2023).
- Sher, D. Footwear Industry Leads in Race for 3D Printed Consumer Products. Available online: https://www.3dprintingmedia.network/footwear-industry-leads-in-race-for-3d-printed-consumer-products (accessed on 31 March 2024).
- Scott, C. Dr. Scholl’s Partners with Wiivv for 3D Printed Custom Insoles, 3D Printing Industry. Available online: https://3dprint.com/233413/dr-scholls-partners-with-wiivv/ (accessed on 31 March 2024).
- Sher, D. SmarTech Issues New Report Projecting Footwear AM and 3D Printed Footwear Will Generate $6.5 Billion Yearly Revenues by 2029. SmarTech. Available online: https://www.smartechanalysis.com/news/smartech-projects-3d-printed-footwear-6-5-billion-yearly-revenues-by-2029/ (accessed on 31 March 2024).
- Kutnjak-Mravlinčić, S. Influence of 3D Print Parameters Produced by Fused Deposition Process and Geometry of Lattice Structures on Properties of 3D Printed Products from Acrylonitrile/Butadiene/Styrene. Ph.D. Thesis, University of Zagreb Faculty of Textile Technology, Zagreb, Croatia, 21 May 2021. [Google Scholar]
- HRN EN ISO 604; ISO 604:2002; EN ISO 604:2003; Plastics—Determination of Compressive Properties. Croatian Standards Institute: Zagreb, Croatia, 2003.
- Kutnjak-Mravlinčić, S.; Pilipović, A.; Godec, D. Influence of orientation on mechanical properties in fused deposition modelling. J. Leather Footwear 2020, 68, 4–13. [Google Scholar] [CrossRef]
- Kutnjak-Mravlinčić, S.; Sutlović, A.; Godec, D.; Krišković, T. Application of 3D printing from acrylonitrile/butadiene/styrene in the realization of prototypes of heels of women’s shoes. Tekst. J. Text. Cloth. Technol. 2022, 71, 48–56. [Google Scholar]
- Wang, M.; Liu, L.; Ren, Y.; Xu, G.; Yi Wang, Y. Investigation of Heated Nozzle Temperature in ABS Specimens Fabricated Based on Fiber Bragg Grating During Fused Deposition Modeling Process. Integr. Ferroelectr. 2020, 208, 177–180. [Google Scholar] [CrossRef]
- Spahiu, T.; Ehrmann, A.; Almeida, H.; Jimeno-Morenilla, A.; Kyratsis, P. Footwear products and the role of industry 4.0 for sustainable production. In Proceedings of the VI International Conference “Modern Trends and Innovations in the Textile Industry”, Belgrade, Serbia, 14–15 September 2023. [Google Scholar]
- Mallakpour, S.; Radfar, Z.; Mustansar Hussain, C. Advanced Application of Additive Manufacturing in the Footwear Industry: From Customized Insoles to Fully 3D-Printed Shoes. In Additive Manufacturing Materials and Technologies, Medical Additive Manufacturing; Elsevier GmbH: Berlin, Germany, 2024; pp. 153–178. [Google Scholar]
- Gelaziene, E.; Milasiene, D. Influence of the Type of Plastic and Printing Technologies on the Compressive Behavior of 3D-Printed Heel Prototypes. Materials 2023, 16, 1930. [Google Scholar] [CrossRef]
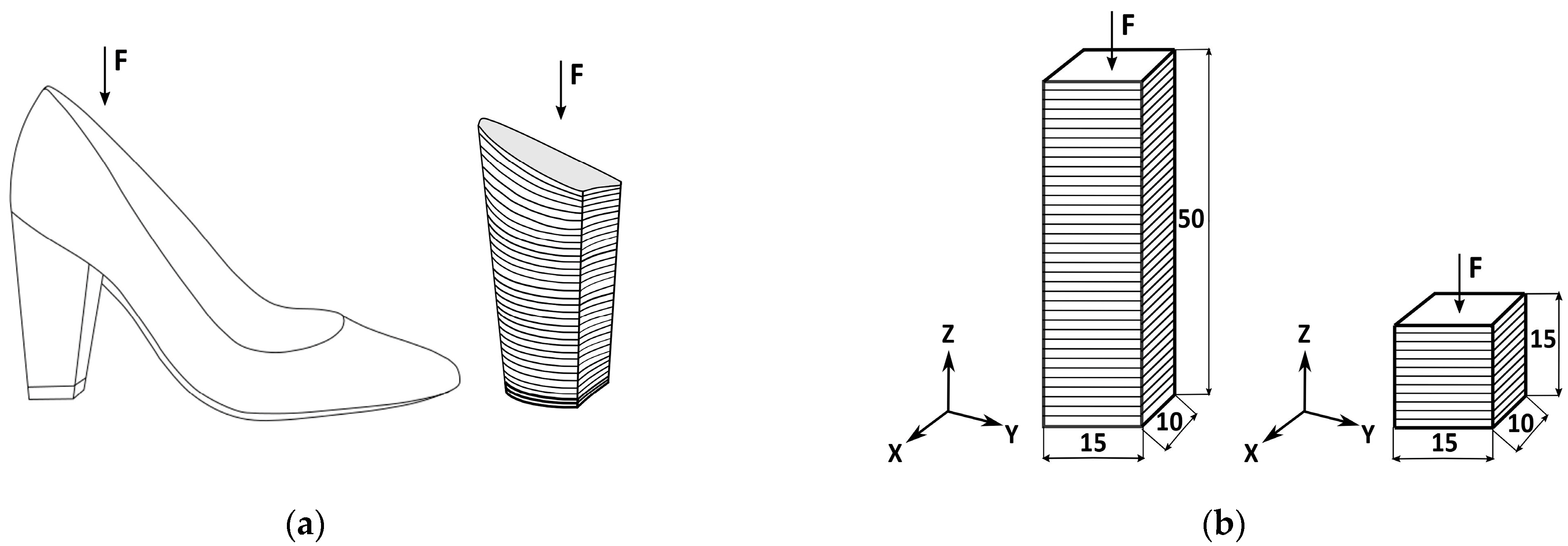










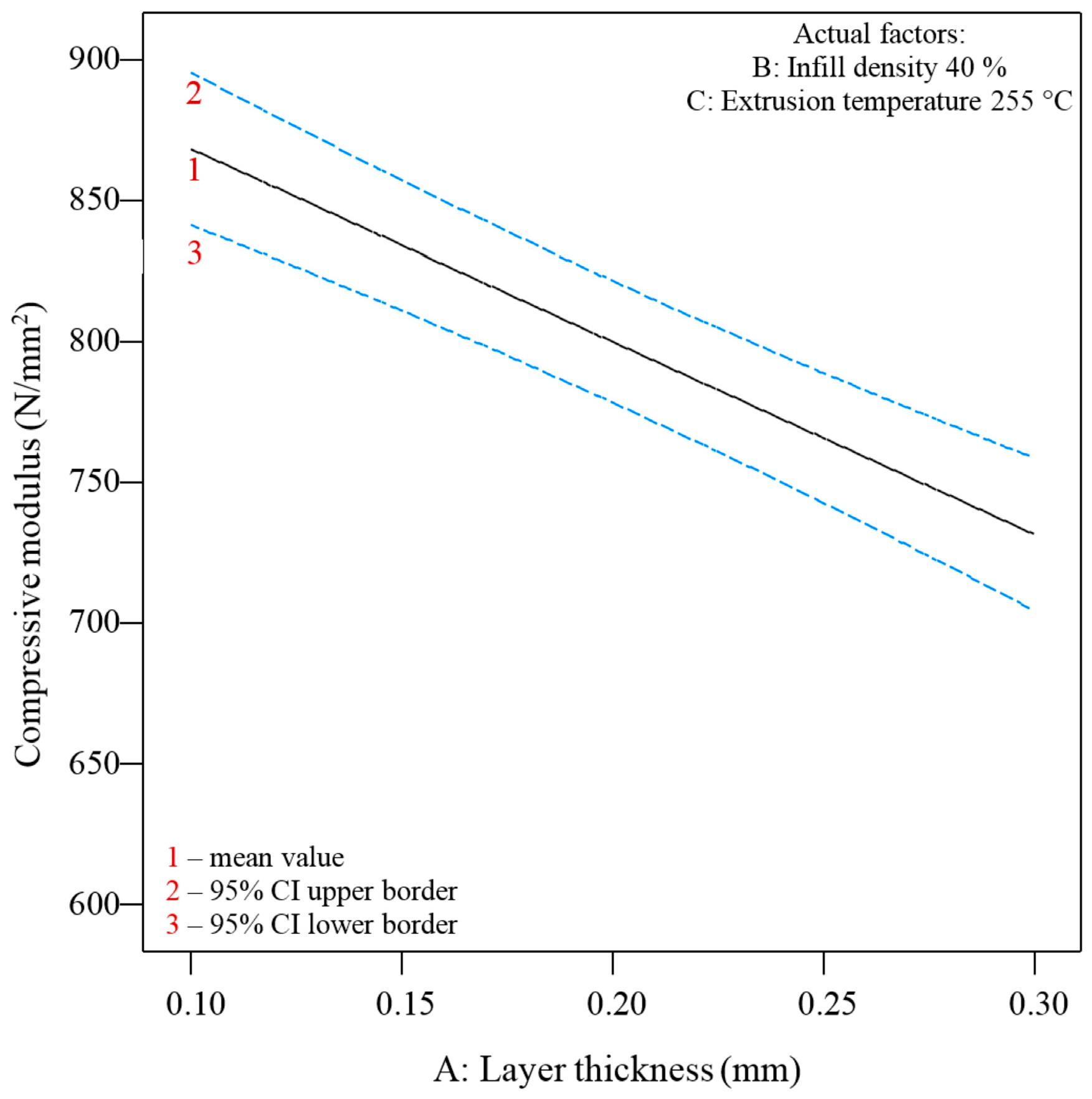
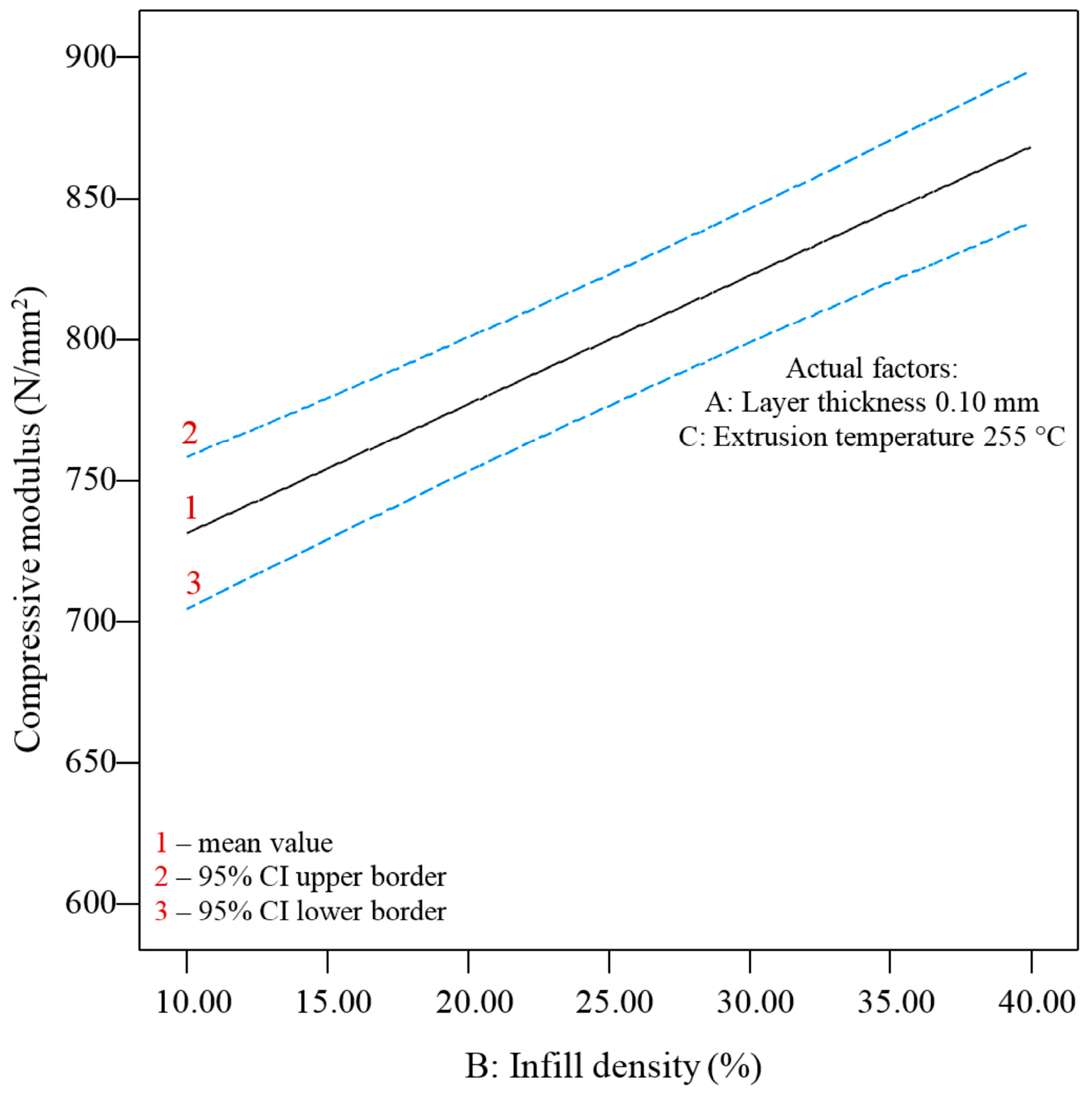
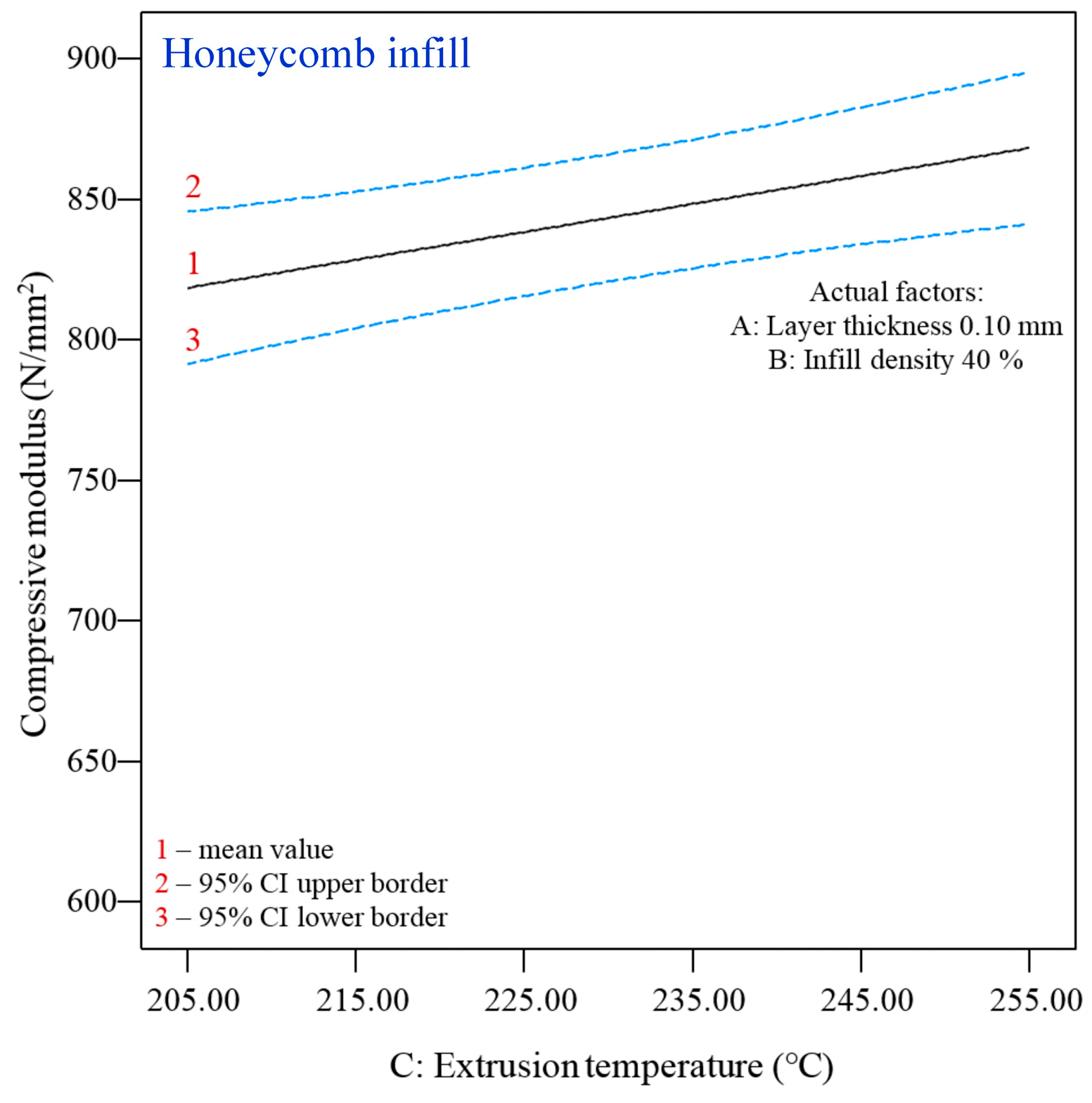

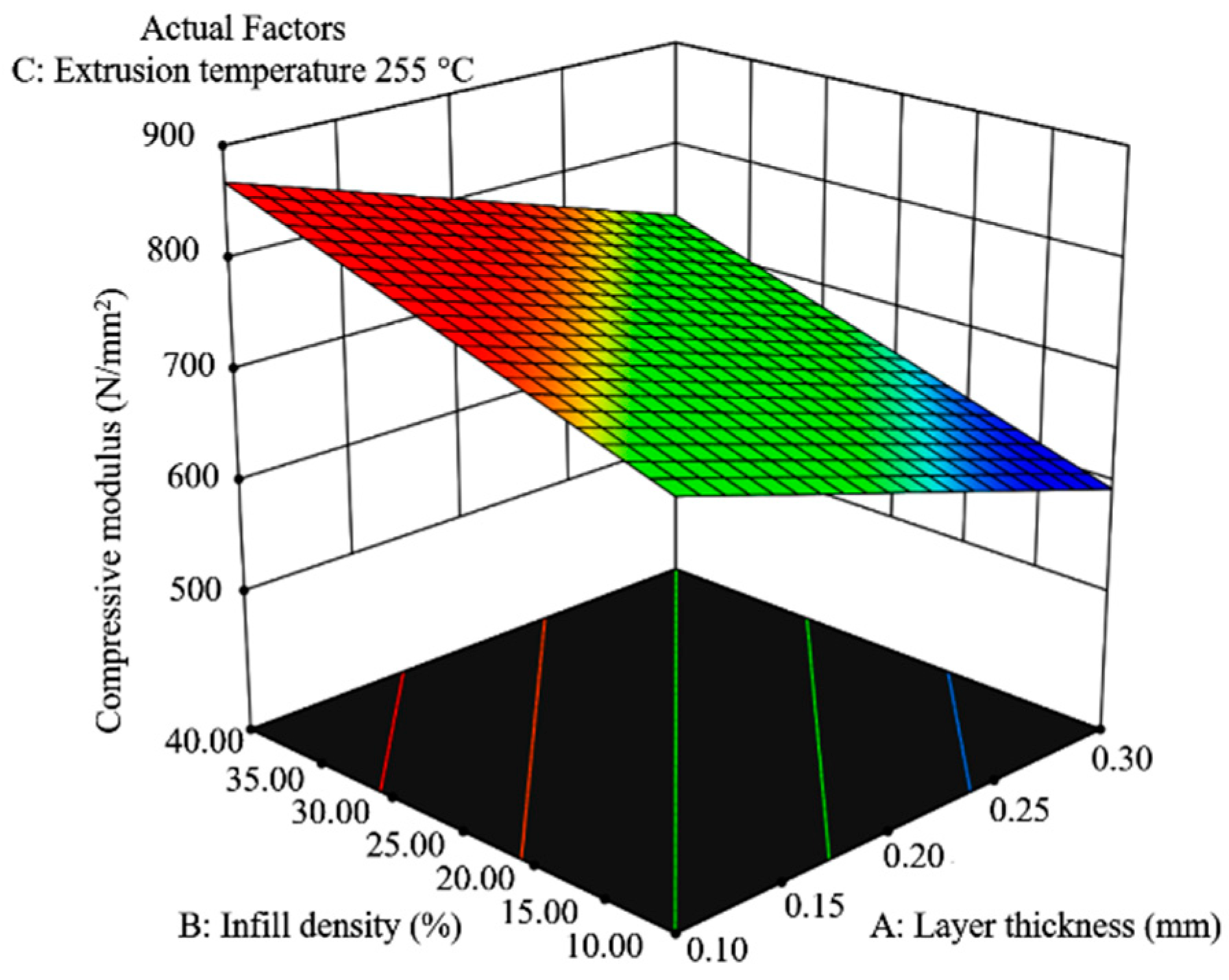


| Levels | Layer Thickness mm | Infill Density % | Extrusion Temperature °C |
|---|---|---|---|
| −1.682 | 0.10 | 10 | 205 |
| −1 | 0.15 | 15 | 215 |
| 0 | 0.20 | 25 | 230 |
| 1 | 0.25 | 35 | 245 |
| 1.682 | 0.30 | 40 | 255 |
| Run | Factor 1: Layer Thickness LT, mm | Factor 2: Infill Density ID,% | Factor 3: Temperature ϑ, °C |
|---|---|---|---|
| 1 | 0.20 | 25 | 230 |
| 2 | 0.15 | 35 | 245 |
| 3 | 0.20 | 40 | 230 |
| 4 | 0.10 | 25 | 230 |
| 5 | 0.20 | 25 | 230 |
| 6 | 0.20 | 25 | 230 |
| 7 | 0.20 | 25 | 255 |
| 8 | 0.20 | 25 | 205 |
| 9 | 0.15 | 15 | 245 |
| 10 | 0.15 | 15 | 215 |
| 11 | 0.25 | 35 | 245 |
| 12 | 0.20 | 25 | 230 |
| 13 | 0.30 | 25 | 230 |
| 14 | 0.25 | 15 | 215 |
| 15 | 0.25 | 15 | 245 |
| 16 | 0.20 | 25 | 230 |
| 17 | 0.20 | 10 | 230 |
| 18 | 0.15 | 35 | 215 |
| 19 | 0.25 | 35 | 215 |
| Trial Number | Factor 1 | Factor 2 | Factor 3 | Linear Infill 45° | Honeycomb Infill | ||
|---|---|---|---|---|---|---|---|
| A: Layer Thickness LT, mm | B: Infill Density ID,% | C: Temp. ϑ, °C | Compressive Strength ± SD σx (N/mm2) | Compressive Modulus ± SD Ec (N/mm2) | Compressive Strength ± SD σx (N/mm2) | Compressive Modulus ± SD Ec (N/mm2) | |
| 1 | 0.20 | 25 | 230 | 26.12 ± 0.23 | 565.32 ± 13.59 | 30.96 ± 0.67 | 733.12 ± 4.49 |
| 2 | 0.15 | 35 | 245 | 37.09 ± 0.85 | 836.89 ± 8.36 | 33.81 ± 1.43 | 804.53 ± 18.81 |
| 3 | 0.20 | 40 | 230 | 38.99 ± 0.40 | 808.38 ± 8.02 | 32.98 ± 0.82 | 772.91 ± 5.16 |
| 4 | 0.10 | 25 | 230 | 35.55 ± 0.90 | 823.13 ± 12.31 | 32.70 ± 0.24 | 778.43 ± 27.07 |
| 5 | 0.20 | 25 | 230 | 30.90 ± 0.61 | 717.28 ± 3.23 | 29.73 ± 0.50 | 723.16 ± 3.81 |
| 6 | 0.20 | 25 | 230 | 30.92 ± 0.73 | 724.63 ± 1.00 | 30.78 ± 0.65 | 707.53 ± 17.59 |
| 7 | 0.20 | 25 | 255 | 32.63 ± 0.70 | 755.46 ± 7.08 | 30.30 ± 0.72 | 725.37 ± 1.59 |
| 8 | 0.20 | 25 | 205 | 29.42 ± 0.06 | 671.05 ± 1.31 | 29.98 ± 0.14 | 689.67 ± 5.02 |
| 9 | 0.15 | 15 | 245 | 23.61 ± 0.38 | 539.24 ± 8.78 | 28.53 ± 1.44 | 695.55 ± 9.45 |
| 10 | 0.15 | 15 | 215 | 28.70 ± 0.15 | 675.96 ± 2.96 | 27.84 ± 1.28 | 695.20 ± 14.67 |
| 11 | 0.25 | 35 | 245 | 38.15 ± 0.79 | 747.05 ± 10.29 | 31.44 ± 0.31 | 738.11 ± 12.06 |
| 12 | 0.20 | 25 | 230 | 30.93 ± 0.30 | 712.41 ± 7.15 | 29.24 ± 0.06 | 706.58 ± 6.31 |
| 13 | 0.30 | 25 | 230 | 23.54 ± 0.41 | 497.94 ± 7.68 | 28.01 ± 0.27 | 646.33 ± 0.93 |
| 14 | 0.25 | 15 | 215 | 24.67 ± 0.28 | 582.57 ± 4.79 | 24.61 ± 0.87 | 603.46 ± 11.16 |
| 15 | 0.25 | 15 | 245 | 25.93 ± 0.14 | 646.69 ± 10.79 | 26.28 ± 1.02 | 655.59 ± 0.69 |
| 16 | 0.20 | 25 | 230 | 30.87 ± 0.37 | 716.84 ± 7.21 | 29.08 ± 0.23 | 674.96 ± 5.63 |
| 17 | 0.20 | 10 | 230 | 25.37 ± 0.89 | 612.80 ± 12.53 | 25.59 ± 0.37 | 622.47 ± 9.08 |
| 18 | 0.15 | 35 | 215 | 36.21 ± 1.02 | 835.79 ± 4.11 | 31.52 ± 0.74 | 768.44 ± 11.75 |
| 19 | 0.25 | 35 | 215 | 33.17 ± 1.16 | 733.88 ± 2.95 | 30.29 ± 0.40 | 683.91 ± 10.29 |
| Source | Sum of Squares | DoF | Mean Square | F-Value | p-Value | Remark |
|---|---|---|---|---|---|---|
| Model | 356.90 | 2 | 178.45 | 32.56 | <0.0001 | Significant |
| A—Layer thickness | 47.99 | 1 | 47.99 | 8.76 | 0.0092 | Significant |
| B—Infill density | 308.91 | 1 | 308.91 | 56.36 | <0.0001 | Significant |
| Residual | 87.69 | 16 | 5.48 | |||
| Lack of fit | 69.37 | 12 | 5.78 | 1.26 | 0.4476 | Not significant |
| Pure Error | 18.32 | 4 | 4.58 | |||
| Corrected Total | 444.59 | 18 |
| Compressive Strength σc [N/mm2] | |
|---|---|
| Standard deviation | 2.34 |
| Mean | 30.67 |
| Coefficient of determination (R-squared (r2)) | 0.8028 |
| Source | Sum of Squares | DoF | Mean Square | F-Value | p-Value | Remark |
|---|---|---|---|---|---|---|
| Model | 102.83 | 4 | 25.71 | 55.73 | <0.0001 | Significant |
| A—Layer thickness | 21.30 | 1 | 21.30 | 46.17 | <0.0001 | Significant |
| B—Infill density | 76.31 | 1 | 76.31 | 165.43 | <0.0001 | Significant |
| C—Temperature | 2.96 | 1 | 2.96 | 6.41 | 0.0239 | Significant |
| B2 | 2.26 | 1 | 2.26 | 4.90 | 0.0439 | Significant |
| Residual | 6.46 | 14 | 0.46 | |||
| Lack of fit | 3.44 | 10 | 0.34 | 0.46 | 0.8569 | Not significant |
| Pure Error | 3.02 | 4 | 0.75 | |||
| Corrected Total | 109.29 | 18 |
| Compressive Strength σc [N/mm2] | |
|---|---|
| Standard deviation | 0.68 |
| Mean | 29.67 |
| Coefficient of determination (R-squared (r2)) | 0.9409 |
| Source | Sum of Squares | DoF | Mean Square | F-Value | p-Value | Remark |
|---|---|---|---|---|---|---|
| Model | 1.233 ∙ 105 | 2 | 61,629.98 | 16.83 | 0.0001 | Significant |
| A—Layer thickness | 42,856.25 | 1 | 42,856.25 | 11.71 | 0.0035 | Significant |
| B—Infill density | 80,403.71 | 1 | 80,403.71 | 21.96 | 0.0002 | Significant |
| Residual | 58,575.56 | 16 | 3660.97 | |||
| Lack of fit | 39,900.99 | 12 | 3325.08 | 0.7122 | 0.7090 | Not significant |
| Pure Error | 18,674.57 | 4 | 4668.64 | |||
| Corrected Total | 1.818 ∙ 105 | 18 |
| Compressive Modulus Ec [N/mm2] | |
|---|---|
| Standard deviation | 60.51 |
| Mean | 694.91 |
| Coefficient of determination (R-squared (r2)) | 0.6779 |
| Source | Sum of Squares | DoF | Mean Square | F-Value | p-Value | Remark |
|---|---|---|---|---|---|---|
| Model | 47,778.07 | 3 | 15,926.02 | 67.84 | <0.0001 | Significant |
| A—Layer thickness | 18,690.31 | 1 | 18,690.31 | 79.61 | <0.0001 | Significant |
| B—Infill density | 26,069.58 | 1 | 26,029.56 | 111.05 | <0.0001 | Significant |
| C—Temperature | 3018.18 | 1 | 3018.18 | 12.86 | 0.0027 | Significant |
| Residual | 3521.39 | 15 | 234.76 | |||
| Lack of fit | 1572.40 | 11 | 142.94 | 0.29 | 0.9520 | Not significant |
| Pure Error | 1948.99 | 4 | 487.25 | |||
| Corrected Total | 51,299.46 | 18 |
| Compressive Modulus Ec [N/mm2] | |
|---|---|
| Standard deviation | 15.32 |
| Mean | 706.60 |
| Coefficient of determination (R-squared (r2)) | 0.9314 |
| Parameter/Property | Goal | Lower Limit | Upper Limit | Importance |
|---|---|---|---|---|
| A: Layer thickness | Is in range | 0.10 mm | 0.30 mm | 3 |
| B: Infill density | Is in range | 10% | 40% | 3 |
| C: Extrusion temperature | Is in range | 205 °C | 255 °C | 3 |
| Compressive strength—L45 | Maximize | 36 N/mm2 | 42 N/mm2 | 5 |
| Compressive strength—H | Maximize | 30 N/mm2 | 36 N/mm2 | 5 |
| Compressive modulus—L45 | Maximize | 880 N/mm2 | 920 N/mm2 | 5 |
| Compressive modulus—H | Maximize | 800 N/mm2 | 880 N/mm2 | 5 |
| Parameter/Property | 1 | 2 | 3 |
|---|---|---|---|
| Layer thickness [mm] | 0.10 | 0.10 | 0.10 |
| Infill density [%] | 40.00 | 40.00 | 40.00 |
| Extrusion temperature [°C] | 209.67 | 222.96 | 254.35 |
| Compressive strength [N/mm2] | 41.59 | 41.59 | 41.59 |
| Compressive modulus [N/mm2] | 918.72 | 918.72 | 918.72 |
| Desirability | 0.95 | 0.95 | 0.95 |
| Parameter/Property | 1 | 2 | 3 |
|---|---|---|---|
| Layer thickness [mm] | 0.10 | 0.10 | 0.10 |
| Infill density [%] | 40.00 | 39.85 | 39.66 |
| Extrusion temperature [°C] | 255 | 254.78 | 255 |
| Compressive strength [N/mm2] | 35.70 | 35.68 | 35.66 |
| Compressive modulus [N/mm2] | 868.32 | 867.43 | 866.78 |
| Desirability | 0.76 | 0.74 | 0.73 |
| Print Parameter | Value |
|---|---|
| Layer thickness | 0.10 mm |
| Infill density | 40% |
| Number of shells | 3 |
| Infill build speed | 90 mm/s |
| Shell speed | 40 mm/s |
| Infill pattern | linear 45° |
| Roof thickness | 1.00 mm |
| Extrusion temperature | 210 °C |
| Author | Infill Density, % | Infill Pattern | Layer Thickness, mm | Compressive Strength |
|---|---|---|---|---|
| Oudah et al. [25] | 75 | Tri-hexagon | 0.3 | 37.6 |
| Oudah et al. [25] | 50 | Zigzag | 0.3 | 39.15 |
| Oudah et al. [25] | 75 | Gyroid | 0.2 | 44.64 |
| Ali et al. [30] | 60 | Zigzag | 0.15 | 27.42 |
| Ali et al. [30] | 60 | Gyroid | 0.05 | 27.458 |
| Ali et al. [30] | 60 | Cross | 0.25 | 27.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kutnjak-Mravlinčić, S.; Godec, D.; Pilipović, A.; Sutlović, A. Optimization of the FDM Processing Parameters on the Compressive Properties of ABS Objects for the Production of High-Heeled Shoes. J. Manuf. Mater. Process. 2024, 8, 106. https://doi.org/10.3390/jmmp8030106
Kutnjak-Mravlinčić S, Godec D, Pilipović A, Sutlović A. Optimization of the FDM Processing Parameters on the Compressive Properties of ABS Objects for the Production of High-Heeled Shoes. Journal of Manufacturing and Materials Processing. 2024; 8(3):106. https://doi.org/10.3390/jmmp8030106
Chicago/Turabian StyleKutnjak-Mravlinčić, Suzana, Damir Godec, Ana Pilipović, and Ana Sutlović. 2024. "Optimization of the FDM Processing Parameters on the Compressive Properties of ABS Objects for the Production of High-Heeled Shoes" Journal of Manufacturing and Materials Processing 8, no. 3: 106. https://doi.org/10.3390/jmmp8030106
APA StyleKutnjak-Mravlinčić, S., Godec, D., Pilipović, A., & Sutlović, A. (2024). Optimization of the FDM Processing Parameters on the Compressive Properties of ABS Objects for the Production of High-Heeled Shoes. Journal of Manufacturing and Materials Processing, 8(3), 106. https://doi.org/10.3390/jmmp8030106








