Verifying the Accuracy of 3D-Printed Objects Using an Image Processing System
Abstract
:1. Introduction
2. Related Work
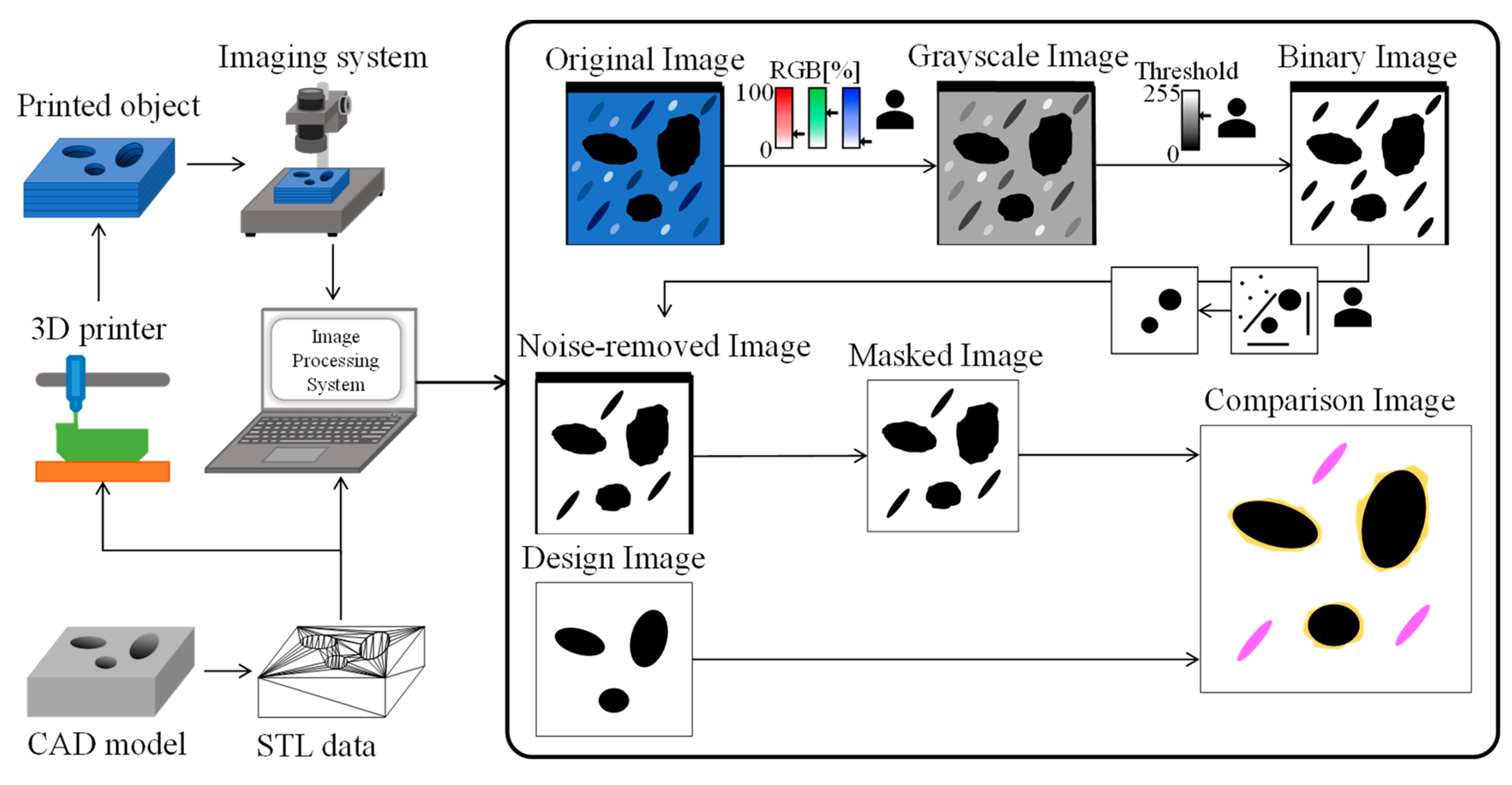
3. Proposed Image Processing System
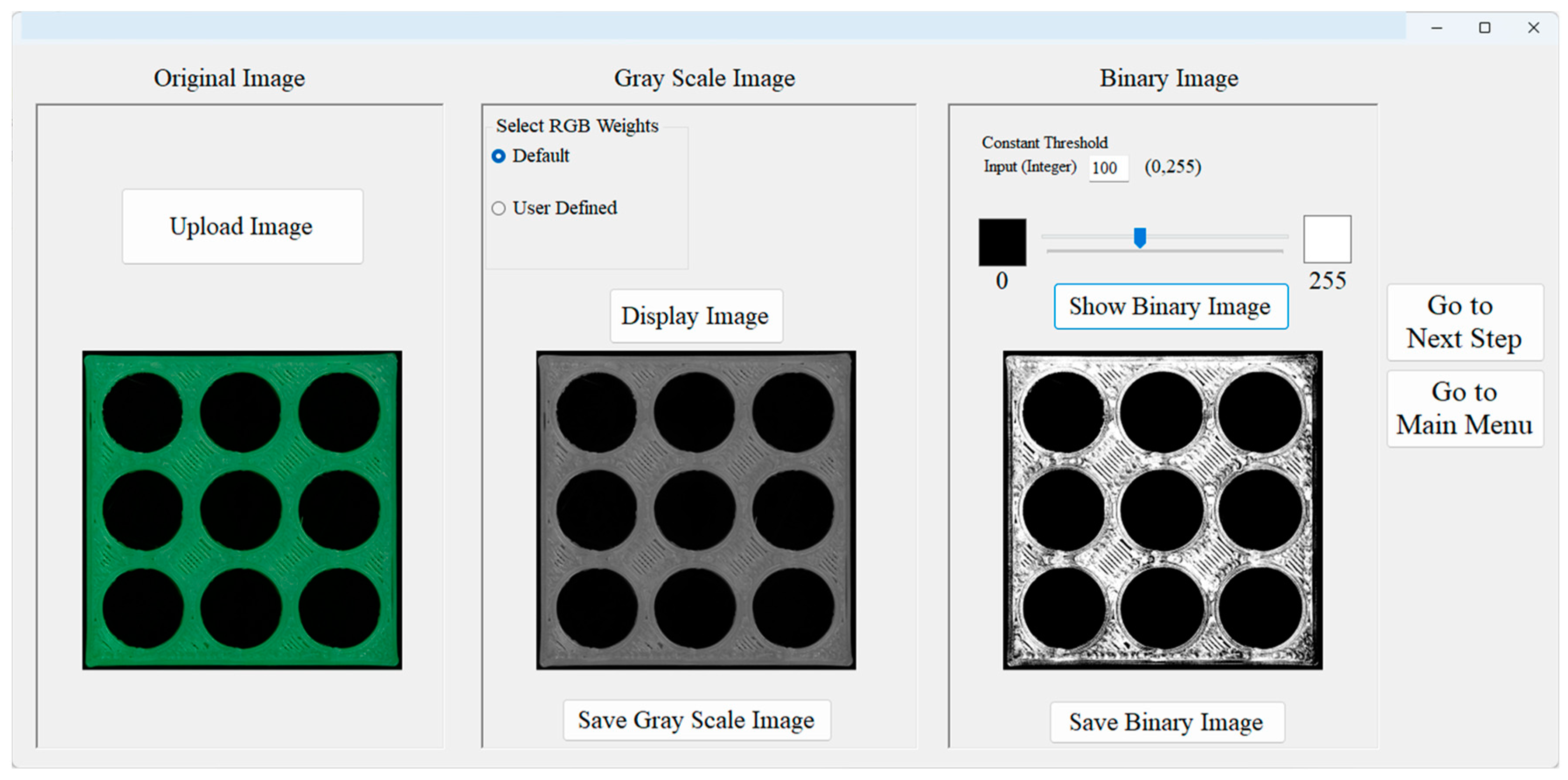
User Interfaces
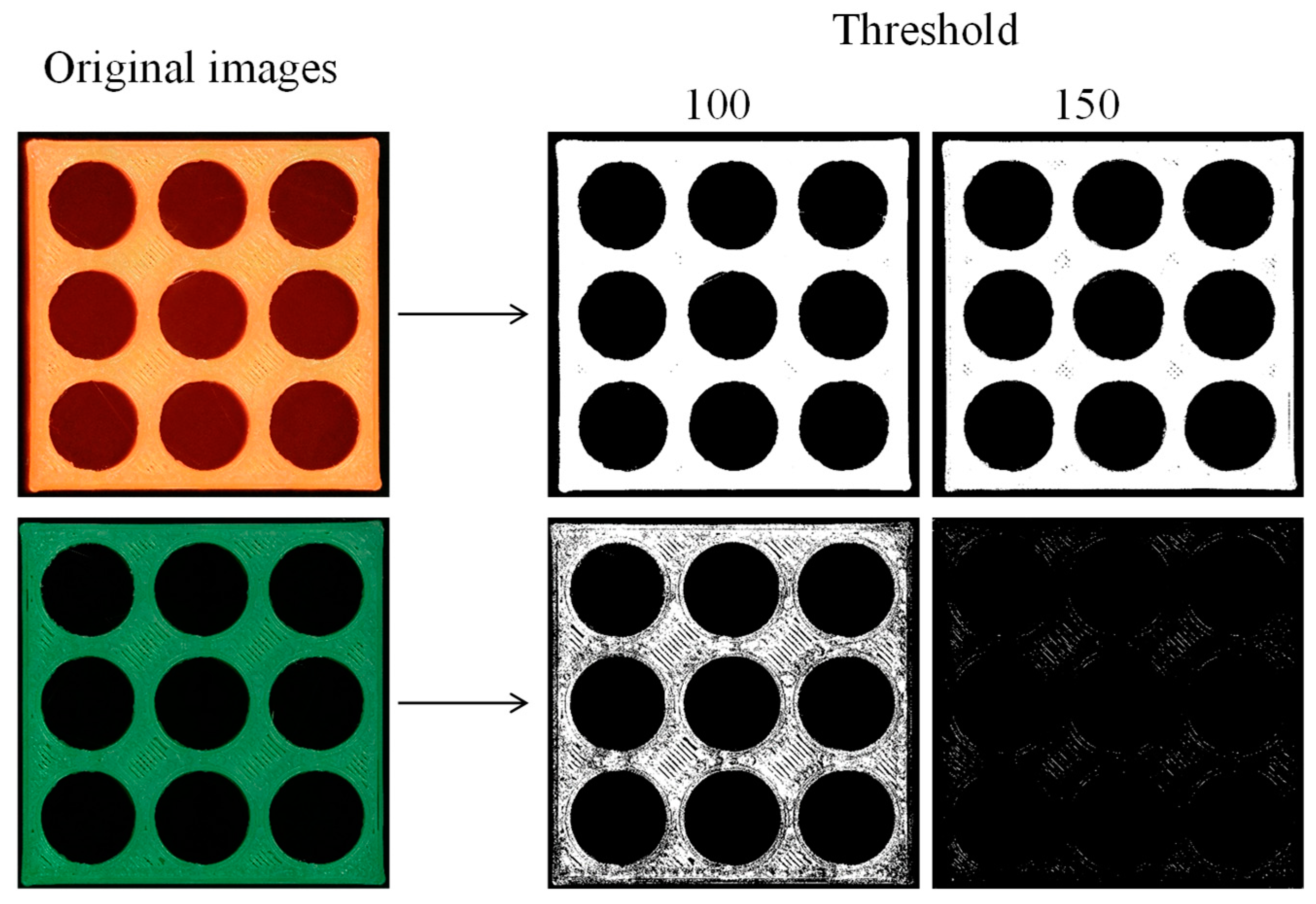
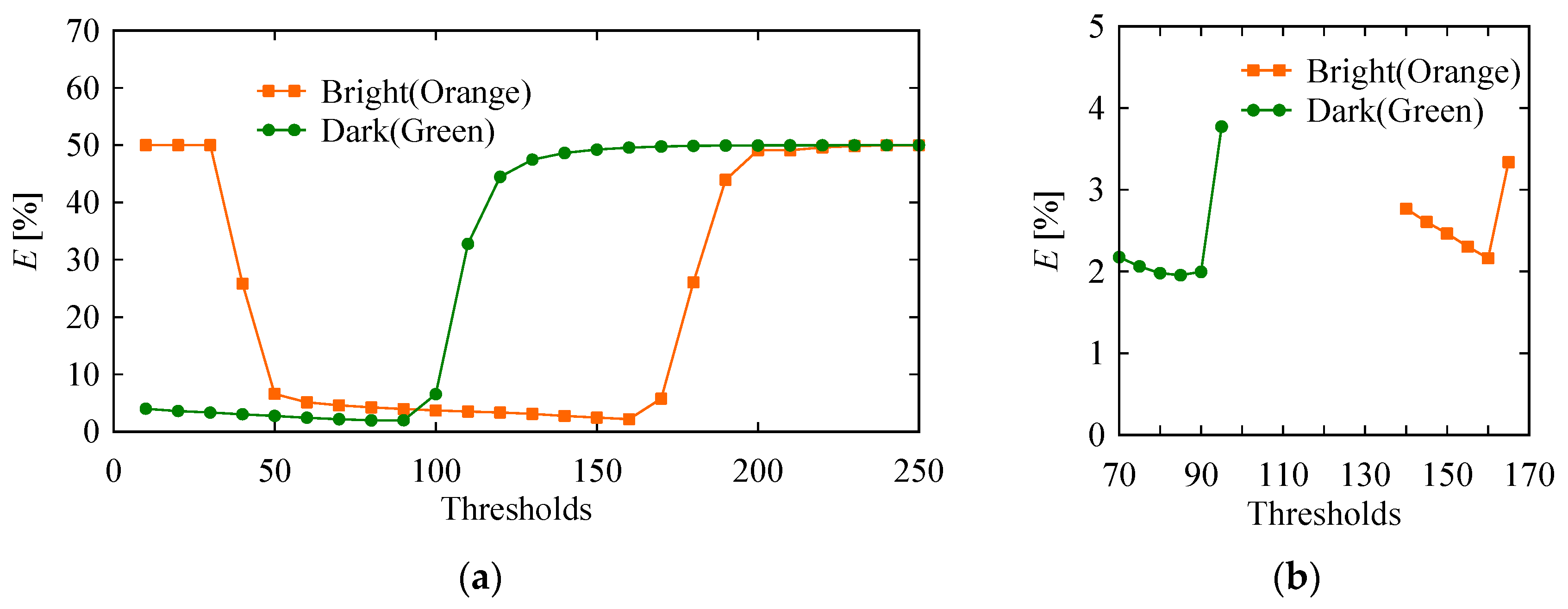
4. Accuracy of a Simple 3D-Printed Object
5. Accuracy of a 3D-Printed Porous Structure (Complex Object)
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bourell, D.L.; Rosen, D.W.; Leu, M.C. The Roadmap for Additive Manufacturing and Its Impact. 3D Print. Addit. Manuf. 2014, 1, 6–9. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies: 3D Printing, Rapid Prototyping, and Direct Digital Manufacturing; Springer: New York, NY, USA, 2015. [Google Scholar]
- Ullah, A.M.M.S.; Tashi; Kubo, A.; Harib, K.H. Tutorials for Integrating 3D Printing in Engineering Curricula. Educ. Sci. 2020, 10, 194. [Google Scholar] [CrossRef]
- Ullah, A.M.M.S.; D’Addona, D.M.; Harib, K.H.; Lin, T. Fractals and Additive Manufacturing. Int. J. Autom. Technol. 2016, 10, 222–230. [Google Scholar] [CrossRef]
- Ullah, A.M.M.S.; Kiuno, H.; Kubo, A.; D’Addona, D.M. A system for designing and 3D printing of porous structures. CIRP Ann. 2020, 69, 113–116. [Google Scholar] [CrossRef]
- Seto, Y.; Ullah, A.M.S.; Kubo, A.; Marilena, D.D.; Teti, R. On the Porous Structuring using Unit Cells. Procedia CIRP 2021, 99, 381–386. [Google Scholar] [CrossRef]
- Ullah, A.S.; D’Addona, D.M.; Seto, Y.; Yonehara, S.; Kubo, A. Utilizing Fractals for Modeling and 3D Printing of Porous Structures. Fractal Fract. 2021, 5, 40. [Google Scholar] [CrossRef]
- Carew, R.M.; Morgan, R.M.; Rando, C. A Preliminary Investigation into the Accuracy of 3D Modeling and 3D Printing in Forensic Anthropology Evidence Reconstruction. J. Forensic Sci. 2019, 64, 342–352. [Google Scholar] [CrossRef] [PubMed]
- Edwards, J.; Rogers, T. The Accuracy and Applicability of 3D Modeling and Printing Blunt Force Cranial Injuries. J. Forensic Sci. 2018, 63, 683–691. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.Y.; Cho, J.W.; Chang, N.Y.; Chae, J.M.; Kang, K.H.; Kim, S.C.; Cho, J.H. Accuracy of three-dimensional printing for manufacturing replica teeth. Korean J. Orthod. 2015, 45, 217–2251. [Google Scholar] [CrossRef]
- Leng, S.; McGee, K.; Morris, J.; Alexander, A.; Kuhlmann, J.; Vrieze, T.; McCollough, C.H.; Matsumoto, J. Anatomic modeling using 3D printing: Quality assurance and optimization. 3D Print. Med. 2017, 3, 6. [Google Scholar] [CrossRef]
- George, E.; Liacouras, P.; Rybicki, F.J.; Mitsouras, D. Measuring and establishing the accuracy and reproducibility of 3D printed medical models. RadioGraphics 2017, 37, 1424–1450. [Google Scholar] [CrossRef]
- Bortolotto, C.; Eshja, E.; Peroni, C.; Orlandi, M.A.; Bizzotto, N.; Poggi, P. 3D printing of CT dataset: Validation of an open source and consumer-available workflow. J. Digit. Imaging 2016, 29, 14–21. [Google Scholar] [CrossRef]
- Herpel, C.; Tasaka, A.; Higuchi, S.; Finke, D.; Kühle, R.; Odaka, K.; Rues, S.; Lux, C.J.; Yamashita, S.; Rammelsberg, P.; et al. Accuracy of 3D Printing Compared with Milling—A Multi-Center Analysis of Try-In Dentures. J. Dent. 2021, 110, 103681. [Google Scholar] [CrossRef] [PubMed]
- Cai, T.; Rybicki, F.J.; Giannopoulos, A.A.; Schultz, K.; Kumamaru, K.K.; Liacouras, P.; Demehri, S.; Small, K.M.; Mitsouras, D. The residual STL volume as a metric to evaluate accuracy and reproducibility of anatomic models for 3D printing: Application in the validation of 3D-printable models of maxillofacial bone from reduced radiation dose CT images. 3D Print. Med. 2015, 1, 2. [Google Scholar] [CrossRef]
- Kim, T.; Lee, S.; Kim, G.B.; Hong, D.; Kwon, J.; Park, J.W.; Kim, N. Accuracy of a simplified 3D-printed implant surgical guide. J. Prosthet. Dent. 2020, 124, 195–201. [Google Scholar] [CrossRef]
- Kwon, J.; Kim, G.B.; Kang, S.; Byeon, Y.; Sa, H.-S.; Kim, N. Accuracy of 3D printed guide for orbital implant. Rapid Prototyp. J. 2020, 26, 1363–1370. [Google Scholar] [CrossRef]
- Yuan, F.; Sun, Y.; Zhang, L.; Sun, Y. Accuracy of chair-side fused-deposition modelling for dental applications. Rapid Prototyp. J. 2019, 25, 857–863. [Google Scholar] [CrossRef]
- Borgue, O.; Panarotto, M.; Isaksson, O. Fuzzy model-based design for testing and qualification of additive manufacturing components. Des. Sci. 2022, 8, e11. [Google Scholar] [CrossRef]
- Li, T.; Li, J.; Ding, X.; Sun, X.; Wu, T. An error identification and compensation method for Cartesian 3D printer based on specially designed test artifact. Int. J. Adv. Manuf. Technol. 2023, 125, 4185–4199. [Google Scholar] [CrossRef]
- Holzmond, O.; Li, X. In situ real time defect detection of 3D printed parts. Addit. Manuf. 2017, 17, 135–142. [Google Scholar] [CrossRef]
- Yu, Z.; Li, X.; Zuo, T.; Wang, Q.; Wang, H.; Liu, Z. High-accuracy DLP 3D printing of closed microfluidic channels based on a mask option strategy. Int. J. Adv. Manuf. Technol. 2023, 127, 4001–4012. [Google Scholar] [CrossRef]
- Montgomery, S.M.; Demoly, F.; Zhou, K.; Qi, H.J. Pixel-Level Grayscale Manipulation to Improve Accuracy in Digital Light Processing 3D Printing. Adv. Funct. Mater. 2023, 33, 2213252. [Google Scholar] [CrossRef]
- Ma, Y.; Potappel, J.; Schutyser, M.A.I.; Boom, R.M.; Zhang, L. Quantitative analysis of 3D food printing layer extrusion accuracy: Contextualizing automated image analysis with human evaluations: Quantifying 3D food printing accuracy. Curr. Res. Food Sci. 2023, 6, 100511. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Vidakis, N.; David, C.; Petousis, M.; Sagris, D.; Mountakis, N. Optimization of key quality indicators in material extrusion 3D printing of acrylonitrile butadiene styrene: The impact of critical process control parameters on the surface roughness, dimensional accuracy, and porosity. Mater. Today Commun. 2023, 34, 105171. [Google Scholar] [CrossRef]
- Eltes, P.E.; Kiss, L.; Bartos, M.; Gyorgy, Z.M.; Csakany, T.; Bereczki, F.; Lesko, V.; Puhl, M.; Varga, P.P.; Lazary, A. Geometrical accuracy evaluation of an affordable 3D printing technology for spine physical models. J. Clin. Neurosci. 2020, 72, 438–446. [Google Scholar] [CrossRef]
- Nguyen, P.; Stanislaus, I.; McGahon, C.; Pattabathula, K.; Bryant, S.; Pinto, N.; Jenkins, J.; Meinert, C. Quality assurance in 3D-printing: A dimensional accuracy study of patient-specific 3D-printed vascular anatomical models. Front. Med. Technol. 2023, 5, 1097850. [Google Scholar] [CrossRef]
- Huang, H.; Xiang, C.; Zeng, C.; Ouyang, H.; Wong, K.K.; Huang, W. Patient-specific geometrical modeling of orthopedic structures with high efficiency and accuracy for finite element modeling and 3D printing. Australas. Phys. Eng. Sci. Med. 2015, 38, 743–753. [Google Scholar] [CrossRef]
- Xia, M.; Nematollahi, B.; Sanjayan, J. Shape Accuracy Evaluation of Geopolymer Specimens Made Using Particle-Bed 3D Printing. In Proceedings of the Second RILEM International Conference on Concrete and Digital Fabrication, Online, 6–9 July 2020; Bos, F.P., Lucas, S.S., Wolfs, R.J.M., Salet, T.A.M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 1011–1019. [Google Scholar]
- Yonehara, S.; Ullah, A.S. Elucidating accuracy of 3D printed porous structure by analyzing images of designed and printed structures. In Proceedings of the International Conference on Design and Concurrent Engineering 2021 & Manufacturing Systems Conference 2021 (iDECON/MS2021), JSME, Virtual, 3–4 September 2021; p. 17. [Google Scholar]
- Okamoto, T.; Yonehara, S.; Ura, S.; Ghosh, A.K. A Metrological System for 3D-Printed Objects. In Proceedings of the 38th American Society for Precision Engineering Annual Meeting, Boston, MA, USA, 12–17 November 2023. [Google Scholar]












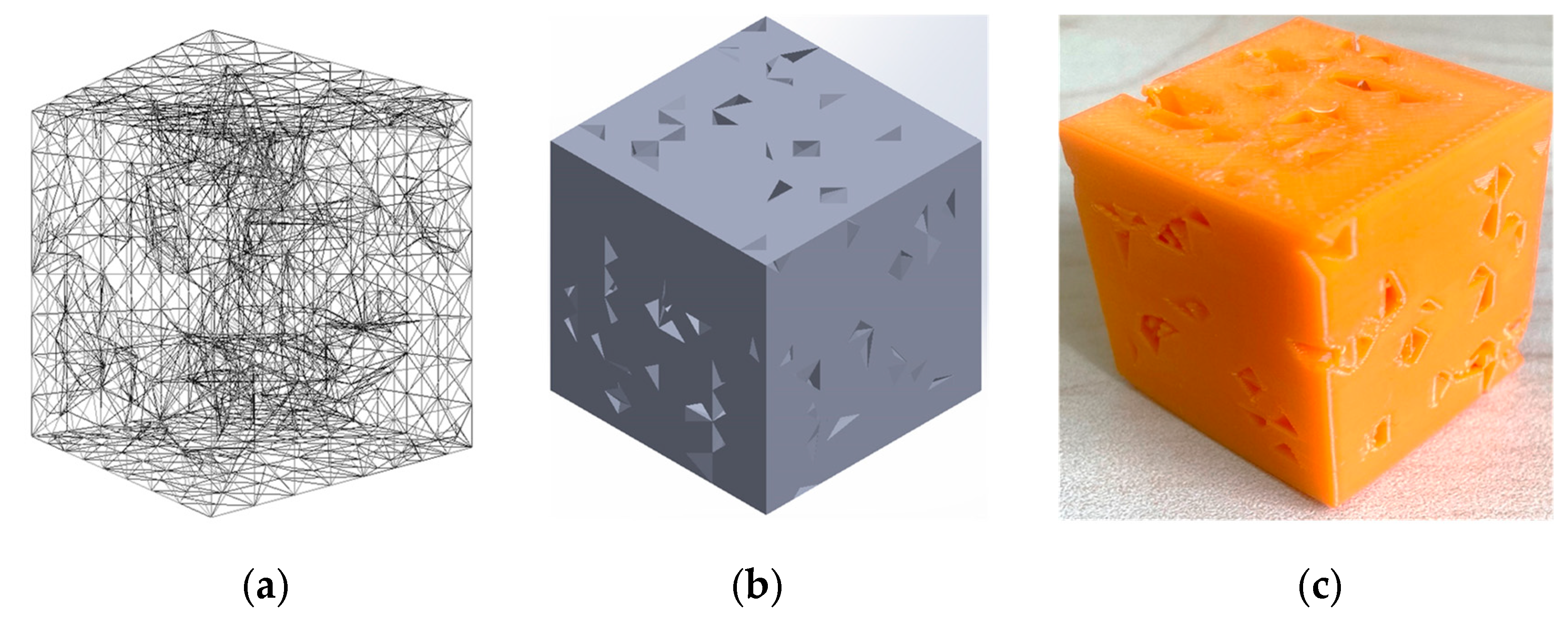


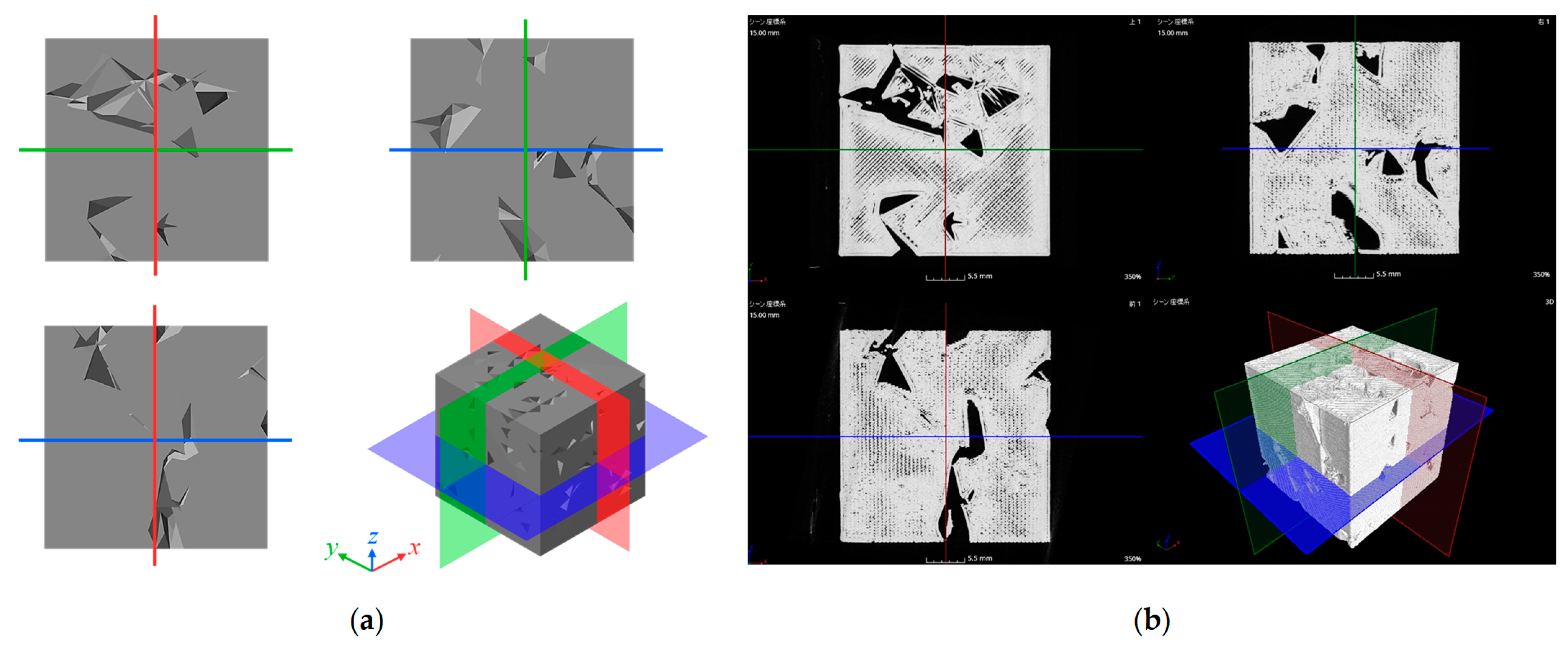

| Items | Descriptions |
|---|---|
| Material | Thermoplastic Filament Made of Poly-Lactic Acid (PLA) |
| Printing technology | Fused Filament Fabrication (FFF) |
| Extrusion width [mm] | 0.4 |
| Extruder temperature [°C] | 205 |
| Printing speed [mm/s] | 50.0 |
| Infill speed [mm/s] | 80.0 |
| Layer height [mm] | 0.25 |
| Infill density [%] | 15 |
| Infill pattern | Grid |
| Infill angles [°] | 45, 135 |
| Printer | Raise3D Pro2™ (Irvine, CA, USA) |
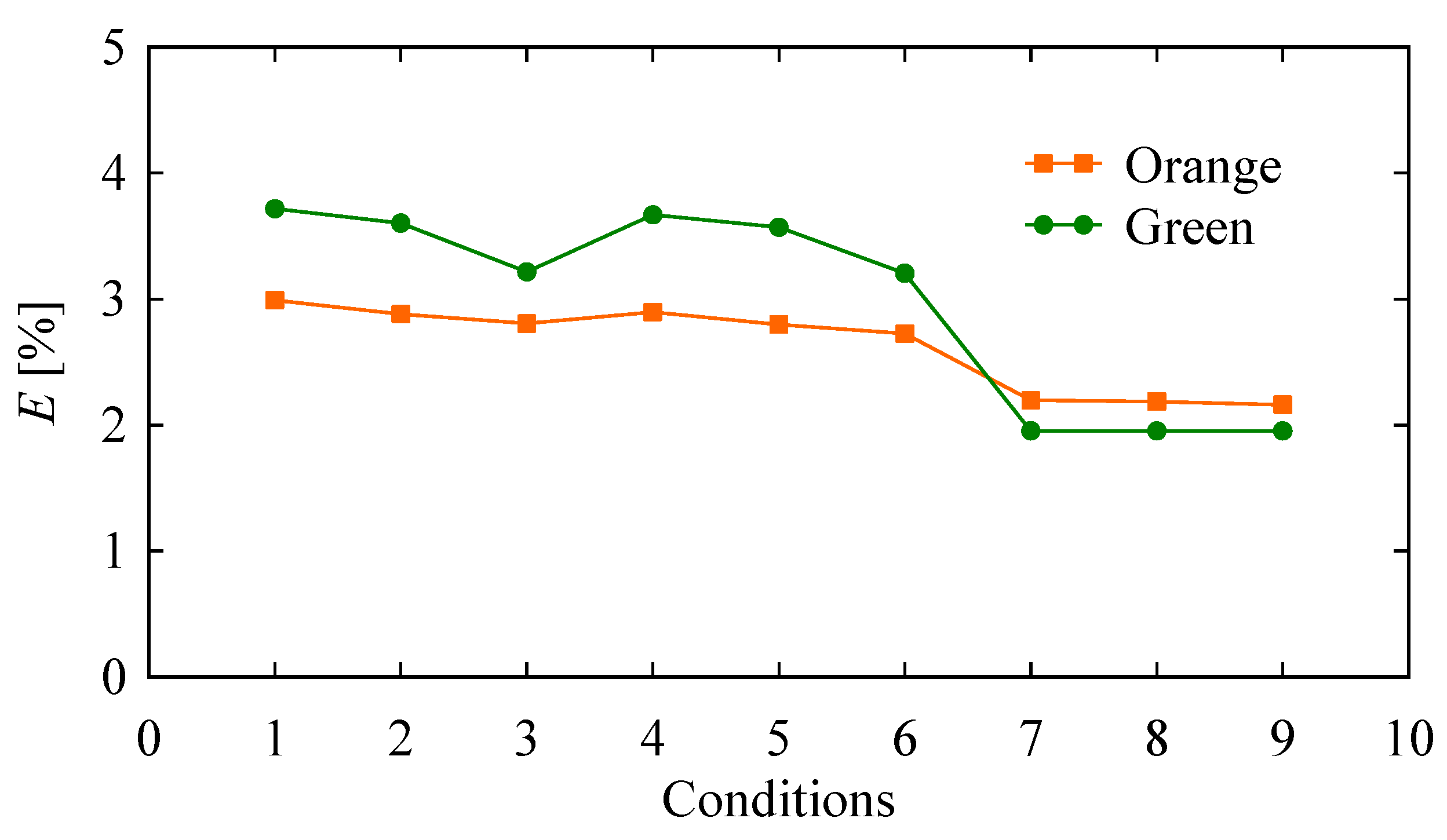
| Conditions | θmin [°] | θmax [°] | pc [Pixels] | wc [Pixels] | Thresholds |
|---|---|---|---|---|---|
| 1 | 0 | 45 | 100 | 50 | For the orange object 160 For the green object 85 |
| 2 | 200 | 100 | |||
| 3 | 500 | 250 | |||
| 4 | 90 | 100 | 50 | ||
| 5 | 200 | 100 | |||
| 6 | 500 | 250 | |||
| 7 | 180 | 100 | 50 | ||
| 8 | 200 | 100 | |||
| 9 | 500 | 250 |
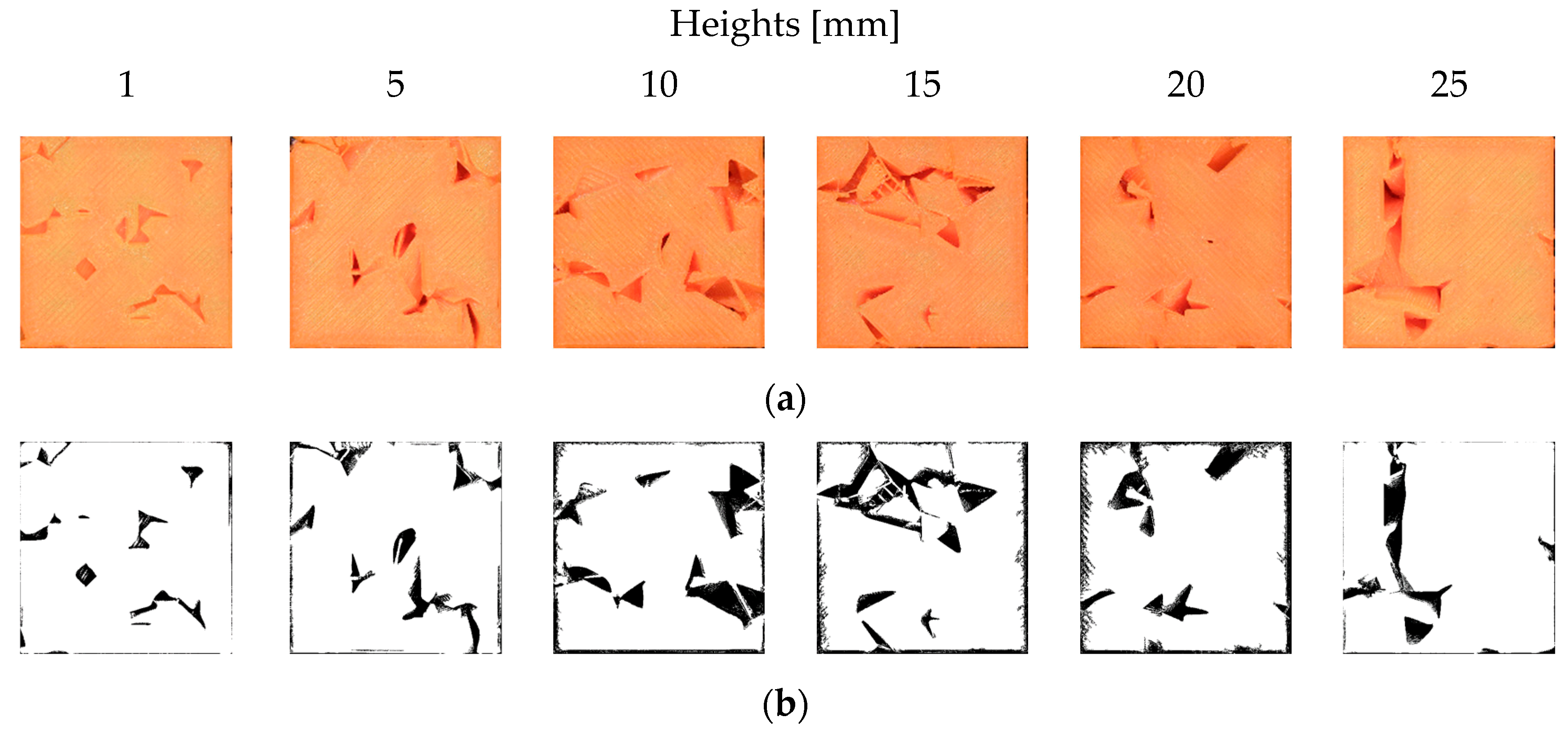
| Heights [mm] | 1 | 5 | 10 | 15 | 20 | 25 |
|---|---|---|---|---|---|---|
| E [%] | 3.85 | 9.29 | 10.89 | 10.50 | 10.74 | 6.90 |
| Height [mm] | 1 | 5 | 10 | 15 | 20 | 25 |
|---|---|---|---|---|---|---|
| E [%] | 2.86 | 3.55 | 4.06 | 3.55 | 2.18 | 3.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okamoto, T.; Ura, S. Verifying the Accuracy of 3D-Printed Objects Using an Image Processing System. J. Manuf. Mater. Process. 2024, 8, 94. https://doi.org/10.3390/jmmp8030094
Okamoto T, Ura S. Verifying the Accuracy of 3D-Printed Objects Using an Image Processing System. Journal of Manufacturing and Materials Processing. 2024; 8(3):94. https://doi.org/10.3390/jmmp8030094
Chicago/Turabian StyleOkamoto, Takuya, and Sharifu Ura. 2024. "Verifying the Accuracy of 3D-Printed Objects Using an Image Processing System" Journal of Manufacturing and Materials Processing 8, no. 3: 94. https://doi.org/10.3390/jmmp8030094
APA StyleOkamoto, T., & Ura, S. (2024). Verifying the Accuracy of 3D-Printed Objects Using an Image Processing System. Journal of Manufacturing and Materials Processing, 8(3), 94. https://doi.org/10.3390/jmmp8030094







