Revealing the Relationship between Critical Inlet Velocity and a Double-Layer Oxide Film Combined with Low-Pressure Casting Technology
Abstract
:1. Introduction
2. Mathematical Model
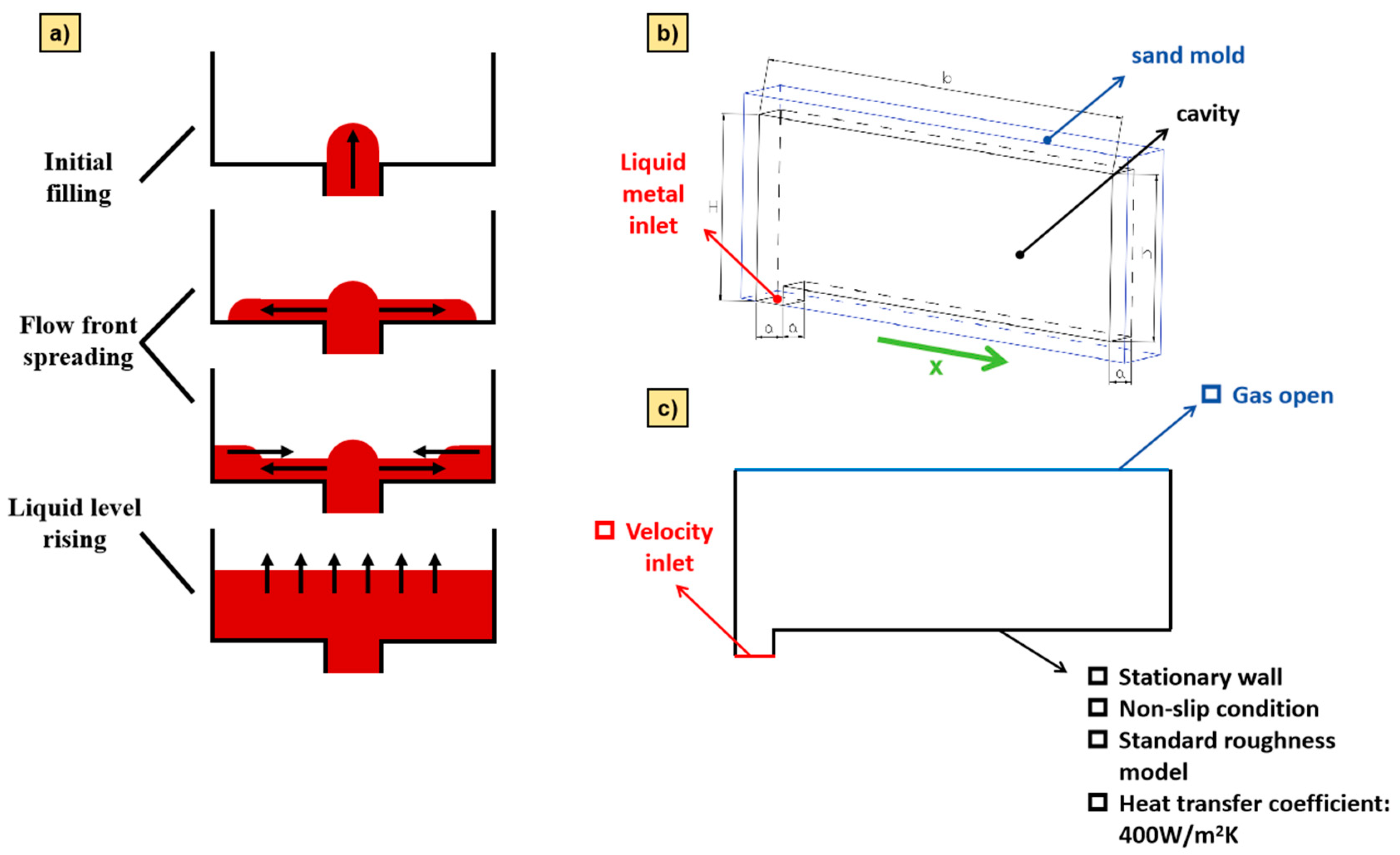
2.1. Typical Structural Model and Streamlining
2.2. Volume Fraction Equation
2.3. Turbulence and Momentum Model
2.4. Surface Tension Equation
2.5. Density and Viscosity Equations
2.6. Thermal Equation
2.7. Material Properties
3. Experimental Methods
3.1. Simulation Scheme
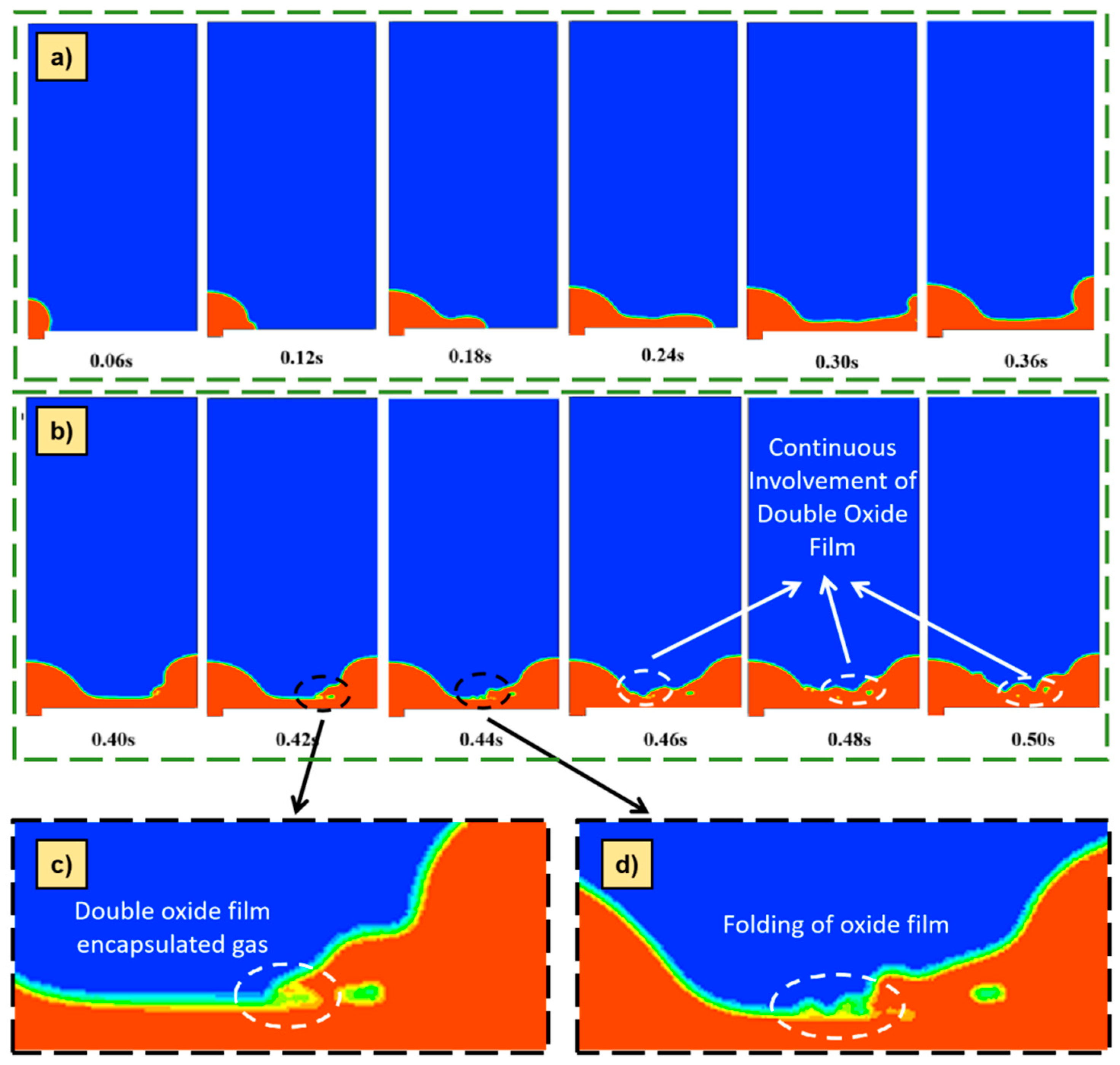
3.2. Numerical Simulation Results for the Determination of the Phenomenon of Gas Entrapment Using a Double Oxide Film Wrapping
3.3. Low-Pressure Casting Validation
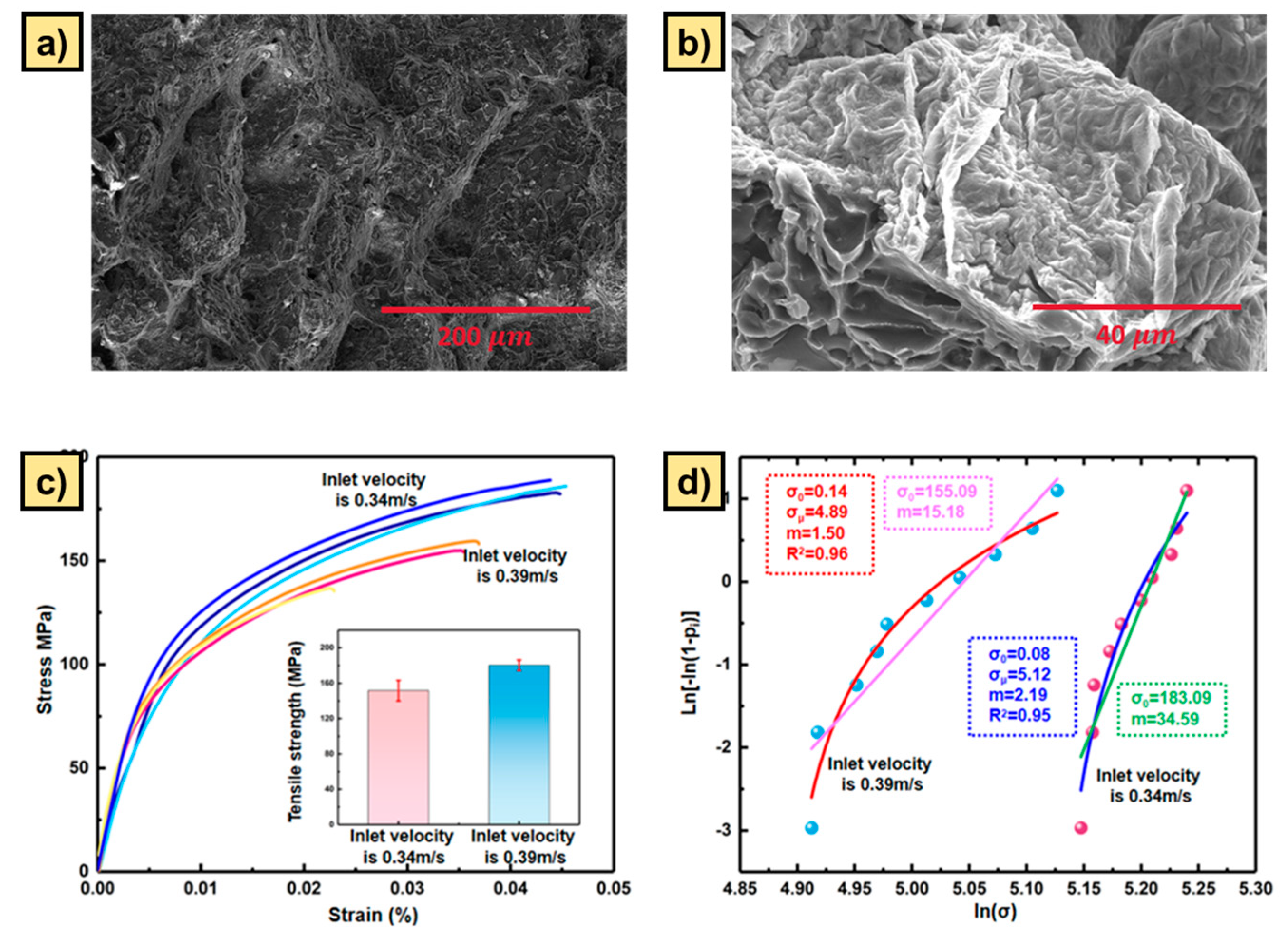
3.4. Mechanical Performance and Reliability Analysis
4. Results and Discussion
4.1. Grid-Independent Verification
4.2. Mechanism of Defect Formation
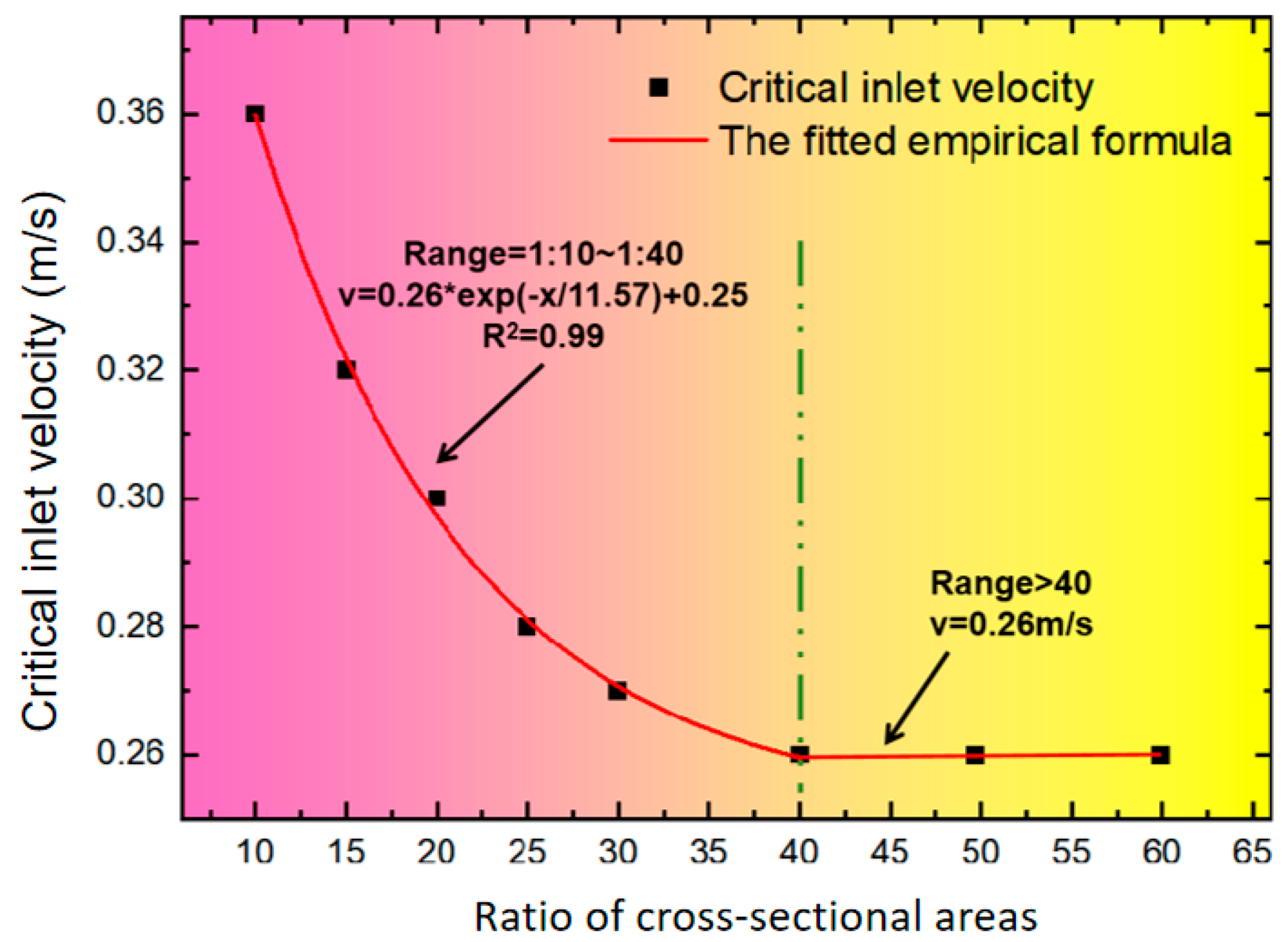
4.3. Calculation of Critical Inlet Velocity
4.4. Casting Experiment and Reliability Analysis
5. Conclusions
- The critical inlet velocity of the spreading stage was obtained based on simulation results. When the ratio of the cross-sectional area change is less than 40, the relationship between the critical velocity and the cross-sectional area ratio follows the empirical formula . The critical inlet velocity remains 0.26 m/s when the ratio of the cross-sectional area exceeds 40.
- The experimental results show that when the inlet velocity is below the critical velocity of 0.5 m/s proposed by Campbell, oxide film defects can still be observed at the tensile fracture of the casting, and the mechanical properties decrease. This proves that the oxide film defects can also be entrained during the spreading stage.
- The critical inlet velocity of the actual casting is larger than the critical inlet velocity of the typical structures. This can be attributed to the difference between cross-sectional shapes of the typical structures and actual castings. The critical velocity obtained from typical structures shows stricter requirements and can be used for the process design of actual castings to eliminate oxide film defects.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, A.A.; Sachdev, A.K.; Apelian, D. Alloy development and process innovations for light metals casting. J. Mater. Process. Technol. 2022, 306, 117606. [Google Scholar] [CrossRef]
- Lai, N.W.; Griffiths, W.D.; Campbell, J. Modelling of the potential for oxide film entrainment in light metal alloy castings. Model. Cast. Weld. Adv. Solidif. Process.-X 2003, 415–422. [Google Scholar]
- Liu, S.G.; Cao, F.Y.; Zhao, X.Y.; Jia, Y.D.; Ning, Z.L.; Sun, J.F. Characteristics of mold filling and entrainment of oxide film in low pressure casting of A356 alloy. Mater. Sci. Eng. A—Struct. Mater. Prop. Microstruct. Process. 2015, 626, 159–164. [Google Scholar] [CrossRef]
- Li, Q.; Hao, Q.T.; Jie, W.Q.; Daan, M. Influence of filling parameters on fatigue properties of A357 alloy produced by counter pressure plaster mold casting. Trans. Nonferrous Met. Soc. China 2013, 23, 1281–1285. [Google Scholar] [CrossRef]
- Fox, S.; Campbell, J. Visualisation of oxide film defects during solidification of aluminium alloys. Scr. Mater. 2000, 43, 881–886. [Google Scholar] [CrossRef]
- Sun, J.Y.; Le, Q.C.; Fu, L.; Bai, J.; Tretter, J.; Herbold, K.; Huo, H.W. Gas entrainment behavior of aluminum alloy engine crankcases during the low-pressure-die-casting process. J. Mater. Process. Technol. 2019, 266, 274–282. [Google Scholar] [CrossRef]
- Viswanath, A.; Manu, M.V.; Savithri, S.; Pillai, U.T.S. Numerical simulation and experimental validation of free surface flows during low pressure casting process. J. Mater. Process. Technol. 2017, 244, 320–330. [Google Scholar] [CrossRef]
- Puga, H.; Barbosa, J.; Azevedo, T.; Ribeiro, S.; Alves, J.L. Low pressure sand casting of ultrasonically degassed AlSi7Mg0.3 alloy: Modelling and experimental validation of mould filling. Mater. Des. 2016, 94, 384–391. [Google Scholar] [CrossRef]
- Niu, Z.C.; Liu, G.Y.; Li, T.; Ji, S.X. Effect of high pressure die casting on the castability, defects and mechanical properties of aluminium alloys in extra-large thin-wall castings. J. Mater. Process. Technol. 2022, 303, 117525. [Google Scholar] [CrossRef]
- Duan, Z.Q.; Chen, W.P.; Pei, X.L.; Hou, H.; Zhao, Y.H. A multimodal data-driven design of low pressure die casting gating system for aluminum alloy cabin. J. Mater. Res. Technol. 2023, 27, 2723–2736. [Google Scholar] [CrossRef]
- Dong, G.J.; Li, S.D.; Ma, S.Z.; Zhang, D.S.; Bi, J.; Wang, J.; Starostenkov, M.D.; Xu, Z. Process optimization of A356 aluminum alloy wheel hub fabricated by low-pressure die casting with simulation and experimental coupling methods. J. Mater. Res. Technol. 2023, 24, 3118–3132. [Google Scholar] [CrossRef]
- Sulaiman, S.; Hamouda, A.M.S. Modeling of the thermal history of the sand casting process. J. Mater. Process. Technol. 2001, 113, 245–250. [Google Scholar] [CrossRef]
- Tiryakioglu, M.; Yousefian, P.; Eason, P.D. Quantification of Entrainment Damage in A356 Aluminum Alloy Castings. Metall. Mater. Trans. A—Phys. Metall. Mater. Sci. 2018, 49, 5815–5822. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Liu, J.H.; Chen, J.M.; Wen, F.L.; Jia, R.; Ma, Q.X. Optimization of residual stress in low-pressure casting of ZL205A alloys. J. Manuf. Process. 2023, 99, 338–350. [Google Scholar] [CrossRef]
- Aniszewski, W.; Ménard, T.; Marek, M. Volume of Fluid (VOF) type advection methods in two-phase flow: A comparative study (vol 97, pg 52, 2014). Comput. Fluids 2017, 152, 193–194. [Google Scholar] [CrossRef]
- Homayonifar, P.; Babaei, R.; Attar, E.; Shahinfar, S.; Davami, P. Numerical modeling of splashing and air entrapment in high-pressure die casting. Int. J. Adv. Manuf. Technol. 2008, 39, 219–228. [Google Scholar] [CrossRef]
- Zhai, Y.Y.; Fuhrman, D.R.; Christensen, E.D. Numerical simulations of flow inside a stone protection layer with a modified k-w turbulence model. Coast. Eng. 2024, 189, 104469. [Google Scholar] [CrossRef]
- Fernández-Fidalgo, J.; Cueto-Felgueroso, L.; Ramírez, L.; Martínez, A.; Nogueira, X. Pore-scale simulation of multiphase flows using equations of state that preserve the correct surface tension. Comput. Methods Appl. Mech. Eng. 2024, 428, 117072. [Google Scholar] [CrossRef]
- Huang, G.J.; Xie, S.S.; Cheng, L. Simulation and Experiment on Direct Continuous Casting Process of Lead Frame Copper Alloy. In Proceedings of the 10th International Conference on Numerical Methods in Industrial Forming Processes (NUMIFORM 2010), Pohang, Republic of Korea, 13–17 June 2010; pp. 515–522. [Google Scholar]
- Li, T.; Davies, J.M.T. Evolution of Entrainment Defects Formed in Mg-Y Alloy Castings. Metall. Mater. Trans. A—Phys. Metall. Mater. Sci. 2020, 51, 5389–5400. [Google Scholar] [CrossRef]
- Seydani, M.Z.; Krimi, A.; Khelladi, S.; Bedel, M.; El Mansori, M. 3D numerical simulation and experimental validation of resin-bonded sand gravity casting: Filling, cooling, and solidification with SPH and ProCAST approaches. Therm. Sci. Eng. Prog. 2024, 47, 102329. [Google Scholar] [CrossRef]
- Green, N.R.; Campbell, J. Influence in oxide film filling defects on the strength of Al-7si-Mg Alloy Castings. Trans. Am. Foundry Soc. 1994, 102, 341–347. [Google Scholar]
- Yang, H.H.; Zhang, Z.H.; Tan, C.H.; Ito, M.K.; Pan, P.; Wang, X.S. Rotating Bending Fatigue Microscopic Fracture Characteristics and Life Prediction of 7075-T7351 Al Alloy. Metals 2018, 8, 210. [Google Scholar] [CrossRef]
- Jia, X.; Cheng, Z.; Guo, B. Nonlinear Fitting Based Weibull Distribution Parameter Confidence Interval Estimation Method. CN201811441043.8, 7 August 2020. [Google Scholar]
- Jia, X.; Cheng, Z.; Guo, B. Distribution Function Logarithmic Transformation Based Weibull Distribution Parameter Estimating Method, Involves Estimating Failure Probability of Each Sample Data, and Performing Logarithm Transform by Weibull Distribution Function. CN109101466A, 22 March 2019. [Google Scholar]
- Jian, L.; Jian, P.; Bing, H.; Xie, G.Y. Oxidation kinetics of Haynes 230 alloy in air at temperatures between 650 and 850 °C. J. Power Sources 2006, 159, 641–645. [Google Scholar] [CrossRef]
- Divandari, M.; Campbell, J. Morphology of oxide films of Al5Mg alloy in dynamic conditions in casting. Int. J. Cast Met. Res. 2005, 18, 187–192. [Google Scholar] [CrossRef]
- Song, H.Q.; Zhang, L.Y.; Cao, F.Y.; Shen, H.X.; Ning, Z.L.; Huang, Y.J.; Zhao, X.Y.; Gu, X.; Qiu, Z.A.; Sun, J.F. Three-dimensional reconstruction of bifilm defects. Scr. Mater. 2021, 191, 179–184. [Google Scholar] [CrossRef]
- Mirak, A.R.; Divandari, M.; Boutorabi, S.M.A.; Campbell, J. Oxide film characteristics of AZ91 magnesium alloy in casting conditions. Int. J. Cast Met. Res. 2007, 20, 215–220. [Google Scholar] [CrossRef]
- Rashid, A.; Campbell, J. Oxide defects in a vacuum investment-cast Ni-based turbine blade. Metall. Mater. Trans. A—Phys. Metall. Mater. Sci. 2004, 35, 2063–2071. [Google Scholar] [CrossRef]
- Griffiths, W.D.; Lai, N.W. Double Oxide Film Defects in Cast Magnesium Alloy. Metall. Mater. Trans. A 2007, 38, 190–196. [Google Scholar] [CrossRef]
- Bozchaloei, G.E.; Varahram, N.; Davami, P.; Kim, S.K. Effect of oxide bifilms on the mechanical properties of cast Al–7Si–0.3Mg alloy and the roll of runner height after filter on their formation. Mater. Sci. Eng. A 2012, 548, 99–105. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Ning, Z.L.; Cao, F.Y.; Liu, S.G.; Huang, Y.J.; Liu, J.S.; Sun, J.F. Effect of Double Oxide Film Defects on Mechanical Properties of As-Cast C95800 Alloy. Acta Metall. Sin.-Engl. Lett. 2017, 30, 541–549. [Google Scholar] [CrossRef]
- Song, H.Q.; Zhang, L.Y.; Cao, F.Y.; Shen, H.X.; Ning, Z.L.; Huang, Y.J.; Zhao, X.Y.; Gu, X.; Li, L.; Sun, J.F. Structure of oxide bifilms in nickel-aluminium bronze alloys. Appl. Surf. Sci. 2021, 541, 148491. [Google Scholar] [CrossRef]


| Temperature (K) | Surface Tension (mN·m−1) | Density (kg/m−3) | Newtonian Viscosity (kg·m−1·s−1) |
|---|---|---|---|
| 995.15 | 876 | 2390.94 | 0.001152 |
| 979.15 | 882 | 2395.46 | 0.001191 |
| 963.15 | 887.62 | 2399.99 | 0.001233 |
| 947.15 | 892.3 | 2404.51 | 0.001277 |
| 931.15 | 896.92 | 2409.04 | 0.001325 |
| 915.15 | 902.97 | 2413.56 | 0.001376 |
| 899.15 | 907.42 | 2418.09 | 0.001432 |
| 888.15 | 910.14 | 2421.03 | 0.00147 |
| 886.15 | 910.24 | 2430.72 | 0.001484 |
| 883.15 | 910.56 | 2439.45 | 0.001499 |
| 880.15 | 910.67 | 2447.34 | 0.001513 |
| 878.15 | 910.89 | 2454.51 | 0.001528 |
| 874.15 | 911.17 | 2464.15 | 0.001551 |
| 870.15 | 911.39 | 2472.65 | 0.001574 |
| 866.15 | 911.58 | 2480.23 | 0.001598 |
| 861.15 | 911.73 | 2489.16 | 0.00163 |
| 856.15 | 911.83 | 2497.01 | 0.001663 |
| 850.15 | 911.89 | 2505.62 | 0.001706 |
| 844.15 | 911.91 | 2537.13 | 0.001741 |
| 843.15 | 907.91 | 2542.75 | 0.001754 |
| 839.15 | 887.14 | 2547.52 | 0.001777 |
| 831.15 | 871.41 | 2553.11 | 0.001838 |
| Cross-Sectional Area Ratio | 1:10 | 1:15 | 1:20 | 1:25 | 1:30 | 1:40 | 1:50 | 1:60 |
|---|---|---|---|---|---|---|---|---|
| Inlet velocity (m/s) | 0.31 0.32 0.33 0.34 0.35 0.36 0.37 0.38 0.39 0.40 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49 0.50 | |||||||
| a (mm) | 20 | |||||||
| b (mm) | 200 | 300 | 400 | 500 | 600 | 800 | 1000 | 1200 |
| h (mm) | 5 | |||||||
| H (mm) | 200 | |||||||
| Model Structure | Mesh Size (mm) | Convergence | Computation Time | Velocity (m/s) | Relative Error (%) |
|---|---|---|---|---|---|
| 2D | 2.5 | Stable | 17 min 23 s | 0.7906 | - |
| 1 | Stable | 25 min 10 s | 0.7729 | 2.24 | |
| 0.5 | Stable | 31 min 35 s | 0.7597 | 1.71 | |
| 0.25 | Stable | 12 h 16 min | 0.7531 | 0.87 | |
| 0.1 | Stable | 17 h 35 min | 0.7491 | 0.53 | |
| 3D | 10 | Stable | 6 h 13 min | 0.6155 | - |
| 8 | Stable | 9 h 12 min | 0.5983 | 2.79 | |
| 5 | Stable | 29 h 45 min | 0.5917 | 1.10 | |
| 2 | Stable | 56 h 56 min | 0.5866 | 0.86 | |
| 1 | Stable | 179 h 33 min | 0.5823 | 0.73 |
| Cross-Sectional Ratio | Critical Inlet Velocity of Castings (m/s) | Critical Inlet Velocity of Typical Structure (m/s) | Relative Error (%) | |
|---|---|---|---|---|
| Castings A | 1:11.78 | 0.3614 | 0.3439 | 4.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Z.; Zhang, C.; Zhang, L.; Cao, F.; Shen, H.; Jin, Z.; Cao, G.; Zhao, X.; Song, H.; Sun, J. Revealing the Relationship between Critical Inlet Velocity and a Double-Layer Oxide Film Combined with Low-Pressure Casting Technology. J. Manuf. Mater. Process. 2024, 8, 168. https://doi.org/10.3390/jmmp8040168
Qiu Z, Zhang C, Zhang L, Cao F, Shen H, Jin Z, Cao G, Zhao X, Song H, Sun J. Revealing the Relationship between Critical Inlet Velocity and a Double-Layer Oxide Film Combined with Low-Pressure Casting Technology. Journal of Manufacturing and Materials Processing. 2024; 8(4):168. https://doi.org/10.3390/jmmp8040168
Chicago/Turabian StyleQiu, Ziao, Chaojun Zhang, Lunyong Zhang, Fuyang Cao, Hongxian Shen, Zhishuai Jin, Guanyu Cao, Xinyi Zhao, Heqian Song, and Jianfei Sun. 2024. "Revealing the Relationship between Critical Inlet Velocity and a Double-Layer Oxide Film Combined with Low-Pressure Casting Technology" Journal of Manufacturing and Materials Processing 8, no. 4: 168. https://doi.org/10.3390/jmmp8040168
APA StyleQiu, Z., Zhang, C., Zhang, L., Cao, F., Shen, H., Jin, Z., Cao, G., Zhao, X., Song, H., & Sun, J. (2024). Revealing the Relationship between Critical Inlet Velocity and a Double-Layer Oxide Film Combined with Low-Pressure Casting Technology. Journal of Manufacturing and Materials Processing, 8(4), 168. https://doi.org/10.3390/jmmp8040168







