Prediction of Wear Rate by a New Direct Method Using the Friction Coefficient Curve
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Hardness
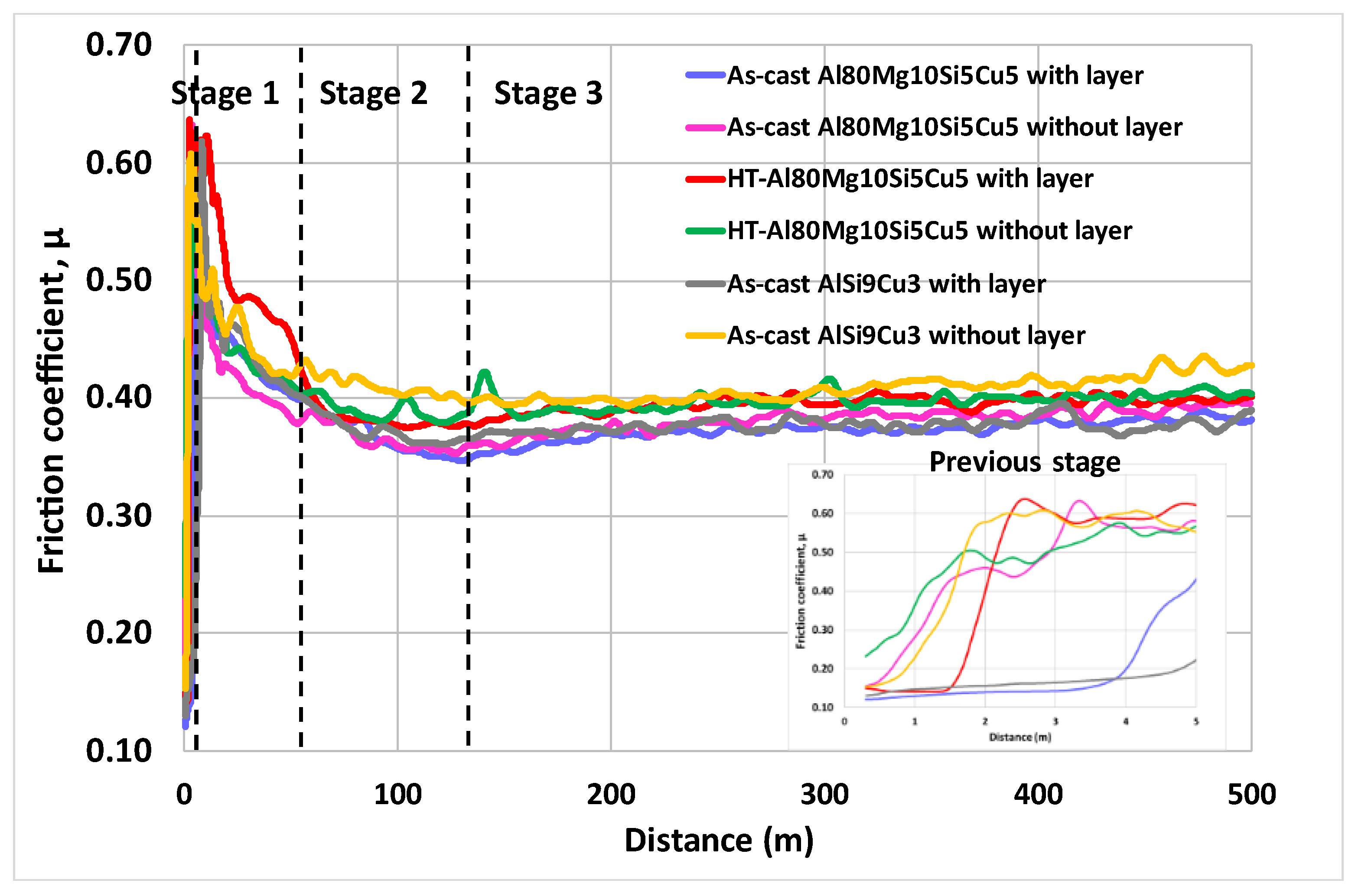
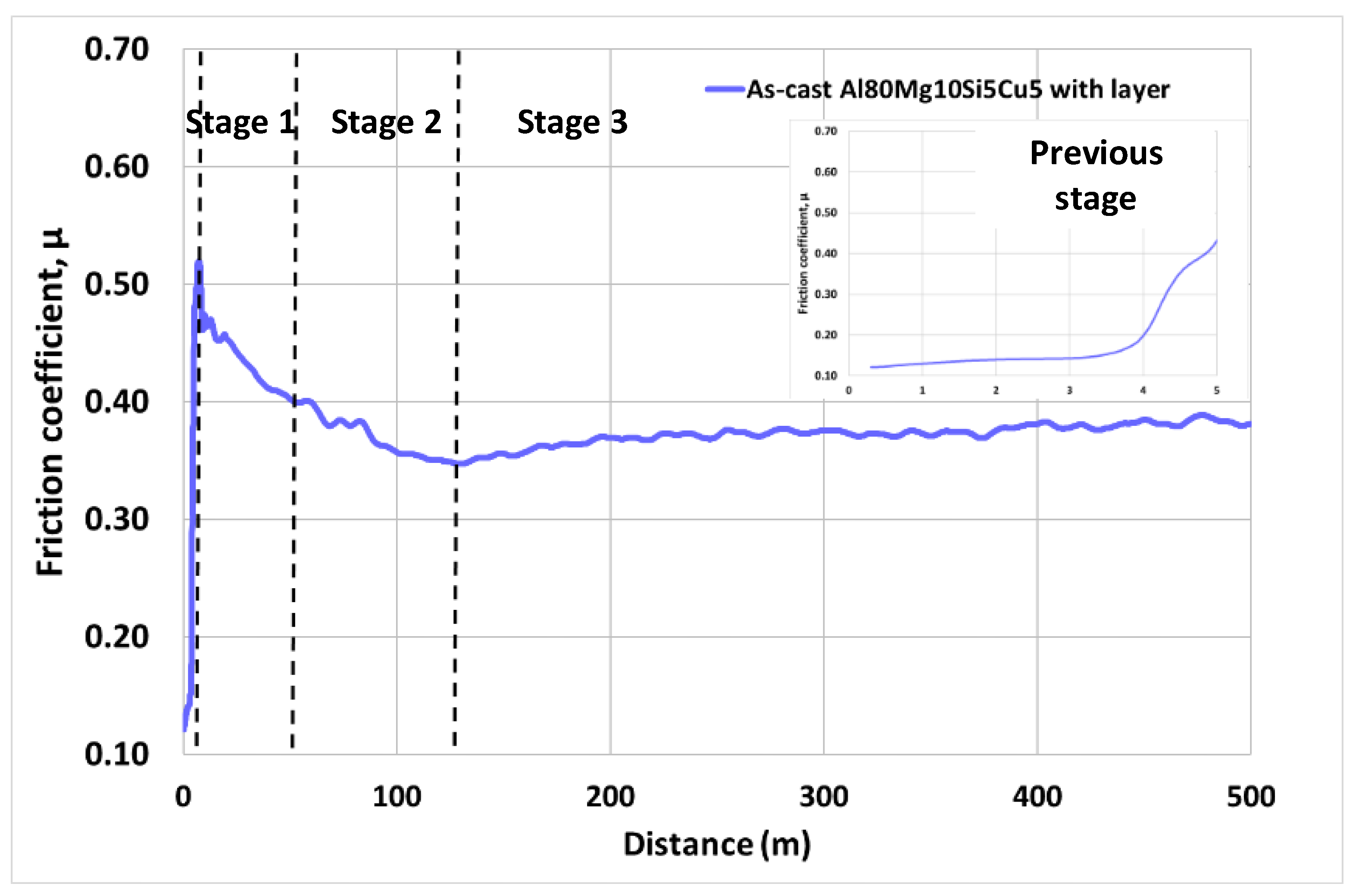
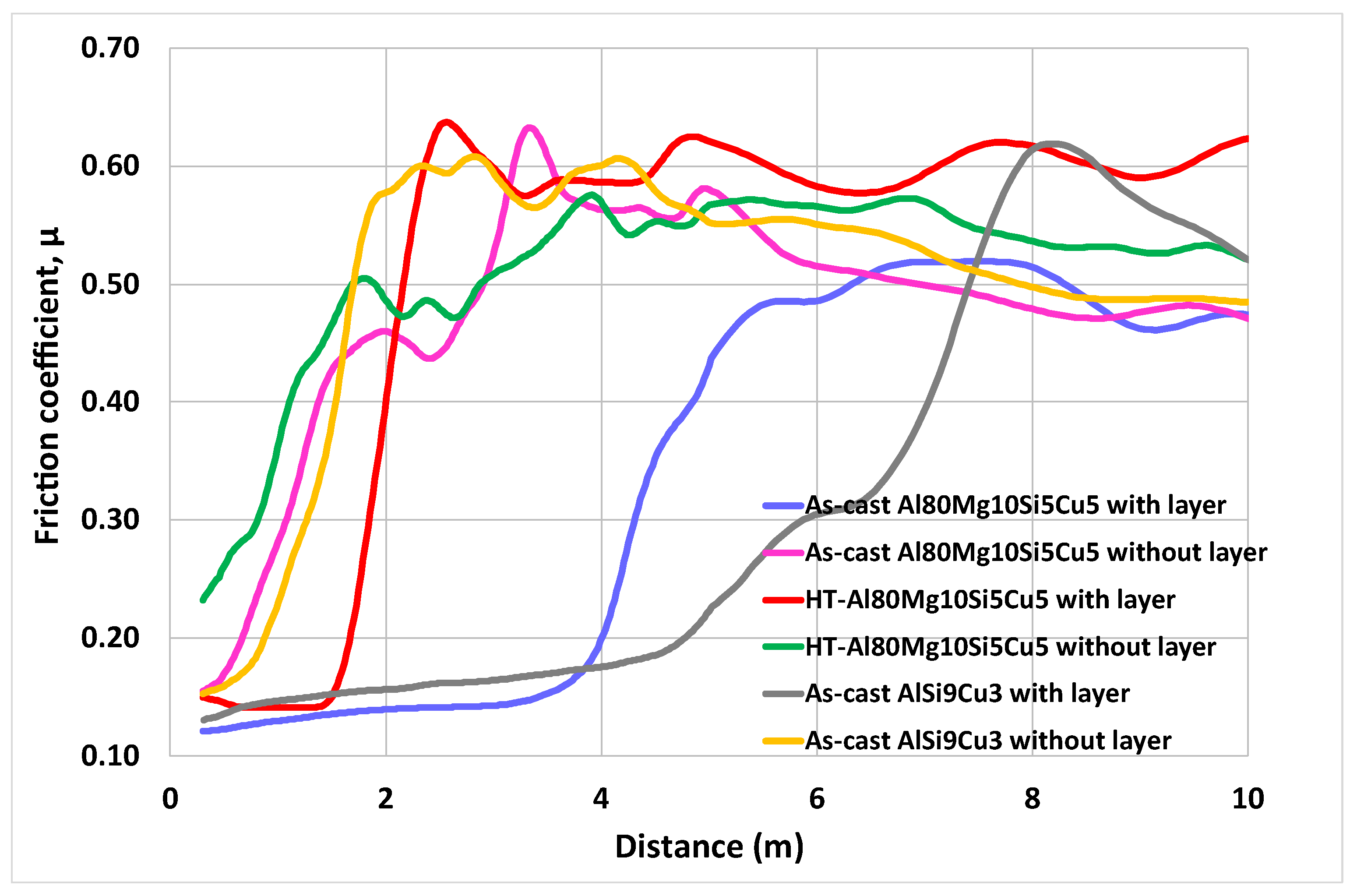
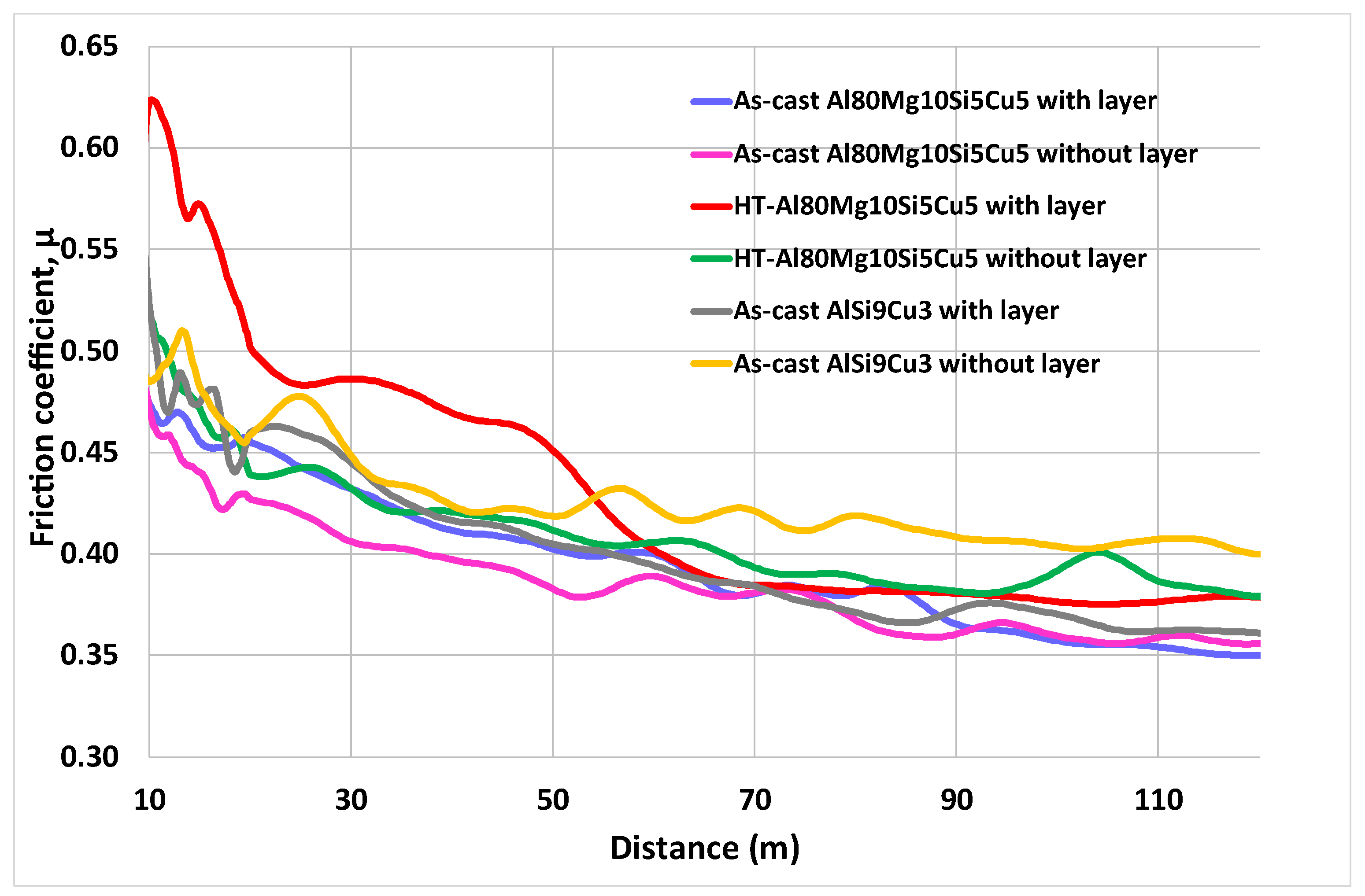
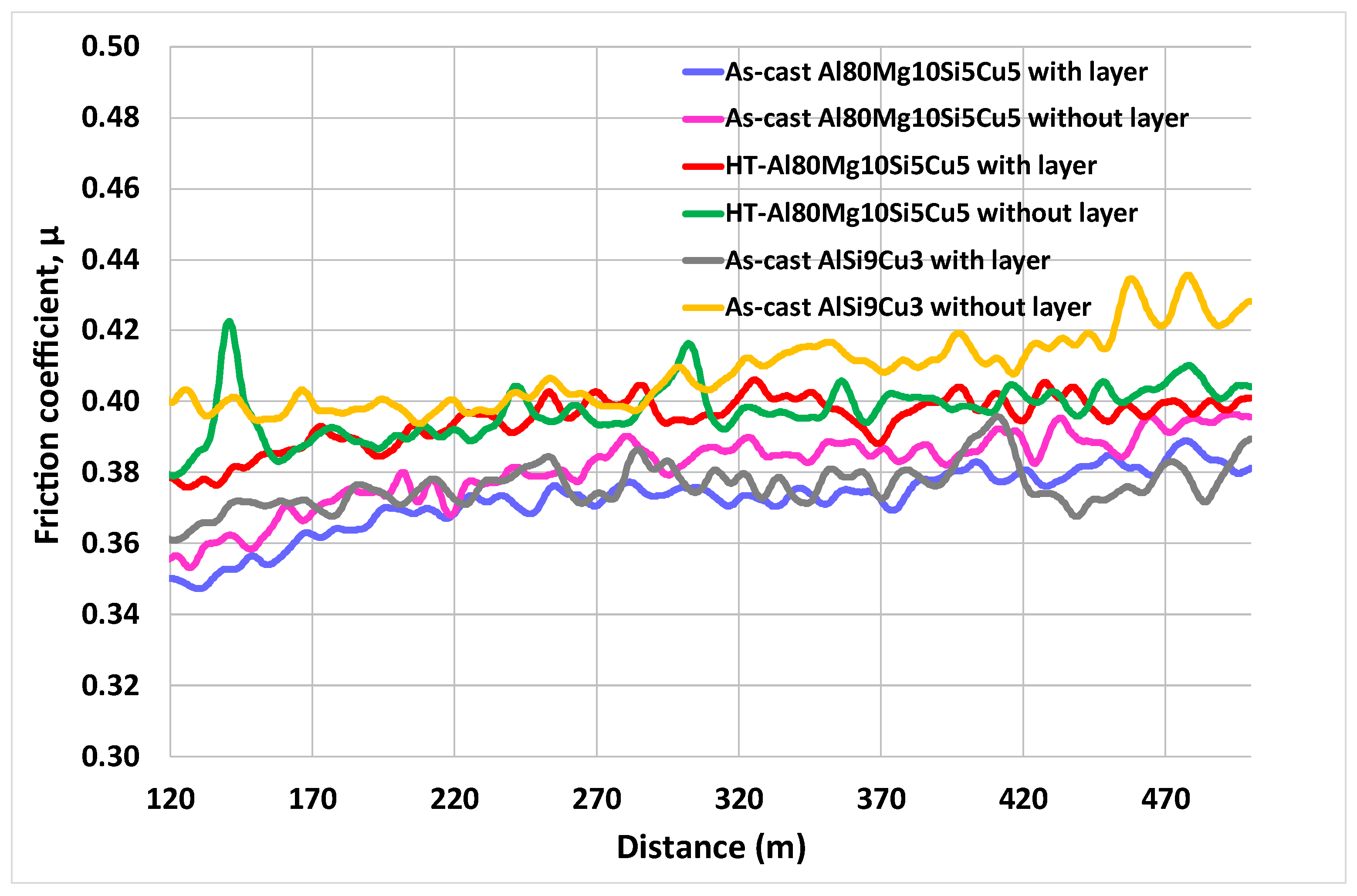
3.2. Friction Coefficient Curves
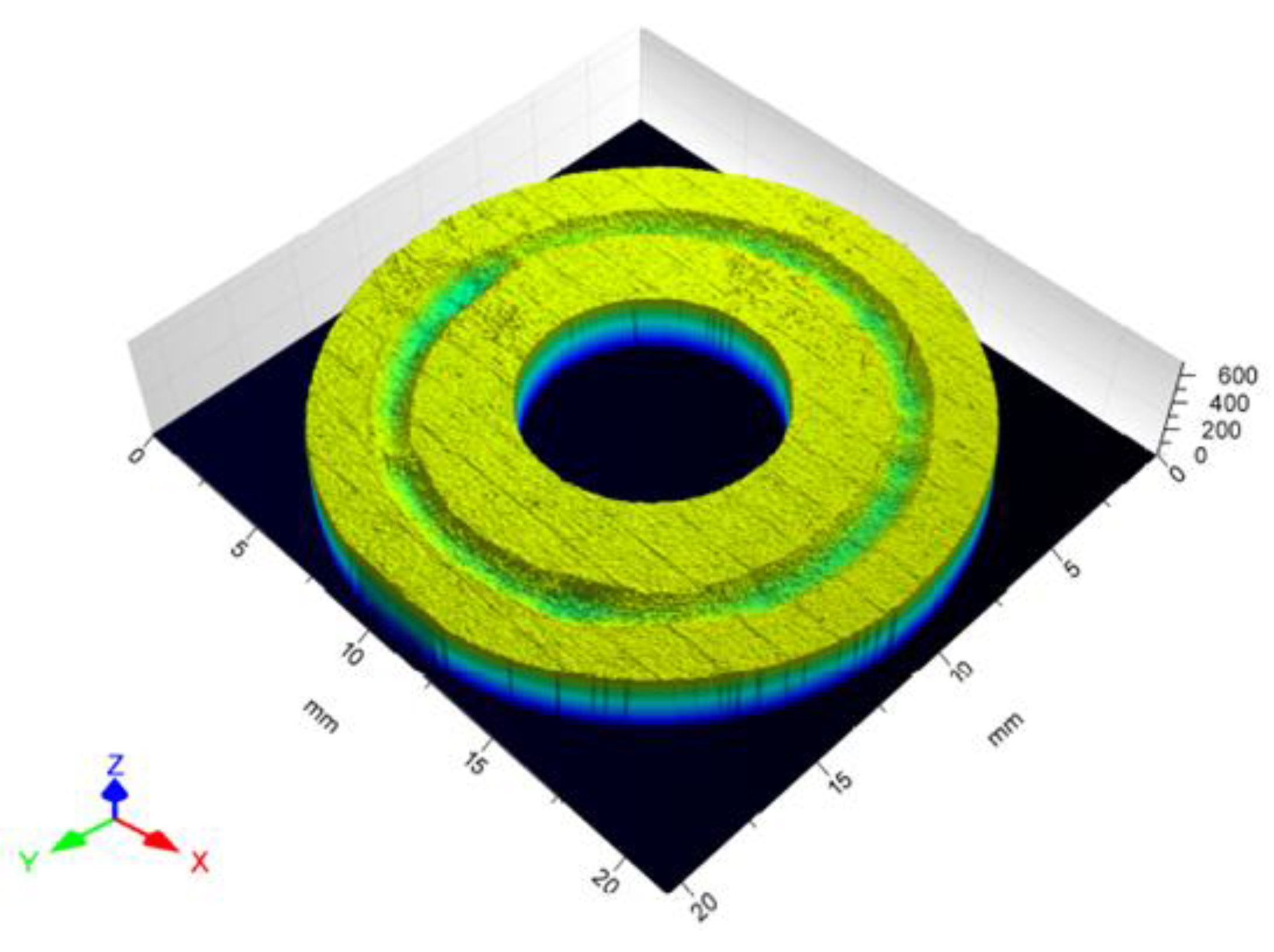
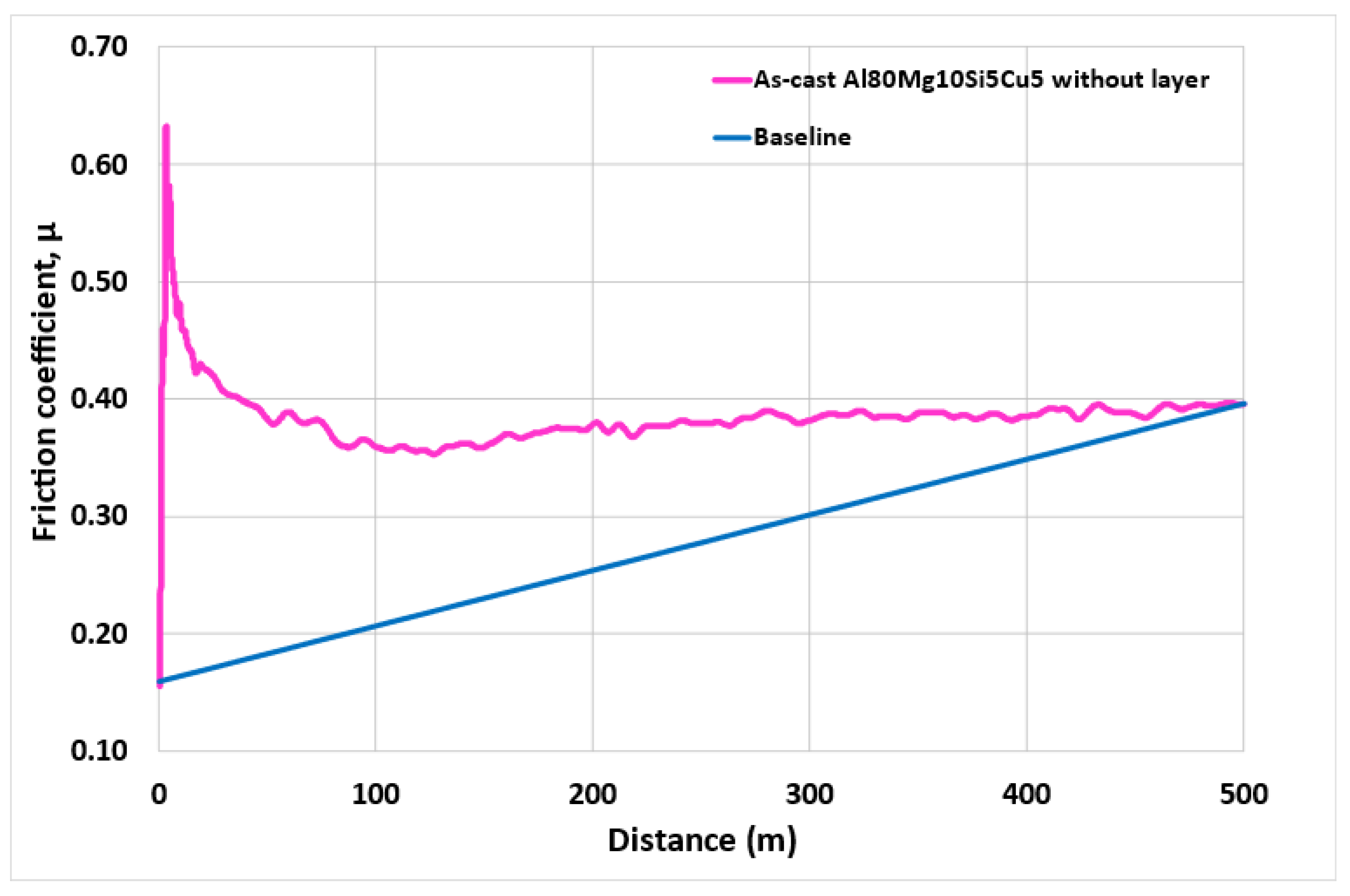
3.3. Determination of Wear Rate Coefficient
3.4. Application of the New Method to Estimate the Wear Rate from the Friction Curve
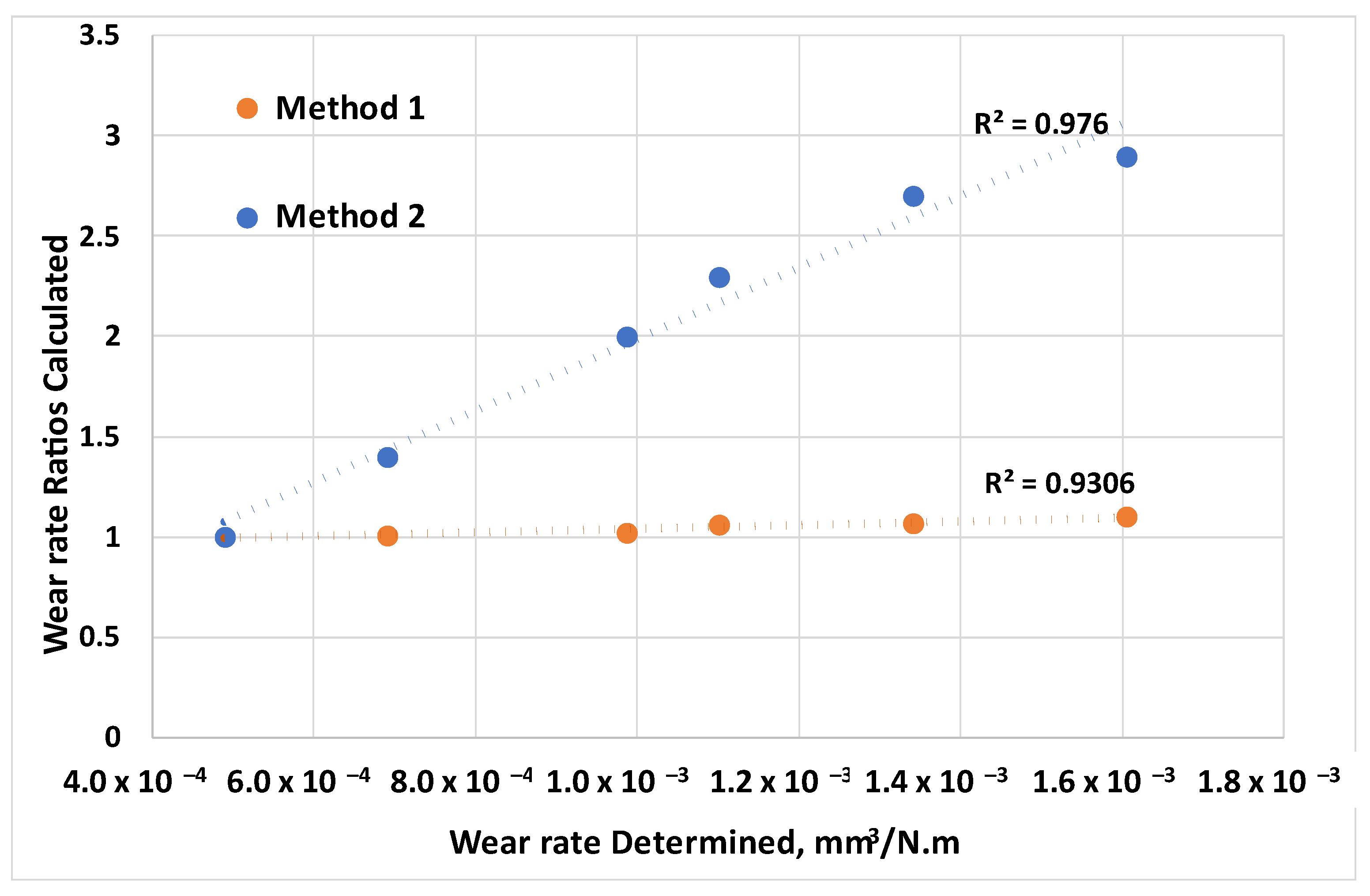
3.5. Comparison of Calculated and Determined Wear Rate Values
4. Discussion
5. Conclusions
- The results presented in this work highlight the significance of the early stages in determining the wear rate.
- The findings demonstrate no clear relations between the coefficient of friction and the wear rate.
- The results also demonstrate that hardness has a greater influence on wear rate than the steady-state friction coefficient.
- The results from studied samples indicate that the area under the curve during the early stages can serve as a quick indicator of wear rate, which was later confirmed by more precise methods like confocal technology that require longer analysis times.
- With a regression coefficient of R2 = 0.976, the correlation coefficient is approximately 0.988, indicating a robust linear relationship. Therefore, the model is expected to predict future observations with a minimal margin of error.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Das, S.; Robi, P.S.; Kumar, P. Tribological properties of (Al)10(FeCoNiCu)90 high entropy alloy. Tribol.—Mater. Surf. Interfaces 2022, 17, 72–80. [Google Scholar] [CrossRef]
- Devaraju, A. A critical review on different types of wear of material. Int. J. Mech. Eng. Technol. 2015, 6, 77–83. [Google Scholar]
- Soares, F.; Manfrinato, M.D.; Gazzola, J.; Rossino, L.S. Determination of the wear resistance of 1020 steel superficially treated in contact with 3104 aluminum alloy using the microwear test compared to the designed wear test evaluated by the moiré optical technique. Matéria 2024, 29, e20240094. [Google Scholar] [CrossRef]
- Swain, B.; Bhuyan, S.; Behera, R.; Mohapatra, S.S.; Behera, A. Wear: A Serious Problem in Industry. In Tribology, 2nd ed.; Patnaik, A., Singh, T., Kukshal, V., Eds.; Intechopen: London, UK, 2021; pp. 1–20. [Google Scholar]
- Neale, M.J. Wear mechanisms. In Lubrication and Reliability Handbook; Elsevier: Amsterdam, The Netherlands, 2001; Volume B19, pp. 1–3. [Google Scholar] [CrossRef]
- Wimmer, M.A.; Fischer, A.; Buscher, R.; Pourzal, R.; Sprecher, C.; Hauert, R.; Jacobs, J.J. Wear mechanisms in metal-on-metal bearings: The importance of tribochemical reaction layers. J. Orthop. Res. 2010, 28, 436–443. [Google Scholar] [CrossRef]
- Jeyaprakash, N.; Yang, C.H. Friction, Lubrication, and Wear. In Tribology in Materials and Manufacturing—Wear, Friction and Lubrication, 2nd ed.; Patnaik, A., Singh, T., Kukshal, V., Eds.; Intechopen: London, UK, 2020; pp. 1–17. [Google Scholar]
- Hemadri, K.; Daniel, A.A.; Kukanur, V.; Nagaral, M. Determination of wear rate and coefficient of friction of Al6262 reinforced with different weight percentage of WC/MoS2 under dry sliding condition. J. Res. Eng. Struct. Mater. 2024, 10, 1125–1138. [Google Scholar] [CrossRef]
- Zawawi, N.N.M.; Azmi, W.H.; Redhwan, A.A.M.; Sharif, M.Z. Coefficient of friction and wear rate effects of different composite nanolubricant concentrations on Aluminium 2024 plate. In Proceedings of the Materials Science and Engineering Conference, Kuantan, Malaysia, 1–2 August 2017. [Google Scholar] [CrossRef]
- Zhang, Y.; Kovalev, A.; Meng, Y. Combined Effect of Boundary Layer Formation and Surface Smoothing on Friction and Wear Rate of Lubricated Point Contacts during Normal Running-in Processes. Friction 2018, 6, 274–288. [Google Scholar] [CrossRef]
- Perfilyev, V.; Moshkovich, A.; Lapsker, I.; Rapoport, L. Friction and Wear of Copper Samples in the Steady Friction State. Tribol. Int. 2010, 43, 1449–1456. [Google Scholar] [CrossRef]
- Yue, T.; Wahab, M.A. Finite Element Analysis of Fretting Wear under Variable Coefficient of Friction and Different Contact Regimes. Tribol. Int. 2017, 107, 274–282. [Google Scholar] [CrossRef]
- Li, L.; Kang, L.; Ma, S.; Li, Z.; Ruan, X.; Cai, A. Finite element analysis of fretting wear considering variable coefficient of friction. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 758–768. [Google Scholar] [CrossRef]
- Xavier, L.F.; Suresh, P. Wear Behavior of Aluminium Metal Matrix Composite Prepared from Industrial Waste. Sci. World J. 2016, 2016, 6538345. [Google Scholar] [CrossRef] [PubMed]
- Pawelec, K.M.; White, A.A.; Best, S.M. Properties and characterisation of bone repair materials. Bone Repair Biomater. 2009, 4, 65–102. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J. A Review of the Friction and Wear Behavior of Particle-Reinforced Aluminum Matrix Composites. Lubricants 2023, 11, 317. [Google Scholar] [CrossRef]
- Marimuthu, U.; Aravindan, S.; Kaliyamoorthy, R. Wear performance of Al–SiC–B4 C hybrid composites under dry sliding conditions. Mater. Des. 2013, 47, 456–464. [Google Scholar] [CrossRef]
- Elhefnawey, M.; Shuai, G.L.; Li, Z.; Nemat-Alla, M.; Zhang, D.T.; Li, L. On Dry Sliding Wear of ECAPed Al-Mg-Zn Alloy: Wear Rate and Coefficient of Friction Relationship. Alex. Eng. J. 2021, 60, 927–939. [Google Scholar] [CrossRef]
- Suh, N.P.; Sridharan, P. Relationship between the coefficient of friction and the wear rate of metals. Wear 1975, 34, 291–299. [Google Scholar] [CrossRef]
- Al-Enzi, F.F.S.; Mohammed, S.S. Prediction Of Hardness And Wear Behaviour Of Friction Stir Processed Cast A319 Aluminum Alloys Using Machine Learning Technique. Eng. Res. J. 2020, 1, 16–26. [Google Scholar]
- Zhu, C.; Jin, L.; Li, W.; Han, S.; Yan, J. The Prediction of Wear Depth Based on Machine Learning Algorithm. Lubricants 2024, 12, 34. [Google Scholar] [CrossRef]
- Wattel, S.; Molinari, J.F. A story of two transitions: From adhesive to abrasive wear and from ductile to brittle regime. J. Chem. Phys. 2024, 160, 014711. [Google Scholar] [CrossRef]
- Popov, V.L. Generalized Archard law of wear based on Rabinowicz criterion of wear particle formation. Facta Univ. Mech. Eng. 2019, 17, 39–45. [Google Scholar] [CrossRef]
- Udoye, N.; Fayomi, O.S.I.; Inegbenebor, A.O. Assessment of Wear Resistance of Aluminium Alloy in Manufacturing Industry-A Review. Procedia Manuf. 2019, 35, 1383–1386. [Google Scholar] [CrossRef]
- Mokhtar, M.O.A. The effect of hardness on the frictional behaviour of metals. Wear 1982, 78, 297–304. [Google Scholar] [CrossRef]
- Qiao, L.; Ramanujan, R.V.; Zhu, J. Effect of Aluminum on the Friction and Wear Behavior of Medium-Entropy Alloys. Adv. Eng. Mater. 2022, 24, 2101475. [Google Scholar] [CrossRef]
- Gopi, V.; Sellamuthu, R.; Sanjivi, A. Measurement of hardness, wear rate and coefficient of friction of surface refined Al-Cu alloy. Procedia Eng. 2014, 97, 1355–1360. [Google Scholar] [CrossRef]
- Alajmi, M.; Shalwan, A. Correlation between Mechanical Properties with Specific Wear Rate and the Coefficient of Friction of Graphite/Epoxy Composites. Materials 2015, 8, 4162–4175. [Google Scholar] [CrossRef] [PubMed]
- Mezlini, S.; Kapsa, P.; Abry, J.C.; Meille, G.; Ribes, H.; Dif, R. Relationship between Hardness and Abrasive Wear for some Aluminium Alloys. Mater. Sci. Forum 2002, 396, 1517–1524. [Google Scholar] [CrossRef]
- Hoic, M.; Skugor, B.; Deur, J.; Tissot, A. Correlation of wear rate, hardness, and density for a dry clutch friction material. In Proceedings of the 7th World Tribology Congress, Lyon, France, 10–15 July 2022. [Google Scholar]
- The Wear of Metals: Theory, Mechanism and Testing. University of Cambridge. Available online: https://www.phase-trans.msm.cam.ac.uk/2011/JG/4.pdf (accessed on 25 December 2024).
- Smith, D.A. Wear and Friction Analysis of Thin Coatings. Available online: https://www.silcotek.com/hs-fs/hub/22765/file-341679011-pdf/docs/t-09-113_silcotek_tribology_testing_final_report.pdf (accessed on 12 November 2024).
- Gregorio, A.V.L.; Silva, T.E.F.; Reis, A.P.; de Jesus, A.M.P.; Rosa, P.A.R. A Methodology for Tribo-Mechanical Characterization of Metallic Alloys under Extreme Loading and Temperature Conditions Typical of Metal Cutting Processes. J. Manuf. Mater. Process. 2022, 6, 46. [Google Scholar] [CrossRef]
- ASTM G133-05; Standard Test Method for Linearly Reciprocating Ball-on-Flat Sliding Wear. ASTM International: West Conshohocken, PA, USA, 2016.
- Federici, M.; Straffelini, G.; Gialanella, S. Pin-on-Disc Testing of Low-Metallic Friction Material Sliding Against HVOF Coated Cast Iron: Modelling of the Contact Temperature Evolution. Tribol. Lett. 2017, 65, 121. [Google Scholar] [CrossRef]
- Morshed, A.; Wu, H.; Jiang, Z. A Comprehensive Review of Water-Based Nanolubricant. Lubricants 2021, 9, 89. [Google Scholar] [CrossRef]
- Mosleh, A.O.; Kotova, E.G.; Kotov, A.D.; Gershman, I.S.; Mironov, A.E. Bearing Aluminum-Based Alloys: Microstructure, Mechanical Characterizations, and Experiment-Based Modeling Approach. Materials 2022, 15, 8394. [Google Scholar] [CrossRef]
- Mathavan, J.; Patnaik, A. Analysis of wear properties of aluminium based journal bearing alloys with and without lubrication. In Proceedings of the Materials Science and Engineering, Bangalore, India, 14–16 July 2016. [Google Scholar] [CrossRef]
- Deuis, R.L.; Subramanian, C.; Yellup, J. Dry sliding wear of aluminium composites—A review. Compos. Sci. Technol. 1997, 57, 415–435. [Google Scholar] [CrossRef]
- Meyveci, A.; Karacan, I.; Caligulu, U.; Durmus, H. Pin-on-disc characterization of 2xxx and 6xxx aluminium alloys aged by precipitation age hardening. J. Alloys Compd. 2010, 491, 278–283. [Google Scholar] [CrossRef]
- Marimuthu, K.; Sornakumar, T. Friction and wear studies of die cast aluminum alloy-aluminum oxide-reinforced composites. Ind. Lubr. Tribol. 2010, 62, 361–371. [Google Scholar]
- Lutfar, M.; Zhang, L.C. An investigation into the friction and wear mechanisms of aluminium high silicon alloy under contact sliding. Wear 2017, 376, 940–946. [Google Scholar] [CrossRef]
- Wang, L.; Cai, J.; Zhou, J.; Duszczyk, J. Characteristics of the Friction Between Aluminium and Steel at Elevated Temperatures During Ball-on-Disc Tests. Tribol. Lett. 2009, 36, 183–190. [Google Scholar] [CrossRef]
- Edacherian, A.; Algahtani, A.; Tirth, V. Investigations of the Tribological Performance of A390 Alloy Hybrid Aluminum Matrix Composite. Materials 2018, 11, 2524. [Google Scholar] [CrossRef]
- Salguero, J.; Vazquez-Martinez, J.M.; Del Sol, I.; Batista, M. Application of Pin-On-Disc Techniques for the Study of Tribological Interferences in the Dry Machining of A92024-T3 (Al-Cu) Alloys. Materials 2018, 11, 1236. [Google Scholar] [CrossRef] [PubMed]
- Talibouya, E.C.; Rosa, M.; Sérgio, P.; Martins, R.; Martins da Cruz, M.P.; Ferreira, V. Investigation of the effects of skewness Rsk and kurtosis Rku on tribological behavior in a pin-on-disc test of surfaces machined by conventional milling and turning processes. Mater. Res. 2021, 24, e20200435. [Google Scholar] [CrossRef]
- Mia, M.; Anwar, S.; Yang, X. Development of interactive friction model for machining considering the instantaneous interfacial characteristics. J. Mater. Process. Technol. 2023, 322, 118203. [Google Scholar] [CrossRef]
- Hashiguchi, K.; Ozaki, S. Constitutive equation for friction with transition from static to kinetic friction and recovery of static friction. Int. J. Plast. 2008, 24, 2102–2124. [Google Scholar] [CrossRef]
- Coban, A.; Boyaci, S. The Calculation of Kinetic and Static Friction Coefficient and Friction Graph Analysis Using Arduino. Phys. Educ. 2020, 56, 013003. [Google Scholar] [CrossRef]
- Tocci, M.; Pola, A.; Girelli, L.; Lollio, F.; Montesano, L.; Gelfi, M. Wear and Cavitation Erosion Resistance of an AlMgSc Alloy Produced by DMLS. Metals 2019, 9, 308. [Google Scholar] [CrossRef]
- Gnanamoorthy, R. Development of a fretting wear test rig and preliminary studies for understanding the fretting wear properties of steels. Mater. Des. 2006, 27, 141–146. [Google Scholar] [CrossRef]
- Leiro, A.; Kankanala, A.; Vuorinen, E.; Prakash, B. The tribological behaviour of carbide-free bainitic steel under rolling/sliding conditions. Wear 2011, 273, 2–8. [Google Scholar] [CrossRef]
- Wu, J.M.; Lin, S.J.; Yeh, J.W.; Chen, S.K.; Huang, Y.S.; Chen, H.C. Adhesive wear behavior of AlxCoCrCuFeNi high-entropy alloys as a function of aluminum content. Wear 2006, 261, 513–519. [Google Scholar] [CrossRef]
- Wen, Q.; Liu, M.; Zhang, Z.; Sun, Y. Experimental Investigation into the Friction Coefficient of Ball-on-Disc in Dry Sliding Contact Considering the Effects of Surface Roughness, Low Rotation Speed, and Light Normal Load. Lubricants 2022, 10, 256. [Google Scholar] [CrossRef]
- Krbata, M.; Eckert, M.; Majerik, J.; Barenyi, I. Wear Behaviour of High Strength Tool Steel 90MnCrV8 in Contact with Si3N4. Metals 2020, 10, 756. [Google Scholar] [CrossRef]
- Orasanu, N.; Voicu, G.; Ungureanu, N. Determination of the static and dynamic friction coefficients for the milling products and their variation with respect to some parameter. In Proceedings of the OPROTEH Conference, Bacau, Romania, 22–24 October 2009. [Google Scholar]
- Maculotti, G.; Goti, E.; Genta, G.; Mazza, L.; Galetto, M. Uncertainty-based comparison of conventional and surface topography-based methods for wear volume evaluation in pin-on-disc tribological test. Tribol. Int. 2021, 165, 107260. [Google Scholar] [CrossRef]
- Torres, A.; Hernandez, A.; García-Atance, G.; Viesca, J.L.; Gonzalez, R.; Hadfield, M. Use of optical profilometry in the ASTM D4172 standard. Wear 2011, 271, 2963–2967. [Google Scholar] [CrossRef]
- Neis, P.D.; Ferreira, N.F.; da Silva, F.P. Comparison between methods for measuring wear in brake friction materials. Wear 2014, 319, 191–199. [Google Scholar] [CrossRef]
- Tomovich, S.; Peng, Z.; Yuan, C.; Yan, X.P. Quantitative Surface Characterisation Using Laser Scanning Confocal Microscopy. In Laser Scanning, Theory and Applications; Intechopen: London, UK, 2011. [Google Scholar] [CrossRef][Green Version]
- Conroy, M.; Armstrong, J. A comparison of surface metrology techniques. J. Phys. Conf. Ser. 2005, 13, 458. [Google Scholar] [CrossRef]
- Klapetek, P.; Valtr, M.; Bursik, P. Non-equidistant scanning approach for millimetre-sized SPM measurement. Nanoscale Res. Lett. 2012, 7, 213. [Google Scholar] [CrossRef] [PubMed]
- Ansari, M.; Hazrati, I.A.; Esmailzadeh, E.; Azadi, S. Wear Rate Estimation of Train Wheels Using Dynamic Simulations and Field Measurements. Veh. Syst. Dyn. 2008, 46, 739–759. [Google Scholar] [CrossRef]
- Villanueva, E.; Vicario, I.; Albizuri, J.; Arruebarrena, G.; Guraya, T. Wear properties of a new Al80Mg10Si5Cu5 multicomponent alloy. Wear 2024, 15, 558–559. [Google Scholar] [CrossRef]
- Lehmhus, D. Advances in Metal Casting Technology: A Review of State of the Art, Challenges and Trends—Part I: Changing Markets, Changing Products. Metals 2022, 12, 1959. [Google Scholar] [CrossRef]
- Sharma, P.; Dwivedi, V.K.; Dwivedi, S.P. Development of high entropy alloys: A review. Mater. Today Proc. 2021, 43, 502–509. [Google Scholar] [CrossRef]
- UNE-EN ISO 1706:2020+A1:2021; Aluminio y Aleaciones de Aluminio. Piezas Moldeadas. Composición Química y Características Mecánicas. Asociación Española de Normalización: Génova, Spain, 2022.
- Otarawanna, S.; Gourlay, C.; Laukli, H.I.; Dahle, A.K. Formation of the surface layer in hypoeutectic Al-alloy high-pressure die castings. Mater. Chem. Phys. 2011, 130, 251–258. [Google Scholar] [CrossRef]
- ASTM G99-17; Standard Test Method for Wear Testing with a Pin-on-Disk Apparatus. ASTM International: West Conshohocken, PA, USA, 2023.
- Timelli, G.; Fabrizi, A.; Vezzù, S.; De Mori, A. Design of Wear-Resistant Diecast AlSi9Cu3(Fe) Alloys for High-Temperature Components. Metals 2020, 10, 55. [Google Scholar] [CrossRef]
- Ghazali, J.; Rainfoth, W.M.; Omar, M.Z. A comparative study of mechanically mixed layers (MMLs) characteristics of commercial aluminium alloys sliding against alumina and steel sliders. J. Mater. Process. Technol. 2008, 201, 662–668. [Google Scholar] [CrossRef]
- Lee, S.J.; Sohn, Y.C.; Kim, C.L. Tribological Effects of Water-Based Graphene Lubricants on Graphene Coatings. Materials 2023, 16, 197. [Google Scholar] [CrossRef] [PubMed]
- Vanna, K.; Venkata, A.; Lumley, R.; Horacio, C. The Skin Effect in High Pressure Die Casting Al Alloys. In Proceedings of the 12th International Conference on Aluminium Alloys, Yokohama, Japan, 5–9 September 2010; pp. 687–692. [Google Scholar]
- Khonsari, M.; Ghatrehsamani, S.; Akbarzadeh, S. On the running-in nature of metallic tribo-components: A review. Wear 2021, 474–475, 203871. [Google Scholar] [CrossRef]
- Devenport, T.M.; Griffin, J.M.; Rolfe, B.F.; Pereira, M.P. Friction and Wear in Stages of Galling for Sheet Metal Forming Applications. Lubricant 2023, 11, 288. [Google Scholar] [CrossRef]
- Pongen, R.; Kumar, A.; Parthiban, P. Study of microstructure and mechanical properties of A713 aluminium alloy having an addition of grain refiners Al-3.5 Ti-1.5C and Al-3Cobalt. Results Phys. 2019, 13, 102105. [Google Scholar] [CrossRef]
- Alkhafaji, A.; Camas, D.; Lopez-Crespo, P.; Al-Asadi, H.; Han, J.G.G.; Hori, M. The Influence of Tool Geometry on the Mechanical Properties and the Microstructure of AA6061-T6 Aluminum Alloy Friction Stir Spot Welding. Materials 2023, 16, 4135. [Google Scholar] [CrossRef]
- Yunyou, J.; Xiuyan, L. The Microstructure Evolution in Early Running-in Stage and its Effect on the Friction Behavior in 304 Stainless Steel. Tribology 2018, 38, 37–43. [Google Scholar] [CrossRef]
- Shaikh, A. Friction and Wear Measurement Techniques; Modern Tribology Handbook, CRC Press: Boca Raton, FL, USA, 2001; p. 13. [Google Scholar]
- Kar, S.; Sahu, B.B.; Kousaka, H. Study of the effect of normal load on friction coefficient and wear properties of CNx thin films. AIP Adv. 2020, 10, 065214. [Google Scholar] [CrossRef]
- Behrens, B.A.; Bouguecha, A.; Vucetic, M.; Chugreev, A. Advanced Wear Simulation for Bulk Metal Forming Processes. In Proceedings of the NUMIFORM 2016: The 12th International Conference on Numerical Methods in Industrial Forming Processes, Troyes, France, 4–7 July 2016; Volume 80, p. 04003. [Google Scholar]
- Ghatrehsamani, S.; Akbarzadesh, S.; Khonsari, M.M. Experimentally verified prediction of friction coefficient and wear rate during running-in dry contact. Tribol. Int. 2022, 170, 107508. [Google Scholar] [CrossRef]
- Bird, J.O.; Chivers, P.J. Engineering and Physical Science. In Newnes (An Imprint of Butterworth-Heinemann Ltd.); Pocket Book: Lugano, Switzerland, 1993; pp. 235–237. [Google Scholar]
- Liu, D.; Luo, J. Energy dissipation through phonon and electron behaviors of superlubricity in 2D materials. In Superlubricity, 2nd, ed.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 145–166. [Google Scholar] [CrossRef]
- Erbas, K.C. On the Newtonian Thermal Analysis of Casting: A Critical Aproach. J. Eng. Sci. 2014, 7, 47–60. [Google Scholar] [CrossRef]
- Villanueva, E.; Vicario, I.; Sanchez, J.M.; Albizuri, J.; Montero, J. Solid Fraction Determination at the Rigidity Point by Advanced Thermal Analysis. Appl. Sci. 2021, 12, 237. [Google Scholar] [CrossRef]
- Emadi, D.; Laurence, W.; Djurdjevic, M.B.; Witold, K.; Sokolowski, J.H. Comparison of Newtonian and Fourier thermal analysis techniques for calculation of latent heat and solid fraction of aluminum alloys. J. Met. 2004, 10, 91–106. [Google Scholar] [CrossRef] [PubMed]
- Rafalski, I.V.; Arabey, A.; Lushchik, P.; Chaus, A. Computer Modeling of Cast Alloys Solidification by Computer-Aided Cooling Curve Analysis; International Doctoral Seminar, Proceedings; Alumni Press: Trnava, Slovakia.
- Hemminger, W.F.; Sarge, S.M. The Baseline Construction and Its Influence On The Measurement Of Heat With Differential Scanning Calorimeters. J. Therm. Anal. Calorim. 1991, 37, 1455–1477. [Google Scholar] [CrossRef]
- Tanski, T.; Snopinski, P.; Roszak, M.; Rusz, S.; Palcek, P. Thermal, structure and phases analysis of the aluminium ENAC-AlMg5Si2Mn alloy. Mater. Sci. Eng. 2015, 22, 54–65. [Google Scholar]



| Reference | Al | Si | Fe | Cu | Mn | Mg | Zn |
|---|---|---|---|---|---|---|---|
| Al80Mg10Si5Cu5 | 78.9 | 5.6 | 0.3 | 4.7 | 0.1 | 10.3 | 0.1 |
| AlSi9Cu3 | 87.2 | 8.3 | 0.6 | 2.4 | 0.2 | 0.2 | 0.7 |
| Test Parameters | Value |
|---|---|
| Load (N) | 15.0 |
| Velocity (m/s) | 0.1 |
| Rotation Speed (rpm) | 127.3 |
| Sliding distance (m) | 500.0 |
| Track diameters (mm) | 15 |
| Environment | Dry air |
| Reference | HV3 |
|---|---|
| As-cast Al80Mg10Si5Cu5 with layer | 136 ± 5 |
| As-cast Al80Mg10Si5Cu5 without layer | 130 ± 13 |
| HT-Al80Mg10Si5Cu5 with layer | 125 ± 6 |
| HT-Al80Mg10Si5Cu5 without layer | 114 ± 12 |
| As-cast AlSi9Cu3 with layer | 114 ± 5 |
| As-cast AlSi9Cu3 without layer | 95 ± 7 |
| Reference | µmax | µsteady-state |
|---|---|---|
| As-cast Al80Mg10Si5Cu5 with a layer | 0.52 ± 0.01 | 0.38 ± 0.006 |
| As-cast Al80Mg10Si5Cu5 without layer | 0.63 ± 0.12 | 0.38 ± 0.008 |
| Thermal-treated Al80Mg10Si5Cu5 with layer | 0.64 ± 0.15 | 0.38 ± 0.008 |
| Thermal-treated Al80Mg10Si5Cu5 without layer | 0.57 ± 0.08 | 0.39 ± 0.007 |
| As-cast AlSi9Cu3 with layer | 0.62 ± 0.03 | 0.38 ± 0.003 |
| As-cast AlSi9Cu3 without layer | 0.61 ± 0.04 | 0.39 ± 0.019 |
| Reference | K (mm3/N.m) |
|---|---|
| As-cast Al80Mg10Si5Cu5 with layer | 4.90 × 10−4 ± 0.39 |
| As-cast Al80Mg10Si5Cu5 without layer | 9.86 × 10−4 ± 0.19 |
| HT-Al80Mg10Si5Cu5 with layer | 1.10 × 10−3 ± 0.43 |
| HT-Al80Mg10Si5Cu5 without layer | 1.34 × 10−3 ± 0.63 |
| As-cast AlSi9Cu3 with layer | 6.90 × 10−4 ± 0.01 |
| As-cast AlSi9Cu3 without layer | 1.61 × 10−3 ± 0.16 |
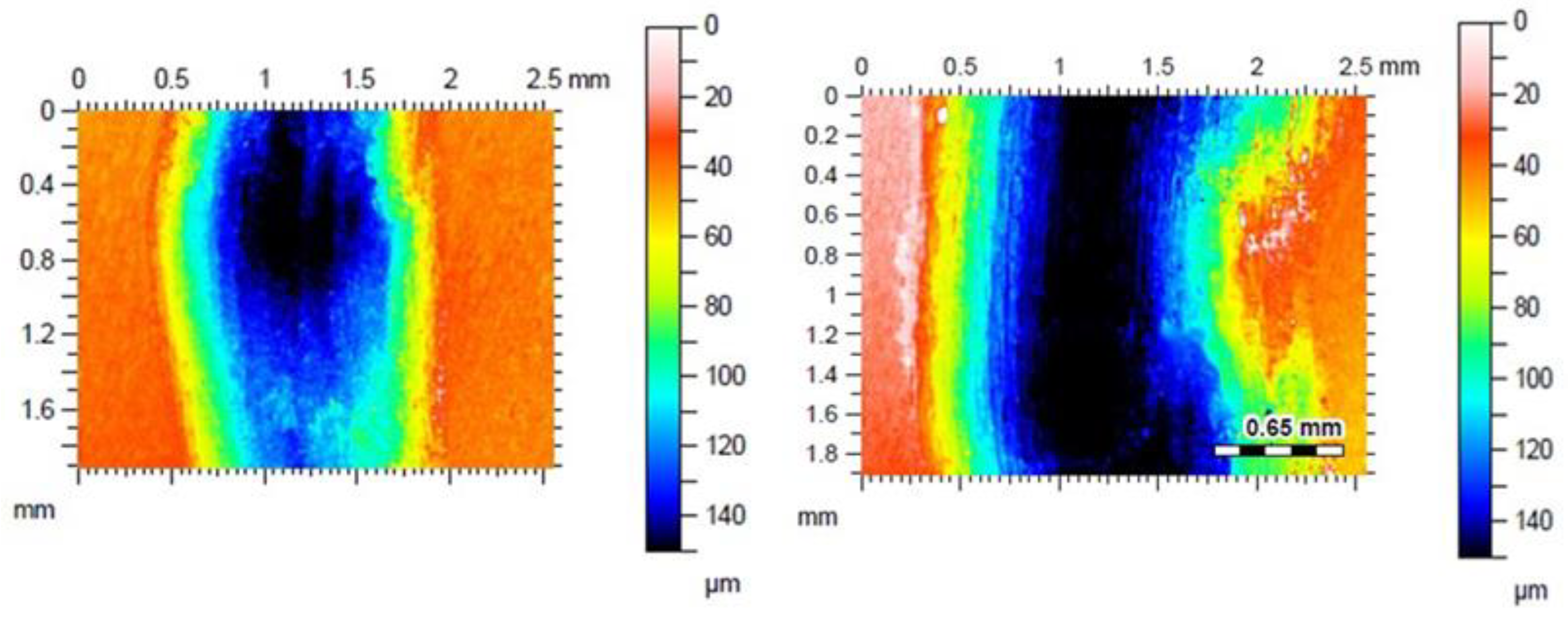
| Reference | Total Area (Units Area) | Area Under 20 m (Units Area) | Area Under 20 m (%) | Ratio Total Area | Ratio Area Under 20 m |
|---|---|---|---|---|---|
| As-cast Al80Mg10Si5Cu5 with layer | 1.882 | 77 | 4 | 1.00 | 1.00 |
| As-cast AlSi9Cu3 with layer | 1.901 | 80 | 4 | 1.01 | 1.40 |
| As-cast Al80Mg10Si5Cu5 without layer | 1.919 | 88 | 5 | 1.02 | 2.00 |
| HT-Al80Mg10Si5Cu5 with layer | 2.003 | 93 | 5 | 1.06 | 2.30 |
| HT-Al80Mg10Si5Cu5 without layer | 2.010 | 106 | 5 | 1.07 | 2.70 |
| As-cast AlSi9Cu3 without layer | 2.070 | 108 | 5 | 1.10 | 2.90 |
| Reference | K (mm3/N.m) | Ratio Total Area | Ratio Area Under 20 m |
|---|---|---|---|
| As-cast Al80Mg10Si5Cu5 with layer | 4.90 × 10−4 | 1.00 | 1.00 |
| As-cast AlSi9Cu3 with layer | 6.90 × 10−4 | 1.01 | 1.40 |
| As-cast Al80Mg10Si5Cu5 without layer | 9.86 × 10−4 | 1.02 | 2.00 |
| Thermal-treated Al80Mg10Si5Cu5 with layer | 1.10 × 10−3 | 1.06 | 2.30 |
| Thermal-treated Al80Mg10Si5Cu5 without layer | 1.34 × 10−3 | 1.07 | 2.70 |
| As-cast AlSi9Cu3 without layer | 1.61 × 10−3 | 1.10 | 2.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villanueva, E.; Albizuri, J.; Caballero, P.; Guraya, T.; Vicario, I. Prediction of Wear Rate by a New Direct Method Using the Friction Coefficient Curve. J. Manuf. Mater. Process. 2025, 9, 6. https://doi.org/10.3390/jmmp9010006
Villanueva E, Albizuri J, Caballero P, Guraya T, Vicario I. Prediction of Wear Rate by a New Direct Method Using the Friction Coefficient Curve. Journal of Manufacturing and Materials Processing. 2025; 9(1):6. https://doi.org/10.3390/jmmp9010006
Chicago/Turabian StyleVillanueva, Ester, Joseba Albizuri, Patricia Caballero, Teresa Guraya, and Iban Vicario. 2025. "Prediction of Wear Rate by a New Direct Method Using the Friction Coefficient Curve" Journal of Manufacturing and Materials Processing 9, no. 1: 6. https://doi.org/10.3390/jmmp9010006
APA StyleVillanueva, E., Albizuri, J., Caballero, P., Guraya, T., & Vicario, I. (2025). Prediction of Wear Rate by a New Direct Method Using the Friction Coefficient Curve. Journal of Manufacturing and Materials Processing, 9(1), 6. https://doi.org/10.3390/jmmp9010006







