Thermal Modelling of Metals and Alloys Irradiated by Pulsed Electron Beam: Focus on Rough, Heterogeneous and Multilayered Materials
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
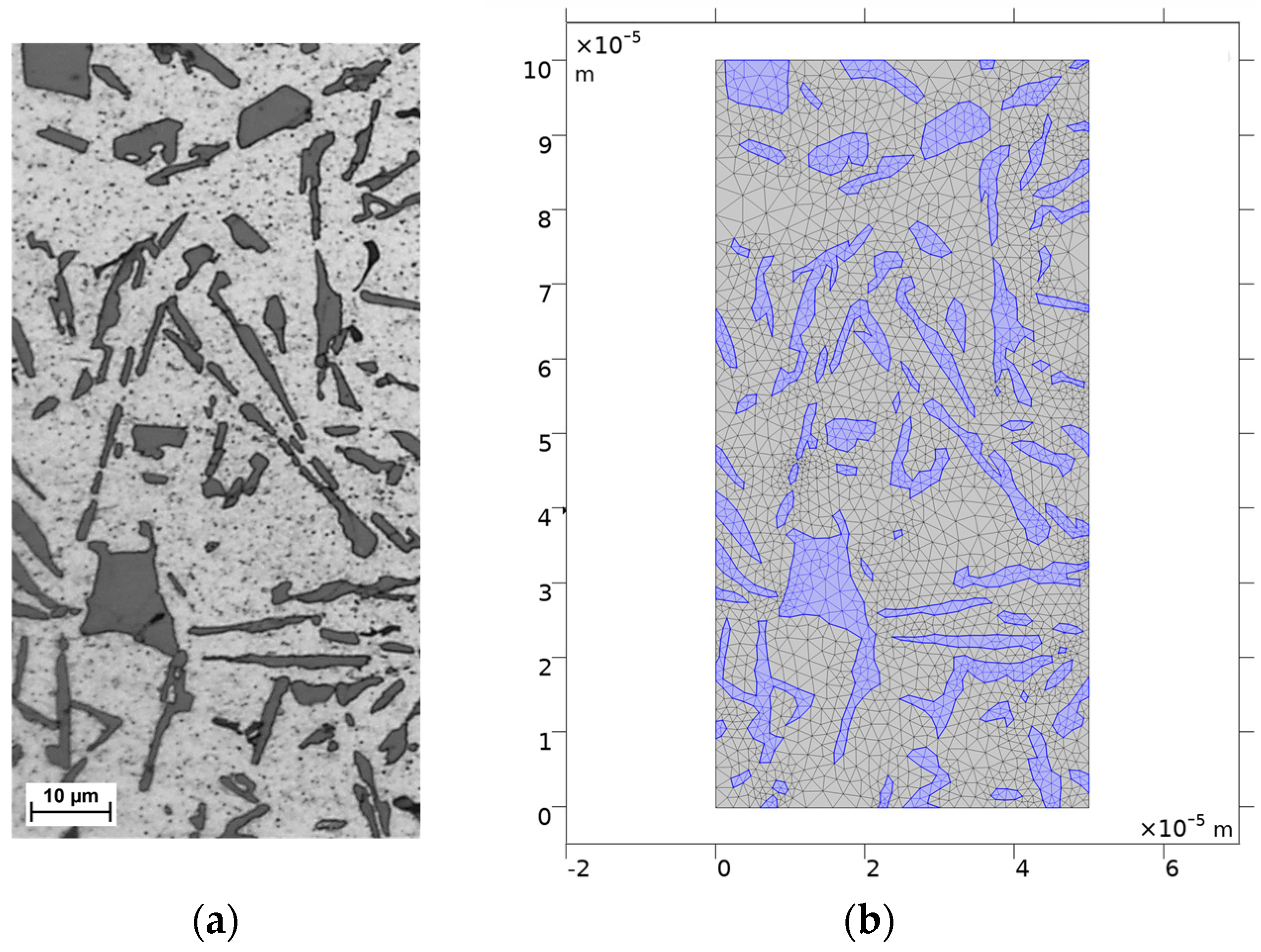
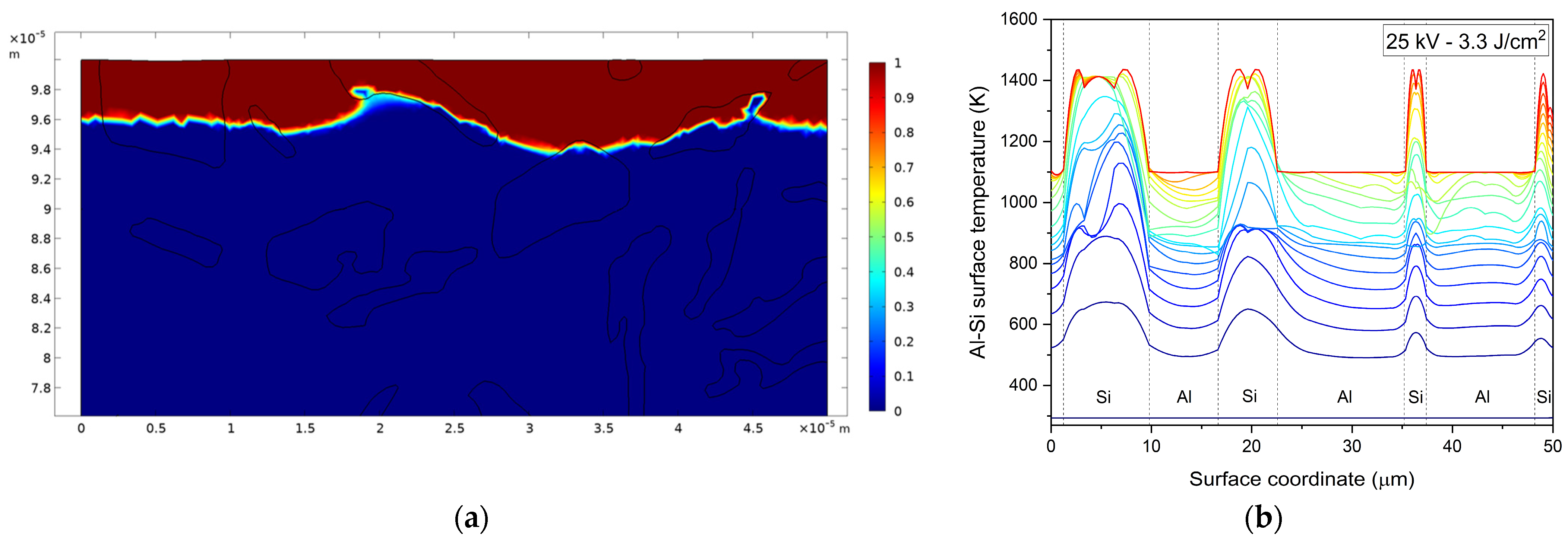
3.2. Al-Si13 Cast Alloy
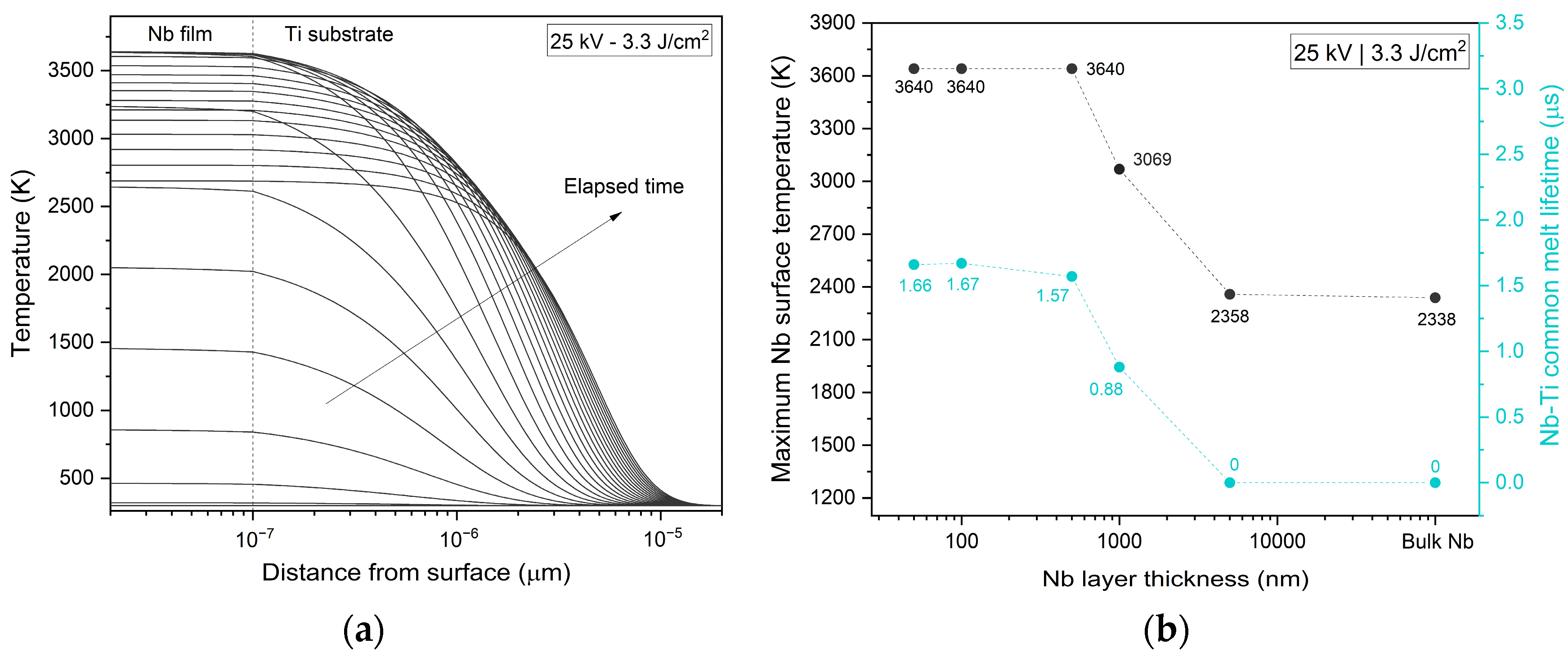
3.3. Ti-Nb Surface Alloy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Proskurovsky, D.I.; Rotshtein, V.P.; Ozur, G.E.; Ivanov, Y.F.; Markov, A.B. Physical foundations for surface treatment of materials with low energy, high current electron beams. Surf. Coat. Technol. 2000, 125, 49–56. [Google Scholar] [CrossRef]
- Rotshtein, V.P.; Proskurovsky, D.I.; Ivanov, Y.F.; Markov, A.B. Surface modification and alloying of metallic materials with low-energy high-current electron beams. Surf. Coat. Technol. 2004, 180, 377–381. [Google Scholar] [CrossRef]
- Proskurovsky, D.I.; Rotshtein, V.P.; Ozur, G.E. Use of low-energy, high-current electron beams for surface treatment of materials. Surf. Coat. Technol. 1997, 96, 117–122. [Google Scholar] [CrossRef]
- Vladimir, R.; Ivanov, Y.; Markov, A. Surface treatment of materials with low-energy, high-current electron beams. Mater. Surf. Process. By Dir. Energy Tech. 2006, 6, 205. [Google Scholar]
- Markov, A.B.; Solovyov, A.V. Melting Thresholds of the Film-Substrate System Irradiated with a Low-Energy High-Current Electron Beam. Russ. Phys. J. 2023, 65, 1893–1899. [Google Scholar] [CrossRef]
- Markov, A.; Yakovlev, E. Calculation of heat regimes for a Cr-Cu surface alloy formed with a low-energy high-current electron beam. J. Phys. Conf. Ser. 2018, 1115, 042010. [Google Scholar] [CrossRef]
- Markov, A.; Yakovlev, E. Calculation of heat regimes for a Ni-Al surface alloy formed on a carbon steel substrate with a low-energy high-current electron beam. J. Phys. Conf. Ser. 2019, 1393, 012130. [Google Scholar]
- Markov, A.; Solovyov, A.; Yakovlev, E.; Pesterev, E.; Petrov, V.; Slobodyan, M. Computer simulation of temperature fields in the Cr (film)-Zr (substrate) system during pulsed electron-beam irradiation. J. Phys. Conf. Ser. 2021, 2064, 012058. [Google Scholar] [CrossRef]
- Markov, A.; Solovyov, A.; Yakovlev, E.; Slobodyan, M. Prediction of the composition of surface alloys formed via pulsed melting of preliminary deposited coatings. Mater. Chem. Phys. 2022, 292, 126821. [Google Scholar] [CrossRef]
- Shepel, D.; Markov, A. Low-energy high-current electron beam heating of target with second-phase microinclusions. Tech. Phys. Lett. 2011, 37, 772–775. [Google Scholar] [CrossRef]
- Vutova, K.; Donchev, V. Electron beam melting and refining of metals: Computational modeling and optimization. Materials 2013, 6, 4626–4640. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Smith, J.; Ge, W.; Lin, F.; Liu, W.K. Multiscale modeling of electron beam and substrate interaction: A new heat source model. Comput. Mech. 2015, 56, 265–276. [Google Scholar] [CrossRef]
- Kurashkin, S.; Rogova, D.; Tynchenko, V.; Petrenko, V.; Milov, A. Modeling of Product Heating at the Stage of Beam Input in the Process of Electron Beam Welding Using the COMSOL Multiphysics System. In Proceedings of the Computational Methods in Systems and Software, Virtual, 14–17 October 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 905–912. [Google Scholar]
- Ansari, P.; Rehman, A.U.; Pitir, F.; Veziroglu, S.; Mishra, Y.K.; Aktas, O.C.; Salamci, M.U. Selective laser melting of 316l austenitic stainless steel: Detailed process understanding using multiphysics simulation and experimentation. Metals 2021, 11, 1076. [Google Scholar] [CrossRef]
- Mayi, Y.A.; Dal, M.; Peyre, P.; Metton, C.; Moriconi, C.; Fabbro, R. An original way of using COMSOL® application builder to enhance multiphysical simulation of laser welding processes. In Proceedings of the COMSOL Conference 2020, Virtual, 7–8 October 2020; pp. 14–15. [Google Scholar]
- Mayi, Y.A.; Dal, M.; Peyre, P.; Bellet, M.; Metton, C.; Moriconi, C.; Fabbro, R. Laser-induced plume investigated by finite element modelling and scaling of particle entrainment in laser powder bed fusion. J. Phys. D Appl. Phys. 2019, 53, 075306. [Google Scholar] [CrossRef]
- Darif, M.; Semmar, N.; Orléans Cedex, F. Numerical simulation of Si nanosecond laser annealing by COMSOL multiphysics. In Proceedings of the COMSOL Conference 2008, Hannover, Germany, 9–11 October 2008; pp. 567–571. [Google Scholar]
- Sabau, A.S.; Porter, W.D. Alloy shrinkage factors for the investment casting of 17-4PH stainless steel parts. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2008, 39, 317–330. [Google Scholar] [CrossRef]
- Fabiocchi, L.; Mariani, M.; Lucchini Huspek, A.; Pozzi, M.; Bestetti, M.; Lecis, N. Low-Energy High-Current Pulsed Electron Beam Surface Treatment on the Tribological Behavior of 17-4PH Steel Produced via Binder Jetting. Lubricants 2025, 13, 42. [Google Scholar] [CrossRef]
- Brandt, R.; Neuer, G. Electrical resistivity and thermal conductivity of pure aluminum and aluminum alloys up to and above the melting temperature. Int. J. Thermophys. 2007, 28, 1429–1446. [Google Scholar] [CrossRef]
- NIST Chemistry—National Institute of Standards and Technology. Available online: https://webbook.nist.gov/ (accessed on 20 February 2025).
- Yamasue, E.; Susa, M.; Fukuyama, H.; Nagata, K. Thermal conductivities of silicon and germanium in solid and liquid states measured by non-stationary hot wire method with silica coated probe. J. Cryst. Growth 2002, 234, 121–131. [Google Scholar] [CrossRef]
- Asensio-Lozano, J.; Vander Voort, G. The Al-Si Phase Diagram. Tech Notes 2009, 5, 5. [Google Scholar]
- Antes, H., Jr. Critical Melting Points and Reference Data for Vacuum Heat Treating. 2010. Available online: https://solarmfg.com/wp-content/uploads/2011/01/Critical-Melting-Point1.pdf (accessed on 20 February 2025).
- Lucchini Huspek, A.; Akdogan, B.; Akhmadeev, Y.H.; Petrikova, E.A.; Ivanov, Y.F.; Moskvin, P.V.; Koval, N.N.; Bestetti, M. Enhancing Microhardness and Corrosion Resistance of Anodic Oxides Grown on Hypoeutectic Al–Si Alloys Pretreated by Low-Energy High-Current Electron Beams. J. Surf. Investig. X-Ray Synchrotron Neutron Tech. 2024, 18, 1135–1145. [Google Scholar] [CrossRef]
- Morini, F.; Bestetti, M.; Franz, S.; Vicenzo, A.; Markov, A.; Yakovlev, E. Synthesis and characterization of ti-nb alloy films obtained by magnetron sputtering and low-energy high-current electron beam treatment. Materials 2021, 14, 3238. [Google Scholar] [CrossRef] [PubMed]
- Mills, K.C. Recommended Values of Thermophysical Properties for Selected Commercial Alloys; Woodhead Publishing: Cambridge, UK, 2002. [Google Scholar]
- Singaravelu, S.; Klopf, J.M.; Krafft, G.; Kelley, M.J. Laser nitriding of niobium for application to superconducting radio-frequency accelerator cavities. J. Vac. Sci. Technol. B 2011, 29, 061803. [Google Scholar] [CrossRef]
- Markov, A.; Yakovlev, E.; Bestetti, M. Synthesis of a Cr-Cu surface alloy using a low-energy high-current electron beam. Results Phys. 2019, 12, 1915–1924. [Google Scholar] [CrossRef]
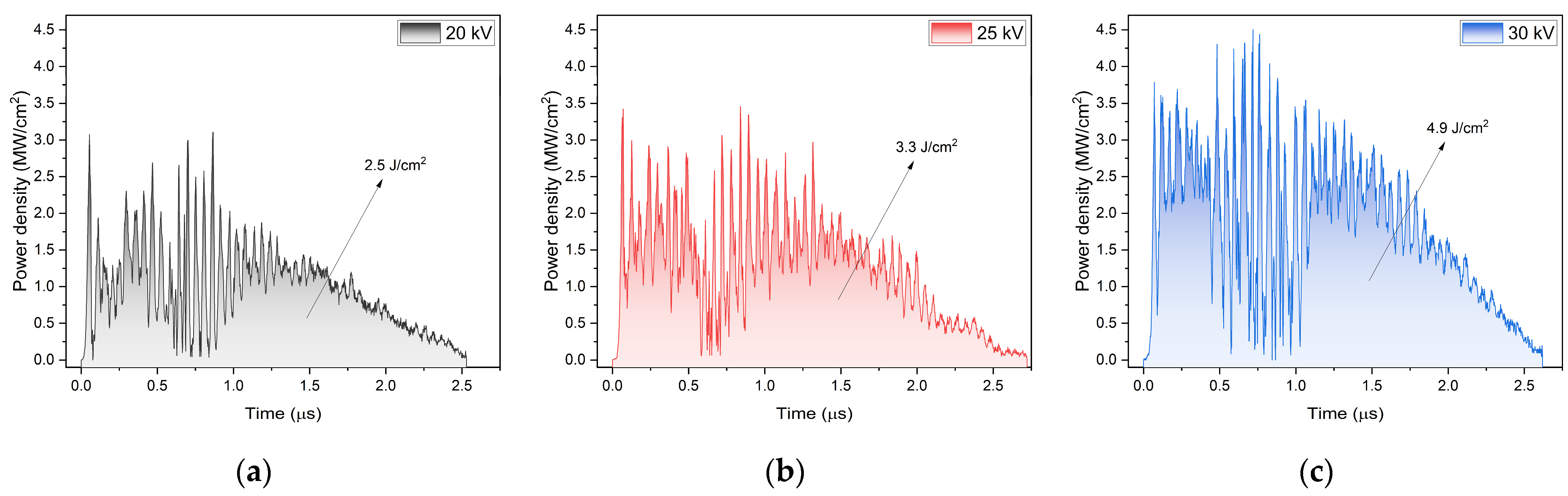
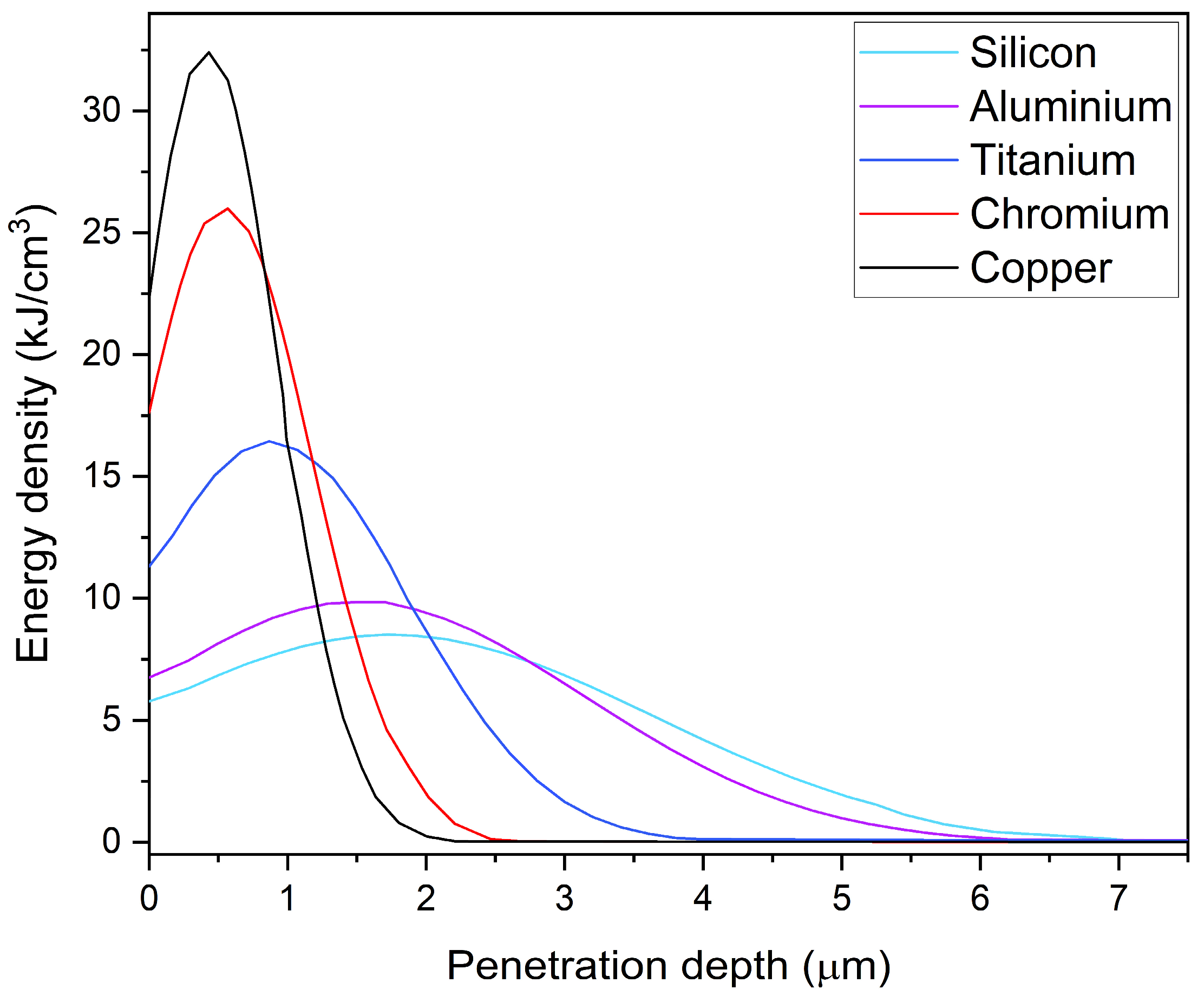
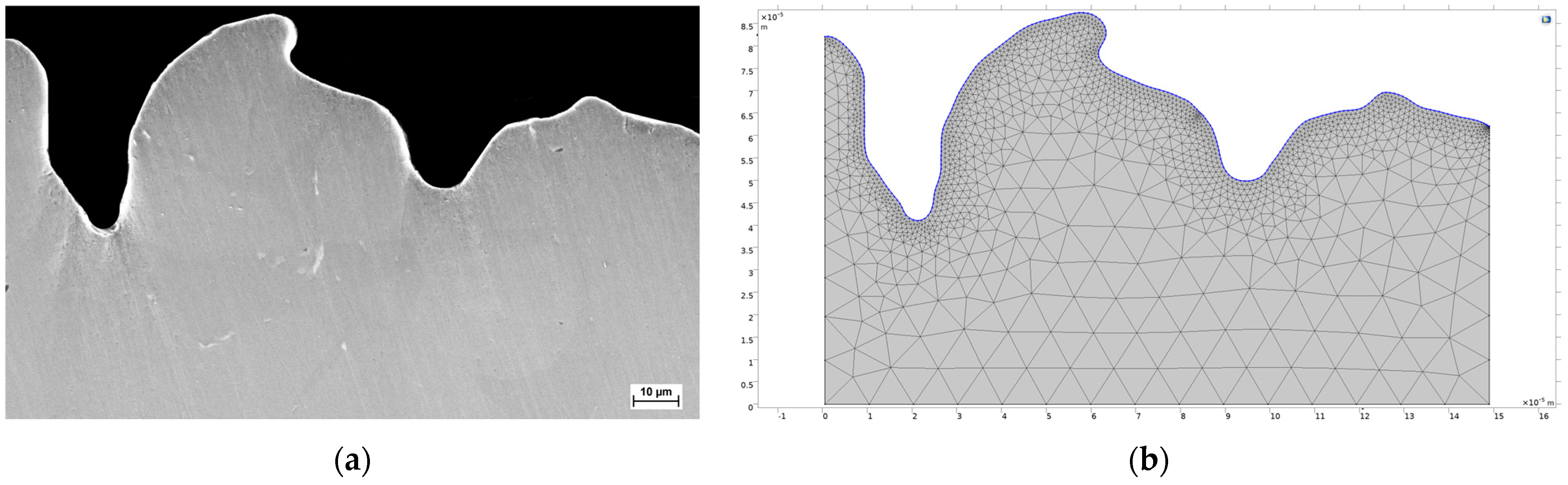
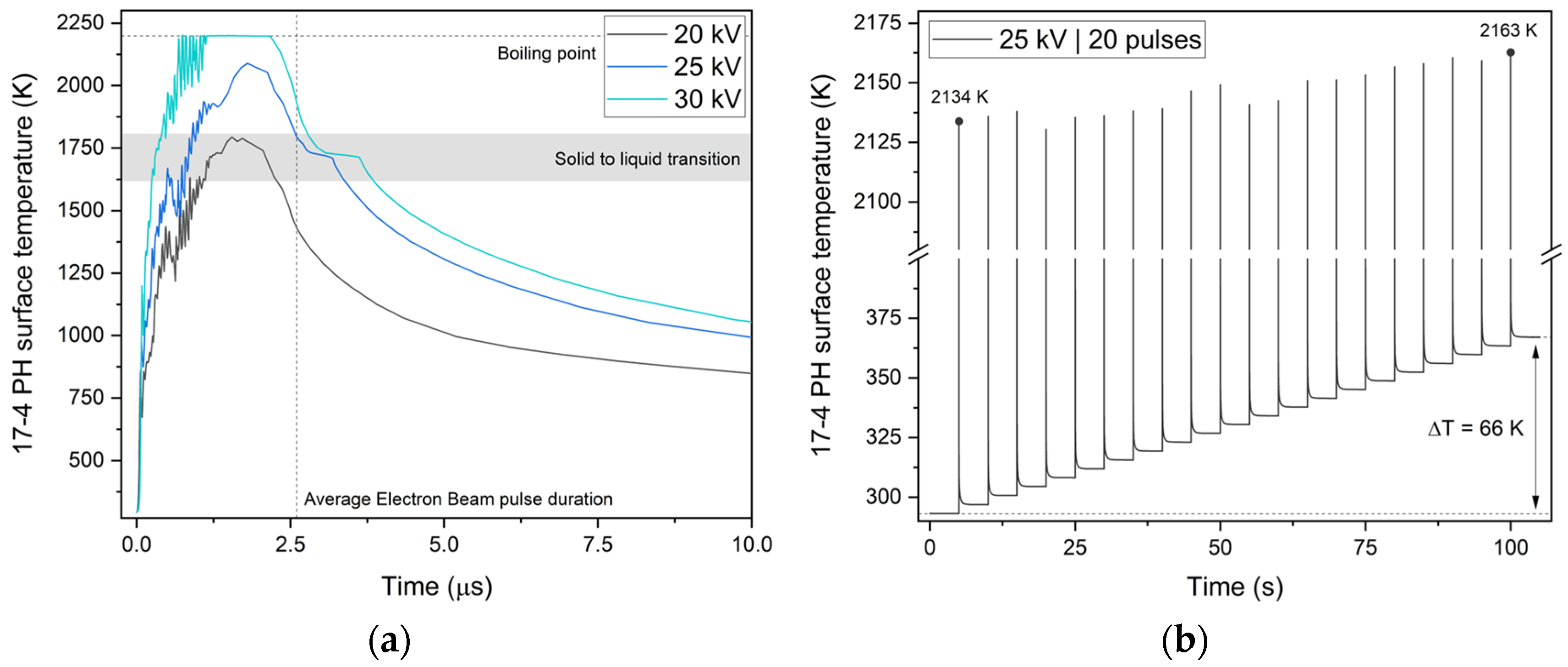

| Parameter | Value | Description |
|---|---|---|
| Ep | 2.5, 3.3, 4.9 J/cm2 | Energy density at 20, 25, 30 kV |
| τp | 2.5 µs | Average pulse duration |
| Np | 1-… | Number of pulses |
| ωp | 0.05–0.1 Hz | Pulse repetition frequency |
| Pirr | 1.8 × 10−4 Torr | Irradiation pressure |
| Tamb | 273.15 K | Ambient temperature |
| RH | 0.35 | Ambient relative humidity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucchini Huspek, A.; Mataloni, V.; Mohtashamifar, A.; Paterlini, L.; Bestetti, M. Thermal Modelling of Metals and Alloys Irradiated by Pulsed Electron Beam: Focus on Rough, Heterogeneous and Multilayered Materials. J. Manuf. Mater. Process. 2025, 9, 130. https://doi.org/10.3390/jmmp9040130
Lucchini Huspek A, Mataloni V, Mohtashamifar A, Paterlini L, Bestetti M. Thermal Modelling of Metals and Alloys Irradiated by Pulsed Electron Beam: Focus on Rough, Heterogeneous and Multilayered Materials. Journal of Manufacturing and Materials Processing. 2025; 9(4):130. https://doi.org/10.3390/jmmp9040130
Chicago/Turabian StyleLucchini Huspek, Andrea, Valentina Mataloni, Ali Mohtashamifar, Luca Paterlini, and Massimiliano Bestetti. 2025. "Thermal Modelling of Metals and Alloys Irradiated by Pulsed Electron Beam: Focus on Rough, Heterogeneous and Multilayered Materials" Journal of Manufacturing and Materials Processing 9, no. 4: 130. https://doi.org/10.3390/jmmp9040130
APA StyleLucchini Huspek, A., Mataloni, V., Mohtashamifar, A., Paterlini, L., & Bestetti, M. (2025). Thermal Modelling of Metals and Alloys Irradiated by Pulsed Electron Beam: Focus on Rough, Heterogeneous and Multilayered Materials. Journal of Manufacturing and Materials Processing, 9(4), 130. https://doi.org/10.3390/jmmp9040130







