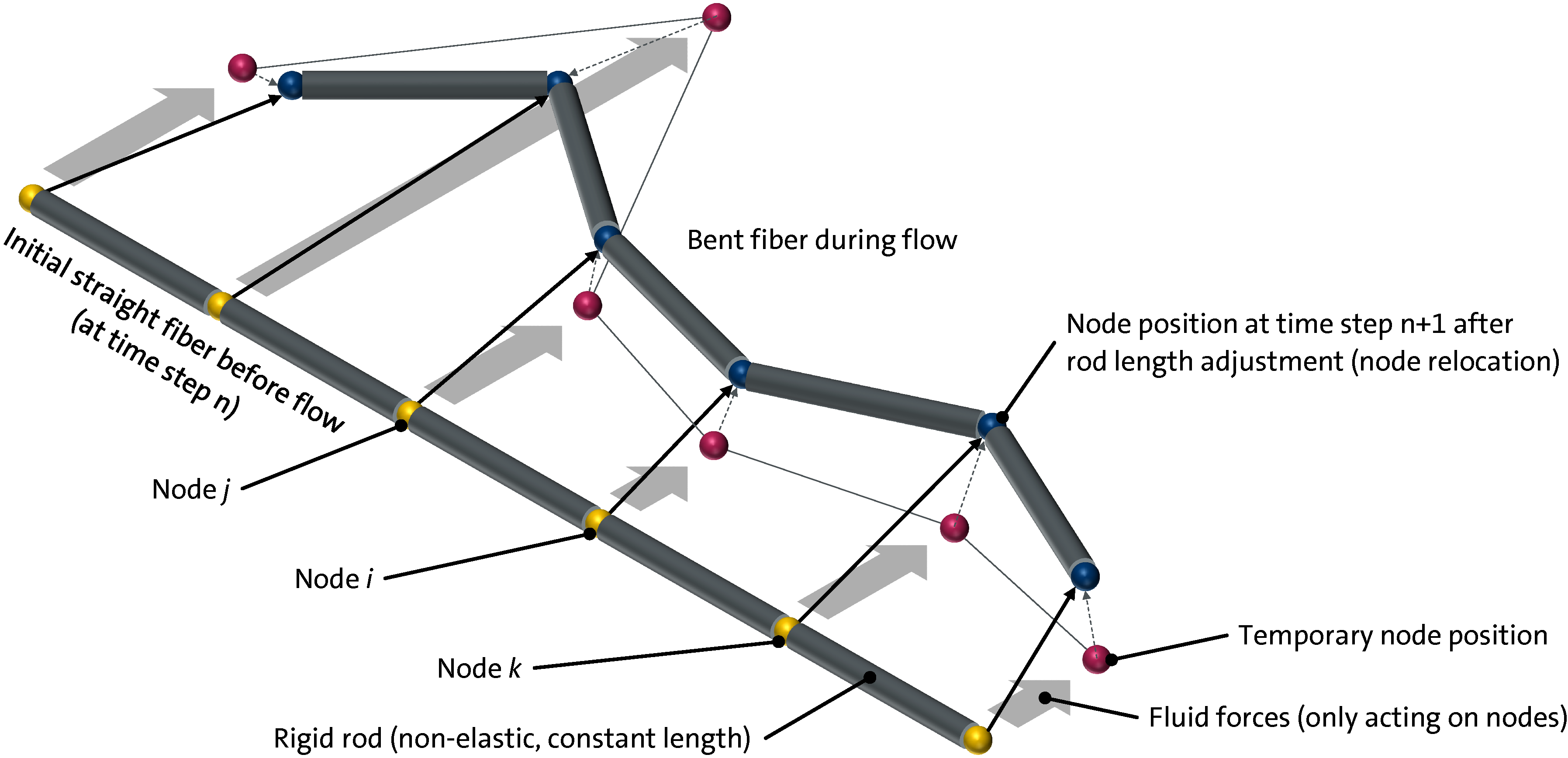
Figure 1.
Schematic illustration of a flexible long fiber modeled with 6 hinge nodes and 5 rods in 3D TIMON shown in its initial straight form and bent after moved by fluid forces and applied rod length adjustments (node relocations).
Figure 1.
Schematic illustration of a flexible long fiber modeled with 6 hinge nodes and 5 rods in 3D TIMON shown in its initial straight form and bent after moved by fluid forces and applied rod length adjustments (node relocations).
Figure 2.
Schematic illustration of a tetra element in the morphing method with one node at the top, 3 nodes at the bottom, and 20 calculation points through the thickness for Light 3D analyses in 3D TIMON CompositePRESS.
Figure 2.
Schematic illustration of a tetra element in the morphing method with one node at the top, 3 nodes at the bottom, and 20 calculation points through the thickness for Light 3D analyses in 3D TIMON CompositePRESS.
Figure 3.
(a) HexMC raw material roll; (b) HexMC mesostructure with randomly in-plane oriented prepreg carbon/epoxy unidirectional (UD) strands.
Figure 3.
(a) HexMC raw material roll; (b) HexMC mesostructure with randomly in-plane oriented prepreg carbon/epoxy unidirectional (UD) strands.
Figure 4.
(a) CAD images of the upper and lower mold half of a research tool with a ribbed hat profile tool insert designed for compression molding of carbon fiber sheet molding compounds (CF-SMCs); (b) CAD geometry of the ribbed hat profile part with varying rib heights and thicknesses.
Figure 4.
(a) CAD images of the upper and lower mold half of a research tool with a ribbed hat profile tool insert designed for compression molding of carbon fiber sheet molding compounds (CF-SMCs); (b) CAD geometry of the ribbed hat profile part with varying rib heights and thicknesses.
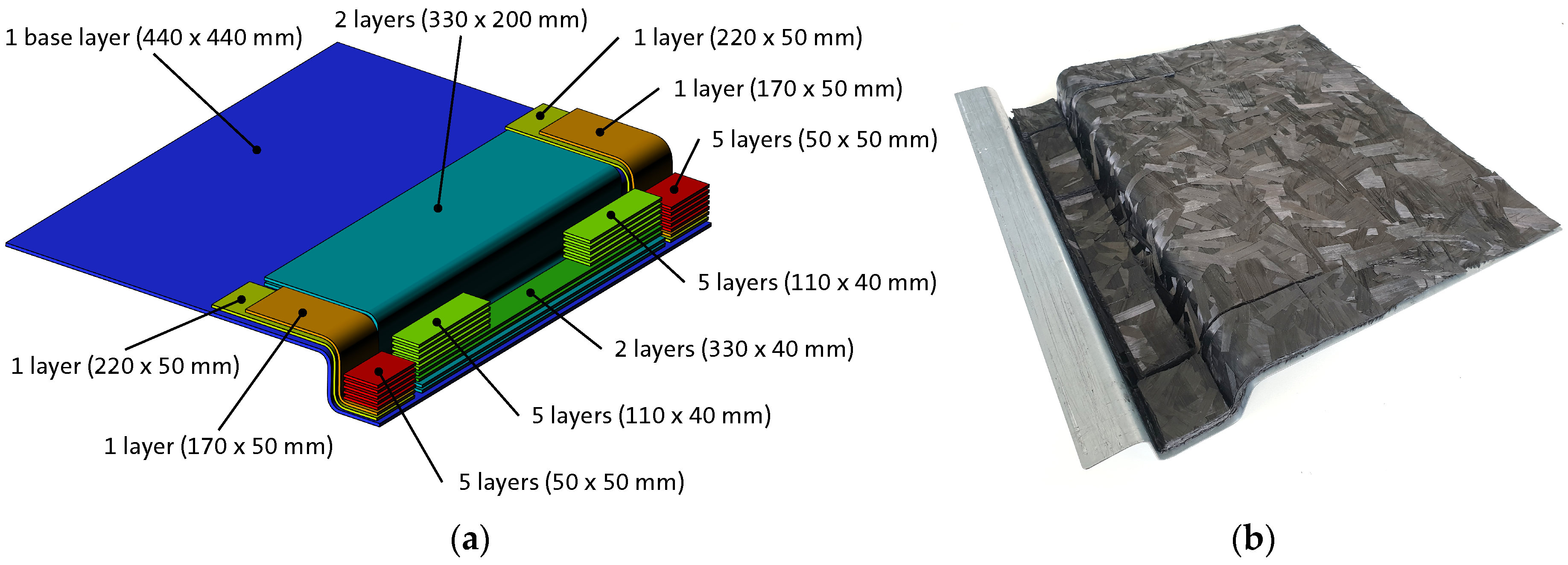
Figure 5.
HexMC charge pattern for ribbed structure part; (a) schematic illustration with dimensions and number of layers per charge package (for visualization purposes the charge package are slightly separated in thickness direction); (b) prepared HexMC charge on a metal preform.
Figure 5.
HexMC charge pattern for ribbed structure part; (a) schematic illustration with dimensions and number of layers per charge package (for visualization purposes the charge package are slightly separated in thickness direction); (b) prepared HexMC charge on a metal preform.
Figure 6.
Schematic illustration of the shimming technique for short shot experiments in a cross-sectional view; (a) initial pre-heating position of the upper mold half; (b) final position of the upper mold half touching the 8.65 mm shims and showing the short shot of the pressed HexMC charge.
Figure 6.
Schematic illustration of the shimming technique for short shot experiments in a cross-sectional view; (a) initial pre-heating position of the upper mold half; (b) final position of the upper mold half touching the 8.65 mm shims and showing the short shot of the pressed HexMC charge.
Figure 7.
Mold filling simulation in 3D TIMON CompositePRESS using the morphing method; (a) cross sectional view of the morphed tetra mesh in the initial open-mold position; (b) pressed back tetra mesh close to end of compression showing the proceeding flow front in the hat brim.
Figure 7.
Mold filling simulation in 3D TIMON CompositePRESS using the morphing method; (a) cross sectional view of the morphed tetra mesh in the initial open-mold position; (b) pressed back tetra mesh close to end of compression showing the proceeding flow front in the hat brim.
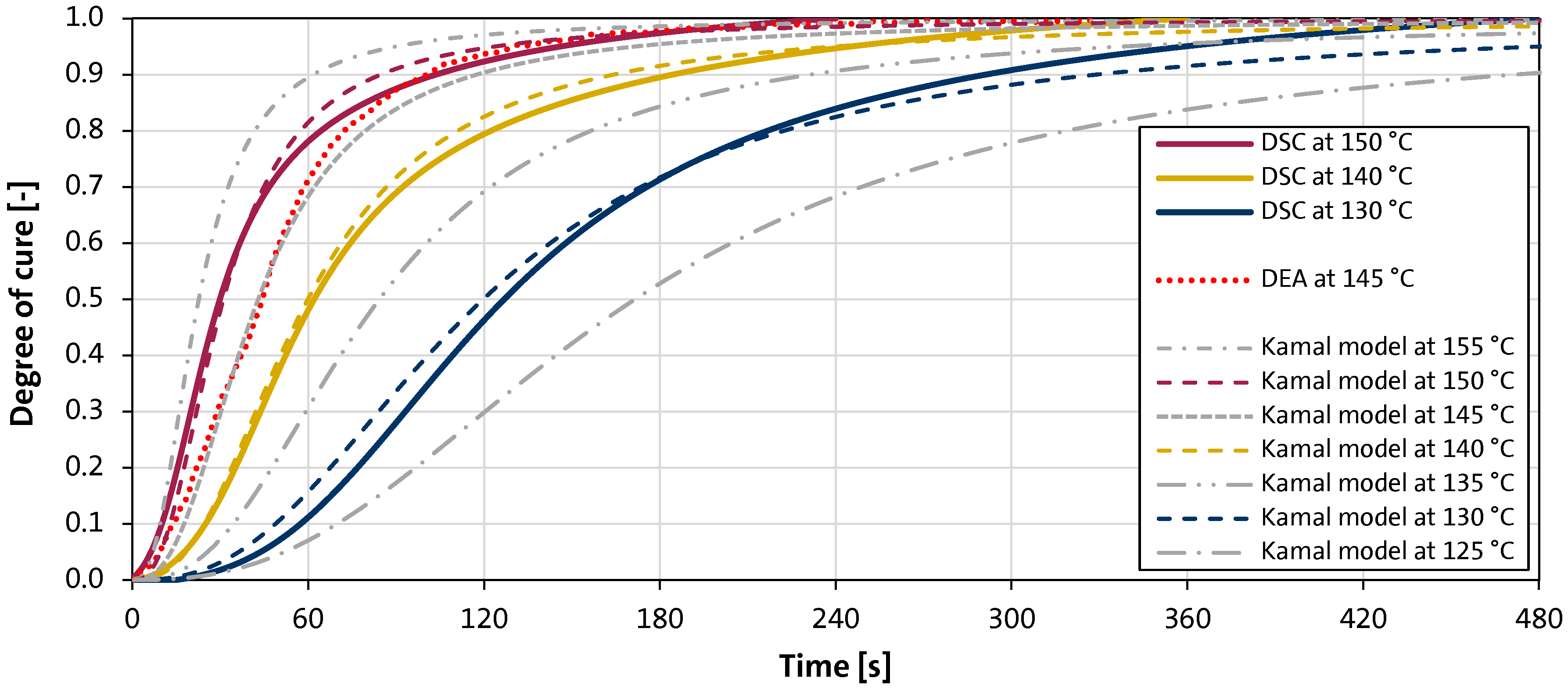
Figure 8.
Isothermal differential scanning calorimetry (DSC) measurements of curing HexMC samples at different temperatures and fitted Kamal model curing curves using the identified parameters given in
Table 4.
Figure 8.
Isothermal differential scanning calorimetry (DSC) measurements of curing HexMC samples at different temperatures and fitted Kamal model curing curves using the identified parameters given in
Table 4.
Figure 9.
HexMC carbon fiber UD strands and a schematic illustration of their numerical counterpart modeled in 3D TIMON CompositePRESS with 4 boundary fibers defining the outer strand dimensions and 11 added inner fibers (here each fiber consists of 20 nodes and 19 rods, indicated on just one boundary fiber) (note: for visualization purposes length specifications are not true to scale).
Figure 9.
HexMC carbon fiber UD strands and a schematic illustration of their numerical counterpart modeled in 3D TIMON CompositePRESS with 4 boundary fibers defining the outer strand dimensions and 11 added inner fibers (here each fiber consists of 20 nodes and 19 rods, indicated on just one boundary fiber) (note: for visualization purposes length specifications are not true to scale).
Figure 10.
(a) Numerically modeled initial charge pattern for the ribbed hat profile part consisting of in-plane randomly oriented UD strands (5 UD strands are highlighted); (b) bottom view of the numerical charge definition where each charge package is colored differently for better discernibility.
Figure 10.
(a) Numerically modeled initial charge pattern for the ribbed hat profile part consisting of in-plane randomly oriented UD strands (5 UD strands are highlighted); (b) bottom view of the numerical charge definition where each charge package is colored differently for better discernibility.
Figure 11.
(a) Exemplary CT measurement setup (note: here, focus object distance (FOD) and the focus detector distance (FDD) are not the ones used for the scans); (b) schematic illustration of merged CT scans with overlap areas.
Figure 11.
(a) Exemplary CT measurement setup (note: here, focus object distance (FOD) and the focus detector distance (FDD) are not the ones used for the scans); (b) schematic illustration of merged CT scans with overlap areas.
Figure 12.
Ribbed structure compression molded with a simple quadratic HexMC charge pattern and unsuited molding parameters showing extensive fiber matrix separation (FMS) (left) compared to a part molded with a pre-heated and optimized charge pattern developed by means of filling simulation studies using 3D TIMON CompositePRESS (right) (plate areas are removed from the ribbed hat profiles).
Figure 12.
Ribbed structure compression molded with a simple quadratic HexMC charge pattern and unsuited molding parameters showing extensive fiber matrix separation (FMS) (left) compared to a part molded with a pre-heated and optimized charge pattern developed by means of filling simulation studies using 3D TIMON CompositePRESS (right) (plate areas are removed from the ribbed hat profiles).
Figure 13.
Three compression molded ribbed structures made of HexMC (plate areas are removed from the ribbed hat profiles) picked for CT scanning and a detailed view on the right hand side showing the middle section of sample #19 in bottom view.
Figure 13.
Three compression molded ribbed structures made of HexMC (plate areas are removed from the ribbed hat profiles) picked for CT scanning and a detailed view on the right hand side showing the middle section of sample #19 in bottom view.
Figure 14.
3D TIMON CompositePRESS fill simulation status compared to a real HexMC short shot using 8.65 mm shims.
Figure 14.
3D TIMON CompositePRESS fill simulation status compared to a real HexMC short shot using 8.65 mm shims.
Figure 15.
3D TIMON CompositePRESS fill simulation status compared to a real HexMC short shot using 4.00 mm shims (numerical and real short shot are shown from different viewing angles).
Figure 15.
3D TIMON CompositePRESS fill simulation status compared to a real HexMC short shot using 4.00 mm shims (numerical and real short shot are shown from different viewing angles).
Figure 16.
(a) Progressing flow front and deformed UD strands during the direct fiber simulation (DFS) with 3D TIMON CompositePRESS at an intermediate time step; (b) DFS result close to the end of compression.
Figure 16.
(a) Progressing flow front and deformed UD strands during the direct fiber simulation (DFS) with 3D TIMON CompositePRESS at an intermediate time step; (b) DFS result close to the end of compression.
Figure 17.
(a) Initial virtual charge configuration with randomly oriented UD strands consisting of 15 fibers each; (b) highlighted UD strand (purple colored) at the plate surface before molding; (c) same UD strand near to the end of its flow path; (d) detailed view showing the 15 slightly deformed single fibers of the flown UD strand (for visualization purposes all other strands are colored in light gray).
Figure 17.
(a) Initial virtual charge configuration with randomly oriented UD strands consisting of 15 fibers each; (b) highlighted UD strand (purple colored) at the plate surface before molding; (c) same UD strand near to the end of its flow path; (d) detailed view showing the 15 slightly deformed single fibers of the flown UD strand (for visualization purposes all other strands are colored in light gray).
Figure 18.
(a) Photo of the initial HexMC charge configuration with randomly oriented UD strands in several charge packages on a metal preform; (b) detailed view of the UD strands in the lower right corner of the base charge; (c) compression molded part; (d) detailed view of the lower right corner of the plate showing the flown and slightly deformed UD strands.
Figure 18.
(a) Photo of the initial HexMC charge configuration with randomly oriented UD strands in several charge packages on a metal preform; (b) detailed view of the UD strands in the lower right corner of the base charge; (c) compression molded part; (d) detailed view of the lower right corner of the plate showing the flown and slightly deformed UD strands.
Figure 19.
Virtual UD strand (colored in blue; initial position blue dotted) in the hat profile area deforming and splitting after flowing into and through a rib shown at two different time steps (all other fibers are colored in light gray).
Figure 19.
Virtual UD strand (colored in blue; initial position blue dotted) in the hat profile area deforming and splitting after flowing into and through a rib shown at two different time steps (all other fibers are colored in light gray).
Figure 20.
(a) Predicted fiber orientation vectors displayed at the part surface of the hat profile; (b) detailed view of a cross section (front view) showing the fiber orientation vectors in the three middle ribs.
Figure 20.
(a) Predicted fiber orientation vectors displayed at the part surface of the hat profile; (b) detailed view of a cross section (front view) showing the fiber orientation vectors in the three middle ribs.
Figure 21.
CT scan of sample #20 showing fiber bundles of split UD strands on the surface of the hat profile’s end brim after a flow length of approximately 100 mm.
Figure 21.
CT scan of sample #20 showing fiber bundles of split UD strands on the surface of the hat profile’s end brim after a flow length of approximately 100 mm.
Figure 22.
(a) CT images of the hat profile middle sections of all three scanned parts (top view; 1 mm of the each part surface is removed to see the inner strand bundle orientations); (b) fiber bundle orientations determined by VGSTUDIO MAX 3.3 on a 5 × 5 mm integration mesh in a wider section of sample #20 displayed as ellipsoids in the end brim and as vectors (1st eigenvector) in the plate brim.
Figure 22.
(a) CT images of the hat profile middle sections of all three scanned parts (top view; 1 mm of the each part surface is removed to see the inner strand bundle orientations); (b) fiber bundle orientations determined by VGSTUDIO MAX 3.3 on a 5 × 5 mm integration mesh in a wider section of sample #20 displayed as ellipsoids in the end brim and as vectors (1st eigenvector) in the plate brim.
Figure 23.
(a) Detailed 3D view of the CT scanned ribbed structure #20 (displayed are density gradients at the part surface; the surface of the hat brims is slightly removed to show the carbon fiber bundle orientations inside the brims); (b) determined FOTs of the same part displayed as ellipsoids in VGSTUDIO MAX 3.3 (analysis based on the process simulation tetra mesh; CT scan data are set to 100% transparency) (red elongated ellipsoids: fibers highly oriented in one direction, green flattened ellipsoids: planar fiber orientation, blue spherical ellipsoids: 3D random fiber orientation).
Figure 23.
(a) Detailed 3D view of the CT scanned ribbed structure #20 (displayed are density gradients at the part surface; the surface of the hat brims is slightly removed to show the carbon fiber bundle orientations inside the brims); (b) determined FOTs of the same part displayed as ellipsoids in VGSTUDIO MAX 3.3 (analysis based on the process simulation tetra mesh; CT scan data are set to 100% transparency) (red elongated ellipsoids: fibers highly oriented in one direction, green flattened ellipsoids: planar fiber orientation, blue spherical ellipsoids: 3D random fiber orientation).
Figure 24.
CAD image of the ribbed structure’s middle section (3D view, superimposed tetra mesh) with all analysis areas used for the comparison of the averaged fiber orientations of all three CT scans with the fiber orientations predicted with 3D TIMON CompositePRESS.
Figure 24.
CAD image of the ribbed structure’s middle section (3D view, superimposed tetra mesh) with all analysis areas used for the comparison of the averaged fiber orientations of all three CT scans with the fiber orientations predicted with 3D TIMON CompositePRESS.
Figure 25.
1st eigenvector (displayed as arrow) of a fiber orientation in 3D space described by the polar angle and the azimuthal angle (Eulerian angles) in a Cartesian coordinate system.
Figure 25.
1st eigenvector (displayed as arrow) of a fiber orientation in 3D space described by the polar angle and the azimuthal angle (Eulerian angles) in a Cartesian coordinate system.
Figure 26.
CAD image of the ribbed structure’s middle section (front view) with the rib analysis areas (white boxes) showing the determined averaged fiber orientations of all three CT scans in green superimposed with the fiber orientations predicted with 3D TIMON CompositePRESS in pink (both displayed as 2D ellipses on the used tetra mesh).
Figure 26.
CAD image of the ribbed structure’s middle section (front view) with the rib analysis areas (white boxes) showing the determined averaged fiber orientations of all three CT scans in green superimposed with the fiber orientations predicted with 3D TIMON CompositePRESS in pink (both displayed as 2D ellipses on the used tetra mesh).
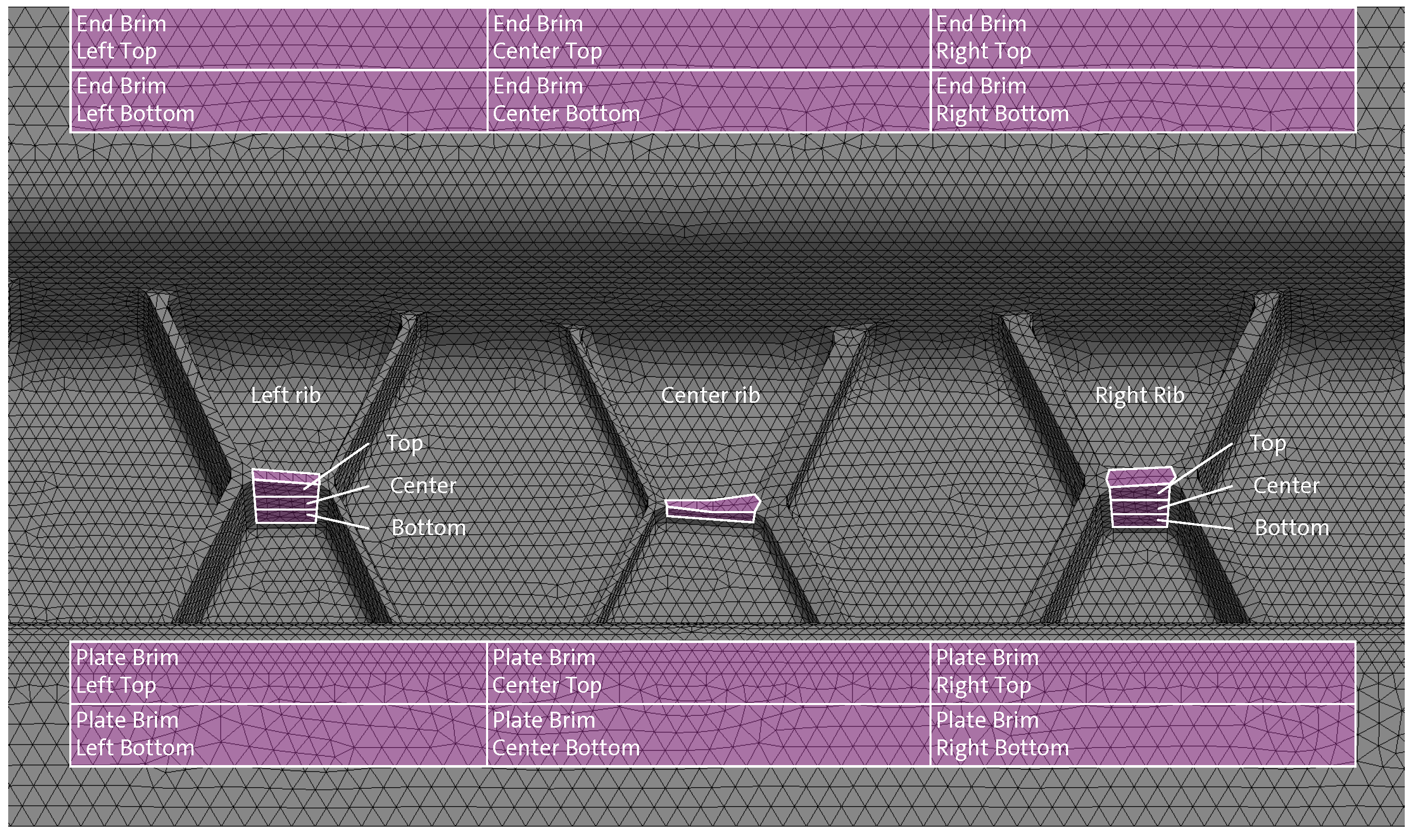
Figure 27.
CAD image of the ribbed structure’s middle section (bottom view) with the brims and head analysis areas (white boxes) showing the determined averaged fiber orientations of all three CT scans in green superimposed with the fiber orientations predicted with 3D TIMON CompositePRESS in pink (both displayed as 2D ellipses on the tetra mesh).
Figure 27.
CAD image of the ribbed structure’s middle section (bottom view) with the brims and head analysis areas (white boxes) showing the determined averaged fiber orientations of all three CT scans in green superimposed with the fiber orientations predicted with 3D TIMON CompositePRESS in pink (both displayed as 2D ellipses on the tetra mesh).
Table 1.
HexMC material properties.
Table 1.
HexMC material properties.
| Material Property | Value/Type | Unit |
|---|
| Fiber | High strength carbon | - |
| Fiber length | 50 | mm |
| Fiber density | 1.80 | g/cm3 |
| Resin | M77 epoxy | - |
| Resin density | 1.22 | g/cm3 |
| UD strand dimensions | 50 × 8 × 0.15 | mm |
| Material density | 1.55 | g/cm3 |
| Nominal fiber weight content | 62 | % |
| Nominal fiber volume content | 57 | % |
| Areal weight | 2000 | g/m2 |
Table 2.
Compression molding processing conditions.
Table 2.
Compression molding processing conditions.
| Molding Parameter | Value | Unit |
|---|
| Mold temperature | 140 | °C |
| Preheating time | 17 | s |
| Pressure | 200 | bar |
| Closing speed | 5 | mm/s |
| Curing time | 480 | s |
| Charge weight | ~1000 | g |
| Mold coverage | ~80 | % |
Table 3.
Cross–Castro–Macosko viscosity model constants.
Table 3.
Cross–Castro–Macosko viscosity model constants.
| Constant | Value | Unit |
|---|
| a | 1.000 × 10−11 | Pa s |
| b | 1.100 × 104 | K |
| D | 1.500 × 101 | - |
| E | −4.000 × 100 | - |
| n | 6.000 × 10−1 | - |
| τ* | 2.000 × 102 | Pa |
| αgel | 8.500 × 10−1 | - |
Table 4.
Kamal curing model constants.
Table 4.
Kamal curing model constants.
| Constant | Value | Unit |
|---|
| m | 6.100 × 10−1 | - |
| n | 1.580 × 100 | - |
| A1 | 1.280 × 107 | 1/s |
| A2 | 6.750 × 1010 | 1/s |
| E1 | 1.187 × 104 | K |
| E2 | 1.159 × 104 | K |
Table 5.
Micro-CT measurement parameters.
Table 5.
Micro-CT measurement parameters.
| Scan Parameter | Value | Unit |
|---|
| Voxel resolution | 59.6 | µm |
| X-ray voltage | 160 | kV |
| X-ray current | 250 | µA |
| Focus object distance (FOD) | 642 | mm |
| Focus detector distance (FDD) | 1500 | mm |
| Integration time | 6 × 200 | ms |
| Projections | 2 × 2400 | - |
| Measuring time per partial scan | 100 | min |
Table 6.
Averaged fiber orientation measurement results for the rib analysis areas of three CT scanned ribbed hat profiles.
Table 6.
Averaged fiber orientation measurement results for the rib analysis areas of three CT scanned ribbed hat profiles.
| Analysis Area | Axx | Ayy | Azz | 1st Eigenvalue | 2nd Eigenvalue | |
|---|
| Left Rib | Top | 0.05 | 0.70 | 0.26 | 0.73 | 0.23 | 79.4° |
| SD | 0.02 | 0.04 | 0.02 | 0.03 | 0.01 | 2.6° |
| Center | 0.06 | 0.60 | 0.34 | 0.65 | 0.30 | 87.0° |
| SD | 0.03 | 0.02 | 0.00 | 0.03 | 0.01 | 15.0° |
| Bottom | 0.07 | 0.61 | 0.32 | 0.65 | 0.28 | 74.8° |
| SD | 0.02 | 0.02 | 0.01 | 0.02 | 0.00 | 1.4° |
| Center Rib | 0.10 | 0.71 | 0.19 | 0.73 | 0.21 | 96.5° |
| SD | 0.03 | 0.06 | 0.04 | 0.07 | 0.04 | 0.6° |
| Right Rib | Top | 0.15 | 0.61 | 0.24 | 0.66 | 0.25 | 101.2° |
| SD | 0.06 | 0.09 | 0.04 | 0.09 | 0.05 | 2.5° |
| Center | 0.12 | 0.54 | 0.34 | 0.61 | 0.30 | 107.2° |
| SD | 0.03 | 0.03 | 0.05 | 0.05 | 0.04 | 3.6° |
| Bottom | 0.09 | 0.49 | 0.42 | 0.60 | 0.32 | 115.5° |
| SD | 0.03 | 0.03 | 0.05 | 0.05 | 0.03 | 3.1° |
| Mean SD | 0.03 | 0.04 | 0.03 | 0.05 | 0.03 | 4.1° |
Table 7.
Averaged fiber orientation measurement results for the brim and head analysis areas of three CT scanned ribbed hat profiles.
Table 7.
Averaged fiber orientation measurement results for the brim and head analysis areas of three CT scanned ribbed hat profiles.
| Analysis Area | Axx | Ayy | Azz | 1st Eigenvalue | 2nd Eigenvalue | |
|---|
| End Brim | Left | Top | 0.27 | 0.70 | 0.03 | 0.73 | 0.25 | 103.5° |
| SD | 0.01 | 0.01 | 0.02 | 0.02 | 0.01 | 19.9° |
| Bottom | 0.42 | 0.55 | 0.03 | 0.63 | 0.34 | 113.5° |
| SD | 0.05 | 0.04 | 0.02 | 0.03 | 0.01 | 13.3° |
| Center | Top | 0.32 | 0.65 | 0.03 | 0.68 | 0.29 | 102.0° |
| SD | 0.03 | 0.01 | 0.02 | 0.01 | 0.01 | 10.6° |
| Bottom | 0.46 | 0.51 | 0.03 | 0.61 | 0.36 | 129.5° |
| SD | 0.01 | 0.01 | 0.02 | 0.03 | 0.01 | 13.0° |
| Right | Top | 0.28 | 0.70 | 0.02 | 0.73 | 0.26 | 97.8° |
| SD | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 3.9° |
| Bottom | 0.40 | 0.57 | 0.02 | 0.65 | 0.33 | 115.9° |
| SD | 0.04 | 0.04 | 0.01 | 0.04 | 0.03 | 11.3° |
| Plate Brim | Left | Top | 0.36 | 0.61 | 0.03 | 0.65 | 0.33 | 96.2° |
| SD | 0.04 | 0.05 | 0.01 | 0.04 | 0.04 | 23.2° |
| Bottom | 0.39 | 0.60 | 0.01 | 0.64 | 0.35 | 97.4° |
| SD | 0.05 | 0.05 | 0.00 | 0.04 | 0.04 | 4.5° |
| Center | Top | 0.38 | 0.58 | 0.04 | 0.63 | 0.35 | 85.1° |
| SD | 0.05 | 0.06 | 0.01 | 0.05 | 0.04 | 18.6° |
| Bottom | 0.45 | 0.54 | 0.01 | 0.61 | 0.37 | 92.4° |
| SD | 0.06 | 0.06 | 0.01 | 0.03 | 0.02 | 17.6° |
| Right | Top | 0.37 | 0.59 | 0.03 | 0.64 | 0.34 | 91.2° |
| SD | 0.04 | 0.05 | 0.01 | 0.05 | 0.04 | 23.1° |
| Bottom | 0.41 | 0.57 | 0.01 | 0.62 | 0.36 | 99.7° |
| SD | 0.04 | 0.04 | 0.01 | 0.05 | 0.04 | 67.6° |
| Head | Left | 0.56 | 0.40 | 0.04 | 0.61 | 0.36 | 156.5° |
| SD | 0.06 | 0.06 | 0.02 | 0.06 | 0.04 | 14.6° |
| Right | 0.51 | 0.44 | 0.05 | 0.58 | 0.37 | 141.3° |
| SD | 0.07 | 0.05 | 0.03 | 0.06 | 0.04 | 19.3° |
| Mean SD | 0.04 | 0.04 | 0.01 | 0.04 | 0.03 | 18.6° |
Table 8.
Predicted fiber orientation results for the rib analysis areas of the ribbed hat profile using 3D TIMON CompositePRESS.
Table 8.
Predicted fiber orientation results for the rib analysis areas of the ribbed hat profile using 3D TIMON CompositePRESS.
| Analysis Area | Axx | Ayy | Azz | 1st Eigenvalue | 2nd Eigenvalue | |
|---|
| Left Rib | Top | 0.12 | 0.53 | 0.34 | 0.54 | 0.34 | 95.8° |
| Absolute error vs. CT scans | 0.08 | 0.16 | 0.09 | 0.19 | 0.11 | 16.4° |
| Center | 0.09 | 0.67 | 0.23 | 0.67 | 0.24 | 88.4° |
| Absolute error vs. CT scans | 0.03 | 0.07 | 0.11 | 0.03 | 0.06 | 1.4° |
| Bottom | 0.10 | 0.78 | 0.13 | 0.79 | 0.12 | 82.6° |
| Absolute error vs. CT scans | 0.03 | 0.16 | 0.19 | 0.14 | 0.16 | 7.8° |
| Center Rib | 0.21 | 0.60 | 0.18 | 0.61 | 0.22 | 84.2° |
|
Absolute error vs. CT scans | 0.12 | 0.11 | 0.01 | 0.12 | 0.01 | 12.3° |
| Right Rib | Top | 0.15 | 0.71 | 0.15 | 0.71 | 0.15 | 94.1° |
| Absolute error vs. CT scans | 0.00 | 0.10 | 0.10 | 0.05 | 0.10 | 7.1° |
| Center | 0.15 | 0.76 | 0.09 | 0.77 | 0.15 | 94.5° |
| Absolute error vs. CT scans | 0.03 | 0.22 | 0.25 | 0.15 | 0.15 | 12.7° |
| Bottom | 0.19 | 0.74 | 0.07 | 0.74 | 0.19 | 92.4° |
| Absolute error vs. CT scans | 0.09 | 0.25 | 0.35 | 0.14 | 0.13 | 23.2° |
| MAE vs. averaged CT scans | 0.06 | 0.15 | 0.16 | 0.12 | 0.10 | 11.6° |
Table 9.
Predicted fiber orientation results for the brim and head analysis areas of the ribbed hat profile using 3D TIMON CompositePRESS.
Table 9.
Predicted fiber orientation results for the brim and head analysis areas of the ribbed hat profile using 3D TIMON CompositePRESS.
| Analysis area | Axx | Ayy | Azz | 1st Eigenvalue | 2nd Eigenvalue | |
|---|
| End Brim | Left | Top | 0.18 | 0.81 | 0.01 | 0.81 | 0.19 | 91.2° |
| Absolute error vs. CT | 0.08 | 0.10 | 0.02 | 0.08 | 0.06 | 12.3° |
| Bottom | 0.29 | 0.70 | 0.01 | 0.70 | 0.29 | 85.7° |
| Absolute error vs. CT | 0.13 | 0.15 | 0.02 | 0.07 | 0.05 | 27.8° |
| Center | Top | 0.45 | 0.54 | 0.02 | 0.55 | 0.43 | 112.1° |
| Absolute error vs. CT | 0.13 | 0.12 | 0.01 | 0.13 | 0.14 | 10.1° |
| Bottom | 0.70 | 0.29 | 0.01 | 0.70 | 0.29 | 1.9° |
| Absolute error vs. CT | 0.24 | 0.22 | 0.02 | 0.10 | 0.07 | 52.5° |
| Right | Top | 0.24 | 0.75 | 0.01 | 0.76 | 0.23 | 97.4° |
| Absolute error vs. CT | 0.05 | 0.05 | 0.01 | 0.03 | 0.02 | 0.4° |
| Bottom | 0.43 | 0.56 | 0.01 | 0.59 | 0.40 | 111.7° |
| Absolute error vs. CT | 0.02 | 0.01 | 0.01 | 0.05 | 0.07 | 4.3° |
| Plate Brim | Left | Top | 0.21 | 0.75 | 0.05 | 0.83 | 0.14 | 109.3° |
| Absolute error vs. CT | 0.15 | 0.14 | 0.02 | 0.17 | 0.19 | 13.1° |
| Bottom | 0.36 | 0.63 | 0.00 | 0.74 | 0.26 | 117.5° |
| Absolute error vs. CT | 0.03 | 0.04 | 0.01 | 0.10 | 0.09 | 20.1° |
| Center | Top | 0.26 | 0.68 | 0.07 | 0.69 | 0.27 | 101.7° |
| Absolute error vs. CT | 0.13 | 0.09 | 0.03 | 0.06 | 0.08 | 16.6° |
| Bottom | 0.32 | 0.66 | 0.01 | 0.68 | 0.30 | 102.5° |
| Absolute error vs. CT | 0.12 | 0.12 | 0.00 | 0.07 | 0.07 | 10.1° |
| Right | Top | 0.29 | 0.64 | 0.07 | 0.67 | 0.29 | 76.1° |
| Absolute error vs. CT | 0.08 | 0.05 | 0.03 | 0.03 | 0.05 | 15.0° |
| Bottom | 0.38 | 0.61 | 0.01 | 0.61 | 0.38 | 87.1° |
| Absolute error vs. CT | 0.03 | 0.04 | 0.01 | 0.01 | 0.02 | 12.5° |
| Head | Left | 0.57 | 0.42 | 0.00 | 0.60 | 0.40 | 20.3° |
| Absolute error vs. CT | 0.01 | 0.02 | 0.04 | 0.01 | 0.04 | 43.8° ** |
| Right | 0.59 | 0.40 | 0.00 | 0.64 | 0.36 | 23.5° |
| Absolute error vs. CT | 0.08 | 0.03 | 0.05 | 0.06 | 0.01 | 62.2° ** |
| MAE vs. averaged CT scans | 0.09 | 0.08 | 0.02 | 0.07 | 0.07 | 21.5° |