Fatigue Life Prediction for Carbon-SMC and Carbon-FRP by Considering Elastic Modulus Degradation

Abstract

In the automotive industry, being lightweight has become an important design factor with the enhancement of environmental regulations. As a result, many studies on the application of composite materials are in progress. Among them, interest in carbon materials, such as carbon sheet molding compound (C-SMC) and carbon-fiber-reinforced plastic (CFRP), which have excellent strength and stiffness, is increasing. However, CFRP is a material that makes it difficult to secure economic feasibility due to its relatively high manufacturing costs and limited mass production, despite its excellent mechanical strength and durability. As a result, many studies have been conducted on C-SMC as an alternative carbon composite material that can be easily mass-produced. In this regard, this study intended to conduct a study on evaluating the fatigue strength of C-SMC and CFRP among mechanical properties due to the lack of clear failure criteria for fatigue design. We investigated the tensile and fatigue strengths of C-SMC and CFRP, respectively. In the case of C-SMC, the mechanical strength tests were conducted for two different width conditions to evaluate the cutting effect and the machining methods to assess the effects of the edge conditions. To evaluate the fatigue failure assessment criteria, the stiffness drop and elastic modulus degradation criteria were applied for each fatigue test result from the C-SMC and CFRP. The results confirmed that the rationality of the failure criteria in terms of the stiffness drop and the application of the fatigue life prediction of C-SMC based on elastic modulus degradation demonstrated promising results.

1. Introduction

Carbon-fiber-reinforced plastic (CFRP) has excellent strength and stiffness. It can be lightweight, making it suitable for the manufacture of simple feature parts for automobiles, and is currently being applied in various ways [1]. However, CFRP is a material that makes it difficult to secure economic feasibility due to its high manufacturing costs and limited mass production, despite its excellent mechanical strength and durability. As a result, many studies have been conducted on carbon sheet molding compound (C-SMC), an alternative carbon composite material that can be mass-produced. C-SMC is a fiberglass-reinforced thermosetting material that has been applied to automobile production for a long time and can be mass-produced. It has excellent lightweight realization and durability. However, it has been suggested that the existing fatigue tests of C-SMC do not have clear failure criteria and that the standard deviation for the fatigue data is quite large, making it difficult to ensure sufficient reliability.

Salkind studied composite fatigue behavior in terms of the damage and failure mechanics [2]. Wang and Chim presented the fatigue life estimation formula of SMC based on elastic modulus degradation [3]. Sieberer et al. investigated the fatigue behavior of C-SMC while accounting for modulus degradation and stiffness [4]. Lin suggested a fatigue damage accumulation formula in composite materials based on elastic modulus degradation [5]. Denton studied the mechanical properties of SMC-R50 under various temperature effects [6]. Echaabi et al. investigated the failure criteria of a composite material according to the stress and strain of various components [7]. Tang et al. investigated the material behavior of SMC under three different cyclic loading conditions, i.e., tension–tension (T–T), compression–compression (C–C), and tension–compression (T–C) [8]. Fleckenstein et al. investigated the influences of different fiber orientations and fiber weight contents on the fatigue strength behavior of this long-fiber reinforced thermosetting material on SMC [9]. Studies have been conducted on the fatigue life of the composite, such as failure criteria of the stiffness drop and fatigue damage accumulation [10,11,12,13,14,15]. Shokrieh et al. investigated the fatigue behavior according to damage modeling of composite laminates [16,17,18]. Jain et al. presented a stress–number of cycles (S–N) curve that considered the effect of the stiffness drop according to the fiber orientation distribution during a fatigue test [19]. Tamboura et al. investigated the damage and fatigue life prediction of short-fiber-reinforced composites [20]. Therefore, even in recent studies, fatigue life prediction by applying the degradation of the elastic modulus according to the stiffness reduction and damage of the composites were being made. The aforementioned studies suggested failure criteria for composites but did not present failure criteria by applying them to C-SMC and CFRP. Furthermore, existing C-SMC and CFRP fatigue test data have a fairly large standard deviation and it is difficult to ensure sufficient reliability. Therefore, C-SMC and CFRP should evaluate the fatigue strength through fatigue tests according to various criteria and apply failure criteria.

In this study, the considerations for each material were classified as an experimental approach and an analytical approach. The experimental approach in this study was conducted based on fatigue and tensile tests, and the analytical approach was conducted via numerical calculations that were based on specific failure criteria. Finally, a new failure criterion for each material was proposed based on the fatigue life estimation.

2. Preparation of Test Specimen

The specimens used for the tensile and fatigue tests had the same dimensions, and the CFRP was designed according to American Society for Testing and Materials (ASTM)D 3039 [21]. Because C-SMC does not have a clear standard, it was designed based on ASTM D 3039 [21] and is shown in Figure 1. There were a total of four cases, three cases for C-SMC and one for CFRP. C-SMC was prepared using flat-plate machining C-SMC-Cut (carbon sheet molding compound cut) specimens and C-SMC-In-mold (carbon sheet molding compound in mold) specimens according to different molding methods. In the case of C-SMC-Cut, the C-SMC-Cut-35 (35 mm width) specimen and the large-width C-SMC-Cut-100 (100 mm width) specimen were produced to investigate the effect of the width of the specimen. The polymer matrix of C-SMC was of the thermosetting type. In addition, the proportion of carbon fiber and epoxy in the composition was 50% each. The distribution method of C-SMC involved cutting the material with a 1-inch width and distribute the top surface of a sheet from above followed by uniform compression. Figure 2 presents the specimen surface magnified by 50 times. According to Figure 2, it was observed that the fiber was randomly distributed in the C-SMC. In this regard, the C-SMC was considered to present relatively isotropic characteristics compared to the CFRP. In the case of CFRP, the fiber presented a constant orientation for each layer, such as 0° and 90°, though the CFRP tended to exhibit anisotropic characteristics, as shown in Figure 3.

Table 1. Number of specimens required for each stress–number of cycles (S–N) curve [22].

Type of Test	Number of Test Specimens
Preliminary and exploratory	6
Research and development testing of components and structures	12
Design allowables data	24
Reliability data	24

shows the number of test specimens for the fatigue tests in ASTM D3479 [22].

3. Estimation of Fatigue Life for C-SMC and CFRP According to the Failure Criteria

In this section, two different criteria are considered for deriving failure criteria and assessing the fatigue life. First, Salkind studied composite fatigue behavior [2]. Composites exhibit different stiffness changes from the metal at fracture. Figure 4 shows the difference in the stiffness change between metal and composite. Figure 5 shows the difference in the number of cycles between the stiffness change and the complete fracture of the composite [2]. The general stiffness behavior of metals and composites under fatigue loading conditions present significant differences for crack initiation and propagation. According to Thomas et al. [23], more than 50% of damage occurs in the first 20% of the life in the composite, which means that a structure or a component is able to survive in a condition with the presence of cracks. In the case of the metal, crack initiation generally occurs after more than 75% of the fatigue life, as presented in Figure 6. Therefore, in this study, the S–N curve at complete fracture was compared with the S–N curve at a specified stiffness drop according to the cycle. By evaluating the fatigue damage, a failure criterion for a particular stiffness drop was determined. The stiffness was obtained by dividing the load range by the displacement range based on Equation (1):

$$\mathrm{Stiffness}=\frac{\mathrm{Maximum}\mathrm{Load}-\mathrm{Minimum}\mathrm{Load}}{\mathrm{Maximum}\mathrm{Displacement}-\mathrm{Minimum}\mathrm{Displacement}}.$$

(1)

To predict the fatigue life of C-SMC, Wang and Chim used a criterion for reducing the elastic modulus of materials during fatigue testing to predict the fatigue life through an equation based on the fatigue damage rate [3]. Figure 7 shows a decrease in the elastic modulus due to different cyclic stresses during fatigue tests [3]. Equations (2)–(4) show the expressions necessary for calculating the fatigue damage rate. The parameter, D, is defined to provide a quantitative measure of the cycle fatigue damage.

$$D=1-\frac{E}{E^{*}},$$

(2)

$$\frac{\mathrm{d}D}{\mathrm{d}N}=A\left(D\right)N^B,$$

(3)

$$N_{\mathrm{f}}={[{{\displaystyle \int }}_0^{D_{\mathrm{f}}}\frac{B+1}{A}\mathrm{d}D]}^{\frac{1}{B+1}},$$

(4)

where E is the current elastic modulus and $E^{*}$ is the initial elastic modulus. A is a function of D, and B is the slope of the material in a log scale. $N_{\mathrm{f}}$ is the number of cycles it takes to achieve fatigue failure and $D_{\mathrm{f}}$ is the elastic modulus based on the failure criterion. Figure 8 shows the evaluation of the $\frac{\mathrm{d}D}{\mathrm{d}N}$ curve to the number of cycles with different cyclic stress magnitudes [3].

In addition, fatigue tests based on the reduced elastic modulus and the predicted fatigue life results were verified through comparative analysis.

Ye investigated a damage accumulation law according to the stiffness drop. Therefore, D according to the change in stiffness is shown in Equation (2) [5]. Figure 9 shows the fatigue damage evolution in the composites.

Damage accumulation occurs in three stages. The damage accumulates rapidly due to the initiation of many cracks at stage one, and through continuous crack growth, the cracks merge and reach fracture at stage three. The crack growth in stage two is based on the Paris law, which defines an equation that describes the fatigue damage accumulation:

$$\frac{\mathrm{d}D}{\mathrm{d}N}=C {\left(\frac{{\sigma }_{\max }^2}{D}\right)}^n,$$

(5)

where C and n are material constants that can be determined by testing specimens at various stress levels. By integrating Equation (5) and noting that D = 0 when N = 0, a simple form of the damage function (Equation (6)) can be obtained:

$$D={\left[\left(n+1\right)CN\right]}^{1/(n+1)}{\sigma }_{\max }^{2n/\left(n+1\right)}.$$

(6)

Equation (7) is derived from Equation (6):

$$N_1=\frac{D_C^{n+1}}{\left(n+1\right)C{\sigma }_{\max }^{2n}}.$$

(7)

Based on this, the fatigue life estimation according to the stiffness drop was applied to various composite materials.

4. Test Results

4.1. Tensile Test

In this section, the results of the tensile tests are described, which were carried out in accordance with the criteria in ASTM D3039 [21]; the detailed test conditions are summarized in

Table 2. Tensile test conditions.

Classification	Condition
Control mode	Displacement
Temperature	Room temperature
Constant head speed	1%
Gauge length	50 mm

.

Comparison of the Tensile Test Results of C-SMC and CFRP

In this section, the tensile test results of the C-SMC and CFRP are presented. In Figure 10 and

Table 3. Tensile test results.

	C-SMC-Cut-35		C-SMC-Cut-100		C-SMC-In-Mold		CFRP
No. of Case	Elastic Modulus (GPa)	Tensile Strength (MPa)	Elastic Modulus (GPa)	Tensile Strength (MPa)	Elastic Modulus (GPa)	Tensile Strength (MPa)	Elastic Modulus (GPa)	Tensile Strength (MPa)
Case1	29.9	206	32.4	233.4	28	201.7	50.8	676.8
Case2	28.1	179	26.4	200.6	36.7	192	59.5	710.3
Case3	29.2	215	30.6	207.7	23	159	55.9	658.4
Case4	-	-	28	193.9	-	-	57.3	711.4
Case5	-	-	26.6	216.3	-	-	58	671.7
Case6	-	-	26.4	217.6	-	-	54.8	626.3
Average	29	200	28.4	211.6	29.3	184.3	56.1	675.8

, the test results show that the tensile strength of CFRP was higher by about 3 times and the elastic modulus was 2 times higher than those of C-SMC. This appeared because C-SMC mainly consists of chopped carbon fiber. As shown in Figure 2, C-SMC has relatively more boundaries in the microstructure of the material. Therefore, when loading is applied to C-SMC, each boundary acts as a crack initiation site, which leads to more frequent crack initiations compared to CFRP. On the other hand, CFRP consists of a fiber matrix that has specific directionality, which has different mechanical properties depending on the directionality. According to Campbell [25] and Jeong and Cho [26], a 0° orientation fiber matrix is designed to endure the axial loading on the CFRP. On the other hand, a 90° orientation fiber matrix is designed to endure the brittle effect. Due to these structural differences, CFRP presents relatively high tensile properties. Therefore, it shows lower strength and stiffness compared to CFRP.

4.2. Fatigue Test

Fatigue tests were carried out according to the specifications in ASTM D3479 [22]. All fatigue tests used the same testing machine (IMT 8802, Instron, UK), with a maximum load capacity of 250 kN, as shown in Figure 11. The stress ratio R was set to 0.1 and was performed at 10 Hz.

All fatigue tests were conducted by determining the fatigue test stress range as fractions of the tensile strength and defining it as a complete fracture due to a sharp drop in the applied load between fatigue tests. This section also explains how the fatigue lives and the S–N curves differed according to each specimen shape and process method.

4.2.1. Effect of the Edge Fabrication in Fatigue Life

In this section, the results of the fatigue tests that were carried out with R = 0.1 and a test frequency of 10 Hz are presented. A comparative evaluation analysis was conducted to evaluate the fatigue strength according to different molding method effects for the flat-plate machining specimen C-SMC-Cut-35 and the specimen C-SMC-In-mold. Figure 12 gives the S–N curves of the C-SMC-Cut-35 and C-SMC-In-mold specimens.

A comparative evaluation indicated that the value of the fatigue strength was about 21% higher for the flat-plate machining C-SMC-Cut-35 specimens than for the C-SMC-In-mold specimens.

4.2.2. Effect of the Specimen Width on the Fatigue Life

In the case of the surface-cut specimens, the flatbed machining specimens were constructed as SMC-Cut-35 and SMC-Cut-100 such that a comparative evaluation was conducted to determine the influence of the width on the fatigue strength and fatigue life. Figure 13 shows the fatigue curves for SMC-Cut-35 and SMC-Cut-100.

The difference in the S–N curve according to width was not significant, as shown in Figure 13. Comparing the fatigue strengths for the two different width cases, Cut-35 presented 90 MPa for the fatigue limit while Cut-100 presented 88.7 MPa. Therefore, it was determined that the specimen size did not significantly affect the fatigue strength and fatigue life in C-SMC.

4.2.3. Comparison of the Fatigue Lives of C-SMC and CFRP

In this section, the fatigue test results of C-SMC and CFRP are compared. Figure 14 shows the S–N curves for all specimens.

The comparisons show that CFRP exhibited a 5 times higher fatigue strength than C-SMC. These fatigue strength differences generally showed that CFRP had higher strength and stiffness than C-SMC, as expected. The reason for this is that C-SMC mainly consists of chopped carbon fiber. Therefore, C-SMC has relatively many boundaries in the microstructure of the material. On the other hand, CFRP consists of a fiber matrix, which has different directionalities. Due to these structural differences, C-SMC may have many initial cracks when subjected to cyclic loads. For this reason, as the cycles progress, the initial crack in C-SMC becomes larger, and as the cracks merge, it can be seen that the cracks progress even under relatively lower loads than in CFRP.

5. Discussion

In this section, the results of the failure criteria application and fatigue life assessment, which was suggested in Section 3, are presented. Each consideration was based on the stiffness drop and elastic modulus degradation criteria.

5.1. Failure Criterion

As discussed in Section 3, the composites showed a distinct difference in the stiffness drop compared to the metallic material. In particular, a complete fracture due to fatigue is very unlikely to be observed. Therefore, the final fracture in this study was defined using two classifications: (1) complete fracture and (2) stiffness drop. Figure 15 and Figure 16 present the S–N curves for various stiffness drops.

According to failure criteria in terms of the stiffness drop, a 10% stiffness drop was considered as a reasonable final fracture condition for C-SMC. In the case of CFRP, it showed a negligible stiffness drop, unlike C-SMC. Therefore, the complete fracture should be a reasonable final fracture criterion for CFRP.

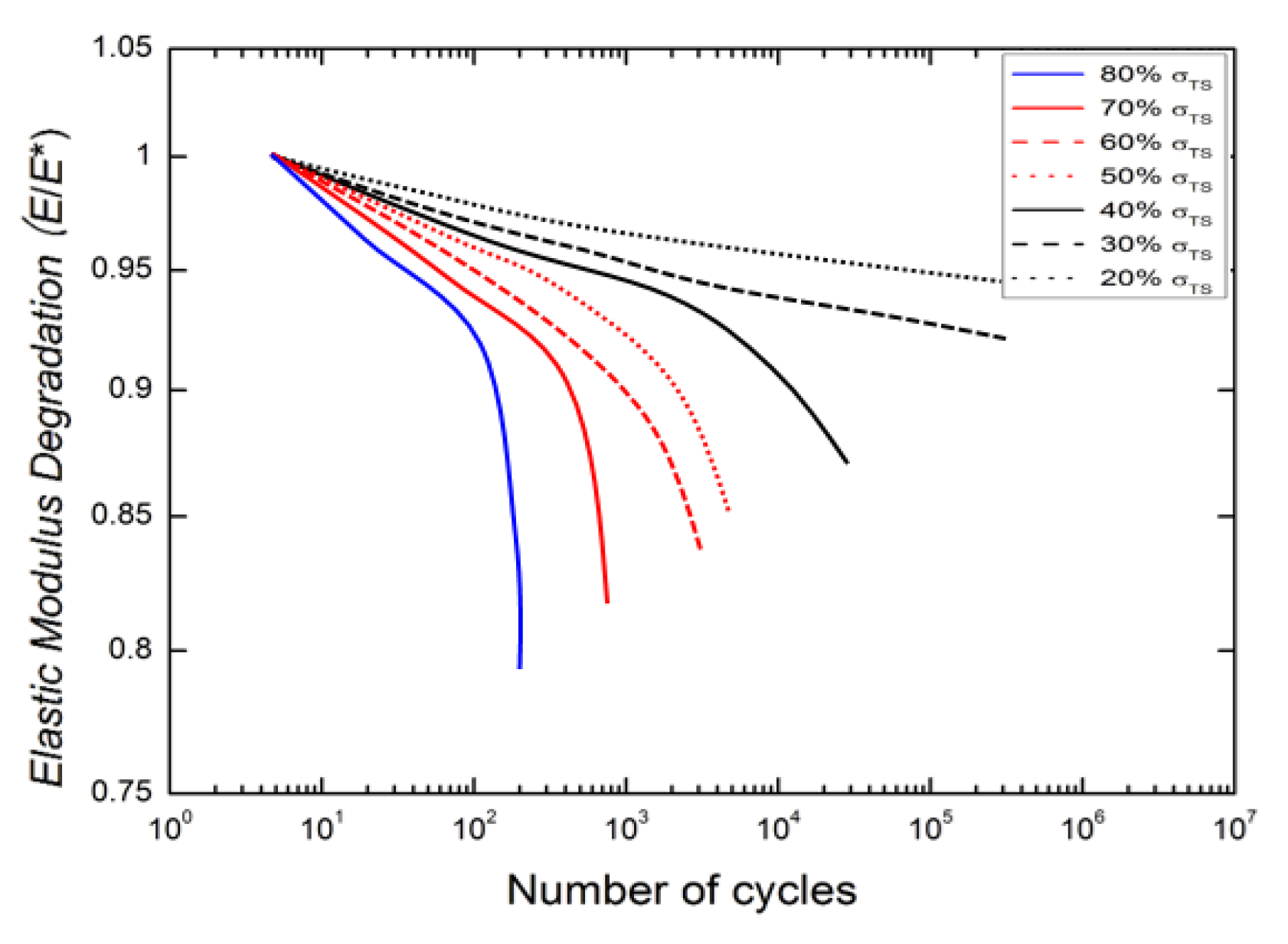
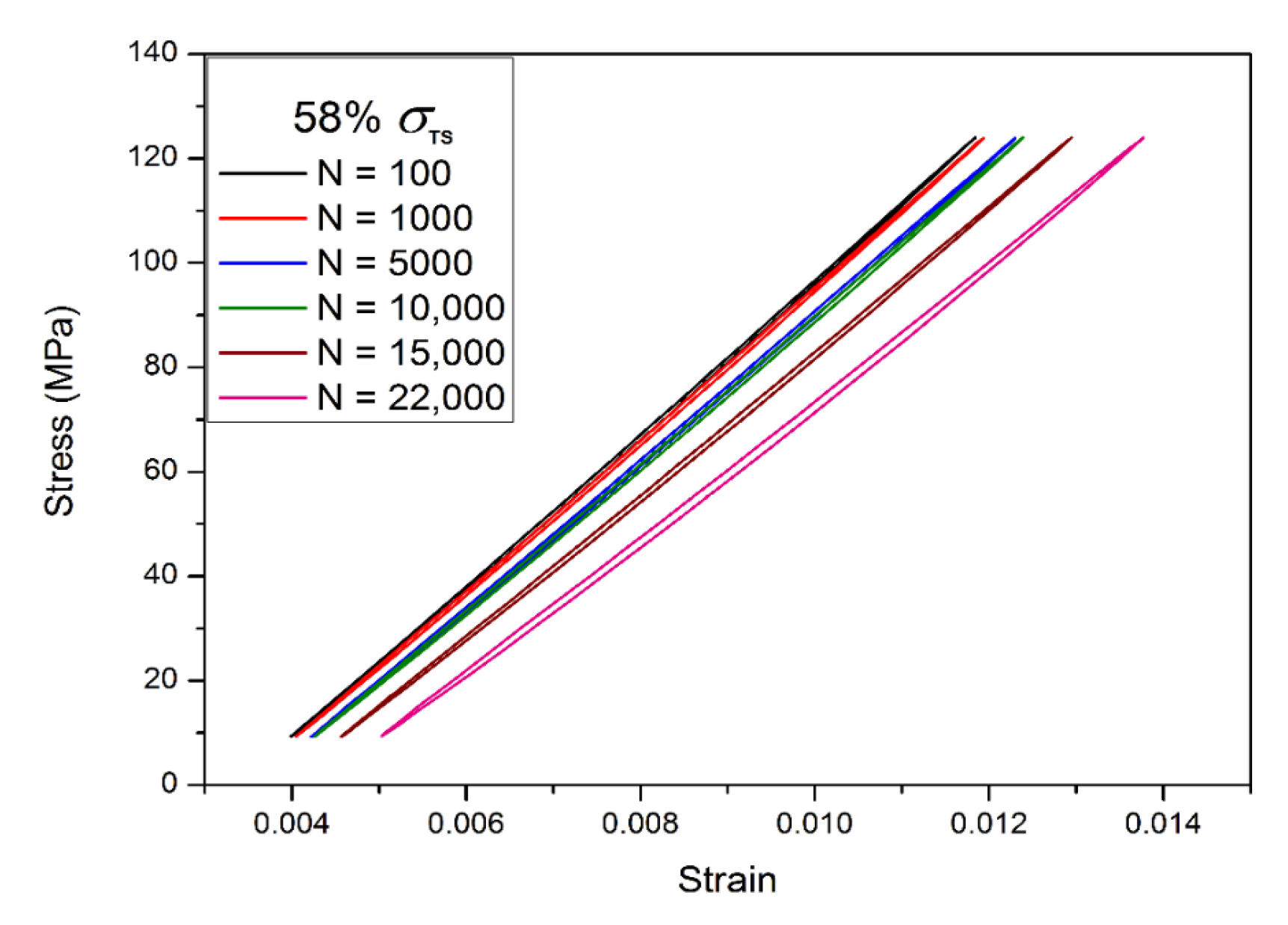
5.2. Fatigue Life Prediction based on the Degradation of Elastic Modulus

In this section, the results of the fatigue life prediction according to elastic modulus degradation during fatigue tests are presented [3]. A dynamic extensometer (Instron, United Kingdom) was installed in the C-SMC-Cut-35 specimen to record the changes in the elastic modulus during fatigue tests. The stress ratio R for the fatigue test was set to 0.1 and the frequency was 3 Hz. The test results were compared with the fatigue life prediction results obtained by applying the fatigue damage rate based on the life calculation formula. Figure 17 and

Table 4. Changes in elastic modulus as a function of the number of cycles.

Stress	N(Cycles)	E(GPa)
55% ${\sigma }_{\mathrm{TS}}$	100	14.8
	1000	14.6
	5000	14.3
	10,000	14.1
	15,000	13.9
	22,000	13.4

show the elastic modulus changing with the cycle. In addition, Figure 17 presents the cyclic softening phenomenon. According to Thomas et al. [23], more than 50% of damage occurs in the first 20% of life in the composite, and much of the crack initiation occurs during this time. Therefore, C-SMC may inherently contain many initial cracks when subjected to cyclic loads. For this reason, as the cycles progress, the initial cracks in C-SMC become larger and the cracks merge. Figure 18 and Figure 19 show the crack initiation of C-SMC via visual observation and digital image correlation (DIC). Therefore, the stiffness due to many crack initiations was reduced, resulting in the cyclic softening phenomenon.

Figure 20 shows the rate of the reduction of the elastic modulus with increasing cycles for each load condition based on the tensile strength. The reasons for the elastic modulus degradation of the C-SMC with increasing cycles for each load condition are as follows. It is known that the fracture modes and physical properties of C-SMC change depending on the fiber orientation distribution. On the other hand, according to [27], the carbon sheet molding compound can be considered isotropic due to the uniformly distributed local fiber orientation. Figure 21 shows the fracture trends of the study of Martulli et al. and the C-SMC in this study. As a result of comparing the fracture tendency, it was found that the C-SMC of this study was similar to the fracture tendency of 0°. In addition, according to the study of Martulli et al., in the C-SMC distributed in the 0° direction, the fiber was mainly broken and reached the fracture condition. In this regard, the results of the SEM analysis of the C-SMC of this study are shown in Figure 22. According to the SEM analysis, the fibers broke and the caused failure, resulting in the elastic modulus degradation of C-SMC. Figure 23 presents the damage rate for each stress value.

Representatively, in the case of 65%${\sigma }_{\mathrm{TS}}$(1) of C-SMC, A(D) was $0.022D^2-0.0035D+0.003$ and B (slope) was −0.045 according to $\mathrm{d}D/\mathrm{d}N$. Based on the elastic modulus degradation ratio and the damage change rate obtained, the fatigue damage change rate was calculated using the fatigue lifetime formula based on Equation (4). Figure 24 compares the damage, D, between the predicted life and the experimental data per cycle.

Here, $D_{\mathrm{f}}$ is the elastic modulus based on the fracture criterion, $N_{\mathrm{Pre}}$ is the number of predicted load cycles and $N_{\mathrm{Exp}}$ is the number of load cycles at the fatigue fracture from the experiment. Figure 25 shows that the fatigue life prediction results based on the elastic modulus degradation and the fatigue life curve from the actual test exhibited an excellent correlation. The error between the experiments and the estimation result based on the elastic modulus degradation was verified to be within 3%. Therefore, it is reasonable that the fatigue life estimation based on the fatigue damage rate is a viable alternative for estimating the fatigue life of C-SMC based on the cyclic stress–strain curves. Furthermore, the fatigue life estimation can predict the S–N curve without a lot of fatigue tests.

6. Conclusions

In this study, a series of fatigue tests for C-SMC and CFRP was conducted to assess the fatigue performance. In terms of the failure assessment criteria, stiffness drop and elastic modulus degradation criteria were applied for each fatigue test result of C-SMC and CFRP. In addition, the fatigue life of C-SMC was predicted based on the elastic modulus degradation. The conclusions from this study are summarized in the following:

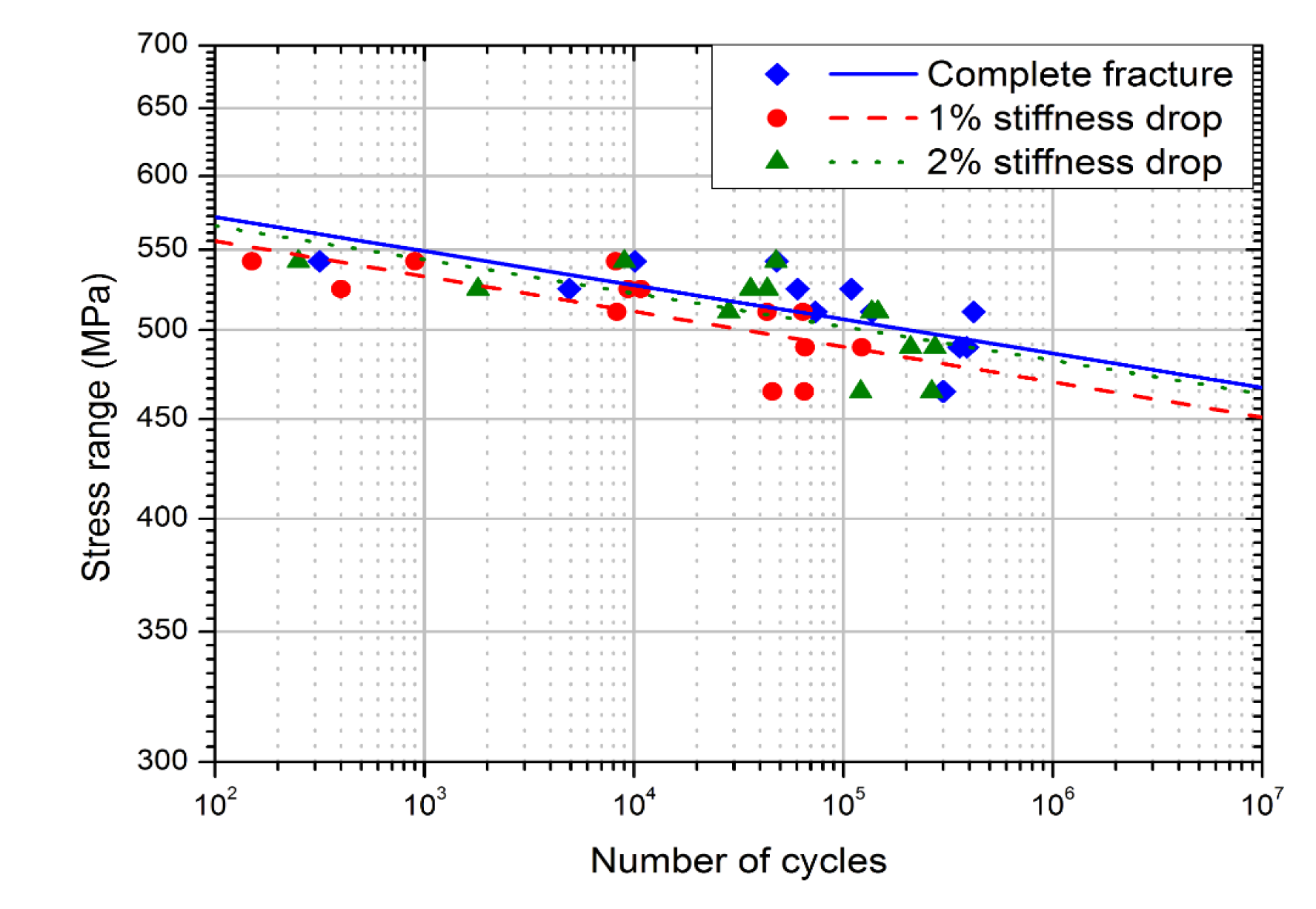
• As a result of the fatigue tests of C-SMC and CFRP, the fatigue strength of C-SMC obtained at 10⁶ cycles was 90 MPa for Cut-35, 88.7 MPa for Cut-100, and 74.5 MPa for In-mold. The fatigue strength of CFRP was determined to be 486.5 MPa. The reason for this was that C-SMC mainly consists of chopped carbon fiber. The relatively lower fatigue strength of C-SMC was attributed to there being many boundaries in the microstructure of the material. On the other hand, CFRP consists of a fiber matrix, which has various directionalities. Due to these structural differences, CFRP was observed to exhibit a relatively higher fatigue strength compared to that of C-SMC.
• In the case of C-SMC, the fatigue strength was evaluated for two different width and edge conditions. Comparing the fatigue strengths for two different width cases, Cut-35 presented 90 MPa for the fatigue limit while Cut-100 presented 88.7 MPa. Regarding the width effect, there was no significant effect on the fatigue strength of C-SMC. As a result of the assessment of the edge conditions, the In-mold condition presented 74.5 MPa for the fatigue limit. Regarding the edge effect, flat-plate machined cases exhibited 21% higher fatigue strengths than molded C-SMCs.
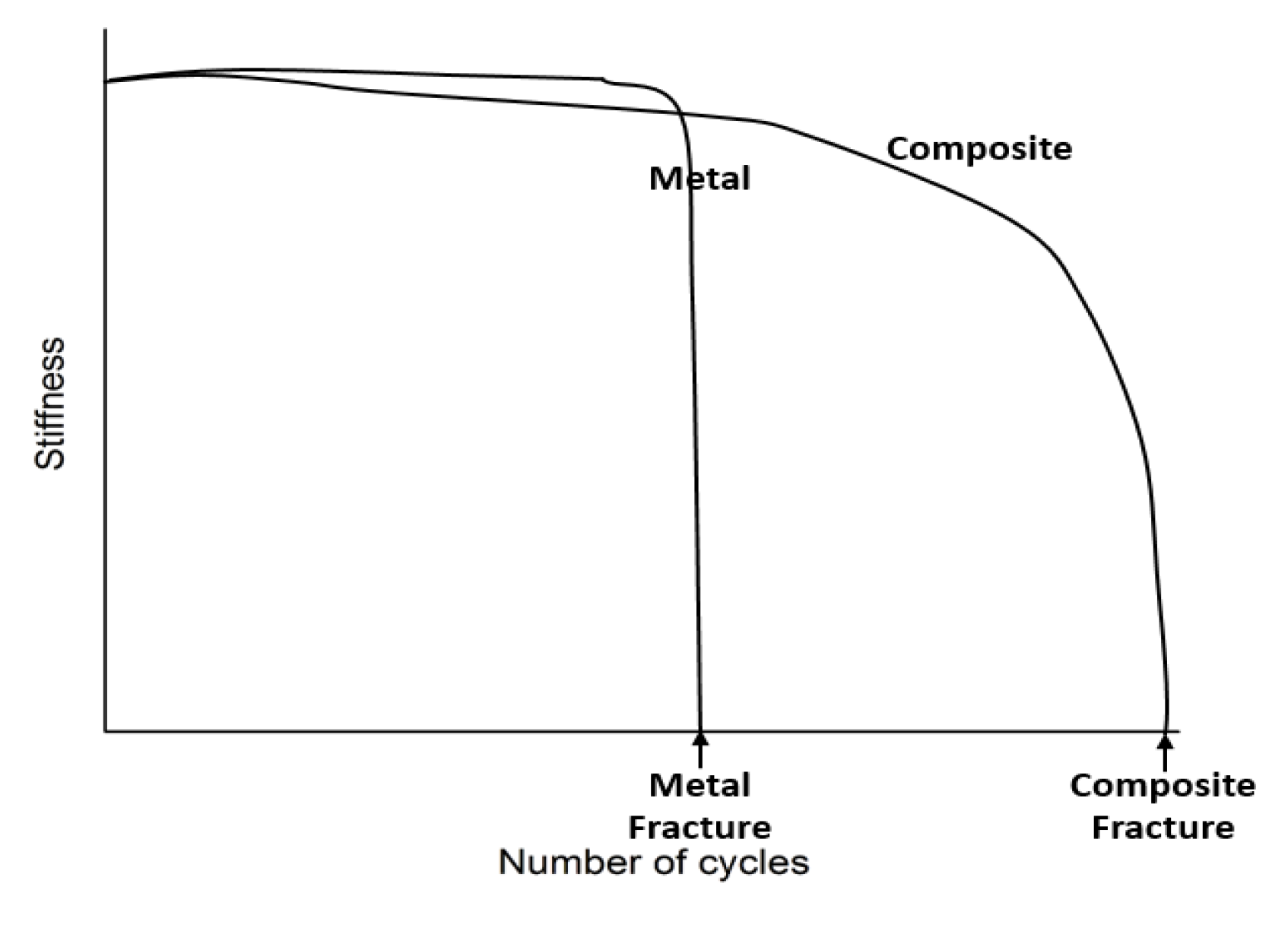
• To assess the proper failure criterion for C-SMC, the stiffness drop criteria were employed in this study. In the case of C-SMC, the fatigue life of C-SMC reached 95% of the fracture life at the 10% stiffness drop point. In this regard, it is considered reasonable to determine the final fatigue life of C-SMC at the 10% stiffness drop. In the case of CFRP, there was no significant stiffness drop. Therefore, the final fatigue life should be considered at the final fracture.
• In this study, a fatigue life estimation method was suggested based on the elastic modulus degradation. Validation for the suggested estimation was conducted via a comparison with the fatigue test result of the C-SMC-Cut-35 case. The fatigue life between the prediction and the experiment was calculated to be less than 3%. Therefore, making a fatigue life prediction of C-SMC by monitoring the elastic modulus degradation is a viable alternative in fatigue design to avoid time-consuming fatigue tests.