Systematic Approach for Finite Element Analysis of Thermoplastic Impregnated 3D Filament Winding Structures—Advancements and Validation
Abstract
:1. Introduction
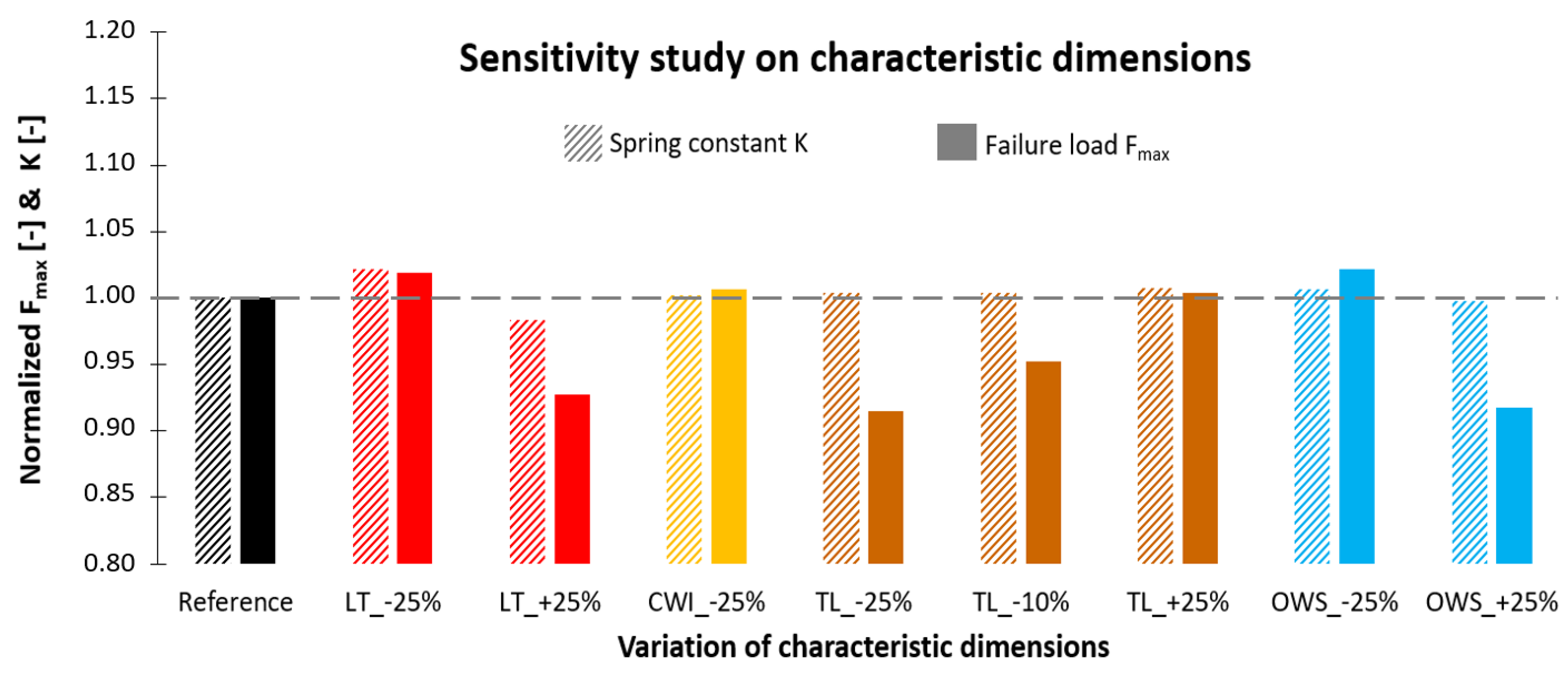
- During modeling of the geometry, more potentially relevant dimensions were found (Section 2.2.2). They are included in this paper’s models and their mechanical effects are examined (Section 3.2.2).
- It has been shown in [8,21] that delamination has an influence on the mechanical behavior (i.e., the load-displacement curve) of tension-loaded simple loops. However, this influence decreases at higher winding numbers. This indicates that at higher winding numbers, mesoscopic modeling may be abandoned in favor of a time-efficient macroscopic modeling approach (Section 2.2.2), which neglects the roving–roving interface (B). Both modeling approaches are compared using the example of simple loops in this paper (Section 3.2.5).
- The loops’ stiffness measured in N/mm, hereafter referred to as spring constant , was overestimated in the simulations in [21]. This deviation as well as possible reasons are examined experimentally (Section 3.2.3). Based on the findings, the fiber-parallel Young’s modulus () of the impregnated roving (A) is adapted to the loops’ effective elastic behavior.
- After intensive consideration of simple loop structures, the knowledge is transferred to the modeling and simulation of inclined loops and thus to three-dimensional fiber skeletons (Section 3.3). Since relative movements between windings and inserts may occur in this case, the insert-roving interface (C) is characterized in this context (Section 3.1).
2. Materials and Methods
2.1. Specimens and Mechanical Testing
2.1.1. Materials
2.1.2. Test Specimens
2.1.3. Test Equipment and Procedures
2.2. Finite Element Modeling
2.2.1. Material Modeling
2.2.2. FE Modeling of the Tensile Tests on Simple Loops
Meso-Modeling
- In [21], discrepancies between simulation results and measurements, as well as uncertainties associated with material characterization, are found. In Section 3.2.3 and Section 3.2.4 of the present work, potential causes are investigated and the material parameters and of the PP-GF roving (A) are adapted by means of reduction factors. The resulting values are given in Table 1.
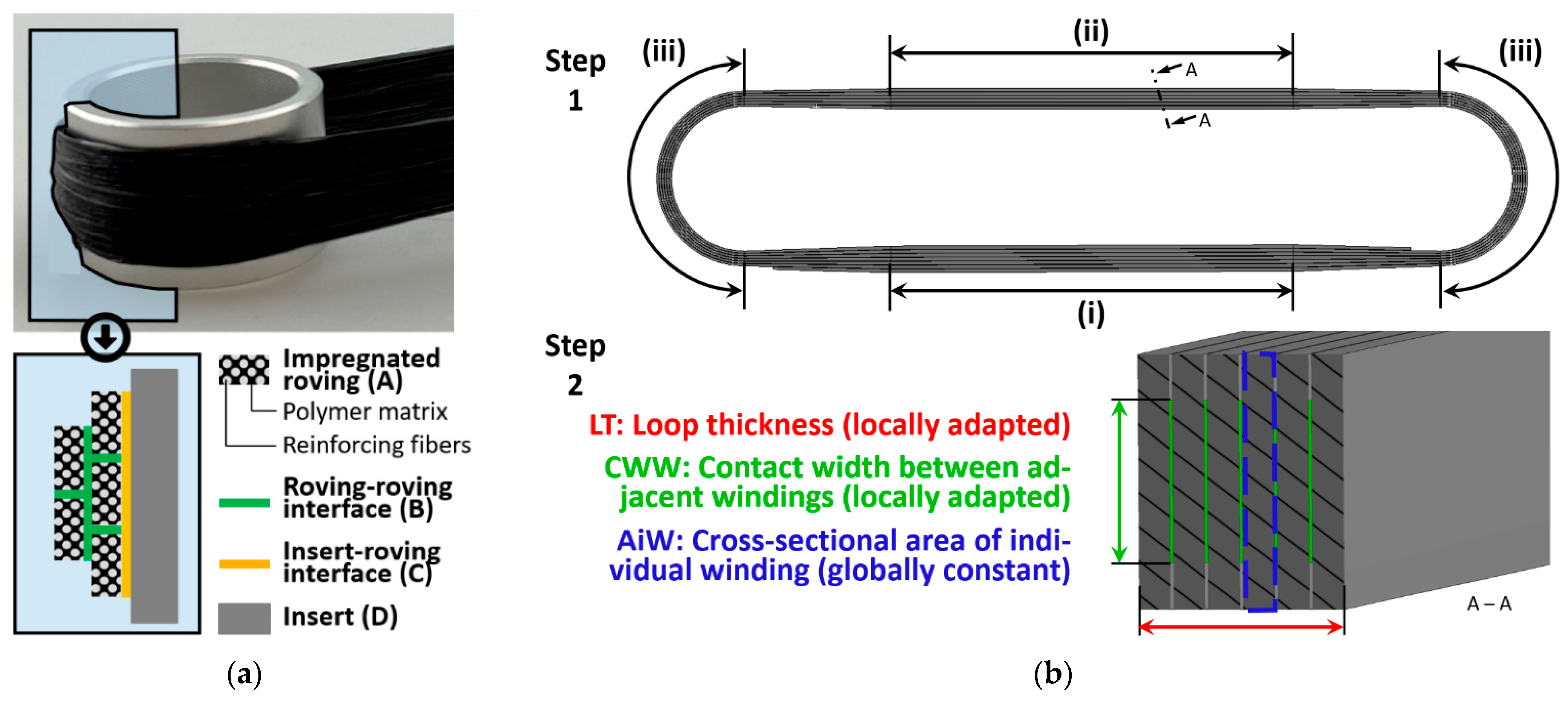
- As shown in Figure 6, further characteristic dimensions are considered and modeled according to the respective measurements given in Table 2. Their mechanical influence—and thus their relevance for precise FE simulations of fiber skeletons—is evaluated in Section 3.2.2.
- To reduce calculation time, the symmetric geometry model is halved.
- Since meshing complex skeleton models with hexahedral SOLID186 elements often leads to poor element quality, all models studied are consistently meshed with tetrahedral SOLID187 elements. SOLID187 is a 10-node 3D solid element with a quadratic shape function and three degrees of freedom per node (x, y and z direction).
- The insert–roving interface (C) is no longer represented by a frictionless contact, but by the friction model described in Section 2.2.1 in combination with the coefficient of friction determined in Section 3.1.
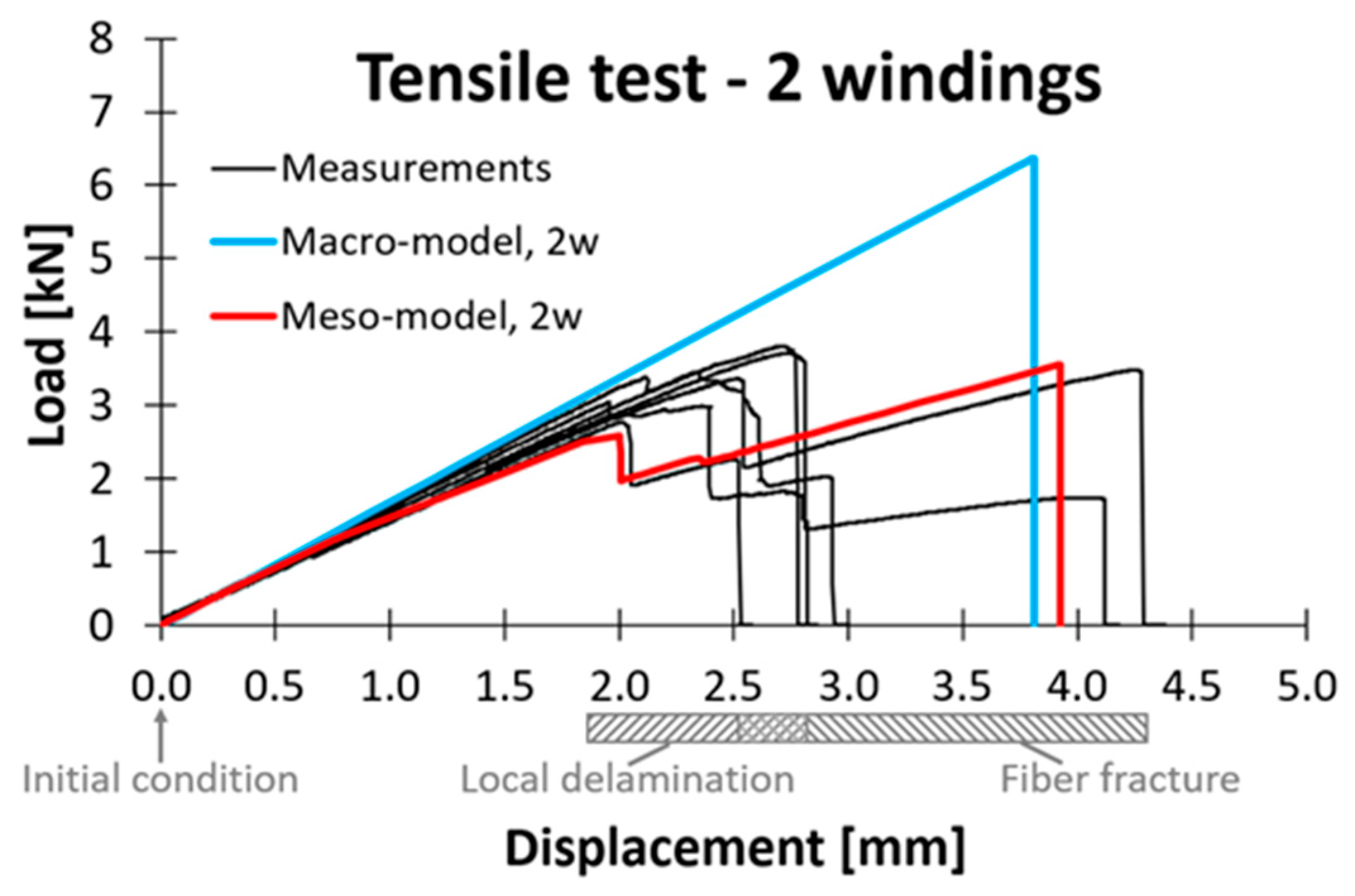
- Geometric non-linearity is considered by activating the corresponding analysis setting in ANSYS Mechanical (“large deflection”). This ensures that deformation-induced changes of the stiffness matrix are determined and adjusted iteratively [31]. Even though the simple loop specimens deformed by only a few millimeters before total failure, the assumption of geometric linearity can lead to unrealistic deformations and stress peaks in the FE simulations. This applies in particular in the context of delamination.

Macro-Modeling
2.2.3. FE Modeling of the Tensile Tests on Inclined Loops
- As shown in Figure 9a, the cross-sections of the outer wraps follow the insert shapes and are therefore not rectangular but rectangle-like: they have a constant wall thickness and parallel edges; however, two of the four edges are not straight. This modeling approach enables a close contact between insert and windings while keeping implementation simple. The inner wraps are modeled in the same way and are connected to the outer wraps by bonded contacts.
- The inserts have different diameters. The two outer wraps therefore do not form a semicircle around the inserts (180° deflection), as is the case with the simple loop. Instead, a larger deflection angle is modeled at the large insert and a smaller one at the small insert. This can also be seen in Figure 9a.
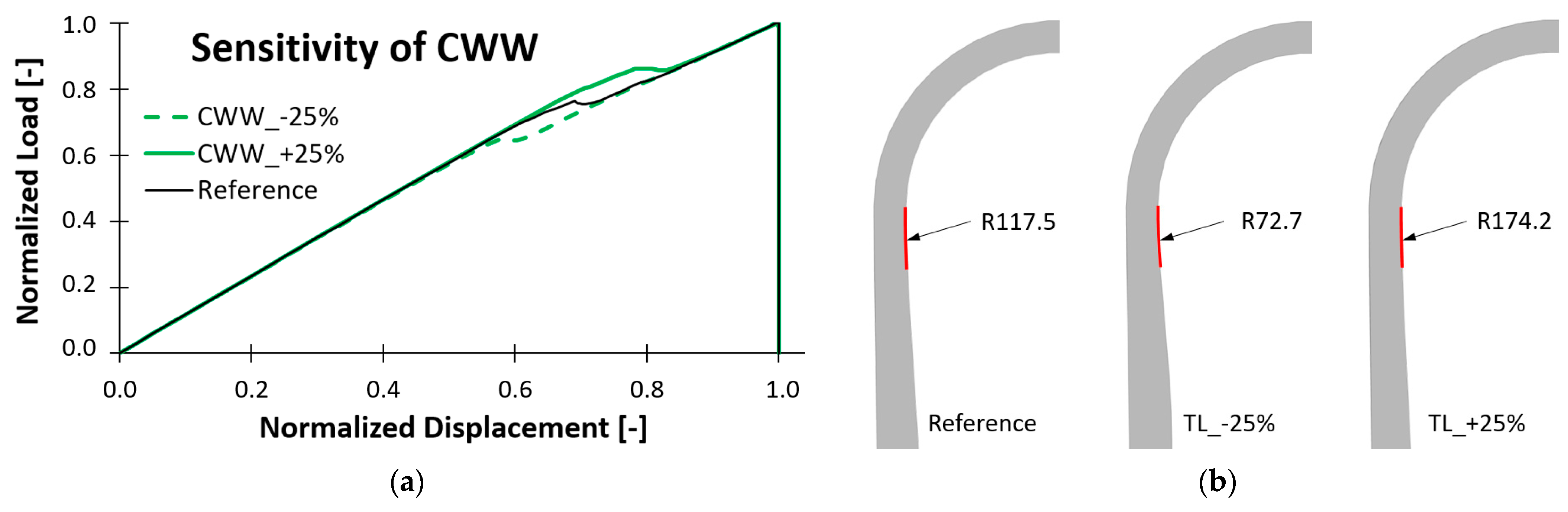
- Due to the twist in the shafts, the OWS and the TL are difficult to measure. The OWS is therefore not considered in the geometry model. Instead, the free shafts are simply centered between the two wrap endings they connect. Based on the recommendations in Section 3.2.2, the TL is set to 25% of the distance between the insert centers.
- The windings are not aligned perpendicularly to the insert axes, but at an incline to them. As can be seen in Figure 9c it is ensured that the outer wraps and the shafts, as well as the transitions connecting them, are all oriented at a uniform angle. Thus, unrealistic bending moments in the windings are avoided.
2.2.4. Geometry, Mesh and Load Step Size Dependencies
3. Results and Discussion
3.1. Characterization of the Insert-Roving Interface (C)
3.2. Investigations on Simple Loop Specimens
3.2.1. Mesh and Load Step Convergence
3.2.2. Mechanical Influence of the Characteristic Dimensions
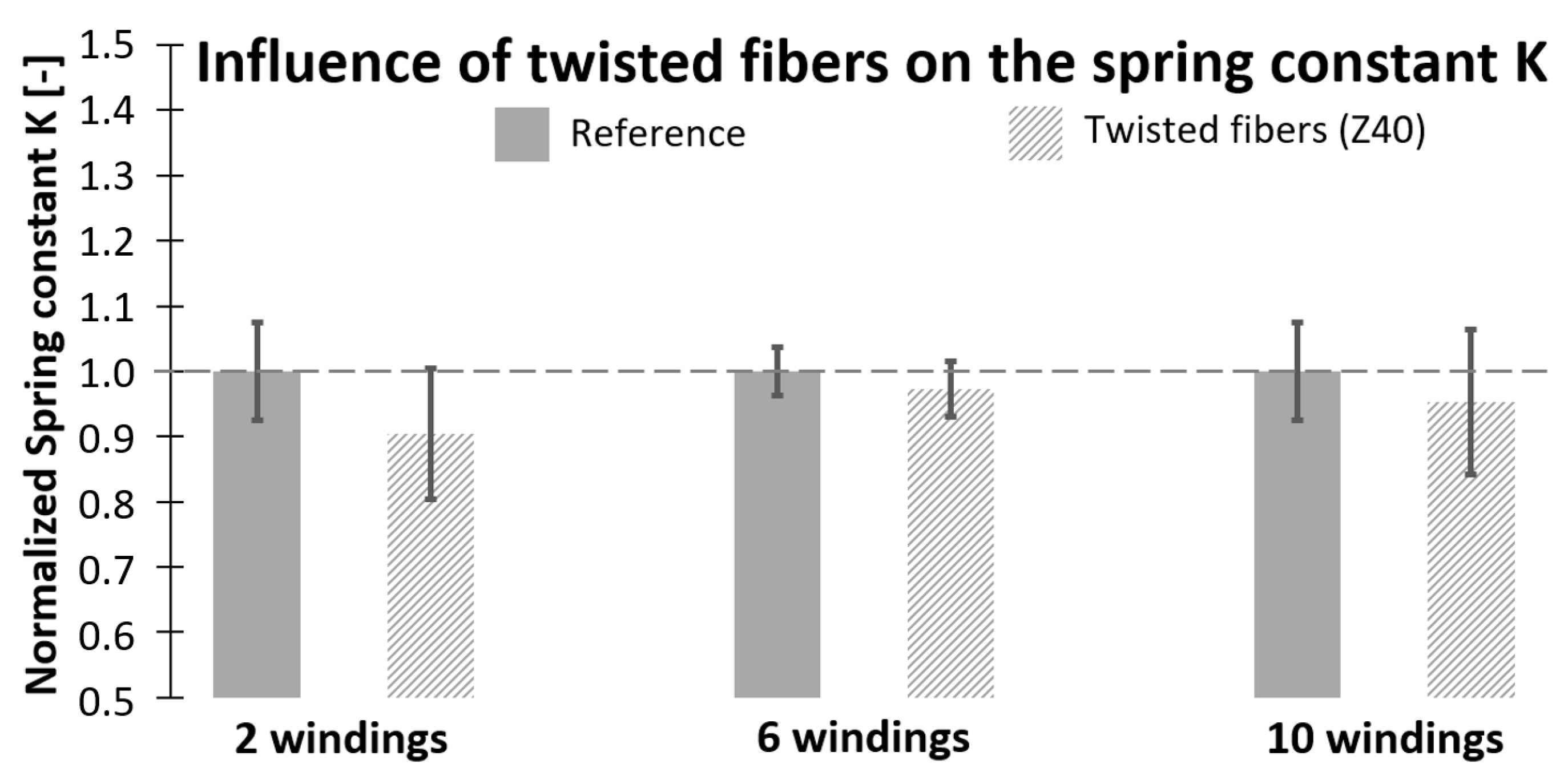
3.2.3. Investigation of the Spring Constant and Adaptation of the Fiber-Parallel Young’s Modulus
3.2.4. Adaptation of the Fiber-Parallel Tensile Strength
3.2.5. Comparison of Meso- and Macroscopic Models
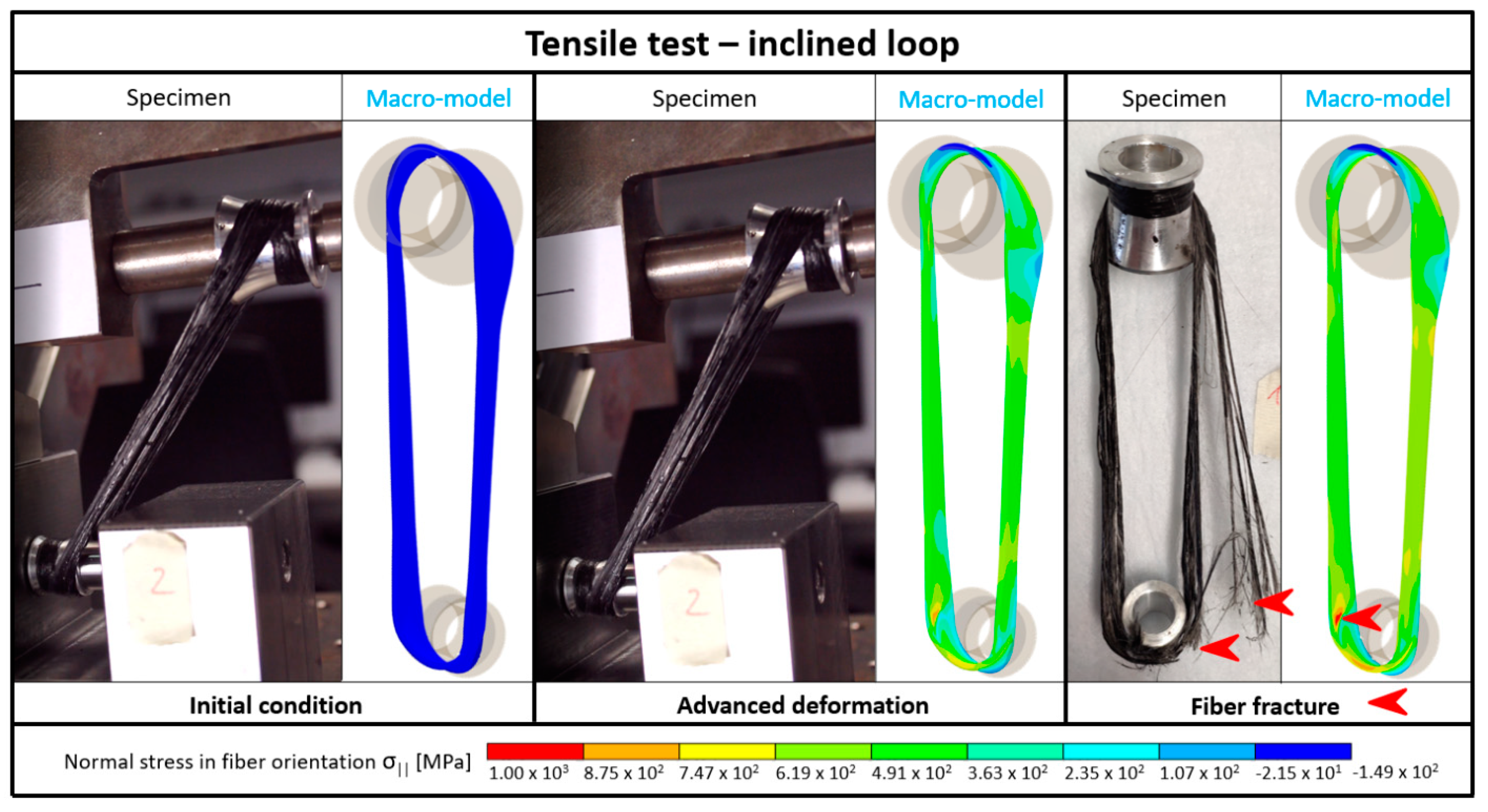
3.3. Validation of the Presented Approach Using the Example of the Inclined Loop
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Minsch, N.; Müller, M.; Gereke, T.; Nocke, A.; Cherif, C. 3D truss structures with coreless 3D filament winding technology. J. Compos. Mater. 2018, 53, 2077–2089. [Google Scholar] [CrossRef]
- Büchler, D.; Elsken, T.; Glück, N.; Sier, M.; Bludszuweit, S. Ultraleichte Raumzelle—Entwicklung von ultraleichten Großstrukturen in Faserverbund- und Hybridbauweise für den Schiffbau. In Statustagung Schifffahrt und Meerestechnik—Tagungsband der Statustagung 2011; GmbH, F.J., Ed.; Schriftenreihe Projektträger Jülich: Jülich, Germany, 2011; pp. 25–45. [Google Scholar]
- Reichert, S.; Schwinn, T.; La Magna, R.; Waimer, F.; Knippers, J.; Menges, A. Fibrous structures: An integrative approach to design computation, simulation and fabrication for lightweight, glass and carbon fibre composite structures in architecture based on biomimetic design principles. Comput. Des. 2014, 52, 27–39. [Google Scholar] [CrossRef]
- Beck, B.; Tawfik, H.; Haas, J.; Park, Y.-B.; Henning, F. Automated 3D Skeleton Winding Process for Continu-ous-Fiber-Reinforcements in Structural Thermoplastic Components. In Advances in Polymer Processing 2020; Hopmann, C., Dahlmann, R., Eds.; Springer Vieweg: Berlin, Germany, 2020; pp. 150–161. [Google Scholar]
- Botzkowski, T.; Galkin, S.; Wagner, S.; Sikora, S.P.; Kärger, L. Experimental and numerical analysis of bolt-loaded open-hole laminates reinforced by winded carbon rovings. Compos. Struct. 2016, 141, 194–202. [Google Scholar] [CrossRef]
- Holzinger, M.; Loy, C.; Gruber, M.; Kugler, K.; Bühler, V. 3D winding of tailor-made thermoplastic rods for locally reinforced injection molded components. In Proceedings of the 5th International Conference & Exhibition on Thermoplastic Composites ITHEC 2020, Bremen, Germany, 13–15 October 2020. [Google Scholar]
- Minsch, N.; Müller, M.; Gereke, T.; Nocke, A.; Cherif, C. Novel fully automated 3D coreless filament winding technology. J. Compos. Mater. 2018, 52, 3001–3013. [Google Scholar] [CrossRef]
- Huber, T. Einfluss Lokaler Endlosfaserverstärkungen auf das Eigenschaftsprofil Struktureller Spritzgießbauteile. Ph.D. Thesis, Karlsruher Institut für Technologie (KIT), Karlsruhe, Germany, 2014. [Google Scholar]
- Schwarz, M. Gezielte Steifigkeits- und Festigkeitssteigerung von Maschinenbauteilen Durch Vorgespannte Ringarmierungen aus Faser-Kunststoff-Verbunden. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2007. [Google Scholar]
- Morozov, E.; Lopatin, A.; Nesterov, V. Finite-element modelling and buckling analysis of anisogrid composite lattice cylindrical shells. Compos. Struct. 2011, 93, 308–323. [Google Scholar] [CrossRef]
- Woods, B.K.; Hill, I.; Friswell, M. Ultra-efficient wound composite truss structures. Compos. Part A Appl. Sci. Manuf. 2016, 90, 111–124. [Google Scholar] [CrossRef] [Green Version]
- Solly, J.; Früh, N.; Saffarian, S.; Aldinger, L.; Margariti, G.; Knippers, J. Structural design of a lattice composite cantilever. Structures 2018, 18, 28–40. [Google Scholar] [CrossRef]
- Bellini, C.; Di Cocco, V.; Iacoviello, F.; Sorrentino, L. Performance index of isogrid structures: Robotic filament winding carbon fiber reinforced polymer vs. titanium alloy. Mater. Manuf. Process. 2021, 1–9. [Google Scholar] [CrossRef]
- Schürmann, H. Konstruieren mit Faser-Kunststoff-Verbunden, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Krystek, J.; Kottner, R.; Bek, L.; Las, V. Validation of the adjusted strength criterion LaRC04 for uni-directional composite under combination of tension and pressure. Appl. Comput. Mech. 2010, 4, 171–178. [Google Scholar]
- Havar, T. Beitrag zur Gestaltung und Auslegung von 3D-Verstärkten Faserverbundschlaufen. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2007. [Google Scholar]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Puck, A. Festigkeitsanalyse von Faser-Matrix-Laminaten: Modelle für die Praxis; Hanser: Munich, Germany, 1996. [Google Scholar]
- Lapczyk, I.; Hurtado, J.A. Progressive damage modeling in fiber-reinforced materials. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2333–2341. [Google Scholar] [CrossRef]
- Kärger, L.; Botzkowski, T.; Galkin, S.; Wagner, S.; Sikora, S.P. Stress analysis and design suggestions for multi-loop carbon roving rosettes to reinforce bolt-loaded open-hole laminates. In Proceedings of the 17th European Conference on Composite Materials ECCM17, Munich, Germany, 26–30 June 2016. [Google Scholar]
- Haas, J.; Hassan, O.N.; Beck, B.; Kärger, L.; Henning, F. Systematic approach for finite element analysis of thermoplastic impregnated 3D filament winding structures—General concept and first validation results. Compos. Struct. 2021, 268, 113964. [Google Scholar] [CrossRef]
- Camanho, P.P.; Matthews, F.L. A Progressive Damage Model for Mechanically Fastened Joints in Composite Laminates. J. Compos. Mater. 1999, 33, 2248–2280. [Google Scholar] [CrossRef]
- Tan, S.C.; Perez, J. Progressive Failure of Laminated Composites with a Hole under Compressive Loading. J. Reinf. Plast. Compos. 1993, 12, 1043–1057. [Google Scholar] [CrossRef]
- Tan, S.C. A Progressive Failure Model for Composite Laminates Containing Openings. J. Compos. Mater. 1991, 25, 556–577. [Google Scholar] [CrossRef]
- Alfano, G.; Crisfield, M.A. Finite element interface models for the delamination analysis of laminated composites: Mechanical and computational issues. Int. J. Numer. Methods Eng. 2001, 50, 1701–1736. [Google Scholar] [CrossRef]
- Ye, J.; Yan, Y.; Li, Y.; Luo, H. Parametric mesoscopic and multi-scale models for predicting the axial tensile response of filament-wound structures. Compos. Struct. 2020, 242, 112141. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, Z.; Ellyin, F. Two-scale analysis of a filament-wound cylindrical structure and application of periodic boundary conditions. Int. J. Solids Struct. 2008, 45, 5322–5336. [Google Scholar] [CrossRef] [Green Version]
- DIN EN ISO 8295:2004-10; Plastics—Film and Sheeting—Determination of the Coefficients of Friction (ISO 8295:1995). Beuth: Berlin, Germany, 2004.
- ANSYS, Inc. Theory Reference—Release 2020 R2; ANSYS Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Rust, W. Nichtlineare Finite-Elemente-Berechnungen mit ANSYS Workbench: Strukturmechanik: Kontakt, Material, große Verformungen; Springer Vieweg: Wiesbaden, Germany, 2020. [Google Scholar]
- ANSYS Inc. Structural Analysis Guide—Release 2020 R2; ANSYS Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
















| Elastic Constants a | |||||||
| PP-GF roving | [MPa] b | [MPa] | [MPa] | [MPa] | [-] | [-] | [-] |
| 23,953 | 3750 | 1225 | 1125 | 0.32 | 0.32 | 0.59 | |
| Aluminum | [MPa] | [-] | |||||
| 71,000 | 0.33 | ||||||
| Strength Values a | |||||||
| PP-GF roving | [MPa] b | [MPa] | [MPa] | [MPa] | [MPa] | [MPa] | |
| 987.9 | 274.0 | 6.7 | 44.6 | 17.0 | 17.8 | ||
| OWS [mm] a (Std. Dev.) | TL [mm] b (Std. Dev.) | AiW [mm2] c | LT [mm] (Std. Dev.) | CWI [mm2] c | CWW [mm] (Std. Dev.) | ||
|---|---|---|---|---|---|---|---|
| 2 windings | (i) | 0.85 (0.20) | 15.80 (7.34) | 2.47 | 1.49 (0.24) | - | 0.33 (0.24) |
| (ii) | 0.85 (0.20) | 15.80 (7.34) | 2.47 | 1.14 (0.16) | - | 0.00 (0.00) | |
| (iii) | - | - | 2.47 | 0.90 (0.11) | 215.56 | 1.96 (1.22) | |
| 6 windings | (i) | 1.11 (0.22) | 23.64 (6.39) | 2.47 | 3.34 (0.16) | - | 0.92 (0.32) |
| (ii) | 1.11 (0.22) | 23.64 (6.39) | 2.47 | 2.55 (0.12) | - | 0.49 (0.19) | |
| (iii) | - | - | 2.47 | 1.91 (0.20) | 304.22 | 3.50 (0.41) | |
| 10 windings | (i) | 1.18 (0.15) | 20.78 (6.67) | 2.47 | 2.82 (0.18) | - | 1.60 (0.40) |
| (ii) | 1.18 (0.15) | 20.78 (6.67) | 2.47 | 2.48 (0.11) | - | 1.37 (0.41) | |
| (iii) | - | - | 2.47 | 1.94 (0.08) | 499.84 | 4.64 (0.65) | |
| OWS [mm] a | TL [mm] a | AiW [mm2] b | LH [mm] c (Std. Dev.) | CWI [mm2] b | CWW [mm] | Inclination [°] d (Std. Dev.) | N [-] | |
|---|---|---|---|---|---|---|---|---|
| (i) | 0.00 | 29.00 | 2.47 | 5.64 (0.31) | - | Neglected in macro-model | 36.58 (0.71) | 5 |
| (ii) | 0.00 | 29.00 | 2.47 | 5.21 (0.06) | - | 36.58 (0.71) | 4 | |
| (iii) | - | - | 2.47 | 10.84 (1.16) | 477.35 | 36.58 (0.71) | 6 | |
| (iv) | - | - | 2.47 | 10.39 (0.31) | 245.40 | 36.58 (0.71) | 7 | |
| (v) | - | - | 2.47 | 9.20 (0.16) | 710.78 | - | 2 | |
| (vi) | - | - | 2.47 | 6.88 (0.29) | 272.84 | - | 2 |
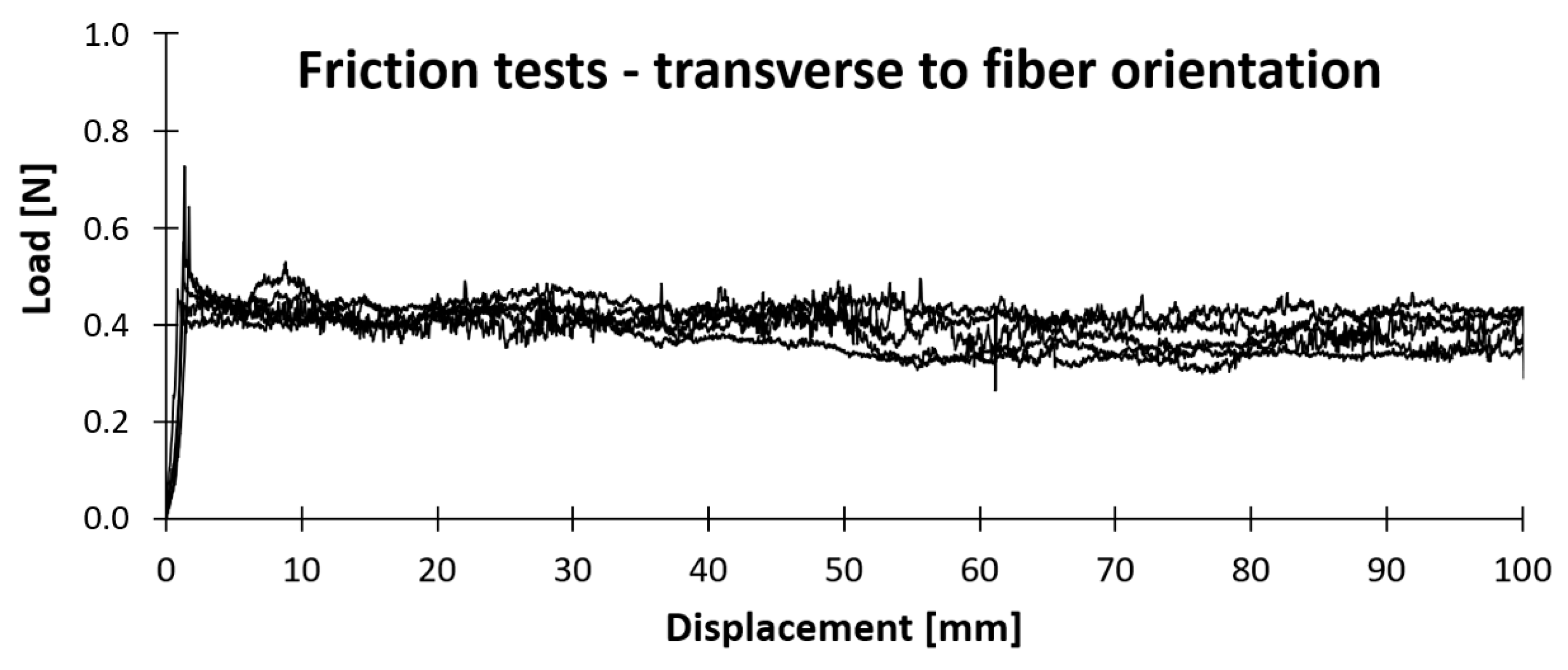
| Friction Coefficients Parallel to Fiber Orientation | Friction Coefficients Transverse to Fiber Orientation | ||
|---|---|---|---|
| [-] (Std. Dev.) | [-] (Std. Dev.) | [-] (Std. Dev.) | [-] (Std. Dev.) |
| 0.21 (0.03) | 0.16 (0.02) | 0.25 (0.05) | 0.19 (0.02) |
| Char. Dimension | Mechanical Relevance | Recommendations |
|---|---|---|
| LT | High | Should be measured in micrographs from each characteristic area and modeled accordingly. |
| CWI | Low | A measurement is not required. CWI must be greater than zero. It is recommended to use the contact area resulting from the height of the windings. |
| TL | High | Should be measured by means of 2D/3D scans and modeled accordingly. If this is not possible, it must be ensured that TL is modeled rather too large than too small: 25 % of the distance between the insert centers can be used as a rule of thumb. |
| OWS | High | Should be measured by means of 2D/3D scans and modeled accordingly. If this is not possible, the shaft should be centered between the wrap endings it connects, knowing that curvatures of the windings and associated stress peaks might be neglected. |
| CWW | High | Should be measured in micrographs from each characteristic area and modeled accordingly. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haas, J.; Aberle, D.; Krüger, A.; Beck, B.; Eyerer, P.; Kärger, L.; Henning, F. Systematic Approach for Finite Element Analysis of Thermoplastic Impregnated 3D Filament Winding Structures—Advancements and Validation. J. Compos. Sci. 2022, 6, 98. https://doi.org/10.3390/jcs6030098
Haas J, Aberle D, Krüger A, Beck B, Eyerer P, Kärger L, Henning F. Systematic Approach for Finite Element Analysis of Thermoplastic Impregnated 3D Filament Winding Structures—Advancements and Validation. Journal of Composites Science. 2022; 6(3):98. https://doi.org/10.3390/jcs6030098
Chicago/Turabian StyleHaas, Jonathan, Daniel Aberle, Anna Krüger, Björn Beck, Peter Eyerer, Luise Kärger, and Frank Henning. 2022. "Systematic Approach for Finite Element Analysis of Thermoplastic Impregnated 3D Filament Winding Structures—Advancements and Validation" Journal of Composites Science 6, no. 3: 98. https://doi.org/10.3390/jcs6030098
APA StyleHaas, J., Aberle, D., Krüger, A., Beck, B., Eyerer, P., Kärger, L., & Henning, F. (2022). Systematic Approach for Finite Element Analysis of Thermoplastic Impregnated 3D Filament Winding Structures—Advancements and Validation. Journal of Composites Science, 6(3), 98. https://doi.org/10.3390/jcs6030098






