Effect of Functionalization with Potassium Atoms on the Electronic Properties of a 3D Glass-like Nanomaterial Reinforced with Carbon Nanotubes: In Silico Study
Abstract
1. Introduction
2. Methods and Approaches
2.1. Bulding of Atomistic Models of GLC Reinforced with SWCNTs
2.2. Calculation Details
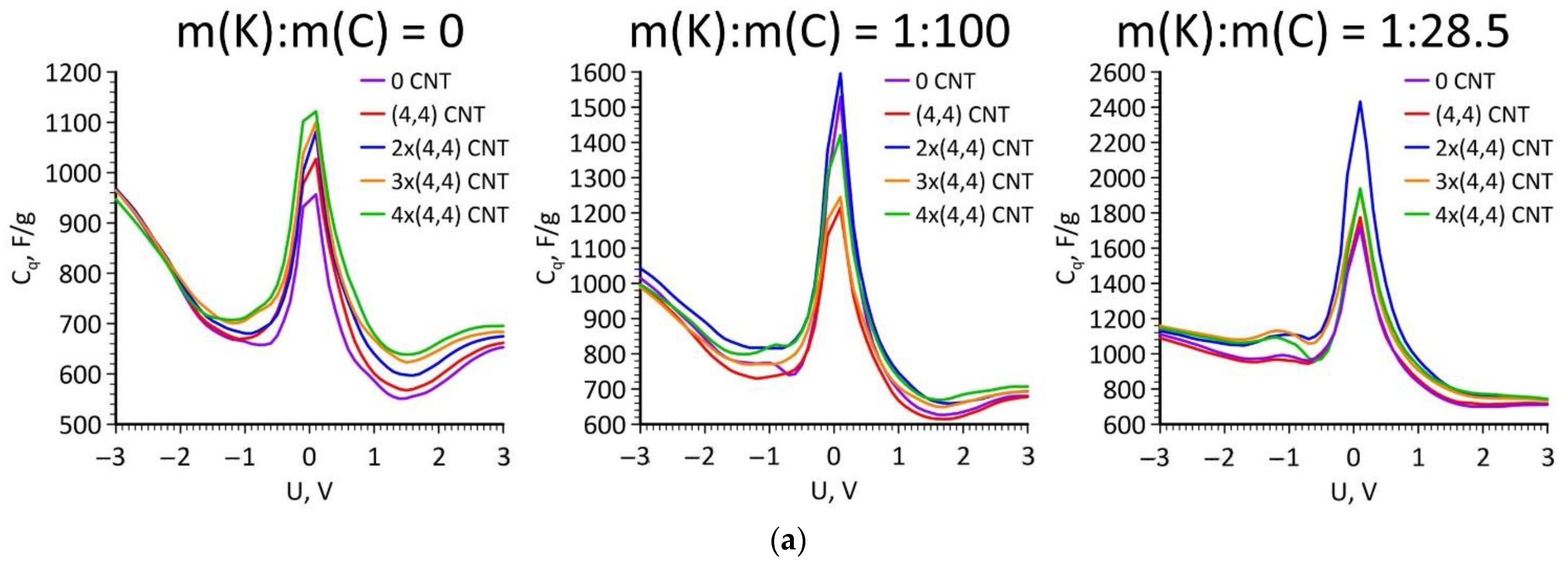
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sharma, S. Glassy Carbon: A Promising Material for Micro and Nanomanufacturing. Materials 2018, 11, 1857. [Google Scholar] [CrossRef] [PubMed]
- Jurkiewicz, K.; Pawlyta, M.; Zygadło, D.; Chrobak, D.; Duber, S.; Wrzalik, R.; Ratuszna, A.; Burian, A. Evolution of glassy carbon under heat treatment: Correlation structure–mechanical properties. J. Mat. Sci. 2018, 53, 3509–3523. [Google Scholar] [CrossRef]
- Bauer, J.; Schroer, A.; Schwaiger, R.; Kraft, O. Approaching theoretical strength in glassy carbon nanolattices. Nat. Mater. 2016, 15, 438–443. [Google Scholar] [CrossRef]
- Slepchenkov, M.M.; Shmygin, D.S.; Zhang, G.; Glukhova, O.E. Controlling the electronic properties of 2D/3D pillared graphene and glass-like carbon via metal atom doping. Nanoscale 2019, 11, 16414–16427. [Google Scholar] [CrossRef] [PubMed]
- Jurkiewicz, K.; Duber, S.; Fischer, H.E.; Burian, A. Modelling of glass-like carbon structure and its experimental verification by neutron and X-ray diffraction. J. Appl. Cryst. 2017, 50, 36–48. [Google Scholar] [CrossRef]
- Zampardi, G.; La Mantia, F.; Schuhmann, W. Determination of the formation and range of stability of the SEI on glassy carbon by local electrochemistry. RSC Adv. 2015, 5, 31166–31171. [Google Scholar] [CrossRef]
- Shimizu, A.; Tachikawa, H. Molecular dynamics simulation on diffusion of lithium atom pair in C150H30 cluster model for glassy carbon at very low temperatures. Electrochim. Acta 2003, 48, 1727–1733. [Google Scholar] [CrossRef]
- Sharma, S.; Kamath, R.; Madou, M. Porous glassy carbon formed by rapid pyrolysis of phenol-formaldehyde resins and its performance as electrode material for electrochemical double layer capacitors. J. Anal. Appl. Pyrolysis 2014, 108, 12–18. [Google Scholar] [CrossRef]
- Bozym, D.J.; Uralcan, B.; Limmer, D.T.; Pope, M.A.; Szamreta, N.J.; Debenedetti, P.G.; Aksay, I.A. Anomalous Capacitance Maximum of the Glassy Carbon–Ionic Liquid Interface through Dilution with Organic Solvents. J. Phys. Chem. Lett. 2015, 6, 2644–2648. [Google Scholar] [CrossRef]
- Palanisamy, S.; Ku, S.; Chen, S.-M. Dopamine sensor based on a glassy carbon electrode modified with a reduced graphene oxide and palladium nanoparticles composite. Microchim. Acta 2013, 180, 1037–1042. [Google Scholar] [CrossRef]
- Cui, F.; Zhang, X. Electrochemical sensor for epinephrine based on a glassy carbon electrode modified with graphene/gold nanocomposites. J. Elec. Chem. 2012, 669, 35–41. [Google Scholar] [CrossRef]
- Tajik, S.; Beitollahi, H. A Sensitive Chlorpromazine Voltammetric Sensor Based on Graphene Oxide Modified Glassy Carbon Electrode. Anal. Bioanal. Chem. Res. 2019, 6, 171–182. [Google Scholar]
- Tajik, S.; Beitollahi, H.; Biparva, P. Methyldopa electrochemical sensor based on a glassy carbon electrode modified with Cu/TiO2 nanocomposite. J. Serbian Chem. Soc. 2018, 83, 863–874. [Google Scholar] [CrossRef]
- Devi, M.; Vomero, M.; Fuhrer, E.; Castagnola, E.; Gueli, C.; Nimbalkar, S.; Hirabayashi, M.; Kassegne, S.; Stieglitz, T.; Sharma, S. Carbon-based neural electrodes: Promises and challenges. J. Neural. Eng. 2021, 18, 041007. [Google Scholar] [CrossRef] [PubMed]
- Uskoković, V. A historical review of glassy carbon: Synthesis, structure, properties and applications. Carbon Trends 2021, 5, 100116. [Google Scholar] [CrossRef]
- Jovanovic, Z.; Kalijadis, A.; Vasiljevic-Radovic, D.; Eric, M.; Lausevic, M.; Mentus, S.; Lausevic, Z. Modification of glassy carbon properties under low energy proton irradiation. Carbon 2011, 49, 3737–3746. [Google Scholar] [CrossRef]
- Serp, P.; Machado, B. Nanostructured Carbon Materials for Catalysis, 1st ed.; Royal Society of Chemistry: London, UK, 2015; pp. 1–45. [Google Scholar]
- Arkhipov, A.; Davydov, S.; Gabdullin, P.; Gnuchev, N.; Kravchik, A.; Krel, S. Field-induced electron emission from nanoporous carbons. J. Nanomater. 2014, 2014, 190232. [Google Scholar] [CrossRef]
- Kravchik, A.E.; Kukushkina, J.A.; Sokolov, V.V.; Tereshchenko, G.F. Structure of nanoporous carbon produced from boron carbide. Carbon 2006, 44, 3263–3268. [Google Scholar] [CrossRef]
- Pykal, M.; Jurečka, P.; Karlický, F.; Otyepka, M. Modelling of graphene functionalization. Phys. Chem. Chem. Phys. 2016, 18, 6351–6372. [Google Scholar] [CrossRef]
- Harris, P.J.F. Fullerene-Related Structure of Commercial Glassy Carbons. Philos. Mag. 2004, 84, 3159–3167. [Google Scholar] [CrossRef]
- Harris, P.J.F.; Tsang, S.C. High-Resolution Electron Microscopy Studies of Non-Graphitizing Carbons. Philos. Mag. A 1997, 76, 667–677. [Google Scholar] [CrossRef]
- Harris, P.J.F. Fullerene-Like Models for Microporous Carbon. J. Mater. Sci. 2013, 48, 565–577. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar, C.N.S.; Korvink, J.G.; Kübel, C. Evolution of Glassy Carbon Microstructure: In Situ Transmission Electron Microscopy of the Pyrolysis. Process. Sci. Rep. 2018, 8, 16282. [Google Scholar] [CrossRef]
- Carpenter, A.C.; Hunt, C.E. High-current, low-cost field emission triode using a reticulated vitreous carbon cathode. J. Vac. Sci. Technol. B 2010, 28, C2C37–C2C40. [Google Scholar] [CrossRef][Green Version]
- Gay, S.; Orlanducci, S.; Passeri, D.; Rossic, M.; Terranova, M.L. Nanoshaping field emitters from glassy carbon sheets: A new functionality induced by H-plasma etching. Phys. Chem. Chem. Phys. 2016, 18, 25364–25372. [Google Scholar] [CrossRef]
- Smith, B.C.; Hunt, C.E.; Brodiec, I.; Carpenter, A.C. High-performance field-emission electron gun using a reticulated vitreous carbon cathode. J. Vac. Sci. Technol. B 2011, 29, 02B108. [Google Scholar] [CrossRef]
- Egorov, N.; Sheshin, E. Carbon-Based Field-Emission Cathodes. In Field Emission Electronics, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 60, pp. 295–367. [Google Scholar]
- Figueiredo, J.L. Functionalization of porous carbons for catalytic applications. J. Mater. Chem. A 2013, 1, 9351–9364. [Google Scholar] [CrossRef]
- Long, C.; Jiang, L.; Wu, X.; Jiang, Y.; Yang, D.; Wang, C.; Wei, T.; Fan, Z. Facile synthesis of functionalized porous carbon with three-dimensional interconnected pore structure for high volumetric performance supercapacitors. Carbon 2015, 93, 412–420. [Google Scholar] [CrossRef]
- Benzigar, M.R.; Talapaneni, S.N.; Joseph, S.; Ramadass, K.; Singh, G.; Scaranto, J.; Ravon, U.; Al-Bahily, K.; Vinu, A. Recent advances in functionalized micro and mesoporous carbon materials: Synthesis and applications. Chem. Soc. Rev. 2018, 47, 2680–2721. [Google Scholar] [CrossRef]
- Glukhova, O.E.; Slepchenkov, M.M. Electronic Properties of the Functionalized Porous Glass-Like Carbon. J. Phys. Chem. C 2016, 120, 17753–17758. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, E.F.; Yan, H.; Kono, Y.; Wen, B.; Bai, L.; Shi, F.; Zhang, J.; Kenney-Benson, C.; Park, C.; et al. Nanoarchitectured Materials Composed of Fullerene-Like Spheroids and Disordered Graphene Layers With Tunable Mechanical Properties. Nat. Commun. 2015, 6, 6212. [Google Scholar] [CrossRef] [PubMed]
- LAMMPS Molecular Dynamics Simulator. Available online: https://www.lammps.org/ (accessed on 15 January 2021).
- Nose, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017; pp. 95–147. [Google Scholar]
- Senftle, T.P.; Hong, S.; Islam, M.M.; Kylasa, S.B.; Zheng, Y.; Shin, Y.K.; Junkermeier, C.; Engel-Herbert, R.; Janik, M.J.; Aktulga, H.M.; et al. The ReaxFF Reactive Force-Field: Development, Applications and Future Directions. Comput. Mater. 2016, 2, 15011–15025. [Google Scholar] [CrossRef]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-Consistent-Charge Density-Functional Tight-Binding Method for Simulations of Complex Materials Properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar] [CrossRef]
- Elstner, M.; Seifert, G. Density Functional Tight Binding. Phil. Trans. R. Soc. 2014, 372, 20120483. [Google Scholar] [CrossRef]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Hourahine, B.; Aradi, B.; Blum, V.; Bonafé, F.; Buccheri, A.; Camacho, C.; Cevallos, C.; Deshaye, M.Y.; Dumitrică, T.; Dominguez, A.; et al. DFTB+, a Software Package for Efficient Approximate Density Functional Theory Based Atomistic Simulations. J. Chem. Phys. 2020, 152, 124101. [Google Scholar] [CrossRef]
- Slepchenkov, M.M.; Barkov, P.V.; Glukhova, O.E. In Silico Study of the Electrically Conductive and Electrochemical Properties of Hybrid Films Formed by Bilayer Graphene and Single-Wall Nanotubes under Axial Stretching. Membranes 2021, 11, 658. [Google Scholar] [CrossRef]
- Kolosov, D.A.; Glukhova, O.E. Boron-Decorated Pillared Graphene as the Basic Element for Supercapacitors: An Ab Initio Study. Appl. Sci. 2021, 11, 3496. [Google Scholar] [CrossRef]
- Mousavi-Khoshdel, S.M.; Jahanbakhsh-bonab, P.; Targholi, E. Structural, electronic properties, and quantum capacitance of B, N and P-doped armchair carbon nanotubes. Phys. Lett. A 2016, 380, 3378–3383. [Google Scholar] [CrossRef]
- Samal, R.; Bhat, M.; Kapse, S.; Thapa, R.; Late, D.J.; Rout, C.S. Enhanced energy storage performance and theoretical studies of 3D cuboidal manganese diselenides embedded with multiwalled carbon nanotubes. J. Colloid Interface Sci. 2021, 598, 500–510. [Google Scholar] [CrossRef] [PubMed]

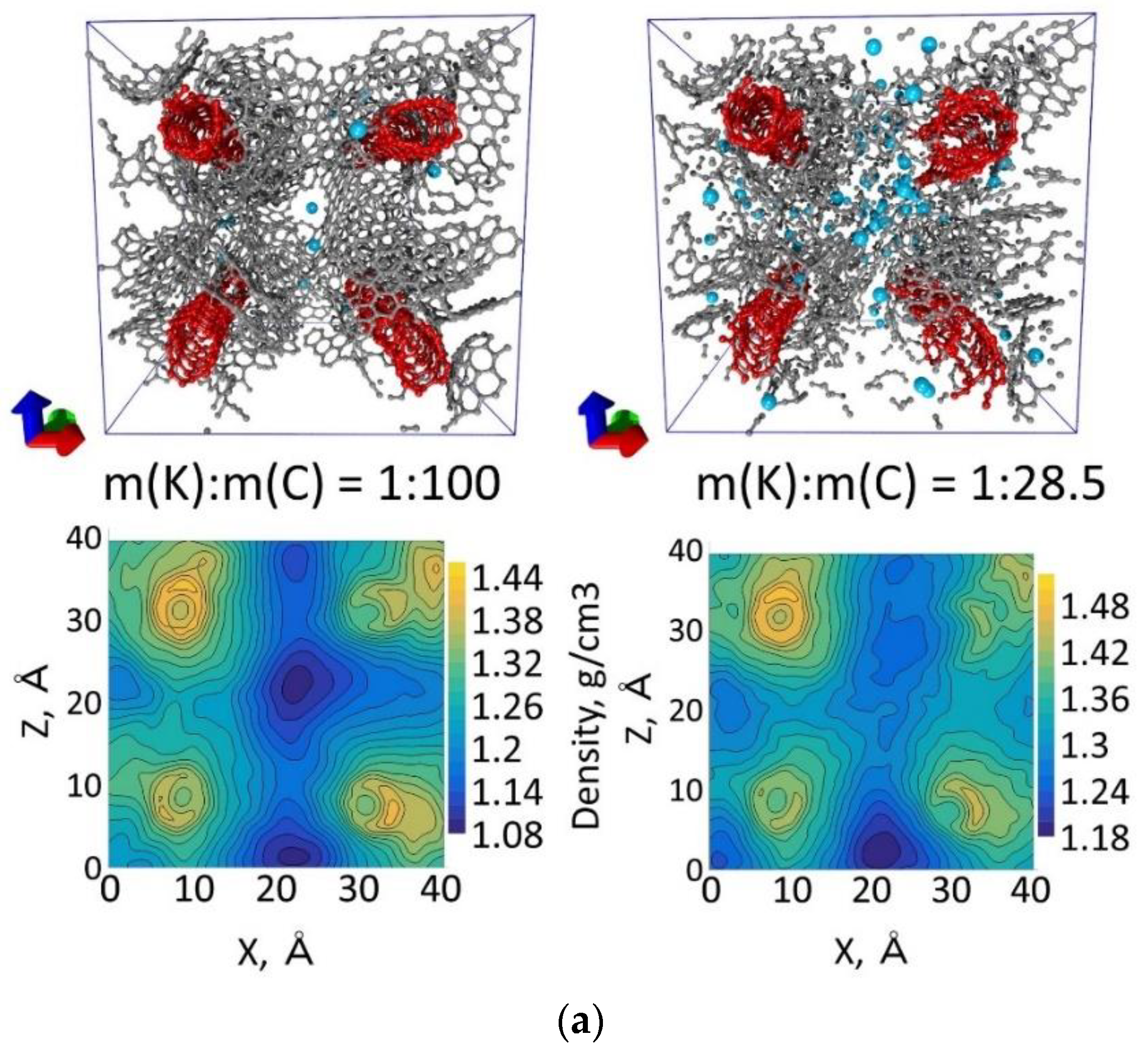
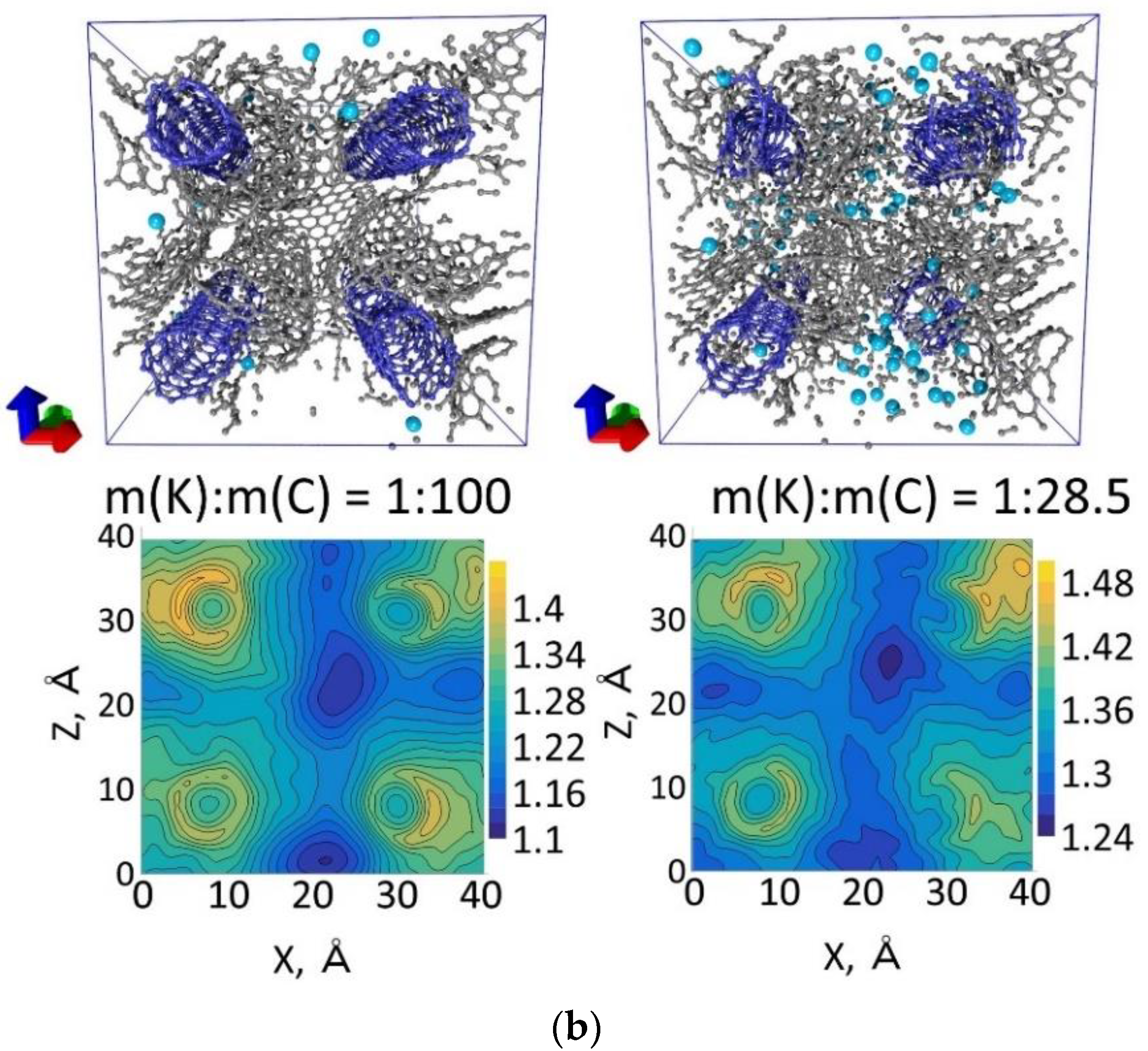
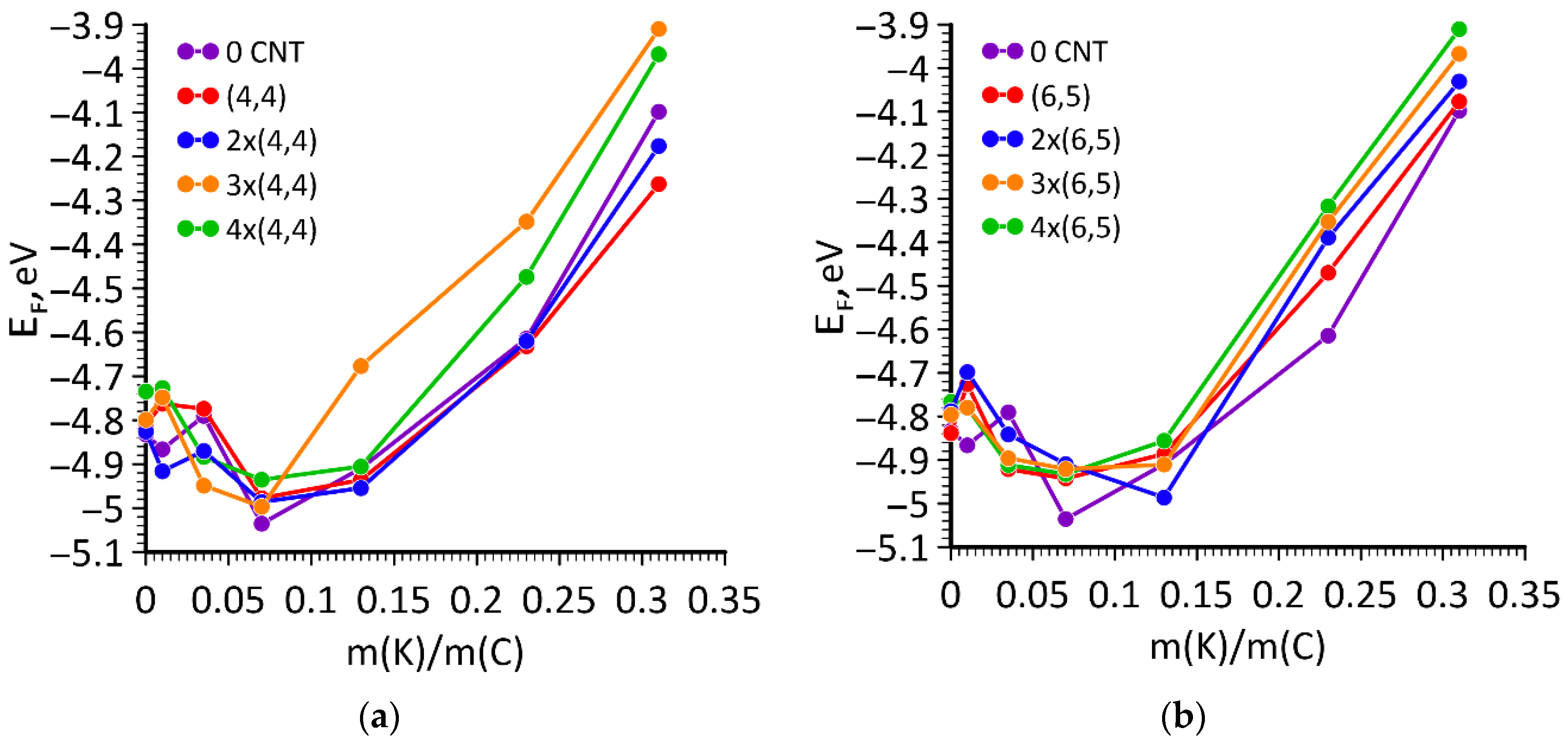
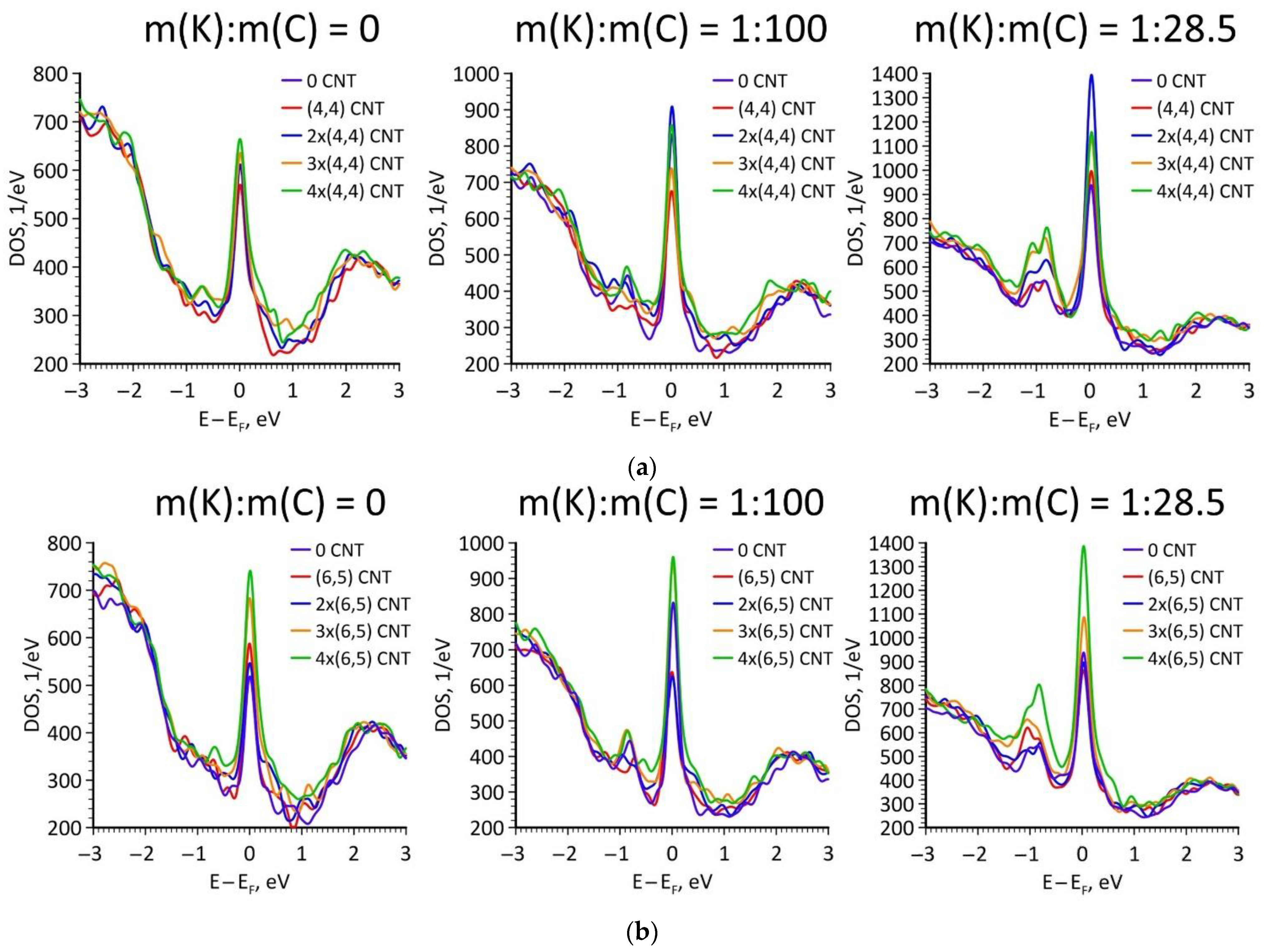

| Number of Atoms in Supercell | % Mass Fraction of Nanotube, % | Density, g/cm3 | Compressibility, GPa−1 | Bulk Modulus, GPa |
|---|---|---|---|---|
| GLC without SWCNTs | ||||
| 3891 | 0 | 1.18 | 0.519 | 1.93 |
| SWCNT (6,5) | ||||
| 4010 | 9.08 | 1.18 | 0.1091 | 9.17 |
| 4111 | 17.71 | 1.32 | 0.0793 | 12.61 |
| 4243 | 25.73 | 1.38 | 0.0539 | 18.55 |
| 4336 | 33.57 | 1.41 | 0.0519 | 19.27 |
| SWCNT (4,4) | ||||
| 3994 | 6.81 | 1.21 | 0.2071 | 4.83 |
| 4093 | 13.29 | 1.24 | 0.1072 | 9.35 |
| 4200 | 19.43 | 1.26 | 0.0788 | 12.69 |
| 4287 | 25.38 | 1.29 | 0.0682 | 14.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrunin, A.A.; Slepchenkov, M.M.; Glukhova, O.E. Effect of Functionalization with Potassium Atoms on the Electronic Properties of a 3D Glass-like Nanomaterial Reinforced with Carbon Nanotubes: In Silico Study. J. Compos. Sci. 2022, 6, 186. https://doi.org/10.3390/jcs6070186
Petrunin AA, Slepchenkov MM, Glukhova OE. Effect of Functionalization with Potassium Atoms on the Electronic Properties of a 3D Glass-like Nanomaterial Reinforced with Carbon Nanotubes: In Silico Study. Journal of Composites Science. 2022; 6(7):186. https://doi.org/10.3390/jcs6070186
Chicago/Turabian StylePetrunin, Alexander A., Michael M. Slepchenkov, and Olga E. Glukhova. 2022. "Effect of Functionalization with Potassium Atoms on the Electronic Properties of a 3D Glass-like Nanomaterial Reinforced with Carbon Nanotubes: In Silico Study" Journal of Composites Science 6, no. 7: 186. https://doi.org/10.3390/jcs6070186
APA StylePetrunin, A. A., Slepchenkov, M. M., & Glukhova, O. E. (2022). Effect of Functionalization with Potassium Atoms on the Electronic Properties of a 3D Glass-like Nanomaterial Reinforced with Carbon Nanotubes: In Silico Study. Journal of Composites Science, 6(7), 186. https://doi.org/10.3390/jcs6070186







