An Efficient Method to Determine the Thermal Behavior of Composite Material with Loading High Thermal Conductivity Fillers
Abstract
:1. Introduction
2. Theory of Calculation: The Improvement of Thermal Conductivity
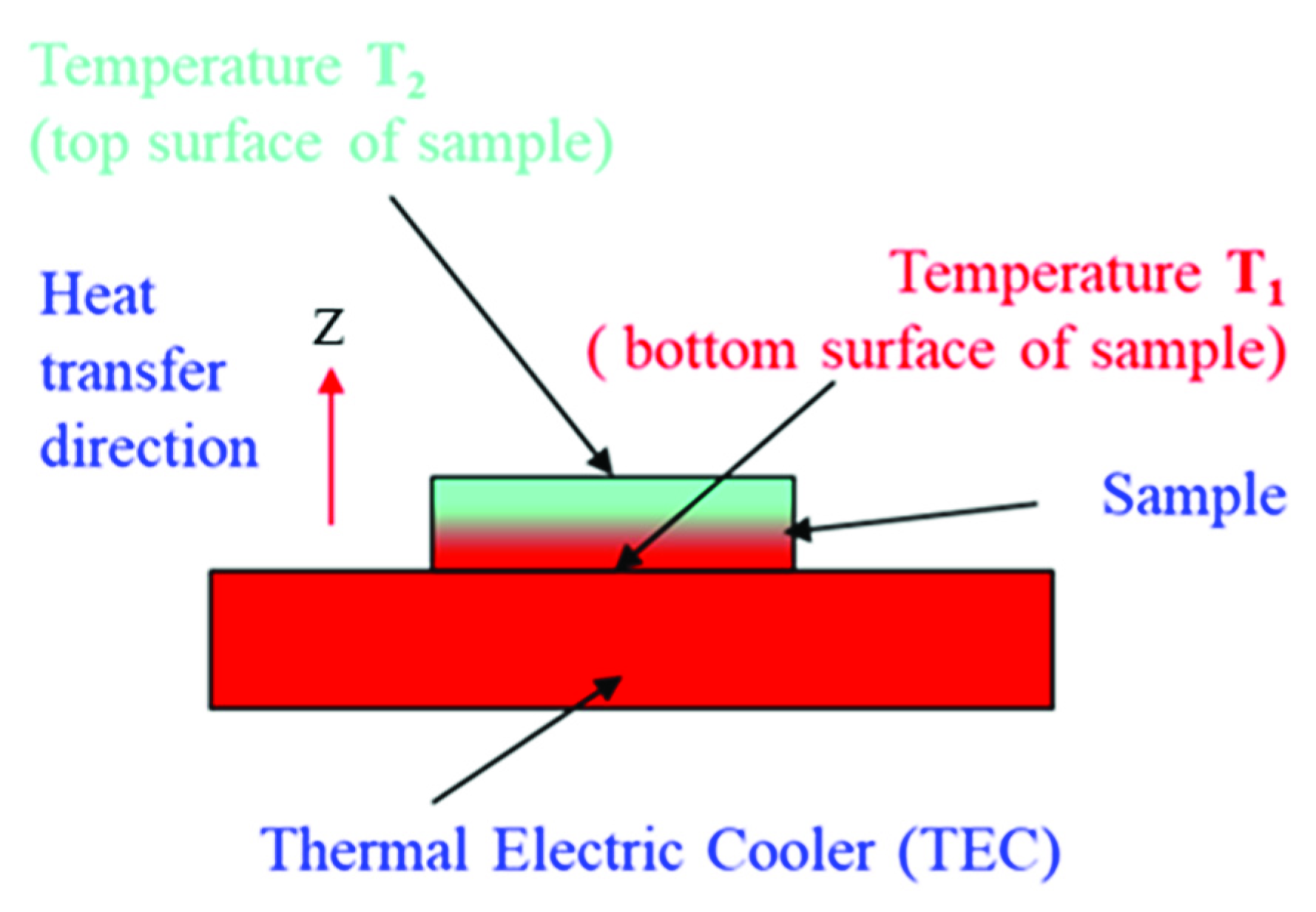
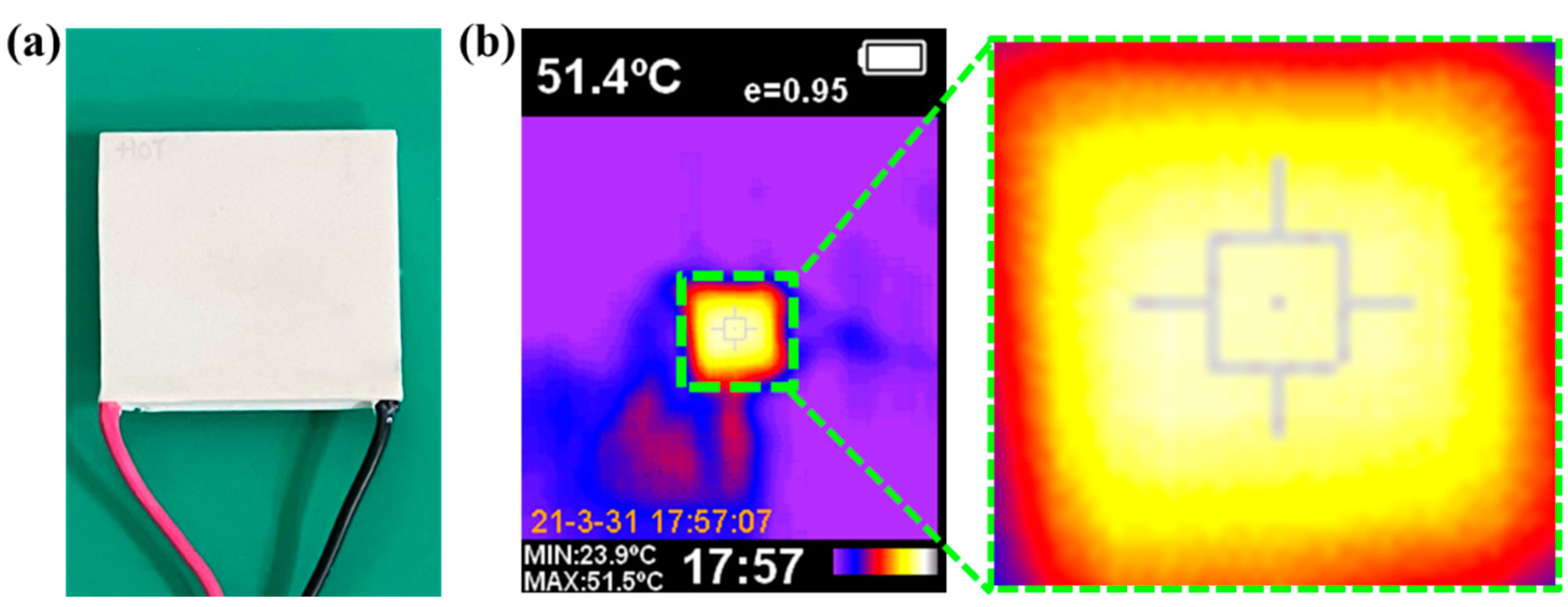
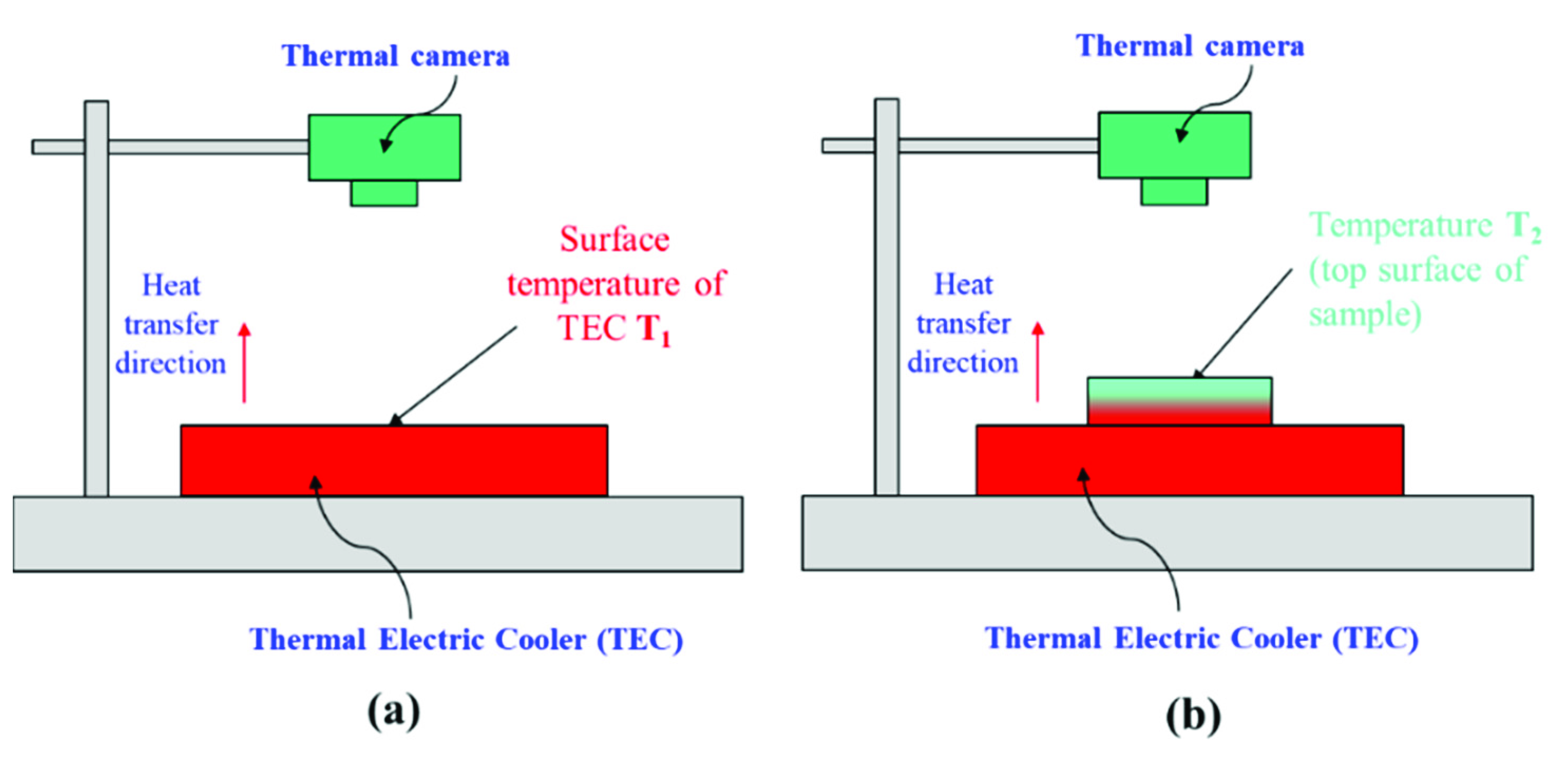
3. Method for Determining the Temperature Value of the Sample’s Two Faces in the Experiment
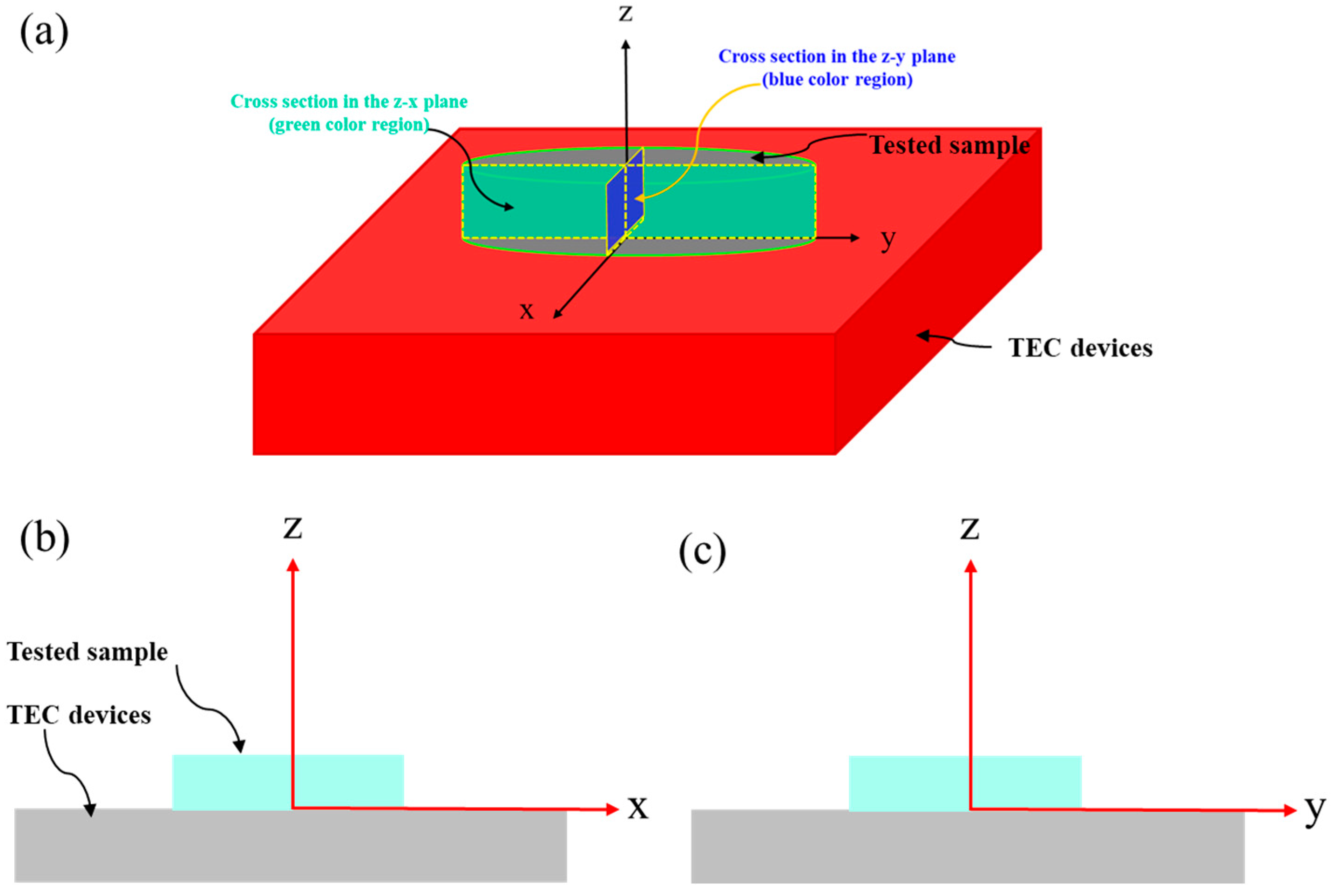
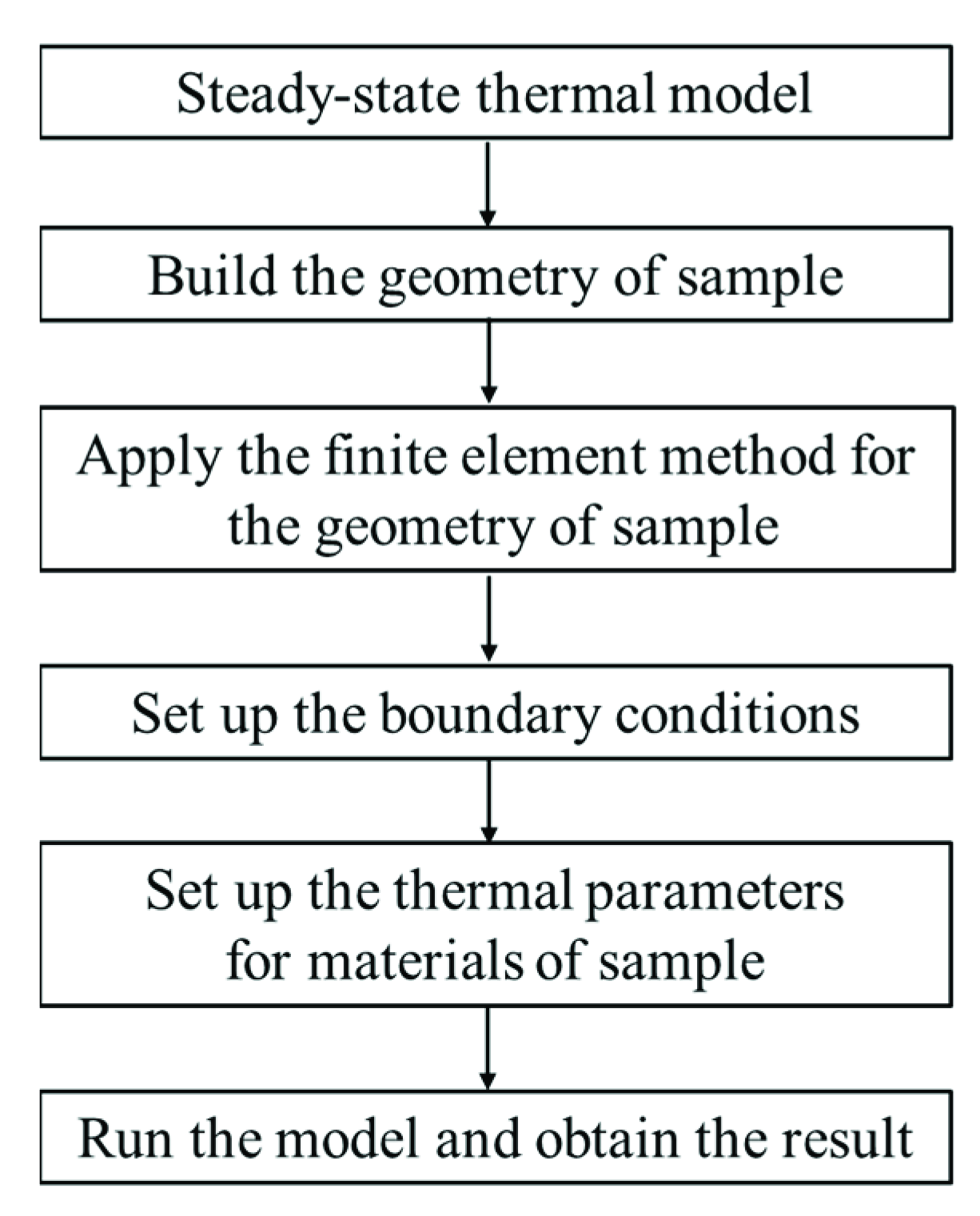
4. Simulation of Temperature Distribution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Narendran, N.; Gu, Y. Life of LED-Based White Light Sources. J. Disp. Technol. 2005, 1, 167–171. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Bettinelli, M.; Sharma, S.-K.; Redlich, B.; Speghini, A.; Karlsson, M. Unraveling the impact of different thermal quenching routes on the luminescence efficiency of the Y3Al5O12:Ce3+ phosphor for white light emitting diodes. J. Mater. Chem. C 2020, 8, 14015. [Google Scholar] [CrossRef]
- Davis, J.L.; Mills, K.-C.; Bobashev, G.; Rountree, K.-J.; Lamvik, M.; Yaga, R.; Johnson, C. Understanding chromaticity shifts in LED devices through analytical models. Microelectron. Reliab. 2018, 84, 149–156. [Google Scholar] [CrossRef]
- Singh, P.; Tan, C.-M. Degradation Physics of High-Power LEDs in Outdoor Environment and the Role of Phosphor in the degradation process. Sci. Rep. 2016, 6, 24052. [Google Scholar] [CrossRef] [Green Version]
- Ying, S.-P.; Fu, H.-K.; Tang, W.-F.; Hong, R.-C. The Study of Thermal Resistance Deviation of High-Power LEDs. IEEE Trans. Electron Devices 2014, 61, 2843–2848. [Google Scholar] [CrossRef]
- Górecki, K.; Ptak, P. Compact Modelling of Electrical, Optical and Thermal Properties of Multi-Colour Power LEDs Operating on a Common PCB. Energies 2021, 14, 1286. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, B.; Gao, Y.; Wu, X.; Chen, J.; Shan, L.; Sun, K.; Zhao, Y.; Yang, K.; Yu, J.; et al. Epoxy Composites with High Thermal Conductivity by Constructing Three-Dimensional Carbon Fiber/Carbon/Nickel Networks Using an Electroplating Method. ACS Omega 2021, 6, 19238–19251. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, Y.; Dai, W.; Wu, Y.; Wang, M.; Hou, X.; Li, H.; Jiang, N.; Lin, C.T.; Yu, J. Anisotropic thermal conductive properties of cigarette filter-templated graphene/epoxy composites. RSC Adv. 2018, 8, 1065. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Z.; Dai, J.; Zhang, Y.; Wang, H.; Wang, A.; Shan, M.; Long, H.; Peng, Y.; Sun, H.; Chen, C. Enhanced Heat Dissipation of Phosphor Film in WLEDs by AlN-Coated Sapphire Plate. IEEE Trans. Electron Devices 2020, 67, 3180–3185. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, Z.; Kang, R.; Chen, Y.; Hou, X.; Wu, Y.; Wang, M.; Wang, B.; Cui, J.; Jiang, N.; et al. Enhanced thermal conductivity of epoxy composites filled with tetrapod-shaped ZnO. RSC Adv. 2018, 8, 12337–12343. [Google Scholar] [CrossRef] [Green Version]
- Hao, W.; Li, L.; Chen, Y.; Li, M.; Fu, H.; Hou, X.; Wu, X.; Lin, C.; Jiang, N.; Yu, J. Efficient thermal transport highway construction within epoxy matrix via hybrid carbon fibers and alumina particles. ACS Omega 2020, 5, 1170–1177. [Google Scholar]
- Peng, C.; Zhang, G.; Sun, R.; Wong, C.P. Investigation of the optical properties of ZnO/epoxy resin nanocomposite: Application in the LED. In Proceedings of the 13th International Conference on Electronic Packaging Technology & High. Density Packaging, Guilin, China, 13–16 August 2012; pp. 376–379. [Google Scholar] [CrossRef]
- Shen, D.; Zhan, Z.; Liu, Z.; Cao, Y.; Zhou, L.; Liu, Y.; Dai, W.; Nishimura, K.; Li, C.; Lin, C.-T.; et al. Enhanced thermal conductivity of epoxy composites filled with silicon carbide nanowires. Sci. Rep. 2017, 7, 2606. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, J.; Li, Q.; Yan, L.; Jia, L.; Huang, X.; Zhao, L.; Ran, Q.; Fu, M. Enhanced thermal conductivity of epoxy composites by constructing aluminum nitride honeycomb reinforcements. Compos. Sci. Technol. 2020, 199, 108304. [Google Scholar]
- Gaska, K.; Rybak, A.; Kapusta, C.; Sekula, R.; Siwek, A. Enhanced thermal conductivity of epoxy–matrix composites with hybrid fillers. Polym. Adv. Technol. 2015, 26, 26–31. [Google Scholar] [CrossRef]
- Rong, Y.; Su, F.; Zhang, L.; Li, C. Highly enhanced thermal conductivity of epoxy composites by constructing dense thermal conductive network with combination of alumina and carbon nanotubes. Compos. Part. A Appl. Sci. Manuf. 2019, 125, 105496. [Google Scholar]
- Kang, R.; Zhang, Z.; Guo, L.; Cui, J.; Chen, Y.; Hou, X.; Wang, B.; Lin, C.-T.; Jiang, N.; Yu, J. Enhanced thermal conductivity of epoxy composites filled with 2D transition metal carbides (MXenes) with ultralow loading. Sci. Rep. 2019, 9, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Huang, Y.; Zeng, X.; Li, Q.; Ren, L.; Sun, R.; Xu, J.; Wong, C. Polymer composite with enhanced thermal conductivity and mechanical strength through orientation manipulating of BN. Compos. Sci. Technol. 2018, 160, 127–137. [Google Scholar] [CrossRef]
- Kraemer, D.; Chen, G. A simple differential steady-state method to measure the thermal conductivity of solid bulk materials with high accuracy. Rev. Sci. Instrum. 2014, 85, 025108. [Google Scholar] [CrossRef]
- Braun Jeffrey, L.; Olson, D.; Gaskins, J.; Hopkins, P. A steady-state thermoreflectance method to measure thermal conductivity. Rev. Sci. Instrum. 2019, 90, 024905. [Google Scholar] [CrossRef] [Green Version]
- Santos, D.; Nunes, W. Thermal properties of polymers by non-steady-state techniques. Polym. Test. 2007, 26, 556–566. [Google Scholar] [CrossRef]
- Singh, A.K.; Panda, B.; Mohanty, S.; Nayak, S.; Gupta, M. Synergistic effect of hybrid graphene and boron nitride on the cure kinetics and thermal conductivity of epoxy adhesives. Polym. Adv. Technol. 2017, 28, 1851–1864. [Google Scholar] [CrossRef]
- Craddock, J.D.; Burgess, J.; Edrington, S.; Weisenberger, M. Method for direct measurement of on-axis carbon fiber thermal diffusivity using the laser flash technique. J. Therm. Sci. Eng. Appl. 2017, 9, 014502. [Google Scholar] [CrossRef]
- Chaudhry, A.U.; Mabrouk, A.N.; Abdala, A. Thermally enhanced polyolefin composites: Fundamentals, progress, challenges, and prospects. Sci. Technol. Adv. Mater. 2020, 21, 737–766. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.comsol.com/heat-transfer-module (accessed on 19 April 2022).
- Available online: https://quickfield.com/transfer.htm (accessed on 19 April 2022).
- Available online: https://www.theseus-fe.com/simulation-software/heat-transfer-analysis (accessed on 19 April 2022).
- Available online: https://www.mscsoftware.com/application/thermal-analysis (accessed on 19 April 2022).
- Incropera, F.; Dewitt, D. Fundamentals of Heat and Mass Transfer, 5th ed.; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Partial Differential Equation Toolbox for Use with MATLAB; The MathWorks, Inc: Natick, MA, USA, 1995.
- Heat Transfer. Available online: https://www.mathworks.com/help/pde/heat-transfer-and-diffusion-equations.html (accessed on 19 April 2022).
- Li, S.; Liu, J.-L.; Ding, L.; Liu, J.-X.; Xu, J.; Peng, Y.; Chen, M.-X. Active Thermal Management of High-Power LED Through Chip on Thermoelectric Cooler. IEEE Trans. Electron. Devices 2021, 68, 1753–1756. [Google Scholar] [CrossRef]
- Huang, B.J.; Chin, C.J.; Duang, C.L. A design method of thermoelectric cooler. Int. J. Refrig. 2000, 23, 208–218. [Google Scholar] [CrossRef]




| Value | Unit | |
|---|---|---|
| Sample thickness | 0.5 | mm |
| Sample width (diameter) | 16 | mm |
| TEC device thickness | 5 | mm |
| TEC device width | 30 | mm |
| Value | Unit | |
|---|---|---|
| Sample thermal conductivity | Ki | W/(m.K) |
| TEC device thermal conductivity | 130 | W/(m.K) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, C.-C.; Nguyen, Q.-K. An Efficient Method to Determine the Thermal Behavior of Composite Material with Loading High Thermal Conductivity Fillers. J. Compos. Sci. 2022, 6, 214. https://doi.org/10.3390/jcs6070214
Tran C-C, Nguyen Q-K. An Efficient Method to Determine the Thermal Behavior of Composite Material with Loading High Thermal Conductivity Fillers. Journal of Composites Science. 2022; 6(7):214. https://doi.org/10.3390/jcs6070214
Chicago/Turabian StyleTran, Chi-Cuong, and Quang-Khoi Nguyen. 2022. "An Efficient Method to Determine the Thermal Behavior of Composite Material with Loading High Thermal Conductivity Fillers" Journal of Composites Science 6, no. 7: 214. https://doi.org/10.3390/jcs6070214
APA StyleTran, C.-C., & Nguyen, Q.-K. (2022). An Efficient Method to Determine the Thermal Behavior of Composite Material with Loading High Thermal Conductivity Fillers. Journal of Composites Science, 6(7), 214. https://doi.org/10.3390/jcs6070214







