Prediction of Damage in Non-Crimp Fabric Composites Subjected to Transverse Crushing: A Comparison of Two Constitutive Models
Abstract
:1. Introduction
2. Physical Experiments
2.1. Materials and Manufacturing
2.2. Material Characterization
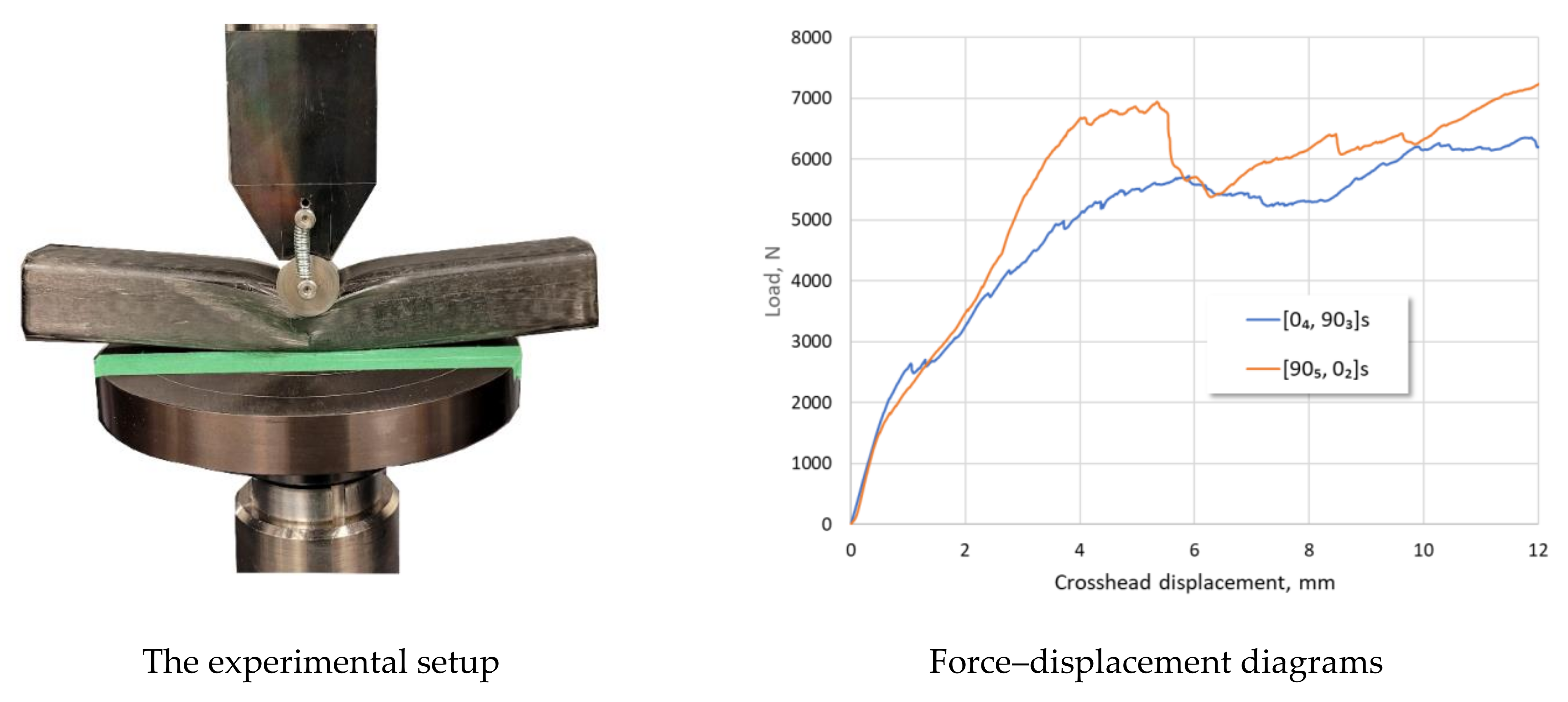
2.3. Component Testing
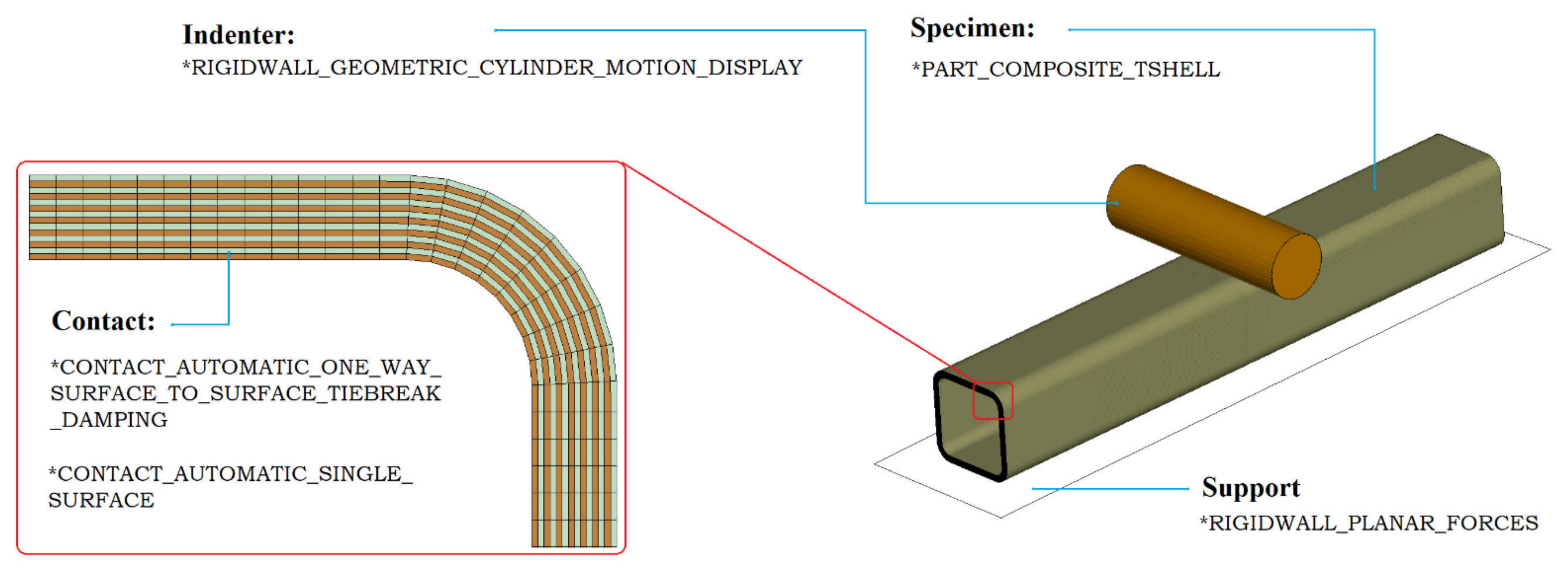
3. Numerical Model
3.1. General Description of the Numerical Model
3.2. Modeling of Intra-Ply Damage
3.2.1. MAT54—*MAT_ENHANCED_COMPOSITE_DAMAGE
- (1)
- (element deletion) parameters;
- (2)
- parameters controlling crashfront softening;
- (3)
- those characterizing material behavior after failure initiation.
3.2.2. MAT58–*MAT_LAMINATED_COMPOSITE_FABRIC
3.3. Modeling of Delamination
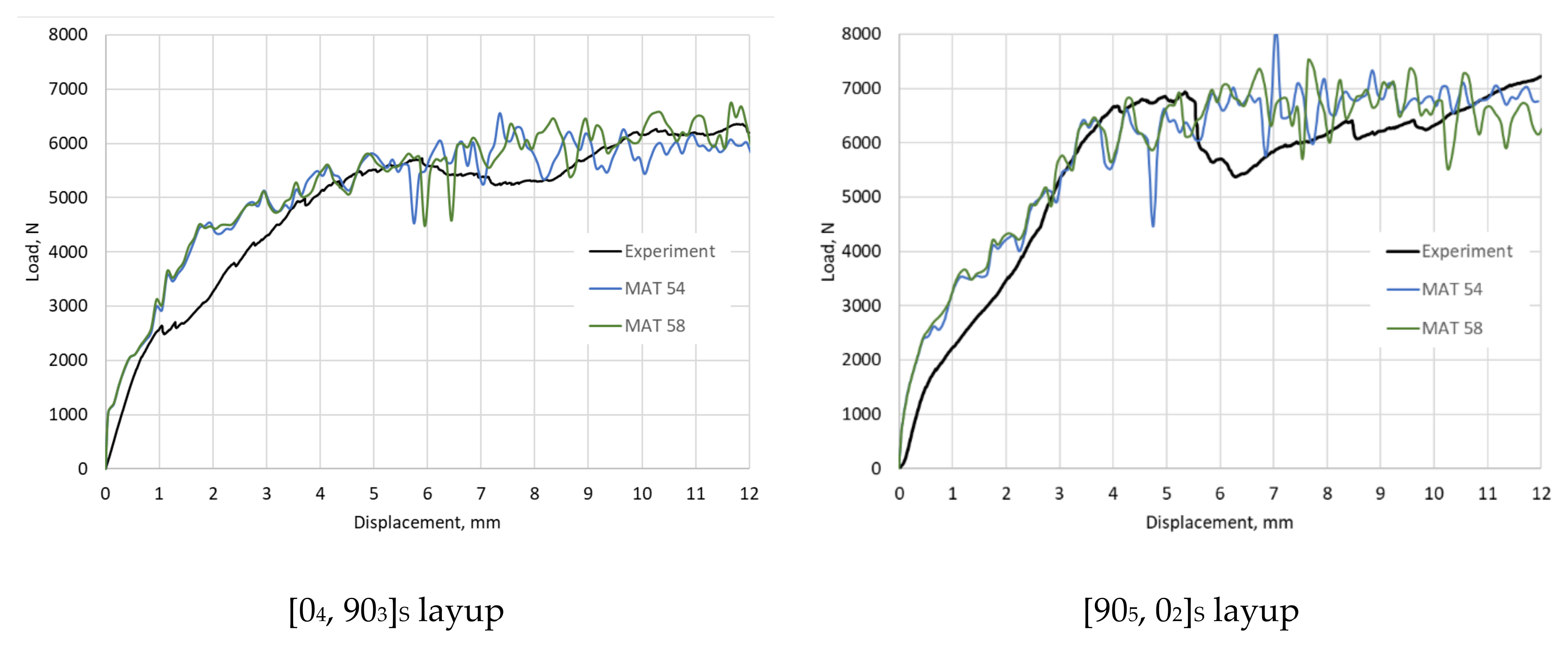
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Middendorf, P.; Metzner, C. Aerospace application of non-crimp fabric composites. In Non-Crimp Fabric Composites, Philadelphia; Woodhead Publishing: Sawston, UK, 2011; pp. 441–449. [Google Scholar]
- Sköck-Hartmann, B.; Gries, T. Automotive applications of non-crimp fabric composites. In Non-Crimp Fabric Composites, Philadelphia; Woodhead Publishing: Sawston, UK, 2011; pp. 461–480. [Google Scholar]
- Adolphs, G.; Skinner, C. Non-crimp fabric composites in wind turbines. In Non-Crimp Fabric Composites, Philadelphia; Woodhead Publishing: Sawston, UK, 2011; pp. 481–493. [Google Scholar]
- Mouli, Y.S.C.; Upadhyay, C.S.; Mohite, P.M. Intra-ply Damage Modeling of Low-Velocity Impact on Composite Laminates. In Proceedings of the 1st International Conference on Emerging Trends in Engineering (ICETE), Hyderabad, India, 22–23 March 2020. [Google Scholar]
- Moncayo, E.; Wagner, H.; Drechsler, K. Benchmarks for Composite Delamination Using LS-Dyna 971: Low Velocity Impact. In Proceedings of the 6th LS-DYNA Anwenderforum, Frankental, Germany, 11 October 2007. [Google Scholar]
- Cherniaev, A.; Pavlova, S.; Pavlov, A.; Komarov, V. Prediction of Load-Bearing Capacity of Composite Parts with Low-Velocity Impact Damage: Identification of Intra- and Inter-Ply Constitutive Models. Appl. Mech. 2020, 1, 5. [Google Scholar] [CrossRef] [Green Version]
- Heimbs, S.; Heller, S.; Middendorf, P. Simulation of low velocity impact on composite plates with compressive preload. In LS-DYNA Anwenderforum; DYNAmore GmbH: Banberg, Germany, 2008. [Google Scholar]
- Aymerich, F.; Dore, F.; Priolo, P. Prediction of impact-induced delamination in cross-ply composite laminates using cohesive interface elements. Compos. Sci. Technol. 2008, 68, 2383–2390. [Google Scholar] [CrossRef] [Green Version]
- Di Caprio, F.; Langella, A.; Lopresto, V.; Caprino, G. Numerical, Experimental and Analytical Correlation for Predicting the Structural Behavior of Composite Structures under Impact. Procedia Eng. 2016, 167, 80–87. [Google Scholar] [CrossRef]
- Long, S.; Yao, X.; Zhang, X. Delamination prediction in composite laminates under low-velocity impact. Compos. Struct. 2015, 132, 290–298. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Zhang, Q.; Huili, Y. Study of fiber modulus effect on impact energy absorption characteristics of composite laminates at normal and oblique impacts. Mater. Res. Express 2019, 6, 085610. [Google Scholar] [CrossRef]
- Cherniaev, A.; Butcher, C.; Montesano, J. Predicting the axial crush response of CFRP tubes using three damage-based constitutive models. Thin-Walled Struct. 2018, 129, 349–364. [Google Scholar] [CrossRef]
- Geier, N.; Szalay, T.; Takács, M. Analysis of thrust force and characteristics of uncut fibres at non-conventional oriented drilling of unidirectional carbon fibre-reinforced plastic (UD-CFRP) composite laminates. Int. J. Adv. Manuf. Technol. 2018, 100, 3139–3154. [Google Scholar] [CrossRef]
- Sapozhnikov, S.; Swolfs, Y.; Lomov, S. Pseudo-ductile unidirectional high modulus/high strength carbon fibre hybrids using conventional ply thickness prepregs. Compos. Part B Eng. 2020, 198, 108213. [Google Scholar] [CrossRef]
- Sy, B.L.; Fawaz, Z.; Bougherara, H. Damage evolution in unidirectional and cross-ply flax/epoxy laminates subjected to low velocity impact loading. Compos. Part A Appl. Sci. Manuf. 2018, 112, 452–467. [Google Scholar] [CrossRef]
- Liv, Y.; Guillamet, G.; Costa, J.; González, E.; Marín, L.; Mayugo, J. Experimental study into compression after impact strength of laminates with conventional and nonconventional ply orientations. Compos. Part B Eng. 2017, 126, 133–142. [Google Scholar] [CrossRef] [Green Version]
- Sabah, S.A.; Kueh, A.; Al-Fasih, M. Comparative low-velocity impact behavior of bio-inspired and conventional sandwich composite beams. Compos. Sci. Technol. 2017, 149, 64–74. [Google Scholar] [CrossRef]
- Vignjevic, R.; Campbell, J.; Hughes, K.; Orłowski, M.; Garcea, S.; Withers, P.; Reed, J. Soft body impact resistance of composite foam core sandwich panels with unidirectional corrugated and tubular reinforcements. Int. J. Impact Eng. 2019, 132, 103320. [Google Scholar] [CrossRef]
- Liu, H.; Falzon, B.; Tan, W. Experimental and numerical studies on the impact response of damage-tolerant hybrid unidirectional/woven carbon-fibre reinforced composite laminates. Compos. Part B Eng. 2018, 136, 101–118. [Google Scholar] [CrossRef] [Green Version]
- Shyr, T.-W.; Pan, Y.-H. Impact resistance and damage characteristics of composite laminates. Compos. Struct. 2003, 62, 193–203. [Google Scholar] [CrossRef]
- Greve, L.; Pickett, A. Modelling damage and failure in carbon/epoxy non-crimp fabric composites including effects of fabric pre-shear. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1983–2001. [Google Scholar] [CrossRef] [Green Version]
- Lomov, S.V.; Bogdanovich, A.E.; Ivanov, D.S.; Mungalov, D.; Karahan, M.; Verpoest, I. A comparative study of tensile properties of non-crimp 3D orthogonal weave and multi-layer plain weave E-glass composites. Part 1: Materials, methods and principal results. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1134–1143. [Google Scholar] [CrossRef]
- Segreto, T.; Bottillo, A.; Teti, R. Advanced ultrasonic non-destructive evaluation for metrological analysis and quality assessment of impact damaged non-crimp fabric composites. Procedia CIRP 2016, 41, 1055–1060. [Google Scholar] [CrossRef]
- Bibo, G.; Hogg, P.; Backhouse, R.; Mills, A. Carbon-fibre non-crimp fabric laminates for cost-effective damage-tolerant structures. Compos. Sci. Technol. 1998, 58, 129–143. [Google Scholar] [CrossRef]
- Berketis, K.; Tzetzis, D. The compression-after-impact strength of woven and non-crimp fabric reinforced composites subjected to long-term water immersion ageing. J. Mater. Sci. 2010, 45, 5611–5623. [Google Scholar] [CrossRef]
- Zhao, L.; Warrior, N.; Long, A. Finite element modelling of damage progression in non-crimp fabric reinforced composites. Compos. Sci. Technol. 2006, 66, 36–50. [Google Scholar] [CrossRef]
- Yin, H.; Li, Q.; Iannucci, L. Meso-scale Finite Element (FE) modelling of biaxial carbon fibre non-crimp-fabric (NCF) based composites under uniaxial tension and in-plane shear. Compos. Struct. 2022, 290, 115538. [Google Scholar] [CrossRef]
- Rouf, K.; Worswick, M.J.; Montesano, J. A multiscale framework for predicting the mechanical properties of unidirectional non-crimp fabric composites with manufacturing induced defects. J. Compos. Mater. 2020, 55, 741–757. [Google Scholar] [CrossRef]
- Costa, S.; Bru, T.; Olsson, R.; Portugal, A. Improvement and validation of a physically based model for the shear and transverse crushing of orthotropic composites. J. Compos. Mater. 2018, 53, 1681–1696. [Google Scholar] [CrossRef]
- Gouskos, D.; Iannucci, L. A failure model for the analysis of cross-ply Non-Crimp Fabric (NCF) composites under in-plane loading: Experimental & numerical study. Eng. Fract. Mech. 2022, 271, 108575. [Google Scholar]
- Senner, T.; Kreissl, S.; Merklein, M.; Meinhardt, M.; Lipp, A. Bending of unidirectional non-crimp-fabrics: Experimental characterization, constitutive modeling and application in finite element simulation. Prod. Eng. 2015, 9, 1–10. [Google Scholar] [CrossRef]
- Soto, A.; González, E.V.; Maimí, P.; Escalera, F.M.D.L.; Aja, J.S.D.; Alvarez, E. Low velocity impact and compression after impact simulation of thin ply laminates. Compos. Part A Appl. Sci. Manuf. 2018, 109, 413–427. [Google Scholar] [CrossRef]
- Feraboli, P.; Wade, B.; DeLeo, F.; Rassaian, M.; Higgins, M.; Byar, A. LS-DYNA MAT54 modeling of the axial crushing of a composite tape sinusoidal specimen. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1809–1825. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, B.; Zheng, D.; Li, Z. Experimental and numerical study on energy absorption performance of CFRP/aluminum hybrid square tubes under axial loading. Thin-Walled Struct. 2020, 155, 106948. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, J.; Ma, Y.; Zhang, Y.; Li, Q. Crushing responses and energy absorption behaviors of multi-cell CFRP tubes. Thin-Walled Struct. 2020, 155, 106930. [Google Scholar] [CrossRef]
- Zhou, G.; Tang, H.; Sun, Q.; Li, D.; Peng, Y.; Zeng, D.; Su, X. Analysis of the crushing behaviors of woven carbon fiber reinforced plastic hat section component under dynamic bending and axial crushing loading. Thin-Walled Struct. 2021, 161, 107426. [Google Scholar] [CrossRef]
- Pohl, C.; Toenjes, M.; Liebold, C.; Ploeckl, M.; Koerber, H.; Gray, L.A.; Colin, D.; Drechsler, K. Numerical prediction of composite damage behavior: A modeling approach including the strain-rate-dependent material response. Compos. Struct. 2022, 292, 115628. [Google Scholar] [CrossRef]
- Mansor, M.; Ahmad, Z.; Abdullah, M. Crashworthiness capability of thin-walled fibre metal laminate tubes under axial crushing. Eng. Struct. 2021, 252, 113660. [Google Scholar] [CrossRef]
- Lanzi, L. Composite stiffened panels in postbuckling: Experiments and dynamic explicit analyses with LS-DYNA. In Proceedings of the 30th Europian Rotor Craft Forum, Marseilles, France, 14–16 September 2004. [Google Scholar]
- Xiao, X.; McGregor, C.; Vaziri, R.; Poursartip, A. Progress in braided composite tube crush simulation. Int. J. Impact Eng. 2009, 36, 711–719. [Google Scholar] [CrossRef]
- Jackson, K.E.; Fasanella, E.L.; Littell, J.D. Development of a continuum damage mechanics material model of a graphite-kevlar hybrid fabric for simulating the impact response of energy absorbing subfloor concepts. In Proceedings of the 73rdAHS International Annual Forum & Technology Display, Fort Worth, TX, USA, 9–11 May 2017. [Google Scholar]
- Reiner, J.; Vaziri, R. Progressive Axial Crushing of Composite Laminates: A Comparison Between LS-DYNA Continuum Damage Models. In Proceedings of the American Society for Composites—Thirty-Third Annual Technical Conference, Seattle, WA, USA, 24–26 September 2018. [Google Scholar]
- Panciroli, R.; Giannini, O. Comparing the impact resistance of flax/epoxy and glass/epoxy composites through experiments and numerical simulations. Compos. Struct. 2021, 264, 113750. [Google Scholar] [CrossRef]
- Metin, F.; Avcı, A. In-plane quasi-static and out-of-plane dynamic behavior of nanofiber interleaved glass/epoxy composites and finite element simulation. Compos. Struct. 2021, 270, 114085. [Google Scholar] [CrossRef]
- Yan, J.; Liu, Y.; Yan, Z.; Bai, F.; Shi, Z.; Si, P.; Huang, F. Ballistic characteristics of 3D-printed auxetic honeycomb sandwich panel using CFRP face sheet. Int. J. Impact Eng. 2022, 164, 104186. [Google Scholar] [CrossRef]
- Wei, Q.; Gu, B.; Sun, B. Ballistic penetration damages and energy absorptions of stacked cross-plied composite fabrics and laminated panels. Int. J. Damage Mech. 2020, 29, 1465–1484. [Google Scholar] [CrossRef]
- Yu, H.; Zhao, H.; Shi, F. Bending Performance and Reinforcement of Rocker Panel Components with Unidirectional Carbon Fiber Composite. Materials 2019, 12, 3164. [Google Scholar] [CrossRef] [Green Version]
- No. D3039/D3039M-17; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. Annual Book of ASTM Standards: West Conshohocken, PA, USA, 2017.
- Chamis, C.C.; Sinclair, J.H. Ten Deg. Off-Axis Tensile Test for Intralaminar Shear Characterization of Fiber Composites; NASA Technical Note (TN-D-8215); National Aeronautics and Space Administration: Washington, DC, USA, 1976.
- No. D 5528-01 (Reapproved 2007); Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites1. Annual Book of ASTM: West Conshohocken, PA, USA, 2007.
- Carlsson, L.A.; Adams, D.F.; Pipes, R.B. Characterization of Delamination Failure. In Experimental Characterization of Advanced Composite Materials; CRC Press: Boca Raton, FL, USA, 2014; pp. 250–262. [Google Scholar]
- Lo, K.; Chim, E.-M. Compressive Strength of Unidirectional Composites. J. Reinf. Plast. Compos. 1992, 11, 838–896. [Google Scholar] [CrossRef]
- Chamis, C.C. Simplified composite micromechanics equations for hygral, thermal and mechanical properties. In Proceedings of the Thirty-Eight Annual Conference of Society of the Plastics Industry (SPI) Reinforced Plastics/Composites Institute, Houston, TX, USA, 7–11 February 1983. [Google Scholar]
- Livermore Software Technology Corporation (LSTC). LS-DYNA ® Keyword User’s Manual Volume II: Material Models; LSTC: Canonsburg, PA, USA, 2013. [Google Scholar]
- Matzenmiller, A.; Lubliner, J.; Taylor, L.R. A constitutive model for anisotropic damage in fiber-composites. Mech. Mater. 1995, 20, 125–152. [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation (LSTC). LS-DYNA ® Keyword User’s Manual Volume I; LSTC: Canonsburg, PA, USA, 2019. [Google Scholar]
- Graf, T.; Haufe, A.; Andrade, F. Adhesives modeling with LS-DYNA: Recent developments and future work. In Proceedings of the Nordic LS-DYNA Forum, Stuttgart, Germany, 6–8 October 2014. [Google Scholar]








| # | Test Type | In-Plane Dimensions, mm × mm | Number of NCF Layers | Test Procedure |
|---|---|---|---|---|
| 1 | Longitudinal tensile test | 250 × 15 | 8 | ASTM D3039 [48] |
| 2 | Transverse tensile test | 175 × 25 | 14 | ASTM D3039 [48] |
| 3 | 10°off-axis tensile test | 250 × 15 | 8 | Ref [49] |
| 4 | Double-cantilever beam (DCB) test (specimen with Teflon insert) | 125 × 25 | 32 | ASTM 5528b [50] |
| 5 | End-notched flexure (ENF) test (specimen with Teflon insert) | 120 × 25 | 32 | Ref [51] |
| Property | Units | Mean Value |
|---|---|---|
| Longitudinal Young’s modulus, | MPa | 149,018 |
| Transverse Young’s modulus, | MPa | 6071 |
| Major in-plane Poisson’s ratio, | - | 0.32 |
| In-plane shear modulus, | MPa | 4217 |
| Longitudinal tensile strength, | MPa | 2060 |
| Longitudinal compressive strength *, | MPa | 1539 |
| Transverse tensile strength, | MPa | 29.1 |
| Transverse compressive strength *, | MPa | 126.6 |
| In-plane shear strength, | MPa | 44.5 |
| Longitudinal tensile strain-at-failure, | % | 1.37 |
| Transverse tensile strain-at-failure, | % | 0.40 |
| In-plane shear strain-at-failure, | % | 1.71 |
| Mode I strain energy release rate, GIc | 0.66 | |
| Mode II strain energy release rate, GIIc | 2.77 | |
| Shear stress at onset of non-linearity | MPa | 30 |
| Shear strain at onset of non-linearity | % | 0.711 |
| Parameter | Meaning | Units | Value | Comment for the Chosen Initial Value |
|---|---|---|---|---|
| DFAIL | Maximum strains for directional straining at which element will be eroded. | mm/mm | – | Disabled to control elements’ erosion by timestep (TFAIL) and effective strain (EPS) only. |
| TFAIL | Element is deleted when its time step is smaller than the given value. | s | 10−7 | Element is deleted when current timestep is less 10−7s |
| EPS | Effective failure strain | mm/mm | 0.55 | Chosen as to be significantly higher than any directional strain at failure initiation, as used in [12] |
| SOFT | Softening reduction factor for material strength in crash front elements | – | 0.90 | Slight (10%) reduction of strength in crashfront elements is assumed |
| SOFT2 | Optional transverse softening reduction factor | – | no input | Softening is assumed to be isotropic |
| PFL | Percentage of layers which must fail until crash front is initiated | – | 100 | Default value |
| BETA | Weighting factor for shear term in tensile fiber mode (see Equation (1)) | – | 0 | No effect of shear stresses on fiber tensile failure (max stress criterion), which usually provides good agreement with experimental data. |
| SLIMT1 | Factor to determine the minimum stress limit after stress maximum (fiber tension). | – | 0.010 | Small but non-zero residual strength is assumed after tensile failure to avoid numerical instabilities |
| SLIMC1 | Factor to determine the minimum stress limit after stress maximum (fiber tension). | – | 0.375 | A post-calibration value obtained in [12] |
| SLIMT2 | Factor to determine the minimum stress limit after stress maximum (matrix tension). | – | 0.010 | Small but non-zero residual strength is assumed after tensile failure to avoid numerical instabilities |
| SLIMC2 | Factor to determine the minimum stress limit after stress maximum (matrix compression). | – | 0.375 | A post-calibration value obtained in [12] |
| SLIMS | Factor to determine the minimum stress limit after stress maximum (shear). | – | 1.000 | A recommended value [54] |
| FBRT | Reduction factor for fiber tensile strength after matrix compressive failure | – | 0 | A zero effect of transverse matrix cracking on fiber tensile strength is assumed |
| YCFAC | Reduction factor for compressive fiber strength Xc after matrix compressive failure | – | 12 | Assume no influence of the matrix failure on the longitudinal compressive strength |
| Parameter | Meaning | Units | Value | Comment for the Chosen Initial Value |
|---|---|---|---|---|
| TFAIL | Timestep for automatic element deletion | s | 10−7 | Element is deleted when current timestep is less 10−7 s |
| ERODS | Maximum effective strain for element failure. If lower than zero, element fails when the effective strain calculated from the full strain tensor exceeds ERODS | mm/mm | −0.55 | Chosen as to be significantly higher than any directional strain at failure initiation |
| SOFT | Softening reduction factor for material strength in crash front elements | – | 0.90 | Slight (10%) reduction of strength in crashfront elements is assumed |
| SLIMT1 | Factor to determine the minimum stress limit after stress maximum (fiber tension) | – | 0.010 | Small but non-zero residual strength is assumed after tensile failure to avoid numerical instabilities |
| SLIMC1 | Factor to determine the minimum stress limit after stress maximum (fiber tension). | – | 0.375 | A post-calibration value obtained in [12] |
| SLIMT2 | Factor to determine the minimum stress limit after stress maximum (matrix tension) | – | 0.010 | Small but non-zero residual strength is assumed after tensile failure to avoid numerical instabilities |
| SLIMC2 | Factor to determine the minimum stress limit after stress maximum (matrix compression) | – | 0.375 | A post-calibration value obtained in [12] |
| SLIMS | Factor to determine the minimum stress limit after stress maximum (shear) | – | 1.000 | A recommended value [54] |
| Property | Unit | Value | Rationale |
|---|---|---|---|
| NFLS | MPa | 75.00 | The ultimate strength of bulk epoxy resin multiplied by a scaling factor of 0.95 to account for the mesh dependency (see the recommendation provided in [57] for meshes with element sizes of 0.7 mm). |
| SFLS | MPa | 43.30 | Assumed as (von Mises criterion) |
| G_Ic | 0.66 | Measured experimentally, see Table 1 | |
| G_IIc | 2.77 | Measured experimentally, see Table 1 | |
| CN | MPa/mm | 200,000 | CN = Eepoxy/δRRR, where Eepoxy is the Young’s modulus of epoxy matrix (~3650 MPa) and δRRR is the thickness of the interlaminar resin-rich region (typically within 0.01 and 0.10 mm). Thus, the lower and upper bounds for CN correspond to 36,500 MPa/mm and 365,000 MPa/mm, accordingly. This averages to 200,000 MPa/mm as an estimate for the CN parameter. |
| CT2CN | - | 0.37 | CT2CN = CT/CN = Gepoxy/Eepoxy = 1/2 × (1 + νepoxy), where Gepoxy and νepoxy are the shear modulus and the Poisson’s ratio (~0.35) of epoxy resin, correspondingly. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazemian, M.; Cherniaev, A. Prediction of Damage in Non-Crimp Fabric Composites Subjected to Transverse Crushing: A Comparison of Two Constitutive Models. J. Compos. Sci. 2022, 6, 224. https://doi.org/10.3390/jcs6080224
Kazemian M, Cherniaev A. Prediction of Damage in Non-Crimp Fabric Composites Subjected to Transverse Crushing: A Comparison of Two Constitutive Models. Journal of Composites Science. 2022; 6(8):224. https://doi.org/10.3390/jcs6080224
Chicago/Turabian StyleKazemian, Milad, and Aleksandr Cherniaev. 2022. "Prediction of Damage in Non-Crimp Fabric Composites Subjected to Transverse Crushing: A Comparison of Two Constitutive Models" Journal of Composites Science 6, no. 8: 224. https://doi.org/10.3390/jcs6080224
APA StyleKazemian, M., & Cherniaev, A. (2022). Prediction of Damage in Non-Crimp Fabric Composites Subjected to Transverse Crushing: A Comparison of Two Constitutive Models. Journal of Composites Science, 6(8), 224. https://doi.org/10.3390/jcs6080224







