Describing the Material Behavior of Steel and Carbon Fiber Reinforced Composites Using a Combined Damage-Plasticity Approach
Abstract
:1. Introduction
1.1. Challenges
1.2. Objective
- Development and implementation of a material model for the description of the mechanical material behavior of unidirectional metal fiber reinforced plastics.
- Application and validation of a description method for the mechanical behavior of SCFRP in the FEM.
- Experimental characterization of the mechanical material behavior of SCFRP with the aim of material model parameterization and validation of the numerical predictions.
2. Combining the MTL Model with a 1D Plasticity Model
2.1. 1D Plasticity Model
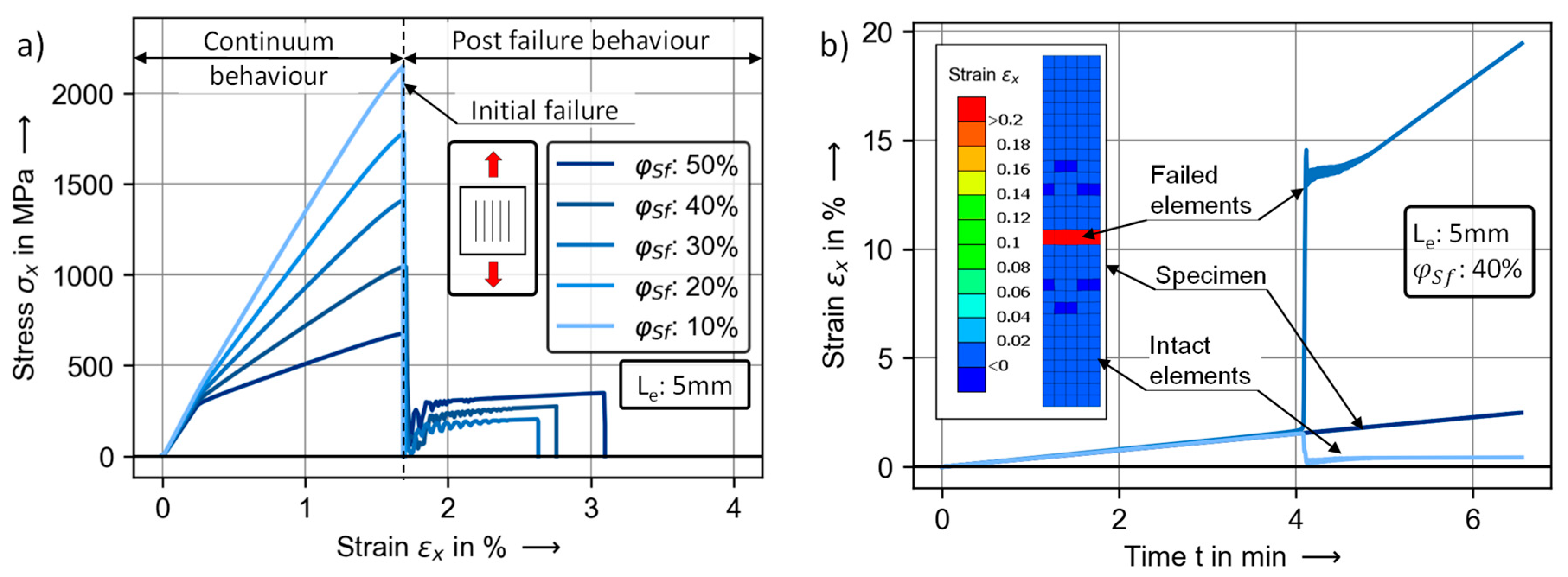
2.2. Damage Model
3. Experimental Work
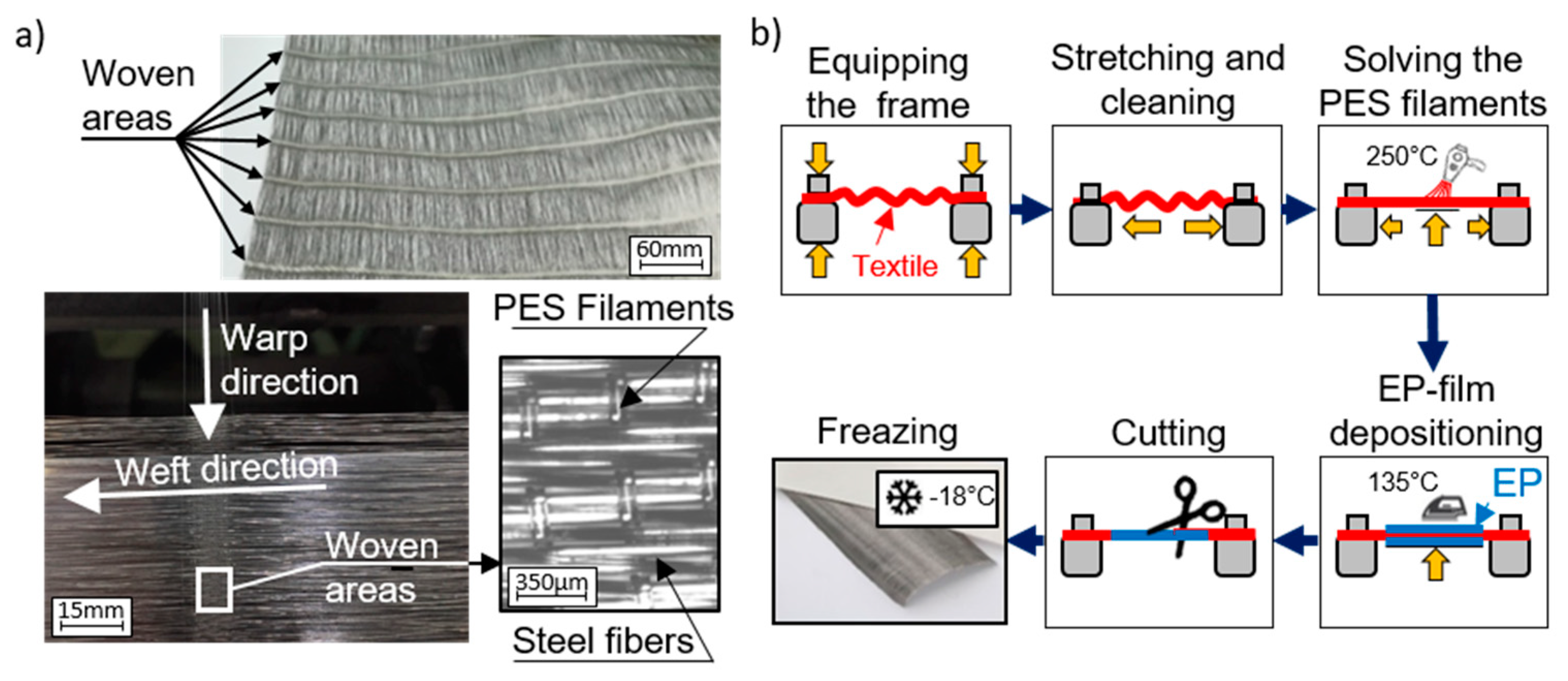
3.1. Laminate Manufacturing
3.2. Specimen Preparation and Test Setup
4. Numerical Predictions and Model Validation
- The numerical investigations were performed using the explicit solver LS-Dyna.
- The sample geometries were modeled with rectangular, fully integrated shell elements (LS-Dyna element type 16) [53]. The element size was varied as described in the following sections.
- The degrees of freedom of the nodes belonging to the shell elements were locked in the area of the fixed clamping, and a prescribed displacement was set in the area of the load introduction.
- In order to be able to determine a structural response comparable to the experimental results, force sensors in the cross section and displacement sensors were modeled at the clamping areas of the sample geometry.
- The mapping of the experimentally investigated laminate structures was carried out using the laminated shell strategy using the *PART_COMPOSITE method of LS-Dyna (see Figure 4).
- The material model *MAT_LAMINATED_COMPOSITE_FABRIC [53] implemented for LS-Dyna was used in combination with the failure criterion according to HASHIN [54] to represent the material behavior of CFRP layers. The material behavior of the SFRP layers was mapped with the material model described in chapter 2.
4.1. Material Model Parameterization
4.2. Prediction of the SCFRP Material Behavior in FEA
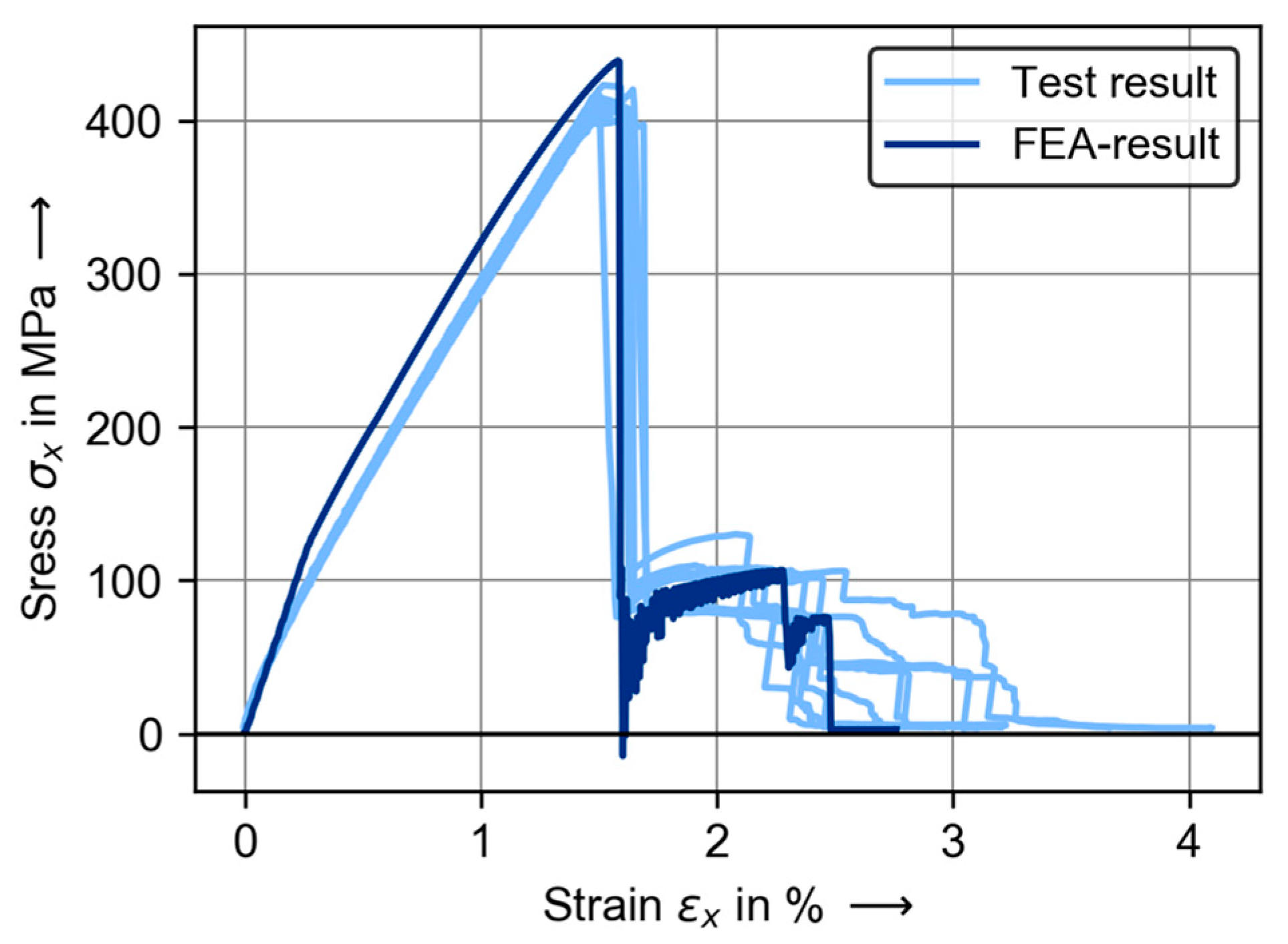
4.3. Validation of the Numerical Predictions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rao, S.; Daniel, I.M.; Gdoutos, E.E. Mechanical Properties and Failure Behavior of Cord/Rubber Composites. Appl. Compos. Mater. 2004, 11, 353–375. [Google Scholar] [CrossRef]
- Van den Abeele, F. Impact Damage Models for Steel Fibre Reinforced Composite Materials. Ph.D. Thesis, Universität Gent, Gent, Belgium, 2006. [Google Scholar]
- Meichsner, A.; Voll, N.; Maier, M. Experimentelle Und Numerische Untersuchung Des Deformations-Und Bruchverhaltens von Edelstahltextilverstärkten Kunststoffen Und LFT-Werkstoffen. Z. Kunstst. J. Plast. Technol. 2008, 5, 48–70. [Google Scholar]
- Schmeer, S.; Steeg, M.; Maier, M.; Mitschang, P. Metal Fibre Reinforced Composite–Potentialities and Tasks. Adv. Compos. Lett. 2009, 18, 096369350901800. [Google Scholar] [CrossRef] [Green Version]
- Hasselbruch, H.; Von Hehl, A.; Zoch, H.W. Properties and Failure Behavior of Hybrid Wire Mesh/Carbon Fiber Reinforced Thermoplastic Composites under Quasi-Static Tensile Load. Mater. Des. 2014, 66, 429–436. [Google Scholar] [CrossRef]
- Hannemann, B.; Backe, S.; Schmeer, S.; Balle, F.; Breuer, U.P. New Multifunctional Hybrid Polymer Composites Reinforced by Carbon and Steel Fibers. In Proceedings of the ICCM20, Copenhagen, Denmark, 19 July 2015. [Google Scholar]
- Lehmann, B.; Selvarayan, S.K.; Ghomeshi, R.; Gresser, G.T. Carbon Fiber Reinforced Composite–Toughness and Structural Integrity Enhancement by Integrating Surface Modified Steel Fibers. Mater. Sci. Forum 2015, 825–826, 32. [Google Scholar] [CrossRef]
- Mosleh, Y.; Clemens, D.; Gorbatikh, L.; Verpoest, I.; van Vuure, A.W. Penetration Impact Resistance of Novel Tough Steel Fibre-Reinforced Polymer Composites. J. Reinf. Plast. Compos. 2015, 34, 624–635. [Google Scholar] [CrossRef]
- Vanclooster, K.; Barburski, M.; Lomov, S.V.; Verpoest, I.; Deridder, F.; Lanckmans, F. Experimental Characterization of Steel Fibre Knitted Fabrics Deformability. Exp. Tech. 2015, 39, 16–22. [Google Scholar] [CrossRef]
- Breuer, U.P.; Hannemann, B.; Schmeer, S.; Balle, F.; Backe, S. Metal and Carbon—The Development of a New Multifuctional Material for Primary Structures. In Proceedings of the DLRK 2016, Brunswick, Germany, 13 September 2016. [Google Scholar]
- McBride, A.K.; Turek, S.L.; Zaghi, A.E.; Burke, K.A. Mechanical Behavior of Hybrid Glass/Steel Fiber Reinforced Epoxy Composites. Polymers 2017, 9, 151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brien, C.; Mcbride, A.; Zaghi, A.E.; Burke, K.; Hill, A. Mechanical Behavior of Stainless Steel Fiber-Reinforced Composites Exposed to Accelerated Corrosion. Materials 2017, 10, 772. [Google Scholar] [CrossRef] [Green Version]
- Swolfs, Y.; De Cuyper, P.; Callens, M.G.; Verpoest, I.; Gorbatikh, L. Hybridisation of Two Ductile Materials–Steel Fibre and Self-Reinforced Polypropylene Composites. Compos. Part. A Appl. Sci. Manuf. 2017, 100, 48–54. [Google Scholar] [CrossRef]
- Arun Prakash, V.R.; Jaisingh, S. Mechanical Strength Behaviour of Silane Treated E-Glass Fibre, Al-6061 and SS-304 Wire Mesh Reinforced Epoxy Resin Hybrid Composites. Def. Technol. 2018. [Google Scholar] [CrossRef]
- Backe, S.; Balle, F.; Hannemann, B.; Schmeer, S.; Breuer, U.P. Fatigue Properties of Multifunctional Metal- and Carbon-Fiber-Reinforced Polymers and Intrinsic Capabilities for Damage Monitoring. Fatigue Fract. Eng. Mater. Struct. 2018, 42, 143–151. [Google Scholar] [CrossRef] [Green Version]
- Truong, G.T.; Tran, H.; Choi, K.K. Tensile Behavior of On- and Off-Axis Carbon Fiber Reinforced Polymer Composites Incorporating Steel Wire Mesh. Mech. Mater. 2019, 137, 103131. [Google Scholar] [CrossRef]
- Hannemann, B. Multifunctional Metal-Carbon-Fibre Composites for Damage Tolerant and Electrically Conductive Lightweight Structures. Ph.D. Thesis, TU-Kaiserslautern, Kaiserslautern, Germany, 2017. [Google Scholar]
- Ahmed, T. Hybrid Composite Structures: Multifunctionality through Metal Fibres. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 2009. [Google Scholar]
- Hübler, M.; Nissle, S.; Gurka, M.; Breuer, U.P. Fiber-Reinforced Polymers with Integrated Shape Memory Alloy Actuation: An Innovative Actuation Method for Aerodynamic Applications. CEAS Aeronaut. J. 2016, 7, 567–576. [Google Scholar] [CrossRef]
- Gurka, M.; Nissle, S.; Hübler, M.; Kaiser, M. Active Vortex Generator Deployed on Demand by Active Hybrid Composites From Shape Memory Alloys and Fiber Reinforced Polymers. In Proceedings of the ASME 2017, Snowbird, UT, USA, 18 September 2017; p. V001T08A001. [Google Scholar]
- Nissle, S.; Gurka, M. Characterization of the Load Transfer between Fiber Reinforced Composites and Shape Memory Alloys for Active Hybrid Structures. In Proceedings of the ECCM18, Athens, Greece, 25–28 June 2018. [Google Scholar]
- Hannemann, B.; Backe, S.; Schmeer, S.; Balle, F.; Breuer, U.P. Improved Mechanical and Electrical Properties of CFRP Multiaxial Laminates by Embedded Metal Fibers. In Proceedings of the ECCM16, Sevilla, Spain, 22–26 June 2016. [Google Scholar]
- Bauer, C.; Hannemann, B.; Glatt, E.; Schmeer, S. Micromechanical Simulation of a Multifunctional Hybrid Composite with Continuous Steel and Carbon Fiber Reinforcement. In Proceedings of the ACCE, Detroit, MI, USA, 6 September 2017. [Google Scholar]
- Raju, B.; Hiremath, S.R.; Roy Mahapatra, D. A Review of Micromechanics Based Models for Effective Elastic Properties of Reinforced Polymer Matrix Composites. Compos. Struct. 2018, 204, 607–619. [Google Scholar] [CrossRef]
- Sabuncuoglu, B.; Orlova, S.; Gorbatikh, L.; Lomov, S.V.; Verpoest, I. Micro-Scale Finite Element Analysis of Stress Concentrations in Steel Fiber Composites under Transverse Loading. J. Compos. Mater. 2015, 49, 1057–1069. [Google Scholar] [CrossRef]
- Swolfs, Y.; McMeeking, R.M.; Verpoest, I.; Gorbatikh, L. The Effect of Fibre Dispersion on Initial Failure Strain and Cluster Development in Unidirectional Carbon/Glass Hybrid Composites. Compos. Part. A Appl. Sci. Manuf. 2015, 69, 279–287. [Google Scholar] [CrossRef] [Green Version]
- Utzig, L.; Karch, C.; Rehra, J.; Hannemann, B.; Schmeer, S. Modelling and Simulation of Effective Strength of Hybrid Polymer Composites Reinforced by Carbon and Steel Fibres. J. Mater. Sci. 2017, 53, 667–677. [Google Scholar] [CrossRef]
- Jalalvand, M.; Czél, G.; Wisnom, M.R. Damage Analysis of Pseudo-Ductile Thin-Ply UD Hybrid Composites—A New Analytical Method. Compos. Part. A Appl. Sci. Manuf. 2015, 69, 83–93. [Google Scholar] [CrossRef] [Green Version]
- Marom, G.; Fischer, S.; Tuler, F.R.; Wagner, H.D. Hybrid Effects in Composites: Conditions for Positive or Negative Effects versus Rule-of-Mixtures Behaviour. J. Mater. Sci. 1978, 13, 1419–1426. [Google Scholar] [CrossRef]
- Rehra, J.; Hannemann, B.; Schmeer, S.; Hausmann, J.; Breuer, U.P. Approach for an Analytical Description of the Failure Evolution of Continuous Steel and Carbon Fiber Hybrid Composites. Adv. Eng. Mater. 2019, 21, 1800565. [Google Scholar] [CrossRef]
- Swolfs, Y.; Gorbatikh, L.; Verpoest, I. Fibre Hybridisation in Polymer Composites: A Review. Compos. Part. A Appl. Sci. Manuf. 2014, 67, 181–200. [Google Scholar] [CrossRef]
- Wu, G.; Yang, J.M. Analytical Modelling and Numerical Simulation of the Nonlinear Deformation of Hybrid Fibre–Metal Laminates. Model. Simul. Mater. Sci. Eng. 2005, 13, 413. [Google Scholar] [CrossRef]
- Matthews, F.L.; Davies, G.A.O.; Hitchings, D.; Soutis, C. Finite Element Modelling of Composite Materials and Structures; Elsevier: Amsterdam, The Netherlands, 2000; ISBN 978-1-85573-892-8. [Google Scholar]
- Soden, P.D.; Kaddour, A.S.; Hinton, M.J. Recommendations for Designers and Researchers Resulting from the World-Wide Failure Exercise. Compos. Sci. Technol. 2004, 64, 589–604. [Google Scholar] [CrossRef]
- Kaddour, A.S.; Hinton, M.J. Benchmarking of Triaxial Failure Criteria for Composite Laminates: Comparison between Models of ‘Part (A)’ of ‘WWFE-II’. J. Compos. Mater. 2012, 46, 2595–2634. [Google Scholar] [CrossRef]
- Deuschle, H.M.; Puck, A. Application of the Puck Failure Theory for Fibre-Reinforced Composites under Three-Dimensional Stress: Comparison with Experimental Results. J. Compos. Mater. 2013, 47, 827–846. [Google Scholar] [CrossRef]
- Callens, M.G.; De Cuyper, P.; Swolfs, Y.; Gorbatikh, L.; Verpoest, I. Hybridization of Ductile Steel Fibre and Self-Reinforced Composites. In Proceedings of the 9th International Conference on Composite Science and Technology ICCST, Sorrento, Italy, 24–26 April 2013; pp. 24–26. [Google Scholar]
- Callens, M.G. Development of Ductile Stainless Steel Fibre Composites. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 2014. [Google Scholar]
- Gerberich, W.W. Fracture Mechanics of a Composite with Ductile Fibers. J. Mech. Phys. Solids 1971, 19, 71–87. [Google Scholar] [CrossRef]
- Chen, J.-F.; Morozov, E.V. A Consistency Elasto-Viscoplastic Damage Model for Progressive Failure Analysis of Composite Laminates Subjected to Various Strain Rate Loadings. Compos. Struct. 2016, 148, 224–235. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Y.; Ai, S.; He, C.; Tao, Y.; Yang, Y.; Fang, D. A Constitutive Model for Elastoplastic-Damage Coupling Effect of Unidirectional Fiber-Reinforced Polymer Matrix Composites. Compos. Part. A Appl. Sci. Manuf. 2020, 130, 105736. [Google Scholar] [CrossRef]
- Ge, J.; He, C.; Liang, J.; Chen, Y.; Fang, D. A Coupled Elastic-Plastic Damage Model for the Mechanical Behavior of Three-Dimensional (3D) Braided Composites. Compos. Sci. Technol. 2018, 157, 86–98. [Google Scholar] [CrossRef]
- Johnson, A.F.; Pickett, A.K.; Rozycki, P. Computational Methods for Predicting Impact Damage in Composite Structures. Compos. Sci. Technol. 2001, 61, 2183–2192. [Google Scholar] [CrossRef] [Green Version]
- Ladeveze, P.; LeDantec, E. Damage Modelling of the Elementary Ply for Laminated Composites. Compos. Sci. Technol. 1992, 43, 257–267. [Google Scholar] [CrossRef]
- Ren, R.; Le, G.; Zhong, J.; Ma, D.; He, Q. Numerical Research on Elasto-Plastic Behaviors of Fiber-Reinforced Polymer Based Composite Laminates. Compos. Struct. 2019, 207, 364–372. [Google Scholar] [CrossRef]
- Xiao, X. A Coupled Damage-Plasticity Model for Energy Absorption in Composite. Int. J. Damage Mech. 2010, 19, 727–751. [Google Scholar] [CrossRef]
- Matzenmiller, A.; Lubliner, J.; Taylor, R.L. A Constitutive Model for Anisotropic Damage in Fiber-Composites. Mech. Mater. 1995, 20, 125–152. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters. Available online: https://digital.library.unt.edu/ark:/67531/metadc54697/ (accessed on 10 December 2020).
- Ziegler, H. A Modification of Prager’s Hardening Rule. Quart. Appl. Math. 1959, 17, 55–65. [Google Scholar] [CrossRef] [Green Version]
- Schweizerhof, K.; Weimar, K.; Münz, T.; Rottner, T. Crashworthiness Analysis with Enhanced Composite Material Models in LS-DYNA- Merits and Limits. Available online: http://www.dynasupport.com/howtos/material/composite-models/composite_paper.pdf (accessed on 10 December 2020).
- Galántai, A. The Theory of Newton’s Method. J. Comput. Appl. Math. 2000, 124, 25–44. [Google Scholar] [CrossRef] [Green Version]
- Kühn, F.; Rehra, J.; May, D.; Schmeer, S.; Mitschang, P. Dry Fiber Placement of Carbon/Steel Fiber Hybrid Preforms for Multifunctional Composites. Adv. Manuf. Polym. Compos. Sci. 2019, 5, 37–49. [Google Scholar] [CrossRef]
- Hallquist, J.O. LS-DYNA Theory Manual-March 2006. 680. Available online: https://www.lstc.com/dynamat/pdfs/mat_104_theory.pdf (accessed on 20 July 2022).
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]






| Label | Stacking Sequence | Microstructure | ||
|---|---|---|---|---|
| L = longitudinal; T = transvers; S = shear; UD = unidirectional; MD = multidirectional; 20, 30 or 45 = steel fiber volume fraction | sf = steel fiber; cf = carbon fiber; = middle symmetric ply | ) | ) | ) |
| SFRP_UD_L | 58.92 vol.% | 0 vol.% | 41.08 vol.% | |
| SFRP_UD_T | 59.48 vol.% | 0 vol.% | 40.52 vol.% | |
| SFRP_SL_S | 59.73 vol.% | 0 vol.% | 40.27 vol.% | |
| CFRP_UD_L | 0 vol.% | 61.49 vol.% | 38.51 vol.% | |
| CFRP_UD_T | 0 vol.% | 62.35 vol.% | 37.75 vol.% | |
| CFRP_SL_S | 0 vol.% | 60.16 vol.% | 39.84 vol.% | |
| SCFRP_UD_30 | 32.50 vol.% | 28.35 vol.% | 39.15 vol.% | |
| SCFRP_UD_45 | 45.39 vol.% | 18.40 vol.% | 36.21 vol.% | |
| SCFRP_MD_20 | 18.36 vol.% | 40.89 vol.% | 40.75 vol.% | |
| Label | Feasible Tests | Related Standard | Specimen Size (W × H × T) | Gauge Length | Test Speed | Purpose |
|---|---|---|---|---|---|---|
| SFRP_L | 8 | DIN EN ISO 527-5 | 250 × 15 × 1 | 150 | 4 mm/min | Parametrization of the SFRP-Model |
| SFRP_T | 9 | DIN EN 2597 | 150 × 10 × 2 | 50 | 2 mm/min | |
| SFRP_S | 8 | EN ISO 14,129 | 250 × 25 × 2 | 150 | 4 mm/min | |
| CFRP_L | 8 | DIN EN ISO 527 | 250 × 15 × 1 | 150 | 2 mm/min | Parametrization of the CFRP-Model |
| CFRP_T | 9 | DIN EN 2597 | 150 × 10 × 2 | 50 | 2 mm/min | |
| CFRP_S | 10 | EN ISO 14,129 | 250 × 25 × 2 | 150 | 4 mm/min | |
| SCFRP_UD30 | 10 | DIN EN ISO 527-5 | 150 × 15 × 1 | 50 | 2 mm/min | Validation of the unidirectional prediction |
| SCFRP_UD45 | 10 | DIN EN ISO 527-5 | 150 × 15 × 1 | 50 | 2 mm/min | |
| SCFRP_MD | 10 | DIN EN ISO 527-4 | 250 × 15 × 2 | 150 | 2 mm/min | Validation of the multidirectional prediction |
| Label | Result Type | in GPa | in GPa | in GPa | in MPa | in MPa | in MPa | in % | in % |
|---|---|---|---|---|---|---|---|---|---|
| SFRP | Test | 90.3 ± 5.4 | 12.4 ± 0.28 | 3.68 ± 0.09 | 462 ± 64 | 21.9 ± 2.7 | 51.8 ± 0.42 | 20.6 ± 2.8 | 0.19 ± 0.04 |
| Fitting | 93.7 | 12.95 | 3.7 | 428.8 | 25.7 | 54.2 | 19.3 | 0.24 | |
| CFRP | Test | 141.5 ± 4.8 | 9.1 ± 0.94 | 4.43 ± 0.14 | 2312 ± 112 | 76.5 ± 5.6 | 79.5 ± 1.5 | 1.5 ± 0.04 | 1.01 ± 0.17 |
| Fitting | 145.8 | 9.31 | 4.8 | 2550.13 | 78.6 | 73.8 | 1.58 | 1.12 |
| Label | Result Type | in GPa | in MPa | in MPa | in % | in MPa | in % | in MPa |
|---|---|---|---|---|---|---|---|---|
| SCFRP UD30 | Test | 109.4 ± 0.02 | 224.1 ± 18.9 | 1540 ± 10.9 | 1.68 ± 0.03 | 131.3 ± 8.7 | 11.9 ± 3.9 | 23.46 ± 3.7 |
| FEA | 110.65 | 270.45 | 1635.45 | 1.58 | 119.73 | 11.2 | 22.85 | |
| SCFRP UD45 | Test | 97.8 ± 0.08 | 195.1 ± 18.9 | 912.4 ± 10.9 | 1.75 ± 0.09 | 266.6 ± 30.9 | 17.8 ± 2.9 | 47.81 ± 9.8 |
| FEA | 98.54 | 210.64 | 970.35 | 1.58 | 261.95 | 7.41 | 32.47 |
| Label | Result Type | in GPa | in MPa | in MPa | in % | in MPa | in % | in MPa |
|---|---|---|---|---|---|---|---|---|
| SCFRP MD20 | Test | 40.12 ± 1.06 | 81.5 ± 7.06 | 412.2 ± 6.59 | 1.52 ± 0.05 | 85 ± 8.52 | 3.14 ± 0.45 | 0.88 ± 0.33 |
| FEA | 45.15 | 120.56 | 425.79 | 1.5 | 98.53 | 2.51 | 0.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehra, J.; Andriß, C.; Schmeer, S.; Breuer, U.P. Describing the Material Behavior of Steel and Carbon Fiber Reinforced Composites Using a Combined Damage-Plasticity Approach. J. Compos. Sci. 2022, 6, 235. https://doi.org/10.3390/jcs6080235
Rehra J, Andriß C, Schmeer S, Breuer UP. Describing the Material Behavior of Steel and Carbon Fiber Reinforced Composites Using a Combined Damage-Plasticity Approach. Journal of Composites Science. 2022; 6(8):235. https://doi.org/10.3390/jcs6080235
Chicago/Turabian StyleRehra, Jan, Christian Andriß, Sebastian Schmeer, and Ulf P. Breuer. 2022. "Describing the Material Behavior of Steel and Carbon Fiber Reinforced Composites Using a Combined Damage-Plasticity Approach" Journal of Composites Science 6, no. 8: 235. https://doi.org/10.3390/jcs6080235
APA StyleRehra, J., Andriß, C., Schmeer, S., & Breuer, U. P. (2022). Describing the Material Behavior of Steel and Carbon Fiber Reinforced Composites Using a Combined Damage-Plasticity Approach. Journal of Composites Science, 6(8), 235. https://doi.org/10.3390/jcs6080235








