Influence of Thermal and Thermomechanical Stimuli on Dental Restoration Geometry and Material Properties of Cervical Restoration: A 3D Finite Element Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. FE Model Generation
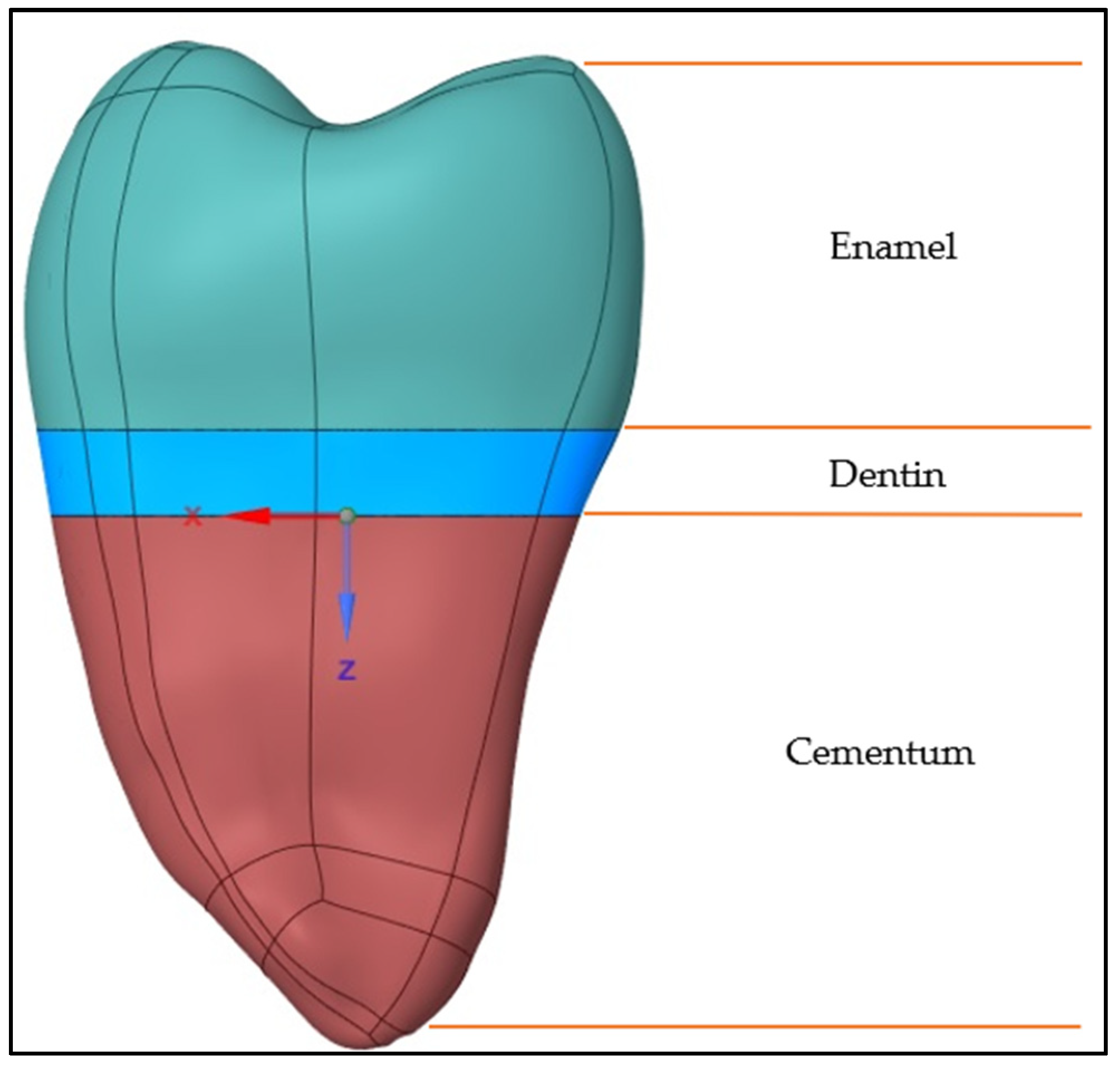
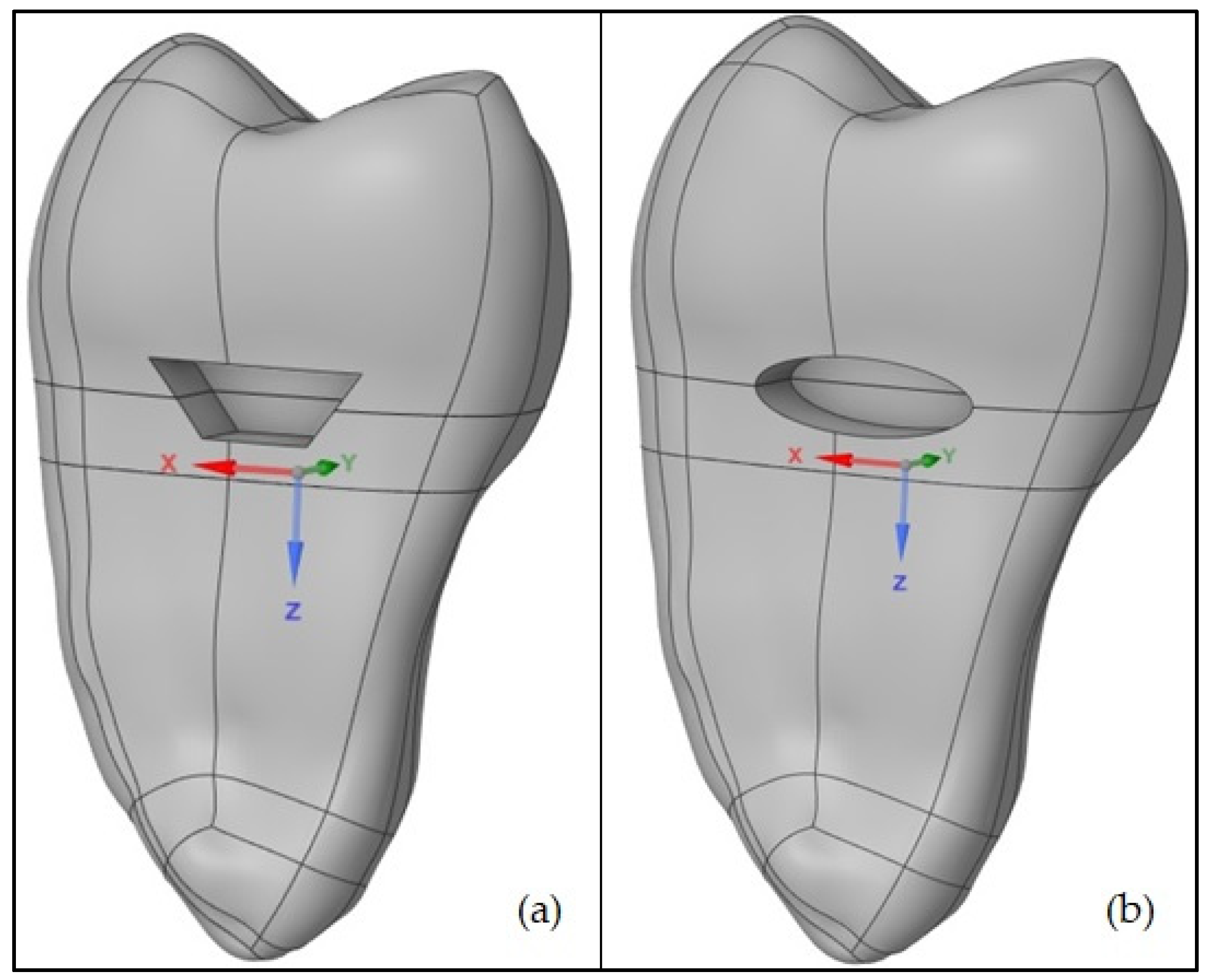
2.2. Cervical Cavity of a Premolar Tooth
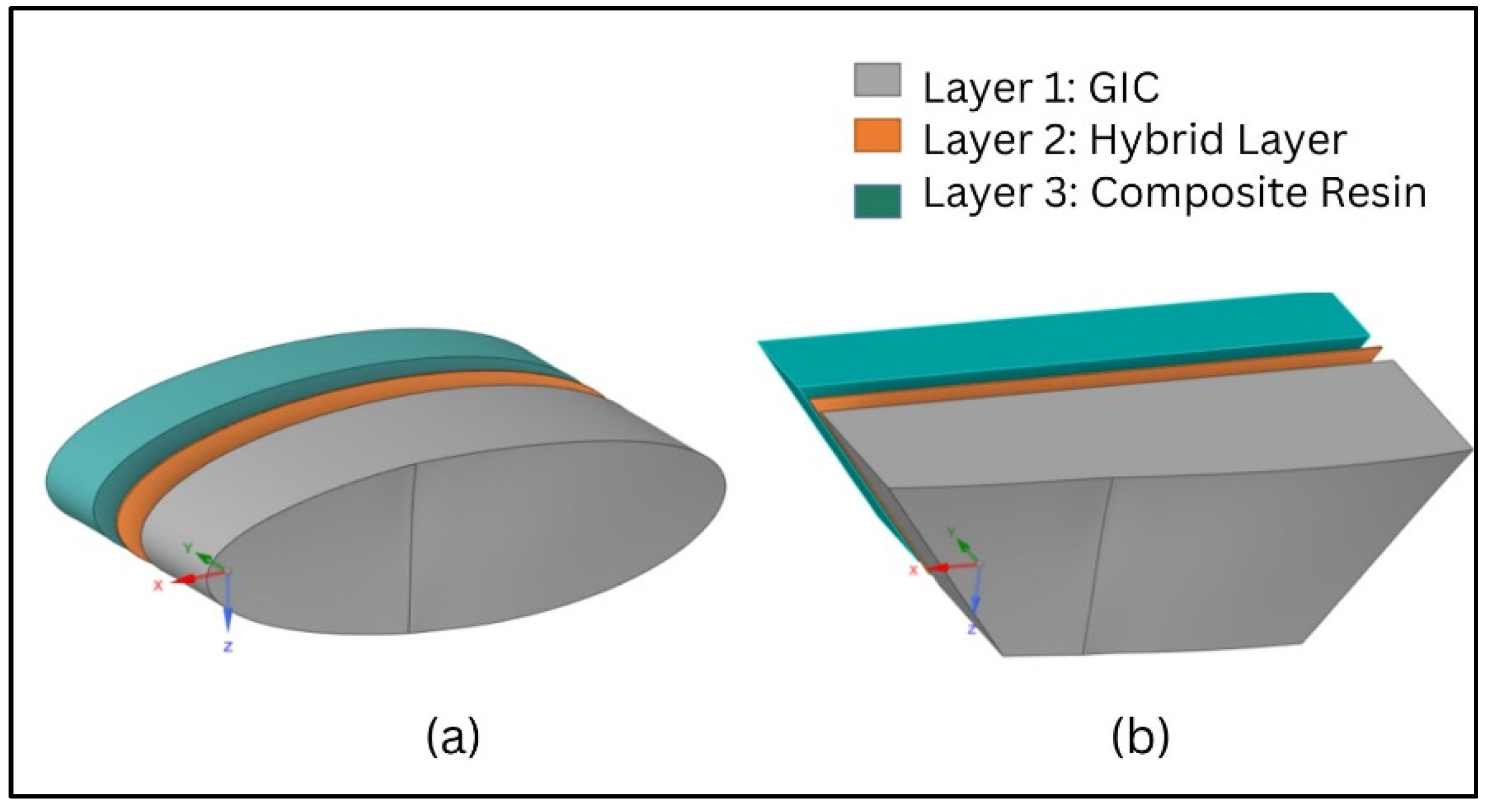
2.3. Material Properties
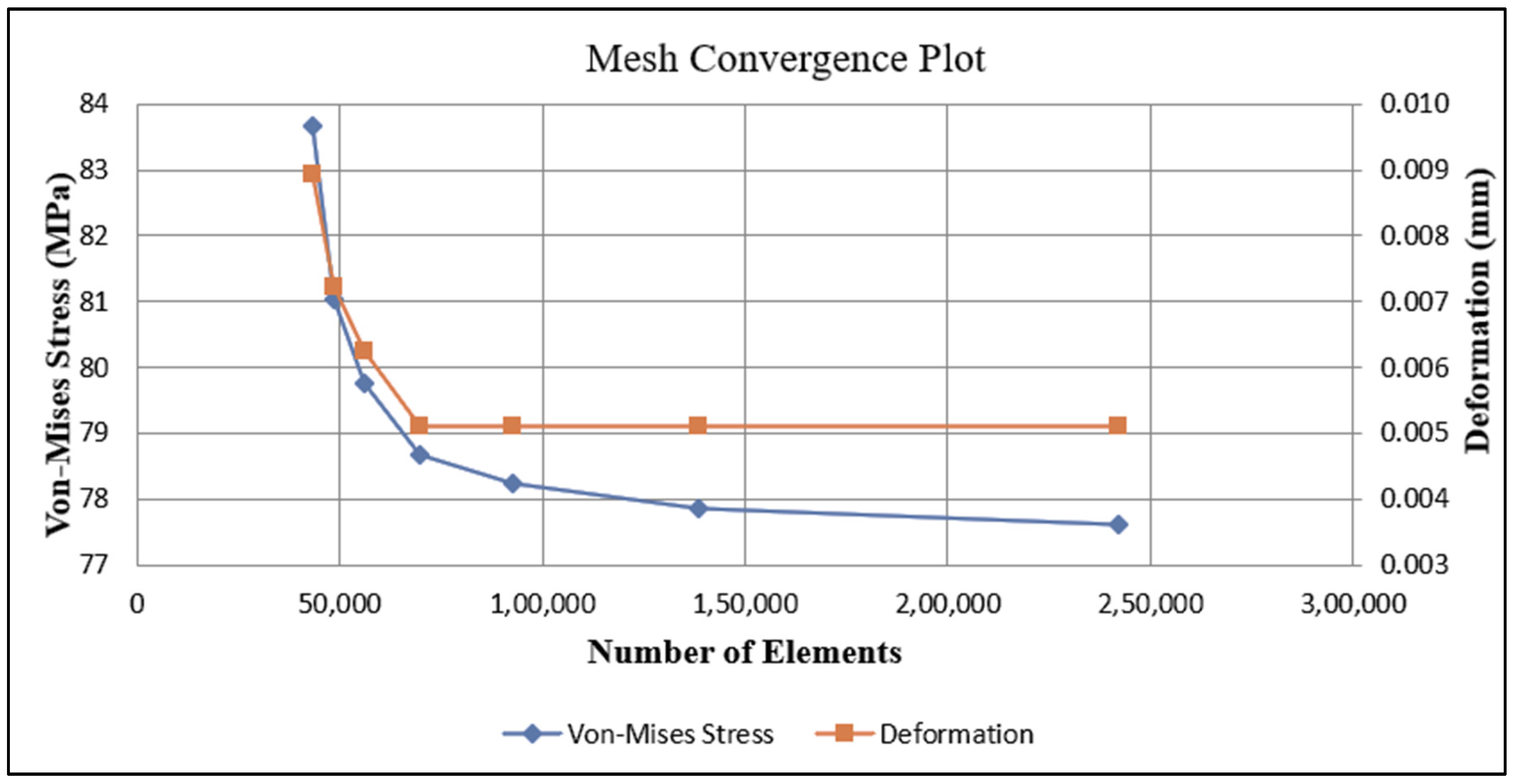
2.4. Meshing
3. Results
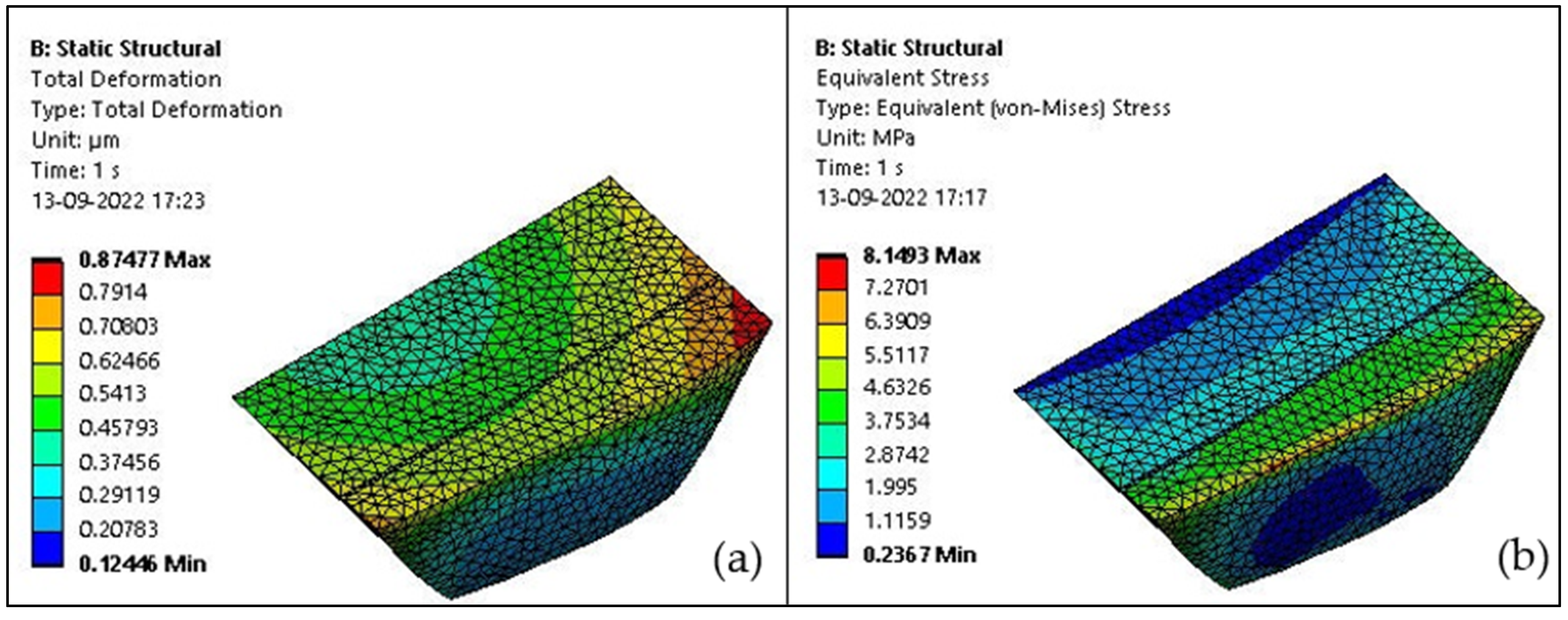
3.1. Thermal Analysis on Trapezoidal Cavity at 5 °C
3.2. Thermal Analysis on Trapezoidal Cavity at 55 °C
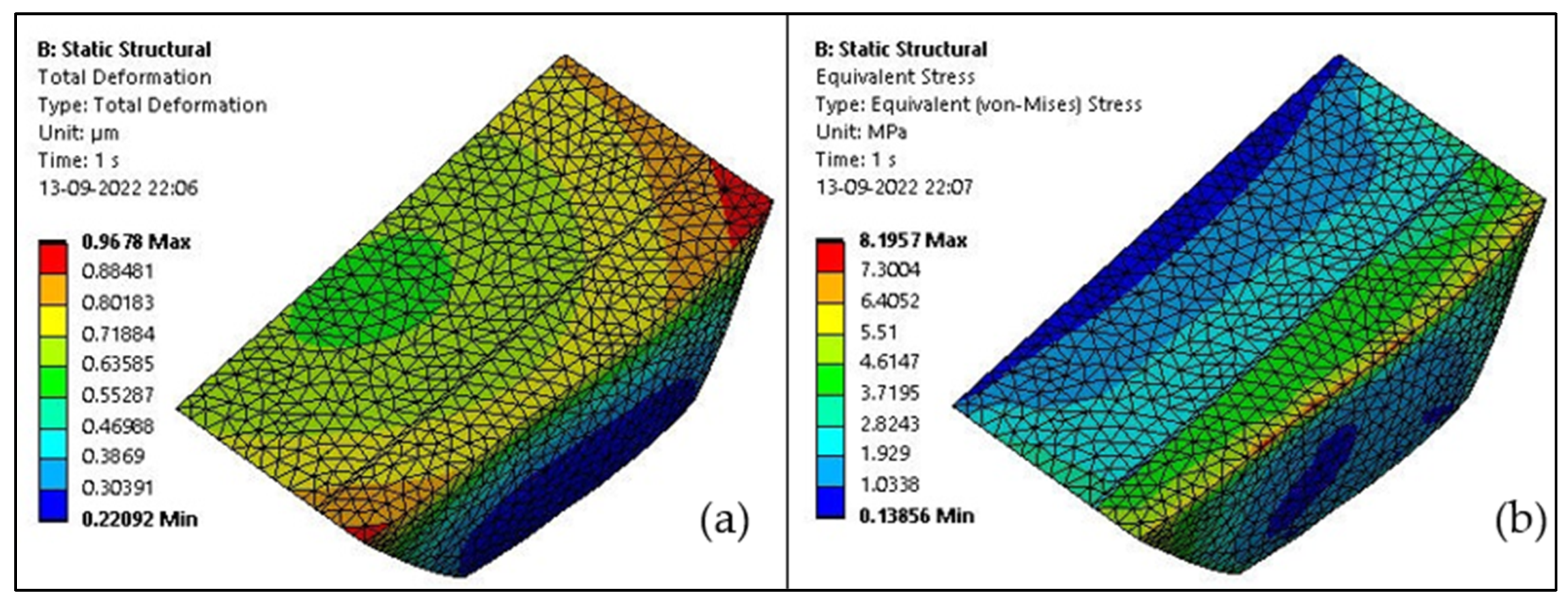
3.3. Thermomechanical Analysis on a Trapezoidal Cavity at 5 °C
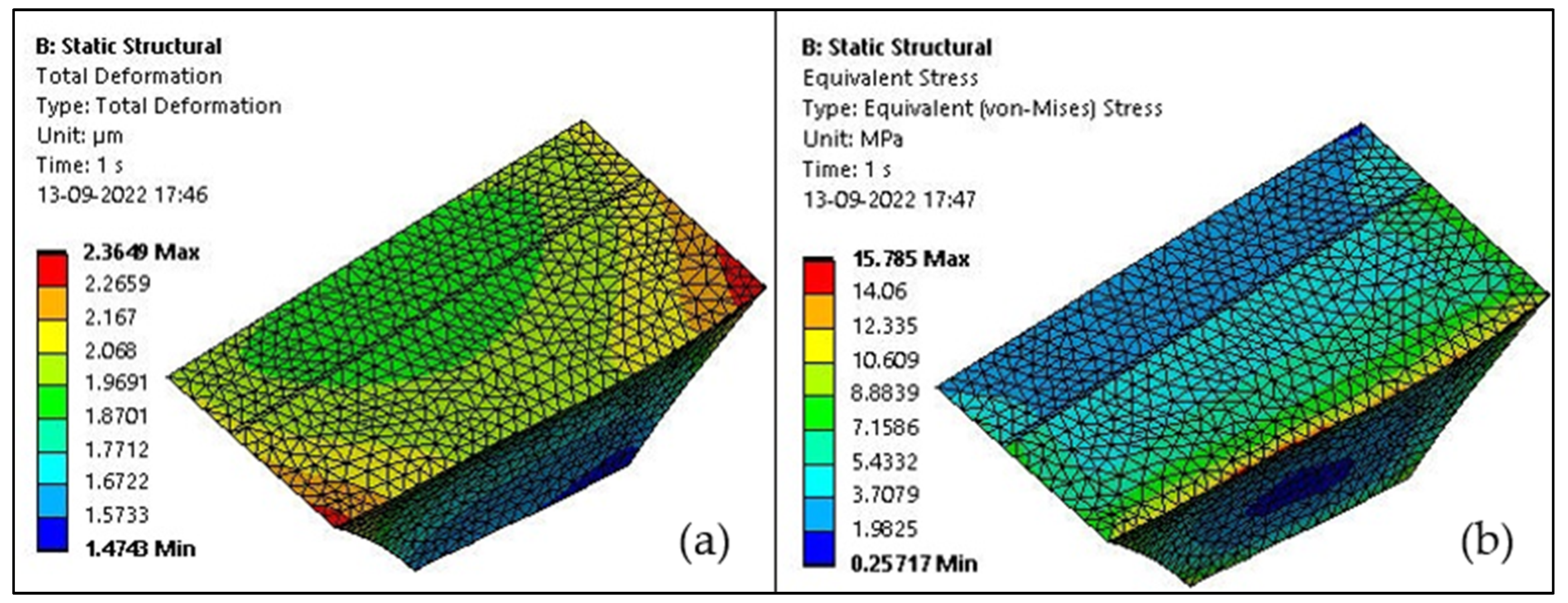
3.4. Thermomechanical Analysis on a Trapezoidal Cavity at 55 °C
3.5. Thermal Analysis on Elliptical Cavity at 5 °C
3.6. Thermal Analysis on Elliptical Cavity at 55 °C
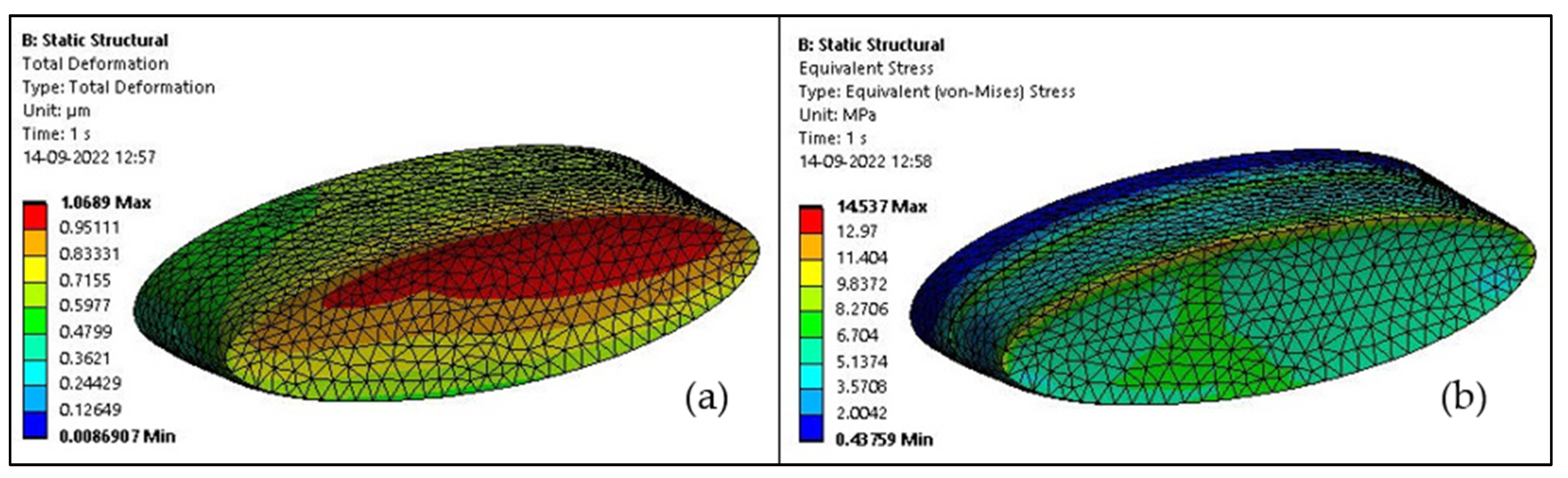
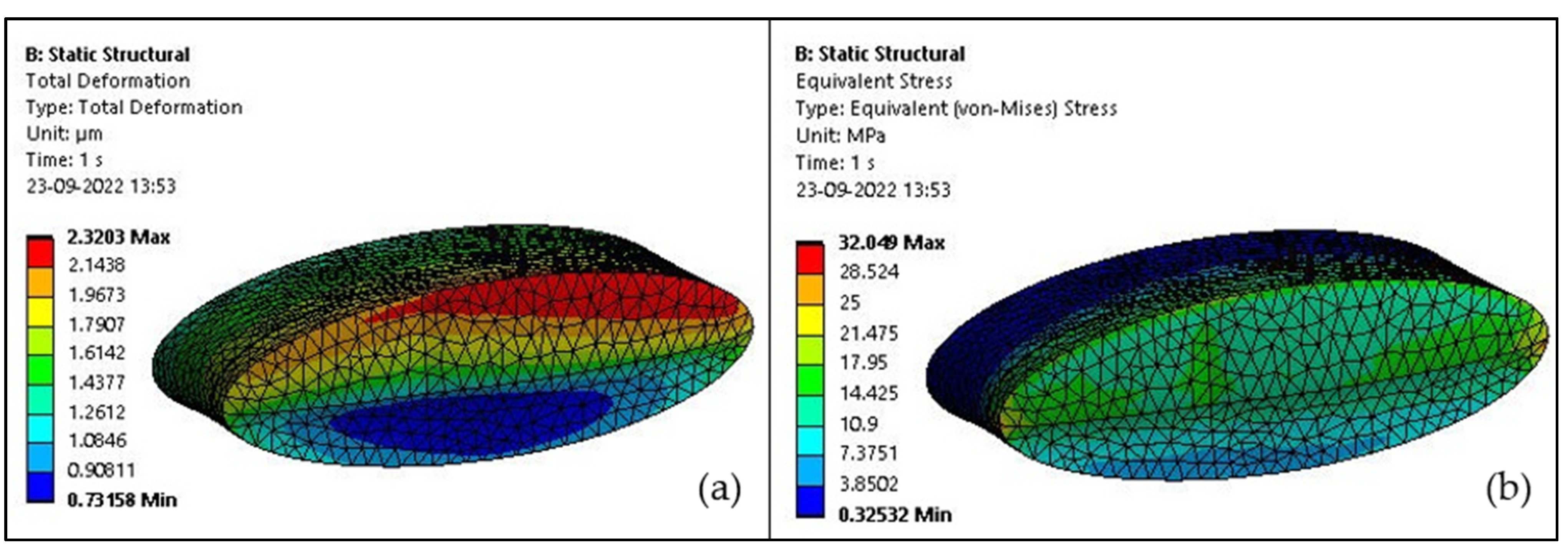
3.7. Thermomechanical Analysis on Elliptical Cavity at 5 °C
3.8. Thermomechanical Analysis on Elliptical Cavity at 55 °C
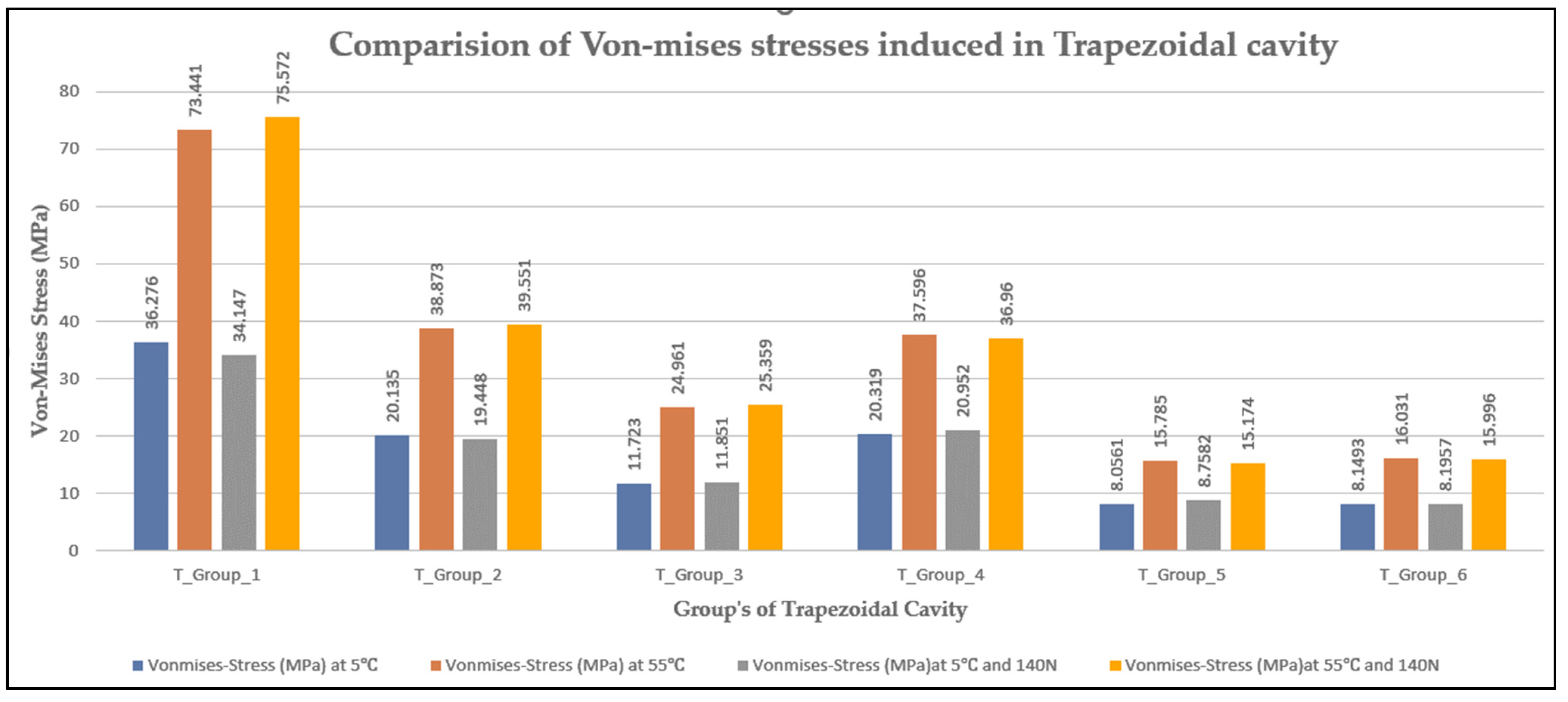
3.9. Comparison of von Mises Stresses and Deformation in Trapezoidal Cavity Restoration
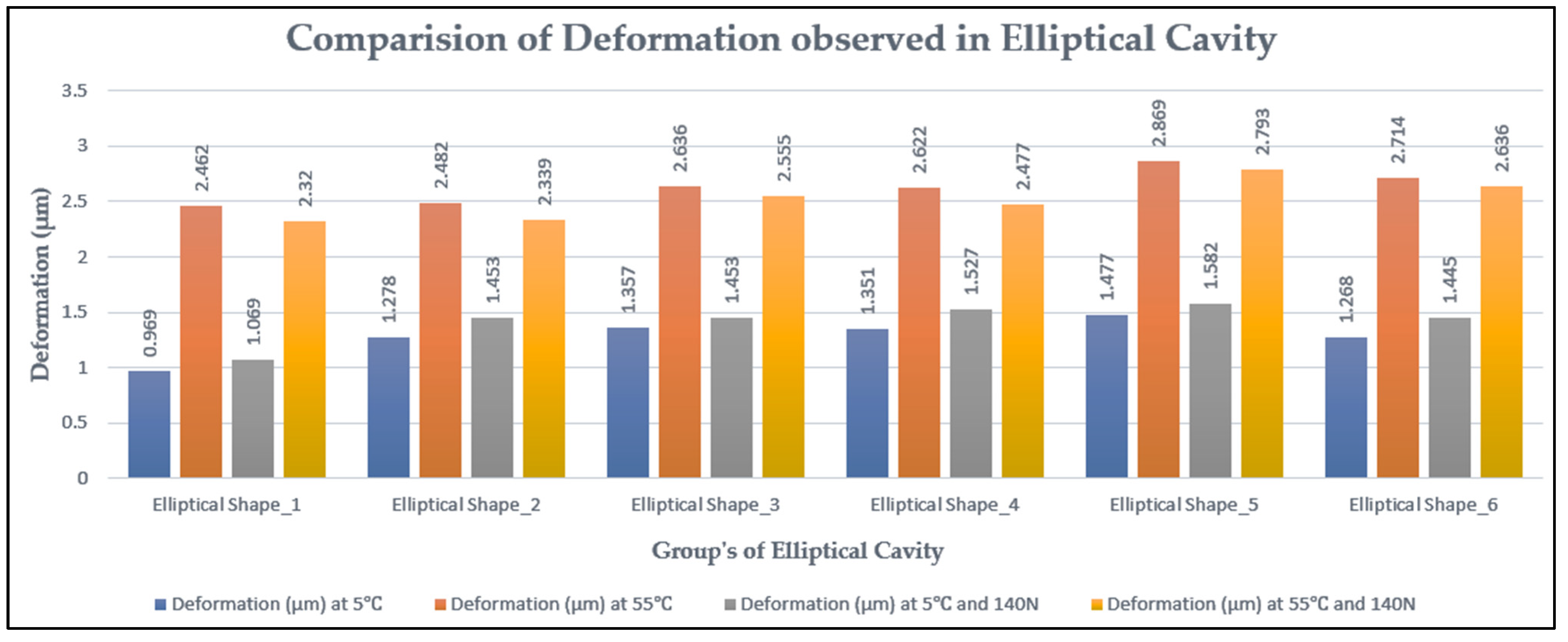
3.10. Comparison of von Mises Stresses and Deformation in Elliptical Cavity Restoration
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pai, S.; Nayak, N.; Awasthi, S.; Acharya, S.R.; Bhat, V.; Patil, V. Effect of thickness of various restorative materials and hybrid layer on stress distribution of direct cervical restorations of teeth using a three-dimensional structural finite element analysis. Eng. Sci. 2021, 16, 281–287. [Google Scholar] [CrossRef]
- Cakici, E.B.; Guler, M.S.; Guler, C.; Cakici, F.; Sen, S. Finite element analysis of thermal stress distribution in different restorative materials used in class V cavities. Niger. J. Clin. Pract. 2016, 19, 30. [Google Scholar] [CrossRef] [PubMed]
- Sen, D.; Patil, V.; Smriti, K.; Varchas, P.; Ratnakar, R.; Naik, N.; Kumar, S.; Saxena, J.; Kapoor, S. Nanotechnology and Nanomaterials in Dentistry: Present and Future Perspectives in Clinical Applications. Eng. Sci. 2022, 20, 14–24. [Google Scholar] [CrossRef]
- Babaei, B.; Shouha, P.; Birman, V.; Farrar, P.; Prentice, L.; Prusty, G. The effect of dental restoration geometry and material properties on biomechanical behaviour of a treated molar tooth: A 3D finite element analysis. J. Mech. Behav. Biomed. Mater. 2022, 125, 104892. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-Y.; Kim, B.-S.; Kim, H.; Cho, S.-Y. Occlusal Stress Distribution and remaining crack propagation of a cracked tooth treated with different materials and designs: 3D finite element analysis. Dent. Mater. 2021, 37, 731–740. [Google Scholar] [CrossRef] [PubMed]
- Browning, W.D.; Brackett, W.W.; Gilpatrick, R.O. Two-year clinical comparison of a microfilled and a hybrid resin-based composite in non-carious Class V lesions. Oper. Dent. 2000, 25, 46–50. [Google Scholar] [PubMed]
- Palmer, D.S.; Barco, M.T.; Billy, E.J. Temperature extremes produced orally by hot and cold liquids. J. Prosthet. Dent. 1992, 67, 325–327. [Google Scholar] [CrossRef]
- Toparli, M.; Gokay, N.; Aksoy, T. An investigation of temperature and stress distribution on a restored maxillary second premolar tooth using a three-dimensional finite element method. J. Oral Rehabil. 2000, 27, 1077–1081. [Google Scholar] [CrossRef]
- Jiang, W.; Bo, H.; YongChun, G.; LongXing, N. Stress distribution in molars restored with inlays or onlays with or without endodontic treatment: A three-dimensional finite element analysis. J. Prosthet. Dent. 2010, 103, 6–12. [Google Scholar] [CrossRef]
- Moeen, F.; Nisar, S.; Dar, N. A step by step guide to finite element analysis in dental implantology. Pak. Oral Dent J. 2014, 34, 164–169. [Google Scholar]
- Gateau, P.; Sabek, M.; Dailey, B. In vitro fatigue resistance of glass ionomer cements used in post-and-coreapplications. J. Prosthet. Dent. 2001, 86, 149–155. [Google Scholar] [CrossRef] [PubMed]
- Ausiello, P.; Franciosa, P.; Martorelli, M.; Watts, D.C. Numerical Fatigue 3D-FE modeling of indirect composite-restored posterior teeth. Dent. Mater. 2011, 27, 423–430. [Google Scholar] [CrossRef] [PubMed]
- Korioth, T.W.; Versluis, A. Modeling the mechanical behavior of the jaws and their related structures by finite element (FE) analysis. Crit. Rev. Oral Biol. Med. 1997, 8, 90–104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ye, Q.; Spencer, P. Analyses of material-tissue interfaces by Fourier transform infrared, Raman spectroscopy, and chemometrics. In Material-Tissue Interfacial Phenomena; Woodhead Publishing: Sawston, UK, 2017; pp. 231–251. [Google Scholar]
- Belli, S.; Eskitaşcio, G.; Eraslan, O.; Senawongse, P.; Tagami, J. Effect of hybrid layer on stress distribution in a premolar tooth restored with composite or ceramic inlay: An FEM study. J. Biomed. Mater. Res. Part B Appl. Biomater. 2005, 74, 665–668. [Google Scholar] [CrossRef] [PubMed]
- Valin Rivera, J.L.; Gonçalves, E.; Vinicius Soares, P.; Milito, G.; Ricardo Perez, J.O.; Palacios Roque, G.F.; Valin Fernández, M.; Figueredo Losada, H.; Araújo Pereira, F.; Garcia del Pino, G.; et al. The Restored Premolars Biomechanical Behavior: FEM and Experimental Moiré Analyses. Appl. Sci. 2022, 12, 6768. [Google Scholar] [CrossRef]
- Eliguzeloglu, E.; Eraslan, O.; Omurlu, H.; Eskitascıoglu, G.; Belli, S. Effect of hybrid layer and thickness on stress distribution of cervical wedge-shaped restorations. Eur. J. Dent. 2010, 4, 160–165. [Google Scholar] [CrossRef] [Green Version]
- Sundfeld, R.H.; Valentino, T.A.; de Alexandre, R.S.; Briso, A.L.F.; Sundefeld, M.L.M.M. Hybrid layer thickness and resin tag length of a self-etching adhesive bonded to sound dentin. J. Dent. 2005, 33, 675–681. [Google Scholar] [CrossRef]
- Sorrentino, R.; Aversa, R.; Ferro, V.; Auriemma, T.; Zarone, F.; Ferrari, M.; Apicella, A. Three-dimensional finite element analysis of strain and stress distributions in endodontically treated maxillary central incisors restored with different post, core and crown materials. Dent Mater. 2007, 23, 983–993. [Google Scholar] [CrossRef]
- Aykul, H.; Toparli, M.; Dalkiz, M. A calculation of stress distribution in metal-porcelain crowns by using three-dimensional finite element method. J. Oral Rehabil. 2002, 29, 381–386. [Google Scholar] [CrossRef]
- Yang, H.-S.; Lang, L.A.; Guckes, A.D.; Felton, D.A. The effect of thermal change on various dowel-and-core restorative materials. J. Prosthet. Dent. 2001, 86, 74–80. [Google Scholar] [CrossRef]
- Toparli, M.; Aykul, H.; Sasaki, S. Temperature and thermal stress analysis of a crowned maxillary second premolar tooth using three-dimensional finite element method. J. Oral Rehabil. 2002, 30, 99–105. [Google Scholar] [CrossRef] [PubMed]
- Anusavice, K.J.; Hojjatie, B. Influence of incisal length of ceramic and loading orientation on stress distribution in ceramic crowns. J. Dent. Res. 1988, 67, 1371–1375. [Google Scholar] [CrossRef] [PubMed]
- Gulec, L.; Ulusoy, N. Effect of endocrown restorations with different CAD/CAM materials: 3D finite element and Weibull analyses. BioMed Res. Int. 2017, 2017, 5638683. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nabih, S.M.; Ibrahim, N.I.; Elmanakhly, A.R. Mechanical and thermal stress analysis of hybrid ceramic and lithium disilicate based ceramic CAD-cam inlays using 3-D Finite Element Analysis. Braz. Dent. Sci. 2021, 24, 1–10. [Google Scholar] [CrossRef]
- Yin, R.; Kim, Y.-K.; Jang, Y.-S.; Lee, J.-J.; Lee, M.-H.; Bae, T.-S. Comparative evaluation of the mechanical properties of CAD/CAM dental blocks. Odontology 2019, 107, 360–367. [Google Scholar] [CrossRef]
- Lin, C.-L.; Chang, C.-H.; Ko, C.-C. Multifactorial analysis of a mod restored human premolar using auto-mesh finite element approach. J. Oral Rehabil. 2001, 28, 576–585. [Google Scholar] [CrossRef]
- Ausiello, P.; Apicella, A.; Davidson, C.L. Effect of adhesive layer properties on stress distribution in composite restorations—A 3D finite element analysis. Dent. Mater. 2002, 18, 295–303. [Google Scholar] [CrossRef]
- Rees, J.S.; Hammadeh, M.; Jagger, D.C. Abfraction lesion formation in maxillary incisors, canines and premolars: A finite element study. Eur. J. Oral Sci. 2003, 111, 149–154. [Google Scholar] [CrossRef]
- Federlin, M.; Krifka, S.; Herpich, M.; Hiller, K.-A.; Schmalz, G. Partial ceramic crowns: Influence of ceramic thickness, preparation design and luting material on fracture resistance and marginal integrity in vitro. Oper. Dent. 2007, 32, 251–260. [Google Scholar] [CrossRef]
- Dejak, B.; Mlotkowski, A. Three-dimensional finite element analysis of strength and adhesion of composite resin versus ceramic inlays in molars. J. Prosthet. Dent. 2008, 99, 131–140. [Google Scholar] [CrossRef]
- Güler, M.S. Evaluation of stress distribution of different restorative materials in class V cavities. Atatürk Üniversitesi Diş Hekim. Fakültesi Derg. 2019, 28, 518–523. [Google Scholar] [CrossRef]
- Kotousov, A.; Kahler, B.; Swain, M. Analysis of interfacial fracture in dental restorations. Dent. Mater. 2011, 27, 1094–1101. [Google Scholar] [CrossRef]
- Bai, K.; Zhang, T.H.; Yang, Z.Y.; Song, F.; Yang, X.D.; Wang, K. Anisotropic, gradient and metal-like mechanical behaviors of teeth and their implications on tooth functions. Chin. Sci. Bull. 2007, 52, 2310–2315. [Google Scholar] [CrossRef] [Green Version]
- Singh, V.; Misra, A.; Marangos, O.; Park, J.; Ye, Q.; Kieweg, S.L.; Spencer, P. Fatigue life prediction of dentin–adhesive interface using micromechanical stress analysis. Dent. Mater. 2011, 27, e187–e195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yahyazadehfar, M.; Ivancik, J.; Majd, H.; An, B.; Zhang, D.; Arola, D. On the mechanics of fatigue and fracture in teeth. Appl. Mech. Rev. 2014, 66, 030803. [Google Scholar] [CrossRef] [PubMed]
- Sharma, D.; Kudva, V.; Patil, V.; Kudva, A.; Bhat, R.S. A Convolutional Neural Network Based Deep Learning Algorithm for Identification of Oral Precancerous and Cancerous Lesion and Differentiation from Normal Mucosa: A Retrospective Study. Eng. Sci. 2022, 18, 278–287. [Google Scholar] [CrossRef]
- Prabhu, N.; Shetty, D.K.; Naik, N.; Shetty, N.; Kalpesh Parmar, Y.; Patil, V.; Sooriyaperakasam, N. Application of finite element analysis to evaluate optimal parameters for bone/tooth drilling to avoid thermal necrosis. Cogent Eng. 2021, 8, 1876582. [Google Scholar] [CrossRef]






| Materials | Young’s Modulus of Elasticity (GPa) | Poisson’s Ratio | Thermal Expansion Coefficient (1/°C) | Thermal Conductivity (W/m °C) |
|---|---|---|---|---|
| Enamel | 80 | 0.33 | 11 × 10−6 | 0.84 |
| Dentin | 20 | 0.31 | 11.4 × 10−6 | 0.63 |
| Cementum | 13.7 | 0.3 | 10 × 10−6 | 5.8 |
| Hybrid Layer | 7.7 | 0.3 | 39 × 10−6 | 2.61 |
| Composite Resin | 15 | 0.24 | 34 × 10−6 | 1.26 |
| Glass Ionomer Cement | 10.8 | 0.3 | 35 × 10−6 | 0.615 |
| Groups | The Thickness of Layers of Restorative Materials | ||
|---|---|---|---|
| Glass Ionomer Cement (mm) | Hybrid Layer (mm) | Composite Resin (mm) | |
| Group 1 | 1 | 0.03 | 2 |
| Group 2 | 2 | 0.03 | 1 |
| Group 3 | 1.5 | 0.03 | 1.5 |
| Group 4 | 1.5 | 0.06 | 1.5 |
| Group 5 | 1 | 0.06 | 2 |
| Group 6 | 2 | 0.06 | 1 |
| Elements | von Mises Stress (MPa) | Deformation (mm) | % Change | Outer Body Element Size (mm) | Restorative Material Element Size (mm) | Temperature (°C) | Load (N) |
|---|---|---|---|---|---|---|---|
| 242,118 | 77.621 | 0.005 | −2.667 | 0.4 | 0.2 | 55 | 140 |
| 138,530 | 77.864 | 0.005 | −1.040 | 0.5 | 0.2 | 55 | 140 |
| 92,594 | 78.225 | 0.005 | −0.581 | 0.6 | 0.2 | 55 | 140 |
| 69,607 | 78.682 | 0.00512 | 0 | 0.7 | 0.2 | 55 | 140 |
| 56,325 | 79.748 | 0.006 | 1.355 | 0.8 | 0.2 | 55 | 140 |
| 48,533 | 81.026 | 0.007 | 2.979 | 0.9 | 0.2 | 55 | 140 |
| 43,347 | 83.676 | 0.009 | 6.347 | 1 | 0.2 | 55 | 140 |
| Shape | Thermal Loading | |
|---|---|---|
| 5 °C | ||
| Trapezoidal | Deformation (μm) | von Mises Stress (MPa) |
| Group 1 | 2.369 | 36.276 |
| Group 2 | 1.077 | 20.135 |
| Group 3 | 0.899 | 11.723 |
| Group 4 | 0.879 | 20.319 |
| Group 5 | 0.869 | 8.758 |
| Group 6 | 0.874 | 8.149 |
| Shape | Thermal Loading | |
|---|---|---|
| 55 °C | ||
| Trapezoidal | Deformation (μm) | von Mises Stress (MPa) |
| Group 1 | 5.209 | 73.441 |
| Group 2 | 2.797 | 38.873 |
| Group 3 | 2.526 | 24.961 |
| Group 4 | 2.466 | 37.596 |
| Group 5 | 2.368 | 16.031 |
| Group 6 | 2.364 | 15.785 |
| Shape | Thermomechanical Loading | |
|---|---|---|
| 5 °C and 140 N | ||
| Trapezoidal | Deformation (μm) | von Mises Stress (MPa) |
| Group 1 | 2.471 | 34.147 |
| Group 2 | 1.166 | 19.448 |
| Group 3 | 0.988 | 11.851 |
| Group 4 | 0.097 | 20.952 |
| Group 5 | 0.978 | 8.758 |
| Group 6 | 0.967 | 8.196 |
| Shape | Thermomechanical Loading | |
|---|---|---|
| 55 °C and 140 N | ||
| Trapezoidal | Deformation (μm) | von Mises Stress (MPa) |
| Group 1 | 5.123 | 75.572 |
| Group 2 | 2.69 | 39.551 |
| Group 3 | 2.429 | 25.359 |
| Group 4 | 2.367 | 36.96 |
| Group 5 | 2.293 | 15.996 |
| Group 6 | 2.191 | 15.174 |
| Shape | Thermal Loading | |
|---|---|---|
| 5 °C | ||
| Elliptical | Deformation (μm) | von Mises Stress (MPa) |
| Group 1 | 0.969 | 14.657 |
| Group 2 | 1.278 | 18.418 |
| Group 3 | 1.357 | 18.207 |
| Group 4 | 1.351 | 17.999 |
| Group 5 | 1.477 | 27.899 |
| Group 6 | 1.268 | 16.655 |
| Shape | Thermal Loading | |
|---|---|---|
| 55 °C | ||
| Elliptical | Deformation (μm) | von Mises Stress (MPa) |
| Group 1 | 2.462 | 32.331 |
| Group 2 | 2.482 | 35.753 |
| Group 3 | 2.636 | 35.343 |
| Group 4 | 2.622 | 34.94 |
| Group 5 | 2.869 | 54.156 |
| Group 6 | 2.714 | 41.283 |
| Shape | Thermomechanical Loading | |
|---|---|---|
| 5 °C and 140 N | ||
| Elliptical | Deformation (μm) | von Mises Stress (MPa) |
| Group 1 | 1.069 | 14.537 |
| Group 2 | 1.453 | 18.876 |
| Group 3 | 1.453 | 18.497 |
| Group 4 | 1.527 | 18.719 |
| Group 5 | 1.582 | 28.886 |
| Group 6 | 1.445 | 17.23 |
| Shape | Thermomechanical Loading | |
|---|---|---|
| 55 °C and 140 N | ||
| Elliptical | Deformation (μm) | von Mises Stress (MPa) |
| Group 1 | 2.320 | 32.049 |
| Group 2 | 2.339 | 35.479 |
| Group 3 | 2.555 | 35.068 |
| Group 4 | 2.477 | 34.236 |
| Group 5 | 2.793 | 54.206 |
| Group 6 | 2.636 | 37.049 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma Uppangala, R.; Pai, S.; Patil, V.; Smriti, K.; Naik, N.; Shetty, R.; Gunasekar, P.; Jain, A.; Tirupathi, J.; Hiremath, P.; et al. Influence of Thermal and Thermomechanical Stimuli on Dental Restoration Geometry and Material Properties of Cervical Restoration: A 3D Finite Element Analysis. J. Compos. Sci. 2023, 7, 6. https://doi.org/10.3390/jcs7010006
Sharma Uppangala R, Pai S, Patil V, Smriti K, Naik N, Shetty R, Gunasekar P, Jain A, Tirupathi J, Hiremath P, et al. Influence of Thermal and Thermomechanical Stimuli on Dental Restoration Geometry and Material Properties of Cervical Restoration: A 3D Finite Element Analysis. Journal of Composites Science. 2023; 7(1):6. https://doi.org/10.3390/jcs7010006
Chicago/Turabian StyleSharma Uppangala, Rohan, Swathi Pai, Vathsala Patil, Komal Smriti, Nithesh Naik, Raviraj Shetty, Pranesh Gunasekar, Amritanshu Jain, Jeswanthi Tirupathi, Pavan Hiremath, and et al. 2023. "Influence of Thermal and Thermomechanical Stimuli on Dental Restoration Geometry and Material Properties of Cervical Restoration: A 3D Finite Element Analysis" Journal of Composites Science 7, no. 1: 6. https://doi.org/10.3390/jcs7010006
APA StyleSharma Uppangala, R., Pai, S., Patil, V., Smriti, K., Naik, N., Shetty, R., Gunasekar, P., Jain, A., Tirupathi, J., Hiremath, P., Patil, S., & Rathnakar, R. (2023). Influence of Thermal and Thermomechanical Stimuli on Dental Restoration Geometry and Material Properties of Cervical Restoration: A 3D Finite Element Analysis. Journal of Composites Science, 7(1), 6. https://doi.org/10.3390/jcs7010006








