Study of the Structural, Electrical, and Mechanical Properties and Morphological Features of Y-Doped CeO2 Ceramics with Porous Structure
Abstract
:1. Introduction
2. Experimental Section
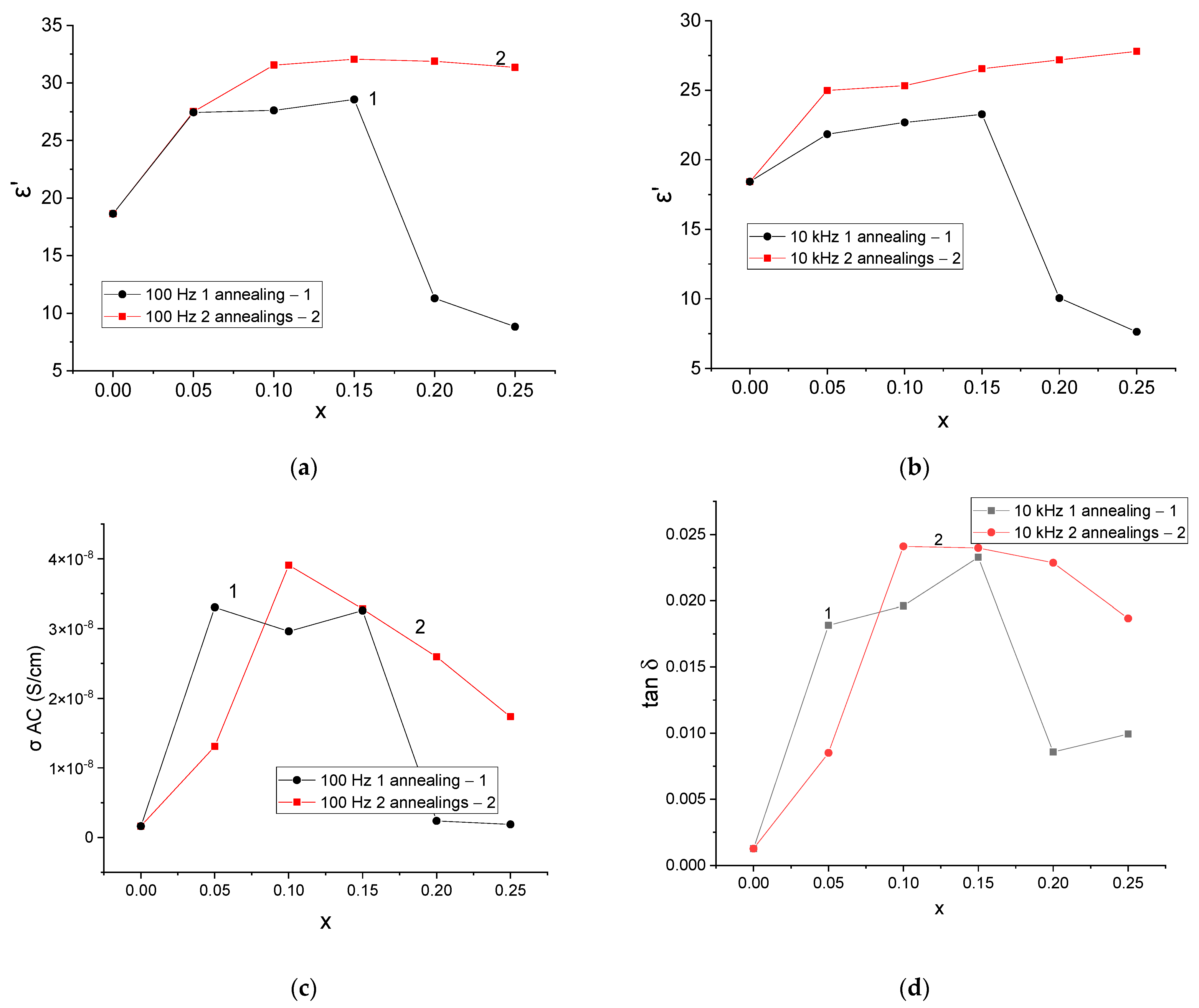
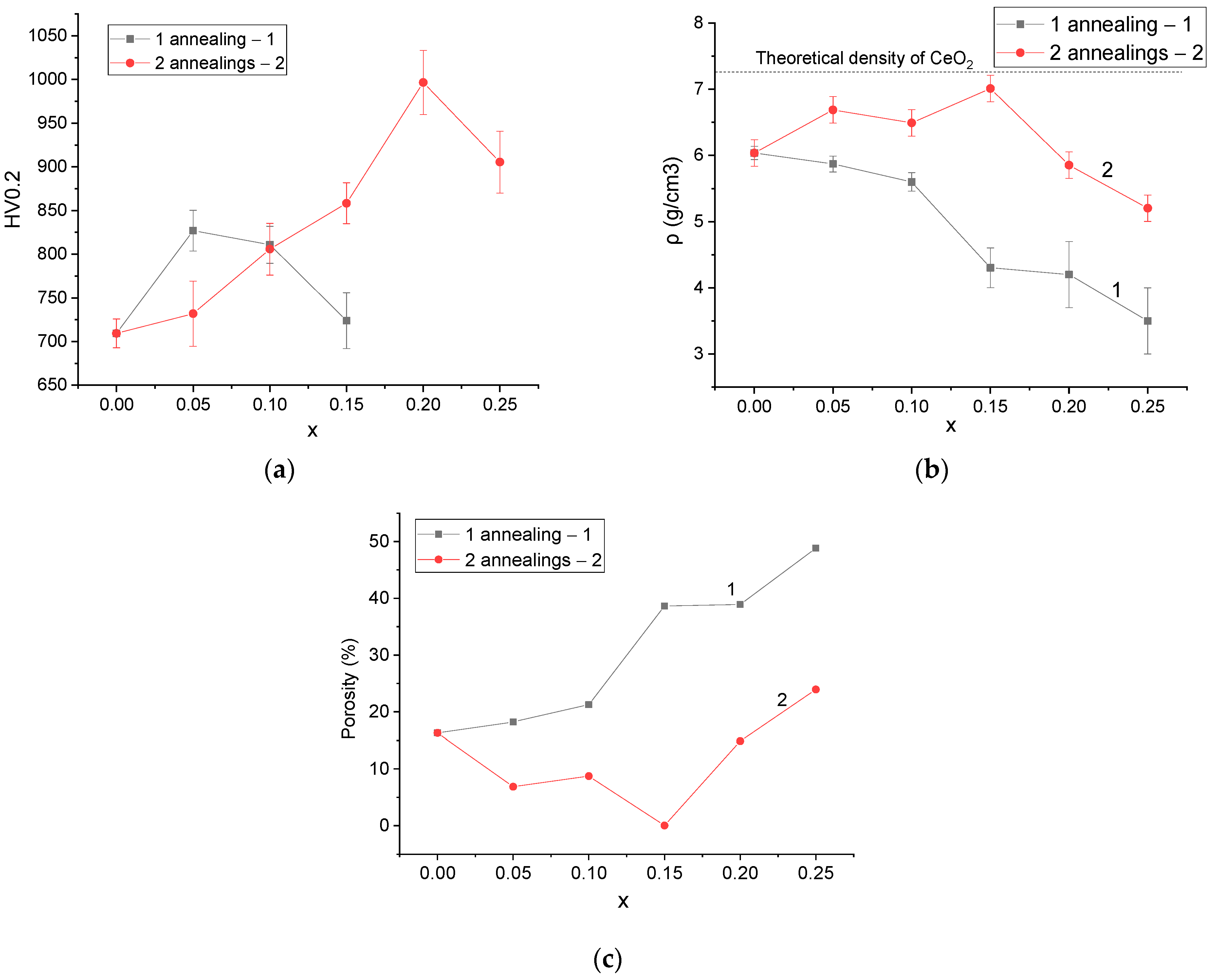
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Middleburgh, S.C.; Lee, W.E.; Rushton, M.J.D. Ceramics in the nuclear fuel cycle. In Advanced Ceramics for Energy Conversion and Storage; Guillon, O., Ed.; Elsevier Series on Advanced Ceramic Materials; Woodhead Publishing Limited: Sawston, UK, 2019; ISBN 978-0-08-102784-4. [Google Scholar]
- Mistarihi, Q.M.; Raj, V.; Kim, J.H.; Ryu, H.J. Thermal Conductivity of Mo-Reinforced ZrO2 Composites Fabricated by Spark Plasma Sintering for Inert Matrix Fuels. Mater. Des. 2017, 134, 476–485. [Google Scholar] [CrossRef]
- Degueldre, C.; Paratte, J.M. Concepts for an Inert Matrix Fuel, an Overview. J. Nucl. Mater. 1999, 274, 1–6. [Google Scholar] [CrossRef]
- Momin, N.; Manjanna, J.; Kobayashi, S.; Aruna, S.T.; Senthil Kumar, S.; Nayaka, G.P. Synthesis and Ionic Conductivity of Calcium-Doped Ceria Relevant to Solid Oxide Fuel Cell Applications. Mater. Adv. 2022, 3, 8780–8791. [Google Scholar] [CrossRef]
- Meng, Q.-L.; Lee, C.; Ishihara, T.; Kaneko, H.; Tamaura, Y. Reactivity of CeO2-Based Ceramics for Solar Hydrogen Production via a Two-Step Water-Splitting Cycle with Concentrated Solar Energy. Int. J. Hydrogen Energy 2011, 36, 13435–13441. [Google Scholar] [CrossRef]
- Choi, J.; Yeon, J.H.; Yook, S.H.; Shin, S.; Kim, J.Y.; Choi, M.; Jang, S. Multifunctional Nafion/CeO2 Dendritic Structures for Enhanced Durability and Performance of Polymer Electrolyte Membrane Fuel Cells. ACS Appl. Mater. Interfaces 2021, 13, 806–815. [Google Scholar] [CrossRef]
- Nelson, A.T.; Rittman, D.R.; White, J.T.; Dunwoody, J.T.; Kato, M.; McClellan, K.J. An Evaluation of the Thermophysical Properties of Stoichiometric CeO2 in Comparison to UO2 and PuO2. J. Am. Ceram. Soc. 2014, 97, 3652–3659. [Google Scholar] [CrossRef]
- Suzuki, K.; Kato, M.; Sunaoshi, T.; Uno, H.; Carvajal-Nunez, U.; Nelson, A.T.; McClellan, K.J. Thermal and Mechanical Properties of CeO2. J. Am. Ceram. Soc. 2018, 102, 1994–2008. [Google Scholar] [CrossRef]
- Frieß, F.; Liebert, W. Inert-Matrix Fuel for Transmutation: Selected Mid- and Long-Term Effects on Reprocessing, Fuel Fabrication and Inventory Sent to Final Disposal. Prog. Nucl. Energy 2022, 145, 104106. [Google Scholar] [CrossRef]
- Kozlovskiy, A.L.; Zdorovets, M.V.; Shlimas, D.I. Study of the Morphological and Structural Features of Inert Matrices Based on ZrO2–CeO2 Doped with Y2O3 and the Effect of Grain Sizes on the Strength Properties of Ceramics. Metals 2022, 12, 1687. [Google Scholar] [CrossRef]
- Zhang, T.; Ma, J.; Kong, L.; Chan, S.; Kilner, J. Aging Behavior and Ionic Conductivity of Ceria-Based Ceramics: A Comparative Study. Solid State Ion. 2004, 170, 209–217. [Google Scholar] [CrossRef]
- Eguchi, K.; Setoguchi, T.; Inoue, T.; Arai, H. Electrical Properties of Ceria-Based Oxides and Their Application to Solid Oxide Fuel Cells. Solid State Ion. 1992, 52, 165–172. [Google Scholar] [CrossRef]
- Zhao, K.; Du, Y. Calcium-Doped Ceria Materials for Anode of Solid Oxide Fuel Cells Running on Methane Fuel. J. Power Sources 2017, 347, 79–85. [Google Scholar] [CrossRef]
- Grover, V.; Tyagi, A.K. Phase Relations, Lattice Thermal Expansion in CeO2–Gd2O3 System, and Stabilization of Cubic Gadolinia. Mater. Res. Bull. 2004, 39, 859–866. [Google Scholar] [CrossRef]
- Nakajima, A.; Yoshihara, A.; Ishigame, M. Defect-Induced Raman Spectra in doped CeO2. Phys. Rev. B 1994, 50, 13297–13307. [Google Scholar] [CrossRef]
- Mandal, B.P.; Grover, V.; Roy, M.; Tyagi, A.K. X-ray Diffraction and Raman Spectroscopic Investigation on the Phase Relations in Yb2O3- and Tm2O3-Substituted CeO2. J. Am. Ceram. Soc. 2007, 90, 2961–2965. [Google Scholar] [CrossRef]
- Souza, E.C.C.; Brito, H.F.; Muccillo, E.N.S. Optical and Electrical Characterization of Samaria-Doped Ceria. J. Alloys Compd. 2010, 491, 460–464. [Google Scholar] [CrossRef]
- Bhosale, R.R.; Takalkar, G.; Sutar, P.; Kumar, A.; AlMomani, F.; Khraisheh, M. A Decade of Ceria Based Solar Thermochemical H2O/CO2 Splitting Cycle. Int. J. Hydrogen Energy 2019, 44, 34–60. [Google Scholar] [CrossRef]
- Melchionna, M.; Trovarelli, A.; Fornasiero, P. Synthesis and properties of cerium oxide-based materials. In Cerium Oxide (CeO2): Synthesis, Properties and Applications; Scire, S., Palmisano, L., Eds.; Metal Oxides Series; Elsevier Science: Amsterdam, The Netherlands, 2019; ISBN 978-0-12-815662-9. [Google Scholar]
- Doebelin, N.; Kleeberg, R. Profex: A Graphical User Interface for the Rietveld Refinement programBGMN. J. Appl. Crystallogr. 2015, 48, 1573–1580. [Google Scholar] [CrossRef]
- Burbano, M.; Norberg, S.T.; Hull, S.; Eriksson, S.G.; Marrocchelli, D.; Madden, P.A.; Watson, G.W. Oxygen Vacancy Ordering and the Conductivity Maximum in Y2O3-Doped CeO2. Chem. Mater. 2011, 24, 222–229. [Google Scholar] [CrossRef]
- Kim, N.; Stebbins, J.F. Vacancy and Cation Distribution in Yttria-Doped Ceria: An 89Y and 17O MAS NMR Study. Chem. Mater. 2007, 19, 5742–5747. [Google Scholar] [CrossRef]
- Sánchez-Santolino, G.; Salafranca, J.; Pantelides, S.T.; Pennycook, S.J.; León, C.; Varela, M. Localization of Yttrium Segregation within YSZ Grain Boundary Dislocation Cores. Phys. Status Solidi A 2018, 215, 1800349. [Google Scholar] [CrossRef]
- Nath, D.; Singh, F.; Das, R. X-ray Diffraction Analysis by Williamson-Hall, Halder-Wagner and Size-Strain Plot Methods of CdSe Nanoparticles- a Comparative Study. Mater. Chem. Phys. 2020, 239, 122021. [Google Scholar] [CrossRef]
- Rupp, J.L.M.; Infortuna, A.; Gauckler, L.J. Microstrain and Self-Limited Grain Growth in Nanocrystalline Ceria Ceramics. Acta Mater. 2006, 54, 1721–1730. [Google Scholar] [CrossRef]
- Kurian, M.; Kunjachan, C. Investigation of Size Dependency on Lattice Strain of Nanoceria Particles Synthesised by Wet Chemical Methods. Int. Nano Lett. 2014, 4, 73–80. [Google Scholar] [CrossRef]
- Tholkappiyan, R.; Vishista, K. Combustion Synthesis of Mg–Er Ferrite Nanoparticles: Cation Distribution and Structural, Optical, and Magnetic Properties. Mater. Sci. Semicond. Process. 2015, 40, 631–642. [Google Scholar] [CrossRef]
- Rahaman, M.N. Sintering of Ceramics; CRC Press: Boca Raton, FL, USA, 2007; ISBN 978-0-8493-7286-5. [Google Scholar]
- Boch, P.; Leriche, A. Sintering and microstructure of ceramics. In Ceramic Materials: Processes, Properties, and Applications; Boch, P., Ni, J.C., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. ImageJ2: ImageJ for the next Generation of Scientific Image Data. BMC Bioinform. 2017, 18, 529. [Google Scholar] [CrossRef]
- Mochizuki, S. Infrared Optical Properties of Cerium Dioxide. Phys. Status Solidi B 1982, 114, 189–199. [Google Scholar] [CrossRef]
- Shimanouchi, T.; Tsuboi, M.; Miyazawa, T. Optically Active Lattice Vibrations as Treated by the GF-Matrix Method. J. Chem. Phys. 1961, 35, 1597–1612. [Google Scholar] [CrossRef]
- Daniel, M.; Loridant, S. Probing Reoxidation Sites Byin situ Raman Spectroscopy: Differences between Reduced CeO2and Pt/CeO2. J. Raman Spectrosc. 2012, 43, 1312–1319. [Google Scholar] [CrossRef]
- Taniguchi, T.; Watanabe, T.; Sugiyama, N.; Subramani, A.K.; Wagata, H.; Matsushita, N.; Yoshimura, M. Identifying Defects in Ceria-Based Nanocrystals by UV Resonance Raman Spectroscopy. J. Phys. Chem. C 2009, 113, 19789–19793. [Google Scholar] [CrossRef]
- Acharya, S.A.; Gaikwad, V.M.; D’Souza, S.W.; Barman, S.R. Gd/Sm Dopant-Modified Oxidation State and Defect Generation in Nano-Ceria. Solid State Ion. 2014, 260, 21–29. [Google Scholar] [CrossRef]
- McBride, J.R.; Hass, K.C.; Poindexter, B.D.; Weber, W.H. Raman and X-Ray Studies of Ce1−xRExO2−y, Where RE = La, Pr, Nd, Eu, Gd, and Tb. J. Appl. Phys. 1994, 76, 2435–2441. [Google Scholar] [CrossRef]
- Kosacki, I.; Suzuki, T.; Petrovsky, V.; Anderson, H.U.; Colomban, P. Lattice Defects in Nanocrystalline CeO2thin Films. Radiat. Eff. Defects Solids 2001, 156, 109–115. [Google Scholar] [CrossRef]
- Filtschew, A.; Hofmann, K.; Hess, C. Ceria and Its Defect Structure: New Insights from a Combined Spectroscopic Approach. J. Phys. Chem. C 2016, 120, 6694–6703. [Google Scholar] [CrossRef]
- Yamamoto, T.; Momida, H.; Hamada, T.; Uda, T.; Ohno, T. First-Principles Study of Dielectric Properties of Cerium Oxide. Thin Solid Film. 2005, 486, 136–140. [Google Scholar] [CrossRef]
- Gurevich, V.L.; Tagantsev, A.K. Intrinsic Dielectric Loss in Crystals. Adv. Phys. 1991, 40, 719–767. [Google Scholar] [CrossRef]
- Pei, J.; Yin, L.; Zhong, S.; Dang, Z. Suppressing the Loss of Polymer-Based Dielectrics for High Power Energy Storage. Adv. Mater. 2022, 35, 2203623. [Google Scholar] [CrossRef]
- Fan, B.; Liu, F.; Yang, G.; Li, H.; Zhang, G.; Jiang, S.; Wang, Q. Dielectric Materials for High-temperature Capacitors. IET Nanodielectrics 2018, 1, 32–40. [Google Scholar] [CrossRef]
- Selmi, M.; Smida, A.; Kossi, S.E. Effect of Polaron Formation in Conduction and Dielectric Behavior in La0.7Sr0.25KMnO3 Oxide. J. Mater. Sci. Mater. Electron. 2021, 32, 6014–6027. [Google Scholar] [CrossRef]
- Li, C.; Chen, G.; Qiu, X.; Lou, Q.; Gao, X. A Direct Proof for Maxwell–Wagner Effect of Heterogeneous Interface. AIP Adv. 2021, 11, 065227. [Google Scholar] [CrossRef]
- Mironovich, A.Y.; Kostishin, V.G.; Shakirzyanov, R.I.; Mukabenov, A.A.; Melnikov, S.A.; Ril, A.I.; Al-Khafaji, H.I. Effect of the Fe/Ba and Fe/Sr Ratios on the Phase Composition, Dielectric Properties and Magnetic Characteristics of M-Type Hexaferrites Prepared by the Hydrothermal Method. J. Solid State Chem. 2022, 316, 123625. [Google Scholar] [CrossRef]
- Hannay, J.H. The Clausius-Mossotti Equation: An Alternative Derivation. Eur. J. Phys. 1983, 4, 141–143. [Google Scholar] [CrossRef]
- Thompson, D.P.; Dickins, A.M.; Thorp, J.S. The Dielectric Properties of Zirconia. J. Mater. Sci. 1992, 27, 2267–2271. [Google Scholar] [CrossRef]
- Tang, Q.; Gong, J. Effect of Porosity on the Microhardness Testing of Brittle Ceramics: A Case Study on the System of NiO–ZrO2. Ceram. Int. 2013, 39, 8751–8759. [Google Scholar] [CrossRef]
- Shakirzyanov, R.I.; Volodina, N.O.; Kadyrzhanov, K.K.; Kozlovskiy, A.L.; Shlimas, D.I.; Baimbetova, G.A.; Borgekov, D.B.; Zdorovets, M.V. Study of the Aid Effect of CuO-TiO2-Nb2O5 on the Dielectric and Structural Properties of Alumina Ceramics. Materials 2023, 16, 5018. [Google Scholar] [CrossRef]
- Rejab, N.A.; Azhar, A.Z.A.; Ratnam, M.M.; Ahmad, Z.A. The Relationship between Microstructure and Fracture Toughness of Zirconia Toughened Alumina (ZTA) Added with MgO and CeO2. Int. J. Refract. Met. Hard Mater. 2013, 41, 522–530. [Google Scholar] [CrossRef]
- Dudek, M. Ceramic Oxide Electrolytes Based on CeO2—Preparation, Properties and Possibility of Application to Electrochemical Devices. J. Eur. Ceram. Soc. 2008, 28, 965–971. [Google Scholar] [CrossRef]
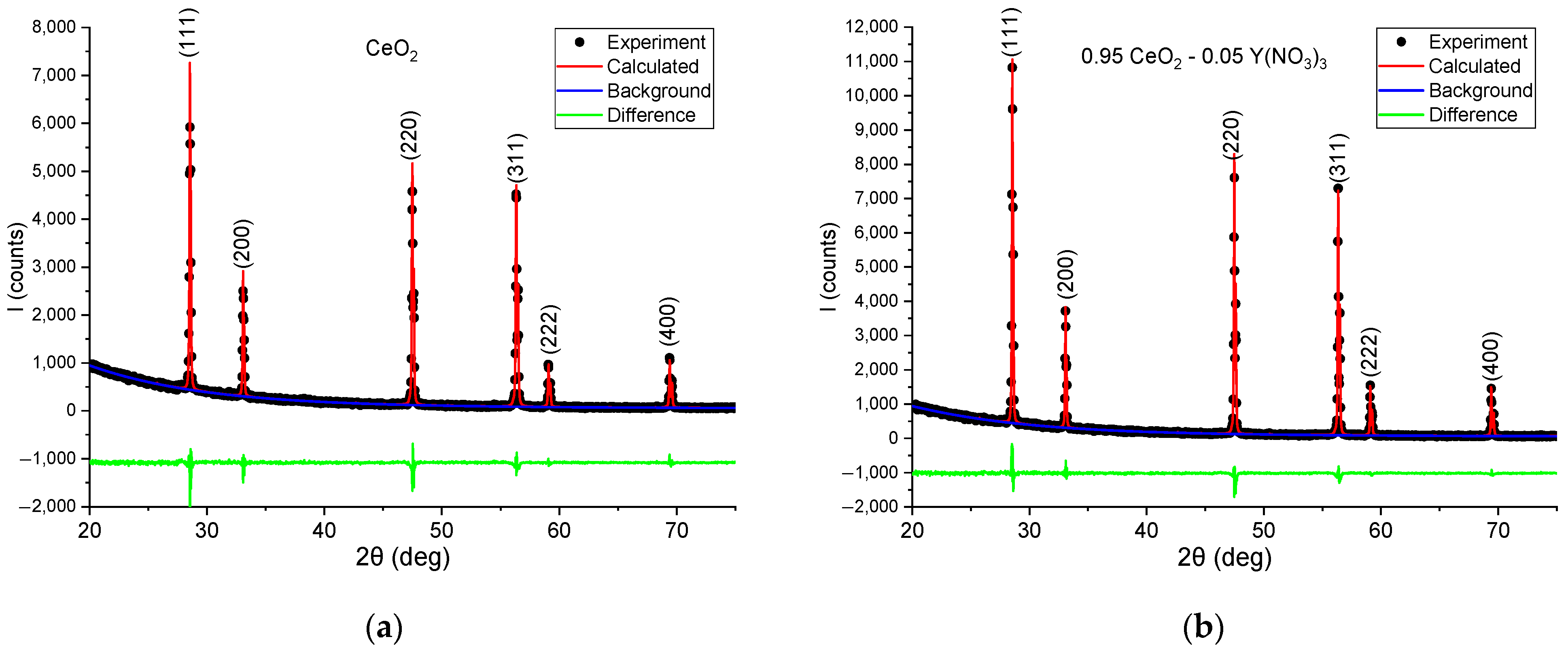






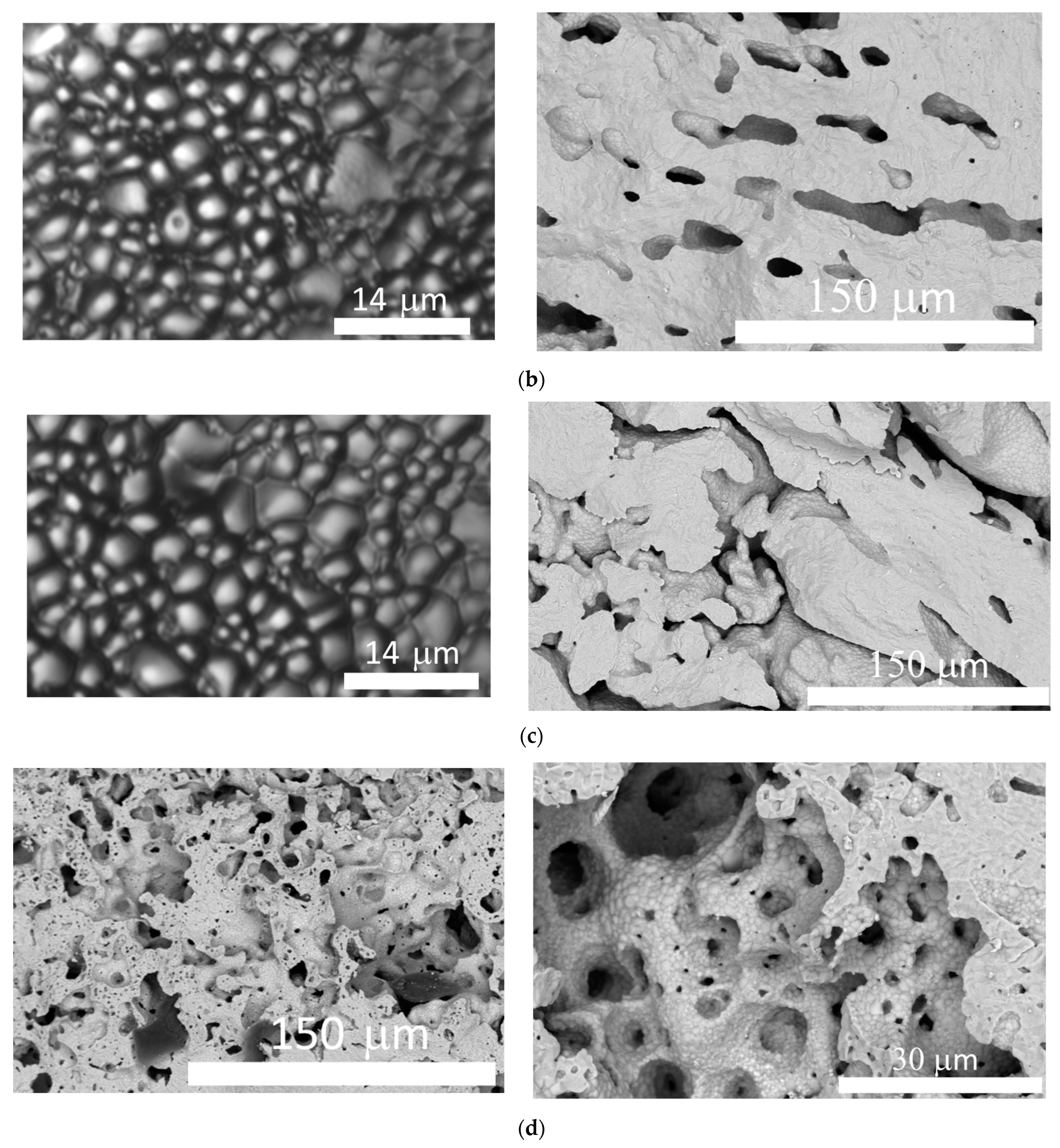

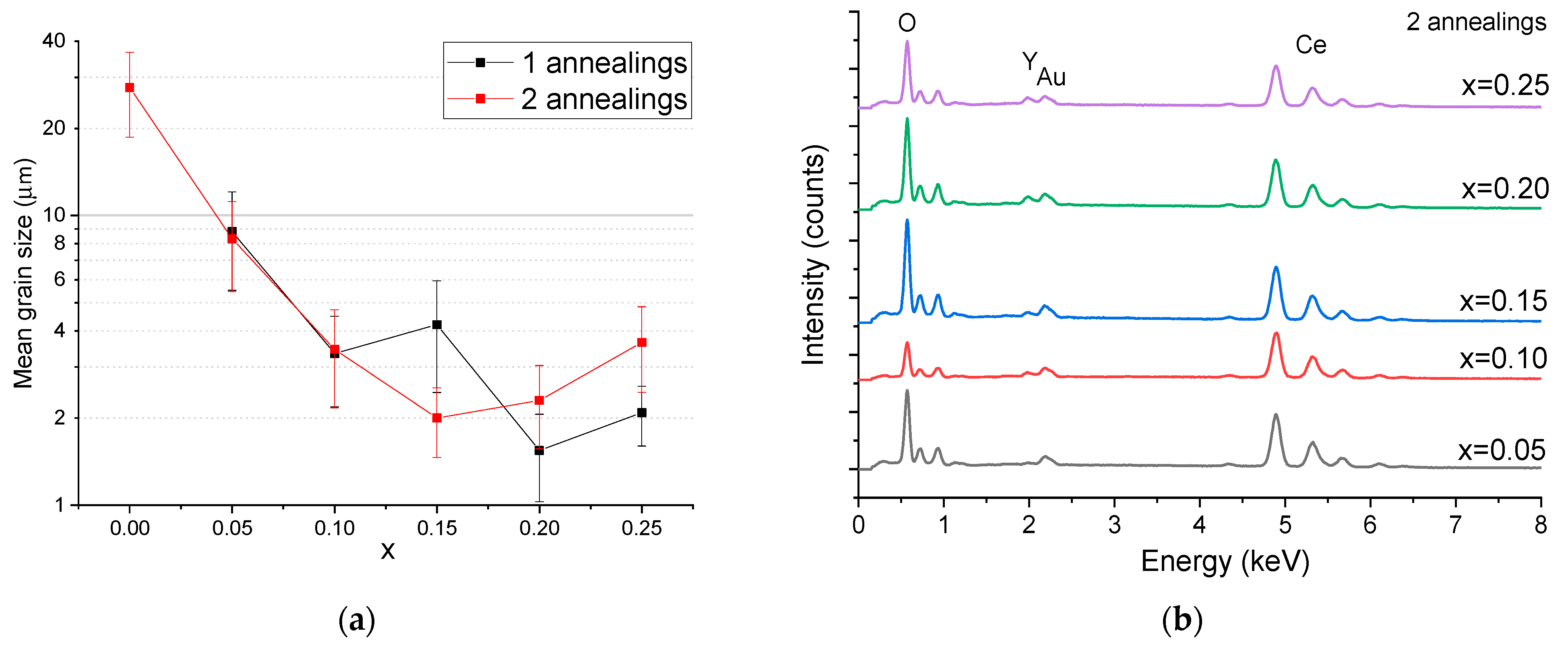
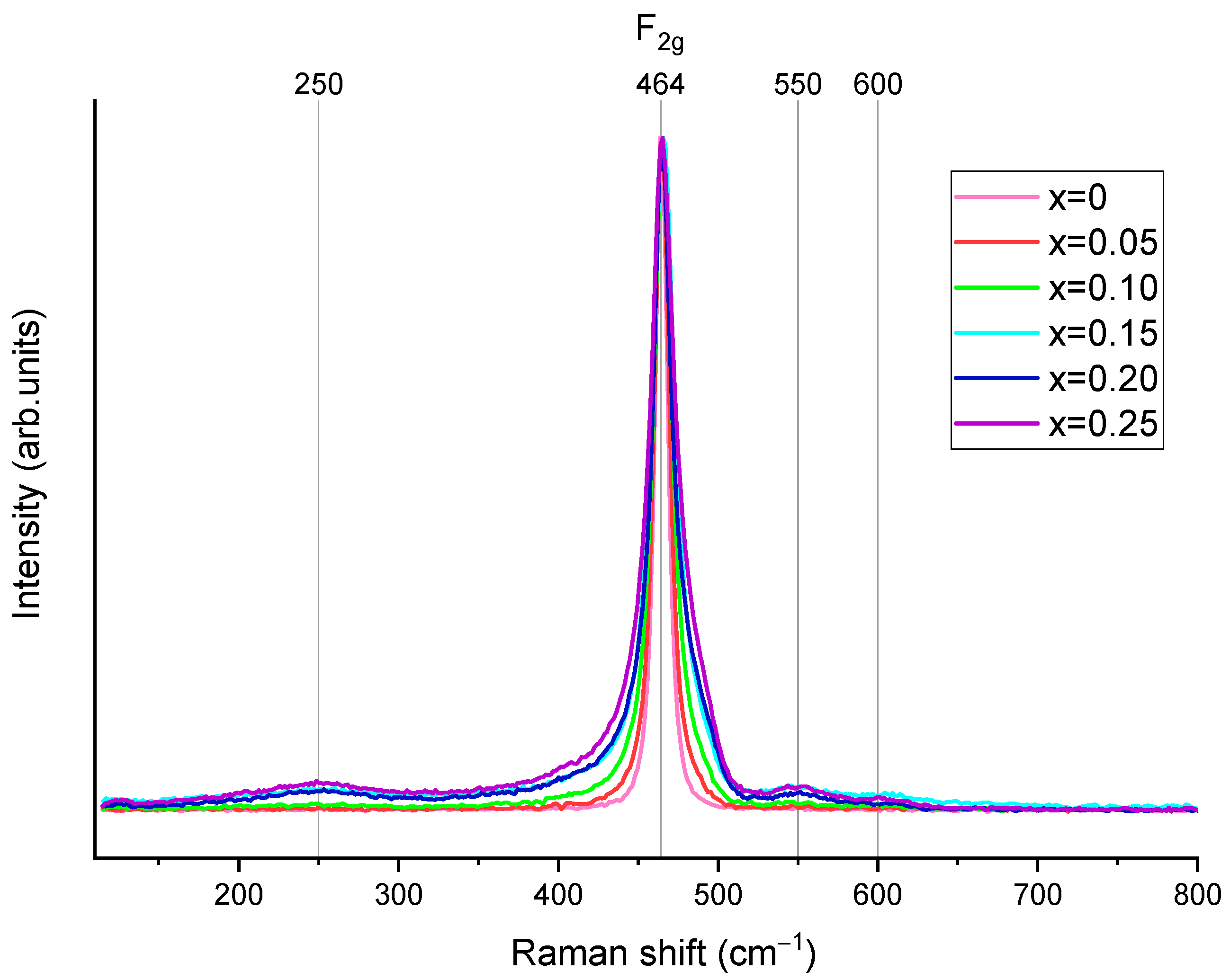


| X | a, Å | X-ray Density, g/cm3 | Rexp | Rwp | GOF | χ2 |
|---|---|---|---|---|---|---|
| 0.00 | 5.411094 ± 0.000052 | 7.215 | 6.63 | 9.47 | 1.43 | 2.04 |
| 0.05 | 5.410745 ± 0.000030 | 7.182 | 6.55 | 7.26 | 1.11 | 1.23 |
| 0.10 | 5.410057 ± 0.000037 | 7.115 | 6.50 | 7.05 | 1.08 | 1.18 |
| 0.15 | 5.408659 ± 0.000074 | 7.015 | 6.46 | 8.89 | 1.38 | 1.89 |
| 0.20 | 5.408249 ± 0.000045 | 6.877 | 5.86 | 6.61 | 1.13 | 1.27 |
| 0.25 | 5.406372 ± 0.000067 | 6.841 | 6.24 | 7.35 | 1.19 | 1.41 |
| x | dav, nm | Dislocation Density∙1015, Line per m2 | Microstrain |
|---|---|---|---|
| 0.00 | 82.1 ± 21.08 | 0.15 | −0.00101 ± 0.00014 |
| 0.05 | 95.1 ± 23.94 | 0.11 | −0.00084 ± 0.00019 |
| 0.10 | 80.7 ± 15.99 | 0.15 | −0.00073 ± 0.00014 |
| 0.15 | 60.7 ± 11.57 | 0.27 | −0.00092 ± 0.00022 |
| 0.20 | 68.2 ± 7.87 | 0.22 | −0.00036 ± 0.00016 |
| 0.25 | 57.7 ± 5.41 | 0.30 | −0.00042 ± 0.00011 |
| x | O Concentration, at.% | Ce Concentration, at.% | Y Concentration, at.% |
|---|---|---|---|
| 0.00—1 annealing | 55.23 ± 4.57 | 42.77 ± 4.24 | - |
| 0.05—1 annealing | 52.20 ± 9.64 | 45.60 ± 9.02 | 0.46 ± 0.11 |
| 0.10—1 annealing | 56.25 ± 4.01 | 39.77 ± 3.75 | 2.06 ± 0.26 |
| 0.15—1 annealing | 61.74 ± 10.76 | 33.79 ± 8.73 | 2.75 ± 1.41 |
| 0.20—1 annealing | 55.92 ± 7.08 | 37.74 ± 7.18 | 4.39 ± 0.52 |
| 0.25—1 annealing | 56.99 ± 6.69 | 35.82 ± 5.82 | 5.22 ± 0.52 |
| 0.05—2 annealings | 58.06 ± 6.08 | 39.50 ± 5.92 | 0.65 ± 0.28 |
| 0.10—2 annealings | 41.77 ± 4.81 | 52.83 ± 4.47 | 2.53 ± 0.59 |
| 0.15—2 annealings | 59.12 ± 4.34 | 37.08 ± 3.88 | 1.39 ± 0.47 |
| 0.20—2 annealings | 62.47 ± 2.19 | 32.19 ± 2.09 | 3.32 ± 0.48 |
| 0.25—2 annealings | 52.01 ± 7.54 | 42.63 ± 6.72 | 2.58 ± 1.01 |
| x | Center | FWHM |
|---|---|---|
| 0 | 464.44 | 8.62 |
| 0.05 | 464.82 | 10.80 |
| 0.10 | 465.31 | 14.27 |
| 0.15 | 465.80 | 18.17 |
| 0.20 | 465.23 | 18.35 |
| 0.25 | 465.46 | 22.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakirzyanov, R.I.; Volodina, N.O.; Kozlovskiy, A.L.; Zdorovets, M.V.; Shlimas, D.I.; Borgekov, D.B.; Garanin, Y.A. Study of the Structural, Electrical, and Mechanical Properties and Morphological Features of Y-Doped CeO2 Ceramics with Porous Structure. J. Compos. Sci. 2023, 7, 411. https://doi.org/10.3390/jcs7100411
Shakirzyanov RI, Volodina NO, Kozlovskiy AL, Zdorovets MV, Shlimas DI, Borgekov DB, Garanin YA. Study of the Structural, Electrical, and Mechanical Properties and Morphological Features of Y-Doped CeO2 Ceramics with Porous Structure. Journal of Composites Science. 2023; 7(10):411. https://doi.org/10.3390/jcs7100411
Chicago/Turabian StyleShakirzyanov, Rafael I., Natalia O. Volodina, Artem L. Kozlovskiy, Maxim V. Zdorovets, Dmitriy I. Shlimas, Daryn B. Borgekov, and Yuriy A. Garanin. 2023. "Study of the Structural, Electrical, and Mechanical Properties and Morphological Features of Y-Doped CeO2 Ceramics with Porous Structure" Journal of Composites Science 7, no. 10: 411. https://doi.org/10.3390/jcs7100411
APA StyleShakirzyanov, R. I., Volodina, N. O., Kozlovskiy, A. L., Zdorovets, M. V., Shlimas, D. I., Borgekov, D. B., & Garanin, Y. A. (2023). Study of the Structural, Electrical, and Mechanical Properties and Morphological Features of Y-Doped CeO2 Ceramics with Porous Structure. Journal of Composites Science, 7(10), 411. https://doi.org/10.3390/jcs7100411








