Comparative Thermoelectric Properties of Polypropylene Composites Melt-Processed Using Pyrograf® III Carbon Nanofibers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Their Processing
2.2. Morphological Analysis
2.3. XRD and Raman Analysis
2.4. DSC Analysis
2.5. Thermoelectric Analysis
3. Results and Discussion
3.1. Morphological Analysis
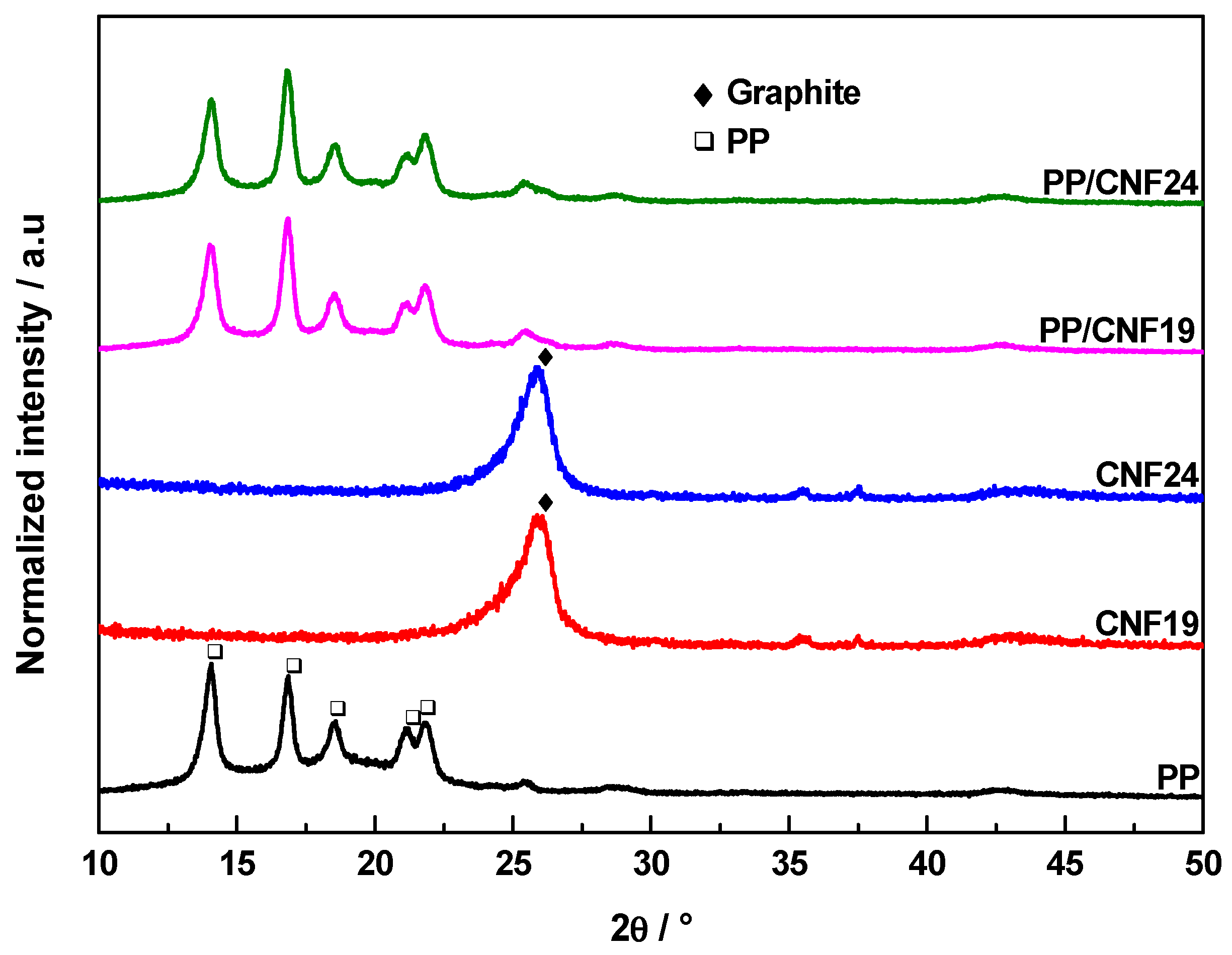
3.2. XRD and Raman Analysis
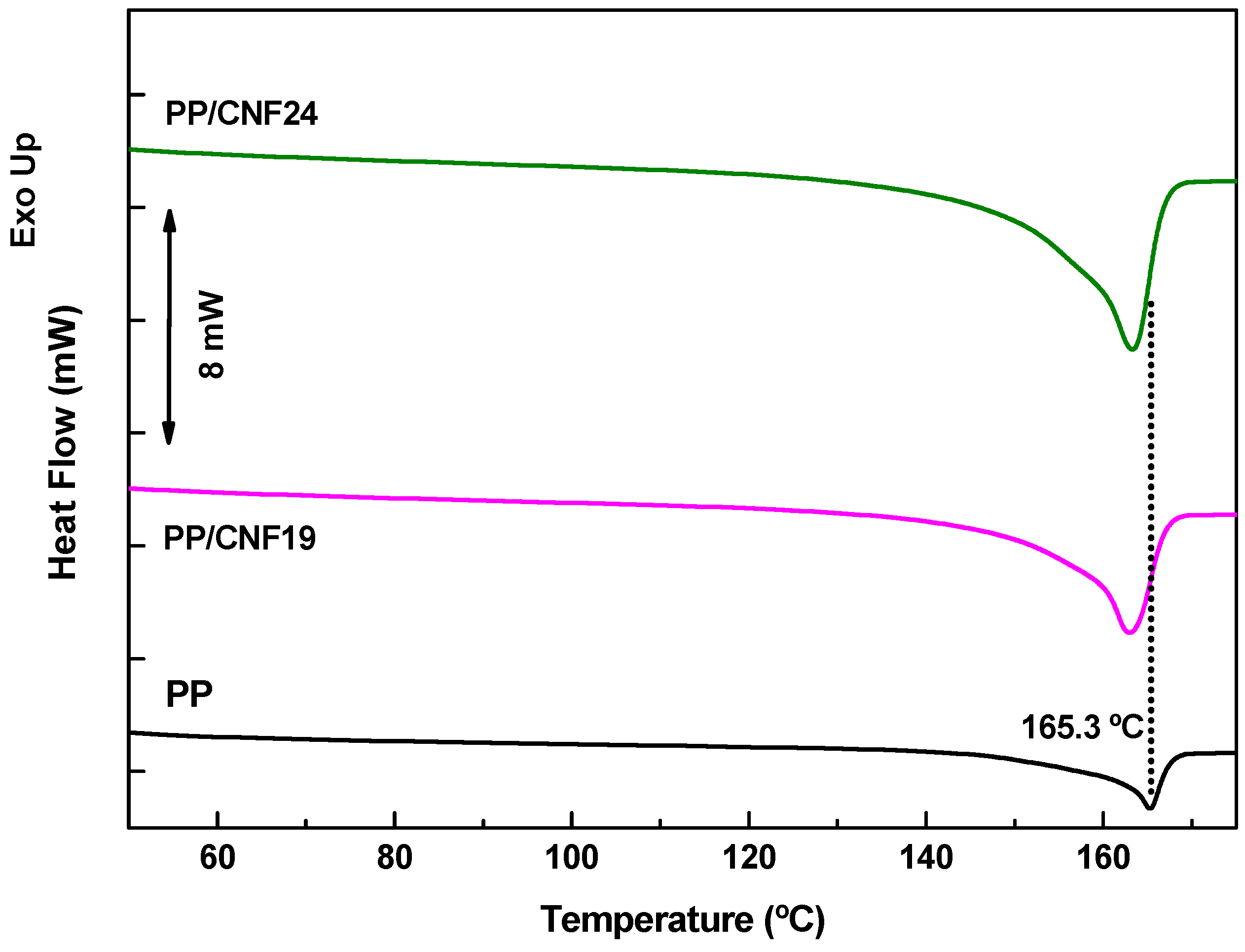
3.3. DSC Analysis
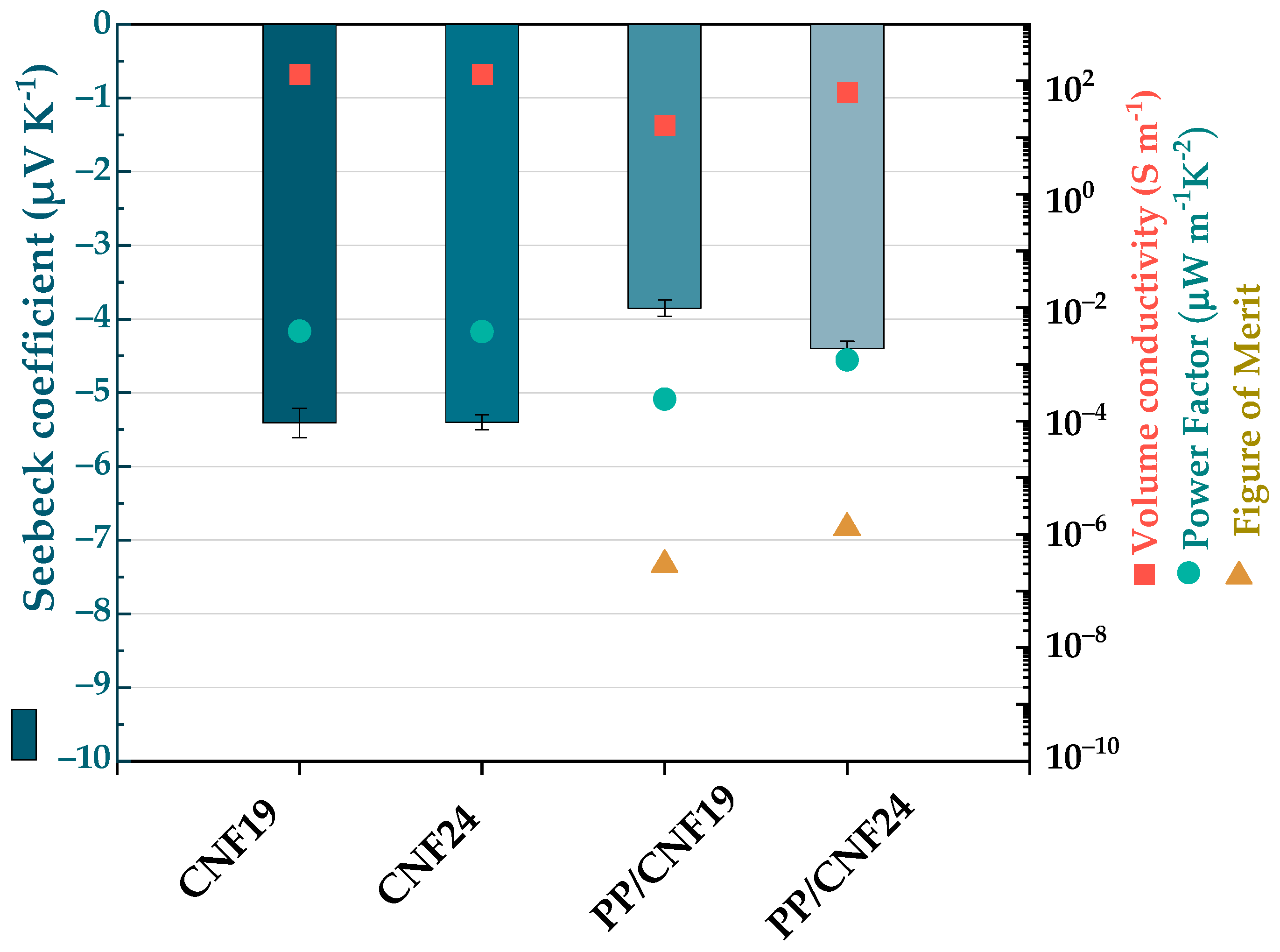
3.4. Thermoelectric Analysis of PP/CNF Composites at 40 °C
3.5. Thermoelectric Analysis of PP/CNF Composites from 40 °C to 100 °C
3.6. Electrical Volume Conductivity and Seebeck Coefficient Modelling of CNFs and PP/CNF Composites
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krause, B.; Barbier, C.; Kunz, K.; Pötschke, P. Comparative study of singlewalled, multiwalled, and branched carbon nanotubes melt mixed in different thermoplastic matrices. Polymer 2018, 159, 75–85. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Y.; Huang, J.; Zhang, J.; Pan, D.; Zhou, J.; Ryu, J.E.; Umar, A.; Guo, Z. Advances in Responsively Conductive Polymer Composites and Sensing Applications. Polym. Rev. 2021, 61, 157–193. [Google Scholar] [CrossRef]
- Zebarjadi, M.; Esfarjani, K.; Dresselhaus, M.S.; Ren, Z.F.; Chen, G. Perspectives on thermoelectrics: From fundamentals to device applications. Energy Environ. Sci. 2012, 5, 5147–5162. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Liu, B. Carbon Nanotube-Based Organic Thermoelectric Materials for Energy Harvesting. Polymers 2018, 10, 1196. [Google Scholar] [CrossRef]
- Nandihalli, N.; Liu, C.-J.; Mori, T. Polymer based thermoelectric nanocomposite materials and devices: Fabrication and characteristics. Nano Energy 2020, 78, 105186. [Google Scholar] [CrossRef]
- Gulrez, S.K.H.; Ali Mohsin, M.E.; Shaikh, H.; Anis, A.; Pulose, A.M.; Yadav, M.K.; Qua, E.H.P.; Al-Zahrani, S.M. A review on electrically conductive polypropylene and polyethylene. Polym. Compos. 2014, 35, 900–914. [Google Scholar] [CrossRef]
- Yadav, D.; Amini, F.; Ehrmann, A. Recent advances in carbon nanofibers and their applications—A review. Eur. Polym. J. 2020, 138, 109963. [Google Scholar] [CrossRef]
- Al-Saleh, M.H.; Sundararaj, U. A review of vapor grown carbon nanofiber/polymer conductive composites. Carbon 2009, 47, 2–22. [Google Scholar] [CrossRef]
- Luo, J.; Cerretti, G.; Krause, B.; Zhang, L.; Otto, T.; Jenschke, W.; Ullrich, M.; Tremel, W.; Voit, B.; Pötschke, P. Polypropylene-based melt mixed composites with singlewalled carbon nanotubes for thermoelectric applications: Switching from p-type to n-type by the addition of polyethylene glycol. Polymer 2017, 108, 513–520. [Google Scholar] [CrossRef]
- Paleo, A.J.; Aribou, N.; Nioua, Y.; Samir, Z.; Fernandes, L.; Moreira, J.A.; Achour, M.E. Electrical properties of melt-mixed polypropylene and as-grown carbon nanofiber composites: Analysis of their interphase via the AC conductivity modeling. J. Compos. Mater. 2022, 56, 1879–1889. [Google Scholar] [CrossRef]
- Vivo, B.D.; Lamberti, P.; Spinelli, G.; Tucci, V.; Guadagno, L.; Raimondo, M. The effect of filler aspect ratio on the electromagnetic properties of carbon-nanofibers reinforced composites. J. Appl. Phys. 2015, 118, 064302. [Google Scholar] [CrossRef]
- Silva, J.; Ribeiro, S.; Lanceros-Mendez, S.; Simões, R. The influence of matrix mediated hopping conductivity, filler concentration, aspect ratio and orientation on the electrical response of carbon nanotube/polymer nanocomposites. Compos. Sci. Technol. 2011, 71, 643–646. [Google Scholar] [CrossRef]
- Dang, Z.-M.; Shehzad, K.; Zha, J.-W.; Hussain, T.; Jun, N.; Bai, J. On Refining the Relationship between Aspect Ratio and Percolation Threshold of Practical Carbon Nanotubes/Polymer Nanocomposites. Jpn. J. Appl. Phys. 2011, 50, 080214. [Google Scholar] [CrossRef]
- Paleo, A.J.; Krause, B.; Cerqueira, M.F.; Melle-Franco, M.; Pötschke, P.; Rocha, A.M. Thermoelectric properties of polypropylene carbon nanofiber melt-mixed composites: Exploring the role of polymer on their Seebeck coefficient. Polym. J. 2021, 53, 1145–1152. [Google Scholar] [CrossRef]
- Paleo, A.J.; Krause, B.; Cerqueira, M.F.; Muñoz, E.; Pötschke, P.; Rocha, A.M. Nonlinear Thermopower Behaviour of N-Type Carbon Nanofibres and Their Melt Mixed Polypropylene Composites. Polymers 2022, 14, 269. [Google Scholar] [CrossRef]
- Mott, N.F. Conduction in glasses containing transition metal ions. J. Non-Cryst. Solids 1968, 1, 1–17. [Google Scholar] [CrossRef]
- Choi, Y.M.; Lee, D.S.; Czerw, R.; Chiu, P.W.; Grobert, N.; Terrones, M.; Reyes-Reyes, M.; Terrones, H.; Charlier, J.C.; Ajayan, P.M.; et al. Nonlinear Behavior in the Thermopower of Doped Carbon Nanotubes Due to Strong, Localized States. Nano Lett. 2003, 3, 839–842. [Google Scholar] [CrossRef]
- Pyrograf Products Inc. Available online: https://apsci.com/products/pyrograf/ (accessed on 11 April 2023).
- Tessonnier, J.-P.; Rosenthal, D.; Hansen, T.W.; Hess, C.; Schuster, M.E.; Blume, R.; Girgsdies, F.; Pfänder, N.; Timpe, O.; Su, D.S.; et al. Analysis of the structure and chemical properties of some commercial carbon nanostructures. Carbon 2009, 47, 1779–1798. [Google Scholar] [CrossRef]
- Paleo, A.J.; Sencadas, V.; van Hattum, F.W.J.; Lanceros-Méndez, S.; Ares, A. Carbon nanofiber type and content dependence of the physical properties of carbon nanofiber reinforced polypropylene composites. Polym. Eng. Sci. 2014, 54, 117–128. [Google Scholar] [CrossRef]
- Paleo, A.J.; Krause, B.; Cerqueira, M.F.; Muñoz, E.; Pötschke, P.; Rocha, A.M. Electronic Features of Cotton Fabric e-Textiles Prepared with Aqueous Carbon Nanofiber Inks. ACS Appl. Eng. Mater. 2023, 1, 122–131. [Google Scholar] [CrossRef]
- Jenschke, W.; Ullrich, M.; Krause, B.; Pötschke, P. Messanlage zur Untersuchung des Seebeck-Effektes in Polymermaterialien. TM—Tech. Mess. 2020, 87, 495–503. [Google Scholar] [CrossRef]
- Krause, B.; Barbier, C.; Levente, J.; Klaus, M.; Pötschke, P. Screening of Different Carbon Nanotubes in Melt-Mixed Polymer Composites with Different Polymer Matrices for Their Thermoelectrical Properties. J. Compos. Sci. 2019, 3, 106. [Google Scholar] [CrossRef]
- Lawrence, J.G.; Berhan, L.M.; Nadarajah, A. Structural transformation of vapor grown carbon nanofibers studied by HRTEM. J. Nanopart. Res. 2008, 10, 1155–1167. [Google Scholar] [CrossRef]
- Nielsen, A.S.; Pyrz, R. A Raman study into the effect of transcrystallisation on thermal stresses in embedded single fibres. J. Mater. Sci. 2003, 38, 597–601. [Google Scholar] [CrossRef]
- Snyder, R.G.; Schachtschneider, J.H. Valence force calculation of the vibrational spectra of crystalline isotactic polypropylene and some deuterated polypropylenes. Spectrochim. Acta 1964, 20, 853–869. [Google Scholar] [CrossRef]
- Lehman, J.H.; Terrones, M.; Mansfield, E.; Hurst, K.E.; Meunier, V. Evaluating the characteristics of multiwall carbon nanotubes. Carbon 2011, 49, 2581–2602. [Google Scholar] [CrossRef]
- Wang, Y.; Alsmeyer, D.C.; McCreery, R.L. Raman Spectroscopy of Carbon Materials: Structural Basis of Observed Spectra. Chem. Mater. 1990, 2, 557–563. [Google Scholar] [CrossRef]
- Knight, D.S.; White, W.B. Characterization of diamond films by Raman spectroscopy. J. Mater. Res. 1989, 4, 385–393. [Google Scholar] [CrossRef]
- Ferrari, A.; Robertson, J. Interpretation of Raman spectra of disordered and amorphous carbon. Phys. Rev. B—Condens. Matter Mater. Phys. 2000, 61, 14095–14107. [Google Scholar] [CrossRef]
- Wunderlich, B.K. Thermal Analysis of Polymeric Materials; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Sui, G.; Zhong, W.-H.; Fuqua, M.A.; Ulven, C.A. Crystalline Structure and Properties of Carbon Nanofiber Composites Prepared by Melt Extrusion. Macromol. Chem. Phys. 2007, 208, 1928–1936. [Google Scholar] [CrossRef]
- Yetgin, S.H. Effect of multi walled carbon nanotube on mechanical, thermal and rheological properties of polypropylene. J. Mater. Res. Technol. 2019, 8, 4725–4735. [Google Scholar] [CrossRef]
- Lozano, K.; Barrera, E.V. Nanofiber-reinforced thermoplastic composites. I. Thermoanalytical and mechanical analyses. J. Appl. Polym. Sci. 2001, 79, 125–133. [Google Scholar] [CrossRef]
- Li, C.; Thostenson, E.T.; Chou, T.-W. Dominant role of tunneling resistance in the electrical conductivity of carbon nanotube–based composites. Appl. Phys. Lett. 2007, 91, 223114. [Google Scholar] [CrossRef]
- Khan, T.; Irfan, M.S.; Ali, M.; Dong, Y.; Ramakrishna, S.; Umer, R. Insights to low electrical percolation thresholds of carbon-based polypropylene nanocomposites. Carbon 2021, 176, 602–631. [Google Scholar] [CrossRef]
- Collins, P.G.; Bradley, K.; Ishigami, M.; Zettl, A. Extreme Oxygen Sensitivity of Electronic Properties of Carbon Nanotubes. Science 2000, 287, 1801–1804. [Google Scholar] [CrossRef]
- Krause, B.; Konidakis, I.; Arjmand, M.; Sundararaj, U.; Fuge, R.; Liebscher, M.; Hampel, S.; Klaus, M.; Serpetzoglou, E.; Stratakis, E.; et al. Nitrogen-Doped Carbon Nanotube/Polypropylene Composites with Negative Seebeck Coefficient. J. Compos. Sci. 2020, 4, 14. [Google Scholar] [CrossRef]
- Krause, B.; Imhoff, S.; Voit, B.; Pötschke, P. Influence of Polyvinylpyrrolidone on Thermoelectric Properties of Melt-Mixed Polymer/Carbon Nanotube Composites. Micromachines 2023, 14, 181. [Google Scholar] [CrossRef]
- Paleo, A.J.; García, X.; Arboleda-Clemente, L.; Van Hattum, F.W.; Abad, M.J.; Ares, A. Enhanced thermal conductivity of rheologically percolated carbon nanofiber reinforced polypropylene composites. Polym. Adv. Technol. 2015, 26, 369–375. [Google Scholar] [CrossRef]
- Fuhrer, M.S.; Holmes, W.; Richards, P.L.; Delaney, P.; Louie, S.G.; Zettl, A. Nonlinear transport and localization in single-walled carbon nanotubes. Synth. Met. 1999, 103, 2529–2532. [Google Scholar] [CrossRef]
- Ivanov, D.K.; Ivanov, K.G.; Uryupin, O.N. Resistance and thermoelectric power of carbon fibers upon changing the conductivity type. Semiconductors 2017, 51, 834–835. [Google Scholar] [CrossRef]
- Paleo, A.J.; Vieira, E.M.F.; Wan, K.; Bondarchuk, O.; Cerqueira, M.F.; Goncalves, L.M.; Bilotti, E.; Alpuim, P.; Rocha, A.M. Negative thermoelectric power of melt mixed vapor grown carbon nanofiber polypropylene composites. Carbon 2019, 150, 408–416. [Google Scholar] [CrossRef]
- Mahan, G.D. Impurity resonances in carbon nanotubes. Phys. Rev. B 2004, 69, 125407. [Google Scholar] [CrossRef]
- Krause, B.; Pötschke, P. Polyethylene Glycol as Additive to Achieve N-Conductive Melt-Mixed Polymer/Carbon Nanotube Composites for Thermoelectric Application. Nanomaterials 2022, 12, 3812. [Google Scholar] [CrossRef] [PubMed]




| PP/CNF Loading | CNF Type | Polypropylene | CNF Loading |
|---|---|---|---|
| PP/CNF19 | PR 19 LHT XT | DaplenTM EE002AE | 5 wt.% |
| PP/CNF24 | PR 24 LHT XT |
| Sample | wG (cm−1) | FWHMG (cm−1) | wD (cm−1) | FWHMD (cm−1) | ID/IG | La (nm) |
|---|---|---|---|---|---|---|
| CNF19 | 1580 | 90 | 1352 | 115 | 0.76 | 5.8 |
| CNF24 | 1583 | 85 | 1352 | 100 | 0.70 | 6.3 |
| PP/CNF19 | 1587 | 50 | 1353 | 75 | 0.70 | 6.3 |
| PP/CNF24 | 1587 | 65 | 1354 | 85 | 0.74 | 5.9 |
| Sample | Tm (°C) | ∆Hm (J g−1) | ∆Xc (%) |
|---|---|---|---|
| PP | 165.3 | 71.4 | 34.5 |
| PP/CNF19 | 162.9 | 107.7 | 55.1 |
| PP/CNF24 | 163.3 | 100.0 | 51.2 |
| Sample | σ (S m−1) | S (µV K−1) | PF (μW m−1K−2) | k (W m−1K−1) | zT |
|---|---|---|---|---|---|
| CNF19 | 131.5 ± 19 | −5.4 ± 0.2 | 3.8 × 10−3 | − | − |
| CNF24 | 131.6 ± 0.1 | −5.4 ± 0.1 | 3.8 × 10−3 | − | − |
| PP/CNF19 | 16.5 ± 0.7 | −3.8 ± 0.1 | 2.4 × 10−4 | 0.25 | 3.0 × 10−7 |
| PP/CNF24 | 62.7 ± 7 | −4.4 ± 0.1 | 1.2 × 10−3 | 0.29 | 1.3 × 10−6 |
| Sample | σ0 (S m−1) | TC (K) | WD (eV) |
|---|---|---|---|
| CNF19 | 63.7 | 89.7 | −7.7 × 10−3 |
| PP/CNF19 | 0.3 | 73.6 × 103 | −6.3 |
| CNF24 | 28.3 | 1.7 × 103 | −0.15 |
| PP/CNF24 | 1.9 | 45.4 × 103 | −3.9 |
| Sample | b (μVK−2) | c (μV) | Tp (K) | Ep − EF (eV) |
|---|---|---|---|---|
| CNF19 | 6.1 × 10−3 | −1.8 × 104 | 9.8 × 102 | 8.5 × 10−2 |
| PP/CNF19 | 4.7 × 10−3 | −1.6 × 104 | 1.1 × 103 | 9.4 × 10−2 |
| CNF24 | 4.2 × 10−3 | −1.8 × 104 | 1.0 × 103 | 8.7 × 10−2 |
| PP/CNF24 | −9.1 × 10−3 | −1.2 × 104 | 1.4 × 103 | 1.2 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paleo, A.J.; Krause, B.; Mendes, A.R.; Tavares, C.J.; Cerqueira, M.F.; Muñoz, E.; Pötschke, P. Comparative Thermoelectric Properties of Polypropylene Composites Melt-Processed Using Pyrograf® III Carbon Nanofibers. J. Compos. Sci. 2023, 7, 173. https://doi.org/10.3390/jcs7040173
Paleo AJ, Krause B, Mendes AR, Tavares CJ, Cerqueira MF, Muñoz E, Pötschke P. Comparative Thermoelectric Properties of Polypropylene Composites Melt-Processed Using Pyrograf® III Carbon Nanofibers. Journal of Composites Science. 2023; 7(4):173. https://doi.org/10.3390/jcs7040173
Chicago/Turabian StylePaleo, Antonio J., Beate Krause, Ana R. Mendes, Carlos J. Tavares, Maria F. Cerqueira, Enrique Muñoz, and Petra Pötschke. 2023. "Comparative Thermoelectric Properties of Polypropylene Composites Melt-Processed Using Pyrograf® III Carbon Nanofibers" Journal of Composites Science 7, no. 4: 173. https://doi.org/10.3390/jcs7040173
APA StylePaleo, A. J., Krause, B., Mendes, A. R., Tavares, C. J., Cerqueira, M. F., Muñoz, E., & Pötschke, P. (2023). Comparative Thermoelectric Properties of Polypropylene Composites Melt-Processed Using Pyrograf® III Carbon Nanofibers. Journal of Composites Science, 7(4), 173. https://doi.org/10.3390/jcs7040173










