Detailed Finite Element Models for the Simulation of the Laser Shock Wave Response of 3D Woven Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Detailed FE Model
2.1.1. Design of the 3D Woven Geometry
2.1.2. Meshing of the Detailed Model
2.1.3. Mesh Density Study for the Detailed Model
2.2. Homogenized FE Model
2.3. Material Models
2.3.1. Fiber Bundles
2.3.2. Matrix
2.3.3. Homogenized Model
2.4. Laser Shock Modeling
3. Results
3.1. Shock Wave Propagation
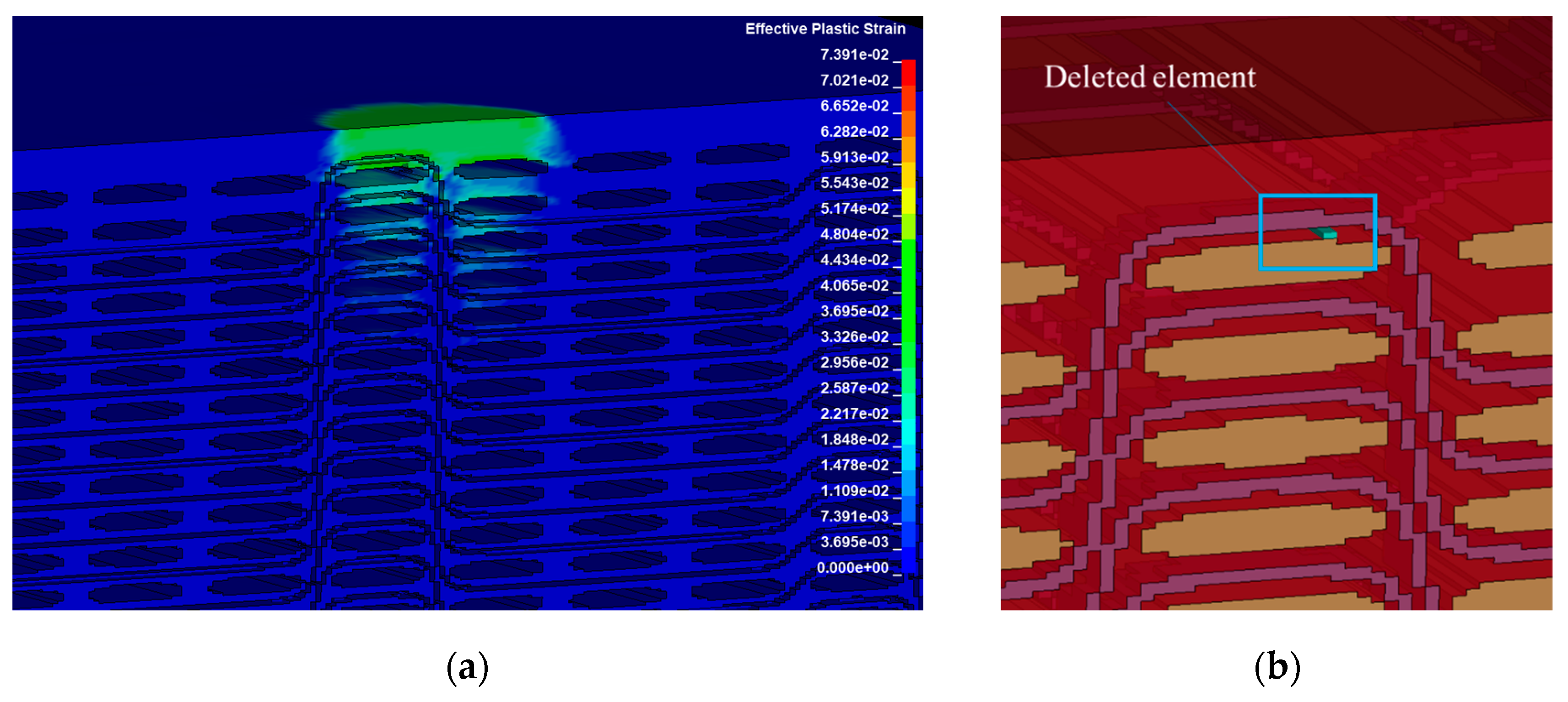
3.2. Damage Accumulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tserpes, K. Adhesive Bonding of Aircraft Structures. In Revolutionizing Aircraft Materials and Processes; Pantelakis, S., Tserpes, K., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 337–357. ISBN 978-3-030-35345-2. [Google Scholar]
- Leite Cavalcanti, W.; Brune, K.; Noeske, M.; Tserpes, K.; Ostachowicz, W.M.; Schlag, M. (Eds.) Adhesive Bonding of Aircraft Composite Structures: Non-Destructive Testing and Quality Assurance Concepts; Springer International Publishing: Cham, Switzerland, 2021; ISBN 978-3-319-92809-8. [Google Scholar]
- Stergiou, V.; Konstantopoulos, G.; Charitidis, C.A. Carbon Fiber Reinforced Plastics in Space: Life Cycle Assessment towards Improved Sustainability of Space Vehicles. J. Compos. Sci. 2022, 6, 144. [Google Scholar] [CrossRef]
- Srinivasan, D.V.; Idapalapati, S. Review of Debonding Techniques in Adhesively Bonded Composite Structures for Sustainability. Sustain. Mater. Technol. 2021, 30, e00345. [Google Scholar] [CrossRef]
- Kormpos, P.; Unaldi, S.; Berthe, L.; Tserpes, K. A Laser Shock-Based Disassembly Process for Adhesively Bonded Ti/CFRP Parts. Processes 2023, 11, 506. [Google Scholar] [CrossRef]
- Ghrib, M.; Berthe, L.; Mechbal, N.; Rébillat, M.; Guskov, M.; Ecault, R.; Bedreddine, N. Generation of Controlled Delaminations in Composites Using Symmetrical Laser Shock Configuration. Compos. Struct. 2017, 171, 286–297. [Google Scholar] [CrossRef]
- Papadopoulos, K.; Tserpes, K.; Unaldi, S.; Sma, I.; Berthe, L.; Karanika, A. Experimental and Numerical Investigation of the Laser Shock-Based Paint Stripping Process on CFRP Substrates. Opt. Laser Technol. 2024, 169, 110068. [Google Scholar] [CrossRef]
- Kormpos, P.; Tserpes, K. An Efficient Numerical Model for the Simulation of Debonding of Adhesively Bonded Titanium/CFRP Samples Induced by Repeated Symmetric Laser Shocks. J. Adhes. 2023. [Google Scholar] [CrossRef]
- Ecault, R.; Touchard, F.; Boustie, M.; Berthe, L.; Dominguez, N. Numerical Modeling of Laser-Induced Shock Experiments for the Development of the Adhesion Test for Bonded Composite Materials. Compos. Struct. 2016, 152, 382–394. [Google Scholar] [CrossRef]
- Ducousso, M.; Marmonier, M.; Cuenca, E.; Marchiano, R.; Coulouvrat, F.; Berthe, L. Acoustic Imaging of the Laser-Driven Shock Wave Propagation in Metallic Materials. In Proceedings of the Forum Acusticum 2020, Virtual, 7–11 December 2020. [Google Scholar] [CrossRef]
- Wielhorski, Y.; Mendoza, A.; Rubino, M.; Roux, S. Numerical Modeling of 3D Woven Composite Reinforcements: A Review. Compos. Part A Appl. Sci. Manuf. 2022, 154, 106729. [Google Scholar] [CrossRef]
- Shah, S.Z.H.; Lee, J.; Megat-Yusoff, P.S.M.; Hussain, S.Z.; Sharif, T.; Choudhry, R.S. Multiscale Damage Modelling of Notched and Un-Notched 3D Woven Composites with Randomly Distributed Manufacturing Defects. Compos. Struct. 2023, 318, 117109. [Google Scholar] [CrossRef]
- Millen, S.L.J.; Dahale, M.; Fisher, T.; Samy, A.; Thompson, K.; Ramaswamy, K.; Ralph, C.; Archer, E.; McIlhagger, A.; Ullah, Z.; et al. Modelling Low-Velocity Impact Damage and Compression after Impact of 3D Woven Structures Considering Compaction. Compos. Struct. 2023, 318, 117104. [Google Scholar] [CrossRef]
- Guo, J.; Wen, W.; Zhang, H.; Cui, H. A Mesoscale Fatigue Progressive Damage Model for 3D Woven Composites. Int. J. Fatigue 2021, 152, 106455. [Google Scholar] [CrossRef]
- Yan, S.; Zeng, X.; Long, A. Meso-Scale Modelling of 3D Woven Composite T-Joints with Weave Variations. Compos. Sci. Technol. 2019, 171, 171–179. [Google Scholar] [CrossRef]
- Zhang, Y.; Tong, J.; Guo, Q.; Guo, J.; Liu, X.; Chen, L. Hierarchical Multiscale Analysis for 3D Woven Composite Leaf Spring Landing Gear. Thin Walled Struct. 2023, 189, 110913. [Google Scholar] [CrossRef]
- Hang, C.; Cui, H.; Liu, H.; Suo, T. Micro/Meso-Scale Damage Analysis of a 2.5D Woven Composite Including Fiber Undulation and in-Situ Effect. Compos. Struct. 2021, 256, 113067. [Google Scholar] [CrossRef]
- Courtois, A.; Marcin, L.; Benavente, M.; Ruiz, E.; Lévesque, M. Numerical Multiscale Homogenization Approach for Linearly Viscoelastic 3D Interlock Woven Composites. Int. J. Solids Struct. 2019, 163, 61–74. [Google Scholar] [CrossRef]
- Zheng, T.; Huang, J.; Huang, K.; Yu, H.; Hong, C.; Guo, L. Different Effects of Interfacial Properties on the Tensile and Compressive Damage Mechanisms of 3D Woven Composites: Multiscale Damage Model and Numerical Comparative Study. Eng. Fract. Mech. 2023, 295, 109741. [Google Scholar] [CrossRef]
- Zheng, T.; Guo, L.; Benedictus, R.; Pascoe, J.-A. Micromechanics-Based Multiscale Progressive Failure Simulation of 3D Woven Composites under Compressive Loading with Minimal Material Parameters. Compos. Sci. Technol. 2022, 219, 109227. [Google Scholar] [CrossRef]
- Leos, A.; Vasylevskyi, K.; Tsukrov, I.; Gross, T.; Drach, B. Evaluation of Process-Induced Residual Stresses in Orthogonal 3D Woven Composites via Nonlinear Finite Element Modeling Validated by Hole Drilling Experiments. Compos. Struct. 2022, 297, 115987. [Google Scholar] [CrossRef]
- Dhimole, V.K.; Chen, Y.; Cho, C. Modeling and Two-Step Homogenization of Aperiodic Heterogenous 3D Four-Directional Braided Composites. J. Compos. Sci. 2020, 4, 179. [Google Scholar] [CrossRef]
- Pham, M.Q.; Bollengier, Q.; Rabe, D.; Lang, T.G.; Häntzsche, E.; Trümper, W.; Cherif, C.; Gereke, T. Meso-Scale Finite Element Model for Rib-Stiffened Composites with Biaxial Weft-Knitted Reinforcements. J. Compos. Sci. 2023, 7, 175. [Google Scholar] [CrossRef]
- Pankow, M.; Waas, A.M.; Yen, C.-F.; Ghiorse, S. Shock Loading of 3D Woven Composites: A Validated Finite Element Investigation. Compos. Struct. 2011, 93, 1347–1362. [Google Scholar] [CrossRef]
- Kyosev, Y.; Boussu, F. (Eds.) Advanced Weaving Technology; Springer International Publishing: Cham, Switzerland, 2022; ISBN 978-3-030-91514-8. [Google Scholar]
- Gardner, M. Mathematical Carnival: A New Round-up of Tantalizers and Puzzles from Scientific American; Vintage Books: New York, NY, USA, 1977; ISBN 978-0-394-72349-5. [Google Scholar]
- Doitrand, A.; Fagiano, C.; Irisarri, F.-X.; Hirsekorn, M. Comparison between Voxel and Consistent Meso-Scale Models of Woven Composites. Compos. Part A Appl. Sci. Manuf. 2015, 73, 143–154. [Google Scholar] [CrossRef]
- Ma, D.; González-Jiménez, Á.; Giglio, M.; Dos Santos Cougo, C.M.; Amico, S.C.; Manes, A. Multiscale Modelling Approach for Simulating Low Velocity Impact Tests of Aramid-Epoxy Composite with Nanofillers. Eur. J. Mech. A/Solids 2021, 90, 104286. [Google Scholar] [CrossRef]
- LS-DYNA Keyword User’s Manual, LS-DYNA R11, Volume I, II, III; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2002.
- Chamis, C.C. Simplified Composite Micromechanics Equations for Strength, Fracture Toughness and Environmental Effects. In SAMPE Quarterly; NASA Lewis Research Center: Cleveland, OH, USA, 1984; Volume 15. [Google Scholar]
- Daniel, I.M.; Ishai, O. Engineering Mechanics of Composite Materials, 2nd ed.; Oxford University Press: New York, NY, USA, 2006; ISBN 978-0-19-515097-1. [Google Scholar]
- Shah, S.P.; Maiarù, M. Effect of Manufacturing on the Transverse Response of Polymer Matrix Composites. Polymers 2021, 13, 2491. [Google Scholar] [CrossRef] [PubMed]
- HEXCEL HexTow IM7 Product Data Sheet; Hexcel: Stamford, CT, USA, 2023.
- 3M Matrix Resin 2894; AMD-747. Automotive & Aerospace Solutions Division 3M Center: St. Paul, MN, USA, November 2017.
- MCA. Interval-Based Computation of the Uncertainty in the Mechanical Properties and the Failure Analysis of Unidirectional Composite Materials. Available online: https://www.mdpi.com/2297-8747/27/3/38 (accessed on 18 September 2023).
- Naik, N.K.; Shankar, P.J.; Kavala, V.R.; Ravikumar, G.; Pothnis, J.R.; Arya, H. High Strain Rate Mechanical Behavior of Epoxy under Compressive Loading: Experimental and Modeling Studies. Mater. Sci. Eng. A 2011, 528, 846–854. [Google Scholar] [CrossRef]
- Fabbro, R.; Peyre, P.; Berthe, L.; Scherpereel, X. Physics and Applications of Laser-Shock Processing. J. Laser Appl. 1998, 10, 265–279. [Google Scholar] [CrossRef]



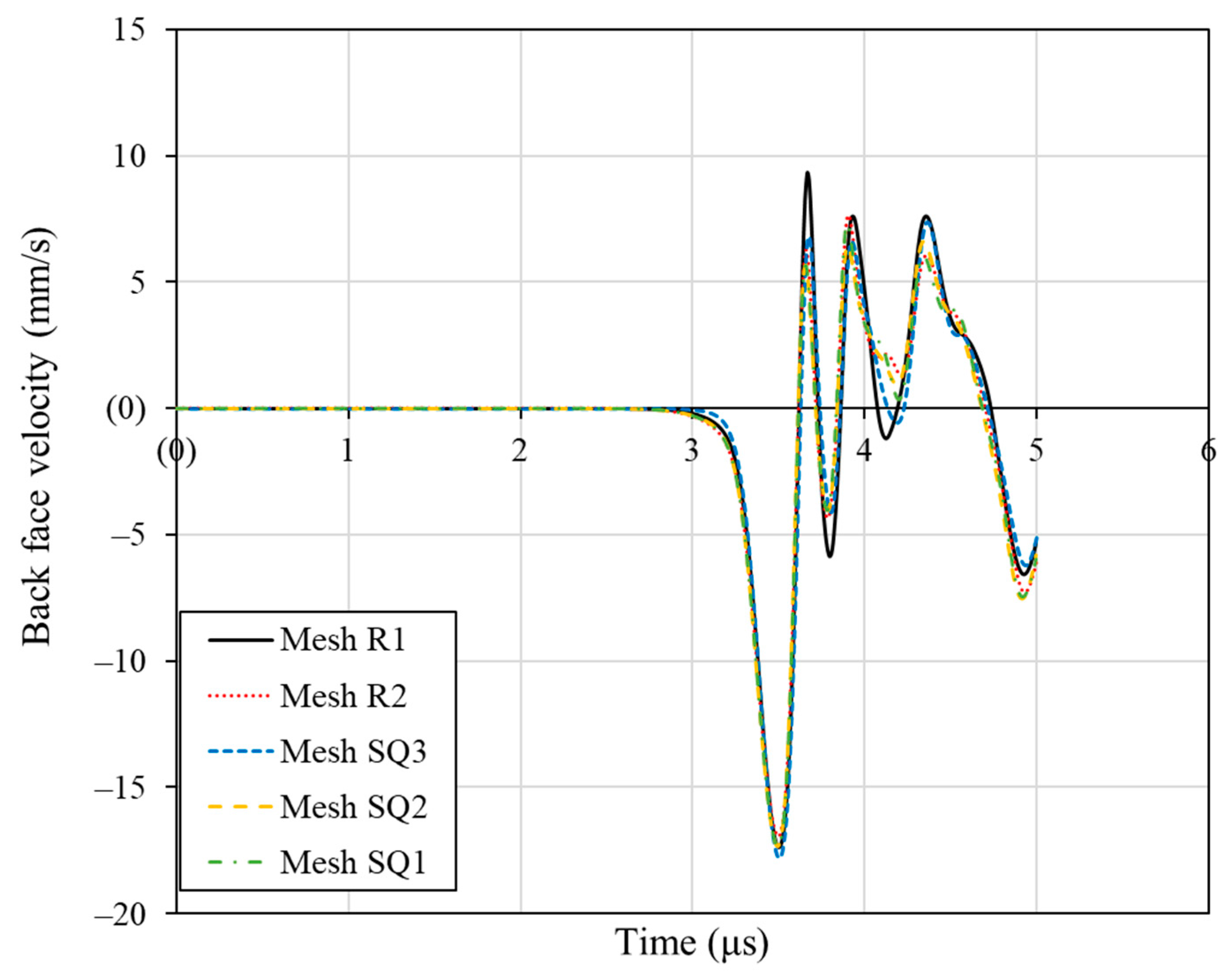
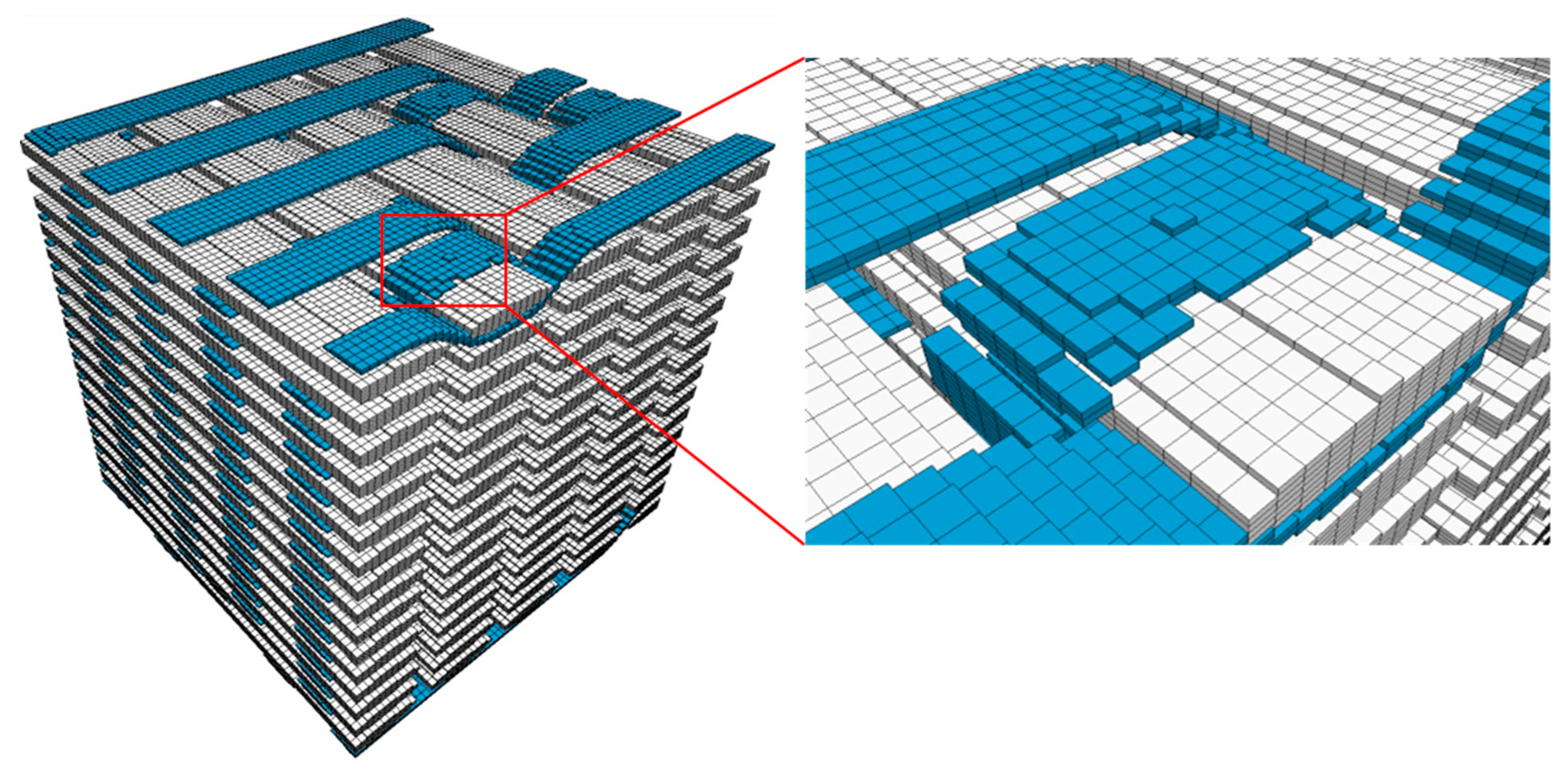

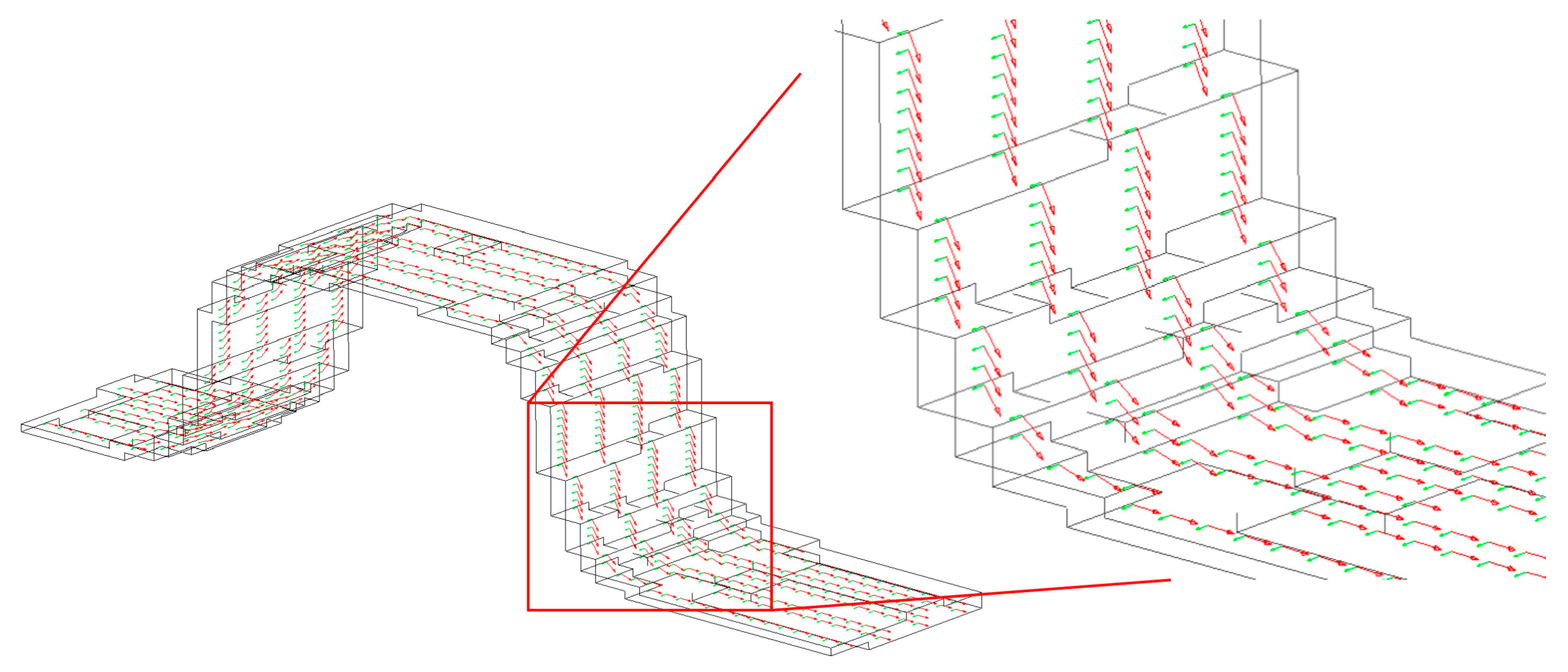




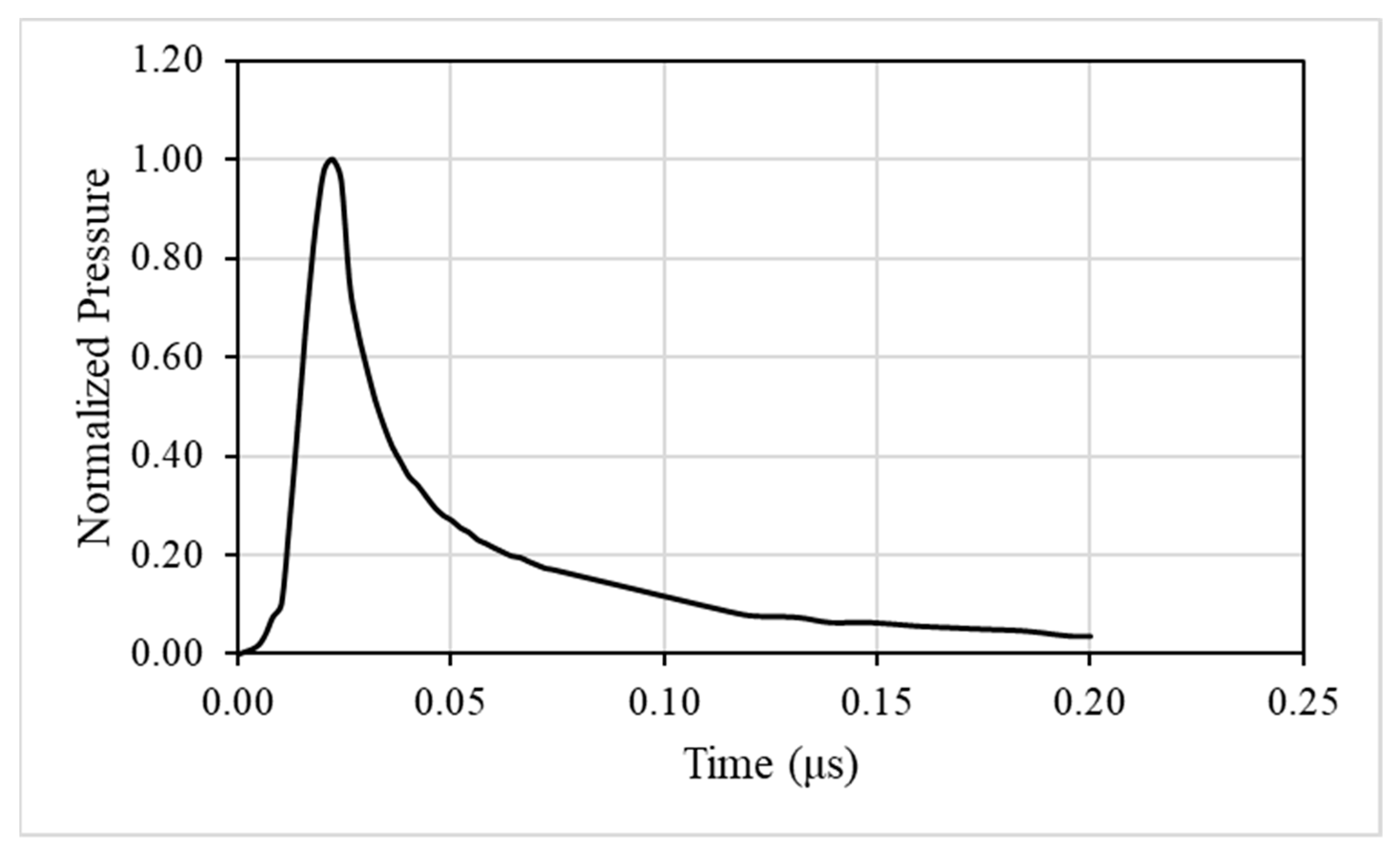







| Name | Element Type | Element Size |
|---|---|---|
| SQ1 | Square | 0.07 mm × 0.07 mm |
| SQ2 | Square | 0.1 mm × 0.1 mm |
| SQ3 | Square | 0.15 mm × 0.15 mm |
| R1 | Rectangle | 0.095 mm × 0.27 mm |
| R2 | Rectangle | 0.05 mm × 0.13 mm |
| Fiber Properties | Reference | |
|---|---|---|
| Elastic modulus, Ef11 (GPa) | 276 | [32] |
| Elastic modulus, Ef22f (GPa) | 19.5 | [32] |
| Elastic modulus, Ef33 (GPa) | 19.5 | [32] |
| Shear modulus, Gf12 (GPa) | 70 | [32] |
| Shear modulus, Gf23 (GPa) | 7.8 | [32] |
| Poisson’s ratio, Vf12 | 0.28 | [32] |
| Poisson’s ratio, Vf23 | 0.25 | [32] |
| Tensile strength, Fft (MPa) | 5516 | [33] |
| Matrix Properties | Reference | |
|---|---|---|
| Elastic modulus, Em (GPa) | 3.2 | [34] |
| Poisson’s ratio, Vm | 0.31 | [34] |
| Shear modulus, Gm (GPa) | 1030.53 | [34] |
| Tensile strength, Fmt (MPa) | 96 | [34] |
| Compressive strength, Fmc (MPa) | 96 | [34] |
| Shear strength, Fms (MPa) | 80 | [35] |
| Composite Fiber Bundle Properties | |
|---|---|
| Longitudinal elastic modulus, E11 (GPa) | 262.36 |
| Transverse elastic modulus, E22, E33 (GPa) | 15.54 |
| Shear modulus, G12 (GPa) | 16.11 |
| Shear modulus, G23 (GPa) | 5.87 |
| Poisson’s ratio, v12 | 0.282 |
| Poisson’s ratio, v23 | 0.268 |
| Longitudinal tensile strength, F1t (MPa) | 5245 |
| Transverse tensile strength, F2t, F3t (MPa) | 64.00 |
| Longitudinal compressive strength, F1c (MPa) | 20,610.69 |
| Transverse compressive strength, F2c, F3c (MPa) | 64.00 |
| Shear strength, F23 (MPa) | 57.57 |
| Shear strength, F12 (MPa) | 80 |
| Strain Rate, (1/s) | Strength, Xc (MPa) | Young’s Modulus, E (GPa) | Ultimate Strain, ɛmax (%) |
|---|---|---|---|
| 0.001 | 120 | 3.5 | 3.4 |
| 683 | 194 | 5.43 | 3.3 |
| 728 | 200 | 5.6 | 3.55 |
| 1229 | 206 | 6.13 | 3.5 |
| 1513 | 210 | 7.51 | 2.86 |
| 1890 | 214 | 8.13 | 2.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tserpes, K.; Kormpos, P. Detailed Finite Element Models for the Simulation of the Laser Shock Wave Response of 3D Woven Composites. J. Compos. Sci. 2024, 8, 83. https://doi.org/10.3390/jcs8030083
Tserpes K, Kormpos P. Detailed Finite Element Models for the Simulation of the Laser Shock Wave Response of 3D Woven Composites. Journal of Composites Science. 2024; 8(3):83. https://doi.org/10.3390/jcs8030083
Chicago/Turabian StyleTserpes, Konstantinos, and Panagiotis Kormpos. 2024. "Detailed Finite Element Models for the Simulation of the Laser Shock Wave Response of 3D Woven Composites" Journal of Composites Science 8, no. 3: 83. https://doi.org/10.3390/jcs8030083
APA StyleTserpes, K., & Kormpos, P. (2024). Detailed Finite Element Models for the Simulation of the Laser Shock Wave Response of 3D Woven Composites. Journal of Composites Science, 8(3), 83. https://doi.org/10.3390/jcs8030083







