Mechanisms of Component Degradation and Multi-Scale Strategies for Predicting Composite Durability: Present and Future Perspectives

Abstract

Composite materials, valued for their adaptability, face challenges associated with degradation over time. Characterising their durability through traditional experimental methods has shown limitations, highlighting the need for accelerated testing and computational modelling to reduce time and costs. This study presents an overview of the current landscape and future prospects of multi-scale modelling for predicting the long-term durability of composite materials under different environmental conditions. These models offer detailed insights into complex degradation phenomena, including hydrolytic, thermo-oxidative, and mechano-chemical processes. Recent research trends indicate a focus on hygromechanical models across various materials, with future directions aiming to explore less-studied environmental factors, integrate multiple stressors, investigate emerging materials, and advance computational techniques for improved predictive capabilities. The importance of the synergistic relationship between experimental testing and modelling is emphasised as essential for a comprehensive understanding of composite material behaviour in diverse environments. Ultimately, multi-scale modelling is seen as a vital contributor to accurate predictions of environmental effects on composite materials, offering valuable insights for sustainable development across industries.

1. Introduction

Composite materials and their constituents can undergo long-term degradation under specific environmental conditions. These are often multi-scale and multi-physics phenomena due to the nature of composites and the various environmental effects [1], the prediction of which warrants complex analytical and computational models. Furthermore, experimental campaigns are often limited in characterising the long-term behaviour of composites due to the extensive time scales at which degradation can occur. This said, accelerated testing methodologies [2,3,4,5] and long-term structural monitoring [6,7,8] can help to attenuate this issue. Nevertheless, the characterisation of the many combinations of degradation agents and composite material configurations is associated with significant material and financial expenses. With this in mind, developing accurate and efficient computational tools to predict the long-term durability of composite materials, though not able to fully replace experimental characterisation, would allow for significant cost reductions associated with experimental campaigns.

In this context, the adoption of multi-scale simulation schemes to predict the durability of composites has gained traction in recent decades. By linking the behaviour of materials at several length scales, these strategies allow for obtaining accurate and detailed solutions to complex problems in a way that would be impossible with classical phenomenological models. This being the case, the main goals of the present text are to summarise the state of the art regarding multi-scale strategies for composite material durability predictions and to outline the main future prospects in this field.

1.1. Degradation of Composite Materials

Composite materials are made by combining two or more material constituents so as to exploit their strengths and minimise their weaknesses. They allow for almost infinite material configurations, finding applications in a wide range of industries, including aviation, aerospace [9], and automotive [10], among others. In the industry, most composite structures are valued for their lightweight nature, high strength-to-weight ratio, corrosion resistance, and tailored properties that make them suitable for various specialised uses. Many composite structures are exposed to environmental effects when in service. These include extreme temperatures, humid and oxidative environments, and several others [11]. Because such effects tend to cause decreased lifespans, predicting their durability is of great interest to the community.

The notion of degradation implies that a deleterious change occurs in the chemical structure and physical properties of the material, resulting in deterioration of mechanical or thermophysical properties and even plasticisation, embrittlement, cracking, etc. Degradation exhibits a diverse array of classifications, each associated with distinct environmental influences. These include hydrolytic degradation, characterised by reactions involving water; thermo-oxidative degradation, induced by the combined effects of elevated temperatures and oxygen exposure; photo-oxidative degradation, driven by the interaction of polymers with light and oxygen; mechano-chemical degradation, resulting from mechanical forces; and biodegradation, wherein polymers undergo decomposition through the action of microorganisms in the environment [12,13].

Nevertheless, at the end of the life of the composite, its degradation turns out to be desirable for recycling purposes, as opposed to degradation during service lifetime, which is unwanted due to potential reliability implications. This paradoxical nature of composite material degradation reinforces the necessity of developing accurate models for diverse phenomena to predict the degradation of components and structures during and after their service life [11]. This imperative gains even greater significance in the contemporary industrial landscape, which, driven by environmental considerations, is marked by a discernible shift from thermosets to thermoplastics [14,15].

However, experimental studies regarding the degradation of composite materials are very limited, as such degradation occurs over years or even decades. Often, the exploration of degradation processes leans more towards practical applications, particularly within the framework of monitoring composite structures. Therefore, it can take years or decades to fully verify a component for application under in-service degradation conditions; in addition, the validation process involves extremely high costs. For this reason in particular, qualification by accelerated testing or numerical simulation could substantially decrease both time and costs, and as such represents both the present and future of the composite industry [16].

1.2. Multi-Scale Models

Single-scale phenomenological approaches have been utilised extensively in the context of computational mechanics for predicting the behaviour of different materials and structures. Such approaches are sufficient for many practical problems in engineering, particularly in quasi-static linear elastic simulations. Nonetheless, in many relevant contexts, the global physical behaviour of materials and structures is controlled by complex phenomena that occur at lower scales as well as by their intricate interactions [17], which single-scale phenomenological approaches are unable to model efficiently or accurately. In studying the durability and time-dependent behaviour of composite materials, which is the focus of this review, several phenomenological models remain relevant [1,18,19,20,21]. Nonetheless, employing multi-scale approaches to attain more accurate predictions has gained traction in recent years [11].

Computational multi-scale models emerged during the 1990s and have been continuously developed ever since, as the scientific community strives for more precise and accurate predictive tools in engineering [22]. Nowadays, the extensive amount of research devoted to these multi-scale approaches has provided highly accurate models for predicting and studying the behaviour of several classes of heterogeneous materials. For instance, multi-scale strategies have been established to model the failure of concrete [23] as well as of metallic [24,25,26] and polymer composite [27,28,29] structures. Furthermore, these strategies have been employed to solve mechanical problems at different combinations of length scales including at the macro- and meso-scales [30], the macro- and micro-scales [31,32], the meso- and micro-scales [33,34], the macro-, meso-, and micro-scales [35,36], and the micro- and nano-scales [37,38].

The main drawback of multi-scale approaches is that they tend to be computationally intensive. Several authors have explored techniques for enhancing the efficiency of these predictive models without significant losses of accuracy. Within this context, parallel computing [39], sub-incrementation schemes [40], and adaptive strategies [41,42] have all been studied over the past two decades. Moreover, reduced order modelling has become a hot topic of research, with machine learning techniques [43,44] employed to achieve fast simulations and precise numerical solutions. With this in mind, although multi-scale models are being continuously developed, delving into more complex formulations such as second-order computational homogenisation [45] that can speed up multi-scale simulations has become a focal point for researchers.

Developing accurate multi-scale models to predict the long-term behaviour of composite materials may warrant the inclusion of discrete mechanical theories such as molecular dynamics that can simulate physical and chemical phenomena at lower scales. That said, the adoption of efficient scale-bridging strategies that can help to avoid excessive computational costs is paramount.

1.3. Main Goal and Outline

The adoption of multi-scale numerical methods for predicting the environmental aging of composite materials is relatively recent. Nevertheless, in 2022, Krauklis and co-workers [11] systematised the main multi-scale modelling efforts in this field of research. The same authors performed an exhaustive review of the main degradation mechanisms present in composites and their components. Lin and co-workers [46] assessed the role of several multi-scale strategies in the prediction of the environmental degradation of composites. Furthermore, in 2017, Matous and co-workers [47] produced a review on the state of the art in the multi-scale modelling of complex solids and structures, highlighting future directions and challenges. In this contribution, we aim to assess the state of the art regarding multi-scale models for durability prediction of composite materials, including the underlying degradation mechanisms, and we expand on previous reviews by incorporating recent developments and discussing the role of more advanced numerical strategies.

To achieve this goal, the remainder of the paper is divided into four sections. In Section 2, the main environmental effects influencing the long-term behaviour of composite materials are discussed, along with a review of some of the most relevant analytical models in this regard. In Section 3, multi-scale approaches utilised in the literature are briefly reviewed, from discrete and continuum mechanics theories to scale-bridging approaches. In Section 4, the most relevant multi-scale modelling efforts in the field of composite material durability are discussed. Finally, in Section 5, the current trends and future prospects in the multi-scale modelling of composite material degradation are summarised.

2. Environmental Effects in Composite Materials

A wide range of composite materials are utilised in modern-day engineering applications. The classification of composites primarily revolves around the nature of the matrix material and the reinforcements, yielding a rich spectrum of materials tailored for specific purposes. The following are among the most widely used categories of composites:

• Polymer matrix composites (PMCs): PMCs constitute a prominent category of composite materials, wherein a polymer matrix binds reinforcing elements to create materials of enhanced strength and versatility. This category can be divided into two sub-categories, namely, particulate composites and fibre-reinforced polymers (FRPs). The latter group is likely one of, if not the most utilised and researched composite materials types in engineering. The fibre reinforcements can be, for example, carbon, glass, or aramid embedded in a polymer matrix such as epoxy, polyester, vinyl ester, or many others.
• Concrete-based composites: Advancements in civil engineering have led to the growing reinforcement of traditional concrete structural elements with high-strength fibres, additives, steel, or FRP bars [48,49,50,51]. The introduction of such reinforcement leads to valuable increases in the strength-to-weight ratio and durability of concrete structures. Nonetheless, they can exhibit time-dependent behaviour under certain environmental and loading conditions [52,53,54,55,56]. Furthermore, in civil construction many structural elements are permanently exposed to degradation agents such as water. This has motivated the scientific community to put notable efforts into optimising both the design of concrete-based composite structures [57,58,59,60] and the production aggregate [61,62,63], to improve durability while utilising more sustainable production routes.

In researching better composites for specific situations, a number of emerging trends in the field of composites are shaping the future of materials science. Examples of such advanced composites include:

• Biocomposites: From the point of view of sustainability, these composites use natural fibres and a biodegradable polymeric matrix, contributing to the growing emphasis on environmentally conscious material solutions [64]. The long-term behaviour of biodegradable polymers, in particular, is already the focus of extensive research [65,66,67,68,69].
• Carbon nanotubes (CNTs): The use of carbon nanotubes as fibre reinforcement offers exceptional electrical conductivity as well as great strength [70,71].
• Hybrids: Hybrid composite materials consist of mixtures of different types of reinforcements and/or matrices, resulting in a synergistic blend of properties appropriate for the application requirements [72].

Within the context of the present work, ceramic matrix composites (CMCs) and carbon–carbon composites are not further addressed, as they do not exhibit significant susceptibility to environmental degradation. Moreover, metal matrix composites (MMCs), despite undergoing deterioration under specific environments (namely, corrosion and creep), were considered to be outside the scope of this text. Therefore, the emphasis is placed primarily on concrete-based and polymer matrix composites, as these are the most widely researched in the scientific community regarding long-term degradation; more specifically, the latter have mostly been studied as fibre-reinforced polymers (FRPs).

Nowadays, the approach of certifying a component ultimately goes down to the ply level, without considering the properties of the micro-constituents. However, at the molecular scale, the structure itself can determine local properties which can affect higher scales; for instance, the structure of the monomers can affect the solubility and local affinity to surfaces, which in turn can influence the hydrolysis of a polymeric matrix. Incorporating these finer details into certification processes can enhance the accuracy and reliability of models, ultimately leading to better predictions of material behaviour and performance.

2.1. Hygrothermal Aging of FRPs

This section of the work focuses on one of the most extensively studied environmental degradation effects, namely, hygrothermal degradation. Hygrothermal degradation refers to deterioration or damage that occurs in materials, especially polymers or composites, due to the combined effects of moisture and temperature.

FRPs can usually be divided into three micro-constituents: the fibres (reinforcement), the polymeric matrix, and the composite interphase. Each behaves differently under the environmental effects that they are subject to, warranting degradation models for each constituent. This approach emphasises the necessity of nuanced multi-scale investigations for the accurate prediction of degradation.

Figure 1 illustrates the effects of hygrothermal environments on the degradation of FRPs along with the manifestation of such degradation in the various constituents. The different phenomena presented in the image are described in the following sections.

2.1.1. Fibre Degradation Models

Although the most common type of fibres in FRPs are glass fibres (GFs) and carbon fibres (CFs), the increasing use of alternatives such as basalt, aramid [75], and natural fibres [76,77] has attracted growing interest in the research community. The careful study of the hygrothermal degradation of each of these fibre types is crucial for modelling the behaviour of composite structures under these environmental conditions.

In order to model the degradation of glass fibres, it is necessary to understand the molecular mechanism of interactions. Herein, it is understood that degradation means the mass loss of the glass fibres [78].

When in contact with water, several chemical reactions may occur simultaneously. At first, the reactions take place at independent rates, known as Phase I. Later, in Phase II, the process becomes limiting and dominates the behaviour [79]. In the initial disorderly Phase I, several processes occur at the same time, such as ion exchange, gel formation, and dissolution. In the longer term, hydrolytic degradation is governed by the glass dissolution mechanism and follows the zero-order reaction kinetics. It must be noted that these kinetics depend on the surface in contact, which is proportional to the radius; therefore, as the dissolution continues, the radius decreases, and hence the rate of mass loss also decreases [11].

There are several models applicable to glass fibre hygrothermal degradation, including the shrinking cylinder model [80], the contracting cylinder model [81], and the dissolving cylinder zero-order kinetics (DCZOK) presented by Krauklis and Echtermeyer [82]. The latter model can predict the dissolution in phase II under various environmental conditions (temperature, stress, pH) as well as the mass loss, fibre radius, crack growth, and strength loss kinetics. The DCZOK assumes that:

• In surface area calculations, all fibres are considered to have the same beginning radius, while the cross-sectional surface area at the ends of the fibres is assumed to be insignificant.
• The length and density of the GFs are both assumed to remain constant throughout the dissolving process.

Moreover, the following equation models the reduction of the glass fibre radius [82]:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}t\le t_{st}:\hfill & r\left(t\right)=r_0-\frac{K_0^l{\xi }_{\mathrm{sizing}}}{{\rho }_{\mathrm{glass}}}t\hfill \\ t>t_{st}:\hfill & r\left(t\right)=r_{t_{st}}-\frac{K_0^{II}{\xi }_{\mathrm{sizing}}}{{\rho }_{\mathrm{glass}}}\left(t-t_{st}\right)\hfill \end{array}\right.\end{array}$$

(1)

where r is the glass fibre radius after time t, $r_0$ is the initial glass fibre radius, ${\rho }_{glass}$ is the density of glass fibre, $K_0^I$ and $K_0^{II}$ are the rate constants for Phase I and Phase II, respectively, ${\xi }_{sizing}$ is the protective effect of sizing, and $r_{t_{st}}$ is the glass fibre radius after time $t_{st}$ when the steady state is reached.

As previously mentioned, the DCZOK model takes into account the influence of temperature, acidity, and mechanical stresses. The increase in temperature tends to accelerate the dissolution, as it follows the Arrhenius principle [83,84]:

$$K=A{e}^{-\frac{E_A(pH,\sigma )}{RT}}.$$

(2)

The activation energy $E_A$ depends on the acidity of the solution and stresses. The acidity has greater influence over dissolution, which accelerates in the extreme values of the pH spectrum, and decreases the degradation rate in the neighbourhood of the neutral value [85].

All three environmental conditions affect the interactions between the material, environmental energy, and activated interactions, and consequently impact the dissolution rate constants $K_0$ [11]:

$$\frac{\partial m}{\partial t}=2n\pi l\left(r_0{K}_0{\xi }_{\mathrm{sizing}}-\frac{{\left(K_0{\xi }_{\mathrm{sizing}}\right)}^2}{{\rho }_{\mathrm{glass}}}t\right);$$

(3)

substituting the dissolution rate constant $K_0$ by eq:Arrenhuiseq, we have

$$\frac{\partial m}{\partial t}=2n\pi l\left(r_{0}A{e}^{-\frac{E_A(pH,\sigma )}{RT}}{\xi }_{sizing}-\frac{{\left(A{e}^{-\frac{E_A(pH,\sigma )}{RT}}{\xi }_{sizing}\right)}^2}{{\rho }_{glass}}t\right),$$

(4)

where m is the total cumulative mass dissolved after time t, l and n are the length and the number of glass fibres, respectively, $K_0$ is the rate constant, A is the pre-exponential factor, R is the gas constant (8.314 J/mol.K), T is the temperature in Kelvin, and $E_A$ is the activation energy, which is a function of the acidity (pH) and the mechanical stress ($\sigma$).

Therefore, the complete expression of the dissolving cylinder zero-order kinetics model is provided as follows [82].

$$\begin{array}{c}\hfill \left\{\begin{array}{c}t\le t_{st}:m_{\mathrm{dissolved}}=n\pi l\left(2r_0{K}_0^{I}t-\frac{K_0^{I2}}{{\rho }_{\mathrm{glass}}}{t}^2\right)\hfill \\ t>t_{st}:m_{\mathrm{dissolved}}=m_{{\mathrm{dissolved}}_{t_{st}}}+n\pi l\left(2r_{t_{st}}{K}_0^{II}\left(t-t_{st}\right)-\frac{K_0^{II2}}{{\rho }_{\mathrm{glass}}}{\left(t-t_{st}\right)}^2\right)\hfill \end{array}\right.\end{array}$$

(5)

It should be noted that $m_{{dissolved}_{tst}}$ and $r_{t_{st}}$ are the mass loss and the fibre radius, respectively, after time $t_{st}$ when Phase I ends. The mechanical strength of a fibre ${\widehat{\sigma }}_f$ can be described by the Griffith equation [86]:

$${\widehat{\sigma }}_f=\sqrt{\frac{2E\gamma }{\pi a}}=\frac{K_{Ic}}{\gamma \sqrt{\pi a}}$$

(6)

where E is the Young’s modulus, $\gamma$ is the surface energy of the fibre, $K_{IC}$ and a are the fracture toughness and crack length, respectively, and Y is the geometry factor considered for a rod with a crack, which can be found in the work of Bush [87].

Furthermore, Echtermeyer et al. have issued the hypothesis that the crack length a returns to the initial crack length $a_0$ as the process evolutes, and that the velocity of fracture is calculated by the difference in the crack growth and the radius shrinkage due to water degradation [78]:

$$a\left(t\right)=a_0+\left(\frac{da}{dt}-\frac{dr}{dt}\right)t$$

(7)

where $\frac{da}{dt}$ is the crack growth rate and $\frac{dr}{dt}$ is the rate of the fibre’s radius. Starting from this equation, and through the introduction of other equations described by Echermeyer et al. [78], we arrive at the final equation

$$a\left(t\right)=a_0+\frac{\left(\vartheta -{\xi }_{\mathrm{sizing}}\right)K_0}{{\rho }_{\mathrm{glass}}}t.$$

(8)

It should be noted that $\vartheta$ is the crack sharpness amplification factor. Combining the classic concepts of Griffith [86] with the crack growth kinetics model allows for the prediction of the strength of glass fibre over time:

$$\left\{\begin{array}{cc}t\le t_{st}:\hfill & {\widehat{\sigma }}_f\left(t\right)=\frac{{\widehat{\sigma }}_{f0}}{\sqrt{1+\frac{K_0^I\left(\vartheta -{\xi }_{\mathrm{sizing}}\right)}{a_0{\rho }_{\mathrm{glass}}}t}}\hfill \\ t>t_{st}:\hfill & {\widehat{\sigma }}_f\left(t\right)=\frac{{\widehat{\sigma }}_f^I}{\sqrt{1+\frac{K_0^{II}\left(\vartheta -{\xi }_{\mathrm{sizing}}\right)}{a_0{\rho }_{\mathrm{glass}}}t}}\hfill \end{array}\right.$$

(9)

where ${\widehat{\sigma }}_f$ is the strength after time t, ${\widehat{\sigma }}_{f0}$ is the static strength, and ${\widehat{\sigma }}_f^I$ stands for the strength at the end of Phase I.

Although this state-of-the-art model can predict the degradation of glass fibres, the DCZOK model is unable to link the fibre strength loss to the composite laminate’s strength loss, as the effect of the encapsulation of the glass fibre in a polymer matrix is not yet fully understood [88]. It is known that both the matrix and the interphase protect and slow down the degradation of the fibres [89]. Even the orientation of the fibres can influence their dissolution, with fibres oriented in the hoop direction tending to degrade slower than those oriented transversely, as reported by Krauklis et al. [89].

Regarding the effects of other liquids on glass fibre properties, in the literature there is only one study for toluene, which reported that the fibres are inert with regard to this degradation agent [78].

Concerning the hygrothermal degradation of carbon fibres, there is only one study, from Echtermeyer et al. [78], whose main conclusion was that these fibres are in fact chemically inert with regard to both water and toluene. This was demonstrated via experimental testing, which showed that carbon fibres did not show any strength changes within the experimental error.

Currently, there is a notable lack of degradation models specifically designed for basalt fibres. Nevertheless, the environmental aging and stability of basalt fibres have been explored in various studies. Notably, the work of Wei et al. (2011) focused on the degradation of a BFRP in seawater solutions, although basalt fibre degradation itself was not their primary focus [90]. Similarly, Fan et al. [91] and Glaskova-Kuzmina et al. [92] delved into the hygrothermal aging context for BFRP, though without studying basalt fibre degradation separately. Wu et al. (2015) investigated the degradation of the tensile properties of basalt fibres and BFRP in diverse corrosive environments [93]. They concluded that basalt fibres are resistant to corrosion in salt and water solutions, while they show reduced resistance in alkaline and acidic solutions. In addition, they observed that when the fibres have greater strength under to these corrosive environments when embedded in the matrix, which can be explained by the protective effect granted by the matrix [93]. More recently, Le Gué et al. (2024) tested basalt fibres in seawater under different temperature conditions, observing a decrease in strength of 40–60%, followed by stabilisation at a plateau which was mainly influenced by the temperature [94].

Aramid fibres are renowned for their exceptional strength, high modulus, and abrasive resistance. However, aramid fibres can undergo degradation under specific environmental conditions and/or mechanical stresses. The main mechanisms of aramid fibres in the scope of environmental degradation are hydrolysis, oxidation, and thermal decomposition. The works of Horta et al. [95,96] have contributed immensely to understanding the degradation kinetics of diverse aramid fibres, such as MPD-I and PPD-T.

In the literature, there is no model for the degradation and loss of properties of natural fibres, although it is known that they are essentially subject to plasticisation and swelling due to water absorption as well as to biodegradation by microorganisms [76,77]. Moreover, degradation in the alkaline and mineral-rich environment of thecement matrix was studied by Wei [97], who concluded that an alkaline environment tends to increase water absorption, leading to quicker degradation. However, due to the uncertainties in the kinetics data and lack of parameterisation for mineralisation, further investigation of the degradation of natural fibres in cement matrices remains necessary.

The following is a summary of fibre degradation during hygrothermal aging:

• The degradation of glass fibres is well-documented, with established mechanisms and defined models guiding the current understanding.
• Carbon fibres are unaffected, and are able to withstand hygrothermal conditions.
• Basalt fibres have been extensively studied in composite contexts; however, the lack of a specific fibre degradation model currently presents a challenge.
• Aramid fibres with well-established degradation mechanisms can form the basis for developing future models.
• While the mechanism of deterioration in natural fibres is recognised, there is no precise model for hygrothermal environments.

2.1.2. Matrix Degradation Models

Understanding the phenomenological causes of degradation is crucial; however, equally essential is the ability to articulate these phenomena through mathematical formulations. In this section, existing constitutive models that describe the degradation of various components in composite materials, namely, the polymer matrix and interphase, are assessed.

Solubility

Exposure to liquid environments is a key factor in the degradation of composite materials, with effects predominantly manifesting within the material bulk rather than on its surface. Degradation in such environments is often driven by solubility effects, as discussed by Arnold [98]. The overall solubility of a liquid within a composite is influenced by its solubility in the polymer matrix, reinforcement, and interphase region, as well as by the presence of liquid in voids, cracks, and debonded regions. Most degradation phenomena occur at the polymer matrix level, where the solubility of liquid molecules in a polymer is primarily dictated by the degree of chemical interaction between the liquid and polymer molecules. Enhanced solubility is typically observed when there is good chemical compatibility, characterised by similar secondary bond forces. Solubility theories employ a thermodynamic energy balance, positing that for a liquid molecule to dissolve in a polymer, the overall free energy change must be negative. This change comprises an entropy term, favouring mixing and increasing with temperature, and an enthalpy term, which is dependent on chemical interactions and solubility parameters. Hansen [99] introduced a model considering dispersive, polar, and hydrogen bonding interactions independently. This model employs three terms: ${\delta }_{\mathrm{d}},{\delta }_{\mathrm{p}}$, and ${\delta }_{\mathrm{h}}$, accounting for these interactions. The terms are related to dispersive, polar, and hydrogen bonding, respectively [98]. Solubility is maximised when minimising the following expression:

$${\left[{\left({\delta }_{\mathrm{dp}}-{\delta }_{\mathrm{ds}}\right)}^2+{\left({\delta }_{\mathrm{pp}}-{\delta }_{\mathrm{ps}}\right)}^2+{\left({\delta }_{\mathrm{hp}}-{\delta }_{\mathrm{hs}}\right)}^2\right]}^{1/2}$$

(10)

where parameters with the subscript p refer to the polymer and those with s to the solution. This approach generally yields good correlations, showing higher solubility in combinations where polymer and liquid solubility parameters are closely aligned, although it is not universally applicable [98].

Diffusion

Degradation in liquid environments can also be related to water diffusion. For polymers, this phenomenon can normally be described using Fickian models. For a majority of polymers and polymer composites, diffusion is the dominant mechanism of water uptake. It is represented by Fick’s second law, which for orthotopic materials in Cartesian coordinates is [100]

$$\frac{\partial c}{\partial t}=\nabla ·(D\nabla c)=D_{11}\frac{{\partial }^{2}c}{\partial x^2}+D_{22}\frac{{\partial }^{2}c}{\partial y^2}+D_{33}\frac{{\partial }^{2}c}{\partial z^2},$$

(11)

where $c(x,y,z,t)$ is the concentration of the diffusing water at a point with coordinates $(x$, $y,z)$ in Cartesian space at time $t,D$ is the positive definite symmetric matrix of diffusion coefficients $D_{\mathrm{ij}}$, and $D_{11},D_{22}$, and $D_{33}$ are the diffusion constants in directions 1, 2, and 3, respectively. The directional diffusivities can be determined from weight gain curves for samples with edges/faces sealed by an impermeable material to eliminate water diffusion from two of three directions, although this approach can be limited by the possibility of dissolution or degradation when subjected to prolonged exposure to water and elevated temperatures.

The structural micromechanical model can also predict diffusivity in anisotropic materials, though only if the diffusion parameters of the microconstituent are known. In contrast, in isotropic materials the diffusion is characterised by the coefficient D. The water content $w\left(t\right)$ is obtained as follows [11]:

$$\frac{w\left(t\right)-w_0}{w_{\infty }-w_0}=1-\frac{8}{{\pi }^6}\sum _{k=1}^{\infty }\sum _{n=1}^{\infty }\sum _{m=1}^{\infty }\frac{{\left[1-{(-1)}^k\right]}^2{\left[1-{(-1)}^n\right]}^2{\left[1-{(-1)}^m\right]}^2}{k^2{n}^2{m}^2}{e}^{-{\lambda }_{k,n,m}^{2}Dt}$$

(12)

where

$${\lambda }_{k,n,m}^2={\lambda }_k^2+{\lambda }_n^2+{\lambda }_m^2={\left(\frac{\pi k}{h}\right)}^2+{\left(\frac{\pi n}{b}\right)}^2+{\left(\frac{\pi m}{l}\right)}^2$$

(13)

and where $w_{\infty }$ and $w_0$ are the equilibrium and initial water contents, respectively, while $h, b$, and l are the geometrical features of the arbitrary body. In the case of the assumption of a 1D diffusion problem, the previous equation can be simplified as follows:

$$w\left(t\right)=w_{\infty }\left[1-\frac{2}{{\pi }^2}\sum _{k=1}^{\infty }\frac{{\left[1-{(-1)}^k\right]}^2}{k^2}{e}^{\left[-{\left(\frac{\pi k}{h}\right)}^{2}Dt\right]}\right]$$

(14)

which can be approximated by the following equation:

$$w\left(t\right)=w_{\infty }\left[1-e^{-7.3{\left(\frac{Dt}{h^2}\right)}^{0.75}}\right]=w_{\infty }[1-G\left(t\right)].$$

(15)

Additionally, in the first phase of water absorption, the previous equation can be simplified to

$$w\left(t\right)=4w_{\infty }\sqrt{\frac{Dt}{\pi h^2}}.$$

(16)

However, Fickian diffusion possesses two requisites, namely, linearity of w vs. $\sqrt{t}$ at the early stage (which is valid for most cases) and that $w\left(t\right)$ asymptotically approaches an equilibrium at the late stage. If the second condition is not achieved, the behaviour is known as non-Fickian diffusion.

Non-Fickian diffusion can be described by two-phase sorption models. The Langmuir two-phase model distinguishes between a free diffusion phase and a bound phase of a penetrant, with the latter not involving diffusion [101]. This model utilises Fick’s law for free-phase water, where the concentration gradient serves as the driving force for diffusion. This model adds two probability parameters $\alpha$ and $\beta$, which respectively correspond to the probability of a water molecule transitioning from combined state to free phase and the opposite [101]:

$$w\left(t\right)=w_{\infty }\left[1-\frac{\beta }{\alpha +\beta }{e}^{-\alpha t}-\frac{\alpha }{\alpha +\beta }G\left(t\right)\right].$$

(17)

Other two-phase models are based on distinct approaches, such as considering the viscoelastic nature of polymer [102], a conceptual approach viewing a polymer as a two-phase system [103], or the coupled action of water diffusion and structural relaxation in the polymer network [104].

An important aspect to emphasise here is the fact that although the non-Fickian models provide good results, Fick’s model remains the most appropriate model for hydrothermal degradation, as noted by Krauklis et al. [11].

Plasticisation

Plasticisation results in increased flexibility of the polymer chains due to exposure to low molecular liquids, for instance, water. It leads to the softening of the polymer, i.e., the glass transition temperature $T_g$ decreases and, assuming that the shift function [105] is known, can be estimated using the time–temperature–plasticisation superposition principle (TTPSP):

$$log\left(a_{\mathit{\text{dry-to-plast}}}\right)=-\frac{-E_A}{2.303R}\left(\frac{1}{T_{g_{plast}}}-\frac{1}{T_{g_{dry}}}\right),$$

(18)

where $a_{\mathit{\text{dry-to-plast}}}$ is the shift function, $E_A$ is the activation energy, and $T_{g_{plast}}$ and $T_{g_{dry}}$ are the glass transition temperatures of the plasticised and dry material, respectively [11].

While other properties may also suffer from plasticisation, such as thermal, dielectric, and other mechanical properties, these are connected to changes in the molecular level [106].

Swelling

When exposed to water or humidity, some polymers can suffer from hygroscopic swelling, in which the volume increases and mechanical properties can deteriorate. Diverse works that have researched the swelling of FRPs [107,108,109,110].

Hygroscopic swelling of polymers tends to be isotropic and linear with the water content:

$${\epsilon }_h=\beta w$$

(19)

where ${\epsilon }_h$ is the hygroscopic strain, $\beta$ is the coefficient of the hygroscopic expansion (CHE), and w is the moisture concentration [111]. It should be noted that in orthotopic laminates the coefficient of hygroscopic expansion differs in the directions, which requires ${\beta }_x,{\beta }_y$, and ${\beta }_z$ to be be determined via experimental testing.

It is possible to analytically predict hygroscopic swelling with a model based on linear elasticity, which was validated by both finite element analysis and experimental results in the work of Krauklis and colleagues [112]. The axial swelling can be calculated by assuming a parallel model with the fibre and matrix:

$${\epsilon }_x={\epsilon }_f=\frac{{\sigma }_f}{E_f}=\frac{{\sigma }_m}{E_f}\frac{1-V_f}{V_f}=\frac{E_m{\epsilon }_m}{E_f}\frac{1-V_f}{V_f},$$

(20)

$${\beta }_x=\frac{{\epsilon }_x}{W_c}=\frac{{\sigma }_m}{W_c{E}_f}\frac{1-V_f}{V_f}=\frac{E_m{\epsilon }_m}{W_c{E}_f}\frac{1-V_f}{V_f}=\frac{E_m{\beta }_m}{E_f}\frac{1-V_f}{V_f},$$

(21)

where ${\epsilon }_x$ is the composite axial strain, ${\epsilon }_f$ is the fibre axial strain, ${\sigma }_f$ is the stress transferred to the fibre, $E_f$ is the Young’s modulus of the fibre, ${\sigma }_m$ is the stress in the matrix, $E_m$ is the Young’s modulus of the matrix, ${\epsilon }_m$ is the matrix swelling strain, $V_f$ is the fibre volume fraction, ${\beta }_x$ is the axial swelling coefficient, $W_c$ is the moisture content in the composite, and ${\beta }_m$ is the matrix swelling coefficient.

On the other hand, the transverse swelling strain is considered as a serial connection between the matrix and the fibres, as follows:

$${\epsilon }_y=V_f{\epsilon }_f+(1-V_f){\epsilon }_m.$$

(22)

Since the transverse swelling is null for the fibres, we have

$${\epsilon }_y=(1-V_f){\epsilon }_m,$$

(23)

$${\beta }_y=\frac{{\epsilon }_y}{W_c}=\frac{(1-V_f){\epsilon }_m}{W_c}=(1-V_f)\frac{W}{W_c}{\beta }_m,$$

(24)

where ${\epsilon }_y$ is the composite transverse swelling strain and W is the moisture content in the matrix.

Hydrolysis

The hydrolysis process involves the insertion of water molecules into the polymer chain, resulting in breakage of the covalent bonds. This can weaken the overall structure of the polymer and reduce its mechanical properties. Examples of polymers that suffer irreversible degradation by hydrolysis include polyamides, studied in detail in the works of Mazan et al. [113,114], who reported that the main mechanisms of property change were chemi-crystallisation and induced chain scission. In addition, they were able to perform multi-scale simulation of the degradation phenomena based on a quantitative structure–property relationship (QSPR) approach [113].

On the other hand, Vieira et al. studied the hydrolytic degradation of biodegradable polymers and found that the decreases in time dependence of the tensile strength $\sigma$ in PLA-PCL blends was related to the reduction of molecular weight $M_n$ [66,115]. As a first-order kinetic mechanism, the hydrolytic damage $d_h$ can be defined as

$$\begin{array}{c}\hfill d_h=1-\frac{{\sigma }_t}{{\sigma }_0}=1-\frac{M_{nt}}{M_{n0}}=1-e^{-ut},\end{array}$$

(25)

where the subscripts 0 and t refer to the parameters at the initial time and after time t has elapsed, respectively, and u is the degradation rate. It should be noted that it is possible to use this approach for other types of polymers as well.

2.1.3. Interphase Degradation Models

The interphase, referred to as the sizing in the context of FRPs, plays a crucial role in determining the performance and properties of composite materials. The sizing can be a thin layer of chemical treatment or coating on the surface of the reinforcing fibres, and has the following main functions:

• Adhesion: Sizing promotes a better adhesion between the fibres and the polymer matrix by creating chemical bonds or interactions at the interface, thereby ensuring strong bonds.
• Protection: Sizing can shield the fibres from environmental factors that would otherwise lead to degradation, such as moisture or chemical exposure.
• Stress/load transfer: Sizing ensures that the load is efficiently distributed throughout the composite, optimizing its mechanical performance [116].

Nonetheless, the quality of the interphase highly depends on the adhesional contact and the presence of flaws, which can be created or grown due to hydrolysis, as seen in Figure 2. These can eventually lead to debonding between the reinforcement and the matrix, splitting, and matrix cracks [117,118]. However, there is currently no direct measurement approach that can quantify the interphase loss due to environmental aging; thus, the research community is very keen to develop modelling techniques for the interphase.

In [117], an approach was proposed for hygrothermal aging of glass fibre-reinforced polymers based on mass balance and the already-known aging mechanism. Notwithstanding this, the connection between the mass loss and the interfacial loss remains to be achieved. The mass balance can be expressed by the following equation [11]:

$$\begin{array}{cc}\hfill m_{interphase}\left(t\right)=& m_{dry}+m_{wateruptake}\left(t\right)+m_{oxidation}\left(t\right)\hfill \\ & -m_{leaching}\left(t\right)-m_{glassdissolution}\left(t\right)\hfill \\ & -m_{gravimetric}\left(t\right)\hfill \end{array}$$

(26)

This Equation (26) allows the degradation kinetics of the interphase to be deduced; however, there is still no proper connection between the mass loss and strength loss [117].

2.2. Thermo-Oxidative Aging of FRPs

Thermo-oxidative aging of Fibre-Reinforced Polymers (FRPs) is a process in which the material undergoes degradation due to elevated temperatures and oxidative environments. This process can significantly impact the mechanical, thermal, and chemical properties of FRPs, affecting their performance and reliability in various applications.

The fibres tend to be resistant to such effects, although the matrix is susceptible to deterioration of its properties. At the molecular level, the polymer chain might suffer from chain scission and crosslinking [119]. The former involves the breaking of chemical bonds within molecular chains, reducing their length and molecular weight, which leads to a decrease in the glass transition temperature and increases the crystallisation and embrittlement of the matrix over time. Meanwhile, the latter diminishes molecular mobility by linking chains, which also leads to embrittlement of the polymer matrix. This contributes to the formation of microcracks and negatively impacts the fatigue life of the material.

In 2021, Bahrololoumi et al. [120] provided a computationally efficient model to describe mechanical performance loss due to chemical aging caused by competition between chain scission and crosslink formation/dissolution. The chemical oxidation rate during thermo-oxidative aging is characterized as follows [121]:

$$-\frac{d\left[P\right]}{dt}=k{\left[P\right]}^q$$

(27)

where $\left[P\right]$ is the chemical compound concentration of P, k is the coefficient of reaction rate, and q is the reaction order, which is usually equal to 1. Under homogeneous conditions, low stretches throughout aging, and no diffusion-limited oxidation, k follows the Arrhenius function and is only temperature-dependent, as provided by the following mathematical equation:

$$k={\tau }_0{e}^{-\frac{E_a}{RT}}$$

(28)

where ${\tau }_0\left[s^{-1}\right]$ is a pre-exponential factor, $R=8.314$ [J/(K·mol)] is the ideal gas constant, $E_a$ [J/mol] is the activation energy of the chemical reaction, and T is the temperature. Then, solving Equation (27) and substituting into Equation (28) provides

$$\left[P\right]=A_0{e}^{(-{\tau }_0{e}^{-\frac{E_a}{RT}}t)},$$

(29)

where $A_0$ is a function of the temperature.

2.3. Photo-Oxidative Aging of FRPs

When subject to UV light, most reinforcements for FRP composites, with the exception of some natural fibres, tend to be generally resistant to photo-oxidative degradation. Manufacturers often apply protective coatings or incorporate UV stabilizers; when in service, it may be desirable to avoid contact with light.

However, photo-oxidative effects have a more significant impact on the matrix than on the fibres, which can involve chain scission, backbone modifications, and/or photo-oxidative crosslinking [11].

In 2021, Mohammadi et al. [122], based on the work mentioned in the subsection on the thermo-oxidative effect [120], developed a constitutive model for predicting changes in the mechanical behaviour of elastomers that encompasses both thermo-oxidative and photo-oxidative aging, as it seems difficult to separate these effects. Their approach is based on the assumption of homogeneous aging, which is only relevant in ultra-thin samples exposed to UV in the abundance of oxygen. Additionally, it can predict inelastic responses such as permanent setting and the Mullins effect. They used a different set of parameters in their models. There are two types of components: one based only on temperature, and another based on both temperature and UV radiation intensity. The model is able to obtain the decay function, which is used to link the molecular scale to higher scales in the function of the elapsed time t:

$${\rho }_0\left(t\right)=e^{(-\tau {\mathrm{\Gamma }}^{\gamma }{e}^{-E_{a_{ref}}^{\prime }}{a}_{T}t)}$$

(30)

where

$$log\left(a_T\right)=E_a^{\prime }\left(\frac{T}{T_{ref}}-1\right)$$

(31)

and

$$E_{a_{ref}}^{\prime }=\frac{E_a}{R{T}_{ref}},$$

(32)

where $T_{ref}$ is the reference temperature that is selected for shifting the data from different times T into a reference curve, $\tau \left[s^{-1}\right]$ is a pre-exponential factor, $a_T$ is the horizontal shift factor [122], $\mathrm{\Gamma }$ is a nondimensional parameter that reflects the effect of UV, and $\gamma$ is another function parameter for UV radiation. Hence, in the absence of UV, the parameter $\gamma$ is null and the model turns into a thermo-oxidative model [122].

In 2022, Najmeddine et al. [123] developed another model consisting of a purely physio-chemically-based constitutive framework to predict the mechanical performance of semi-crystalline LDPE in response to photo-oxidative aging.

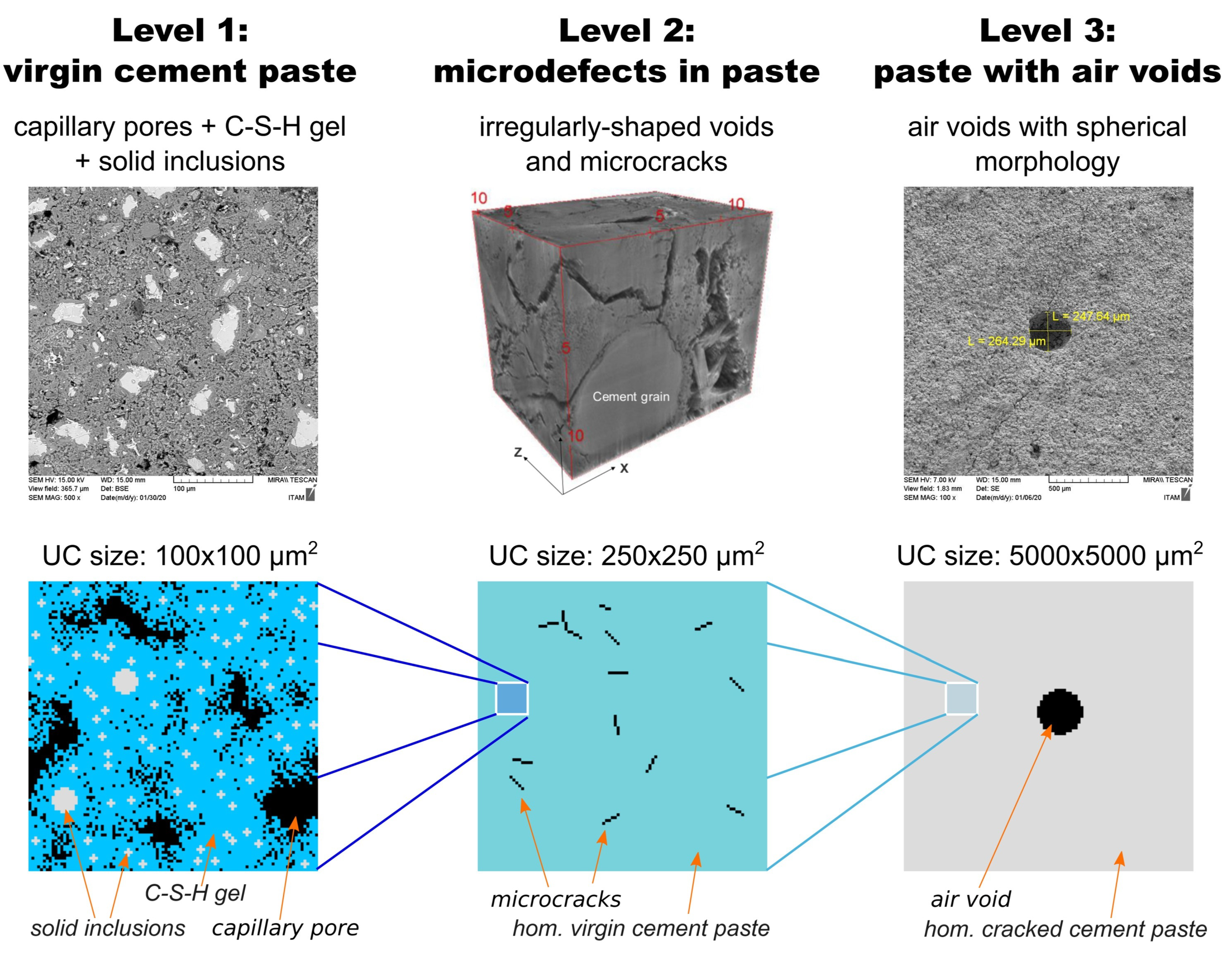
2.4. Aging of Cement-Based Materials

Another type of material often subject to environmental degradation is cement-based composites. The research community is highly interested in this matter due to economic, environmental, and safety concerns associated with infrastructure. Research aims to improve the resilience and sustainability of concrete structures, contributing to the development of more efficient and durable construction materials. Furthermore, multi-scale approaches are often used when studying degradation in this context due to the heterogeneous and complex nature of concrete-based materials.

Concrete-based composites are mostly subject to environmental effects that lead to their deterioration, such as chemical attacks (e.g., chloride [124], acid [125], etc.), physical weathering [126], and temperature [127], among others. The reinforcements employed in these structures exhibits versatility, manifesting in either metallic forms such as steel or high-strength alloys or in the form of fibre-reinforced polymers (FRPs) incorporating glass, carbon, or basalt fibres. Therefore, the longevity and performance of the reinforcements are contingent upon the specific material chosen and the environmental conditions to which they are exposed.

In 2016, Gasch et al. [128] proposed a coupled thermomechanical–hygromechanical model based on the micro-pre-stress solidification theory to analyse the time-dependent deformation of hardened concrete on a structural scale. This model accounts for several aspects of hardened concrete, including aging, creep, drying shrinkage, thermal dilation, and tensile cracking.

Another example of degradation where multi-scale simulation was used can be found in the work of Hlobil et al. (2022) [129], which focused on the strength scale in hardened cement pastes with microstructural defects and the deterioration of the CSH gel.

This approach essentially divides the modelled discretisation of te real cement paste microstructure into three hierarchical levels, as shown in Figure 3:

• Virgin state (defect-free): This level is the smallest one, where the mixture of solid inclusions is embedded into an amorphous CSH gel, all surrounded by large capillary pores.
• Microdefects in the paste: physical defects in the form of microcracks and voids appear primarily within the CSH gel.
• Paste with air voids: Bulk cement paste contains air voids (≥100 μm) that can be identified by visual inspection.

It should be noted that the strength of the material decreases when increasing the specimen size, which is known as the size effect [130]. This model uses two dimensionless parameters that allow for efficient computational generation of generic virtual microstructures used for model evaluation. The first refers to the “gel/space ratio” to describe the space-filling effect of the amorphous hydrate within the capillary porosity during hydration [129]:

$${\gamma }_{CSH}=\frac{{\mathrm{\Phi }}_{CSH}}{{\mathrm{\Phi }}_{CSH}+{\mathrm{\Phi }}_{cappor}}$$

(33)

where ${\mathrm{\Phi }}_{CSH}$ is the volume fraction of the amorphous CSH gel and ${\mathrm{\Phi }}_{cappor}$ is the volume fraction of capillary porosity of hardened cement paste. On the other hand, the second parameter calculates the volume of “solid inclusions” in the virgin cement paste microstructure, stated mathematically as follows:

$${\varphi }_{\mathrm{incl}}=\frac{{\sum }_{\mathrm{solid}=1}^n{\varphi }_{\mathrm{solid}}}{{\sum }_{\mathrm{phase}=1}^n{\varphi }_{\mathrm{phase}}}$$

(34)

where the nominator sums the volume fractions of the unreacted solid phases and crystalline hydrates in the microstructure, while the denominator sums the volume fractions of all the phases together [129].

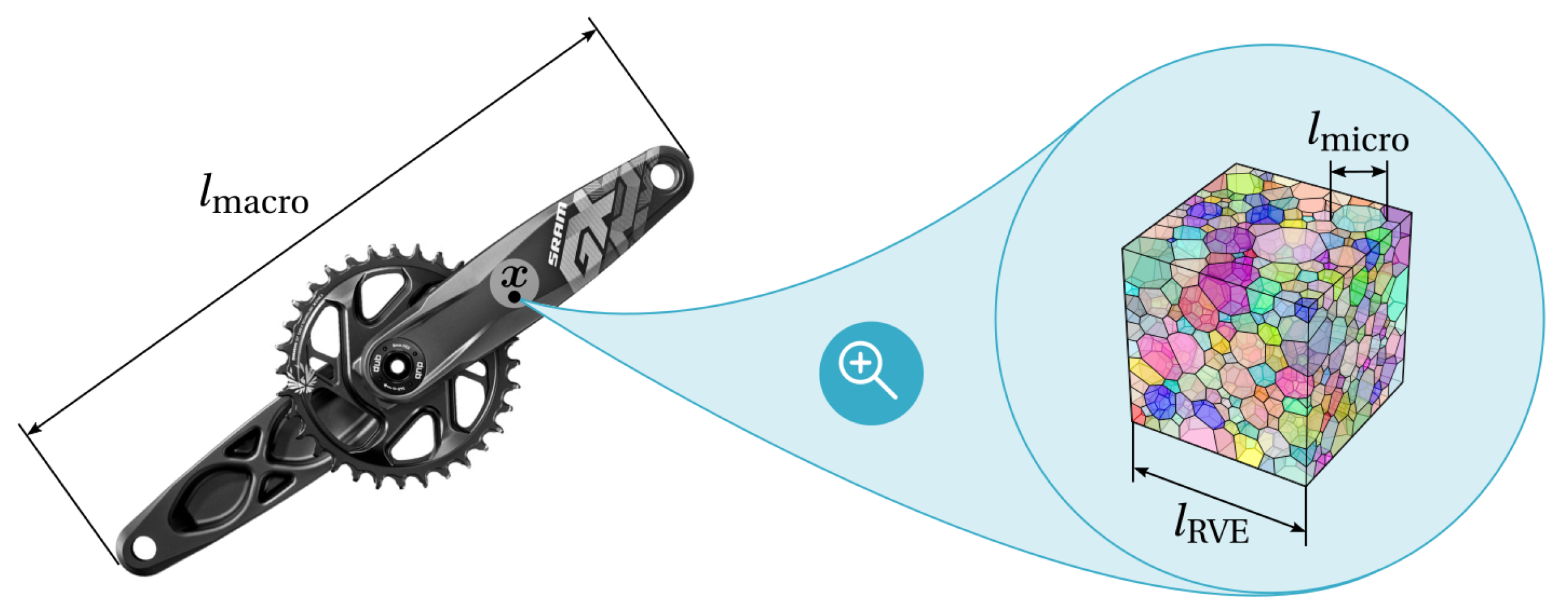
3. Multi-Scale Methods in Structural Mechanics

Throughout the past century, most of the progress in material and mechanical modelling has been achieved by focusing on the physics of phenomenological descriptions at a particular scale. Any multi-scale method aims to establish a bridge between such single-scale models [47]. Several scale-bridging strategies have been developed and utilised in recent years, with homogenisation approaches taking centre stage in the realm of Integrated Computational Materials Engineering (ICME) in linking the microstructural features of engineering materials to their macroscopic behaviour and attaining process–structure–property–performance relations (for more details, see the works of Horstemeyer [131,132]). Furthermore, as previously mentioned, simulating composite material degradation at several different length and time scales may involve material behaviours that cannot be described within the standard continuum hypothesis, as degradation phenomena often occur at the molecular level. With this in mind, discrete theories which model matter as groups of particles, atoms, or molecules must be adopted in order to link the macroscopic degradation of a composite material to the underlying chemical processes occurring at the molecular scale.

In this section, the single-scale models that can be used to model material behaviour at the atomistic, nano-, micro-, meso-, and macro-scales are briefly presented, before assessing the main strategies for scale bridging.

3.1. Discrete Models: Mechanics at Low Length Scales

The continuum hypothesis has been assumed in civil, mechanical, and aeronautical design since the dawn of engineering, and is a cornerstone of classical solid and structural mechanics. Nevertheless, it is generally only valid for length scales above the micron (${10}^{-6}$). Below this level, matter must be visualised as a group of interacting particles and modelled with discrete mechanical theories.

The work of Lin et al. [46] assessed the role of multi-scale methods in the study of the durability of FRP composites, particularly molecular dynamics simulations, displaying the potential of micro- and nano-mechanics for the accurate simulation of the long-term performance of composite materials. In this section, models for description of the physical behaviour of materials at low length and time scales are outlined and discussed.

3.1.1. Density Functional Theory

The formalism of density functional theory (DFT) was first introduced in the pioneering works of Hohenberg, Kohn, and Sham [133,134] during the 1960s. Thereafter, Runge and Gross [135] extended DFT for time-dependent systems, allowing the modelling of subatomic interactions. From then on, several authors applied and extended DFT-based numerical strategies to solve physical and chemical problems at the quantum scale [136,137,138,139,140]. Such strategies also show promise in the field of materials science, where accurately predicting the behaviour of subatomic particles and their interactions is of critical importance when modelling materials at higher scales [141]. For instance, quantum phenomena play a crucial role in chemical reactions, which are of utter importance to material degradation. The quantitative understanding of material properties from the fundamental laws of quantum mechanics is one of the main goals of research into DFT today [142]. That said, DFT is particularly relevant for the development of nano- and metamaterials [143], including the development and study of carbon nanostructures such as CNTs [144,145,146]. Furthermore, DFT models are an interesting avenue to obtain the properties of atomic potentials for molecular dynamics simulations [147,148,149]. Therefore, within a multi-scale effort, a DFT approach can be adopted to model complex phenomena at the subatomic or quantum scale.

Because DFT-based calculations typically span the smallest length scales (<10⁻⁹) [47], they often become computationally demanding. Hybrid quantum mechanical/molecular mechanical (QMMM) [150,151,152] and ab initio molecular dynamics (AIMD) [153,154,155,156] methods have been developed to increase numerical efficiency with minimal accuracy losses [46].

3.1.2. Molecular Dynamics Simulations

The foundation of molecular dynamics (MD) theory dates back to the 1950s, when Fermi and co-workers proposed the numerical simulation of the equations of motion of a many-body system, subject to several choices of force laws [157]. In these simulations, atomic potentials or molecular force fields are utilised to predict the outcomes of particle interactions and solve the dynamical problem with Newton’s laws of motion. With this in mind, correctly defining the aforementioned potentials for each specific application is crucial to guaranteeing accurate and meaningful results. Additionally, as more complex models of atomic potentials and molecular force fields arise, extensive parameterisation is a growing issue. To overcome this, Zhang and co-workers [158] have recently utilised DFT models and machine learning techniques within a multi-objective framework. Moreover, traditional MD methods cannot account for the formation or breakage of chemical bonds. Adopting reactive force fields such as ReaxFF [159,160] allows for the simulation of these chemical reactions, although it results in an increase in the number of model parameters. Nevertheless, in the particular case of studying degradation phenomena, considering chemical bonding and breakage is an extremely relevant feature.

In certain applications, results from MD simulations can inform physical models at higher length scales. For instance, kinetic approaches allow for a better understanding of interface debonding at the meso-scale for FRP and concrete composite materials in the presence of degradation agents [161]. These strategies generally provide a connection between the molecular geometric, kinematic, and dynamic variables to assess bond breakage. Kinetic theories stem from the work of Bell [162,163], which has been expanded into the Modified Bell’s theory [164,165]. MD simulations can also be employed to predict diffusion coefficients and relaxation times in composite materials [46].

Although MD simulations started in the context of theoretical physics, they have subsequently been utilised in several scientific domains, from medicinal chemistry [166,167] to biology [168,169] and geology [170,171], and are likely the most popular method for simulating physical and chemical problems at lower length scales. With the significant increase in computational power observed over the past decades, the limits of MD simulations have also changed, with increasing numbers of particles now included in simulations. This is illustrated in Figure 4 for the particular case of microbiology. That said, MD-based methods can be applied to solve problems at the nano-scale (${10}^{-9}$) and above [172], although simulating systems above the micron-level (${10}^{-6}$) quickly becomes computationally exhausting, especially for traditional MD.

In the context of materials science, MD-based strategies have been employed to study the relationship between nano-scale material features and their resulting physical properties [173,174,175]. Furthermore, several authors have adopted MD simulations to study the fracture behaviour of cross-linked polymers [176,177] and the structural response of nanomaterials [178,179], including CNTs [180,181,182]. A discrete model of a CNT within a polyethylene matrix developed in the work of Hamaekers [181] is shown in Figure 5. Finally, efficient strategies for the generation of microscopic representative volume elements (RVEs) have been devised using MD simulations [183,184,185].

Figure 4. Evolution of MD simulation size in the field of microbiology. Reproduced with permission from [186]. Copyright Springer Nature.

Figure 4. Evolution of MD simulation size in the field of microbiology. Reproduced with permission from [186]. Copyright Springer Nature.

Figure 5. Discrete model of a CNT of 67.5 Å and 1136 atoms long within a polyethylene matrix. Reproduced with permission from [181]. Creative Commons CC BY license.

Figure 5. Discrete model of a CNT of 67.5 Å and 1136 atoms long within a polyethylene matrix. Reproduced with permission from [181]. Creative Commons CC BY license.

MD simulations have also been introduced to study the durability of composite materials. In this context, MD simulations have enhanced the study of the degradation of the interface between high-strength fibres and epoxy resins in hygrothermal [187] and seawater environments [188], the degradation of epoxy resins in FRPs in alkaline [189] and seawater [190] environments, and the effect of hygrothermal and chloride environments on the interfacial strength of vinyl ester–glass fibre composites [191]. The role of MD remains limited to the study of the underlying chemical reactions in a decoupled fashion, the outcomes of which are then used to inform either simulations at higher length scales or the analysis of experimental results. Furthermore, the small time scales simulated by MD (usually below ${10}^{-6}$ seconds [47]) contrast heavily with the large time spans at which the degradation of composite materials might take place, which can encumber the direct coupling between MD and continuum simulations. Nevertheless, even within this limited scope of applicability, MD has already provided valuable inputs for the prediction of composite material durability. Moreover, further coupling between MD and continuum mechanics simulations could be an interesting prospect in the future to increase predictive and modelling power beyond what has been achieved through parameter transfer and upscaling, although computational cost could be a concern.

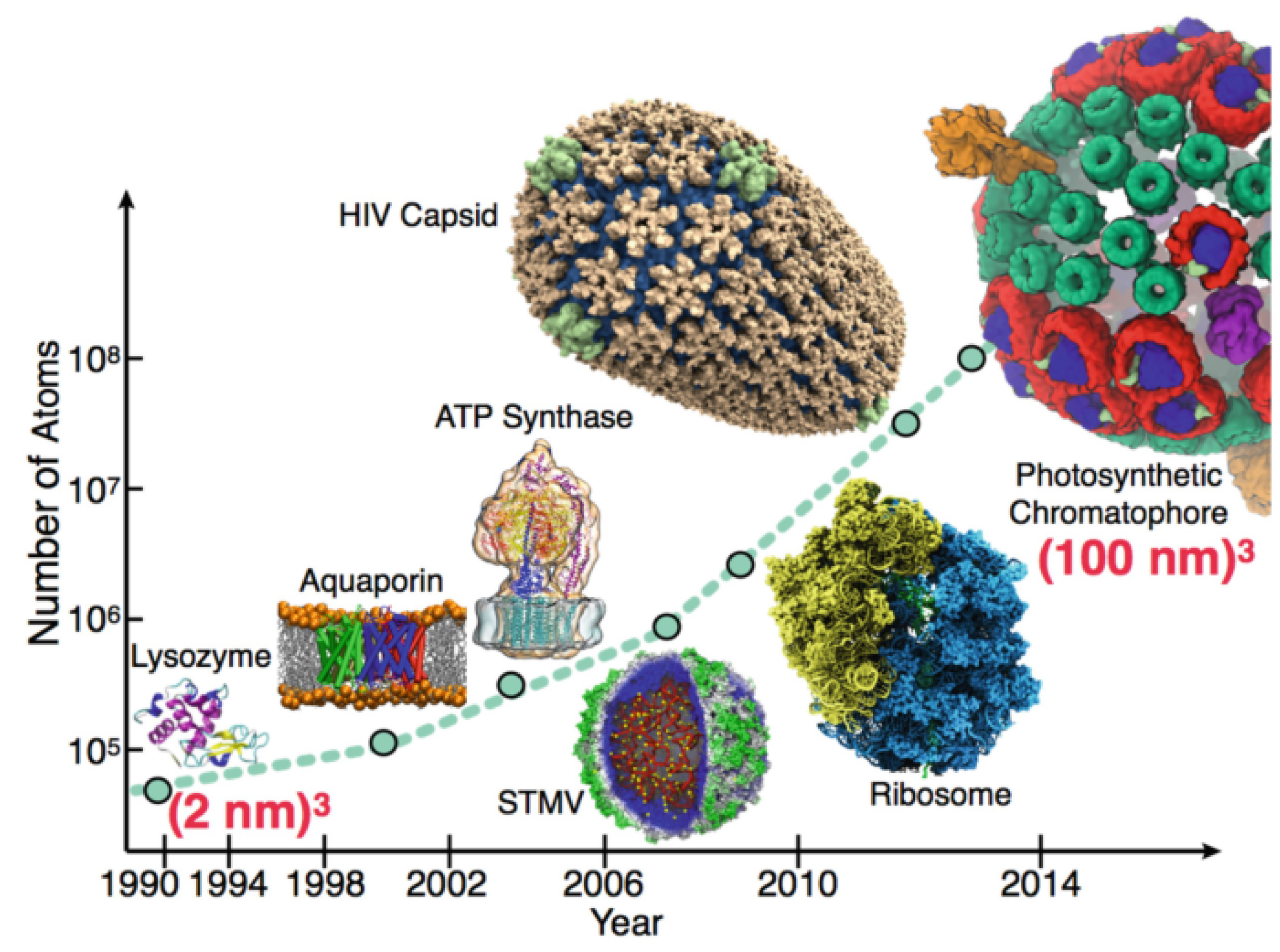
3.1.3. Coarse-Grained Methods

Coarse-grained molecular dynamics (CGMD) was initially proposed by Rudd and Broughton [192] in an attempt to reduce the computational costs of MD simulations, particularly when modelling larger systems (i.e., length scales near ${10}^{-6}$). To this end, particle interactions are generally replaced by the interactions of pseudoatoms which represent molecular or functional groups, thereby reducing the degrees of freedom of the system. In this setting, several strategies can be employed to derive the physical properties of said groups through direct MD simulations. An alternative coarse-grained method is coarse-grained dissipative particle dynamics (CGDPD) [193,194,195].

3.1.4. Other Methods

Other statistical methods can also be used to simulate matter at lower scales. The Monte Carlo (MC) method, for instance, can be utilised to achieve approximate solutions for physical problems by extensive statistical sampling. It was introduced in the 1950s in the field of statistical thermodynamics [196], and has subsequently been adopted in materials science [197,198,199]. Furthermore, hybrid methods have been developed to study the behaviour of materials at length scales which are only partially continuum-based. This is the case for discrete dislocation plasticity models [131,200,201] as well as for the quasi-continuum method [202,203,204,205], which could potentially be adopted for composite degradation modelling in the future.

3.2. Continuum Models

Above the micron level (${10}^{-6}$), the validity of the continuum approximation is restored, and continuum models have been developed to model and simulate all types of materials science and engineering problems. Continuum mechanics theory (see Bonet [206] and Holzapfel [207] for further reading) is widely assumed in almost all mechanical, civil, and aeronautical design problems, with the definition of constitutive relations defining the mechanical response of a material under a given set of loading conditions. These constitutive equations essentially relate physical properties in a way that is specific to a given material, and more often than not are derived in a phenomenological manner, i.e., from empirical observation of the material’s response. That said, constitutive models have been developed for a myriad of materials under numerous conditions, including linear elastic, viscoelastic, elastoplastic and elastoviscoplastic, and viscoelastic–viscoplastic behaviours [208] as well as creep, fatigue, and continuum damage [209].

In the case of FRPs, three distinct length scales (above the micron) can usually be considered: (i) the macro-scale, which accounts for phenomena at the laminate or component level, where homogenised properties are often assumed for simplicity; (ii) the meso-scale, which includes ply-level mechanics; and (iii) the micro-scale, which involves interactions at the constituent level. Generally speaking, continuum models are employed to describe material behaviour at each of these scales, although their nature can differ. Nonlinear effects such as elastoplasticity and damage can be considered at any of these three scales or at several of them. Below these scales, discrete mechanical approaches are usually more appropriate for modelling purposes. The reader is referred to the works of Orifici and colleagues [210], Kanoute and colleagues [211], Soutis and Beaumont [212], and Elmasry and colleagues [213] for further details on FRP constitutive and multi-scale modelling. A computational model of these three scales in the case of a hybrid composite laminate is depicted in Figure 6, which illustrates the interactions between the different composite constituents at each length scale. In this case, a micro-scale model containing a set of fibres, a resin, and an interface is uniformly stacked to form a fabric at the meso-scale level, which is then scaled up to the macroscopic scale by piling up meso-scale models. For further details, interested readers are referred to the original work by Zhao et al. [214].

In the analysis of cement-based composites, several relevant length scales arise [215]: (i) the macro-scale, where the material is usually assumed to be homogeneous; (ii) the meso-scale, where hard and stiff coarse aggregates are embedded in a softer mortar matrix; (iii) the mortar scale, which includes the cement paste (matrix), the finer aggregate particles, and the interface between them, that is, the so-called Interfacial Transition Zone (ITZ); and (iv) the paste scale, which lies below the mortar scale and is comprised of a complex system of pores of varying sizes, below which is the CSH gel scale. Continuum approaches are usually limited to the mortar scale; further reading regarding the computational modelling of concrete is provided in [216,217,218].

The Finite Element Method (FEM) is the go-to numerical method for simulating material and structural behaviour; for further reading, see [219,220]. It is utilised to solve the partial differential equations that define the boundary value problem under analysis. Additionally, when path-dependent constitutive models are assumed, it includes an adequate numerical integration algorithm. The FEM has grown into one of the most popular numerical methods in engineering since its earliest development in the 1960s, and is widely available for use in several software packages. Nonetheless, many research groups have their own in-house finite element codes, which can often include advanced features or methodologies. Meshless methods [221,222] and adaptive mesh refinement strategies [223,224,225] are among these advanced features.

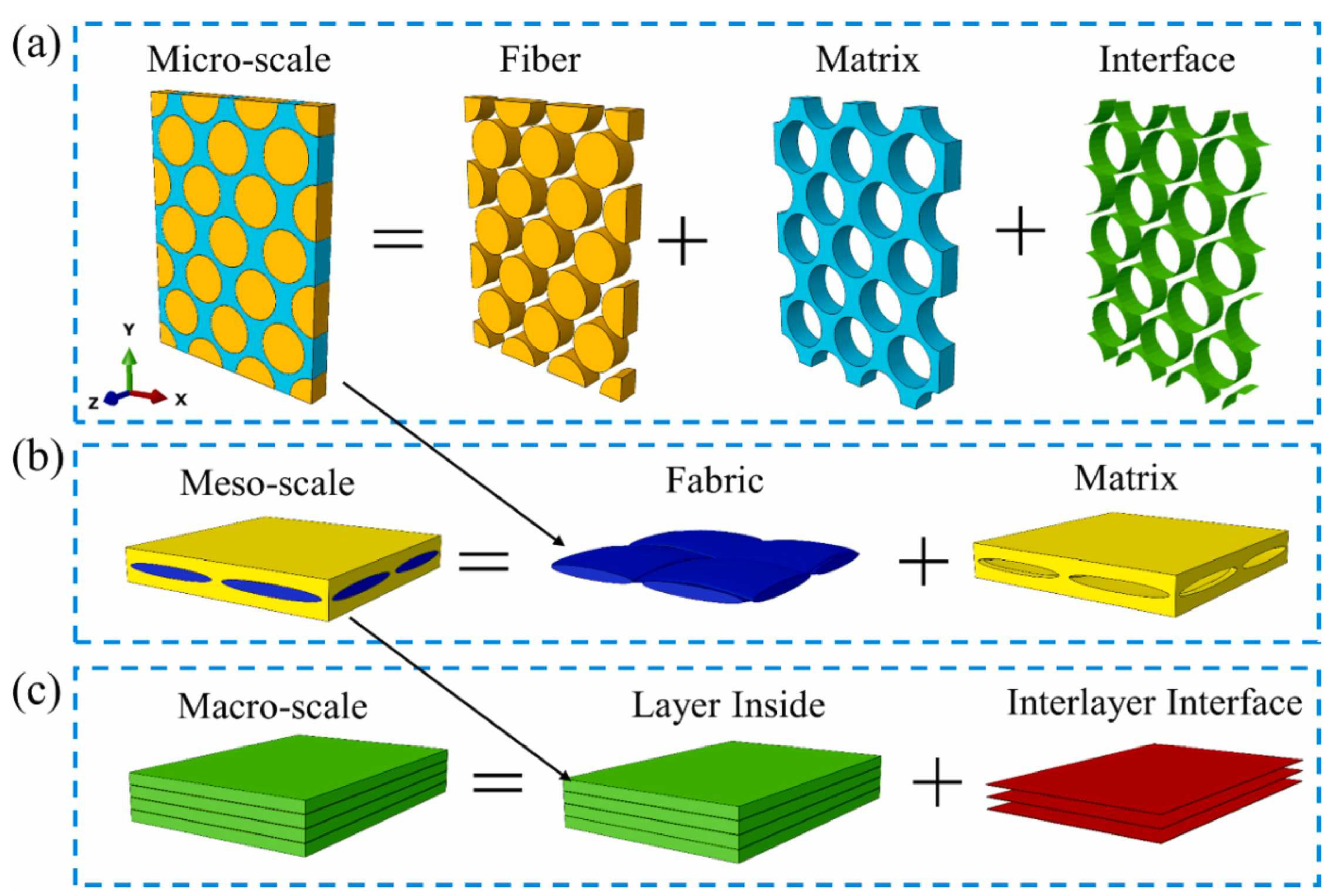
3.3. Scale-Bridging Strategies

Up to this point, several single-scale mechanical theories have been mentioned and described; however, to perform multi-scale analyses, these models must be connected, which can be accomplished through several strategies. Matous and co-workers [47] have systematised the various single- and multi-scale approaches utilised to model and study heterogeneous media at several length scales. In the aforementioned text, the authors state that multi-scale methods can be classified according to the underlying problem formulation or algorithmic scheme. In the present work, such methods are split according to the formulation and solution of the physical problem. The studies by Geers and co-workers [226,227] are also valuable contributions regarding the state of the art of homogenisation-based multi-scale strategies, while the work of Gooneie and co-workers [228] provides a useful review on multi-scale simulations of polymeric materials.

3.3.1. Concurrent Methods

In concurrent solution schemes, multiple time and length scales are formulated and included in a single domain and tackled simultaneously. In practice, these strategies are either used for high-accuracy simulations, in an approach coined Direct Numerical Simulation (DNS), or include adaptive schemes, which allow for the easing of computational demands. DNS results are often utilised as references for more intricate predictive methods, as they do not contain any specific assumptions regarding scale transition or linkage. In practice, however, this approach can be inefficient, particularly if high spatial or temporal resolution is needed. To address this, several adaptive schemes have been developed in recent years to increase the resolution in regions of interest, providing accurate solutions without compromising efficiency. These strategies are particularly attractive for the solution of fracture and damage problems, with several models proposed to address crack propagation [229,230] and continuum damage propagation [231,232].

Although concurrent strategies are not the most popular in the context of computational mechanics, they could be interesting for predicting degradation, as they allow for considering the effects of chemical interactions on the macroscopic properties of the material within small regions of the domain. This approach has been implemented for simulating corrosion in metals [233].

3.3.2. Hierarchical Methods

Most multi-scale methods utilised in engineering are of a hierarchical nature. Hierarchical methods range from analytical procedures to coupled hierarchical simulations. Nevertheless, most hierarchical approaches are based on the concept of homogenisation, which revolves around averaging theorems. In its simplest form, homogenisation can be analytical, utilising micro-mechanics based averaging, such as the rule of mixtures, or the theorems introduced by Hill [234] or Willis [235].

At the other end of the spectrum, computational homogenisation (CH) is one of the most common methods for coupled multi-scale simulations. This method has been the focus of extensive research since the late 1990s, and is essentially based on the nested solution of two boundary value problems, one at each scale [227], in a strategy commonly referred to as FE². It has been utilised to solve problems related to fracture and damage mechanics [236,237], contact mechanics [238,239], mechanically-induced phase transformations [240,241], and even heat conduction [242], among others.

In CH-based strategies, the lower length scales are usually modelled with recourse to unit cells or representative volume elements (RVEs). The latter was first introduced by Hill [234], and defines the RVE as a volume of material sufficiently large such that it captures the mean constitutive response of the microstructure. To that end, the RVE must be statistically representative of the material’s microscopic features and heterogeneities. Moreover, the principle of scale separation is a cornerstone of CH-based multi-scales models. This principle states that the characteristic length of the RVE, denoted by $l_{\mathrm{RVE}}$, must simultaneously be much smaller than the characteristic length of the macroscopic domain $l_{\mathrm{macro}}$ and much larger than the characteristic dimension of its microstructural features $l_{\mathrm{micro}}$. This principle is depicted in Figure 7. Moreover, in a CH-based strategy, the macroscopic problem is solved by replacing the standard constitutive equations at each integration point of the finite element mesh with the solution of an equilibrium problem at a lower length scale driven by the macroscopic deformation gradient (see Figure 8).

CH-based methods have already been utilised in the context of composite material degradation (see Section 4), and could be further introduced in this field of study in light of their widespread application for the solutions of complex multi-scale and multi-physics problems. Advanced CH-based strategies such as second order CH [45,244,245] and asymptotic homogenisation [246,247,248] could also be applicable to degradation modelling in the future.

Apart from CH, hierarchical approaches include strategies based on parameter identification and parameter transfer, which have already seen significant application in degradation modelling thanks to their comparative simplicity and compatibility with discrete mechanics models. In essence, these strategies, often referred to as numerical homogenisation approaches, rely on identifying critical design parameters at the macroscopic level, which can be predicted with simulations at lower length scales. In contrast to CH-based models, these approaches relate different scales in a decoupled fashion, as the results from lower scales influence the material behaviour at the macro-scale, while the opposite is most often not the case. This is associated with lower computational demand, but can come at the cost of reduced accuracy and predictive power. Nevertheless, its simplicity remains one of its key advantages.

Furthermore, with the growing development of machine learning and robust optimisation frameworks along with their application to materials science and engineering, there is unprecedented potential for the improvement of parameter identification procedures in multi-scale modelling in terms of both predictive power and efficiency [249,250]. CH-based reduced order modelling (ROM) efforts are set to benefit from the growing development and introduction of these approaches. In essence, ROM techniques rely on reducing the dimensionality and complexity of computational models to attain approximate solutions at lower computational cost. In 2017, Bessa and co-workers presented a unified framework for the data-driven analysis of materials [251] and proposed self-consistent clustering ROM, which resulted in subsequent contributions [44,252,253]. Other ROM approaches based on the proper orthogonal decomposition method [254,255,256,257], transformation field analysis [258,259,260], wavelet representation [261], and nonlinear manifolds [262] have gained popularity as well. Finally, surrogate models have been utilised for multi-scale analysis of complex materials [263,264,265,266]. A promising example of the use of surrogate models to speed up multi-scale simulations is the work of Maia et al. [267], which developed physically reccurrent neural networks (PRNNs) to capture the complex path-dependent behaviour of heterogeneous solids.

3.3.3. Hybrid Methods

Hybrid multi-scale methods include multi-grid approaches [268], the generalised finite element method [269], and other strategies. These methods essentially share the properties of both concurrent and hierarchical approaches, resulting in hybrid scale-bridging schemes. The quasi-continuum method can be included in this category of multi-scale strategies as well.

Scale bridging is a crucial step in the formulation of any multi-scale strategy. As has already been highlighted in this section, it is a determining factor in the computing demand and predictive power of multi-scale methods. That said, each approach has its own advantages, underlying assumptions, and drawbacks, which should be carefully considered before application to a particular problem. In the coming years, the progressive development of efficient computational strategies is likely to raise the bar for multi-scale methods in terms of efficacy and efficiency.

Finally, coupled multi-scale simulation schemes are much more common when linking two scales which are modelled with the same type of mechanical theories, i.e., discrete or continuum. Direct coupling between discrete and continuum simulations remains a rare occurrence due to the different natures of these models and their different main state and algorithmic variables. Nevertheless, this could be an avenue for future developments, as these models are usually only linked through parameter transfer or upscaling, meaning that macro-scale phenomena do not have any influence on the simulated material behaviour at lower scales, as such simulations are performed prior to the actual macroscopic ones.

3.4. Multi-Scale Modelling and Experimental Testing

High-fidelity computational multi-scale modelling of materials cannot be separated from their experimental characterisation. In fact, balancing the relationship between experimental characterisation and computational modelling is crucial for ensuring efficient testing campaigns and accurate numerical predictions.

Testing is mainly used in two phases of the computational modelling cycle. On the one hand, experimental data can be used to calibrate the material parameters of complex constitutive models to ensure accurate numerical predictions. In such cases, the characterisation tests necessary for the calibration of material parameters depend on the modelling strategy and the number of length scales at play. Generally speaking, the calibration of multi-scale models requires the definition of material properties at the lower scales, as the behaviour of the system at such scales is used to predict its response at the larger length-scales. For the multi-scale modelling of composite aging, for instance, parameters regarding the material response under relevant degradation mechanisms at lower scales are needed to obtain its macroscopic behaviour. Micro- and nano-indentation tests under specific environmental effects [270,271,272] are one example of the experimental tests required to calibrate these multi-scale models. On the other hand, experimental validation is often necessary to corroborate final computational results, in which case computational models that have already been calibrated with empirical data generally warrant another set of experimental results. This highlights the importance of experimental testing for accurate numerical modelling.

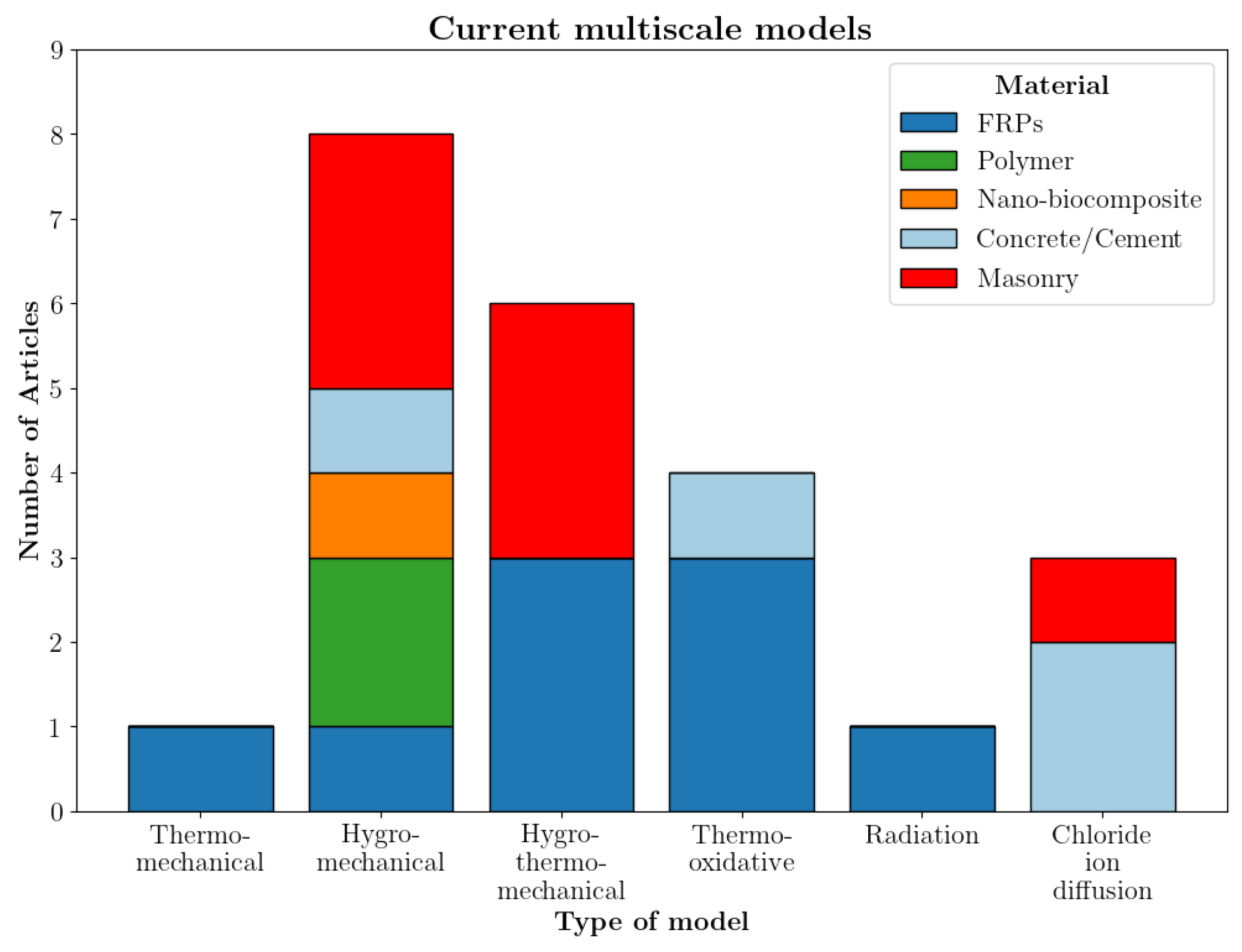
4. Multi-Scale Durability Predictions for Composite Materials

Predicting the degradation of composite materials using multi-scale strategies is still a very recent topic in the literature. However, a number of works have already proven the feasibility of this novel approach. In this section, these works are systematised and discussed, starting with a presentation of the modular paradigm for multi-scale composite durability predictions. Subsequently, the main works devoted to multi-scale analysis of polymer-based composite material degradation are divided and presented according to the environmental agent involved, before briefly touching on the state of the art regarding cement-based composites. It is worth noting that a few polymer studies are included, as a significant aspect of degradation in FRPs lies within the polymeric matrix, allowing these studies to be readily adapted for FRPs.

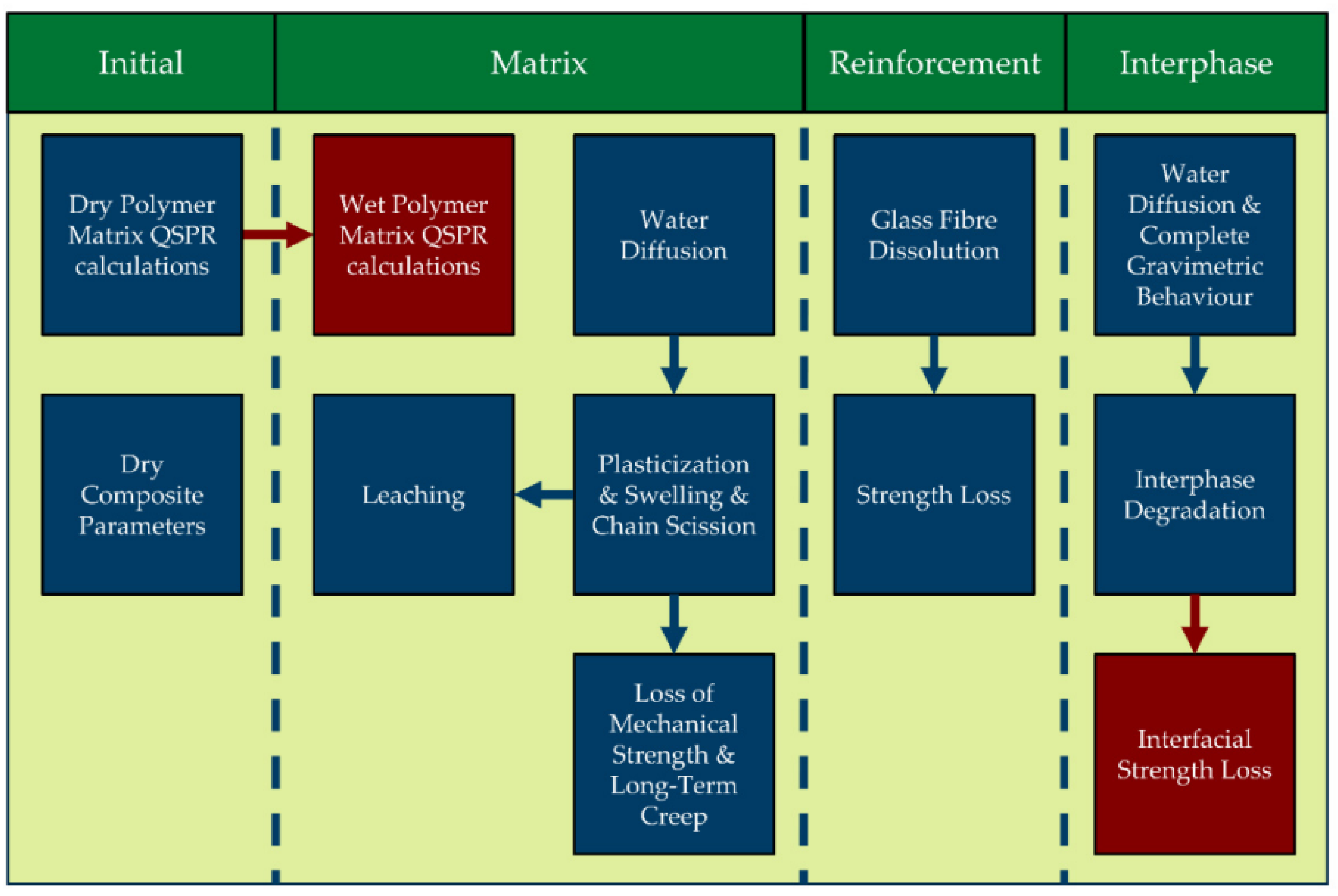
4.1. Modular Paradigm

The modular paradigm was first presented in the work of Echtermeyer and colleagues [16], and has been further expanded in the works of Krauklis and colleagues [11,88,273]. In essence this approach attempts to break down composite material degradation into several blocks, or modular groups, which correspond to each microconstituent, as depicted in Figure 9. The main goal is to obtain a unified composite degradation predictor that can account for all relevant environmental effects on a wide range of materials and constituents.

As shown in Figure 9, this approach is divided into four main modular groups: the initial properties, matrix degradation, reinforcement degradation, and interphase degradation. Calculating the properties of the virgin material is the first step in this procedure, which can usually be accomplished through standard engineering calculations. Thereafter, the three remaining modular groups concern the environmental degradation of each of the composite material’s constituents.

The modular approach is far from fulfilling its potential as a unified tool for durability predictions, as there remains much to explore in this field of research. Nevertheless, as new and more accurate numerical models are developed to perform multi-scale degradation predictions on relevant materials and constituents and under the effect of the relevant degradation agents, this strategy could be extremely useful for the robust assessment of composite material durability. In the meantime, it could help to enlighten the research community with regard to the current research gaps and necessary developments.

4.2. Thermomechanical Model

The pioneering multiscale durability model for composite materials was introduced in 2005 by Lévêque et al. [274]. The examination of the coupling between thermomechanical loading and thermal ageing effects is vital for evaluating the performance of polymer matrix composites with extended service life in aeronautical applications. Thermal aging introduces intricate molecular-scale phenomena capable of significantly altering mechanical properties and reducing the lifespan of composite materials. The aforementioned paper outlines an approach incorporating various aspects, including viscoelastic behaviour, thermomechanical damage, and degradation from physical and chemical aging, into a multi-scale model. The investigated material was a carbon fibre/epoxy matrix composite (IMS/977-2).

4.3. Hygromechanical Models

In 2014, Kojic et al. introduced a hierarchical multi-scale model combining molecular dynamics and finite element methods [275]. By employing numerical homogenisation, this model identifies crucial material parameters such as the bulk diffusion coefficients and distances from solid surfaces while accounting for surface interaction effects. This approach ensures coherence in mass release curves across microstructural and continuum models, allowing it to be applied in large-scale scenarios. The model’s effectiveness was demonstrated through its application to two distinct geometrical and material setups, namely, tightly packed silica nanospheres and a complex fibrous structure surrounding the nanospheres. This methodology was validated experimentally and successfully used to analyse glucose diffusion. It offers a versatile platform for forecasting mass diffusion in intricate biological environments and composite materials, with potential applications spanning various domains, including drug delivery and the development of nanoporous catalysts.

Advancing this line of research, Mazan et al. [113,114] took a step further in 2015 by developing a multi-scale model that integrates diffusion, chemical kinetics, structure–property relationships, and composite models. Their comprehensive approach streamlined property predictions, forecasting density, and crystallinity evolution in polyamide 11 during aging. The study’s success in predicting mechanical properties underscored the potential of multi-scale modelling as a complement to accelerated aging tests, particularly in understanding the intricate effects of diffusion.

In 2018, Obeid et al. [276] delved into the hygromechanical behaviour of polyamide-6 during the transient stage of humid aging tests, emphasising the importance of considering plasticisation effects and local dependence on moisture content for material parameters. While broader in scope, the study highlighted the intricate relationship between diffusion, mechanical behaviour, and aging effects.

In a 2021 study by Riaño et al. [277], a multi-scale model was utilised to simulate the effects of humid tropical aging on a unidirectional composite (E-glass fibres/epoxy), with a specific focus on the interphase region. The study employed ABAQUS to create numerical micromodels for predicting the composite’s mechanical behaviour under monotonic transverse traction. Validation of the models involved comparisons with experimental results, underscoring the significance of accounting for the composite interphase in numerical simulations.

In their recent work, Ghabezi et al. [278] investigated the long-term behaviour of glass/epoxy and carbon/epoxy composites using tensile strength and nanoindentation tests. For nanoindentation, they employed a Berkovich indenter according to standardised methods, assessing the elastic modulus and hardness based on the maximum depth or load, with the load measured as a function of the penetration depth. In fibrous composite micromechanical simulations, the bulk properties of the fibre and matrix constituents are commonly used to predict composite properties and failure behaviour. This study observed a decrease in tensile strength for both materials due to aging and exposure to elevated temperatures and seawater. While nanoindentation showed minimal changes in modulus for glass/epoxy matrices, significant reductions over time were observed in carbon/epoxy matrices. Extrapolations using empirical models accurately predicted the tensile strength of aged samples, with nonlinear models showing superior accuracy for long-term predictions. The study employed both linear and nonlinear models to predict the long-term behaviour of glass/epoxy and carbon/epoxy composites. The linear model assumes a constant degradation mechanism based on the Arrhenius relation described in Equation (2), and allows for calculation of the time shift factor at different temperatures. Nonlinear models assume that the degradation rate decreases over time, and utilise exponential functions to represent this behaviour. The underlying degradation mechanism in these models is the debonding of the fibre–matrix interface. Both models help to understand the long-term performance of composites by predicting their behaviour under different aging conditions. In the final part of this study, multi-scale modelling based on ABAQUS was used to predict the macroscale elastic modulus based on the microscale resin elastic properties measured by nanoindentation, with a deviation from experimental results of less than 10% for both unaged and aged composites.

4.4. Hygromechanical–Thermomechanical Models

In 2017, Ullah et al. [279] proposed a coupled hygromechanical–thermomechanical computational model for fibre-reinforced polymers within the framework of computational homogenisation (CH). Parallel to the depiction in Figure 8, this hierarchical model incorporates thermal and moisture transport variables in the scale bridging procedure, adding to the standard mechanical and kinematic quantities, as illustrated in Figure 10. A degradation model based on experimental data is incorporated, allowing for the prediction of mechanical property evolution over time. The computational framework (implemented in MoFEM FE software) utilises hierarchic basis functions and is designed for distributed memory high-performance computing. The study focused on the representative volume element (RVE) of a plain weave textile composite consisting of yarns embedded in a matrix. The computational framework involved one-way coupling, with mechanical analysis dependent on thermal and moisture transport analyses. The conductivity matrices for thermal (${\overline{\mathbf{K}}}_T$) and moisture (${\overline{\mathbf{K}}}_c$) transport analyses were determined from the CH of the underlying RVEs, calculated once and used subsequently for macro-level heat transfer and moisture transport analyses. A macro-level three-dimensional plate structure with a hole was considered, subject to thermal and moisture boundary conditions as well as uniform mechanical pressure. The macro-level thermal and moisture transport problems were both solved with a time step of 10 days, for a total duration of 1000 days. The simulation results showed the damage evolution as well as the temperature and moisture concentration fields (see Figure 11), indicating the stiffness degradation in the macroscopic structure.

Expanding on this, in 2019 Rocha et al. [280] delved into the hygrothermal aging degradation of unidirectional glass/epoxy composites. Combining experiments and multi-scale numerical modelling, their study explored aging mechanisms by immersing specimens in demineralised water, conducting interlaminar shear tests, and employing advanced fracture analysis. This study built upon the computational foundations laid by Ullah et al., integrating diffusion analysis and models for fibre–matrix debonding in order to more comprehensively understand the aging process.

In 2021, Guo et al. [281] introduced a groundbreaking multi-scale modelling approach, significantly advancing the assessment of hygrothermal aging damage and the prediction of mechanical properties in accelerated cycles. Investigating moisture diffusion coefficients for epoxy resins under diverse conditions, their study explored moisture absorption in fibre-reinforced composites and laminates while considering fibre volume fraction effects. An efficient algorithm utilising disturbance and perfect elastic collisions was used to generate a random fibre distribution for a specified volume fraction ($V_f$) [282]. The process involves arranging fibres regularly in a square array, initiating spontaneous collisions with random velocities, and ensuring periodicity by handling boundary crossings. After a brief perturbation time, the algorithm produces an RVE with a representative random fibre configuration, mimicking the real microstructure of composites. This research highlighted differences in the distribution of the maximum principal residual stress among various fibre arrays, emphasising microcrack generation from stress concentrations in the interface region. An exponential function was introduced to describe reversible changes in constituent properties under hygrothermal conditions. The defect hypothesis characterised irreversible aging damage, revealing substantial drops in transverse modulus, transverse tensile strength, and transverse compression strength after nine severe accelerated hygrothermal aging cycles. Within the laminate FEM model, 3D strain-form Hashin criteria and an improved traction-separation cohesive law were applied and validated against experimental data. Integrated within a global searching genetic algorithm framework, hygrothermal aging variables were optimized for different accelerated conditions. Considering composite design within the global searching genetic algorithm (GA), N (number of defects surrounding a single fibre) and $r_v/r_f$ (ratio between the radius of a semicircular defect and the fibre radius) were regarded as hygrothermal aging design variables for intralaminar elements. Simultaneously, $\gamma$ and $D_c$ represented reduction factors for the strength and fracture energy of interlaminar elements. This algorithm aims to find variable combinations fitting the ILSS experimental results for each accelerated hygrothermal aging condition. The proposed micro-scale and macro-scale models were considered as a generalised function $\psi$ to bridge the design variables and algorithm target.

$$\psi \left(N,\frac{r_v}{r_f},\gamma ,D_c\right)=\left\{\begin{array}{c}0\le N\le 12\\ 8\%\le \frac{r_v}{r_f}\le 24\%\\ 0<\gamma \le 1\\ 0<D_c\le 1\end{array}\right.$$

(35)

The investigation involved four accelerated hygrothermal cycles, and incorporated temperature and duration variations to simulate diverse aging conditions.

Table 1. Final FEM results after nine accelerated hygrothermal aging cycles. Reproduced with permission from [281].

Ageing Condition	$\left(\mathit{N},\frac{{\mathit{r}}_{\mathit{z}}}{{\mathit{r}}_{\mathit{f}}},\mathit{\gamma },{\mathit{D}}_{\mathit{c}}\right)$	ILSS (MPa) (Error)
AHCl	$(8,10\%,0.90,0.92)$	79.87 (2.65%)
AHC2	$(9,14\%,0.85,0.88)$	75.74 (3.88 %)
AHC3/4	$(10,18\%,0.78,0.80)$	70.61 (1.29%)

presents the FEM results for ILSS after these cycles, which showcase good agreement with experimental data, demonstrating the potential of this approach.

4.5. Thermo-Oxidative Aging Models

In 2011, Upadhyaya et al. [283] pioneered a mechanism-based multi-scale model focused on predicting the lifespan of high-temperature polymer matrix composites (HTPMC) during thermo-oxidative aging. This groundbreaking model considered molecular-level damage, specifically inter-crosslink chain scission in a thermoset polymer, and successfully simulated delamination failure in an aged unidirectional IM-7/PETI-5 composite. The model’s accuracy was validated against experimental test data, marking a significant step in understanding aging mechanisms at elevated temperatures.

Expanding on this, in 2019 Shi et al. [284] delved into the multi-scale aging mechanisms influencing impact fracture behaviours in 3D four-directional and five-directional braided composites under thermo-oxidative conditions. Through experiments and high-speed camera recordings, the researchers identified oxidation-induced crack widths and established a multi-scale finite element analysis (FEA) model. This model unveiled interface failure, stress distribution, and energy absorption at the microstructure level, providing insights into how braided structures influence impact fracture properties. Their study emphasised matrix degradation and interfacial weakening as the primary degradation mechanisms.

In a more recent investigation by Miao et al. [285], the focus shifted to exploring thermo-oxidative aging effects on carbon fibre/epoxy plain-woven composites. This study employed a hierarchical multi-scale model to consider the deterioration of structural integrity at the micro-, meso-, and macro-scales along with matrix degradation and interface debonding at the micro-level and pre-formed interlaminar cracks at the macro-scale. The results indicated a noticeable influence of interface damage and matrix degradation on the micro-scale properties, leading to a reduction in mechanical properties at the meso-scale. The finite element results also suggested that interlaminar cracks formed during thermal aging played a crucial role in delamination failure at the macro-scale.

4.6. Radioactive Aging Models

Investigating the environmental durability of plant fibre-reinforced polymer composites holds significant importance for assessing their properties and longevity. Ramie fibre, a type of natural cellulose fibre, is renowned for its superior tensile modulus compared to jute and flax, and can even rival the tensile modulus of glass fibres. Considering this context, Zhao et al. [214] investigated the UV aging behaviour of R/C hybrid composites in a PETG matrix using a multi-scale finite element (FE) model. Their study accurately predicted mechanical property degradation in good agreement with experimental results. They developed a progressive damage FE model integrating micro-, meso-, and macro-scale representations. Ramie fibre (RF) and carbon fibre (CF) fabrics were employed with PETG pellets to fabricate composite specimens comprising six different fibre arrangements. The study conducted a three-point bending fracture simulation at the macroscopic level. As the number of aging days increased, a gradual decrease in the strength of the interface properties was observed. Interfacial strength retention for composites with different aging duration was normalised, offering insights into the effects of aging. The results provided in Figure 12 demonstrate good agreement between the FE and experimental results for the flexural stress vs. strain curves, while analysis of the stress distribution reveals patterns based on the configuration of the composites and duration of aging.

Table 2. Comparison of the flexural modulus of composites. Reproduced with permission from [214].

	Flexural Modulus (After 28 Days of UV Ageing) (GPa)
	EXP	FEM (error)
${[R/R/R/R]}_s$	4.4	3.9 (11%)
${[R/C/R/C]}_s$	11.4	11.1 (2.6%)
${[C/R/C/R]}_s$	26.7	26.4 (1.1%)
${[\mathrm{R}/\mathrm{R}/\mathrm{C}/\mathrm{C}]}_s$	12.4	12.9 (4%)
${[C/C/R/R]}_s$	23.5	23.7 (0.9%)

showcases a minimal error between the experimental and FE results for the flexural modulus, validating the model’s accuracy in predicting elastic modulus changes in R/C composites with UV aging. This approach demonstrates the potential for cost and time savings in the characterisation of composite materials under UV aging.

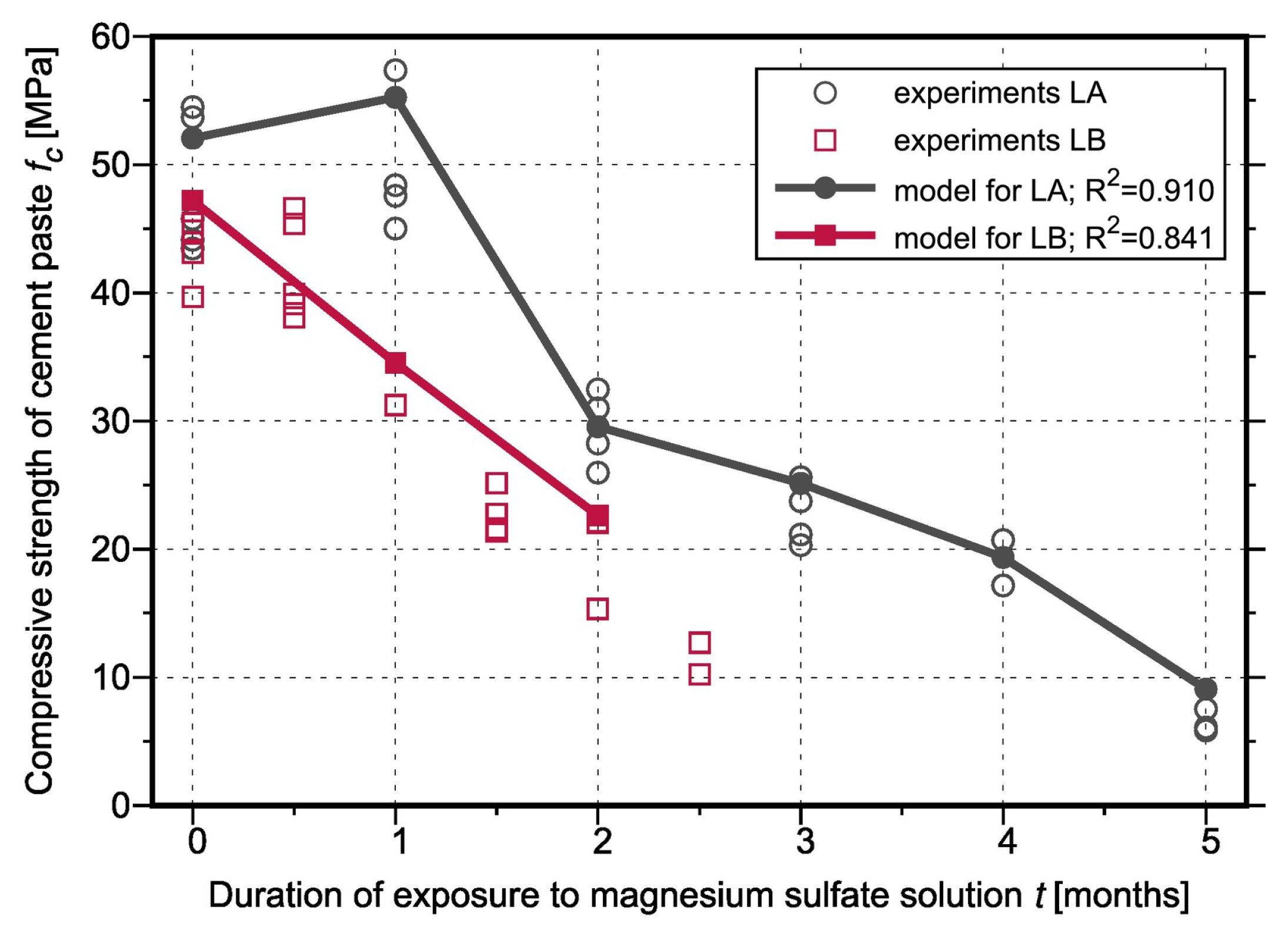
4.7. Aging Models for Cement-Based Materials

Recent research has extensively delved into the complex aging of cement-based composite materials, employing multi-scale modelling approaches to unravel intricate processes and predict material behaviour. The following chronological narrative highlights key contributions to understanding aging mechanisms.

In 2016, Honorio et al. [286] introduced a multi-scale model integrating analytical homogenisation and numerical methods. This model assessed the aging effects on the viscoelastic properties of cement-based materials, specifically focusing on the solidification of non-aging constituents and exploring various aging mechanisms impacting relaxation and creep.

In 2021, Liu et al. [287] investigated the degradation of chloride ion resistance in cement-based materials induced by freezing–thawing (F-T) action. Utilising micro-computed tomography characterisation and numerical modelling, the study identified micro-cracks induced by F-T action as crucial factors affecting chloride ion diffusivity at the micro- and meso-scales.

In 2022, Hlobil et al. [129] introduced a comprehensive multi-scale computational model designed to analyse the microstructure of hardened cement paste. Utilising advanced imaging techniques, their study revealed a highly heterogeneous microstructure consisting of discrete compounds characterised by diverse morphology and distinct chemical composition. To facilitate a nuanced understanding, their model categorised the microstructure into three levels, each representing a distinct length scale, as previously mentioned in Section 2.4. The primary goal of this model is to elucidate the mechanical behaviour of hardened cement paste across length scales ranging from 1 μm to 5 mm. The separation factors between these levels are meticulously chosen, and adhere to continuum mechanics principles. The introduction of dimensionless parameters such as the gel/space ratio and solid inclusions volume fraction serves to simplify the representation and computational generation of generic virtual microstructures, enhancing the model’s practical applicability.

Notably, the paper underscores the model’s specific emphasis on understanding the vulnerability of CSH gel to both physical and chemical damage. This includes a focus on the nanomechanical strength and the macroscopic load-bearing capacity of the material during chemical attacks, providing valuable insights into the intricate interplay between microstructural features and material behaviour. Furthermore, the paper introduces a computational model that predicts and monitors the structural degradation of hardened cement paste during chemical attack. This involves assessing changes in compressive strength and accounting for alterations in the microstructural phase assemblage coupled with nanostructural degradation of the CSH gel. Two independent factors, Δphys and Δchem, are introduced to modify the tensile strength of the CSH gel, reflecting physical damage and nanostructural modifications induced by the chemical attack, respectively. Blind model predictions calibrated using analytical microstructure-based equations demonstrate a notable correlation with the experimental results, as depicted in Figure 13. This showcases the model’s efficacy in capturing and predicting the material’s behaviour under the complex conditions of chemical attack. The presented computational model stands as a valuable tool for advancing the understanding of cementitious materials and their response to environmental challenges.

In 2023, Mou et al. [288] explored recycled aggregate concrete, employing a five-phase multi-scale model for the effective chloride diffusion coefficient. This comprehensive study considered the phases and interfacial transition zones, showcasing the model’s accuracy in predicting chloride diffusion coefficients and contributing to the understanding of degradation mechanisms.

Finally, a series of interconnected studies by Castellazzi and collaborators presented a chronological exploration of multi-scale modelling in the context of masonry structures under environmental conditions. Commencing with Sykora et al. [289], who delved into fully coupled transient heat and moisture transport, subsequent works by Castellazzi et al. [290,291] advanced the realm of hygrothermal modelling, emphasising salt crystallisation predictions and introducing a multi-scale analysis framework. This multi-scale approach is a recurring theme, extending to the study of environmental aging in masonry strengthened with composites by De Miranda et al. [292]. Grementieri et al. [293] further applied multi-scale modelling to explore moisture migration in fibre-reinforced polymer (FRP) composite masonry, while their subsequent work [294] focused on salt transport during drying.

4.8. Discussion

According to our research, the current status of multi-scale models capable of predicting environmental effects on composite materials is outlined in Figure 14. The chart displays the number of articles for each type of environmental model and each material. Hygromechanical models are the most prevalent, covering a diverse range of materials, with at least one article for each type. Notably, some researchers have extended their studies to include thermal effects, resulting in six hygromechanical–thermomechanical models. In this category, the primary focus has been on FRPs and masonry materials.

For thermo-oxidation, four articles delve into the subject, primarily concentrating on FRPs but also extending to concrete and other cementitious materials. The issue of chloride ion diffusion, particularly relevant to construction materials such as concrete, has garnered some attention, with three articles addressing this concern.

In the realm of thermomechanical models, the pioneering work by Léveque et al. stands as the sole representative. While groundbreaking, this model has not been extensively explored, possibly due to the more unpredictable and severe environmental effects imposed by other factors in composite materials.

Despite being represented by only one study, focusing on FRP materials, the research underscores the significance of radiation in the degradation of composite materials. When examining materials more broadly, FRPs and construction composite materials emerge as heavily researched subjects. Additionally, the exploration of newer materials such as nano- and biocomposites is already underway.

Lastly, it is worth noting that these models demonstrate significant efficiency when compared to experimental data across various materials. This efficiency is evidenced by data from sources such as [214,279,281], where the errors range from nearly 0% to a maximum of 10% in the worst-case scenario.

5. Future Prospects

The present state of the art of multi-scale models for predicting environmental effects on composite materials, particularly the formulation of the modular paradigm by Echtermeyer, Krauklis, and colleagues [11,16,88], lays the groundwork for future research and development in this field. Within the existing body of work, several trends and opportunities have surfaced, indicating potential directions for further investigations:

1.

Extension to additional environmental effects: Certain environmental effects, such as radiation, are less explored in the existing literature than other factors. Furthermore, some advanced degradation models have been developed recently, such as the aforementioned DCZOK, offering the potential to improve the accuracy of multi-scale models. Conducting in-depth investigations regarding all relevant environmental effects in engineering and materials science, along with the exploration of the most accurate and efficient degradation models for each, could result in an enriched database and a broader landscape of multi-scale strategies for predicting the durability of composites.

2.

Extension to emerging materials: Due to the increasing introduction of new composite materials with innovative design features and configurations across diverse applications, including nano- and biocomposites in medical contexts [295,296] and thermoplastic matrix composites in the marine and automotive sectors [14,15], it is imperative to delve into the environmental degradation mechanisms affecting these novel materials. Understanding and addressing the unique challenges posed by these materials will play a crucial role in facilitating their successful integration into a wider range of practical applications with assurances of long-term safety and reliability.

3.

Integration and the modular paradigm: Existing models have primarily focused on individual environmental factors, such as hygromechanical and radioactive aging. Future research should aim to develop more comprehensive models that can simultaneously integrate multiple environmental stressors in order to attain the aforementioned modular paradigm for durability predictions. Real-world scenarios involve the simultaneous influence of various environmental factors, and understanding their combined effects is crucial. The development of an integrated database and modelling toolbox for the relevant environmental effects and materials, as proposed in the modular paradigm, would also benefit from the accomplishment of the first and second objectives.

4.

Enhancement of predictive capabilities: Advancements in computational techniques, including high-performance computing and the progressive use of data-driven frameworks, are set to increase the predictive power and efficiency of multi-scale methods in the coming years. The continuous development of these multi-scale strategies and their subsequent application to degradation modelling of composite structures is paramount to attaining more accurate durability predictions for a greater range of materials and environmental agents. The inclusion of discrete mechanics models has been particularly useful in multi-scale degradation analysis due to the influence of chemical interactions at lower scales in the macroscopic structural response. That said, improving the current scale bridging schemes between MD simulations and continuum mechanics models could lead to even more accurate results. Moreover, the full potential of several numerical strategies, such as the quasi-continuum method, concurrent multi-scale approaches (which are seeing growing efficiency due to smarter adaptive algorithms), asymptotic homogenisation, and second order CH, along with ROM and surrogate approaches such as PRNNs, has yet to be fully investigated in the context of multi-scale composite degradation modelling.

5.

Synergy between experimental testing and computational modelling: Strengthening the relationship between experimental testing and computational modelling through the calibration and validation of multi-scale strategies with adequate and precise empirical measurements is paramount for a sustainable development of multi-scale methods in composite material degradation analysis. Establishing standardised protocols for model validation will enhance the reliability and comparability of results across different studies, and a more robust understanding of material behaviour can be achieved through rigorous validation efforts. Although numerical predictions cannot fully replace empirical testing, this would allow the overall costs associated with experimental campaigns to be reduced in the long term. Furthermore, the introduction of novel experimental techniques such as advanced imaging, sensing, and characterisation methods can provide richer datasets for model validation and calibration. Integrating data from these techniques into multi-scale models could help to enhance their predictive capabilities.

6. Conclusions

In this work, an extensive literature review of the current multi-scale strategies for predicting the durability of composite materials is presented, with great emphasis on the degradation mechanisms governing composite material aging and the computational methodologies that allow for the simulation of complex materials at several different length scales. In addition, the existing works on multi-scale durability predictions for composites are systematised. The main findings are as follows:

• Several multi-scale models integrating environmental degradation display remarkable effectiveness, demonstrating their efficacy by closely matching experimental data.
• To shape the future of multi-scale modelling in predicting environmental effects on composite materials, it is crucial to address the identified trends and opportunities.
• Enriching our understanding of composite material behavior requires an extension of the research landscape to encompass a broader range of environmental factors and emerging materials.
• The reliability and accuracy of durability predictions can be enhanced by integrating multiple degradation models according to the modular paradigm and by leveraging computational advancements in multi-scale strategies.
• Promoting synergy between experimental testing and numerical modelling is vital to ensure adequate calibration and validation of multi-scale predictions while reducing experimental characterisation tests.
• Although advanced numerical strategies cannot completely replace experimental testing, their integration into material and structural degradation studies can mitigate the major shortcomings of experimental testing, such as intensive consumption of time and resources.