Bridging Behavior of Palm Fiber in Cementitious Composite
Abstract
1. Introduction
2. Experimental Program
2.1. Palm Fiber
2.1.1. Density of Palm Fiber
2.1.2. Diameter and Morphology of Palm Fiber
2.2. Mixture Proportion
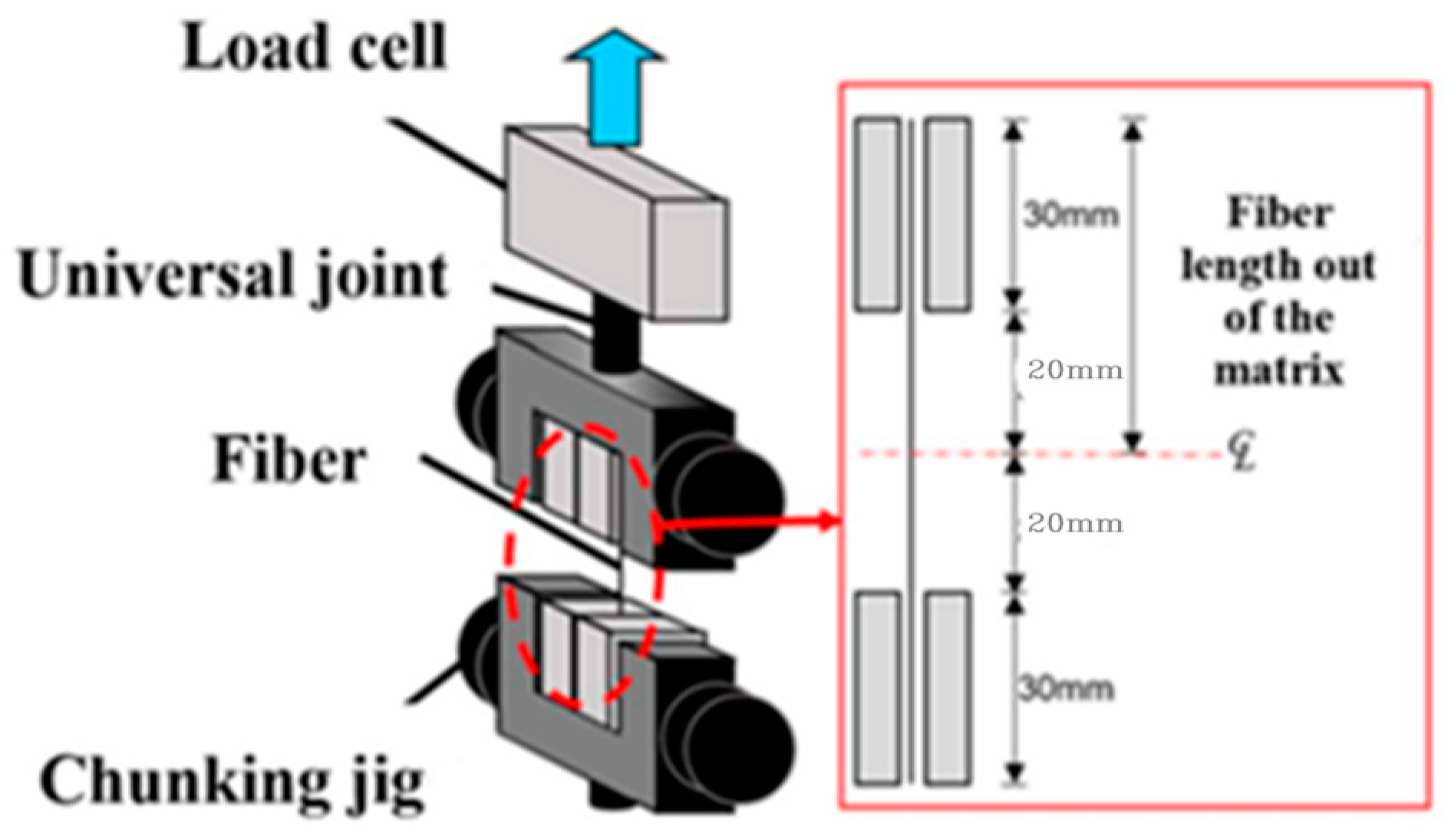
2.3. Specimens for Single Fiber Pullout Test of Palm Fiber
2.4. Loading and Measurement
3. Test Result and Modeling Pullout Behavior
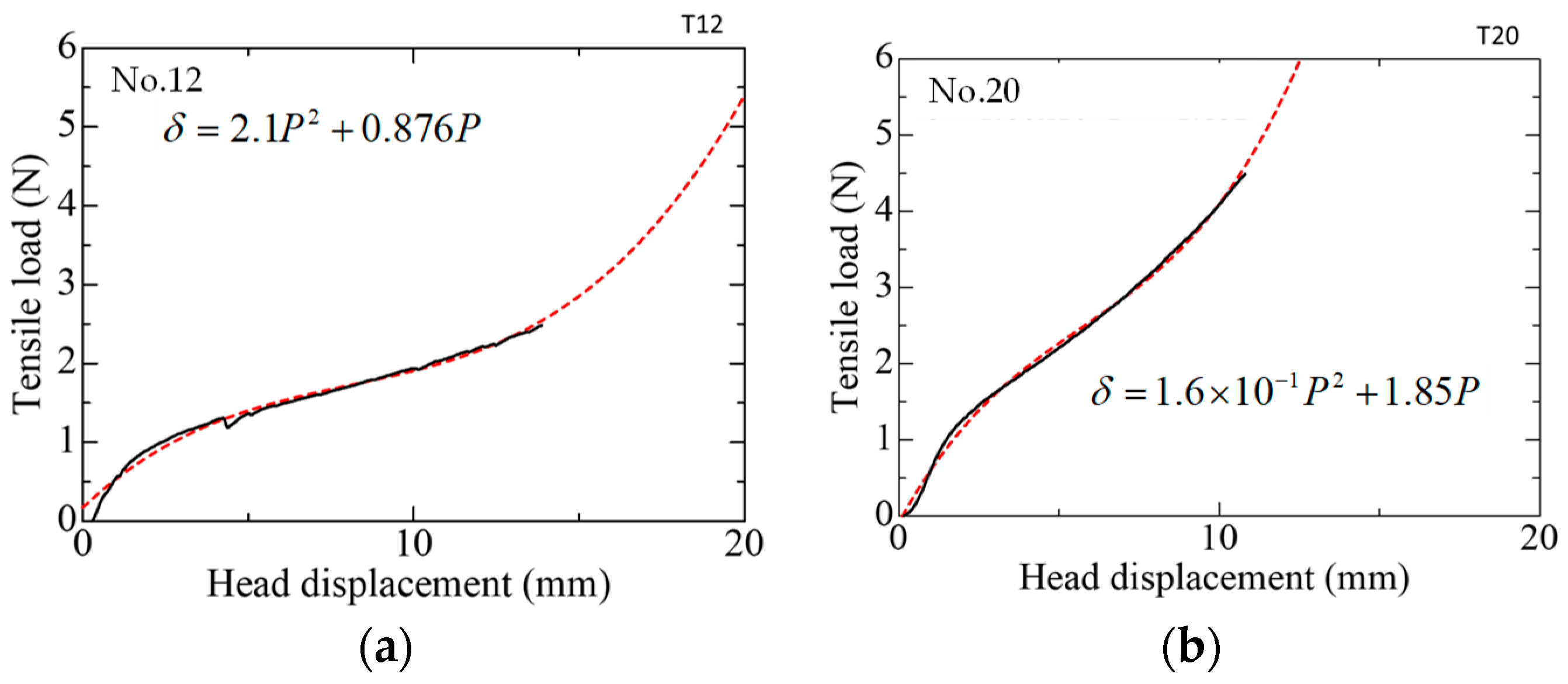
3.1. Uniaxial Tension Test for Single Palm Fiber
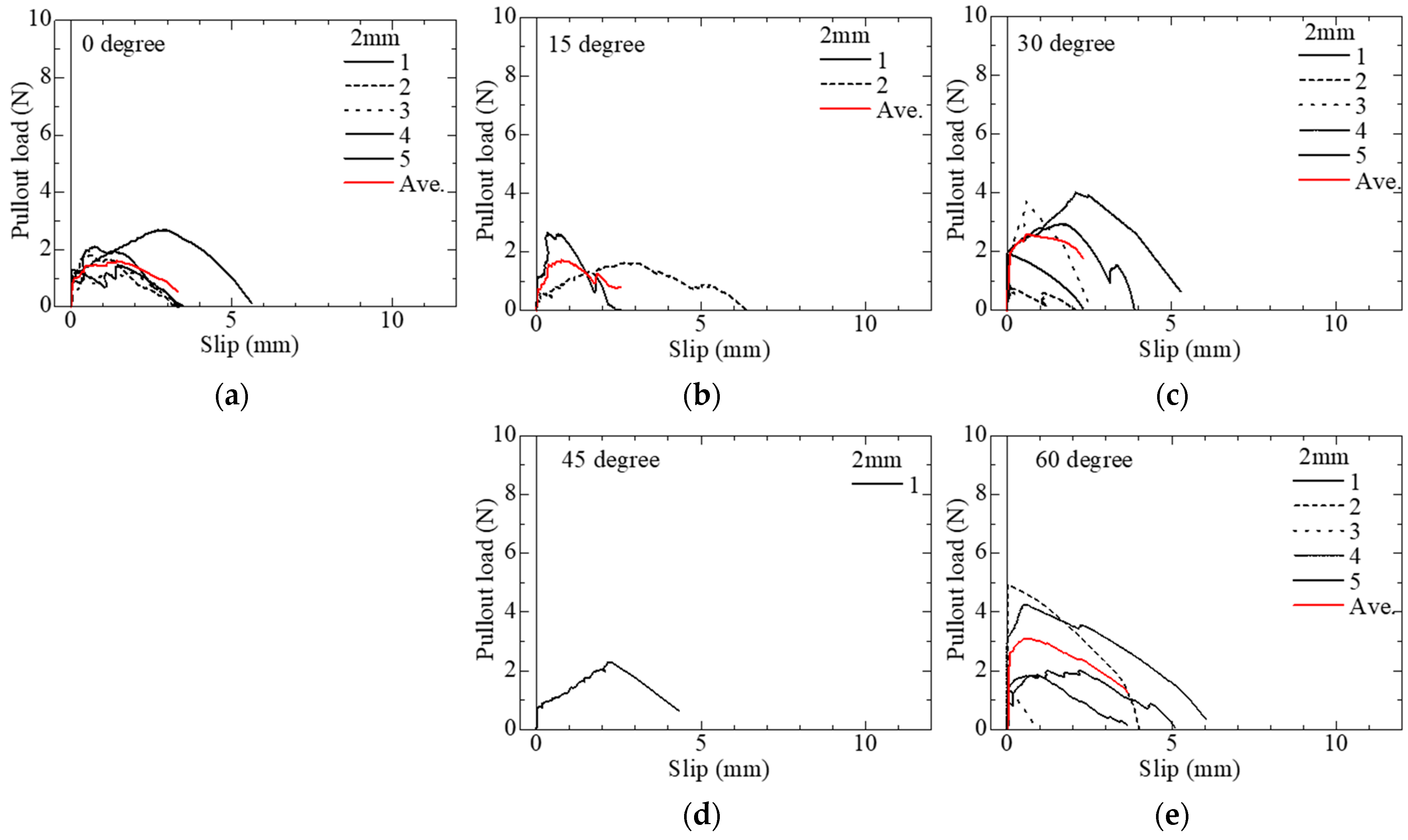
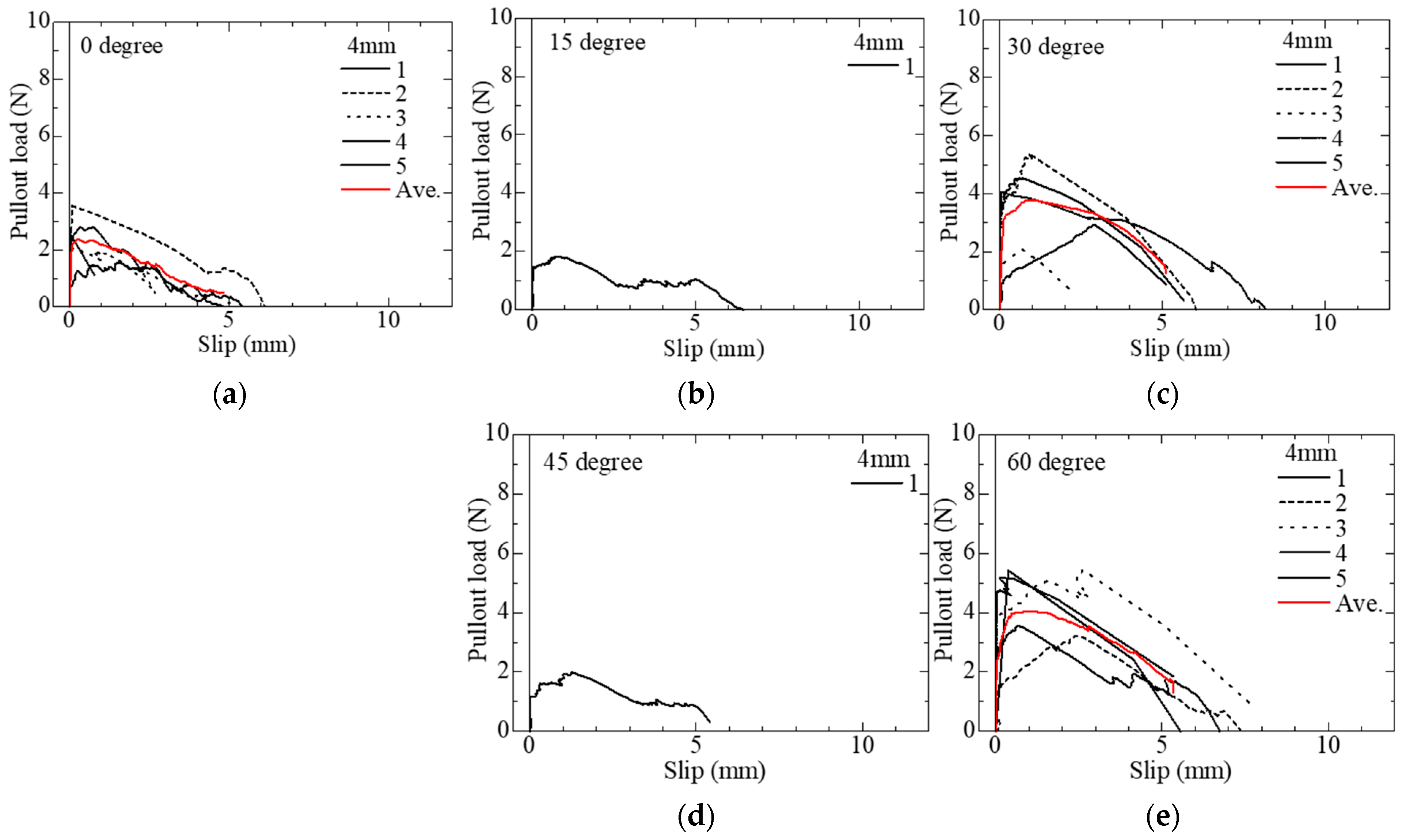
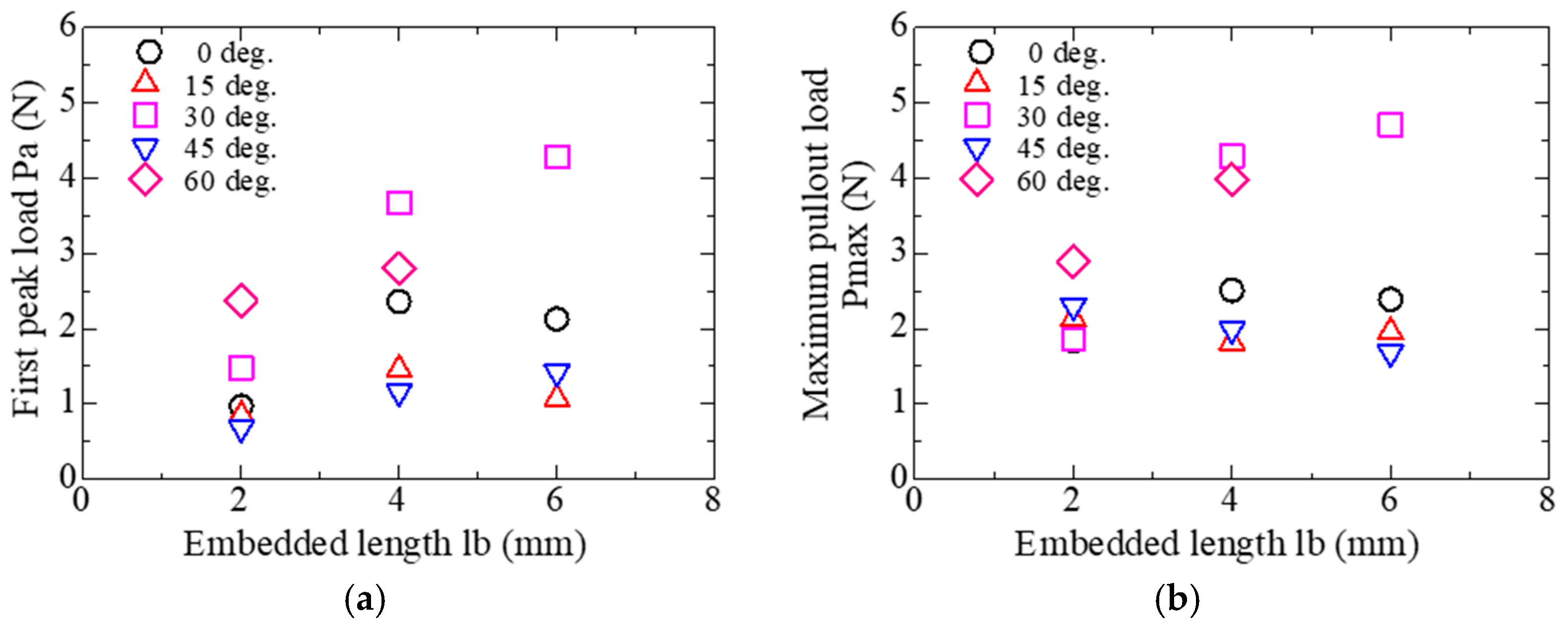
3.2. Single Fiber Pullout Test for Palm Fiber
3.3. Single Fiber Pullout Model
3.3.1. Evaluation of Pullout Load
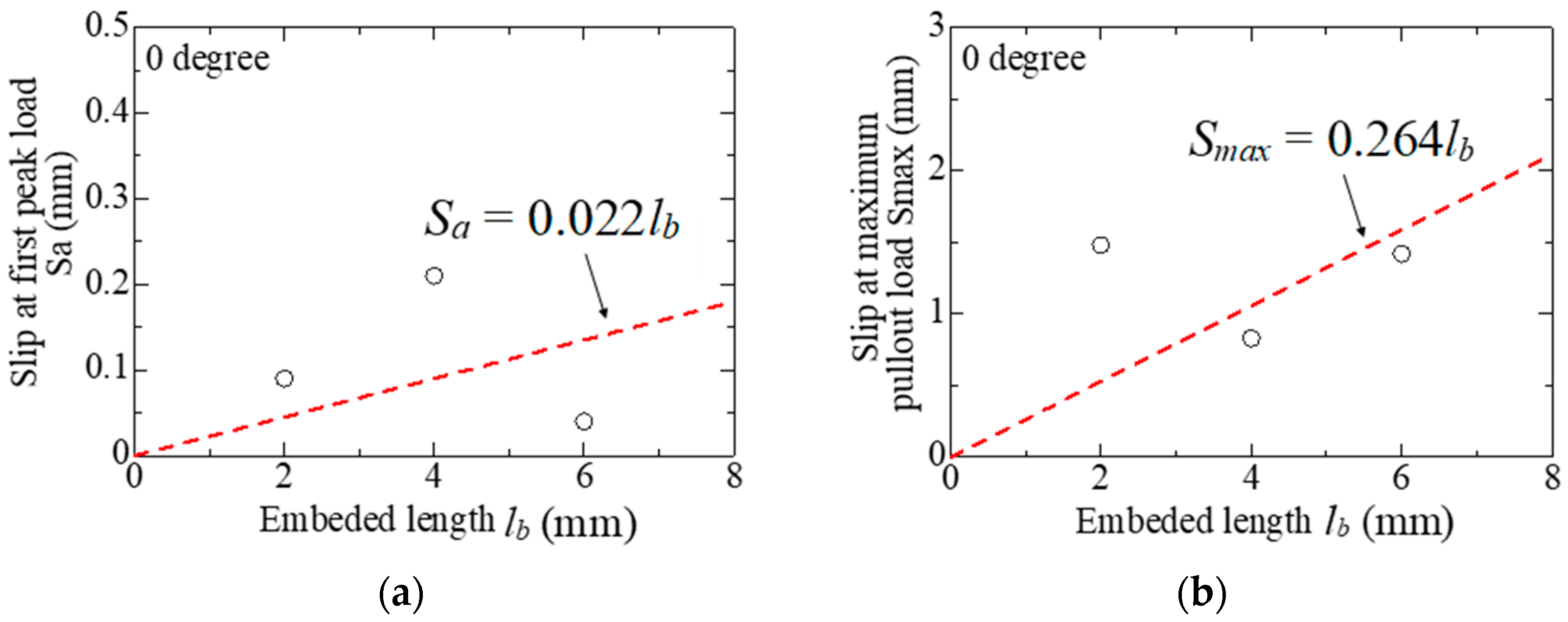
3.3.2. Evaluation of Slip
3.3.3. Snubbing Effect
3.3.4. Apparent Fiber Strength
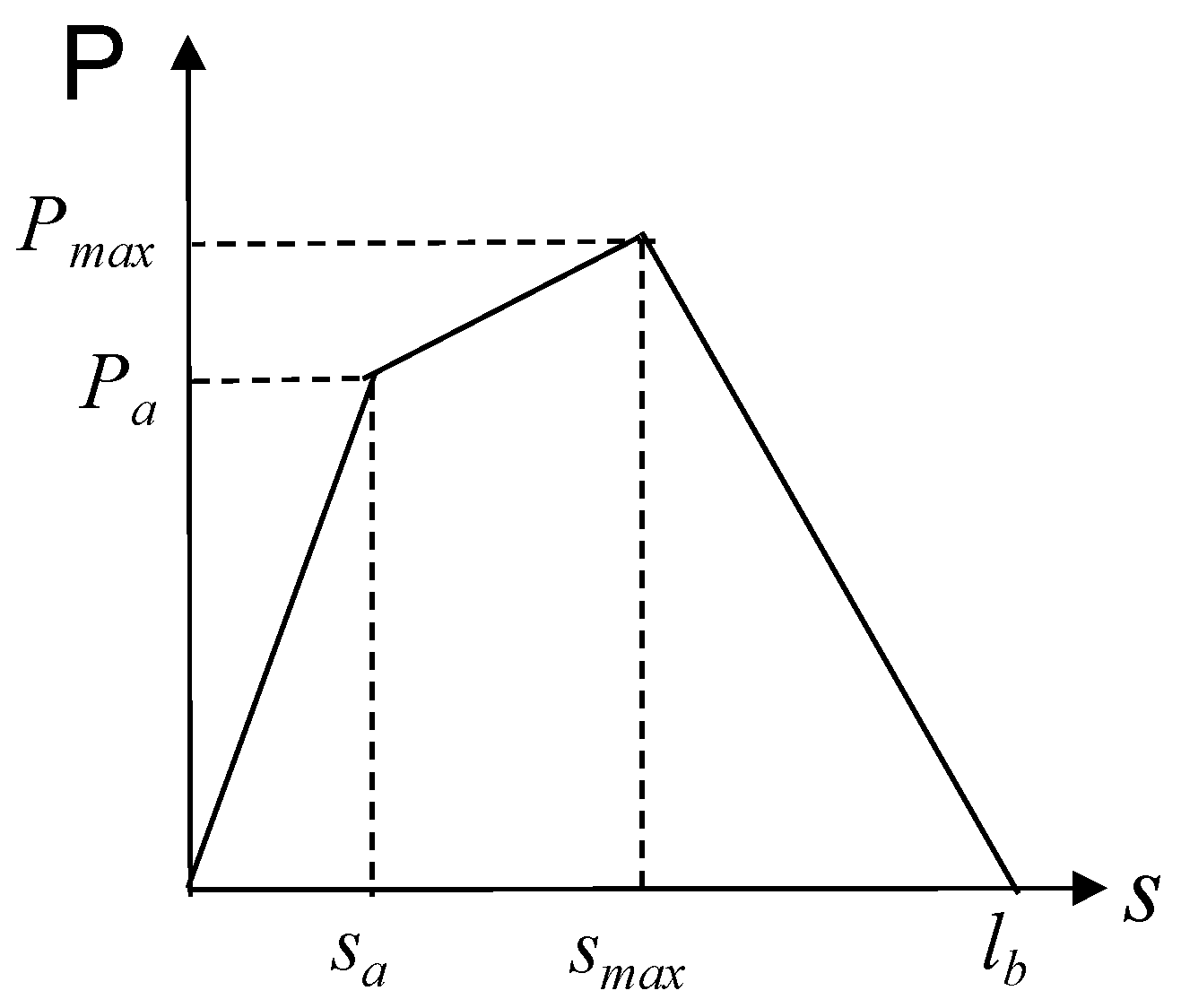
3.4. Trilinear Model of Pullout–Slip Curve
4. Bridging Law of Palm-FRCC
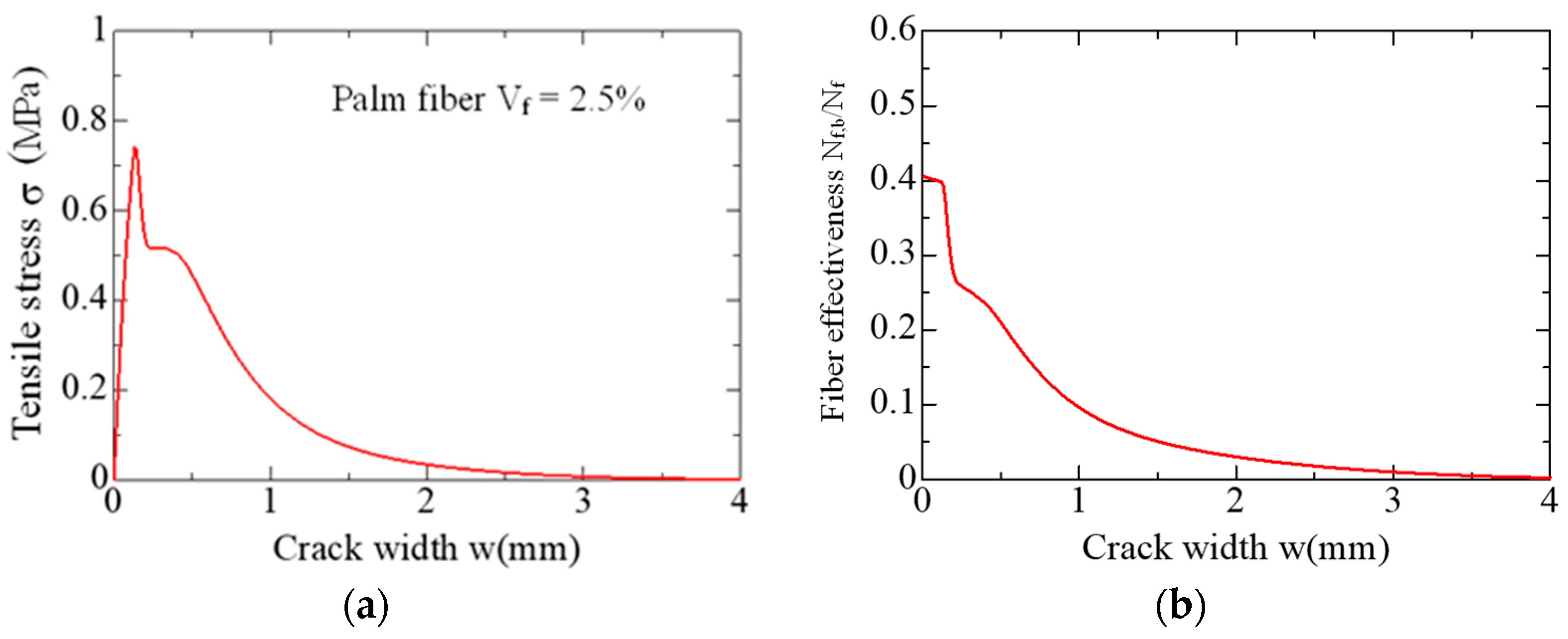
4.1. Calculation Method
4.2. Calculation Results
4.3. Adaptability Assessment of Bridging Law
4.3.1. Four-Point Bending Test
4.3.2. Section Analysis
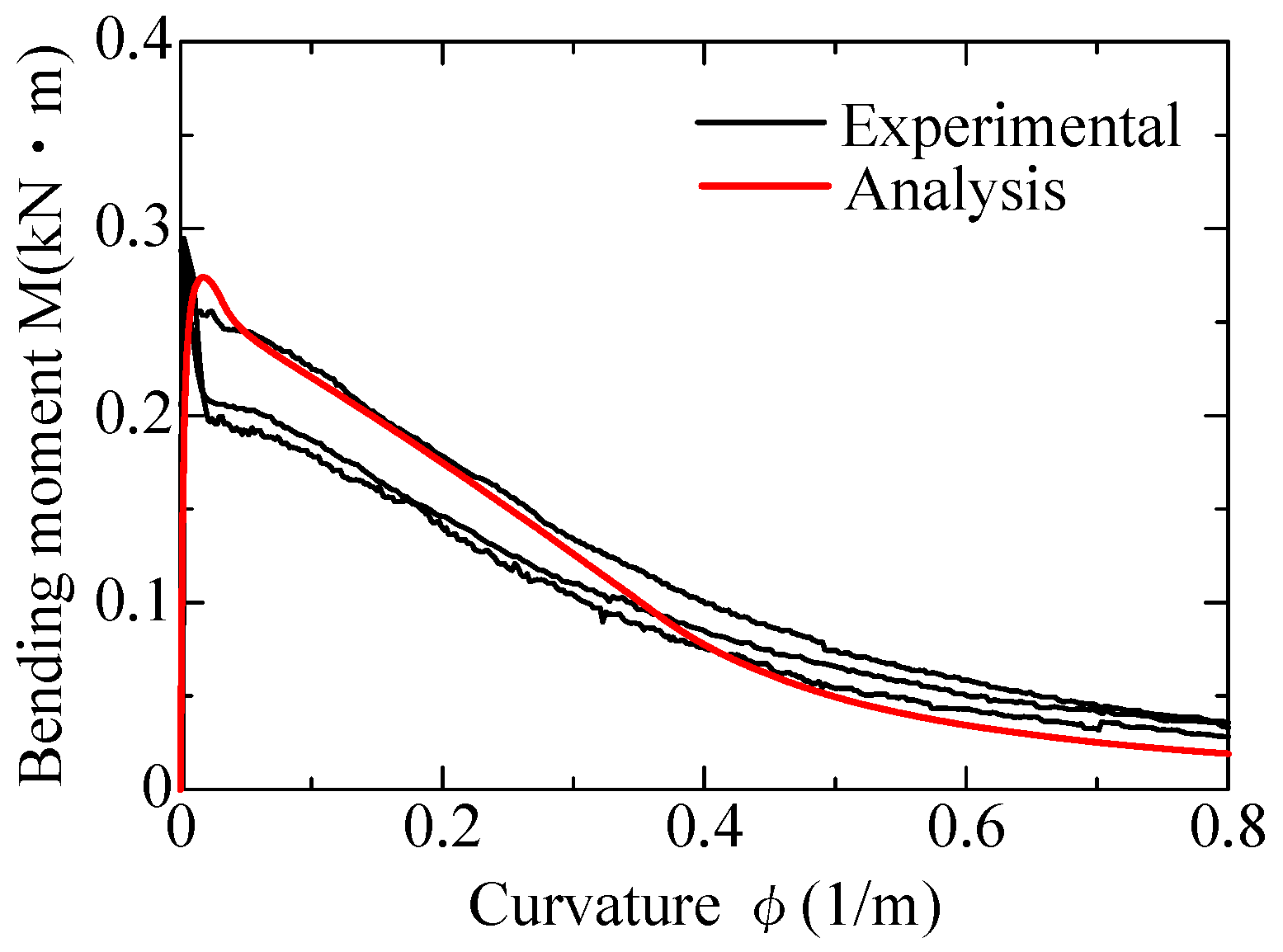
4.3.3. Comparison of Analysis and Experimental Results
5. Conclusions
- In the single fiber pullout test result, the pullout of the fiber from the matrix and fiber rupture were observed. Even though there is variability in the experimental results, a correlation between the slip, embedded length, and angle of inclination was confirmed to some extent.
- A power function relationship between the first peak load and the maximum pullout load with embedded length was found for specimens with 0° angle of inclination. Whereas a linear function relationship was adopted between the slip at the first peak load and at the maximum pullout load with the embedded length.
- The relationship between the normalized pullout load and the inclination angle was examined based on the experimental results. Snubbing effects were considered for the first peak load and maximum pullout load.
- The pullout behavior of a single fiber was modeled using a trilinear model. A tensile stress–crack width relationship model for palm-FRCC was created using the bridging law calculation based on the trilinear model.
- Section analysis was conducted to assess the adaptability of the modeled bridging law calculations. The analysis result of the bending moment–curvature relationship shows a good agreement with the experimental results obtained from the four-point bending test of palm-FRCC.
6. Discussions for Further Research
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Naik, T.R. Sustainability of Concrete Construction. Pract. Period. Struct. Des. Constr. 2008, 13, 98–103. [Google Scholar] [CrossRef]
- Akan, M.Ö.A.; Dhavale, D.G.; Sarkis, J. Greenhouse gas emissions in the construction industry: An analysis and evaluation of a concrete supply chain. J. Clean. Prod. 2017, 167, 1195–1207. [Google Scholar] [CrossRef]
- Kim, D.J.; Naaman, A.E.; El-Tawil, S. Comparative flexural behavior of four fiber reinforced cementitious composites. Cem. Concr. Compos. 2008, 30, 917–928. [Google Scholar] [CrossRef]
- Mechtcherine, V. Towards a durability framework for structural elements and structures made of or strengthened with high-performance fibre-reinforced composites. Constr. Build. Mater. 2012, 31, 94–104. [Google Scholar] [CrossRef]
- Fakharifar, M.; Dalvand, A.; Arezoumandi, M.; Sharbatdar, M.K.; Chen, G.; Kheyroddin, A. Mechanical properties of high performance fiber reinforced cementitious composites. Constr. Build. Mater. 2014, 71, 510–520. [Google Scholar] [CrossRef]
- Jiang, F.; Li, X.; Tian, L.; Yan, T.; Yu, J. Tensile strain-hardening cementitious composites and its practical exploration without reinforcement: A review. Front. Mater. 2022, 9, 1066796. [Google Scholar] [CrossRef]
- Ding, Y.; Yu, K.; Li, M. A review on high-strength engineered cementitious composites (HS-ECC): Design, mechanical property and structural application. Structures 2022, 35, 903–921. [Google Scholar] [CrossRef]
- Onuaguluchi, O.; Banthia, N. Plant-based natural fibre reinforced cement composites: A review. Cem. Concr. Compos. 2016, 68, 96–108. [Google Scholar] [CrossRef]
- Elanchezhian, C.; Ramnath, B.V.; Ramakrishnan, G.; Rajendrakumar, M.; Naveenkumar, V.; Saravanakumar, M.K. Review on mechanical properties of natural fiber composites. Mater. Today Proc. 2018, 5, 1785–1790. [Google Scholar] [CrossRef]
- Croccolo, D.; Agostinis, M.D.; Fini, S.; Liverani, A.; Marinelli, N.; Nisini, E.; Olmi, G. Mechanical Characteristics of Two Environmentally Friendly Resins Reinforced with Flax Fibers. Stroj. Vestn. J. Mech. Eng. 2015, 61, 227–236. [Google Scholar] [CrossRef]
- Mohammed, L.; Ansari, M.N.M.; Pua, G.; Jawaid, M.; Islam, M.S. A Review on Natural Fiber Reinforced Polymer Composite and Its Applications. Int. J. Polym. Sci. 2015, 243947. [Google Scholar] [CrossRef]
- Lotfi, A.; Li, H.; Dao, D.; Prusty, B. Natural fiber–reinforced composites: A review on material, manufacturing, and machinability. J. Thermoplast. Compos. Mater. 2019, 34, 238–284. [Google Scholar] [CrossRef]
- Pacheco-Torgal, F.; Jalali, S. Cementitious building materials reinforced with vegetable fibres: A review. Constr. Build. Mater. 2011, 25, 575–581. [Google Scholar] [CrossRef]
- Laverde, V.; Marin, A.; Benjumea, J.M.; Ortiz, M.R. Use of vegetable fibers as reinforcements in cement-matrix composite materials: A review. Constr. Build. Mater. 2022, 340, 127729. [Google Scholar] [CrossRef]
- Islam, M.S.; Ahmed, S.J. Influence of jute fiber on concrete properties. Constr. Build. Mater. 2018, 189, 768–776. [Google Scholar] [CrossRef]
- Elsaid, A.; Dawood, M.; Seracino, R.; Bobko, C. Mechanical properties of kenaf fiber reinforced concrete. Constr. Build. Mater. 2011, 25, 1991–2001. [Google Scholar] [CrossRef]
- Ren, G.; Yao, B.; Huang, H.; Gao, X. Influence of sisal fibers on the mechanical performance of ultra-high performance concretes. Constr. Build. Mater. 2021, 286, 122958. [Google Scholar] [CrossRef]
- Ali, B.; Azab, M.; Ahmed, H.; Kurda, R.; Ouni, M.H.E.; Elhag, A.B. Investigation of physical, strength, and ductility characteristics of concrete reinforced with banana (Musaceae) stem fiber. J. Build. Eng. 2022, 61, 105024. [Google Scholar] [CrossRef]
- Huang, J.K.; Young, W.B. The mechanical, hygral, and interfacial strength of continuous bamboo fiber reinforced epoxy composites. Compos. Part B Eng. 2019, 166, 272–283. [Google Scholar] [CrossRef]
- Lilargem Rocha, D.; Tambara Júnior, L.U.D.; Marvila, M.T.; Pereira, E.C.; Souza, D.; de Azevedo, A.R.G. A Review of the Use of Natural Fibers in Cement Composites: Concepts, Applications and Brazilian History. Polymers 2022, 14, 2043. [Google Scholar] [CrossRef]
- Qu, W.; Niu, B.; Lv, C.; Liu, J. A Review of Sisal Fiber-Reinforced Geopolymers: Preparation, Microstructure, and Mechanical Properties. Molecules 2024, 29, 2401. [Google Scholar] [CrossRef] [PubMed]
- Ren, G.; Yao, B.; Ren, M.; Gao, X. Utilization of natural sisal fibers to manufacture eco-friendly ultra-high performance concrete with low autogenous shrinkage. J. Clean. Prod. 2021, 332, 130105. [Google Scholar] [CrossRef]
- Thyavihalli Girijappa, Y.G.; Mavinkere Rangappa, S.; Parameswaranpillai, J.; Siengchin, S. Natural Fibers as Sustainable and Renewable Resource for Development of Eco-Friendly Composites: A Comprehensive Review. Front. Mater. 2019, 6, 226. [Google Scholar] [CrossRef]
- Lee, C.H.; Khalina, A.; Lee, S.H. Importance of Interfacial Adhesion Condition on Characterization of Plant-Fiber-Reinforced Polymer Composites: A Review. Polymers 2021, 13, 438. [Google Scholar] [CrossRef]
- Aruna, M.; Shehhi, M. Influence of surface treatments in natural fibre reinforced composites. Int. J. Multiphys. 2020, 14, 129–141. [Google Scholar]
- Santana, H.A.; Júnior, N.S.A.; Ribeiro, D.V.; Cilla, M.S.; Dias, C.M.R. Vegetable fibers behavior in geopolymers and alkali-activated cement based matrices: A review. J. Build. Eng. 2021, 44, 103291. [Google Scholar] [CrossRef]
- Labib, W.A. Plant-based fibres in cement composites: A conceptual framework. J. Eng. Fibers Fabr. 2022, 17, 15589250221078922. [Google Scholar] [CrossRef]
- Oladele, I.O.; Michael, O.S.; Adediran, A.A.; Balogun, O.P.; Ajagbe, F.O. Acetylation Treatment for the Batch Processing of Natural Fibers: Effects on Constituents, Tensile Properties and Surface Morphology of Selected Plant Stem Fibers. Fibers 2020, 8, 73. [Google Scholar] [CrossRef]
- Karimah, A.; Ridho, M.R.; Munawar, S.S.; Adi, D.S.; Ismadi, D.R.; Subiyanto, B.; Fatriasari, W.; Fudholi, A. A review on natural fibers for development of eco-friendly bio-composite: Characteristics, and utilizations. J. Mater. Res. Technol. 2021, 13, 2442–2458. [Google Scholar] [CrossRef]
- Adamu, M.; Alanazi, F.; Ibrahim, Y.E.; Alanazi, H.; Khed, V.C. A Comprehensive Review on Sustainable Natural Fiber in Cementitious Composites: The Date Palm Fiber Case. Sustainability 2022, 14, 6691. [Google Scholar] [CrossRef]
- Saini, K.; Matsagar, V.A.; Kodur, V.R. Recent advances in the use of natural fibers in civil engineering structures. Constr. Build. Mater. 2024, 411, 134364. [Google Scholar] [CrossRef]
- Ardanuy, M.; Claramunt, J.; Filho, R.D.T. Cellulosic fiber reinforced cement-based composites: A review of recent research. Constr. Build. Mater. 2015, 79, 115–128. [Google Scholar] [CrossRef]
- Fan, M.; Fu, F. Introduction: A perspective—Natural fibre composites in construction. In Advanced High Strength Natural Fibre Composites in Construction; Woodhead Publishing: Cambridge, UK, 2017; pp. 1–20. [Google Scholar] [CrossRef]
- Malkapuram, R.; Kumar, V.; Yuvraj, S.N. Recent Development in Natural Fiber Reinforced Polypropylene Composites. J. Reinf. Plast. Compos. 2009, 28, 1169–1189. [Google Scholar] [CrossRef]
- Ahmad, H.; Chhipi-Shrestha, G.; Hewage, K.; Sadiq, R. A Comprehensive Review on Construction Applications and Life Cycle Sustainability of Natural Fiber Biocomposites. Sustainability 2022, 14, 15905. [Google Scholar] [CrossRef]
- Lu, J.X. Recent advances in high strength lightweight concrete: From development strategies to practical applications. Constr. Build. Mater. 2023, 400, 132905. [Google Scholar] [CrossRef]
- Dittenber, D.B.; GangaRao, H.V.S. Critical review of recent publications on use of natural composites in infrastructure. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1419–1429. [Google Scholar] [CrossRef]
- Alhijazi, M.; Zeeshan, Q.; Safaei, B.; Asmael, M.; Qin, Z. Recent Developments in Palm Fibers Composites: A Review. J. Polym. Environ. 2020, 28, 3029–3054. [Google Scholar] [CrossRef]
- Momoh, E.O.; Osofero, A.I. Recent developments in the application of oil palm fibers in cement composites. Front. Struct. Civ. Eng. 2020, 14, 94–108. [Google Scholar] [CrossRef]
- Bamaga, S.O. A Review on the Utilization of Date Palm Fibers as Inclusion in Concrete and Mortar. Fibers 2022, 10, 35. [Google Scholar] [CrossRef]
- Khelifa, H.; Bezazi, A.; Boumediri, H.; del Pino, G.G.; Reis, P.N.B.; Scarpa, F.; Dufresne, A. Mechanical characterization of mortar reinforced by date palm mesh fibers: Experimental and statistical analysis. Constr. Build. Mater. 2021, 300, 124067. [Google Scholar] [CrossRef]
- Momoh, E.O.; Osofero, A.I. Behaviour of oil palm broom fibres (OPBF) reinforced concrete. Constr. Build. Mater. 2019, 221, 745–761. [Google Scholar] [CrossRef]
- Bopda Fokam, C.; Toumi, E.; Kenmeugne, B.; Wiryikfu, N.C.; Mevaa, L. Experimental study of the addition of oil palm mesocarp fiber on the physical and mechanical properties of fiber cement mortar composites. SN Appl. Sci. 2021, 3, 85. [Google Scholar] [CrossRef]
- Lertwattanaruk, P.; Suntijitto, A. Properties of natural fiber cement materials containing coconut coir and oil palm fibers for residential building applications. Constr. Build. Mater. 2015, 94, 664–669. [Google Scholar] [CrossRef]
- Kareche, A.; Agoudjil, B.; Haba, B.; Boudenne, A. Study on the Durability of New Construction Materials Based on Mortar Reinforced with Date Palm Fibers Wastes. Waste Biomass Valorization 2020, 11, 3801–3809. [Google Scholar] [CrossRef]
- Zanichelli, A.; Carpinteri, A.; Fortese, G.; Ronchei, C.; Scorza, D.; Vantadori, S. Contribution of date-palm fibres reinforcement to mortar fracture toughness. Procedia Struct. Integr. 2018, 13, 542–547. [Google Scholar] [CrossRef]
- Aziez, M.N.; Achour, A. Physical and Mechanical Properties of Cement-Based Mortars Reinforced with Treated Date Palm Fibres. All Sciences Preceedings. 2023. Available online: https://as-proceeding.com/index.php/icmar (accessed on 11 September 2024).
- Bonnet-Masimbert, P.A.; Gauvin, F.; Brouwers, H.J.H.; Amziane, S. Study of modifications on the chemical and mechanical compatibility between cement matrix and oil palm fibres. Results Eng. 2020, 7, 100150. [Google Scholar] [CrossRef]
- Oushabi, A.; Sair, S.; Hassani, F.O.; Abboud, Y.; Tanane, O.; Bouari, A.E. The effect of alkali treatment on mechanical, morphological and thermal properties of date palm fibers (DPFs): Study of the interface of DPF–Polyurethane composite. S. Afr. J. Chem. Eng. 2017, 23, 116–123. [Google Scholar] [CrossRef]
- Alatshan, F.; Altlomate, A.M.; Mashiri, F.; Alamin, W. Effect of date palm fibers on the mechanical properties of concrete. Int. J. Sustain. Build. Technol. Urban Dev. 2017, 8, 68–80. [Google Scholar] [CrossRef]
- Kanakubo, T.; Miyaguchi, M.; Asano, K. Influence of Fiber Orientation on Bridging Performance of Polyvinyl Alcohol Fiber-Reinforced Cementitious Composite. ACI Mater. J. 2016, 113, 131–141. [Google Scholar] [CrossRef]
- Ozu, Y.; Miyaguchi, M.; Kanakubo, T. Modeling of Bridging Law for PVA Fiber-Reinforced Cementitious Composite Considering Fiber Orientation. J. Civ. Eng. Archit. 2018, 12, 651–661. [Google Scholar] [CrossRef]
- Sunaga, D.; Koba, T.; Kanakubo, T. Modeling of Bridging Law for Bundled Aramid Fiber-Reinforced Cementitious Composite and its Adaptability in Crack Width Evaluation. Materials 2021, 14, 179. [Google Scholar] [CrossRef] [PubMed]
- Kanakubo, T.; Shi, H.; Wang, J. Influence of Matrix Strength on Bridging Performance of Fiber-Reinforced Cementitious Composite with Bundled Aramid Fiber. J. Compos. Sci. 2022, 6, 131. [Google Scholar] [CrossRef]
- Plagué, T.; Desmettre, C.; Charron, J.P. Influence of fiber type and fiber orientation on cracking and permeability of reinforced concrete under tensile loading. Cem. Concr. Res. 2017, 94, 59–70. [Google Scholar] [CrossRef]
- Kanakubo, T.; Echizen, S.; Wang, J.; Mu, Y. Pullout Behavior of Bundled Aramid Fiber in Fiber-Reinforced Cementitious Composite. Materials 2020, 13, 1746. [Google Scholar] [CrossRef]
- Zhang, J.; Li, V.C. Effect of inclination angle on fiber rupture load in fiber reinforced cementitious composites. Compos. Sci. Technol. 2002, 62, 775–781. [Google Scholar] [CrossRef]
- Kanda, T.; Li, V.C. Interface Property and Apparent Strength of High-Strength Hydrophilic Fiber in Cement Matrix. J. Mater. Civ.Eng. ASCE 1998, 10, 5–13. [Google Scholar] [CrossRef]
- Li, V.C.; Wang, Y.; Backer, S. Effect of inclining angle, bundling and surface treatment on synthetic fibre pull-out from a cement matrix. Composites 1990, 21, 132–140. [Google Scholar] [CrossRef]



















| W/C | FA/B | Unit Weight (kg/m3) | |||
|---|---|---|---|---|---|
| Water | Cement | Fly Ash | Sand | ||
| 0.785 | 0.5 | 380 | 484 | 484 | 484 |
| Specimen Name | Embedded Length (mm) | Inclination Angle (°) | Number of Specimens |
|---|---|---|---|
| P-2mm-0 | 2 | 0 | 5 |
| P-2mm-15 | 15 | 5 | |
| P-2mm-30 | 30 | 5 | |
| P-2mm-45 | 45 | 5 | |
| P-2mm-60 | 60 | 5 | |
| P-4mm-0 | 4 | 0 | 5 |
| P-4mm-15 | 15 | 5 | |
| P-4mm-30 | 30 | 5 | |
| P-4mm-45 | 45 | 5 | |
| P-4mm-60 | 60 | 5 | |
| P-6mm-0 | 6 | 0 | 5 |
| P-6mm-15 | 15 | 5 | |
| P-6mm-30 | 30 | 5 | |
| P-6mm-45 | 45 | 5 | |
| P-6mm-60 | 60 | 5 |
| Name | Angle of Inclination (°) | Embedded Length + (mm) | Pa (N) | Pmax (N) | Sa (mm) | Smax (mm) | Failure Mode |
|---|---|---|---|---|---|---|---|
| 2mm-0-1 | 0 | 2.06 | 0.96 | 2.69 | 0.039 | 2.880 | PO |
| 2mm-0-2 | 0.86 | 1.79 | 0.006 | 0.352 | PO | ||
| 2mm-0-3 | 0.89 | 1.18 | 0.312 | 1.921 | PO | ||
| 2mm-0-4 | 1.29 | 1.45 | 0.028 | 1.545 | PO | ||
| 2mm-0-5 | 0.85 | 2.10 | 0.088 | 0.717 | PO | ||
| 2mm-15-1 | 15 | 2.10 | 1.15 | 2.64 | 0.104 | 0.340 | PO |
| 2mm-15-2 | 0.55 | 1.62 | 0.100 | 2.677 | PO | ||
| 2mm-30-1 | 30 | 2.03 | 1.91 | 1.91 | - * | 0.071 | PO |
| 2mm-30-2 | 0.47 | 0.74 | 0.082 | 0.123 | PO | ||
| 2mm-30-3 | 1.98 | 3.69 | 0.116 | 0.582 | R | ||
| 2mm-30-4 | 2.00 | 4.00 | 0.048 | 2.087 | R | ||
| 2mm-30-5 | 2.05 | 2.93 | 0.156 | 1.619 | PO | ||
| 2mm-45-1 | 45 | 1.90 | 0.68 | 2.30 | 0.017 | 2.268 | PO |
| 2mm-60-1 | 60 | 2.01 | 1.39 | 1.84 | 0.040 | 0.704 | PO |
| 2mm-60-2 | 4.93 | 4.93 | - * | 0.017 | PO | ||
| 2mm-60-3 | 1.44 | 1.44 | - * | 0.013 | PO | ||
| 2mm-60-4 | 3.19 | 4.25 | 0.064 | 0.535 | PO | ||
| 2mm-60-5 | 0.92 | 2.01 | 0.046 | 1.224 | PO |
| Name | Angle of Inclination (°) | Embedded Length + (mm) | Pa (N) | Pmax (N) | Sa (mm) | Smax (mm) | Failure Mode |
|---|---|---|---|---|---|---|---|
| 4mm-0-1 | 0 | 4.05 | 1.22 | 1.59 | 0.218 | 2.422 | PO |
| 4mm-0-2 | 3.55 | 3.55 | - * | 0.074 | PO | ||
| 4mm-0-3 | 2.07 | 2.07 | - * | 0.072 | PO | ||
| 4mm-0-4 | 2.59 | 2.82 | 0.197 | 0.733 | PO | ||
| 4mm-0-5 | 2.58 | 2.58 | - * | 0.019 | R | ||
| 4mm-15-1 | 15 | 4.05 | 1.46 | 1.82 | 0.103 | 0.750 | PO |
| 4mm-30-1 | 30 | 4.09 | 3.29 | 4.53 | 0.060 | 0.705 | PO |
| 4mm-30-2 | 3.66 | 5.39 | 0.061 | 0.901 | R | ||
| 4mm-30-3 | 1.54 | 2.07 | 0.038 | 0.685 | R | ||
| 4mm-30-4 | 4.05 | 4.05 | - * | 0.036 | PO | ||
| 4mm-30-5 | 0.89 | 2.93 | 0.085 | 2.901 | R | ||
| 4mm-45-1 | 45 | 4.05 | 1.16 | 1.99 | 0.067 | 1.250 | PO |
| 4mm-60-1 | 60 | 4.10 | 5.42 | 5.42 | - * | 0.378 | R |
| 4mm-60-2 | 1.18 | 3.21 | 0.022 | 2.372 | PO | ||
| 4mm-60-3 | 3.89 | 5.44 | 0.056 | 2.620 | R | ||
| 4mm-60-4 | 4.72 | 5.18 | 0.113 | 0.200 | PO | ||
| 4mm-60-5 | 2.49 | 3.55 | 0.027 | 0.665 | PO |
| Name | Angle of Inclination (°) | Embedded Length + (mm) | Pa (N) | Pmax (N) | Sa (mm) | Smax (mm) | Failure Mode |
|---|---|---|---|---|---|---|---|
| 6mm-0-1 | 0 | 6.12 | 2.17 | 3.10 | 0.020 | 2.746 | PO |
| 6mm-0-2 | 1.77 | 1.88 | 0.060 | 0.727 | PO | ||
| 6mm-0-3 | 1.72 | 1.72 | 0.033 | 2.040 | PO | ||
| 6mm-0-4 | 2.86 | 2.86 | - * | 0.175 | PO | ||
| 6mm-0-5 | 0.78 | 1.58 | 0.086 | 2.306 | R | ||
| 6mm-15-1 | 15 | 6.03 | 1.46 | 2.52 | 0.024 | 2.171 | PO |
| 6mm-15-2 | 0.67 | 1.40 | 0.021 | 0.324 | PO | ||
| 6mm-15-3 | 1.97 | 3.60 | 0.005 | 1.863 | R | ||
| 6mm-30-1 | 30 | 6.06 | 8.31 | 8.31 | - * | 0.453 | PO |
| 6mm-30-2 | 3.66 | 3.66 | - * | 0.040 | PO | ||
| 6mm-30-3 | 3.20 | 3.20 | - * | 0.745 | PO | ||
| 6mm-30-4 | 1.95 | 3.62 | 0.056 | 3.211 | PO | ||
| 6mm-30-5 | 2.04 | 3.52 | 0.022 | 2.271 | R | ||
| 6mm-45-1 | 45 | 6.06 | 1.61 | 2.12 | 0.373 | 1.360 | PO |
| 6mm-45-2 | 1.32 | 2.11 | 0.100 | 0.659 | R | ||
| 6mm-45-3 | 1.24 | 1.24 | - * | 0.052 | PO | ||
| 6mm-45-4 | 2.30 | 3.21 | 0.072 | 0.220 | R | ||
| 6mm-60-1 | 60 | 6.08 | 3.82 | 3.82 | - * | 0.188 | R |
| 6mm-60-2 | 2.70 | 4.30 | 0.048 | 0.695 | R | ||
| 6mm-60-3 | 0.53 | 1.09 | 0.134 | 0.251 | R | ||
| 6mm-60-4 | 2.61 | 4.02 | 0.069 | 1.239 | R | ||
| 6mm-60-5 | 2.26 | 3.69 | 0.152 | 2.100 | R |
| Parameter | Input Value | |
|---|---|---|
| Cross-sectional area of the fiber, Af (mm2) | 0.023 | |
| Length of fiber, lf (mm) | 12 | |
| Fiber volume fraction (See Section 4.3.2) | 0.025 | |
| Snubbing coefficient | 0.35 | |
| Apparent rupture strength of fiber (MPa) | σfu = 110e0.006ψ | |
| Trilinear model | Maximum pullout load, Pmax (N) | Pmax = 1.6lb0.26 |
| First peak load, Pa (N) | Pa = 0.62lb0.78 | |
| Crack width at Pmax, wmax (mm) | wmax = 0.4lb | |
| Crack width at Pa, wa (mm) | wa = 0.04lb | |
| Elliptic distribution [51] | Orientation intensity, k (kxy = kzx) | 1 |
| Principal orientation angle, θr | 0 | |
| Specimen | Compressive Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|
| Palm-FRCC 3% | 25.2 | 11.8 |
| Sample | Weight of Fiber (g) | Weight of Fiber Passing 2 mm Sieve (g) |
|---|---|---|
| 1 | 4.71 | 0.65 |
| 2 | 6.17 | 0.88 |
| 3 | 5.06 | 0.82 |
| 4 | 8.55 | 1.13 |
| 5 | 6.52 | 0.96 |
| Avg. | 6.20 | 0.89 |
| Percentage of smaller fibers | 14.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abrha, S.F.; Shiferaw, H.N.; Kanakubo, T. Bridging Behavior of Palm Fiber in Cementitious Composite. J. Compos. Sci. 2024, 8, 361. https://doi.org/10.3390/jcs8090361
Abrha SF, Shiferaw HN, Kanakubo T. Bridging Behavior of Palm Fiber in Cementitious Composite. Journal of Composites Science. 2024; 8(9):361. https://doi.org/10.3390/jcs8090361
Chicago/Turabian StyleAbrha, Selamawit Fthanegest, Helen Negash Shiferaw, and Toshiyuki Kanakubo. 2024. "Bridging Behavior of Palm Fiber in Cementitious Composite" Journal of Composites Science 8, no. 9: 361. https://doi.org/10.3390/jcs8090361
APA StyleAbrha, S. F., Shiferaw, H. N., & Kanakubo, T. (2024). Bridging Behavior of Palm Fiber in Cementitious Composite. Journal of Composites Science, 8(9), 361. https://doi.org/10.3390/jcs8090361







