Micro-Scale Numerical Simulation for Residual Strength of CFRP After Cyclic Tensile or Out-of-Plane Shear Loadings Fatigue
Abstract
:1. Introduction
2. Degradable Hashin’s Criteria [35]
3. Determination of Material Constants
4. Numerical Procedures
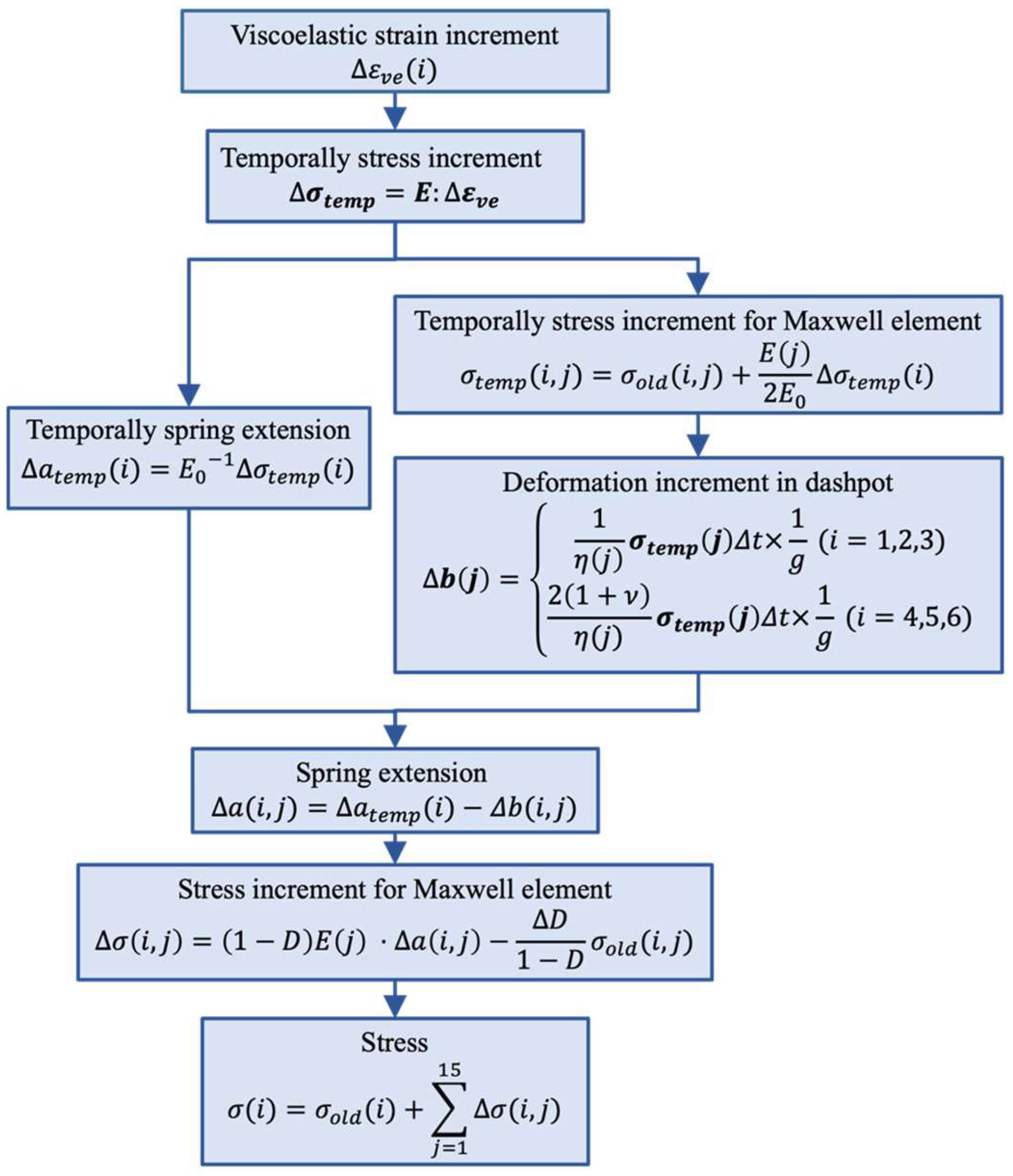
4.1. Analysis Algorithm for the Matrix Resin
4.2. Analysis Model and Conditions
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Banks-Sills, L.; Choron, T.; Simon, I. Effect of number of fatigue cycles on fatigue data: CFRP (prepreg and wet-layup). Fatigue Fract. Eng. Mater. Struct. 2024, 47, 833–848. [Google Scholar] [CrossRef]
- Nishi, Y.; Hosoi, A.; Kawada, H. Evaluation of matrix crack growth in interlaminar toughened quasi-isotropic carbon-fiber reinforced plastic laminates up to the very-high cycle regime by ultrasonic fatigue testing. Compos. Sci. Technol. 2024, 253, 110623. [Google Scholar] [CrossRef]
- Singh, K.K.; Sharma, N. Fatigue behavior of symmetric and asymmetric carbon and basalt fiber-reinforced polymer composites in transverse loading. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 245. [Google Scholar] [CrossRef]
- Lei, Z.; Pan, R.; Sun, W.; Dong, Y.; Wan, Y.; Yin, B. Fatigue damage mechanisms and evolution of residual tensile strength in CFRP Composites: Stacking sequence effect. Compos. Struct. 2024, 330, 117818. [Google Scholar] [CrossRef]
- Gerdes, L.; Mrzljak, S.; Keuntje, J.; Wippo, V.; Jaeschke, P.; Walther, F. Fatigue performance of laser cut carbon fiber-reinforced epoxy and polyamide 6 considering specimen width. Mater./Mater. Test. 2023, 65, 1645–1656. [Google Scholar] [CrossRef]
- Frik, M.; Benkedjouh, T.; Essaidi, A.B.; Boumediene, F. Advancing Damage Assessment of CFRP-Composite through BILSTM and Hilbert Upper Envelope Analysis. Russ. J. Nondestruct. Test. 2023, 59, 1241–1258. [Google Scholar] [CrossRef]
- Jia, Z.; Garnier, C.; Pastor, M.-L.; Rousseau, J.; Gong, X. Experimental investigation of impacted multidirectional laminates under compressive static and cyclic loading. Compos. Struct. 2023, 322, 117335. [Google Scholar] [CrossRef]
- Jia, Z.; Pastor, M.-L.; Garnier, C.; Gong, X. Fatigue life determination based on infrared thermographic data for Multi-Directional (MD) CFRP composite laminates. Compos. Struct. 2023, 319, 117202. [Google Scholar] [CrossRef]
- Morgado, G.F.D.M.; Montagna, L.S.; Gouvêa, R.F.; Guimarães, A.; Passador, F.R.; Rezende, M.C. Fatigue and durability assessment of PA6-based carbon fiber composites for lightweight applications. J. Compos. Mater. 2023, 57, 4227–4238. [Google Scholar] [CrossRef]
- Nishi, Y.; Itoh, S.; Hosoi, A.; Kawada, H. Stress and energy release rate analysis of cross-ply carbon fiber-reinforced plastic laminate with transverse cracks subjected to ultrasonic vibration using a variational approach. Adv. Compos. Mater. 2024, 33, 1224–1238. [Google Scholar] [CrossRef]
- Wu, Y.; Gong, Y.; Tian, D.; Zou, L.; Zhao, L.; Zhang, J.; Hu, N. Influence of curing pressure on the mode I static and fatigue delamination growth behavior of CFRP laminates. Compos. Struct. 2023, 322, 117345. [Google Scholar] [CrossRef]
- Vishe, N.J.; Mulani, S.B.; Roy, S. Repeatable self-healing of composite’s fatigue delamination. Compos. Struct. 2023, 311, 116846. [Google Scholar] [CrossRef]
- Li, X.; Benedictus, R.; Zarouchas, D. Analysis of Stochastic Matrix Crack Evolution in CFRP Cross-Ply Laminates under Fatigue Loading. Eng. Fail. Anal. 2023, 150, 107277. [Google Scholar] [CrossRef]
- Aoki, R.; Higuchi, R.; Yokozeki, T. Progressive damage and residual strength of open-hole thin-ply CFRP laminates under tensile fatigue loading. Compos. Struct. 2023, 314, 116973. [Google Scholar] [CrossRef]
- Mrzljak, S.; Zanghellini, B.; Gerdes, L.; Helwing, R.; Schuller, R.; Sinn, G.; Lichtenegger, H.; Walther, F.; Rennhofer, H. Effect of carbon nanofibre orientation on fatigue properties of carbon fibre-reinforced polymers. J. Compos. Mater. 2023, 57, 1149–1164. [Google Scholar] [CrossRef]
- Guo, Y.-E.; Shang, D.-G.; Zuo, L.-X.; Qu, L.-F.; Cai, D.; Jin, T.; Li, D.-H. Fatigue life prediction considering strength contribution of fibre layers with different orientations for CFRP laminates at high temperature. Compos. Struct. 2023, 306, 116604. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Arai, M.; Yoshimura, A.; Goto, K. Prediction of transverse crack multiplication of CFRP cross-ply laminates under tension-tension fatigue load. Adv. Compos. Mater. 2023, 32, 419–436. [Google Scholar] [CrossRef]
- Aoki, R.; Higuchi, R.; Yokozeki, T. Fatigue simulation for progressive damage in CFRP laminates using intra-laminar and inter-laminar fatigue damage models. Int. J. Fatigue 2021, 143, 106015. [Google Scholar] [CrossRef]
- Mehdizadeh, M.; Khonsari, M.M. On the application of fracture fatigue entropy to variable frequency and loading amplitude. Theor. Appl. Fract. Mech. 2018, 98, 30–37. [Google Scholar] [CrossRef]
- Naderi, M.; Amiri, M.; Khonsari, M.M. On the thermodynamic entropy of fatigue fracture. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 466, 423–438. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. An experimental approach to low-cycle fatigue damage based on thermodynamic entropy. Int. J. Solids Struct. 2010, 47, 875–880. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. A thermodynamic approach to fatigue damage accumulation under variable loading. Mater. Sci. Eng. A 2010, 527, 6133–6139. [Google Scholar] [CrossRef]
- Liakat, M.; Khonsari, M.M. On the anelasticity and fatigue fracture entropy in high-cycle metal fatigue. Mater. Des. 2015, 82, 18–27. [Google Scholar] [CrossRef]
- Sakai, T.; Oya, Y.; Koyanagi, J. Evaluation of volumetric strain on Polyamide 6 by thermodynamic entropy generation. Exp. Mech. 2024, 64, 105–111. [Google Scholar] [CrossRef]
- Kudo, N.; Fujita, R.; Oya, Y.; Sakai, T.; Nagano, H.; Koyanagi, J. Identification of invisible fatigue damage of thermosetting epoxy resin by non-destructive thermal measurement using entropy generation. Adv. Compos. Mater. 2024, 33, 233–249. [Google Scholar] [CrossRef]
- Deng, H.; Mochizuki, A.; Fikry, M.; Abe, S.; Ogihara, S.; Koyanagi, J. Numerical and experimental studies for fatigue damage accumulation of CFRP cross-ply laminates based on entropy failure criterion. Materials 2023, 16, 388. [Google Scholar] [CrossRef]
- Sakai, T.; Takase, N.; Oya, Y.; Koyanagi, J. A possibility for quantitative detection of mechanically induced invisible damage by thermal property measurement via entropy generation for a polymer material. Materials 2022, 15, 737. [Google Scholar] [CrossRef]
- Sato, M.; Hasegawa, K.; Koyanagi, J.; Higuchi, R.; Ishida, Y. Residual Strength Prediction for Unidirectional CFRP Using a Nonlinear Viscoelastic Constitutive Equation Considering Entropy Damage. Compos. Part A 2021, 141, 106178. [Google Scholar] [CrossRef]
- Yamada, N.; Morita, M.; Takamura, M.; Murashima, T.; Oya, Y.; Koyanagi, J. Molecular Dynamics Simulation of Cumulative Microscopic Damage in a Thermosetting Polymer under Cyclic Loading. Polymers 2024, 16, 1813. [Google Scholar] [CrossRef]
- Iwamoto, S.; Oya, Y.; Koyanagi, J. Evaluation of microscopic damage of PEEK polymers under cyclic loadings using molecular dynamics simulations. Polymers 2022, 14, 4955. [Google Scholar] [CrossRef]
- Bryant, M.D.; Khonsari, M.M.; Ling, F.F. On the thermodynamics of degradation. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 2001–2014. [Google Scholar] [CrossRef]
- Li, Y.; Deng, H.; Takamura, M.; Koyanagi, J. Durability analysis of CFRP adhesive joints: A study based on entropy damage modeling using FEM. Materials 2023, 16, 6821. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Toda, K.; Sato, M.; Koyanagi, J. Micro-scale numerical simulation of fatigue failure for CFRP subjected to multiple-amplitude cyclic loadings based on entropy damage criterion. Materials 2023, 16, 6120. [Google Scholar] [CrossRef] [PubMed]
- Kudo, N.; Sekino, T.; Fikry, M.J.M.; Koyanagi, J. Numerical Simulation of the Frequency Dependence of Fatigue Failure for a Viscoelastic Medium Considering Internal Heat Generation. Materials 2024, 17, 6202. [Google Scholar] [CrossRef] [PubMed]
- Koyanagi, J.; Mochizuki, A.; Higuchi, R.; Tan, V.B.C.; Tay, T.E. Finite element model for simulating entropy-based strength-degradation of carbon-fiber-reinforced plastics subjected to cyclic loadings. Int. J. Fatigue 2022, 165, 107204. [Google Scholar] [CrossRef]
- Li, S.; Warrior, N.; Zou, Z.; Almaskari, F. A unit cell for FE analysis of materials with the microstructure of a staggered pattern. Compos. Part A Appl. Sci. Manuf. 2011, 42, 801–811. [Google Scholar] [CrossRef]
- Melro, A.R.; Camanho, P.P.; Andrade Pires, F.M.; Pinho, S.T. Micromechanical analysis of polymer composites reinforced by unidirectional fibres: Part II-Micromechanical analyses. Int. J. Solids Struct. 2013, 50, 1906–1915. [Google Scholar] [CrossRef]
- Li, S.; Jeanmeure, L.F.C.; Pan, Q. A composite material characterisation tool: UnitCells. J. Eng. Math. 2015, 95, 279–293. [Google Scholar] [CrossRef]
- Higuchi, R.; Yokozeki, T.; Nagashima, T.; Aoki, T. Evaluation of mechanical properties of noncircular carbon fiber reinforced plastics by using XFEM-based computational micromechanics. Compos. Part A Appl. Sci. Manuf. 2019, 126, 105556. [Google Scholar] [CrossRef]
- Sato, M.; Shirai, S.; Koyanagi, J.; Ishida, Y.; Kogo, Y. Numerical simulation for strain rate and temperature dependence of transverse tensile failure of unidirectional CFRP. J. Compos. Mater. 2019, 53, 4305–4312. [Google Scholar] [CrossRef]

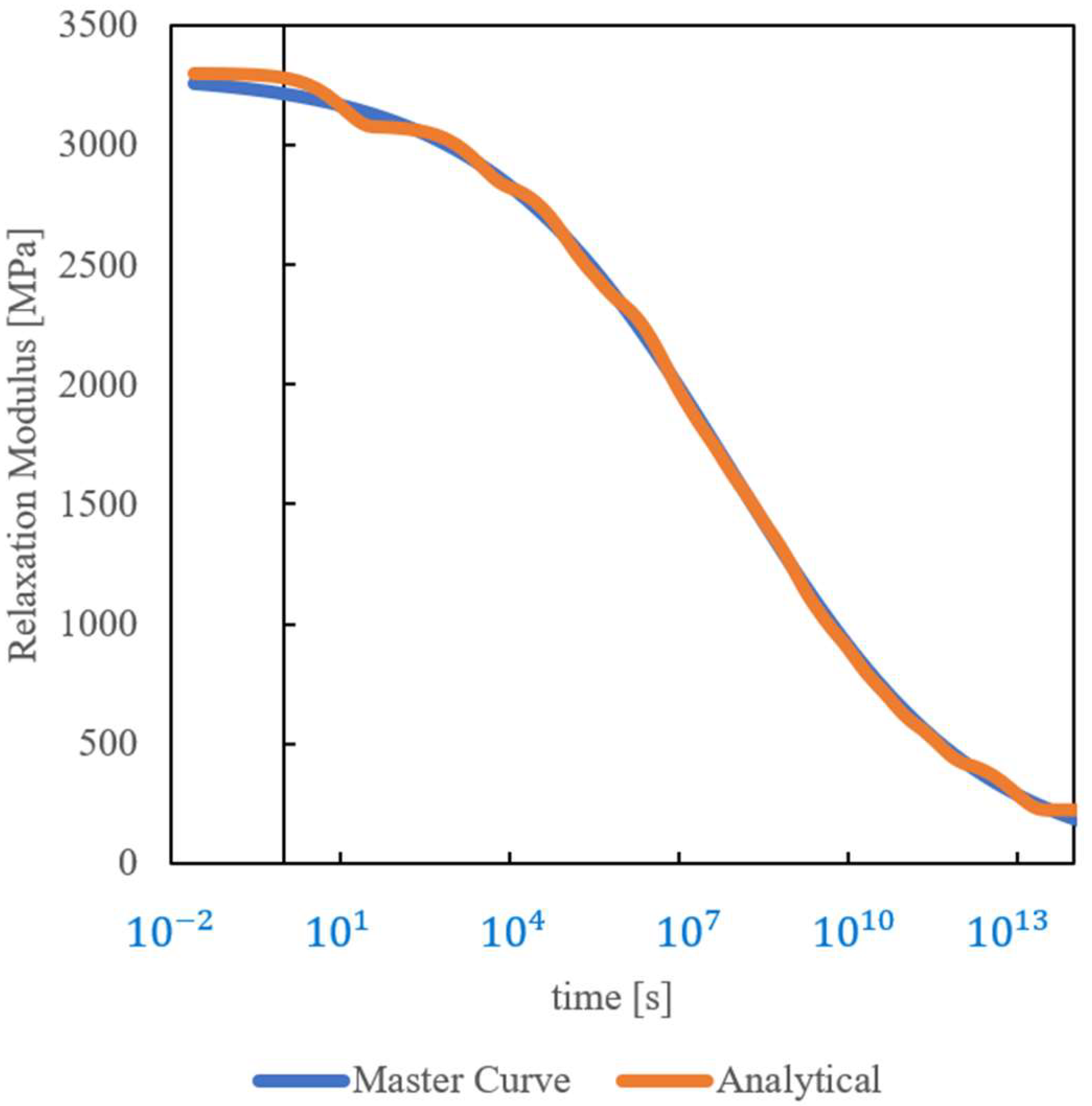









| [MPa] | [MPa·s] | |
|---|---|---|
| 1 | 220 | 2.5 × 103 |
| 2 | 220 | 6.3 × 105 |
| 3 | 220 | 1.6 × 107 |
| 4 | 220 | 6.3 × 107 |
| 5 | 220 | 7.9 × 108 |
| 6 | 220 | 2.0 × 109 |
| 7 | 220 | 7.9 × 109 |
| 8 | 220 | 3.2 × 1010 |
| 9 | 220 | 1.6 × 1011 |
| 10 | 220 | 4.0 × 1011 |
| 11 | 220 | 2.0 × 1012 |
| 12 | 220 | 1.0 × 1013 |
| 13 | 220 | 7.9 × 1013 |
| 14 | 220 | 2.0 × 1015 |
| 15 | 220 | 1.0 × 1035 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekino, T.; Kudo, N.; Koyanagi, J. Micro-Scale Numerical Simulation for Residual Strength of CFRP After Cyclic Tensile or Out-of-Plane Shear Loadings Fatigue. J. Compos. Sci. 2025, 9, 28. https://doi.org/10.3390/jcs9010028
Sekino T, Kudo N, Koyanagi J. Micro-Scale Numerical Simulation for Residual Strength of CFRP After Cyclic Tensile or Out-of-Plane Shear Loadings Fatigue. Journal of Composites Science. 2025; 9(1):28. https://doi.org/10.3390/jcs9010028
Chicago/Turabian StyleSekino, Takumi, Natsuko Kudo, and Jun Koyanagi. 2025. "Micro-Scale Numerical Simulation for Residual Strength of CFRP After Cyclic Tensile or Out-of-Plane Shear Loadings Fatigue" Journal of Composites Science 9, no. 1: 28. https://doi.org/10.3390/jcs9010028
APA StyleSekino, T., Kudo, N., & Koyanagi, J. (2025). Micro-Scale Numerical Simulation for Residual Strength of CFRP After Cyclic Tensile or Out-of-Plane Shear Loadings Fatigue. Journal of Composites Science, 9(1), 28. https://doi.org/10.3390/jcs9010028





