Tensile Strength Predictive Modeling of Natural-Fiber-Reinforced Recycled Aggregate Concrete Using Explainable Gradient Boosting Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Gradient Boosting Algorithms
2.2. Optimization of the Hyperparameters
2.3. Shapley Additive Explanations (SHAP) Methodology
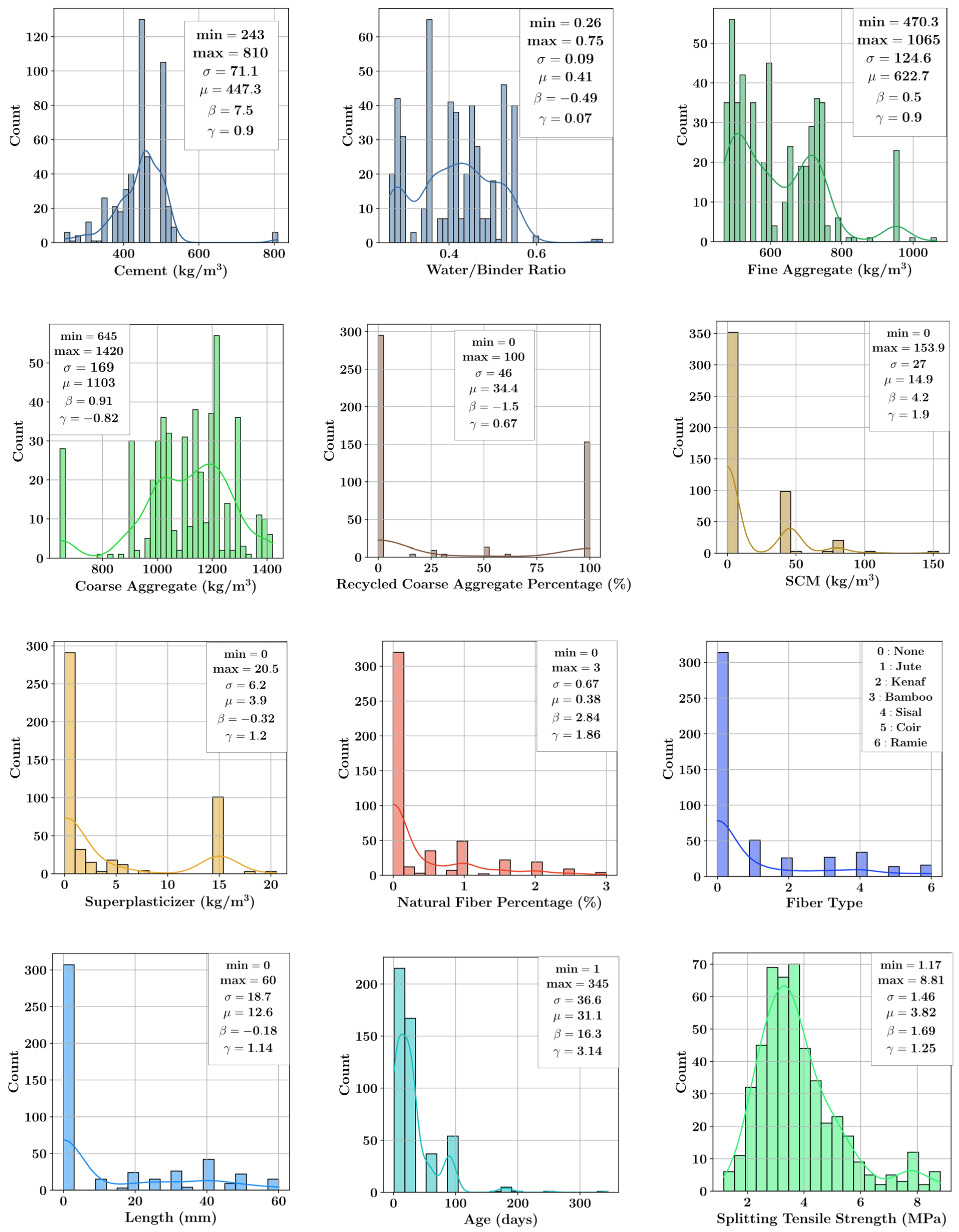
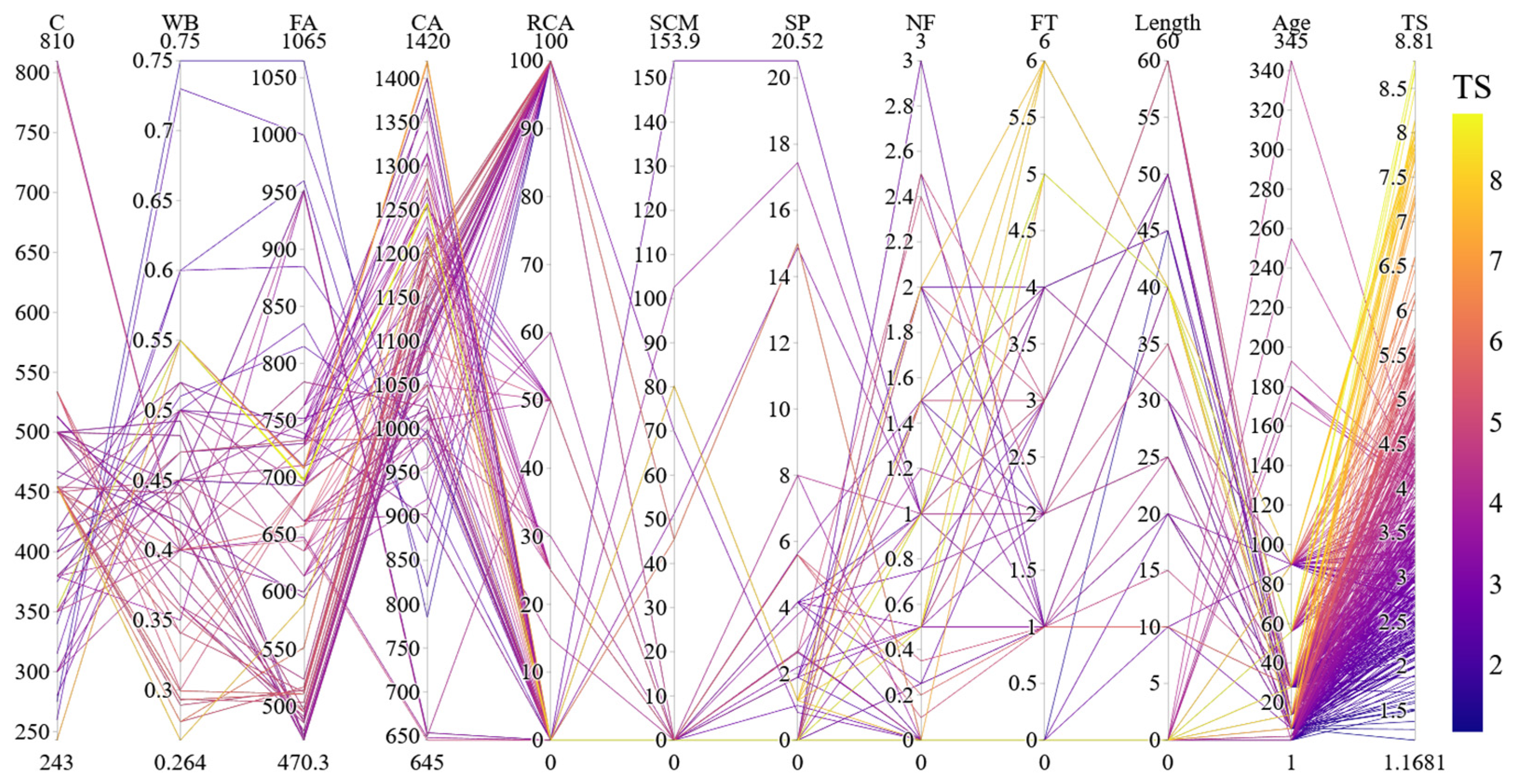
2.4. Statistical Analysis of the Dataset
2.5. Outlier Detection Techniques
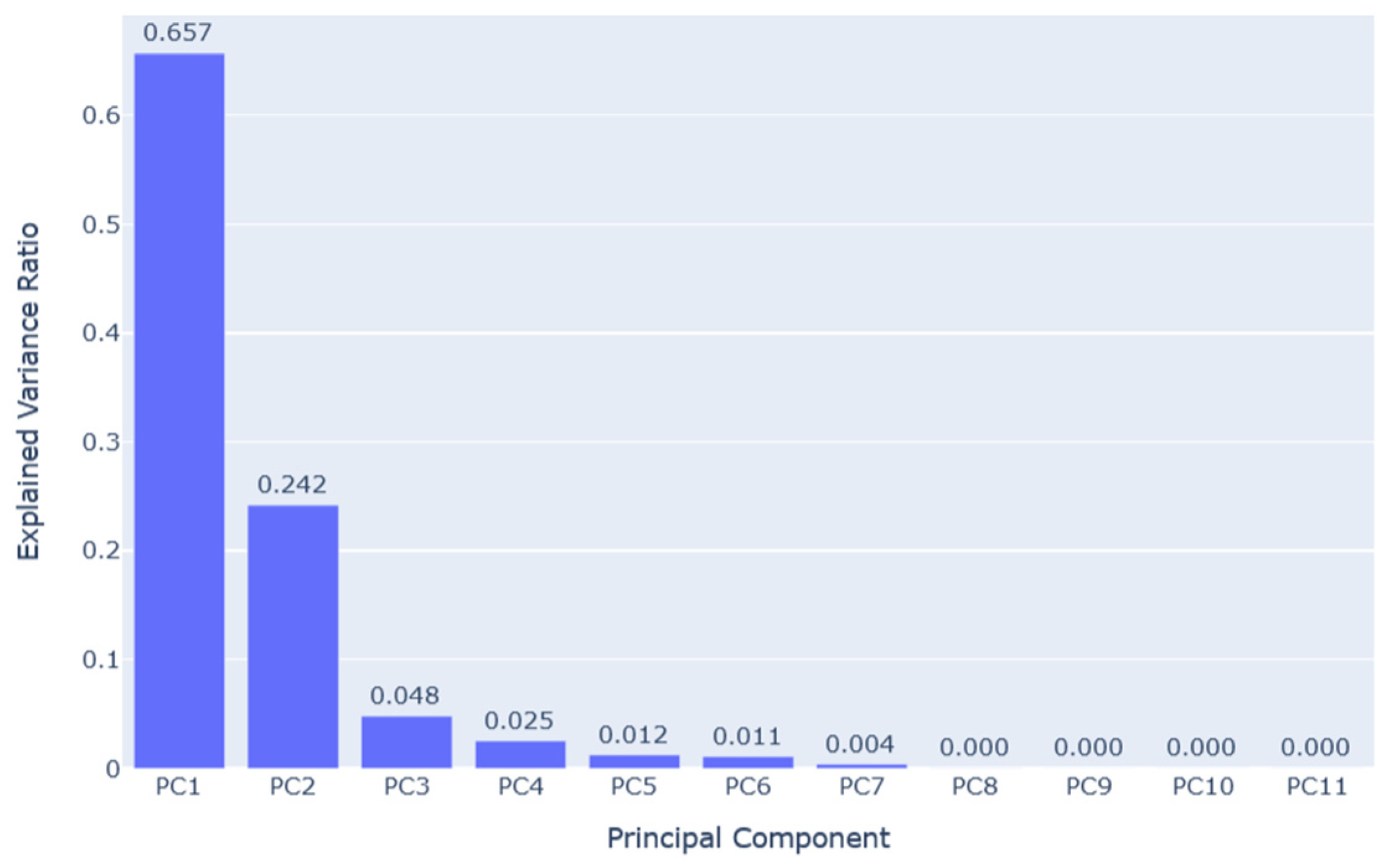
2.5.1. Principal Component Analysis (PCA)
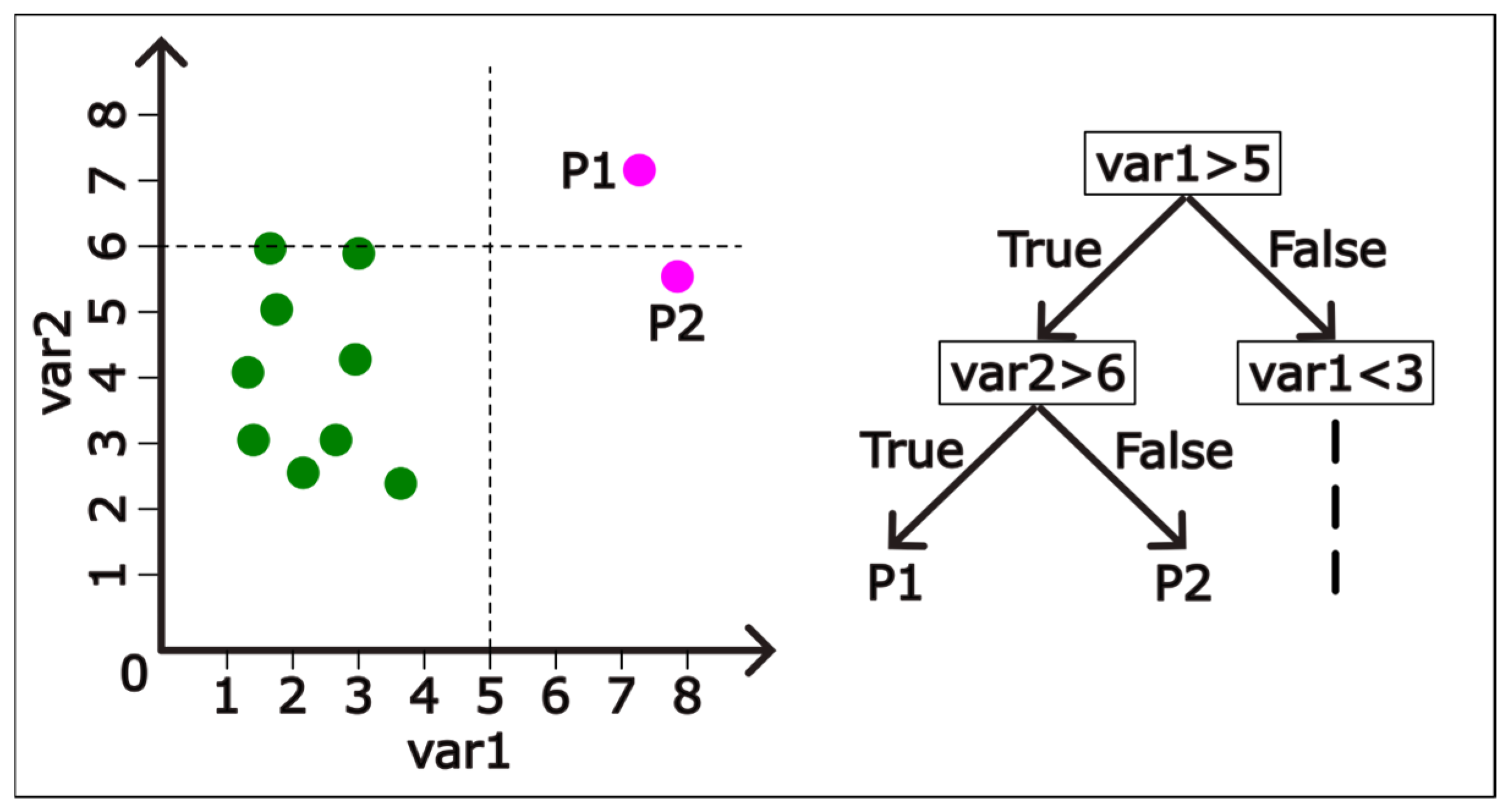
2.5.2. Isolation Forest
3. Results
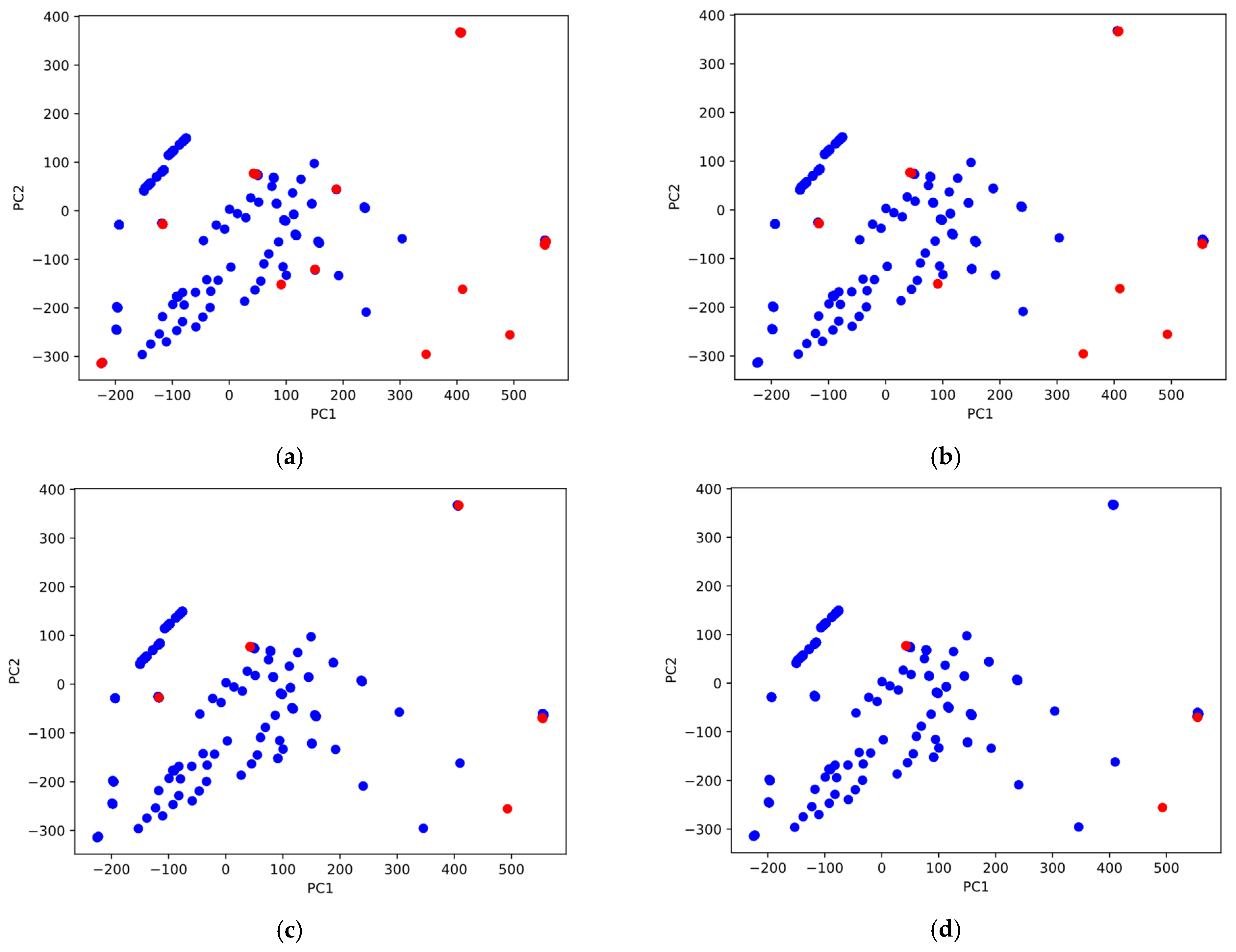
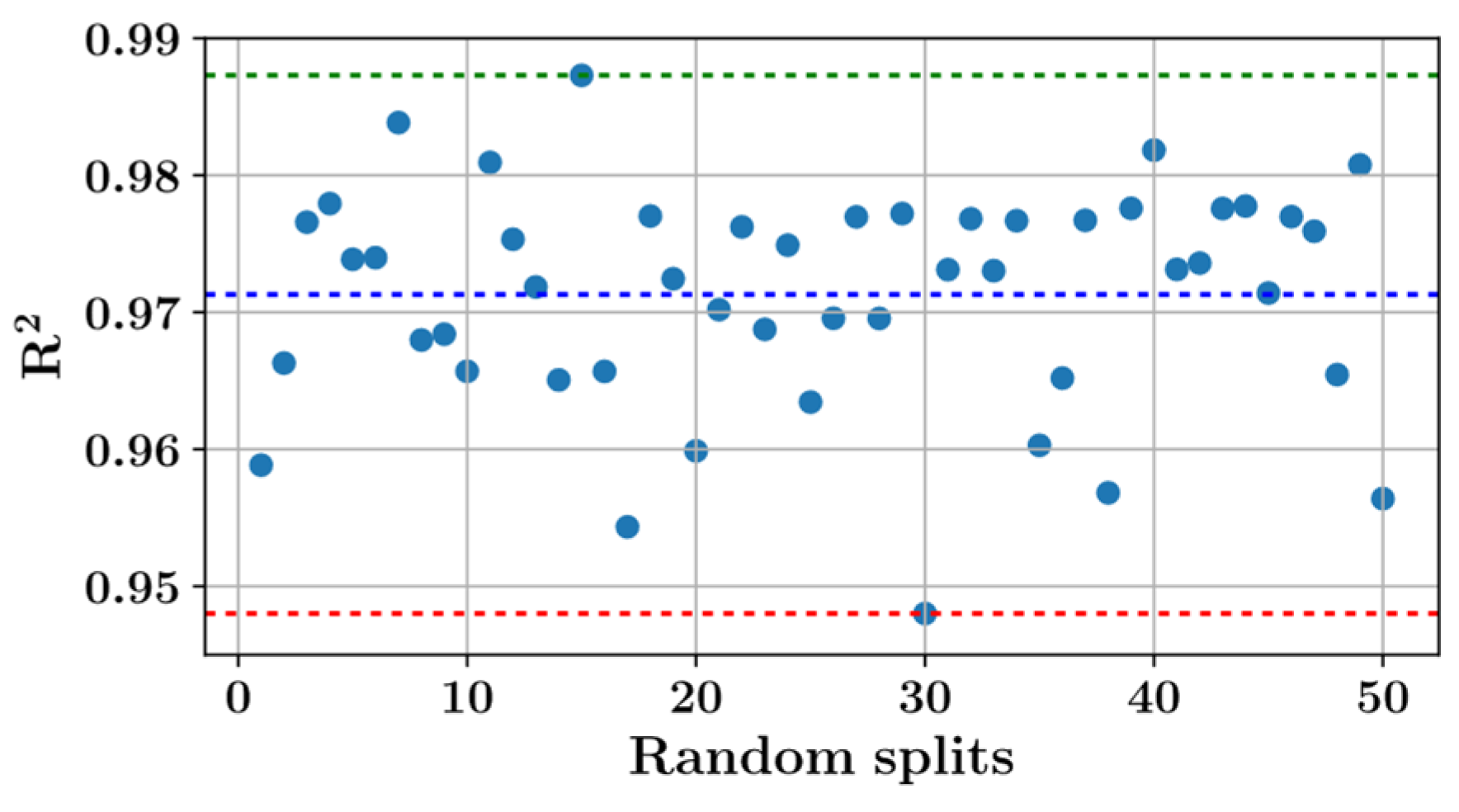
3.1. Outlier Detection Using Isolation Forest and Principal Component Analysis
3.2. Predictions of the LightGBM, XGBoost and Extra Trees Regressors
3.3. Graphical User Interface
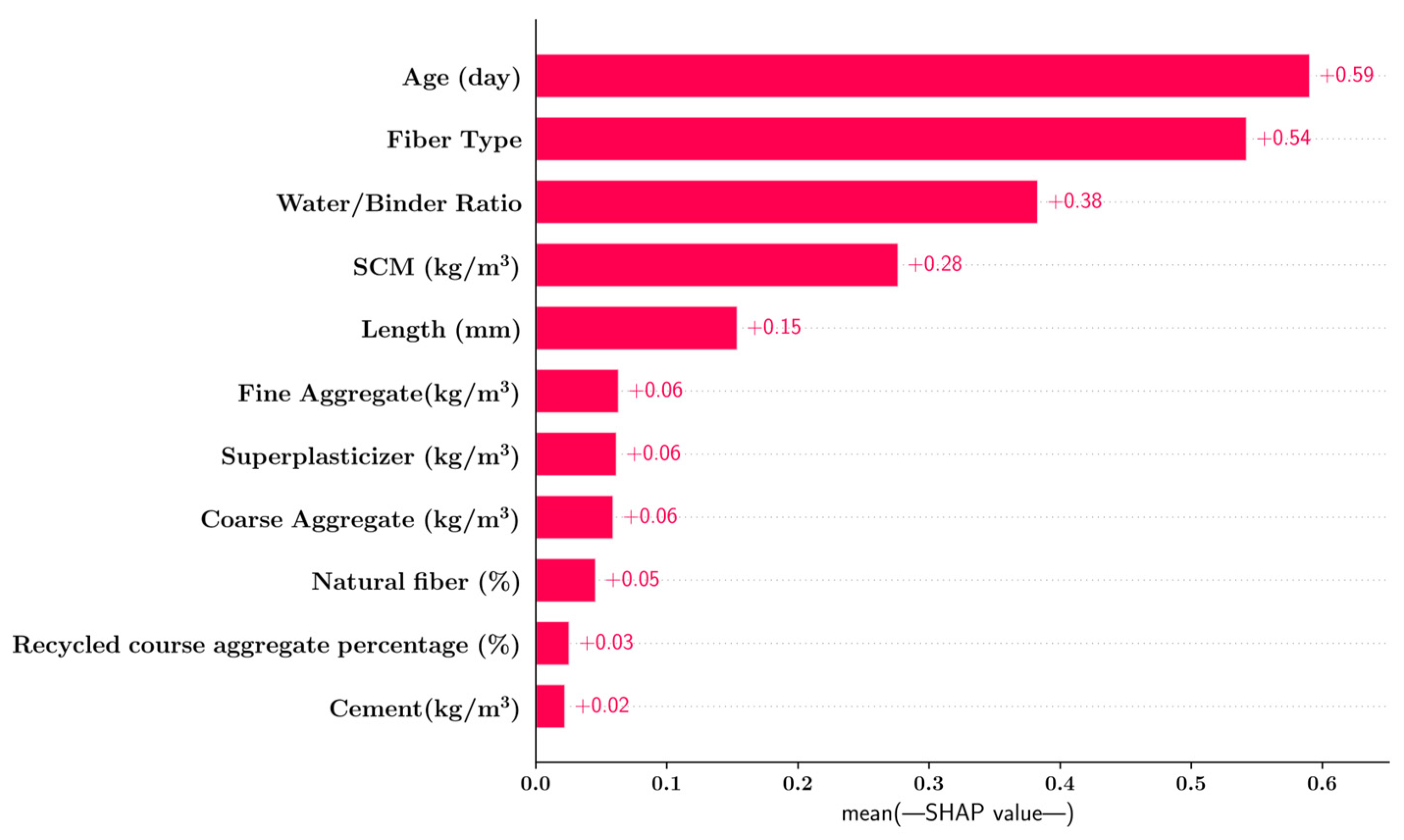
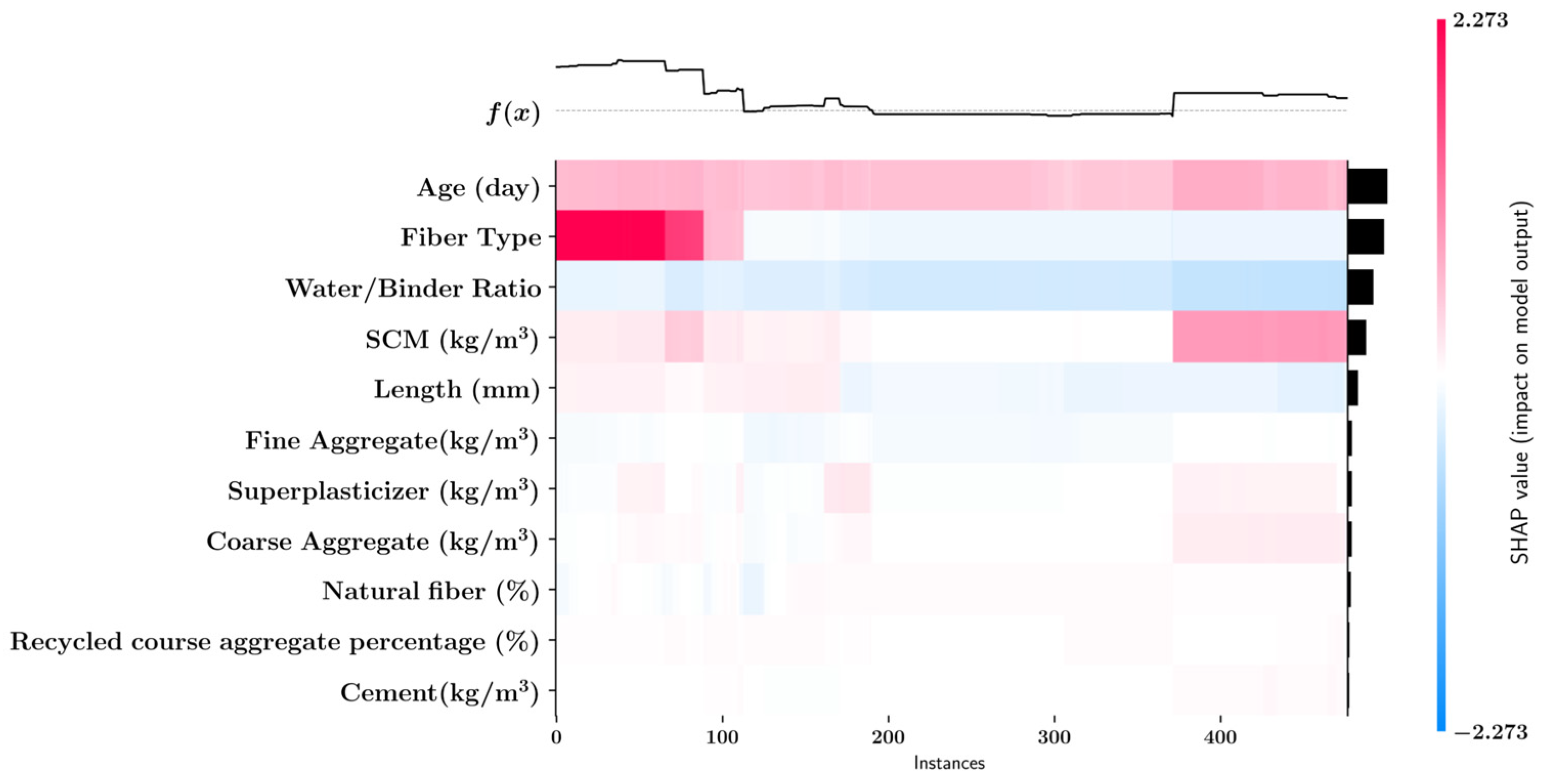
3.4. Feature Importance Analysis Using Shapley Additive Explanations (SHAP)
4. Conclusions
- (1)
- The gradient boosting predictive models predicted the splitting tensile strength of natural fiber reinforced recycled coarse aggregate concrete with an R2 score greater than 0.95. The most accurate predictions were obtained from the extra trees regressor with an R2 score of 0.971 on the test set.
- (2)
- The prediction accuracy of the models could be improved by using principal component analysis and isolation forest as outlier detection techniques. By designating 1% of the data points positioned farthest from the rest of the dataset as outliers, the R2 score of the extra trees model could be enhanced from 0.965 to 0.971 on the test set.
- (3)
- An online graphical user interface has been made available on the Streamlit platform which can be accessed through the link https://splitting-tensile-composite.streamlit.app (accessed on 6 January 2025). It should be noted that the accuracy of the predictions made by the online tool is limited to the range of feature values included in the dataset on which the models were trained. The ranges of the input features are presented in Section 2.4. Further research needs to be carried out in order to expand the range of applicability of the machine learning models.
- (4)
- The impacts of the input features on the machine learning model predictions were quantified using the SHAP methodology. It was observed that the age of the concrete specimens, the type of fiber used and the water/binder ratio had the highest impact on the predicted tensile strength whereas the amount of cement and the percentages of the recycled coarse aggregate and natural fiber had the least impact.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hossain, F.M.Z.; Shahjalal, M.; Islam, K.; Tiznobaik, M.; Alam, M.S. Mechanical properties of recycled aggregate concrete containing crumb rubber and polypropylene fiber. Construct. Build. Mater. 2019, 225, 983–996. [Google Scholar] [CrossRef]
- Huda, S.B.; Alam, M.S. Mechanical and freeze-thaw durability properties of recycled aggregate concrete made with recycled coarse aggregate. J. Mater. Civ. Eng. 2015, 27, 04015003. [Google Scholar] [CrossRef]
- Revilla-Cuesta, V.; Ortega-Lopez, V.; Faleschini, F.; Espinosa, A.B.; Serrano-Lopez, R. Hammer rebound index as an overall-mechanical-quality indicator of self-compacting concrete containing recycled concrete aggregate. Construct. Build. Mater. 2022, 347, 128549. [Google Scholar] [CrossRef]
- Huda, S.B.; Alam, M.S. Mechanical behavior of three generations of 100% repeated recycled coarse aggregate concrete. Construct. Build. Mater. 2014, 65, 574–582. [Google Scholar] [CrossRef]
- Tamanna, K. Mechanical Properties of Rubberized Concrete Containing Recycled Concrete Aggregate and Polypropylene Fiber. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2018. [Google Scholar]
- Su, H. Properties of Concrete with Recycled Aggregates as Coarse Aggregate and As-Received/Surface-Modified Rubber Particles as Fine Aggregate. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2015. [Google Scholar]
- Alam, M.S.; Slater, E.; Billah, A.H.M.M. Green concrete made with RCA and FRP scrap aggregate: Fresh and hardened properties. J. Mater. Civ. Eng. 2013, 25, 1783–1794. [Google Scholar] [CrossRef]
- Limbachiya, M.C.; Leelawat, T.; Dhir, R.K. Use of recycled concrete aggregate in high-strength concrete. Mater. Struct. 2000, 33, 574. [Google Scholar] [CrossRef]
- Islam, M.J.; Shahjalal, M. Effect of polypropylene plastic on concrete properties as a partial replacement of stone and brick aggregate. Case Stud. Constr. Mater. 2021, 15, e00627. [Google Scholar] [CrossRef]
- Chen, A.; Han, X.; Chen, M.; Wang, X.; Wang, Z.; Guo, T. Mechanical and stress-strain behavior of basalt fiber reinforced rubberized recycled coarse aggregate concrete. Construct. Build. Mater. 2020, 260, 119888. [Google Scholar] [CrossRef]
- Alfayez, S.F. Eco-Effifficient Preplaced Recycled Aggregate Concrete Incorporating Recycled Tire Waste Rubber Granules and Steel Wire Fibre Reinforcement. Master’s Thesis, The University of Western Ontario, London, ON, Canada, 2018. [Google Scholar]
- Bittner, C.M.; Oettel, V. Fiber Reinforced Concrete with Natural Plant Fibers—Investigations on the Application of Bamboo Fibers in Ultra-High Performance Concrete. Sustainability 2022, 14, 12011. [Google Scholar] [CrossRef]
- Joachim, L.; Oettel, V. Experimental Investigations on the Application of Natural Plant Fibers in Ultra-High-Performance Concrete. Materials 2024, 17, 3519. [Google Scholar] [CrossRef]
- Beskopylny, A.N.; Shcherban’, E.M.; Stel’makh, S.A.; Chernilnik, A.; Elshaeva, D.; Ananova, O.; Mailyan, L.D.; Muradyan, V.A. Optimization of the Properties of Eco-Concrete Dispersedly Reinforced with Hemp and Flax Natural Fibers. J. Compos. Sci. 2025, 9, 56. [Google Scholar] [CrossRef]
- Jamshaid, H.; Ali, H.; Mishra, R.K.; Nazari, S.; Chandan, V. Durability and Accelerated Ageing of Natural Fibers in Concrete as a Sustainable Construction Material. Materials 2023, 16, 6905. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Xue, S.; Zhang, P.; Tian, Y.; Li, P. Application of Natural Plant Fibers in Cement-Based Composites and the Influence on Mechanical Properties and Mass Transport. Materials 2019, 12, 3498. [Google Scholar] [CrossRef] [PubMed]
- Sadouri, R.; Kebir, H.; Benyoucef, M. The Effect of Incorporating Juncus Fibers on the Properties of Compressed Earth Blocks Stabilized with Portland Cement. Appl. Sci. 2024, 14, 815. [Google Scholar] [CrossRef]
- da Costa Santos, A.C.; Archbold, P. Suitability of Surface-Treated Flax and Hemp Fibers for Concrete Reinforcement. Fibers 2022, 10, 101. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, Y.; Wu, Y. Research on a New Plant Fiber Concrete-Light Steel Keel Wall Panel. Sustainability 2023, 15, 8109. [Google Scholar] [CrossRef]
- Jamshaid, H.; Mishra, R.K.; Raza, A.; Hussain, U.; Rahman, M.L.; Nazari, S.; Chandan, V.; Muller, M.; Choteborsky, R. Natural Cellulosic Fiber Reinforced Concrete: Influence of Fiber Type and Loading Percentage on Mechanical and Water Absorption Performance. Materials 2022, 15, 874. [Google Scholar] [CrossRef]
- Momeni, E.; Omidinasab, F.; Dalvand, A.; Goodarzimehr, V.; Eskandari, A. Flexural Strength of Concrete Beams Made of Recycled Aggregates: An Experimental and Soft Computing-Based Study. Sustainability 2022, 14, 11769. [Google Scholar] [CrossRef]
- Dantas, A.T.A.; Leite, M.B.; de Jesus Nagahama, K. Prediction of compressive strength of concrete containing construction and demolition waste using artificial neural networks. Constr. Build. Mater. 2013, 38, 717–722. [Google Scholar] [CrossRef]
- Felix, E.F.; Possan, E.; Carrazedo, R. A New Formulation to Estimate the Elastic Modulus of Recycled Concrete Based on Regression and ANN. Sustainability 2021, 13, 8561. [Google Scholar] [CrossRef]
- Dai, L.; Wu, X.; Zhou, M.; Ahmad, W.; Ali, M.; Sabri, M.M.S.; Salmi, A.; Ewais, D.Y.Z. Using Machine Learning Algorithms to Estimate the Compressive Property of High Strength Fiber Reinforced Concrete. Materials 2022, 15, 4450. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.; Tian, Y.; Ahmad, W.; Ahmad, A.; Usanova, K.I.; Mohamed, A.M.; Khallaf, R. Machine Learning Prediction Models to Evaluate the Strength of Recycled Aggregate Concrete. Materials 2022, 15, 2823. [Google Scholar] [CrossRef] [PubMed]
- Abed, M.; Mehryaar, E. A Machine Learning Approach to Predict Relative Residual Strengths of Recycled Aggregate Concrete after Exposure to High Temperatures. Sustainability 2024, 16, 1891. [Google Scholar] [CrossRef]
- Rodsin, K.; Ejaz, A.; Wang, H.; Saingam, P.; Joyklad, P.; Khaliq, W.; Hussain, Q.; Boonmee, C. Machine Learning and Regression Models for Evaluating Ultimate Performance of Cotton Rope-Confined Recycled Aggregate Concrete. Buildings 2025, 15, 64. [Google Scholar] [CrossRef]
- Zhu, Y.; Ahmad, A.; Ahmad, W.; Vatin, N.I.; Mohamed, A.M.; Fathi, D. Predicting the Splitting Tensile Strength of Recycled Aggregate Concrete Using Individual and Ensemble Machine Learning Approaches. Crystals 2022, 12, 569. [Google Scholar] [CrossRef]
- Aayaz, R. Natural Fiber-Recycled Aggregate Concrete; Mendeley Data, V1; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar] [CrossRef]
- Guruswamy, K.P.; Thambiannan, S.; Anthonysamy, A.; Jalgaonkar, K.; Dukare, A.S.; Pandiselvam, R.; Jha, N. Coir fibre-reinforced concrete for enhanced compressive strength and sustainability in construction applications. Heliyon 2024, 10, e39773. [Google Scholar] [CrossRef]
- Dayananda, N.; Keerthi Gowda, B.S.; Easwara Prasad, G.L. A study on compressive strength attributes of jute fiber reinforced cement concrete composites. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Beijing, China, 16–18 March 2018; IOP Publishing: Bristol, UK, 2018; Volume 376, p. 012069. [Google Scholar] [CrossRef]
- Aladsani, M.A.; Burton, H.; Abdullah, S.A.; Wallace, J.W. Explainable Machine Learning Model for Predicting Drift Capacity of Reinforced Concrete Walls. ACI Struct. J. 2022, 119, 191–204. [Google Scholar] [CrossRef]
- Wang, C.; Wu, Q.; Huang, S.; Saied, A. Economic hyperparameter optimization with blended search strategy. In Proceedings of the Ninth International Conference on Learning Representations (ICLR 2021), Virtual, 3–7 May 2021. [Google Scholar]
- Wu, Q.; Wang, C.; Huang, C. Frugal Optimization for Cost-related Hyperparameters. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence (AAAI-21), Virtual, 2–9 February 2021. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Mangalathu, S.; Hwang, S.H.; Jeon, J.S. Failure mode and effects analysis of RC members based on machine-learning-based SHapley Additive exPlanations (SHAP) approach. Eng. Struct. 2020, 219, 110927. [Google Scholar] [CrossRef]
- Mangalathu, S.; Shin, H.; Choi, E.; Jeon, J.S. Explainable machine learning models for punching shear strength estimation of flat slabs without transverse reinforcement. J. Build. Eng. 2021, 39, 102300. [Google Scholar] [CrossRef]
- Lyngdoh, G.A.; Zaki, M.; Krishnan, N.A.; Das, S. Prediction of concrete strengths enabled by missing data imputation and interpretable machine learning. Cem. Concr. Compos. 2022, 128, 104414. [Google Scholar] [CrossRef]
- Chen, M.; Park, Y.; Mangalathu, S.; Jeon, J.S. Effect of data drift on the performance of machine-learning models: Seismic damage prediction for aging bridges. Earthq. Eng. Struct. Dyn. 2024, 53, 4541–4561. [Google Scholar] [CrossRef]
- Gewers, F.L.; Ferreira, G.R.; Arruda, H.F.D.; Silva, F.N.; Comin, C.H.; Amancio, D.R.; Costa, L.D.F. Principal component analysis: A natural approach to data exploration. ACM Comput. Surv. (CSUR) 2021, 54, 1–34. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation Forest. In Proceedings of the ICDM ’08: Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation-based anomaly detection. ACM Trans. Knowl. Discov. Data (TKDD) 2012, 6, 3. [Google Scholar] [CrossRef]


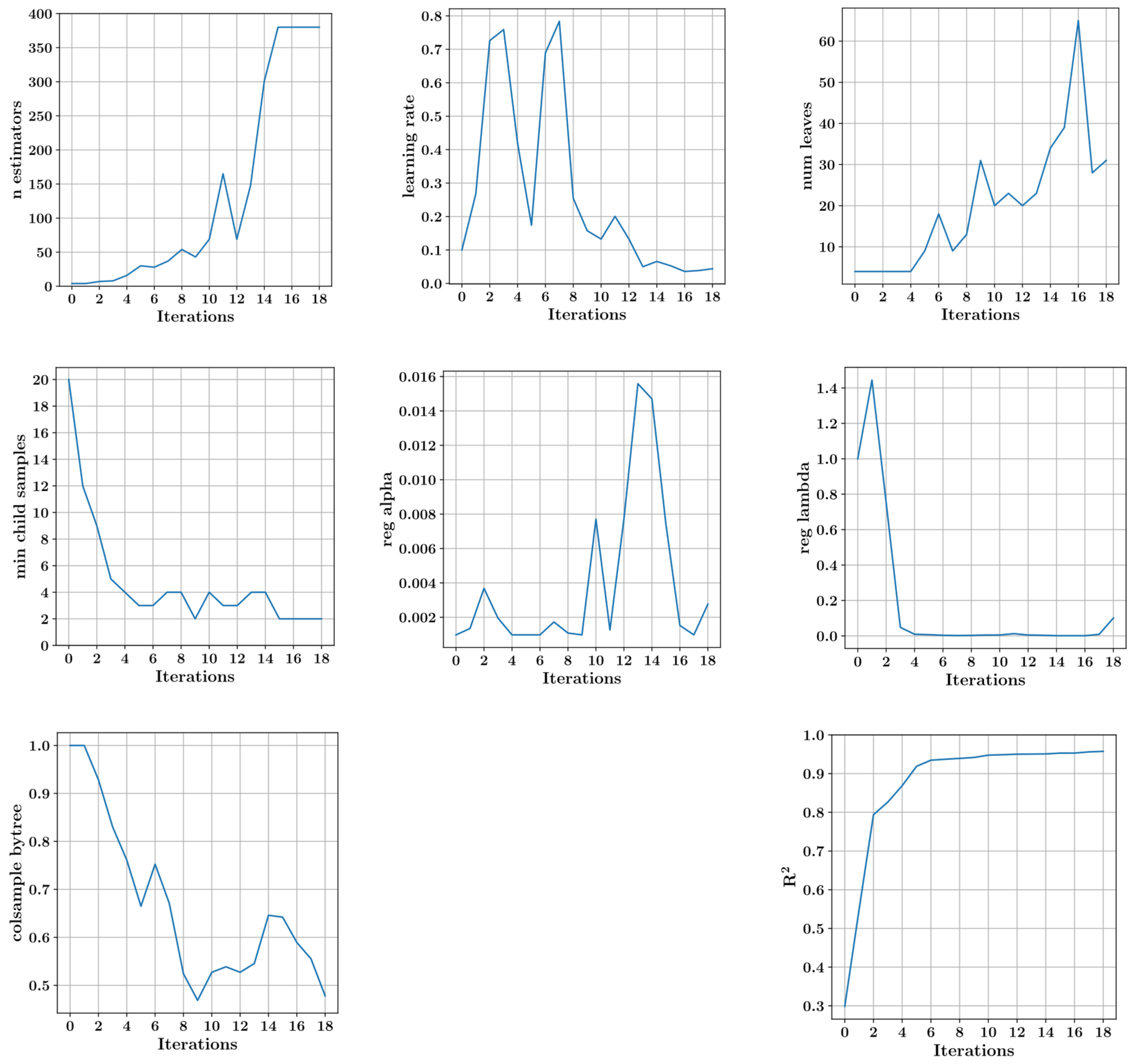



| Algorithm | Optimal Hyperparameters |
|---|---|
| LightGBM | n_estimators: 380, learning_rate: 0.0438, num_leaves: 31, max_depth: −1, min_child_samples: 2, subsample: 1.0, colsample_bytree: 0.4779, reg_alpha: 0.0028, reg_lambda: 0.1005, min_split_gain: 0.0, min_child_weight: 0.001 |
| Extra Trees | n_estimators: 13, max_depth: None, min_samples_split: 2, min_samples_leaf:1, min_weight_fraction_leaf:0.0, max_leaf_nodes: 191, min_impurity_decrease: 0.0, ccp_alpha: 0.0, max_samples: None |
| XGBoost | n_estimators: 96, learning_rate: 0.1868, max_depth: 0, subsample: 0.5599, colsample_bytree: 0.6668, reg_alpha: 0.3023, reg_lambda: 0.00097, min_child_weight: 0.218 |
| Algorithm | R2 Score | |
|---|---|---|
| Training Set | Test Set | |
| LightGBM | 0.993 | 0.946 |
| Extra Trees | 0.992 | 0.971 |
| XGBoost | 0.991 | 0.864 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cakiroglu, C.; Ahadian, F.; Bekdaş, G.; Geem, Z.W. Tensile Strength Predictive Modeling of Natural-Fiber-Reinforced Recycled Aggregate Concrete Using Explainable Gradient Boosting Models. J. Compos. Sci. 2025, 9, 119. https://doi.org/10.3390/jcs9030119
Cakiroglu C, Ahadian F, Bekdaş G, Geem ZW. Tensile Strength Predictive Modeling of Natural-Fiber-Reinforced Recycled Aggregate Concrete Using Explainable Gradient Boosting Models. Journal of Composites Science. 2025; 9(3):119. https://doi.org/10.3390/jcs9030119
Chicago/Turabian StyleCakiroglu, Celal, Farnaz Ahadian, Gebrail Bekdaş, and Zong Woo Geem. 2025. "Tensile Strength Predictive Modeling of Natural-Fiber-Reinforced Recycled Aggregate Concrete Using Explainable Gradient Boosting Models" Journal of Composites Science 9, no. 3: 119. https://doi.org/10.3390/jcs9030119
APA StyleCakiroglu, C., Ahadian, F., Bekdaş, G., & Geem, Z. W. (2025). Tensile Strength Predictive Modeling of Natural-Fiber-Reinforced Recycled Aggregate Concrete Using Explainable Gradient Boosting Models. Journal of Composites Science, 9(3), 119. https://doi.org/10.3390/jcs9030119











