A Study on the Uniaxial Compressive Constitutive Characteristics of Phosphogypsum-Based Irregular-Shaped Bricks (PG-ISBs) for Underground Filling Retaining Walls
Abstract
:1. Introduction
2. Experimental Materials and Methods
2.1. Experimental Materials
2.2. Specimen Mix Ratio
2.3. SEM Observations and Compressive Strength
2.4. Determination of Elastic Modulus
3. Experimental Results and Discussion
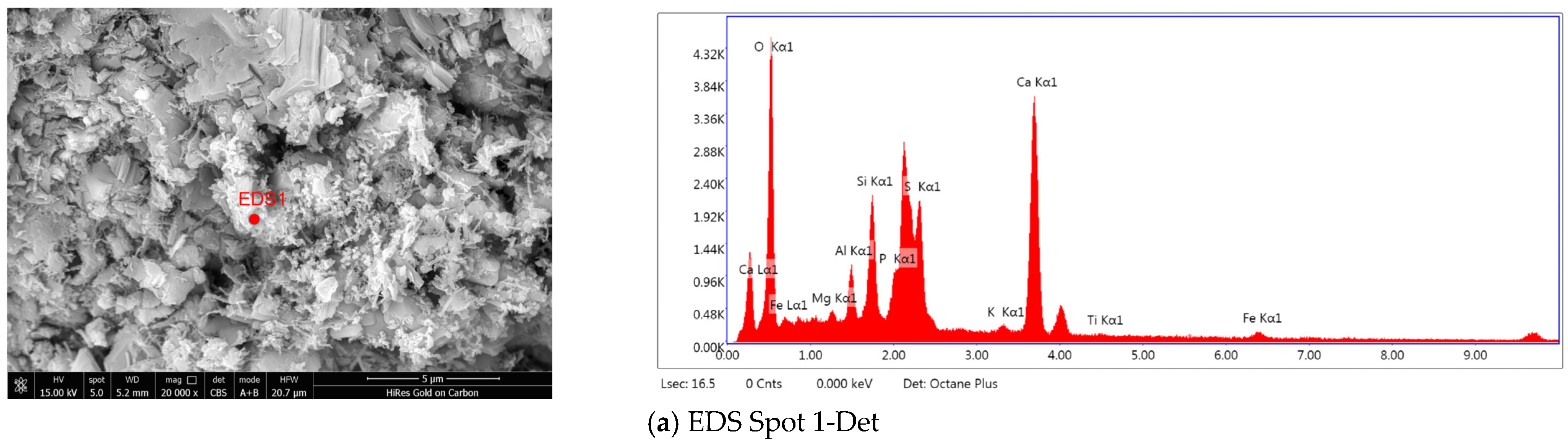
3.1. Scanning Electron Microscopy (SEM) and Energy-Dispersive X-Ray Spectroscopy (EDX) Results
3.2. X-Ray Diffraction (XRD) Results
3.3. Compressive Strength and Elastic Modulus
4. PG-ISB Uniaxial Compression Constitutive Model
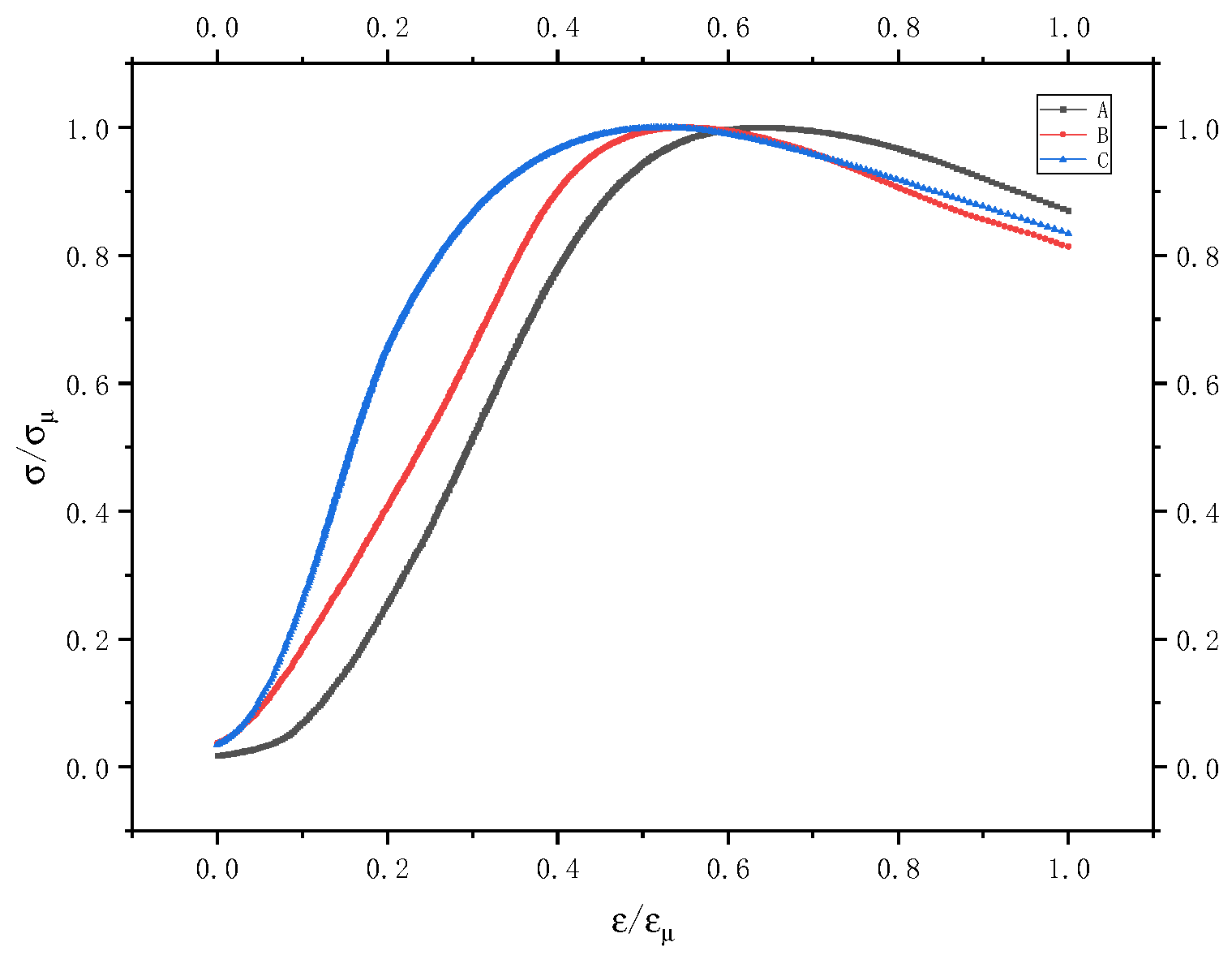
4.1. PG-ISB Stress–Strain Curve
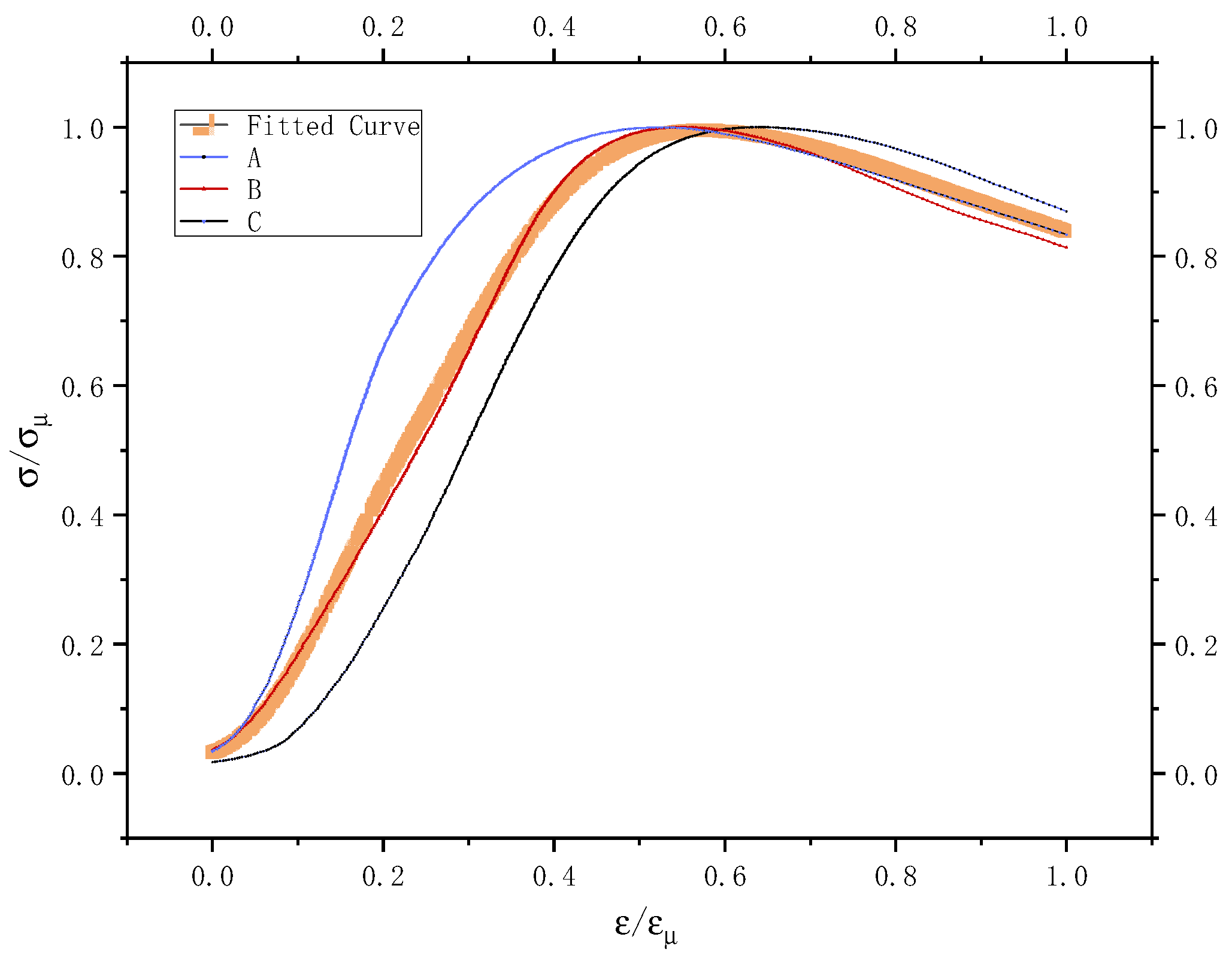
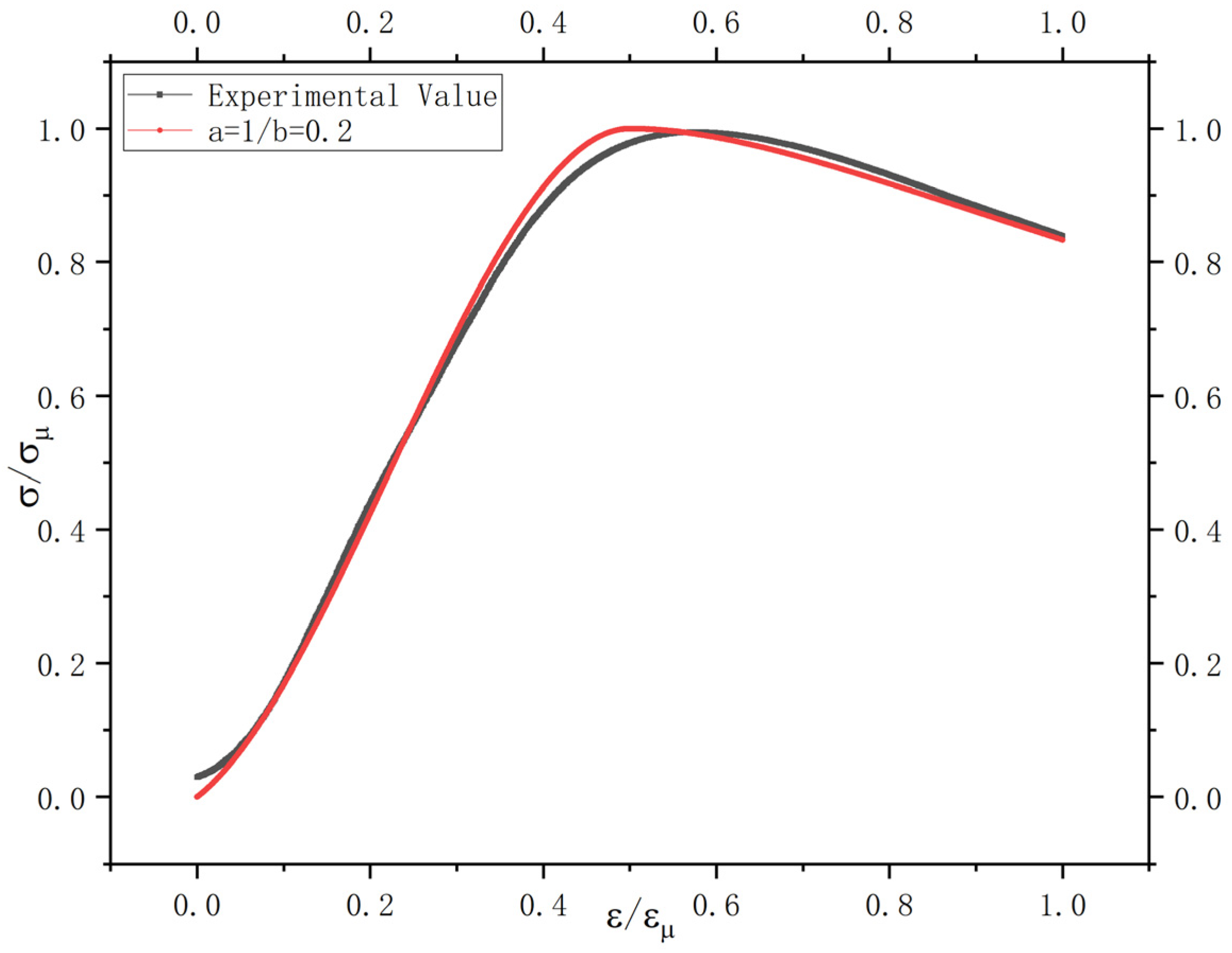
4.2. PG-ISBs Segmented Expression Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, H.; Huang, J. Optimization and Application of Filling Proportion of Phosphogypsum in a Phosphate Mine. Mod. Min. 2024, 40, 185–188. [Google Scholar] [CrossRef]
- Xu, X.; Kong, L.; Li, X.; Lei, B.; Sun, B.; Li, X.; Qu, F.; Pang, B.; Dong, W. Energy conservation and carbon emission reduction of cold recycled petroleum asphalt concrete pavement with cement-stabilized phosphogypsum. Constr. Build. Mater. 2024, 433, 136696. [Google Scholar] [CrossRef]
- Lan, W.; Wu, A.; Wang, Y.; Li, J. Experiments on the Influencing Factors of Filling Strength of Hemihydrate Phosphogypsum. J. Harbin Inst. Technol. 2019, 51, 128–135. [Google Scholar] [CrossRef]
- Qi, C.; Liu, L.; Huang, X.; Wu, Q.; Zhao, X.; Xue, F. Research on the Filling Performance of Undisturbed Phosphogypsum Consolidated by Phosphogypsum-based Cementitious Materials. Non-Met. Mines 2023, 46, 30–34. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, F. Research on Rational Structural Parameters of Filling Retaining Wall and Its Application. Chem. Miner. Process. 2014, 43, 33–35. [Google Scholar]
- Cheng, A.; Du, A.; Yin, D.; Shi, J.; Wang, P. Research on the Determination Method of Filling Retaining Wall Thickness and the Stress Distribution Law Considering the Influence of Boundary Constraints. Met. Mines 2024, 6, 199–211. [Google Scholar] [CrossRef]
- Hao, X.; Liu, H.; Zhao, L.; Yang, H.; Chai, H. Stress Analysis of Filling Retaining Walls in Open Stope Subsequent Filling and Engineering Practice of Construction. Gold 2023, 44, 21–27. [Google Scholar] [CrossRef]
- Deng, G.; Zheng, B.; Li, X. Research on the Construction Technology of Underground Filling Retaining Walls. Min. Technol. 2018, 18, 26–30. [Google Scholar] [CrossRef]
- Li, Z.; Guo, L.; Peng, X.; Zhao, Y.; Yu, B. Flexible Sealing Method and Application of Stope Filling in Underground Mines. J. Min. Saf. Eng. 2024, 41, 86–94. [Google Scholar] [CrossRef]
- GB/T 23456-2018; National Technical Committee for Standardization of Lightweight and Decorative Building Materials (SAC/TC 195). China Standard Press: Beijing, China, 2018.
- Xu, G.; Li, Y.; Pang, R.; Chen, Z.; Ren, X. Constitutive model analysis of Chang’e-5 simulated lunar regolith solidified bodies under compression. Case Stud. Constr. Mater. 2024, 21, e03704. [Google Scholar]









| Types of Materials | CaO | S | SiO2 | P2O5 | Al2O3 | Fe2O3 | K2O | SO3 | Ti2O | MgO |
|---|---|---|---|---|---|---|---|---|---|---|
| Phosphogypsum | 58.97 | 34.05 | 2.89 | 0.97 | 0.61 | 0.31 | 0.14 | - | - | 0.15 |
| Calcium Powder | 5.07 | - | 40.69 | - | 24.66 | 14.52 | 2.10 | 0.76 | 3.11 | - |
| Cementitious Agent | 59.31 | 2.45 | 17.71 | 0.30 | 5.31 | 6.04 | 1.20 | - | 1.14 | 2.21 |
| Construction Brick Debris | 48.33 | 36.22 | 9.87 | 0.87 | 0.61 | 0.31 | 0.14 | 0.55 | 2.11 | 0.16 |
| Materials | Phosphogypsum | Cementitious Agent | Construction Brick Debris | Calcium Powder | Phosphorus Ore Mechanically Processed Sand |
|---|---|---|---|---|---|
| Percentage | 10.36% | 10.36% | 0.52% | 1.04% | 77.72% |
| Project Number | /MPa | |||||
|---|---|---|---|---|---|---|
| Sample A | Sample B | Sample C | Mean Value | |||
| APC | 14.50 | 14.10 | 14.18 | 14.26 | 14.26 | 2.85 |
| Specimen Number | A | B | C |
|---|---|---|---|
| (kN) | 2.90 kN | 2.82 kN | 2.84 kN |
| (kN) | 1.50 kN | 1.41 kN | 1.43 kN |
| (MPa) | 3.42 MPa | 2.56 MPa | 2.85 MPa |
| Rise Section | Descent Segment | ||
|---|---|---|---|
| a | r | b | r |
| 1 | 0.9996 | 0.2 | 0.9897 |
| 2 | 0.9982 | 0.5 | 0.9817 |
| 3 | 0.9917 | 1 | 0.9659 |
| 4 | 0.9791 | 2 | 0.9344 |
| 5 | 0.9594 | 3 | 0.9061 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Xu, G.; Zhao, Z.; Li, H.; He, M.; Wu, W.; Chen, Z. A Study on the Uniaxial Compressive Constitutive Characteristics of Phosphogypsum-Based Irregular-Shaped Bricks (PG-ISBs) for Underground Filling Retaining Walls. J. Compos. Sci. 2025, 9, 157. https://doi.org/10.3390/jcs9040157
Jiang J, Xu G, Zhao Z, Li H, He M, Wu W, Chen Z. A Study on the Uniaxial Compressive Constitutive Characteristics of Phosphogypsum-Based Irregular-Shaped Bricks (PG-ISBs) for Underground Filling Retaining Walls. Journal of Composites Science. 2025; 9(4):157. https://doi.org/10.3390/jcs9040157
Chicago/Turabian StyleJiang, Jixiang, Guihong Xu, Zhenhua Zhao, Hejun Li, Mingwei He, Wenqi Wu, and Ziwei Chen. 2025. "A Study on the Uniaxial Compressive Constitutive Characteristics of Phosphogypsum-Based Irregular-Shaped Bricks (PG-ISBs) for Underground Filling Retaining Walls" Journal of Composites Science 9, no. 4: 157. https://doi.org/10.3390/jcs9040157
APA StyleJiang, J., Xu, G., Zhao, Z., Li, H., He, M., Wu, W., & Chen, Z. (2025). A Study on the Uniaxial Compressive Constitutive Characteristics of Phosphogypsum-Based Irregular-Shaped Bricks (PG-ISBs) for Underground Filling Retaining Walls. Journal of Composites Science, 9(4), 157. https://doi.org/10.3390/jcs9040157






