A Reinforcement Learning Approach for Scheduling Problems with Improved Generalization through Order Swapping
Abstract
1. Introduction
2. Background
2.1. Job Shop Constraints
2.2. Proximal Policy Optimization (PPO)
3. Related Works
4. Methodologies
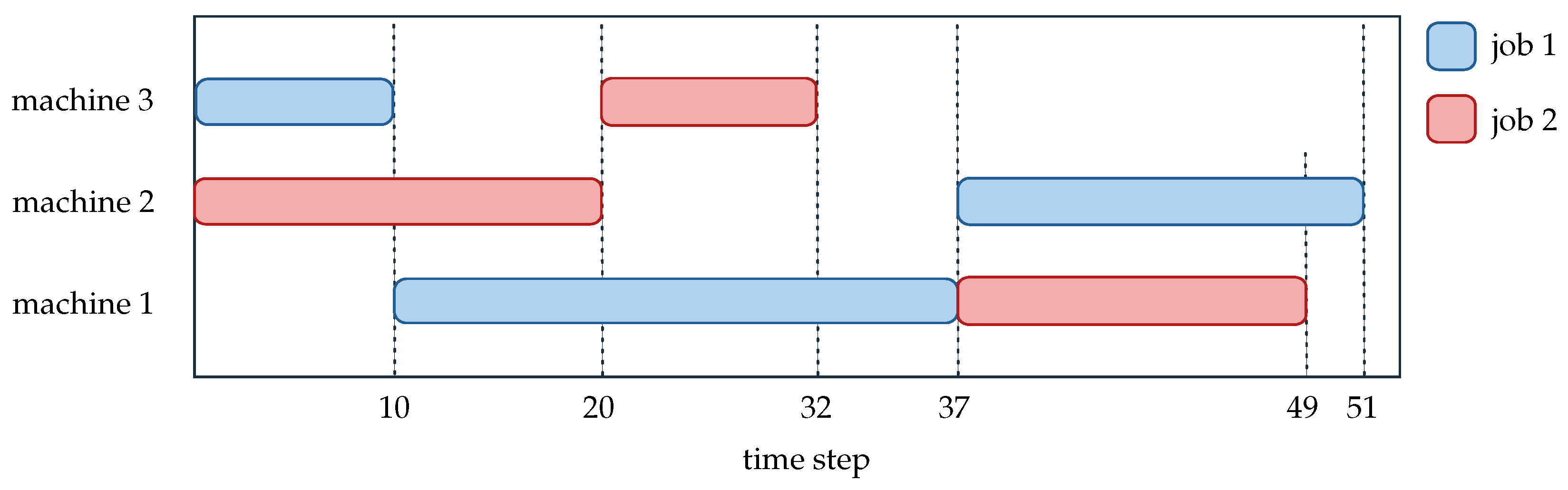
4.1. Environment Outline
- No pre-emption is allowed i.e., operations cannot be interrupted
- Each machine can handle only one job at a time
- No precedence constraints among operations of different jobs
- Fixed machine sequences of each job
4.2. Time Step Transition
4.3. Action Space
4.4. States
4.5. Reward
4.6. Markov Decision Process Formulation
4.7. Generalization
Order Swapping Mechanism (OSM)
5. Experiments
5.1. Model Configuration
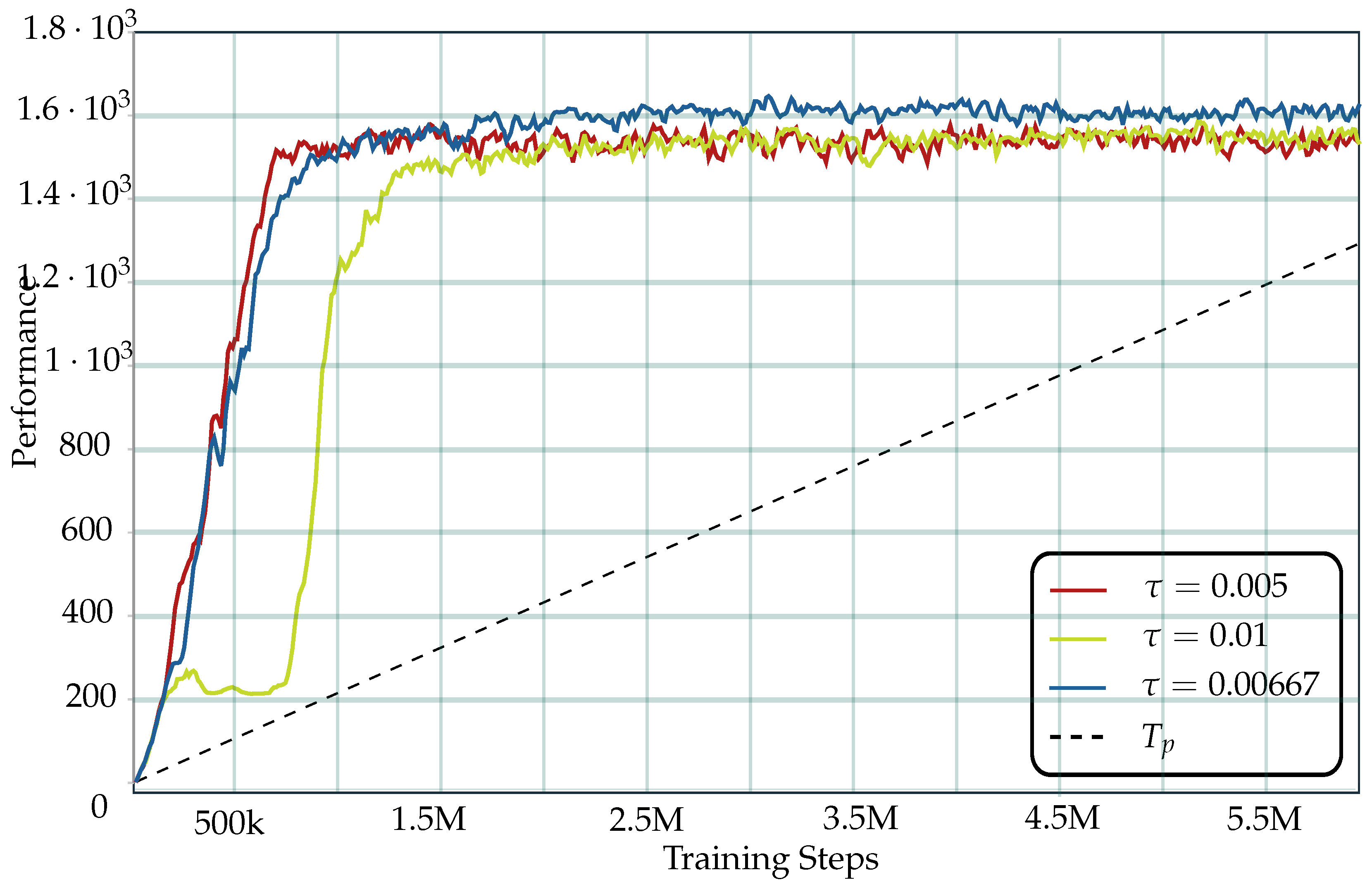
5.2. Training
5.3. Benchmark Instances
5.4. Results
5.5. Generalized Result
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| COP | Combinatorial Optimization Problem |
| DRL | Deep Reinforcement Learning |
| JSSP | Job Shop Scheduling Problem |
| LB | Lower Bound |
| MDP | Markov Decision Process |
| OSM | Order Swapping Mechanism |
| PPO | Proximal Policy Optimization |
References
- Pinedo, M.L. Scheduling; Springer: New York, NY, USA, 2012; pp. 183–215. [Google Scholar]
- Zhang, C.; Song, W.; Cao, Z.; Zhang, J.; Tan, P.S.; Chi, X. Learning to dispatch for job shop scheduling via deep reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 1621–1632. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T.; et al. Mastering chess and shogi by self-play with a general reinforcement learning algorithm. arXiv 2017, arXiv:1712.01815. [Google Scholar]
- Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P.; et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Yan, Z.; Xiang, Q.; Zhan, Q. Vulcan: Solving the Steiner Tree Problem with Graph Neural Networks and Deep Reinforcement Learning. arXiv 2021, arXiv:2111.10810. [Google Scholar]
- Afshar, R.R.; Zhang, Y.; Firat, M.; Kaymak, U. A state aggregation approach for solving knapsack problem with deep reinforcement learning. In Proceedings of the Asian Conference on Machine Learning, PMLR, Bangkok, Thailand, 18–20 November 2020; pp. 81–96. [Google Scholar]
- Manerba, D.; Li, Y.; Fadda, E.; Terzo, O.; Tadei, R. Reinforcement Learning Algorithms for Online Single-Machine Scheduling. In Proceedings of the 2020 15th Conference on Computer Science and Information Systems (FedCSIS), Sofia, Bulgaria, 6–9 September 2020. [Google Scholar] [CrossRef]
- Li, Y.; Carabelli, S.; Fadda, E.; Manerba, D.; Tadei, R.; Terzo, O. Machine learning and optimization for production rescheduling in Industry 4.0. Int. J. Adv. Manuf. Technol. 2020, 110, 2445–2463. [Google Scholar] [CrossRef]
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Demirkol, E.; Mehta, S.; Uzsoy, R. Benchmarks for shop scheduling problems. Eur. J. Oper. Res. 1998, 109, 137–141. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Taillard, E.D. Parallel taboo search techniques for the job shop scheduling problem. ORSA J. Comput. 1994, 6, 108–117. [Google Scholar] [CrossRef]
- Van Laarhoven, P.J.; Aarts, E.H.; Lenstra, J.K. Job shop scheduling by simulated annealing. Oper. Res. 1992, 40, 113–125. [Google Scholar] [CrossRef]
- Pezzella, F.; Morganti, G.; Ciaschetti, G. A genetic algorithm for the flexible job-shop scheduling problem. Comput. Oper. Res. 2008, 35, 3202–3212. [Google Scholar] [CrossRef]
- Cappart, Q.; Moisan, T.; Rousseau, L.M.; Prémont-Schwarz, I.; Cire, A.A. Combining reinforcement learning and constraint programming for combinatorial optimization. In Proceedings of the AAAI Conference on Artificial Intelligence, virtually, 2–9 February 2021; Volume 35, pp. 3677–3687. [Google Scholar]
- Oren, J.; Ross, C.; Lefarov, M.; Richter, F.; Taitler, A.; Feldman, Z.; Di Castro, D.; Daniel, C. SOLO: Search online, learn offline for combinatorial optimization problems. In Proceedings of the International Symposium on Combinatorial Search, Guangzhou, China, 26–30 July 2021; Volume 12, pp. 97–105. [Google Scholar]
- Zhang, Z.; Liu, H.; Zhou, M.; Wang, J. Solving dynamic traveling salesman problems with deep reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 2119–2132. [Google Scholar] [CrossRef]
- d O Costa, P.R.; Rhuggenaath, J.; Zhang, Y.; Akcay, A. Learning 2-opt heuristics for the traveling salesman problem via deep reinforcement learning. In Proceedings of the Asian Conference on Machine Learning, Bangkok, Thailand, 18–20 November 2020; pp. 465–480. [Google Scholar]
- Zhang, R.; Prokhorchuk, A.; Dauwels, J. Deep reinforcement learning for traveling salesman problem with time windows and rejections. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Zhang, W.; Dietterich, T.G. A reinforcement learning approach to job-shop scheduling. IJCAI 1995, 95, 1114–1120. [Google Scholar]
- Deale, M.; Yvanovich, M.; Schnitzuius, D.; Kautz, D.; Carpenter, M.; Zweben, M.; Davis, G.; Daun, B. The space shuttle ground processing scheduling system. Intell. Sched. 1994, 423–449. [Google Scholar]
- Gabel, T.; Riedmiller, M. Distributed policy search reinforcement learning for job-shop scheduling tasks. Int. J. Prod. Res. 2012, 50, 41–61. [Google Scholar] [CrossRef]
- Liu, C.L.; Chang, C.C.; Tseng, C.J. Actor-critic deep reinforcement learning for solving job shop scheduling problems. IEEE Access 2020, 8, 71752–71762. [Google Scholar] [CrossRef]
- Han, B.A.; Yang, J.J. Research on adaptive job shop scheduling problems based on dueling double DQN. IEEE Access 2020, 8, 186474–186495. [Google Scholar] [CrossRef]
- Tassel, P.; Gebser, M.; Schekotihin, K. A reinforcement learning environment for job-shop scheduling. arXiv 2021, arXiv:2104.03760. [Google Scholar]
- Błażewicz, J.; Ecker, K.H.; Pesch, E.; Schmidt, G.; Weglarz, J. Scheduling Computer and Manufacturing Processes; Springer Science & Business Media: Cham, Switzerland, 2001; pp. 273–315. [Google Scholar]
- Mohtasib, A.; Neumann, G.; Cuayáhuitl, H. A study on dense and sparse (visual) rewards in robot policy learning. In Proceedings of the Annual Conference towards Autonomous Robotic Systems; Springer: Cham, Switzerland, 2021; pp. 3–13. [Google Scholar]
- Singh, S.; Cohn, D. How to dynamically merge Markov decision processes. In Proceedings of the 1997 Conference on Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1997; p. 10. [Google Scholar]
- Zhang, T.; Xie, S.; Rose, O. Real-time job shop scheduling based on simulation and Markov decision processes. In Proceedings of the 2017 Winter Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017; pp. 3899–3907. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. Openai gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Raffin, A.; Hill, A.; Gleave, A.; Kanervisto, A.; Ernestus, M.; Dormann, N. Stable-baselines3: Reliable reinforcement learning implementations. J. Mach. Learn. Res. 2021, 22, 12348–12355. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. arXiv 2019, arXiv:1907.10902. [Google Scholar]
- Adams, J.; Balas, E.; Zawack, D. The shifting bottleneck procedure for job shop scheduling. Manag. Sci. 1988, 34, 391–401. [Google Scholar] [CrossRef]
- Fisher, H. Probabilistic learning combinations of local job-shop scheduling rules. Ind. Sched. 1963, 225–251. [Google Scholar]
- Lawrence, S. Resouce Constrained Project Scheduling: An Experimental Investigation of Heuristic Scheduling Techniques (Supplement); Graduate School of Industrial Administration, Carnegie-Mellon University: Pittsburgh, PA, USA, 1984. [Google Scholar]
- Applegate, D.; Cook, W. A computational study of the job-shop scheduling problem. ORSA J. Comput. 1991, 3, 149–156. [Google Scholar] [CrossRef]
- Yamada, T.; Nakano, R. A genetic algorithm applicable to large-scale job-shop problems. In Proceedings of the Second Conference on Parallel Problem Solving from Nature, Brussels, Belguim, 28–30 September 1992; pp. 281–290. [Google Scholar]
- Storer, R.; Wu, S.; Vaccari, R. New search spaces for sequencing instances with application to job shop. Manag. Sci. 1992, 38, 1495–1509. [Google Scholar] [CrossRef]



| Authors | Instance Size Used (Jobs × Machines) |
|---|---|
| Adams, Balas, and Zawack [34] | 10 × 10, 20 × 15 |
| Demirkol, Mehta, and Uzsoy [11] | 20 × 15 to 50 × 20 |
| Fisher [35] | 6 × 6, 10 × 10, 20 × 5 |
| Lawrence [36] | 10 × 10 to 15 × 5 |
| Applegate and Cook [37] | 10 × 10 |
| Taillard [10] | 15 × 15 to 20 × 100 |
| Yamada and Nakano [38] | 20 × 20 |
| Storer, Wu, and Vaccari [39] | 20 × 10 to 50 × 10 |
| Instance | Size (n × m) | MWKR | SPT | Tassel et al. [26] | Han and Yang [25] | Zhang et al. [2] | Ours | LB |
|---|---|---|---|---|---|---|---|---|
| Ft06 | 6 × 6 | - | - | - | - | - | 55 * | 55 |
| La05 | 10 × 5 | 787 | 827 | - | 593 * | - | 593 * | 593 |
| La10 | 15 × 5 | 1136 | 1345 | - | 958 * | - | 958 * | 958 |
| La16 | 10 × 10 | 1238 | 1588 | - | 980 | - | 974 | 945 |
| Ta01 | 15 × 15 | 1786 | 1872 | - | 1315 | 1443 | 1352 | 1231 |
| Ta02 | 15 × 15 | 1944 | 1709 | - | 1336 | 1544 | 1354 | 1244 |
| dmu16 [11] | 30 × 20 | 5837 | 6241 | 4188 | 4414 | 4953 | 4632 | 3751 |
| dmu17 [11] | 30 × 20 | 6610 | 6487 | 4274 | - | 5579 | 5104 | 3814 |
| Ta41 | 30 × 20 | 2632 | 3067 | 2208 | 2450 | 2667 | 2583 | 2005 |
| Ta42 | 30 × 20 | 2401 | 3640 | 2168 | 2351 | 2664 | 2457 | 1937 |
| Ta43 | 30 × 20 | 3162 | 2843 | 2086 | - | 2431 | 2422 | 1846 |
| Instance | Ta01-OSM with 5% | Ta01-OSM with 10% | Ta01-OSM with 15% | MWKR | SPT | Ours | Zhang et al. [2] | LB |
|---|---|---|---|---|---|---|---|---|
| Ta02 | 1491 | 1486 | 1546 | 1944 | 1709 | 1354 | 1544 | 1244 |
| Ta03 | 1443 | 1437 | 1525 | 1947 | 2009 | 1388 | 1440 | 1218 |
| Ta04 | 1568 | 1502 | 1614 | 1694 | 1825 | 1513 | 1637 | 1175 |
| Ta05 | 1599 | 1481 | 1483 | 1892 | 2044 | 1443 | 1619 | 1224 |
| Ta06 | 1776 | 1507 | 1552 | 1976 | 1771 | 1360 | 1601 | 1238 |
| Ta07 | 1526 | 1500 | 1605 | 1961 | 2016 | 1354 | 1568 | 1227 |
| Ta08 | 1631 | 1540 | 1524 | 1803 | 1654 | 1377 | 1468 | 1217 |
| Ta09 | 1662 | 1664 | 1597 | 2215 | 1962 | 1401 | 1627 | 1274 |
| Ta10 | 1573 | 1524 | 1659 | 2057 | 2164 | 1370 | 1527 | 1241 |
| Instance | Ta41-OSM with 5% | Ta41-OSM with 7.5% | Ta41-OSM with 10% | MWKR | SPT | Ours | Zhang et al. [2] | LB |
|---|---|---|---|---|---|---|---|---|
| Ta42 | 2903 | 2831 | 2572 | 3394 | 3640 | 2457 | 2664 | 1937 |
| Ta43 | 2800 | 2651 | 2614 | 3162 | 2843 | 2422 | 2431 | 1846 |
| Ta44 | 2991 | 2751 | 2745 | 3388 | 3281 | 2598 | 2714 | 1979 |
| Ta45 | 2851 | 2812 | 2692 | 3390 | 3238 | 2587 | 2637 | 2000 |
| Ta46 | 2986 | 2842 | 2674 | 3268 | 3352 | 2606 | 2776 | 2006 |
| Ta47 | 2854 | 2807 | 2677 | 2986 | 3197 | 2538 | 2476 | 1889 |
| Ta48 | 2758 | 2753 | 2638 | 3050 | 3445 | 2461 | 2490 | 1937 |
| Ta49 | 2800 | 2646 | 2566 | 3172 | 3201 | 2501 | 2556 | 1961 |
| Ta50 | 2887 | 2654 | 2616 | 2978 | 3083 | 2550 | 2628 | 1923 |
| Instance | Ta41-OSM with 5% | Ta41-OSM with 7.5% | Ta41-OSM with 10% | MWKR | SPT | Ours | Zhang et al. [2] | LB |
|---|---|---|---|---|---|---|---|---|
| Dmu16 | 5413 | 5560 | 4907 | 5837 | 6241 | 4632 | 4953 | 3751 |
| Dmu17 | 5926 | 5911 | 5646 | 6610 | 6487 | 5104 | 5379 | 3814 |
| Dmu18 | 5380 | 5773 | 5287 | 6363 | 6978 | 4998 | 5100 | 3844 |
| Dmu19 | 5236 | 5136 | 4993 | 6385 | 5767 | 4759 | 4889 | 3768 |
| Dmu20 | 5263 | 5318 | 5131 | 6472 | 6910 | 4697 | 4859 | 3710 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vivekanandan, D.; Wirth, S.; Karlbauer, P.; Klarmann, N. A Reinforcement Learning Approach for Scheduling Problems with Improved Generalization through Order Swapping. Mach. Learn. Knowl. Extr. 2023, 5, 418-430. https://doi.org/10.3390/make5020025
Vivekanandan D, Wirth S, Karlbauer P, Klarmann N. A Reinforcement Learning Approach for Scheduling Problems with Improved Generalization through Order Swapping. Machine Learning and Knowledge Extraction. 2023; 5(2):418-430. https://doi.org/10.3390/make5020025
Chicago/Turabian StyleVivekanandan, Deepak, Samuel Wirth, Patrick Karlbauer, and Noah Klarmann. 2023. "A Reinforcement Learning Approach for Scheduling Problems with Improved Generalization through Order Swapping" Machine Learning and Knowledge Extraction 5, no. 2: 418-430. https://doi.org/10.3390/make5020025
APA StyleVivekanandan, D., Wirth, S., Karlbauer, P., & Klarmann, N. (2023). A Reinforcement Learning Approach for Scheduling Problems with Improved Generalization through Order Swapping. Machine Learning and Knowledge Extraction, 5(2), 418-430. https://doi.org/10.3390/make5020025









