1. Introduction
In today’s rapidly evolving digital landscape, computational thinking (CT) has emerged as a crucial skill set, essential not only in computer science but across a diverse range of fields. It plays a pivotal role in problem solving, enabling individuals to approach complex problems using algorithmic and systematic methods. This work centres on the Cross Array Task (CAT) [
1], an activity designed within the Swiss compulsory educational system to evaluate CT skills, particularly students’ proficiency in conceiving and representing algorithms, a set of rules or instructions that should be adopted or followed by an executor, whether human or artificial, to accomplish a given task [
2,
3,
4,
5,
6].
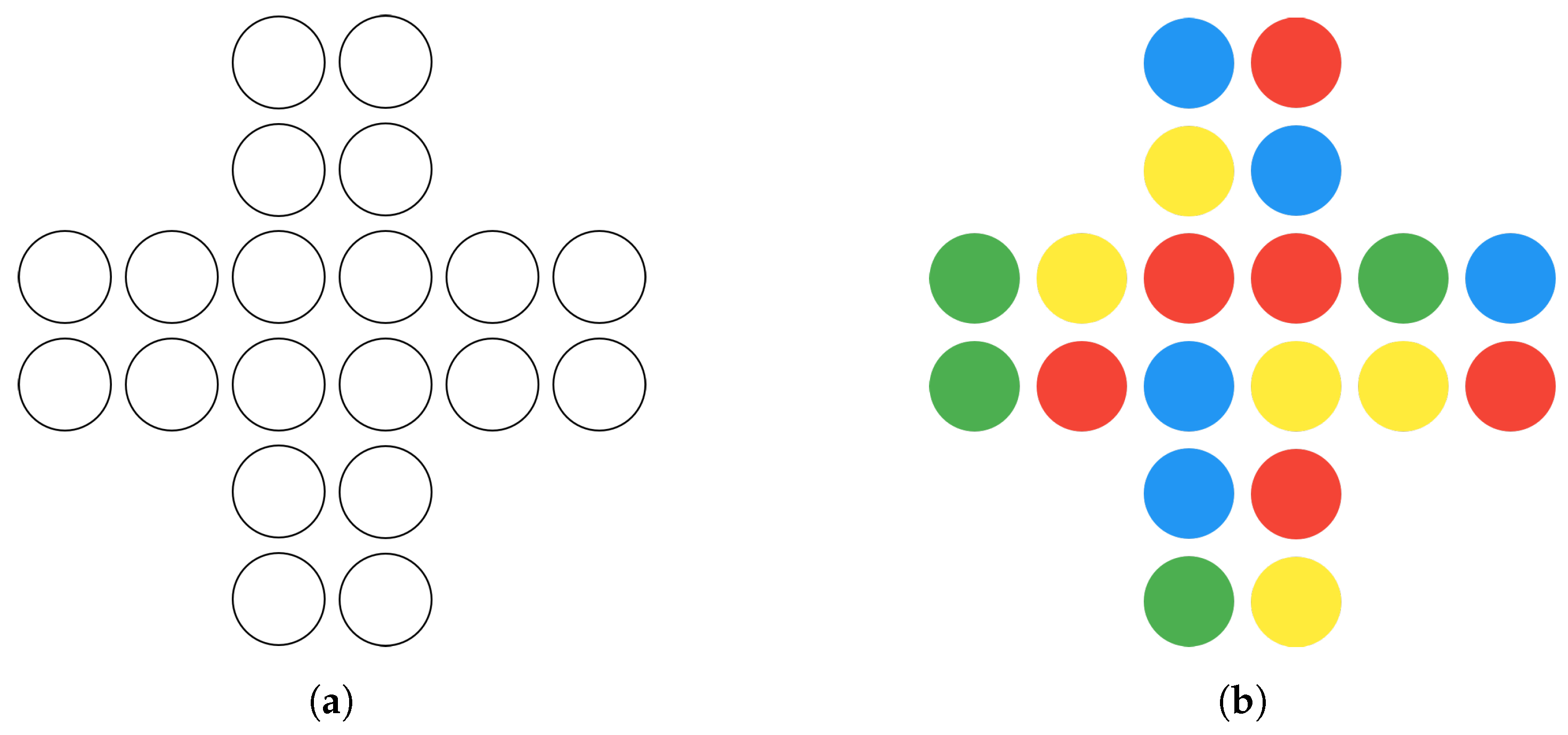
The CAT challenges pupils to deconstruct complex problems, devise sequential strategies, and articulate their solutions. In particular, in this task, participants are required to describe the colouring of a reference cross array board, which resembles a grid with differently coloured dots (see
Figure 1). This can be achieved using verbal instructions, eventually supplemented with gestures, in the unplugged version [
1] or, for example, using a visual block-based programming interface in the virtual version [
7,
8].
During the activity, participants can use different moves, including simple pattern colouring and more advanced actions like the replication of previously executed patterns, to transform the board and achieve the desired outcome. This task is inherently complex due to the multitude of available moves and potential combinations, as well as the freedom given to participants to devise tailored solutions. The challenge is further amplified by the vast array of potential strategies that can be employed. Deciphering the intricate interplay between the different moves and the game board’s configuration is at the heart of this challenge. A nuanced analysis is essential to identifying emerging patterns and determine the most effective moves based on the board’s unique characteristics. This analysis not only influences the choice of moves but also shapes the foundational approach to problem solving, necessitating versatile strategy and execution. As a result, each strategy may demand a completely different construction approach, whether it be employing a pattern copy or a mirror strategy or focusing on identifying the most advantageous patterns. Consequently, every time, the strategy and the approach to tackling the problem change.
The CAT makes significant cognitive demands on participants, requiring consistent identification and strategic application of the most effective moves. Given the task’s classification as an NP problem, known for its logical complexity and intricate problem-solving requirements, it poses a substantial algorithmic challenge, particularly for humans. To address these challenges, there is a burgeoning need to adapt the CAT for machine-based solutions, enabling more efficient resolution through automated processes. This adaptation is well suited to the capabilities of artificial intelligence (AI) and machine learning (ML) methodologies, which can be leveraged to uncover optimal strategies and provide new insights into this complex task.
This research adopts a dual-faceted approach, integrating hybrid meta-heuristic algorithms and reinforcement learning (RL) techniques, which are particularly well suited to tackle the CAT’s challenges. Hybrid meta-heuristic algorithms, with their ability to navigate vast search spaces and escape local minima, provide a robust mechanism for exploring potential solutions and uncovering optimal strategies. Concurrently, RL techniques offer a dynamic and adaptive framework, enabling the model to learn and iteratively improve its performance over time.
Together, these techniques offer a comprehensive solution and novel insights into the CAT, contributing to the broader field of algorithmic problem solving and educational tool development. The broader implications of this research are substantial, particularly in the context of CT, a crucial skill in today’s digital landscape. By elucidating the contributions of AI and ML to CT development and application, this research not only advances our understanding of algorithmic problem solving but also has potential applications in education, serving as a tutoring mechanism to enhance students’ CT and problem-solving capabilities.
2. Literature Review
In recent years, the literature on computational thinking (CT) and algorithmic problem solving has experienced substantial growth, reflecting the escalating significance of these skills in various domains [
2,
9]. Artificial intelligence (AI) and machine learning (ML) have significantly advanced. The emergence of these fields has significantly transformed problem-solving approaches, introducing versatile and advanced methods like genetic algorithms and neural networks for addressing complex issues across various domains [
10,
11,
12,
13,
14,
15,
16]. Employing ML models, encompassing supervised and unsupervised learning, alongside reinforcement learning (RL), has become pivotal in decision making and optimisation processes [
10,
17]. Prominent models such as support vector machine (SVM), decision trees, K-means clustering, principal component analysis (PCA), Q-learning, and Policy Gradient Methods are integral to these sophisticated problem-solving strategies.
Recent studies have explored the synergy between AI and optimisation algorithms, leading to innovative hybrid models that blend various algorithms and techniques, including ensemble methods like random forests and gradient boosting, to effectively address complex and multifaceted problems while enhancing accuracy and robustness [
18,
19,
20,
21].
AI and ML have found applications in diverse fields, solving problems that were once deemed intractable. The domain of education presents a fertile ground for the application of hybrid meta-heuristic algorithms, RL, and AI/ML technologies, particularly in enhancing critical thinking and problem-solving skills. Several literature sources have explored various aspects and applications of these technologies in educational settings [
22,
23].
The RLTLBO [
24] algorithm is an enhanced version of the teaching–learning-based optimisation (TLBO) algorithm [
25] that integrates RL to switch among different learning modes. Although not designed for educational purposes, it simulates how teachers can influence learners and has potential applications in related educational contexts.
Some works explored meta-RL that quickly adapts to new tasks, especially when presented with related tasks [
26,
27,
28]. Although not mentioned, these works could be relevant in education, developing adaptive learning systems and intelligent tutoring systems (ITSs) that adjust to the evolving needs of learners.
Also, the use of hybrid algorithms that combine RL with meta-heuristic methods to solve global optimisation problems has been proposed [
29]. These algorithms could be adapted to address educational challenges, like designing ITSs or optimising educational resources for enhanced learning outcomes.
The current body of research underscores the growing need to leverage AI and ML to enhance educational outcomes, particularly in the context of CT and problem solving. This corpus of work lays robust theoretical groundwork, underscoring the pertinence and timeliness of our inquiry. Nevertheless, a discernible void persists in the literature, especially in the application of AI and ML strategies to intricate problem-solving tasks, such as the CAT [
30].
Our research seeks to address this gap, elucidating how AI and ML can be meticulously tailored to enrich CT and problem-solving aptitudes within educational frameworks. We aim to proffer a holistic analysis delving into the application of hybrid meta-heuristic algorithms and RL techniques to navigate the complex challenges intrinsic to the CAT.
The significance of this study is twofold: it strives to deepen our comprehension of algorithmic problem solving and to forge innovative tutoring methodologies that bolster CT capabilities. In navigating the potentials of AI and ML in this realm, our research aspires to generate practical insights and strategies, with the ultimate objective of cultivating CT and problem-solving proficiency in the digital era, thereby contributing to the enrichment of educational practices.
3. Materials and Methods
This section comprehensively overviews the methodologies and algorithms employed to address the CAT problem. This research was conducted exclusively using computational methodologies. It is important to emphasise that no human participants were involved in this study, and no data were utilised nor collected. Although this study did not involve human participants or use any data, we maintained a rigorous commitment to ethical considerations throughout our research process, ensuring transparency, reproducibility, and the highest standards of computational research integrity. For those interested in exploring our methods further, including the source code, detailed documentation, and all relevant resources necessary for replicating our experiments, please refer to the provided reference [
31].
The CAT’s objective is to develop different algorithms to describe the colouring pattern of a set of 12 cross arrays (each labelled as Graph 1 to Graph 12), characterised by different levels of complexity and based on different types of regularities (see
Figure 2). The schema progression starts with a monochrome design and gradually adds complexity, introducing colours, patterns, repeating modules, and broader symmetric patterns.
The CAT, originally designed for human solving, can be adapted to be efficiently solved by machines through automated processes. The cross-board resembles a grid, where coloured dots are manipulated and referenced using a coordinate system. The primary objective is to colour a board fully white to replicate the reference board precisely. To achieve this, specific moves are employed, categorised into pattern-colouring commands and special action commands. Pattern-colouring commands require defining several parameters: a starting point, a pattern to emulate, a shape to colour (which can be a line, a square, etc.), and, if applicable, a specified length. There are also three special action commands. The fill action allows for colouring all remaining empty dots on the board with a single colour; the copy action permits the replication of previously executed instructions in various areas of the board; the mirror action enables the symmetric colouring of the board along a chosen axis, effectively mirroring parts of the design. These moves and actions constitute the toolkit for solving the CAT, and the challenge lies in using them strategically to achieve the desired board transformation.
The complexity and multifaceted nature of the CAT prompt an exploration into advanced algorithmic solutions. In particular, the realms of artificial intelligence (AI) and machine learning (ML) offer a plethora of methodologies that can be harnessed to tackle the CAT.
The scientific community has developed a wide range of clustering algorithms that are useful in categorising similar moves and optimising problem-solving processes. Among these, K-means [
32,
33,
34] and spectral clustering [
35,
36,
37,
38] are notable examples. Generally, clustering algorithms are oriented towards grouping data based on their similarity. This happens in the absence of predefined labels, unlike what happens in classification processes.
On the other hand, heuristic algorithms, with a particular emphasis on those employing random search strategies, such as Simulated Annealing (SA) [
39,
40,
41], are subject of deep study due to their ability to find globally optimal solutions in scenarios characterised by broad and particularly complex search spaces. The main advantage offered by these methods lies in their ability to avoid the pitfalls of local minima [
42,
43,
44]. At the same time, if properly implemented, they can facilitate the exploration of the search space without the need to analyse it exhaustively.
In parallel, reinforcement learning (RL), a sub-field of ML, focuses on training software to make decisions based on rewards and penalties in specific situations [
45,
46,
47,
48]. This approach has been successfully applied to complex challenges like games and autonomous driving. This work uses three RL models, Advantage Actor–Critic (A2C), Deep Q-Network (DQN), and Proximal Policy Optimization (PPO), each with unique advantages. A2C is an asynchronous RL algorithm that combines the advantages of both policy-based methods (actor) and value-based methods (critic). It uses multiple agents that interact with an environment in parallel, allowing for more efficient exploration and learning. The actor network suggests actions, while the critic network estimates the value of these actions. A2C aims to optimise the balance between exploring new actions and exploiting known effective ones [
49,
50,
51].
DQN is a deep RL algorithm that combines Q-learning with deep neural networks. It is designed to learn a value function (Q-function) that estimates the expected cumulative future rewards for taking various actions in an environment. DQN has been successful in solving complex tasks and games [
48,
52,
53].
Finally, PPO is a RL algorithm that directly optimises the policy function. It belongs to the family of Policy Gradient Methods and is known for its stability and reliability. PPO uses a trust region optimisation approach to update the policy to ensure gradual changes, avoiding large policy updates, which can lead to instability. This makes PPO suitable for a wide range of tasks and provides excellent general performance [
54,
55].
In this paper, we approach the CAT problem by employing two distinct algorithmic methodologies. The first approach uses a hybrid meta-heuristic algorithm, incorporating clustering techniques for move segmentation, random search to assign scores to the moves, and a selection mechanism based on these scores to determine the optimal mode.
In contrast, the second approach utilises RL techniques, specifically focusing on implementing the PPO model. Our adoption of a hybrid approach stems from the CAT problem’s complexity. The clustering component of this approach ensures efficiency by avoiding the coupling of identical or similar moves, enabling more effective exploration and evaluation of solutions. Additionally, the integrated random search is crucial to optimising move evaluations and converging to the best solution.
Within RL, the CAT problem demands a model with high flexibility and robust stability. After exploring various models, including PPO, DQN, and A2C, only PPO demonstrated the versatility and adaptability needed to address the challenges of the CAT problem successfully.
3.1. Hybrid Approach
Our hybrid approach revolves around the strategy of decomposing the problem into two distinct phases, each designed to tackle unique and complex aspects of the CAT problem.
3.1.1. Clustering
The first phase of our approach involves clustering, which is an effective method for organising large numbers of unlabelled data. We use the K-means++ algorithm, which is known for its ability to identify natural clusters within a dataset, for this stage [
56]. Our objective is to group all possible moves within a specific gaming environment into homogeneous clusters based on their similarity. In order to optimise the colour-filling process, we utilise the copy action command to execute each move. Our goal is to colour the board in the most efficient manner possible, which entails maximising the number of dots that can be filled up with a single instruction. After this, our board, represented by a matrix
, is flattened into a vector
, which represents the moves in a multidimensional space. The K-means++ algorithm uses the Euclidean distance to measure the similarity between these vector representations. The output of this phase is a set of move clusters, where each cluster represents a set of moves that are similar from the algorithm’s perspective. The number of clusters is chosen based on the maximum expected moves in the worst-case scenario following heuristics, which may vary based on the rules.
3.1.2. Random Search
The second phase of our hybrid approach employs a random search algorithm. Numerous stochastic search methods have been developed to tackle complex and uncertain optimisation problems, and among these, we draw inspiration from Monte Carlo Tree Search (MCTS) [
57]. MCTS is a stochastic search technique that uses random simulations to guide the exploration of the solution space. Our approach involves simulating the game randomly to assign a score to each move, indicating its functionality concerning both the board and the clustering obtained from the previous step. Here is how we evaluate a game move:
Random move selection: We uniformly select moves at random from permutations of other clusters and then sample a move from each cluster.
Weighted move selection: Each cluster, denoted by A, consists of moves where represents a move within the cluster for all . These moves have associated weights . The probability of selecting is calculated as .
Game simulation: After selecting the moves, a game is simulated using a pseudo-optimal method. Each move is executed using the most frequently used copy action command to ensure replication in the highest number of advantageous cells, following a sequence that maximises coloured cells.
Scoring: At the end of the simulation, we assign a score based on the number of coloured cells. This score is determined in two ways: (i) if the board is incomplete, the score reflects the number of uncoloured cells plus a fixed penalty; (ii) if the board is complete, the score is based on the number of moves used for colouring.
Final score: The final score is calculated as the inverse of the score obtained in the previous step.
This phase serves as the critical step in evaluating the effectiveness of various moves within the game and clustering context, ultimately contributing to the selection of the optimal moves for solving the CAT problem.
3.1.3. Compilation and Selection of Optimal Moves
Once these initial phases are concluded, we compile a set of the best moves for each cluster, as determined by the scores generated through our random search algorithm. These best moves can then be aggregated and harnessed to construct comprehensive solutions for the CAT problem.
In the concluding phase, following this initial assessment, the top-rated moves from each cluster are selected based on their weighted distribution. These chosen moves subsequently undergo a more in-depth examination facilitated by a Depth-First Search (DFS) algorithm. DFS, a thorough exploration algorithm, navigates the entire solution space in a meticulous manner, facilitating the identification of the most promising solutions initially highlighted during the random search phase.
3.2. Proximal Policy Optimization (PPO)
Proximal Policy Optimization (PPO) is a member of the Policy Gradient Methods family [
58], developed by OpenAI in 2017 [
54]. We chose PPO for its ability to stabilise policy updates in RL problems through its Clipped Surrogate Objective method. This technique restricts the policy’s possible changes, discouraging large deviations between the new and old policies, which can cause instability in learning.
Our research employed the PPO algorithm available in the Stable Baselines 3 library [
59], which provides a practical and efficient tool set for implementing models such as PPO. For both the actor and critic, we used a simple Multilayer Perceptron (MLP).
3.2.1. Environment State
The environment, a critical part of our research setup, was developed using the Gym library [
60]. It was designed to represent states as the various configurations of the game board at any given moment, effectively capturing the distribution of both coloured and uncoloured cells. The actions available to the agent are defined by our set of instructions, which it can execute to alter the state of the board. The reward system is structured to reflect the efficacy of the agent’s moves, taking into account both the completeness of the area coloured with a single move and the overall efficiency, as determined by the speed at which the model completes the task. Thus, the agent is encouraged to perform moves that not only cover more area but also solve the puzzle as quickly as possible.
To gauge performance, the environment was equipped with a set of metrics that tracked the agent’s progress and effectiveness:
self.total_reward: This accumulates the total rewards garnered by the agent, reflecting the cumulative success of its actions in terms of area coloured and game completion speed across all played games.
self.total_episodes: This metric keeps a tally of the number of episodes or game instances the agent has completed, providing a count of experiences the agent has learned from.
self.steps: This is a counter for the number of steps taken within a single episode, resetting after each game restart.
In order to achieve more robust training, we added an element of randomness when initialising the starting state, namely, instead of starting with the empty board, we randomly coloured some cells. This modification aimed to encourage the agent to explore the action space more effectively and understand its impact on the game.
3.2.2. Reward Metric
In the environment, the reward metric is derived from the ability of a specific move to colour certain cells within a single step. The reward increases proportionally with the number of cells coloured. However, the reward correspondingly diminishes as the number of steps taken increases. Should the outcome of the colouring be zero or negative, a penalty is applied, suggesting that the move might have been ineffective or potentially detrimental to the board.
To elucidate, if the colouring outcome is positive, the reward is computed as the number of coloured cells divided by the total steps taken plus one; if the colouring outcome is zero or negative, a penalty of −0.5 or −1 is imposed, contingent upon the specific circumstances.
Lastly, upon game completion, an additional reward is allocated based on the completion speed: starting from a value of 9, this bonus decrementally reduces by one for each step undertaken, with a floor value of 1.
3.2.3. Training Process
We trained our model using PPO. To generate training data, we ran 14 separate games in parallel, resulting in batches of size 128. We then trained the model for 30 epochs using the Adam optimiser. This process was repeated for a total of 5M steps. The details about hyperparameters can be found in the
Table 1.
The configuration of hyperparameters in PPO was critical to improving the model’s performance in our study. While PPO is naturally resilient with the Stable Baselines 3 library’s default settings [
59], tailored adjustments helped us to hone its efficacy. By experimenting manually and using a profound comprehension of the underlying mechanisms, we tested several hyperparameter variations and different configurations.
A notable modification was the rise in the entropy coefficient (ent_coef), which was initially 0 and later adjusted to 0.02, 0.03, and finally, 0.05. This alteration aimed to expand the scope of exploration undertaken by the model concerning the CAT problem, which is important, since there is a wide range of potential moves. Insufficient exploration could cause the model to be unable to learn optimal strategies.
Concurrently, we decreased clip_range from 0.2 to 0.15. This parameter aims to limit policy variations in updates, minimising sudden large fluctuations that may occur during the training phase, particularly in a problem such as CAT, where the value of a move can undergo significant changes. Decreasing the clip range was essential to balancing the increased entropy coefficient and ensuring stable policy updates.
Additionally, we chose to increase batch_size from 64 to 128. By increasing the agent’s prior experience before each policy update, we improve the accuracy of the gradient estimate, resulting in decreased update variance and a more stable learning process.
Regarding the number of epochs (n_epochs), we increased this from 10 to 30. A greater number of epochs provides the agent with more opportunities to explore and learn complex game strategies, thus increasing the chance of performance improvement. In the CAT problem context, with its myriad actions and potential strategies, more epochs translate into deeper exploration and the possibility of discovering novel and more effective move combinations.
In summary, given the complexity of the CAT problem, with its vast space of actions and potential states, we chose to increase exploration, gather more experiences, and enhance the agent’s opportunities to explore new move combinations while being cautious not to destabilise the learning process. The final parameters selected, which are both theoretically sound and empirically effective according to our tests, are documented in
Table 1. These values contributed to consistent and superior results compared with all other configurations tested in our experiments.
To quantify the efficacy with which our models manage to interpret the dynamics of the game, we relied on the “explained variance” metric, already integrated into the Stable Baselines 3 library [
59].
4. Results and Discussion
This section presents and discusses the results derived from our research, with the aim of offering a clear interpretation of the data, underscoring both the strengths and limitations of our findings.
Multiple iterations were performed on the inherently non-deterministic meta-heuristic model to comprehend its regular performance and determine the maximum achievable outcome. This methodology recognises the variability of the model’s results and assures that the assessment encompasses its capabilities.
Conversely, the reinforcement learning model was operated systematically on completion of training. The model consistently selects the action with the highest probability. The evaluation of this model centres on the number of instructions required to colour the board entirely and how efficiently it maximises the rewards according to the reward metric.
4.1. Hybrid Approach
The findings of our investigation, outlined in
Table 2, illuminate significant aspects of the resolution strategies employed for the twelve distinct game boards illustrated in
Figure 2. From the derived results, we discerned a considerable disparity in resolution times contingent on the complexity of the board: those necessitating three–four moves for resolution demanded between 5 and 10 min, whereas more straightforward boards requiring at least one–two moves were resolved from a brisk few seconds to a minute.
Two crucial factors influence the algorithm’s choice. As board complexity increases, the number of acceptable combinations decreases. Furthermore, moves that might be effective are challenging for the algorithm to identify, as they may only be optimal when paired with other moves. From a programming perspective, the algorithm sets a limit on DFS, corresponding to the maximum number of moves explored. For instance, if there’s a solution based on three moves, the algorithm first attempts to find a combination of two moves. If we look at the values marked with an asterisk (*) in
Table 2, we can see an example of how in complex boards where there are few solutions of optimal length, the algorithm does not guarantee to find the solution. This may be because the clustering has not split the moves optimally or because the moves struggle to obtain a high score.
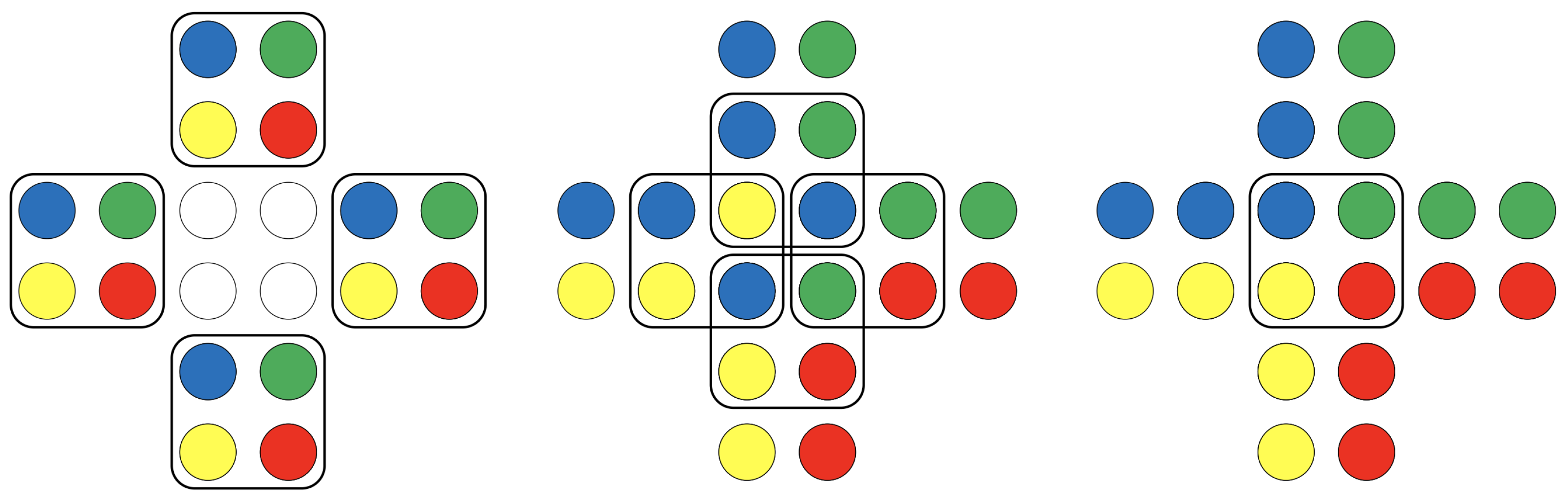
Figure 3 and
Figure 4 depict two intriguing solutions identified by the algorithm.
Figure 3 displays a solution consisting of a single instruction, which is notable due to its inherent complexity. Through an accurate overlay of the move, the algorithm can completely colour the entire board. Conversely,
Figure 4 illustrates a two-move solution, highlighting the effective functioning of cluster division; the two moves only share the central part of the board.
The figures demonstrate the versatility of the hybrid method in resolving problems of different levels of intricacy. It is noteworthy that the technique is capable of producing both complicated and less intuitive solutions for challenging tasks, as well as simple and comprehensible ones for less intricate boards. This adaptability is further demonstrated in other scenarios analysed. When confronted with game configurations that include all four colours or more intricate patterns, the algorithm has a tendency to choose a series of smaller moves, which are then combined in ways that may appear less intuitive. Conversely, in scenarios with fewer elements and more straightforward patterns, the algorithm showcases its ability to generate solutions that are not only efficient but also more easily understandable. This dual capacity demonstrates the hybrid approach’s adaptability in adjusting its solution strategy in response to the complexity of the problem presented.
In conclusion, our findings underscore the profound influence of the board’s complexity and the randomised colour layout on the algorithm’s performance metrics. Despite inherent challenges, our algorithm demonstrates robust efficacy, navigating through all categories of boards associated with the CAT problem within a reasonable time frame.
4.2. Proximal Policy Optimization (PPO)
An initial attempt involved training a basic Proximal Policy Optimization (PPO) model to tackle the 12 distinct game boards. Unfortunately, the model consistently executed erroneous moves. This issue stems from the immense number of potential moves and the drastic variability in board colouring and resolution strategy, which make it incredibly challenging for the model to grasp the game’s underlying logic. Each board introduces new information and invalidates previously learned information.
To mitigate this, a second experiment was conducted. Here, the basic PPO model was trained on a single board, enabling the model to focus on a more stable environment and learn the specific strategies for each one.
This approach yielded the results depicted in
Figure 5, which scrutinises the learning trajectories across different game board schemes. The intricate interplay between the model’s ability to grasp the rules of the game and the game board’s inherent complexities is evident in the ebbs and flows of the explained variance across time steps. The fluctuating learning trajectories for different game board schemes suggest that certain board configurations might inherently be more challenging for the model to navigate than others. For instance, while PPO for Graph 7 exhibits considerable variation in the initial stages, its trajectory gradually stabilises. Conversely, PPO for Graph 11 shows sustained variability throughout, indicating persistent challenges. The model’s learning is non-linear, with periods of rapid understanding followed by plateaus or even regression. This could be attributed to the complexities introduced by individual game boards, as each one adds new information while simultaneously invalidating some previously acquired knowledge. The early stages of training, as reflected in the left half of
Figure 5, indicate a steep learning curve for the model. This could be a phase of initial exploration where the model tries to figure out the game’s mechanics. The latter half of the graph, with more pronounced oscillations, might represent a fine-tuning phase where the model optimises its strategy. There are evident troughs in the explained variance, suggesting moments when the model might be stuck in local minima. Yet, the subsequent increases highlight the model’s ability to navigate out of these challenges, albeit not consistently. While the models were capable of completing the game board optimally or sub-optimally, a significant issue arose, as evidenced by the low explained variance depicted in
Figure 5. This outcome suggests that the model, despite achieving victory, failed to understand the game thoroughly. It managed to improve only certain strategies, lacking the versatility required. It becomes evident that while the model might excel or at least show promise in certain configurations, it struggles in others, emphasising the need for a more generalised strategy. These insights bolster the argument for a more nuanced training approach. Techniques like curriculum learning, where the model is gradually introduced to more complex tasks, could be beneficial. Similarly, ensemble methods that utilise multiple models’ predictions might offer a more robust solution, capitalising on the strengths of individual models across various game board schemes.
Table 3 presents the results achieved with PPO. In this analysis, we focus on presenting the results from more complex graph instances, excluding the simplest cases that can be resolved with just a single move. This is because the model identifies the optimal strategy easily in these cases and tends to apply the copy move consistently across similar situations. This behaviour is expected, because this move is effective and also yields the highest possible score in these elementary scenarios. Consequently, including these trivial instances would not add significant value to our understanding of the model’s capabilities, as its ability to solve them does not challenge its problem-solving mechanisms. The model yields slightly more extended solutions than those previously displayed for the hybrid approach in
Table 2. However, it consistently performs flawlessly on simpler boards. These findings illustrate the versatility and robustness of the PPO model in adapting and solving varying levels of problem complexity. Even PPO struggles on complex boards where the optimal solution is difficult to find, as observed from the values marked with an asterisk (*) in
Table 3. This could be due to the complex challenge of properly exploring all feasible moves, identifying the best correlations, and subsequently finding the solution, compared with other setups with simpler and more efficient solutions.
Subsequently, various PPO models were tested on Graph 10, incorporating random start, a clip range value of 0.15, and entropy coefficients of 0.02–0.05. This experimentation yielded the results shown in
Figure 6, while
Figure 7 illustrates the difference with respect to the previous model.
The integration of random start into the PPO model was aimed at facilitating better exploration of the environment.
Figure 6 sheds light on how different entropy coefficients, when used alongside random start, can influence the model’s learning journey. There’s a clear disparity in the explained variance trajectories when comparing models with different entropy coefficients. Higher entropy, as seen in the model with entropy of 0.05, leads to more pronounced fluctuations. This might be indicative of the model taking more diverse actions, resulting in varying levels of success and failure. The model with entropy of 0.01 appears to offer a slightly smoother learning curve, perhaps finding a better balance between exploration (trying new moves) and exploitation (leveraging known successful strategies). The increased volatility seen in the 0.05 entropy model underscores the challenge of navigating with excessive randomness. While exploration is essential, overdoing it can cause the model to deviate significantly from optimal strategies.
The juxtaposition of learning trajectories in
Figure 7 provides a comprehensive understanding of the effect of initialisation on model training. It is evident from the trajectories that models employing random start generally demonstrate better explained variance, especially in the latter stages. This underscores the potential benefits of avoiding biases in initial conditions and allowing the model to explore the environment more comprehensively. The model that does not employ random start appears to hit a plateau, suggesting that it might get trapped in specific sub-optimal strategies, unable to find its way out. While random start can be advantageous, the initial stages of learning seem more chaotic. It is likely that the model, due to the lack of any predetermined strategy, takes a longer time to identify promising strategies. Despite the clear advantages of random start, the oscillations in explained variance indicate that fine tuning, perhaps with adaptive entropy coefficients, could be beneficial.
Figure 8 demonstrates how the average reward of the models rises during training, indicating that our agent acquires the ability to navigate the environment to achieve maximum reward accumulation. If we combine this observation with those made previously, it is evident that our PPO model can predict future performance with high explained variance. Additionally, it yields high rewards, indicating a strong grasp of the operating environment.
An example of a solution generated by the PPO model for Graph 10 is illustrated in
Figure 9. The identified solution strategy is composed of two vertical instructions featuring alternating yellow and blue patterns. When combined, these instructions successfully colour the entire board, underscoring the efficacy and accuracy of the PPO model in formulating coherent and comprehensive solutions.
In conclusion, PPO models are highly adept at solving the CAT problem, albeit requiring substantial time and resources for training. The primary advantage is that when developed with random start and augmented entropy, it can resolve the game board and assist in resolving various game boards from a non-empty start. This feature renders it useful for third-party applications in progress games.
4.3. Comparative Analysis and Discussion
This subsection provides a comparative analysis of the results obtained from the hybrid approach and the PPO model in addressing the CAT problem. The analysis aims to elucidate the differences in performance and the underlying reasons for these differences, thereby offering a clearer understanding of the relative strengths and weaknesses of these algorithms in this context. To facilitate the comparison between the two models, alongside depicting the solution found with visual means, we aimed to extend the PPO metric, introduced in
Section 3.2.2, to the hybrid approach.
Table 4 encapsulates the key performance metrics for both methods across various problem instances. We would like to note that boards with a single-move solution are not considered, as both methods always yield the same result for both. Significant observations arise from the data presented regarding the quality of solutions and differences between the two approaches. Firstly, the nature of the instructions selected by the respective models highlights discrepancies in their resolution behaviour. The hybrid approach appears to prioritise simpler moves, resulting in less intuitive but complex combinations; conversely, the PPO model adopts more elaborate moves, resulting in generally more intuitive solutions.
The table shows the strategies chosen by the two approaches (i.e., the different moves chosen to complete the game) for different boards. We, therefore, have an illustration not only of the number of moves chosen but also of the types of moves chosen. To compare the two approaches, the reward metric is also added.
On the one hand, this distinction appears to be influenced by the hybrid approach’s strategy of assessing moves for their combinational effectiveness. In this context, less complex moves are often more versatile and adaptable, enabling them to fit a variety of combinations and scenarios. As a result, these moves tend to achieve higher scores because they are more likely to work with other moves.
The PPO model, on the other hand, leverages its exploratory capabilities to learn and harness the complex interplay among moves. It does not solely prioritise adaptability, but instead, it seeks to explore a diverse range of moves, including those that are more intricate. It assesses the effectiveness of these complex moves over a broad spectrum of situations, progressively refining its choice to favour moves that, although possibly less versatile, can navigate toward solutions in a more direct and often more optimised manner.
Regarding the length of solutions, meaning the number of selected instructions, the hybrid approach demonstrates superiority in more complex problems, finding more concise solutions compared with PPO.
Regarding the reward, the two models exhibit comparable performance. A higher score is assigned to solutions with a greater number of instructions if they are characterised by higher speed and quality, as evidenced in the case of Graph 11. This demonstrates how a numerically less optimal solution can still achieve higher scores, thus showing room for improvement in the metrics.
In general, PPO tends to come up with solutions that have more instructions compared with the hybrid approach. Therefore, if both methods discover solutions of equal length, the solution produced by PPO has the highest reward. This is because the model is designed to optimise the reward, so it chooses moves that can initially colour more. However, this approach can lead to mitigating losses in shorter solutions, as in the case of Graph 11, but not in solutions that require many moves, as in Graph 12, since the metric tends to penalise the model more and more as the model employs more moves to complete the solution.
In summary, it can be said that both models demonstrate effectiveness in addressing the CAT problem, but they differ significantly in the type of solution generated. While the hybrid approach often generates fewer instructions that result in more complex combinations, the PPO model favours slightly more extensive but simpler-to-interpret solutions, characterised by more moves.
5. Conclusions
In the face of swift technological transformations, the significance of computational thinking (CT) skills cannot be overstated, especially in the educational domain. This study, anchored in the Swiss educational system’s needs, scrutinises the Cross Array Task (CAT) as both an evaluative instrument for assessing students’ algorithmic proficiency and a complex problem ripe for computational analysis. The goal of this study is to expand the boundaries of algorithmic research by exploring computational strategies that can optimally solve this task.
Our rigorous analysis unearthed the nuanced challenges posed by the CAT, a task that, on the surface, appears deceptively simple yet demands a profound level of strategic reasoning. By adopting a hybrid approach, leveraging clustering techniques with score-based evaluations, and harnessing the Proximal Policy Optimization (PPO) reinforcement learning (RL) model, we have carved out new paths for solving and understanding the intricacies of this educational tool.
Comparing our findings with existing research, it is evident that the hybrid method represents a significant stride in the CAT problem’s algorithmic landscape. Traditional methods have often struggled with the balance between optimisation and variability, a concern that the hybrid approach addresses with finesse. Furthermore, the intricacies and potential of RL, as highlighted in this study, underscore the need for a more refined exploration of its applications in future research.
While both the hybrid and PPO models demonstrate commendable performance, they are each constrained by specific limitations, particularly in complex scenarios with numerous colours and intricate board configurations. For the hybrid approach, the main bottleneck arises from the clustering mechanism and the metric used to measure move similarity. This can result in different moves being erroneously grouped together, which may obscure the efficacy of potentially optimal moves. Consequently, the algorithm might fail to evaluate and select the best strategies accurately. The PPO model, by virtue of considering all possible moves, ostensibly benefits from a broader learning scope, capturing the nuances of move interactions and board dynamics. However, this same breadth also introduces a significant challenge; the diversity of game boards and the expansive search space can overwhelm the learning process, potentially leading to subpar strategies. Moreover, the PPO model’s inability to effectively manage multiple types of board configurations further compounds this complexity, complicating the discernment of move-to-board inter-dependencies. These results represent further confirmation of how not only meta-heuristic methods but also RL models are able to address an NP-hard problem adequately.
Looking ahead, we see potential in using advanced methods like meta-reinforcement learning (meta-RL) and general-purpose in-context learning as alternative methodologies. Meta-RL, for example, could help us create smarter educational tools that not only tailor learning experiences to individual student profiles but also excel in generalising to new problem-solving scenarios that are significantly distinct from those encountered during training [
27]. Also, using general-purpose learning technologies could help us design systems capable of addressing a wider array of problems with minimal manual tuning, thus surpassing the capabilities of current manually-designed approaches [
28]. Employing these cutting-edge technologies could result in more efficient and effective learning interventions, potentially leading to superior problem-solving strategies that are both innovative and broadly applicable across the diverse landscape of educational challenges.
This study carries profound practical implications for CT education. By incorporating our algorithms into educational technologies, such as the virtual CAT application, we can enhance the learning experience, making the activities more interactive and tailored to individual needs. One promising avenue for such integration is the development of intelligent tutoring systems (ITSs) that adapt to individual learning styles and student’s proficiency [
61,
62,
63].
While the promise is significant, integrating these complex algorithms into user-friendly systems is not without its challenges. They must be designed to maintain educational focus without complexity overwhelming the learner. Moreover, the interfaces should be clear and provide constructive feedback to support learning. Additionally, the deployment of such systems must navigate issues of accessibility; the risk of dependency on algorithms; and the need for a flexible, current curriculum.
Even with these challenges, incorporating our algorithms into ITSs has the potential to revolutionise how students learn CT, enhancing their problem-solving abilities and their understanding of CT concepts.
In conclusion, this research not only offers a comprehensive understanding of the CAT problem but also charts a path for future studies and practical applications. Through a judicious blend of hybrid methodologies and RL, the study has expanded the horizons of algorithmic solutions in the realm of CT and education.