Spherical Tree-Structured SOM and Its Application to Hierarchical Clustering

Abstract

When analyzing high-dimensional data with many elements, a data visualization that maps the data onto a low-dimensional space is often performed. By visualizing the data, humans can intuitively understand the structure of the data in the high-dimensional space. The self-organizing map (SOM) is one such data visualization method. We propose a spherical tree-structured SOM (S-TS-SOM), which speeds up the search for winner nodes and eliminates the unevenness of learning due to the position of the winner nodes by placing the nodes on a sphere and applying the tree search method. In this paper, we confirm that the S-TS-SOM can achieve the same results as a normal spherical SOM while reducing the learning time. In addition, we confirm the granularity of clustering on the tree structure of the S-TS-SOM.

1. Introduction

Because of the recent developments in data science, various types of data are now analyzed in many fields. When analyzing data, if the structure of the data is unknown in advance, it is necessary to first understand the structure of the data and then select the analysis methods according to the task. If the data to be analyzed consist of few elements, it is easy to understand the structure of the data. However, in the case of high-dimensional data with many elements, it is difficult for humans to grasp the structure of the data. Therefore, data visualization that maps high-dimensional data onto low-dimensional space with two or three dimensions is often performed. By visualizing these data, humans can intuitively understand the structure of the data in the high-dimensional space. Various methods have been proposed for data visualization, and a self-organizing map (SOM) is one such data visualization method [1,2].

The SOM maps high-dimensional data onto a low-dimensional map and expresses the similarity between data points using distance on the map. Similar data are placed close to each other on the map, and dissimilar data are placed far from each other on the map. A brief description of the SOM algorithm is as follows. First, the SOM arranges nodes that have reference vectors initialized with random values in a two-dimensional grid. In the learning phase, a SOM determines the winner node, which is the reference vector closest to the input vector, and updates the winner node’s reference vector and its neighbors’ reference vectors so that they are closer to the input vector. Learning in the SOM is performed by repeatedly determining the winner node and updating the reference vectors of the winner node and its neighbors.

In recent years, large amounts of data have accumulated because of the development of various web services, and hence the number of data to be analyzed has increased. Generally, when visualizing a large number of data using a SOM, the number of nodes in the map is set to a large number. However, as the number of nodes increases, the SOM needs more time to search for the winner nodes. In addition, because the SOM usually arranges nodes in a two-dimensional grid, there are edges to the map. Therefore, according to the position of winner nodes, e.g., the center or edge of the map, the update area sizes are different. This means that learning is not uniform but depends on the positions of the winner nodes. To solve both these problems, we propose a spherical tree-structured SOM (S-TS-SOM). The S-TS-SOM arranges nodes on a spherical surface and applies a tree search method to speed up the search for the winner nodes while eliminating the edges of the map. We compare the effectiveness of the S-TS-SOM with a conventional spherical SOM (S-SOM) using the benchmark data MNIST [3].

The S-TS-SOM builds a tree structure and determines the winner nodes using a tree search method. In addition to speeding up the search, the advantage of the tree structure is that we can obtain different granularities of clustering in the tree structure. In this paper, we examine whether the granularity of clustering can be found in the tree structure of the S-TS-SOM. The main contributions of this paper can be summarized as follows.

(1)

We propose the S-TS-SOM, which applies a tree search method to the S-SOM, to speed up the search for winner nodes and eliminate the edges of the map.

(2)

We examine the effectiveness of the S-TS-SOM by comparing it with the S-SOM using a benchmark dataset.

(3)

We examine whether the granularity of clustering can be determined using the tree structure of the S-TS-SOM.

The remainder of this paper is organized as follows. Section 2.1 introduces work related to this study. Section 2.2 presents the proposed method, the S-TS-SOM. In Section 3.1 and Section 3.2, we evaluate the effectiveness of the S-TS-SOM by comparing it with the S-SOM using the benchmark dataset MNIST. Section 3.3 examines whether the granularity of clustering can be found using the tree structure of the S-TS-SOM. Section 4 presents the discussion and future work.

2. Materials and Methods

2.1. Related Work

First, we describe a SOM and other methods used for data visualization. A SOM is a type of artificial neural network proposed by Kohonen. It maps high-dimensional data onto a low-dimensional map and expresses the similarity of the data using distance. On the map, similar data are placed close to each other, and dissimilar data are placed far from each other. This characteristic enables the SOM to be used for data visualization. By visualizing the data, humans can intuitively grasp the relationships among the data in a high-dimensional space. WEBSOM is an example of an application that is used as a tool for data visualization. WEBSOM makes it easy to search for documents that are similar to a query document by arranging many documents onto a two-dimensional map according to similarity [4].

We describe the SOM algorithm as follows: Figure 1 shows the structure of the SOM. It has nodes $m_i\left(i=1,\dots I\right)$ with reference vector m_i. First, each reference vector is initialized with a random value. In the SOM, the node with the reference vector that is closest to the input vector $x_j\left(j=1,\dots J\right)$ that was selected from the input set is determined to be the winner node $m_c$. After the winner node is determined, the reference vectors of the winner node and its neighborhood nodes are updated so that they are closer to the value of the input vector using the following formula:

$$m_i\left(t+1\right)=m_i\left(t\right)+h_{ci}\left[x_j\left(t\right)-m_i\left(t\right)\right]$$

(1)

$$h_{ci}\left(t\right)=\alpha \left(t\right)\exp \left(-\frac{d_{ci}{}^2}{2{\sigma }^2\left(t\right)}\right),$$

(2)

where $h_{ci}$ is a neighborhood function determined by the positions of winner node $m_c$ and node $m_i$, $d_{ci}$ is the distance between the nodes $m_c$ and $m_i$ on the map, $\alpha \left(t\right)$ is the learning rate, and $\sigma \left(t\right)$ is a function that determines the size of the update area; $\alpha \left(t\right)$ and $\sigma \left(t\right)$ are set to decrease as the number of updates increases. By repeatedly determining the winner node and updating the reference vectors, the SOM is trained. The algorithm described above is a common technique called online learning. By contrast, batch learning that does not depend on the order of input has also been proposed [5]. In batch learning, after the winner node of all inputs is determined, the map is updated using the following formula:

$$m_i\left(t+1\right)=\frac{{\sum }_{j=1}^J{h}_{cj}{,}_i{x}_j}{{\sum }_{j=1}^J{h}_{cj}{,}_i}$$

(3)

$$h_{cj}{,}_i\left(t\right)=\exp \left(-\frac{d_{cj,i}{}^2}{2{\sigma }^2\left(t\right)}\right).$$

(4)

In addition to the SOM, principal component analysis (PCA) and t-distributed stochastic neighbor embedding (t-SNE) are common dimensional reduction or compression methods [6,7]. PCA searches for the axes with the large variances in the data and removes axes with small variances to reduce the dimensions. Note that PCA is based on the assumption that the magnitude of the variance represents the characteristics of the data. t-SNE regards the distance between data points as a probability and compresses the dimensions so that the distances between data points in the high- and low-dimensional spaces are the same. Here, we introduced PCA and t-SNE as typical methods. However, many other methods continue to be proposed [8,9]. Similar to the SOM, PCA and t-SNE are mainly used for data visualization. The major difference between the SOM and other dimensional reduction or compression methods such as PCA and t-SNE is that the SOM uses nodes for learning. Therefore, using a SOM, we obtain not only the coordinates of the input data in the low-dimensional space but also the codebook vectors from the nodes.

As mentioned in the Introduction, if the number of nodes in a SOM increases, the number of search nodes needed to determine the winner nodes increase, and the calculation time increases. Therefore, a tree-structured SOM (TS-SOM), which uses the tree search method in the SOM, was proposed [10]. The structure of a TS-SOM is shown on the left-hand side of Figure 2. A TS-SOM is a SOM composed of multiple layers and has a structure in which the number of nodes increases from the upper layers to the lower layers. The nodes of the upper layer have links to the nodes of lower layer, and the winner nodes determined in the upper layer assist the search for the lower layer’s winner nodes to speed up the search for the winner nodes. The right-hand side of Figure 2 shows how to determine the winner node in a TS-SOM. The lower winner node is determined from the child node group that has a link from the winner node determined in the upper layer. As in a SOM, the nodes of each layer in a TS-SOM are arranged in a two-dimensional grid pattern. Therefore, a TS-SOM also has map edges.

Next, we describe the shape of the SOM. Normally, the SOM arranges nodes on a two-dimensional grid pattern for learning. Therefore, a SOM is a map with edges. The presence of the edges of the map causes a difference in the size of the update area of a winner node at the center of the map and a winner node at the edge of the map. Figure 3 shows the update area according to the position of the winner node. In addition, because of the characteristics of the SOM, if the map has an edge, the SOM tends to collect data at the edges of the map. Therefore, to eliminate differences in the size of the update area, the torus SOM, which has a map without edges, and the spherical SOM (S-SOM), which arranges nodes on a spherical surface, were proposed [11,12]. Figure 4 shows the map shapes of the torus SOM and the S-SOM. In the torus SOM, by connecting the edges of the map as shown in the Figure 4, the edges of the map are eliminated. The torus SOM can learn uniformly regardless of the position of the winner nodes. However, when the map is visualized, it is necessary to consider the connections between the edges of the map, which make it difficult for humans to intuitively understand the result. In this study, we chose to arrange nodes on a sphere for intuitive visibility. Intuitive visibility is achieved by drawing the spherical map in three dimensions and rotating the spherical map for viewing.

When clustering data, how finely the data should be clustered strongly depends on the target task. For example, if the data are uniformly distributed, it is difficult to automatically determine the optimal number of clusters. Furthermore, for data with small categories within large categories, the hyperparameters need to be adjusted depending on the size of the target category. Generally, for such data, a dendrogram is created by performing hierarchical clustering, and the number of clusters is arbitrarily determined according to the task. In addition to hierarchical clustering, a SOM with multiple layers can be used to arbitrarily determine the number of clusters. The TS-SOM, which is the basis of the method proposed in this paper, is composed of multiple layers, and has a structure in which the number of nodes increases from the upper layers to the lower layers. Therefore, the data are classified more finely toward the lower layers, and clustering results with different granularities can be obtained in each layer. In addition to the TS-SOM, the hierarchal feature map (HFM) has also been proposed [13,14]. Moreover, the GH-SOM, which enables the HFM to learn adaptively, and a method that makes the TS-SOM learn adaptively, have been proposed [15,16,17].

2.2. S-TS-SOM

In this section, we describe the S-TS-SOM. The basic structure is the same as that of a TS-SOM. However, in an S-TS-SOM, nodes are evenly arranged on a spherical surface to eliminate the edges of the map. In this paper, we use polyhedrons inscribed in a sphere to arrange the nodes on the spherical surface. The nodes are arranged as follows. First, we divide the icosahedron and stack it, as shown in Figure 5. Next, nodes are placed on each surface of the polyhedrons, and links are added from the nodes of the inner layer to the nodes of the outer layer. Using this process, the tree structure is constructed for each face of the polyhedron, as shown in Figure 6. In the method proposed in this paper, except for the outermost layer’s nodes, the tree structure is created such that each node has four links to the outer layer’s nodes. The direction of layering is not important because it does not change the underlying concept. However, for the sake of explanation, we create the structure such that the outer layer has more nodes.

An S-TS-SOM has multiple layers, each layer has a node $m_{i_l}\left(i_l=1,\dots I_l\right)$, and node $m_{i_l}$ has a reference vector $m_{i_l}$. Here, $l$ indicates the level of the layer, and $l=0,1,2,\dots L$ in order from the inner layer to the outer layer. In addition, $i_l$ indicates the node number of the $l$th layer. We used an icosahedron for the innermost polyhedron, and because we divide the icosahedron to increase the number of layers, the number of nodes in each layer is expressed by the following formula.

$$I_l=20\times 4^l$$

(5)

The learning algorithm of the S-TS-SOM is as follows. First, we initialize the reference vectors of the 0th layer nodes with random values. The 0th layer is trained using the SOM algorithm. In a SOM, the node with the reference vector that is closest to the input vector that was selected from the input set is determined to be the winner node. After determining the winner node, the reference vectors of the winner node and its neighborhood nodes are updated so that they are closer to the value of the input vector. By repeatedly determining the winner node and updating the reference vectors, the SOM is trained. In this paper, Euclidean distance is used to measure the similarity between the input and reference vectors. For layers other than the 0th layer, the winner node is determined using the winner node of the inner layer. If the winner node in the $l$th layer of $x_j\left(j=1,\dots J\right)$ selected from the input vector set is $m_{c_l, j}$, the winner node in the $l+1$th layer is determined from the child node set $c_l, j$, which has links from node $m_{c_l, j}$. The update method of each layer is the same as that used in a SOM. Update methods include online learning and batch learning methods. We adopt batch learning because it is not affected by the order of the input data. After determining the winner nodes of all the input vectors in the $l$th layer, the reference vectors of the $l$th layer are updated by the following formula.

$$m_{i_l}\left(t+1\right)=\frac{{\sum }_{j=1}^J{h}_{c_{l}j}{,}_{i_l}{x}_j}{{\sum }_{j=1}^J{h}_{c_{l}j}{,}_{i_l}}$$

(6)

$$h_{c_{l}j}{,}_{i_l}\left(t\right)=\exp \left(-\frac{{\theta }_{c_{l}j,i_l}^2}{2{\sigma }^2\left(t\right)}\right),$$

(7)

Here, $h_{c_{l}j}{,}_{i_l}$ is a neighborhood function obtained from the positions of winner node $m_{c_l, j}$ and node $m_{i_l}$. In addition, ${\theta }_{c_{l}j,i_l}$ is the angle between winner node $m_{c_l, j}$ and node $m_{i_l}$, as seen from the center of the sphere; $\sigma \left(t\right)$ is a function that determines the size of the update area; $\sigma \left(t\right)$ is set to decrease as the number of updates increases. When the learning of the $l$th layer is completed, the nodes of the $l+1$ th layer are initialized by the following formula, and the $l+1$ th layer is trained:

$$m_{i_{l+1}}=\frac{{\sum }_{i_l=1}^{I_l}{h}_{i_l,i_{l+1} }{m}_{i_l}}{{\sum }_{i_l=1}^{I_l}{h}_{i_l,i_{l+1}}}$$

(8)

$$h_{i_l, i_{l+1}}=\exp \left(-\frac{{\theta }_{i_l,i_{l+1}}^2}{2{\sigma }_{l+1}^2}\right)$$

(9)

Here, ${\sigma }_{l+1}$ is the parameter for initializing the reference vectors of the $l$ + 1 th layer.

When the number of updates of each layer is defined as $T_l$, the number of nodes searched during learning for one input vector is expressed by the following formula.

$$20\left(T_0+1\right)+\sum _{l=1}^{L}4(T_l+1)$$

(10)

We use this formula in Section 3 to compare the performance of the S-TS-SOM and S-SOM.

The learning process of the S-TS-SOM is described below.

(1)

Train the 0th layer using the SOM algorithm.

(2)

Add a competitive layer.

(3)

Search for the winner nodes in the added layer.

(4)

Update the reference vectors of the added layer using the neighborhood function.

(5)

Repeat steps 3 to 4 a certain number of times.

(6)

If the number of layers is the same as a pre-determined number, the learning is finished. Otherwise, the process returns to step 2.

3. Results

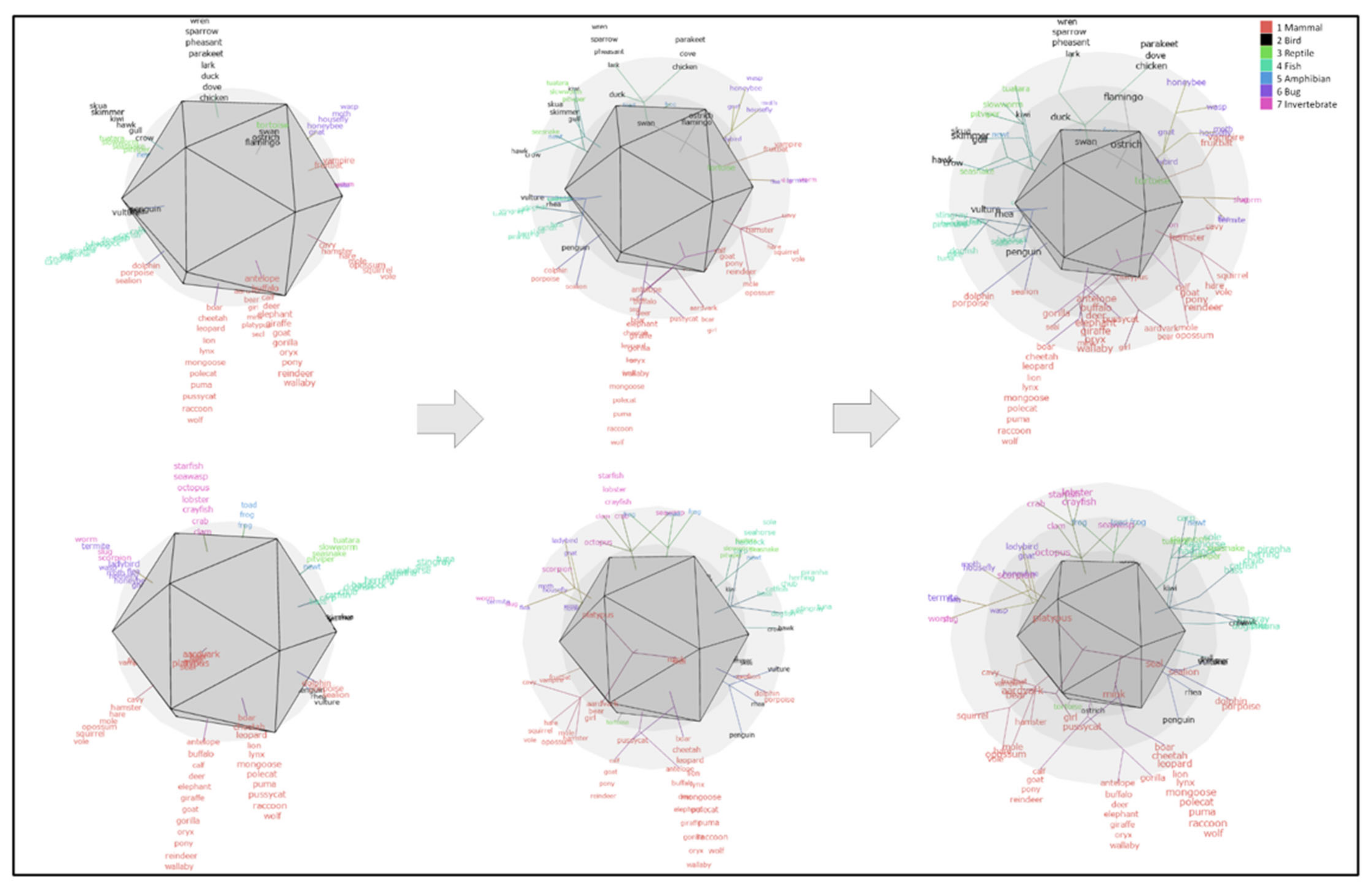
3.1. Visualization Experiment

First, we evaluate the S-TS-SOM as a visualization tool. Here, we use the MNIST benchmark dataset. MNIST is a dataset of images consisting of 10 categories, with 60,000 training data, and 10,000 test data. Handwritten numbers from “0” to “9” are drawn on each image. Each image in MNIST is 28 × 28 pixels. Similar to SOM, S-TS-SOM needs to convert the data to a vector format. Therefore, 28 × 28 data are inputted by transforming them into a vector of 784 elements.

For reasons of visualization, we used a total of 1000 images (100 extracted from each category) as the training data. We set the number of layers of the S-TS-SOM to $L=4$. Parameter ${\sigma }_{l+1}$ was set to decrease as the inner layers become outer layers. (${\sigma }_1,{\sigma }_2,{\sigma }_3,{\sigma }_4=90°,45°,22.5°,11.25°$). In addition, the $\sigma \left(t\right)$ of each layer was set to decay linearly with the number of updates, with ${\sigma }_{l+1}$ as the initial value. The $\sigma \left(t\right)$ of the 0th layer was set with 180° as the initial value. We set the number of updates for each layer to 100. Figure 7 shows the result. For comparison, we show the result of the S-SOM in Figure 8. We placed the nodes of the S-SOM on the faces of the polyhedron, set the number of the S-SOM updates to 100, and updated the map by batch learning. The $\sigma \left(t\right)$ of the S-SOM was set with 180° as the initial value. For the sake of clarity, we added colors to the MNIST images according to each category. The results show that similar images are gathered close to each other on the maps generated by both the S-TS-SOM and S-SOM. These results indicate that the S-TS-SOM is working properly as a visualization tool.

3.2. Quantitative Evaluation of Clustering

Here, we quantitatively compare the clustering performance of the S-TS-SOM and S-SOM. We used the purity and normalized mutual information (NMI) clustering indicators to evaluate the performance [18]. These two indicators take a value from 0 to 1, and values close to 1 indicate a high performance. Purity is calculated by counting the most dominant labels in each cluster and dividing by the number of data. Purity is simple to calculate. However, purity can easily be increased to 1 by increasing the number of clusters. By contrast, the calculation of NMI is complicated. However, it is calculated considering the number of clusters. NMI is close to 1 when the labels for each cluster are not mixed, and the number of clusters is close to the number of original categories. To calculate the purity and NMI clustering indicators, the true category labels are required. We used a total of 70,000 MNIST images as the experimental data. Therefore, in this experiment, the purity and NMI will be high if the data are correctly classified.

We set the number of outermost nodes to 80, 320, 1280, and 5120 for both the S-TS-SOM and S-SOM. We calculated the purity and NMI by treating the data placed on the same winner node as belonging to one cluster. We set the number of S-TS-SOM updates to 100 for each layer and the number of S-SOM updates to 100. We set ${\sigma }_{l+1}$ and $\sigma \left(t\right)$ in the same way as in Section 3.1. The 0th layer of the S-TS-SOM and S-SOM were initialized with random values. Therefore, we present the average of the results of the five trials in

Table 1. Performance of the S-TS-SOM and S-SOM.

	(1) S-T S-SOM				(2) S-SOM				(1)/(2)
Number of Outermost Nodes	Number of Search Nodes	Purity	NMI	Time (s)	Number of Search Nodes	Purity	NMI	Time (s)	Purity	NMI	Time (s)
80	24 × 101	0.761	0.481	215.13	80 × 101	0.787	0.508	235.07	0.967	0.948	0.915
320	28 × 101	0.822	0.443	409.06	320 × 101	0.823	0.449	941.17	0.998	0.986	0.435
1280	32 × 101	0.864	0.409	789.74	1280 × 101	0.844	0.401	3678.23	1.024	1.020	0.215
5120	36 × 101	0.895	0.381	2011.44	5120 × 101	0.858	0.365	16,560.32	1.043	1.046	0.121

. This table reveals that the S-TS-SOM and S-SOM have almost the same performance with respect to purity and NMI.

In addition to the calculation of purity and NMI, we compared the learning time of the S-TS-SOM and S-SOM to examine whether the S-TS-SOM could be trained more quickly than the S-SOM. We used Python for model creation and calculation and used a PC with an Intel(R) Core (TM) i7-10870 2.20 GHz/5.0 GHz and 64 GB DDR4 memory. The “Time” column in Table 1 lists the learning time of each model. Because the number of updates for each layer of the S-TS-SOM was set to 100, the number of nodes searched during learning for one input vector is (20 + 4L) × 101 from Formula (10). By contrast, in the S-SOM, the number of nodes searched for one input vector is 20 × 4L × 101.

In addition to the difference in the number of searched nodes, the S-TS-SOM initializes and updates the reference vectors in multiple layers. Moreover, because of the differences in the algorithms, the number of searched nodes does not directly reflect the difference in the learning times of the S-TS-SOM and S-SOM. However, the learning time of the S-TS-SOM was shorter than the learning time of the S-SOM. Moreover, as the number of nodes increased, the difference between the S-TS-SOM and S-SOM learning times increased.

From the experiments, we confirmed that an S-TS-SOM has almost the same clustering performance as a S-SOM but a shorter learning time.

3.3. Data Clustering Utilizing the Tree Structure of the S-TS-SOM

The S-TS-SOM proposed in this paper has a structure in which the number of nodes increases from the inner to outer layers. Therefore, we believe that by checking the results for each layer, we can obtain results with different data classification granularity. We consider that the layers closer to the inner layer have a smaller number of nodes, so the data are more roughly classified. Moreover, the layers closer to the outer layer have a larger number of nodes, so the data are more finely classified. In this section, we check the results of each layer of the S-TS-SOM to determine if the adjustment of the number of clusters is successful.

We used the Zoo dataset of UCI as the experimental data [19]. The Zoo dataset is composed of 101 species of animals, where each animal has 17 attributes. We used 16 attributes as the input and excluded the “type” attribute. Therefore, each animal was treated as a vector with 16 elements. Because the “legs” attribute is not a Boolean value, we used the value divided by the maximum value in the “legs” attribute as the input. The “type” attribute classifies each animal into an animal type using a number from one to seven. We set the number of layers of the S-TS-SOM to L = 2 and the number of updates for each layer to 100. Figure 9 shows the results. In Section 3.1, we presented only the outermost layer of the S-TS-SOM. However, the other layers are also shown in Figure 9, and the labels are color-coded according to the “type” attribute. In Figure 9, the top row shows the front of the map, and the bottom row shows the back of the map. We plotted the data placed on the same winner node in the same direction as seen from the center of the sphere. If only one data point was placed at a node in a layer other than the outermost layer, the branch growth was stopped for the sake of visibility.

In the results of Figure 9, in the 0th layer, the clusters are roughly formed according to each “type” attribute. As the number of layers increases, we can see that the clusters branch into smaller clusters. Note that some data have stopped branching because the input values are the same.

Table A1. Animals with the same input values.

aardvark, bear

antelope, buffalo, deer, elephant, giraffe, oryx

bass, catfish, chub, herring, piranha

boar, cheetah, leopard, lion, lynx, mongoose, polecat, puma, raccoon, wolf

calf, goat, pony, reindeer

chicken, dove, parakeet

crayfish, lobster

crow, hawk

dogfish, pike, tuna

dolphin, porpoise

flea, termite

fruitbat, vampire

gull, skimmer, skua

haddock, seahorse, sole

hare, vole

housefly, moth

lark, pheasant, sparrow, wren

mole, opossum

slug, worm

shows the groups of data with the same input value. From this experiment, we confirmed that the S-TS-SOM can extract the granularity of clustering on the tree structure by checking each layer after the data were learned.

4. Conclusions

In this paper, we proposed the S-TS-SOM, which uses a tree search method on a spherical surface to eliminate the edges of the map in the SOM and speed up the search for winner nodes. In addition, we confirmed the effectiveness of the S-TS-SOM by comparing the visualization performance and clustering performance with the S-SOM using the MNIST dataset. As a result, the S-TS-SOM placed similar images close to each other on the map equally as well as the S-SOM. Additionally, when we checked purity and NMI while changing the number of nodes to measure clustering performance, the difference between the values of the S-TS-SOM and S-SOM was within 0.1. When we measured the learning time, the ratio of the learning time of the S-TS-SOM to that of the S-SOM became shorter at 0.915, 0.435, 0.215, and 0.121 as the number of nodes in the map increased. The results show that the S-TS-SOM obtained the same performance as the S-SOM while speeding up the search for winner nodes.

We furthermore confirmed that the granularity of clustering could be found on each layer of the S-TS-SOM that learned the Zoo dataset. Hence, the S-TS-SOM is able to organize the map into a tree structure that reflects the granularity of the clustering.

As a limitation, the S-TS-SOM has more hyperparameters than the S-SOM because the former initializes and updates the map of each layer. In this paper, we did not investigate the influence of the hyperparameters of the S-TS-SOM. In the future, we will investigate the influence of the hyperparameters and compare the proposed method with other data visualization and clustering methods. In addition, we will develop a data search system that makes use of the tree structure of the S-TS-SOM.