Abstract
The main issue to tune controlled devices by the application of a DC magnetic field comes up against the high value of the field’s intensity required for their implementation. This work presents an implementation of magneto-dielectric materials (MDM) specifically manufactured for their integration in antenna devices operating in VHF band. The twofold objective is: (i) reduction in antenna size, (ii) frequency tuning of the antenna using a low intensity magnetic control. A notable permeability variation of MDM samples is observed when the symmetry of the lines of the control field, with an intensity less than 10 Oe, is consistent with the one of the structures in the magnetic domains. The MDM allows a miniaturization of 20% of an inverted-F antenna (IFA) antenna structure, and an agility of about 2.5% for a control field of 1.5 Oe.
1. Introduction
The common use of connected objects these last few years has led to a special need of both electrically small, cost effective and performing antennas. Antenna miniaturization becomes a real challenge at UHF and VHF frequency bands, since the wavelength are large at those frequencies. The designers of electrically small antennas are always facing a tradeoff involving the electrical size of the antenna, its frequency bandwidth and its radiation efficiency, following the fundamental laws of physics described in [1,2,3,4]. For applications requiring long-range communications, antenna radiation properties are crucial to achieve a correct link budget. This critical issue particularly arises for airborne systems industry, where the need of small antennas at VHF frequencies is also justified by a limitation in weight and aerodynamic drag. In this kind of application, antennas frequency bandwidth is often sacrificed, in order to achieve small antennas with sufficient radiation properties. A possible solution to overcome the limited bandwidth issue is to design a frequency reconfigurable antenna that covers the used communication channel. Classical frequency reconfigurability techniques using electronic components, such as varactors, digitally tunable capacitors, or switches to tune antenna’s frequency response, are often used, in order to solve the narrow bandwidth issue of small antennas [5]. These techniques can be used to artificially increase total antenna operating bandwidth, either by matching the antenna to the required narrow instant band, or by fine tuning the narrow operating band of miniature antenna that can be sensitive to their close changing environment. The drawback using those techniques is to introduce additional losses in antenna structure leading to reduce its radiation performances. In this work, a frequency agility technique based on tunable polycrystalline magneto-dielectric material (MDM) is proposed for fine-tuning the frequency response of an electrically small antenna designed in VHF band. MDM belong to the class of “multiferroic materials”, wherein magnetic, electric and mechanical responses might be interlinked. A magnetostrictive material, for example, may exhibit in certain cases a change in magnetization (M) in the presence of an electric field (E). For instance, [6] focused on composite magnetoelectric structures which associate piezoelectric substrates and magnetostrictive layers, in order to get a variation of microwave permeability, thanks to an electric field generated under a voltage of 125 V. However, the required electric voltage is prohibitive for actual applications. For this reason, the implementation of the magnetostrictive properties of ferrites have not been retained in this study. Thanks to a relative permittivity (εr) and a relative permeability (µr) both greater than one, MDM has been used these last few years as suitable materials for antenna miniaturization [7,8,9,10]. A DC biasing current generating a magnetic static field in the MDM is used to tune antenna’s frequency response. The problem using DC magnetic field comes up against the value of the fields intensity required for their implementation, due to the importance of the demagnetizing effects linked to the discontinuities of magnetization, which appear in particular on the surface of the material. It is established that these effects are weaker when the polycrystalline material has a toroidal shape, as the magnetic walls adopt the orthoradial symmetry [11]. The permeability is then easily modified by a magnetic field of the same symmetry, without any noticeable impact of demagnetizing effects. A fabricated antenna, using samples of polycrystalline MDM specifically designed to meet this objective is presented.
2. Materials and Methods
2.1. Antenna Design Description
The proposed electrically small frequency reconfigurable antenna is designed to work at VHF band starting from a geometry of an inverted-F antenna (IFA) as described in Figure 1. The IFA is a compact low-profile antenna proposed in the 1960s by King [12]. Its operating principle is based on a transmission line section producing a quarter-wave resonator, since it is short-circuited at one end and open at the other. Frequency agility of this antenna is studied by changing the properties of the short circuit with the use of MDM. Some miniaturization technics have been implemented to further reduce the size of this compact antenna.
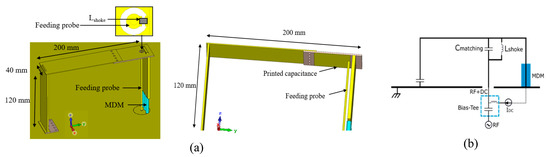
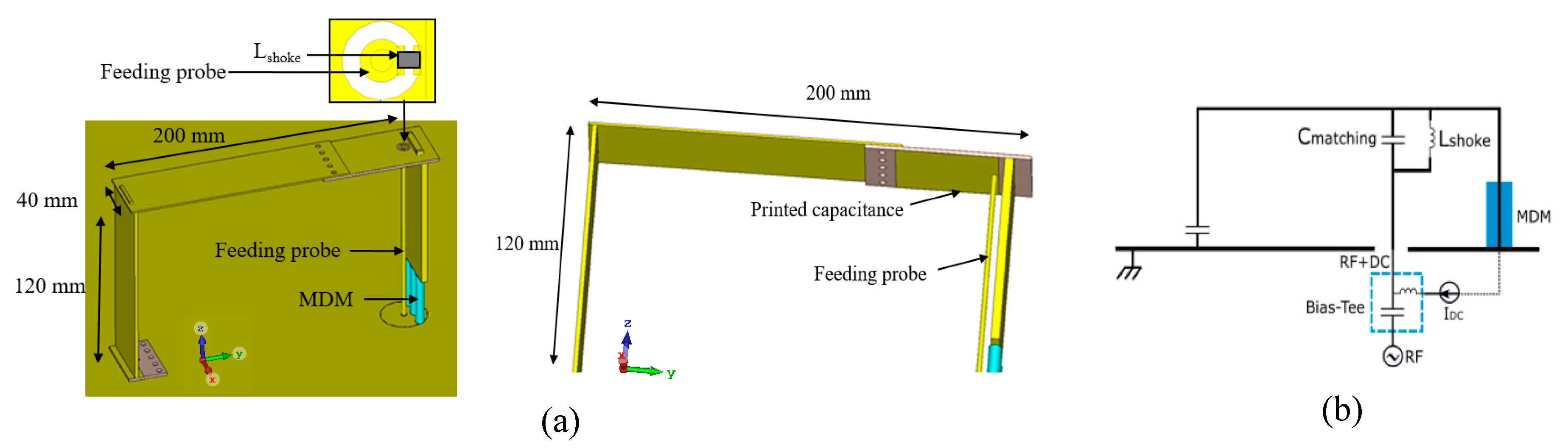
Figure 1.
(a) Antenna design and (b) schematic view of the antenna with the biasing circuit.
The developed antenna is composed of a conductive strip of 40 × 440 mm² (λ0/107 × λ0/10) above a circular ground plane, with a diameter of 1250 mm (~λ0/4). λ0 is the wavelength calculated at the resonance frequency of 70 MHz. The antenna height is 120 mm, which corresponds to λ0/36. Ground plane dimensions are chosen according to the targeted application, especially to meet aircraft reference tests condition. The left side of the conductor strip is bent, and incorporates a capacitive termination for antenna miniaturization issue. A feeding probe is connected to a metallic strip of 47 × 40 mm² (λ0/91 × λ0/107), printed on FR4 substrate (εr = 4.3, tan δe = 0.02). This metallic strip forms a metal-insulator-metal (MIM) capacitance of 31 pF with the top conductor of the antenna, assuring antenna matching to 50 Ω impedance at the frequency of interest.
On the other side, antenna’s strip is bent to be shorted to the ground plane using a vertical strip for upper part and three conductive wires for lower part. The three wires are loaded with the tunable MDM (blue cylinders). Three short-circuits are used instead of one following the work described in [13], due to material’s shape constraint. This previous work has shown that loading the antenna with MDM around its short circuits, where the currents are strong, is optimal toward miniaturization, because the antenna is more sensitive to magnetic material’s properties. The MDM loading strategy must respond to different constraints aimed to substantially miniaturize the antenna, by limiting its volume and weight for aeronautics application. It is interesting to note that the current control of loading MDM to ensure antenna’s frequency response tuning can be easily integrated into this antenna structure, which has short circuits. DC current is injected via the antenna feeding probe and flows through the short-circuit wires thanks to a RF block inductor of 0.8 µH connected at the strip. As shown in the schematic view, a bias-tee working below 100 MHz and limited to 5 A currents is used to introduce the DC current combined to RF feeding of the antenna. The designed antenna is electrically small with a k.a of 0.2 calculated at the resonance frequency. k is the wave number (k = 2π/λ) and a is the radius of the smallest sphere enclosing the antenna and its electrical image through the ground plane. According to the fundamental work proposed in [2], the definition of electrically small antennas follows the condition k.a < 0.5.
2.2. Structural and Main Electromagnetic Features of MDM Samples
The materials used for this application of small and frequency reconfigurable antenna are polycrystalline soft ferrites prepared by the Lab-STICC [14,15]. For confidentiality reasons, the presentation of the materials will not be detailed. They were obtained from chemically synthesized powders. These powders were placed in a mold, which gives a toroidal shape to the sample by means of uniaxial pressing. The sample was then subjected to a suitable heat treatment. We present here two samples, called S2 and S6, which differ both in their chemical compositions and in the applied heat treatments. Volume density is close to 90% for S6 and lies between 95% and 99% for S2.
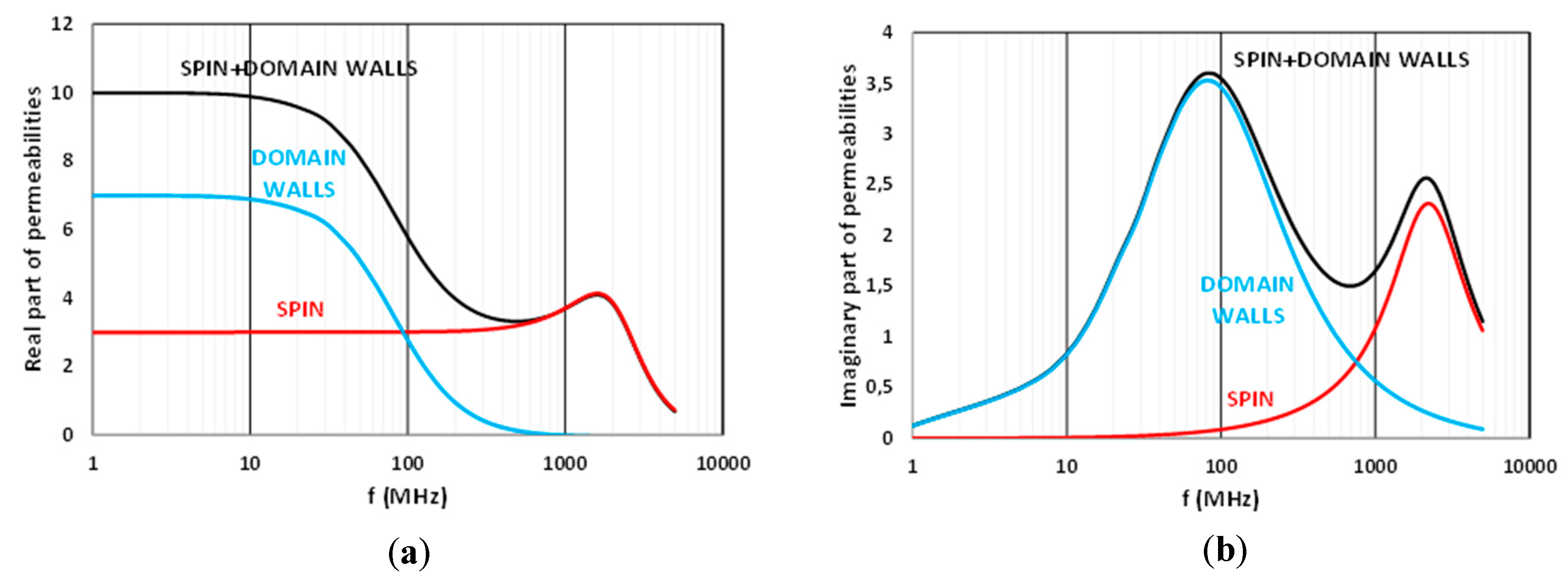
Generally speaking, the dynamic permeability of a polycrystalline material is the sum of two contributions, which are due (a) to magnetic walls displacements, and (b) to spin gyroresonance (Figure 2).
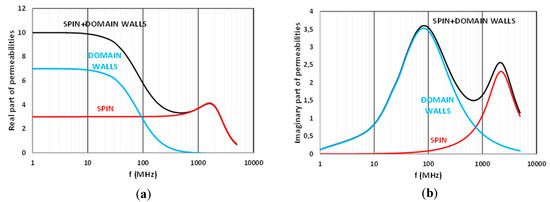
Figure 2.
Walls displacements and spin gyroresonance contributions to the complex permeability µ = µ’-jµ″ of a polycrystal of infinite size (a) Real part µ’ and (b) Imaginary part µ″.
Magnetic walls displacements phenomenon is very sensitive to the presence of a static magnetic field. With regard to the second contribution, in the general case, the spin resonance occurs in the effective field, which is the sum of the anisotropy field Ha and the applied field Hext. In the present study, Hext is much lower than Ha. With this hypothesis, and in contrast to the magnetic wall’s contribution, the spin resonance is insensitive to Hext. In the study presented here, the mobilization of the domain walls by a static field plays a key role. Moreover, in the frequent case where the material is of finite size, the permeability is also sensitive to demagnetizing effects. These are caused by discontinuities in the magnetizing flux, which can occur at the physical boundaries of the sample (shape effect), as well as at the grain level due to porosity (internal effects). These demagnetizing effects can be detrimental, because their presence requires, when permeability has to be changed, the application of a strong magnetic field proportional to the magnetization. As an example, the initial magnetic state of a soft ferrite depends on two parameters, which are: the magnetocrystalline anisotropy field and the demagnetizing field, this one is being related to the spontaneous magnetizing flux. Since the former intensity is lower that the latter one, it plays a much smaller role in the domain walls organization. Thus, while the magnetocrystalline anisotropy field is of the order of 300–800 Oe, the demagnetizing field related to the shape of the sample can reach 1300 Oe (in the case of a spherical sample).
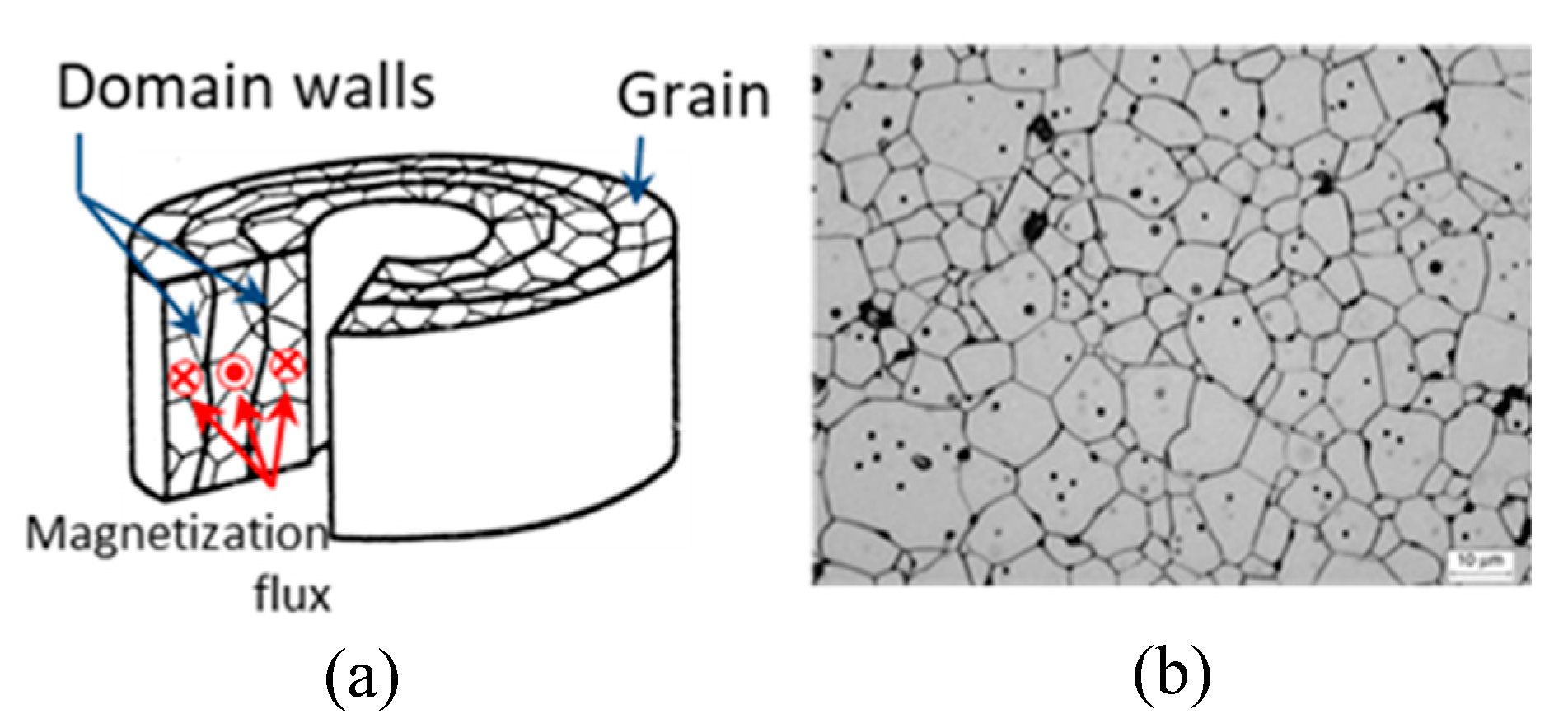
In ideal polycrystalline materials, the shape demagnetizing effects are minimized by the formation of magnetic walls showing orthoradial symmetry, which allow the closure of the magnetizing flux in the sample. This is the concept of the “magnetic torus” (Figure 3), developed by Globus [11]. The application of a static magnetic field of orthoradial symmetry leads to the displacement of the magnetic walls in the sample, thus varying its permeability. In addition, ferrimagnetic polycrystalline materials obtained by powder sintering usually show natural porosity (Figure 3).
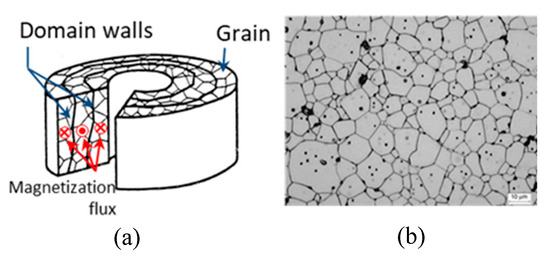
Figure 3.
(a) The concept of the magnetic torus. (b) General aspect of the microstructure of a polycrystalline ferrite, with intragranular and intergranular porosity.
The porosity acts as a brake in the displacement of the walls, as well as in the generation of internal demagnetizing effects. An example of internal demagnetizing effect is given in Figure 4, showing that the presence of a non-magnetic phase in a heterogeneous magnetic material leads to discontinuities of the magnetizing flux lines (areas framed in red), generating demagnetizing effects. Consequently, it significantly influences the magnetization processes by displacement of walls, and therefore permeability. Porosity is an adjustment parameter for permeability, which is therefore important to control as well as possible.

Figure 4.
Illustration of an internal demagnetizing mechanism. (Dark spheres represent magnetic particles, the non-magnetic phase is colored in grey). (Figure adapted from [16]).
There are usually two distinct contributions to porosity, and, thus, to internal demagnetizing effects, the proportions of which vary according to the firing temperature of the ceramic. These are: (i) intragranular porosity that consists of a multitude of small pores (Figure 3). This determines the movement of the walls on which it acts as a brake. Its influence is greatest on the small reversible wall movements (initial permeability). This porosity can be pushed back to the limits of grain boundaries during the material synthesis, by applying a higher firing temperature; (ii) intergranular porosity that is distributed in more or less large pores pushed back to the limits of the grains during their growth.
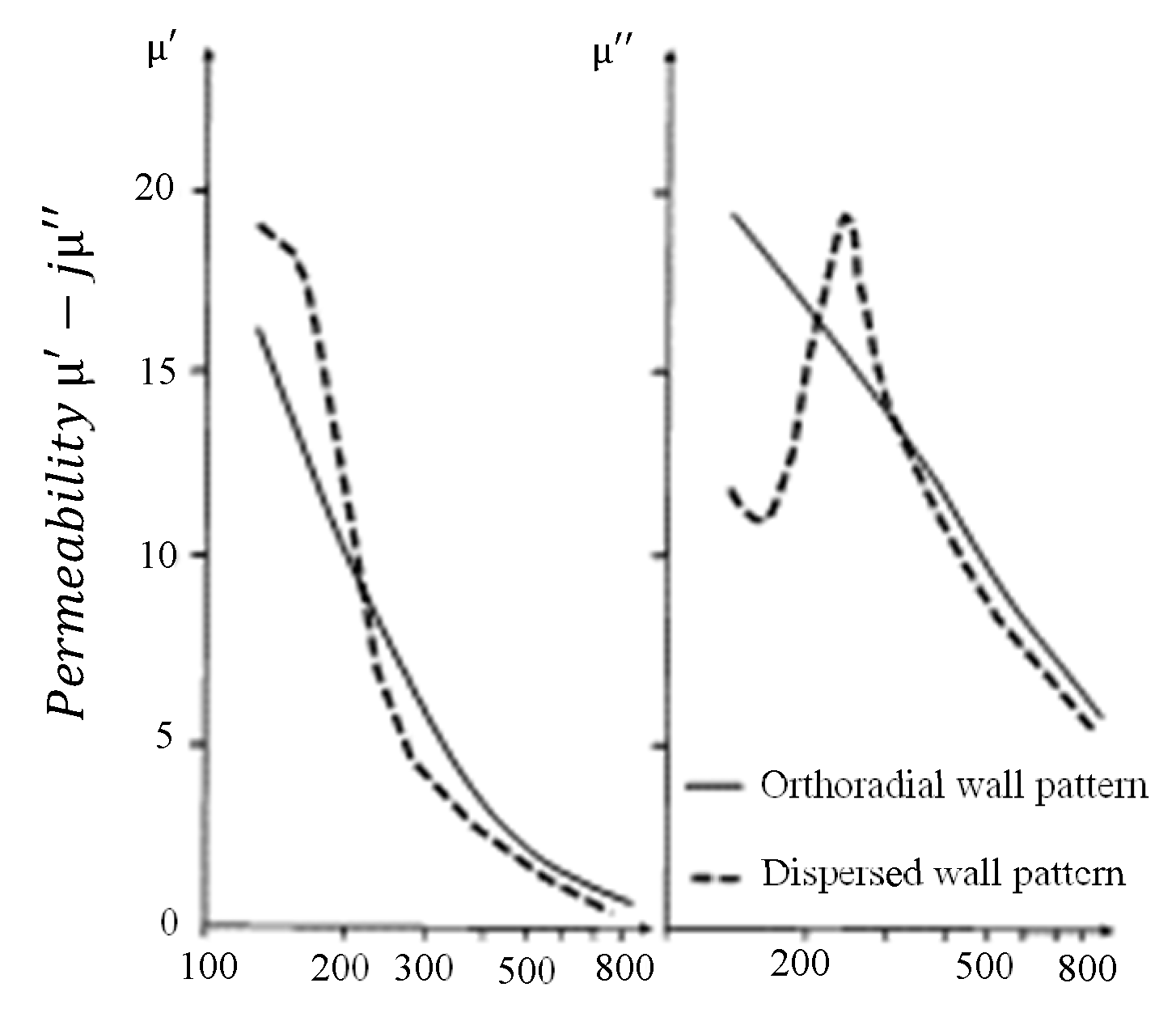
Finally, the dispersion of the walls with respect to the orthoradial symmetry, due to the presence of porosities, has a strong influence on the variation of permeability as a function of frequency (Figure 5). It was demonstrated in [17] that the permeability of a ferrite torus depends on whether it is non-defective or porous. The distribution of the walls is orthoradially symmetrical in the first case, while the walls are dispersed in the second case [17].
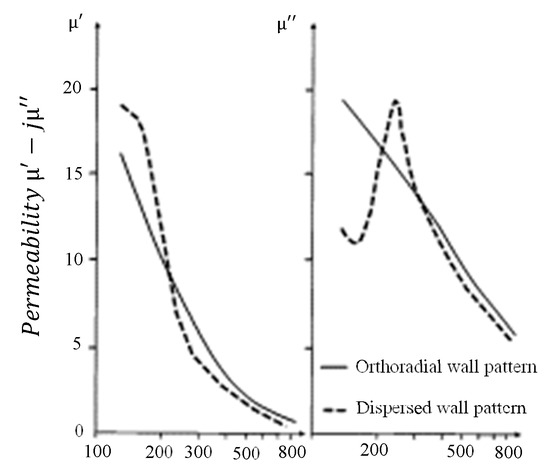
Figure 5.
The permeability of a ferrite torus depends on whether it is non-defective or porous. The related wall pattern is orthoradial in the first case, and dispersed in the second case (figure adapted from [17]).
3. Results
3.1. Measurements of Sample’s Permeability Dynamics as a Function of an Applied DC Magnetic Field
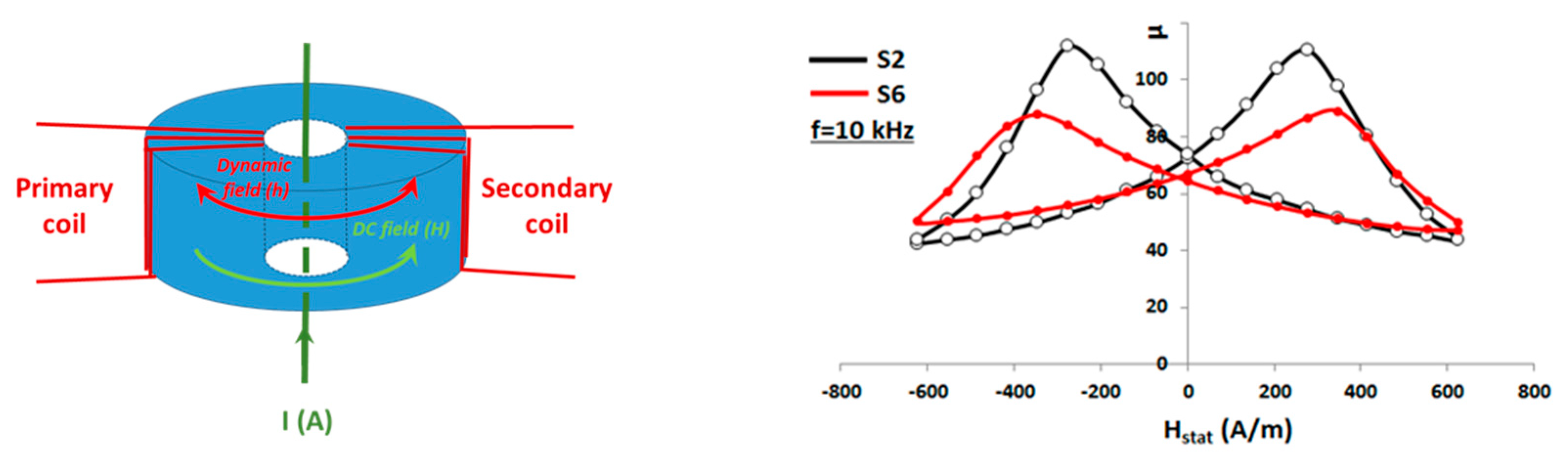
At first, the real part of the permeability of the toroidal samples was measured at f = 10 kHz, by the transformer method (Figure 6), using a hysteresis meter with lock-in amplifier. The maximum change in permeability obtained when the DC field is varied between zero and its maximum value is called the permeability dynamic Δµ. Orthoradial symmetry common to the polarization field H (generated by a control current I) and to the microwave field h respects the symmetry of the sample, thus avoiding the creation of demagnetizing effects other than those related to grain boundaries and porosity. The measurement results (Figure 6) show for samples S2 and S6 a dynamic Δµ close to 70 and 30, respectively, for a static field varying between 0 A/m and 526 A/m (mean value calculated over the volume of the sample), i.e., 6.6 Oe, corresponding to a maximum current of 9 A. However, these first results do not give any information on the imaginary µ″ part of the permeability and have to be confirmed in the working frequency band of the antenna.
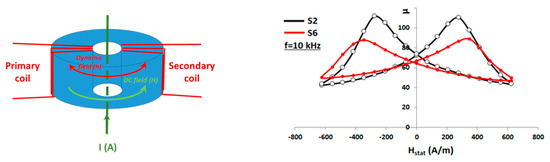
Figure 6.
The transformer method and the permeability dynamics of samples S2 and S6 measured at frequency f = 10 kHz.
Subsequently, the variation of permeability in the VHF frequency band under the action of a DC magnetic field controlled by a current limited to 5 A, was measured. The measurement set-up consists in a vectorial network analyzer (VNA), two ETL TEEBX 4013 bias tees (1 MHz–5430 MHz/up to 5 A and 48 V DC), an APC7 coaxial transmission line, a DC power supply and an Ampere meter, to control the static current travelling in the coaxial line. In this measurement cell, a static current travelling in the inner conductor generates a static magnetic field orthoradial to the toroid axis, thus, in the same direction than the dynamic magnetic field (Figure 7) [18].

Figure 7.
APC7 measurement cell loaded with a ferrite toroidal sample. Both DC and AC magnetic fields have orthoradial symmetry (only HDC is represented).
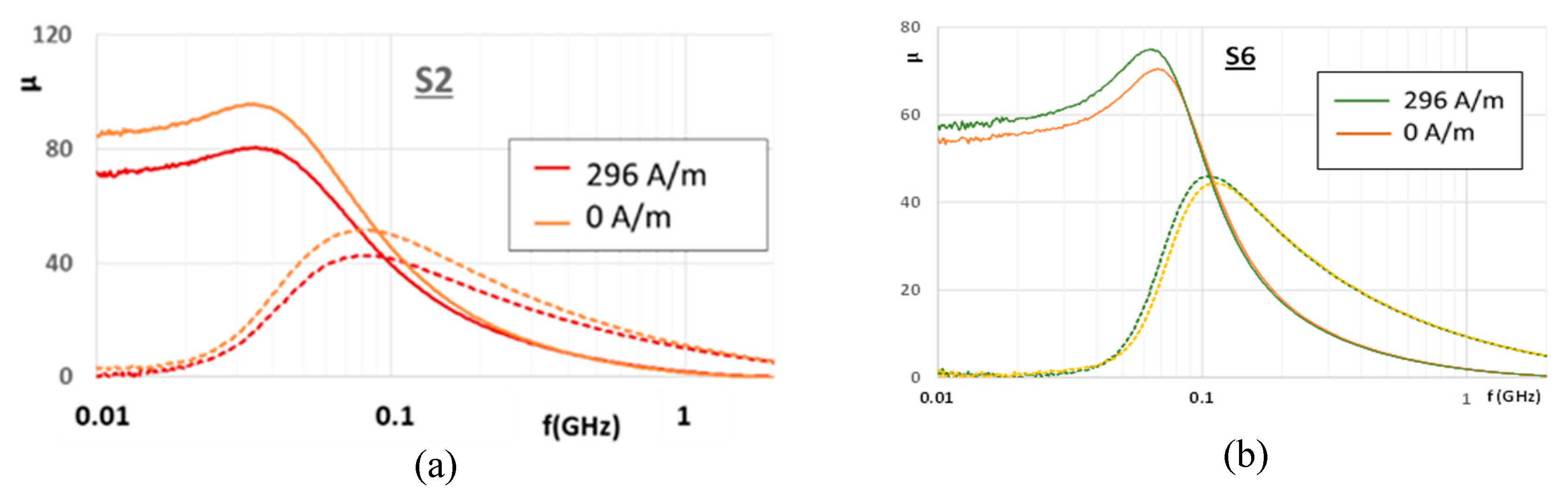
As in the transformer measurement method, the configuration of fields in this transmission line allows avoiding shape demagnetizing effects to occur. This specific measurement set-up was calibrated in order to take into account the variations of S-parameters as a function of applied DC current when no sample or a dielectric sample is characterized, and thus to ensure that measured variations come from a change of sample’s permeability. The results, obtained with a maximum DC current of 5 A which produced an average field strength equal to 296 A/m (i.e., 3.7 Oe, mean value calculated over the volume of the sample) are presented in Figure 8a,b. In the frequency range 10–80 MHz, the permittivity and the dielectric loss tangent remained almost constant. For S2 and S6 the following values (ε’, tgδε) were measured: (16, 0.025) for S2, (14.5, 0.03) for S6, which testified to the high electrical resistivity of the materials. These results confirm for both samples the existence of permeability dynamics in the VHF band (with relative variations equal to 14% for S2, and 7% for S6), which can be exploited to tune frequency response of the IFA antenna.
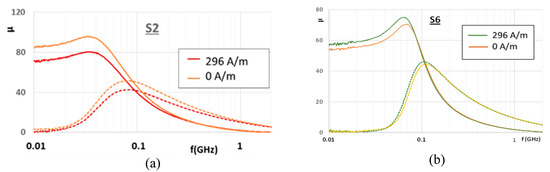
Figure 8.
Permeability variations of (a) S2 sample and (b) S6 sample as a function of the frequency of the HF field, for two intensities of the DC field (insert: the values of the averaged DC field over the sample, limited here to 3.7 Oe, i.e., 296 A/m.) Real and imaginary parts are full and dashed lines, respectively.
3.2. Frequency Agility Potential of IFA Loaded with S2 MDM
According to Figure 8, the S2 type MDM shows a better potential toward antenna miniaturization and frequency agility compared to S6 material, since it exhibits a higher permeability with a higher dynamic range of tunability in the frequency band of interest (10 MHz to 100 MHz). For these reasons, the S2 material has been selected for our application to load the IFA antenna in VHF band.
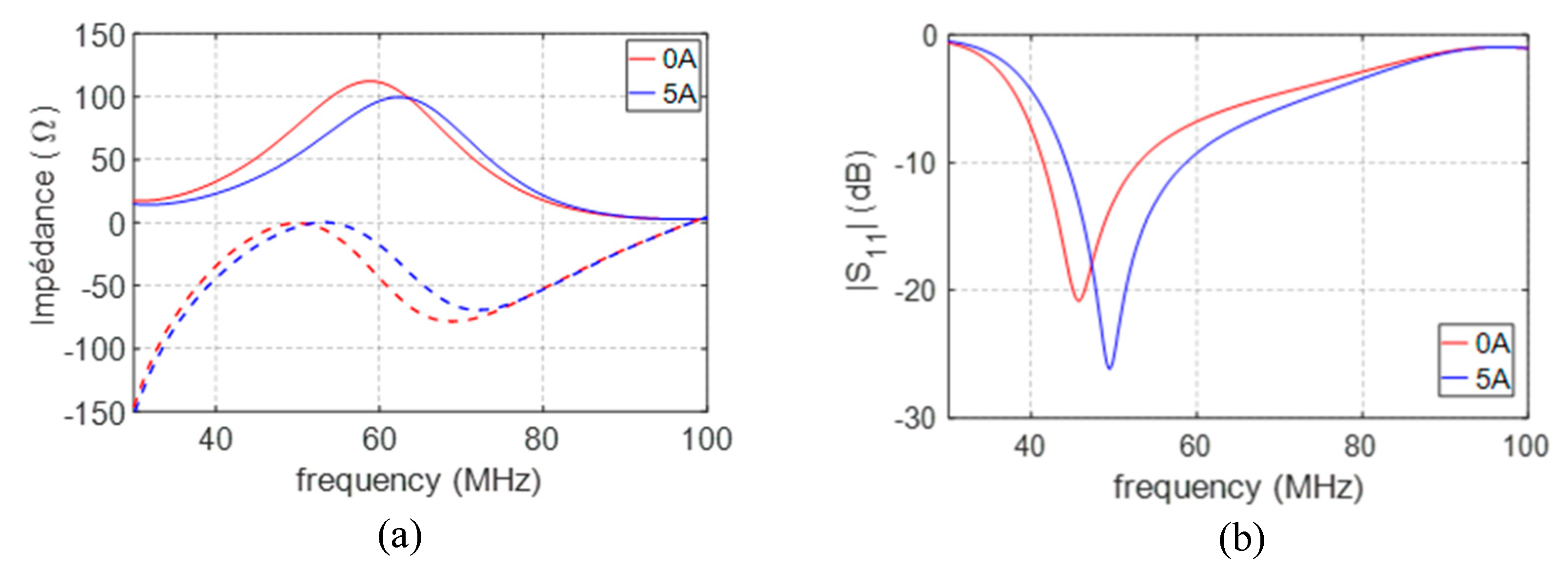
The input impedance of the antenna at the vicinity of resonance frequency and the 50 Ω reflection coefficient obtained with a full 3D electromagnetic (EM) simulator are respectively plotted in Figure 9a,b, with a biasing current varying from 0 A to 5 A. The frequency agility observed on the resonance frequency is 6%. The resonance frequency is considered where antenna’s real part impedance reaches a maximum amplitude. The antenna’s operation frequency, with an agility of 8.2%, achieves a frequency bandwidth of 26 MHz from 40 MHz to 66 MHz, with respect to −7 dB reflected power. The antenna’s operation frequency is defined at the minimum value of |S11|, with the lowest reflections at the input of the antenna. This frequency agility obtained with the MDM S2 is lower than 10%, mainly due to the limited quantity of MDM used for practical reasons. This first demonstration of agility presents a not wide enough frequency excursion for multi-frequency antennas applications, but it offers a suitable opportunity for our application looking for a fine tuning of electrically small antenna’s frequency response shifted with the close changing environment.
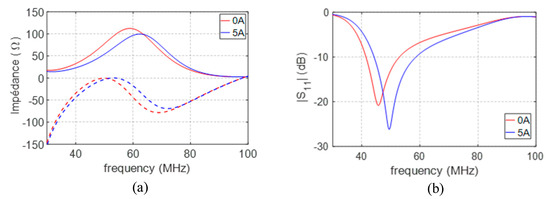
Figure 9.
The antenna’s frequency agility with a tuning current between 0 A and 5 A on (a) input impedance and (b) reflection coefficient.
It is important to notice that the frequency agility of the antenna is different from the dynamic range of tunability expected from the MDM. The link between the two is not direct, and can be explained qualitatively, since it depends on antenna topology (see electrical antenna model from [19]), and on the material’s location inside the antenna geometry, as shown in [10]. The MDM dynamic range Δµ is driven by the static current intensity flowing on shorting wires and the induced magnetic field in the material. The antenna’s frequency response is governed by the resonance conditions of the transmission line [19]. The MDM is present on a small portion of the antenna, and mainly modifies the short-circuit conditions of the antenna (its inductance). The increase of MDM permeability is synonymous with higher equivalent shorting post inductance, which then reduces the resonant frequency of the antenna, but with a dilution effect.
3.3. Antenna’s Frequency Agility Measurement
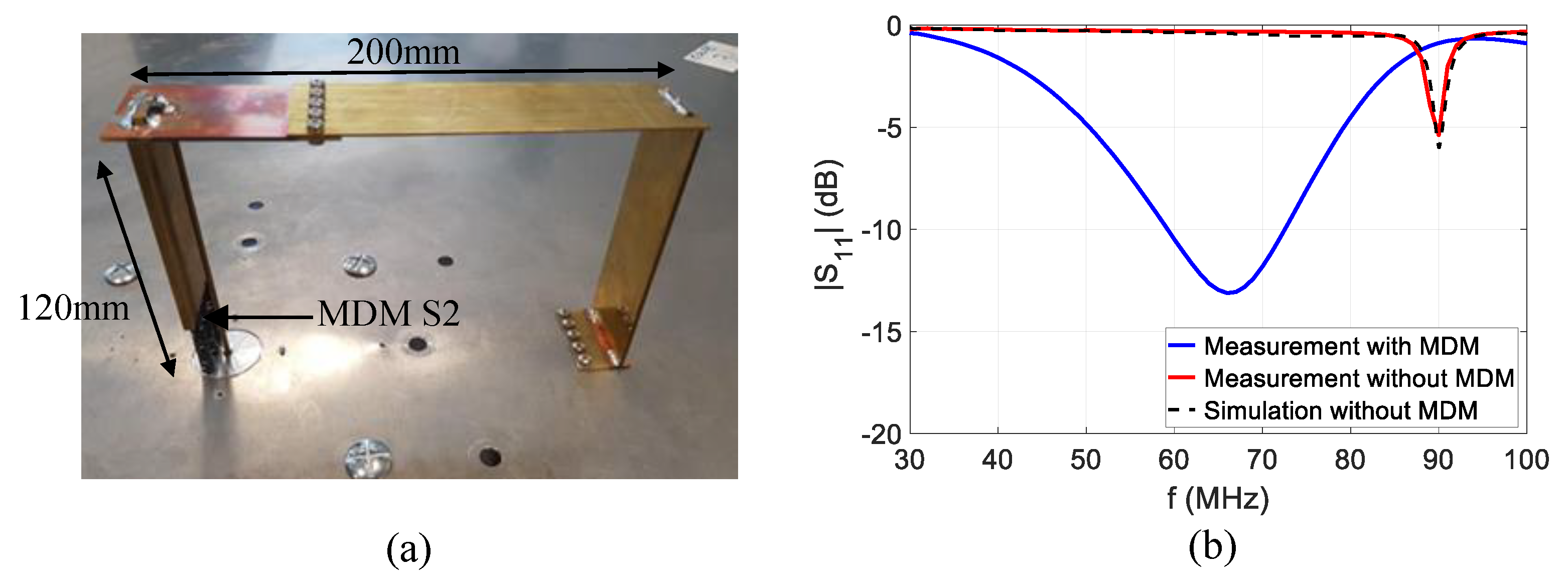
The fabricated IFA antenna loaded with S2 MDM is shown in Figure 10a. A preliminary measurement is carried out on the antenna without MDM in order to validate the design. The antenna’s frequency response obtained by simulation without MDM meets measurement results, as shown in Figure 10b. This preliminary result is important, as it leads to avoid any interrogation about antenna design during agility characterization with the material. A comparison between the antenna’s operation frequency measurement with and without MDM is also plotted on Figure 10b. This figure shows that the use of MDM to load the IFA antenna leads to a miniaturization factor of 27%, as observed on the operation frequency shift between 90 MHz (without MDM) and 66 MHz (with MDM-0A).
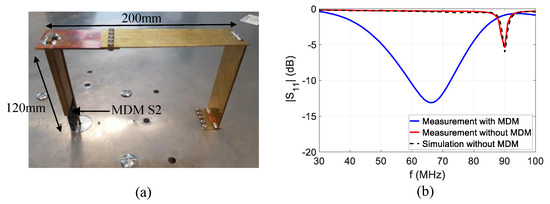
Figure 10.
(a) Fabricated inverted-F antenna (IFA) antenna loaded with magneto-dielectric material (MDM) S2, (b) measurement of the resonance frequency shift with and without MDM.
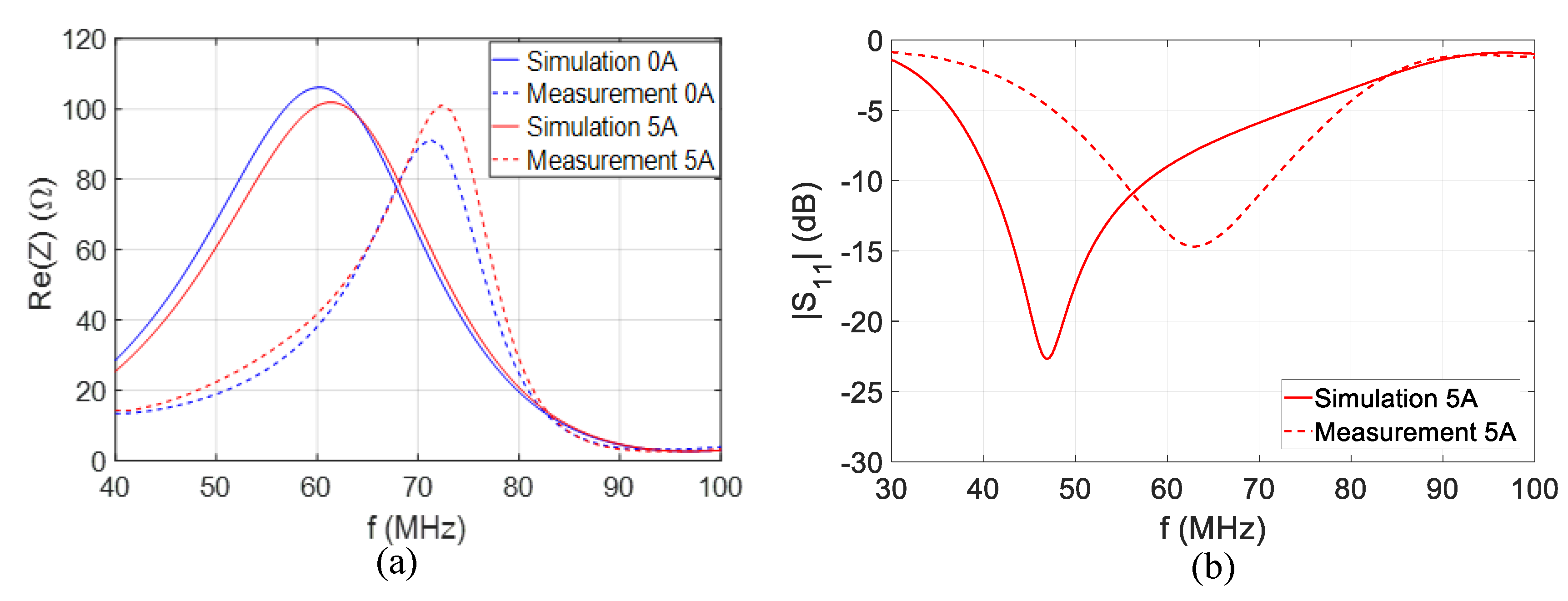
The measurement results of the impedance and operation frequency of IFA antenna loaded with S2 material are compared to the simulations with the same biasing condition, and are plotted in Figure 11a,b, respectively.
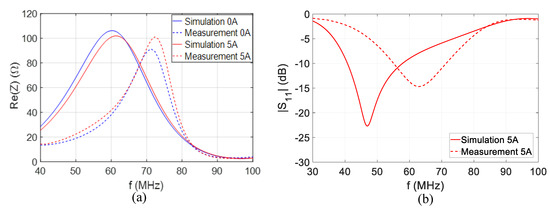
Figure 11.
(a) Real part of impedance measurement and simulation comparison in the same biasing condition, and (b) simulated and measured antenna operation frequencies with 5 A bias current.
As shown in Figure 10a, the measured frequency agility is about 2% around 75 MHz. This frequency agility is lower than the values of 6% expected from the EM simulations (Figure 9). This difference is related to the experimental conditions using a bias tee supporting currents limited to 5 A. As a result, the maximum current biasing MDM on each of three short-circuit is 1.67 A for the experimentations. In the simulation (Figure 9), the maximum potential of agility has been considered with 5 A on each antenna’s short-circuit (the MDM has been designed to provide maximum tunability with this DC current value). The comparison of antenna’s real part input impedance between measurement and simulation considering the 5 A biasing current split is plotted in Figure 10b. The frequency agility obtained in simulations considering the limited current measurement conditions is 2.5%, which is comparable to measurement results. These results confirm the frequency agility of the MDM S2 and its decent model of permeability dynamics used in simulation tools and extracted from material characterization [18]. Nevertheless, a frequency shift of 19% is observed, considering impedance measurement and simulation results at a biasing current of 0 A (Figure 11a). The same phenomenon is observed in Figure 11b, which shows a frequency shift of 26% on the antenna’s operation frequencies, with a biasing current of 5 A. This difference is probably due to MDM model inaccuracy in terms of permittivity and permeability properties, which can be readjusted in the simulator, in order to fit with measurement results.
3.4. Measurement Results of IFA’s Radiation Properties Loaded with S2 MDM
Radiation properties of the fabricated IFA loaded with MDM S2 has been characterized in VHF anechoic room at CEA-Leti. Two orthogonal cut planes have been considered for the measurement of antenna’s radiation pattern (Figure 12a,b). Simulated and measured gain patterns in H plane and E plane are plotted at their respective resonance frequencies 62 MHz and 72 MHz, for a biasing current of 0 A in Figure 12c,d. Given the limited experimental frequency agility of the antenna, gain patterns are not plotted for other biasing currents as similar results are obtained. The gain measurement level has appeared higher than the simulated one and possible uncertainties regarding the material’s magnetic losses have been readjusted in a simulation to the value of tan δm = 0.17 (instead of 0.65 [18]), in order to fit the measured radiated field level of the antenna.
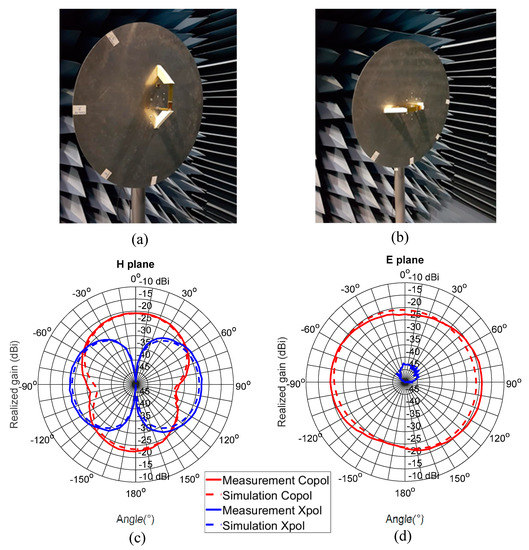
Figure 12.
Two cut planes considered for radiation pattern measurement (a) H plane illustration, (b) E plane illustration, (c) antenna gain patterns in the H plane and (d) gain patterns in the E plane.
Figure 12c,d show a good agreement of antenna gain patterns between the simulation and measurement with a maximum gain of −20 dBi. This low value of gain is partially impacted by the high value of magnetic losses of the MDM. Nevertheless, this low gain value associated with the bandwidth (quality factor) is quite in accordance with fundamental limits of electrically small antenna (k.a = 0.2) [2].
4. Conclusions
This work has demonstrated the frequency agility of a miniaturized IFA, thanks to a particular loading technique using a specific tunable magneto dielectric material S2. The fabricated IFA has been measured in VHF band achieving a frequency agility of 2% around 70 MHz, in agreement with the simulation results. Improving the biasing circuit, the model and quantity of the used material will offer a better potential for antenna frequency tunability in VHF band.
5. Patents
The deposit of an international patent describing the chemical process of a reconfigurable magneto-dielectric material fabrication for tunable antenna applications has been undertaken in 2020 (in progress).
Author Contributions
All of the authors have contributed substantially to the work reported. L.B. has contributed to the writing of all the paragraphs dealing with antenna application and more generally to the review and editing of this research article. He has also contributed to the conceptualization, design, analysis and measurement of the antenna loaded with the MDM. J.-L.M. has contributed to the writing and reviewing of the paragraphs dealing with the materials. He also contributed with the material conceptualization and fabrication. A.C. and V.L. has contributed to the review of the article with a scientific contribution with material measurement and the definition of its model. C.D. has supervised the research project supporting the work reported in this article. He has a major contribution in the funding acquisition and contributed to the conceptualization, methodology and review of the work. All authors have read and agreed to the published version of the manuscript.
Funding
This research work is partially funded by public grant overseen by the French National Research Agency (ANR-15-CE24-0030, MISTRAL project).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chu, L.J. Physical limitations of omni-directional antennas. J. Appl. Phys. 1948, 19, 1163–1175. [Google Scholar] [CrossRef]
- Wheeler, H.A. Fundamental limitations of small antennas. Proc. IRE 1947, 35, 1479–1484. [Google Scholar] [CrossRef]
- Harrington, R.F. Effect of antenna size on gain, bandwidth, and efficiency. J. Res. Natl. Bur. Stand. 1960, 64D, 1–12. [Google Scholar] [CrossRef]
- Yaghjian, A.D.; Best, S.T. Impedance, bandwidth, and Q of antennas. IEEE Trans. Antennas Propag. 2005, AP-53, 1298–1324. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, C.; Pan, H.K.; Fathy, A.E.; Nair, V.K. Frequency-Reconfigurable Antennas for Multiradio Wireless Platforms. IEEE Microw. Mag. 2009, 10, 66–83. [Google Scholar] [CrossRef]
- Laur, V.; Queffelec, P.; Rasoanoavy, F.; Lebedev, G.; Viala, B.; Pham, M.T. Microwave Magnetoelectric Couplings in FeCoB/Piezoelectric Bilayers. IEEE Trans. Mag. 2013, 49, 1060–1063. [Google Scholar] [CrossRef]
- Niamien, C.; Collardey, S.; Sharaiha, A.; Mahdjoubi, K. Compact Expressions for Efficiency and Bandwidth of Patch Antennas Over Lossy Magneto-Dielectric Materials. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 63–66. [Google Scholar] [CrossRef]
- Louzir, A.; Minard, P.; Pintos, J. Parametric study on the use of magneto-dielectric materials for antenna miniaturization. In Proceedings of the 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada, 11–17 July 2010; 2010. [Google Scholar] [CrossRef]
- Kabalan, A.; Sharaiha, A.; Tarot, A.C.; Mattei, J.L.; Souriou, D.; Queffelec, P. Impact of magneto-dielectric materials on the miniaturization of UWB monopole antennas. In Proceedings of the 2018 International Workshop on Antenna Technology (iWAT), Shanghai, China, 5–7 March 2018. [Google Scholar]
- Batel, L.; Pintos, J.-F.; Delaveaud, C. Design of a monopolar wire-plate antenna loaded with magneto-dielectric material. Eucap 2017. [Google Scholar] [CrossRef]
- Globus, A. Universal hysteresis loop for soft ferrimagnetic polycristals. Physics B 1977, 86, 943–944. [Google Scholar] [CrossRef]
- King, R.; Harrison, C.; Denton, D. Transmission-line missile antennas. IRE Trans. Antennas Propag. 1960, 8, 88–90. [Google Scholar] [CrossRef]
- Batel, L.; Delaveaud, C.; Pintos, J.F. Miniaturization of a Monopolar Wire-Plate Antenna Using Magneto-Dielectric Material. In Proceedings of the 2019 IEEE International Workshop on Antenna Technology (iWAT), Miami, FL, USA, 3–6 March 2019; pp. 91–94. [Google Scholar] [CrossRef]
- Mattei, J.-L.; Le Guen, E.; Chevalier, A.; Tarot, A.C. Experimental determination of magnetocrystalline anisotropy constants and saturation magnetostriction constants of NiZn and NiZnCo ferrites intended to be used for natennas miniaturization. J. Magn. Magn. Mater. 2015, 374. [Google Scholar] [CrossRef]
- Mattei, J.-L.; Souriou, D.; Chevalier, A. Magnetic and dielectric properties in the UHF frequency band of half-dense Ni-Zn-Co ferrites ceramics with Fe-excess and Fe-deficiency. J. Magn. Magn. Mater. 2017, 447. [Google Scholar] [CrossRef]
- Mattei, J.-L.; Le Floc’h, M. Percolative behaviour and demagnetizing effects in disordered heterostructures. J. Magn. Magn. Mater. 2003, 257, 335–345. [Google Scholar] [CrossRef]
- Le Floc’h, M.; Globus, A. Effects of perpendicular stresses on the magnetization processes of polycrystalline magnetic materials. J. Appl. Phys. 1987. [Google Scholar] [CrossRef]
- Doumouya, V.; Kabalan, A.; Chevalier, A.; Mattei, J.-L.; Tarot, A.-C.; Delaveaud, C.; Sharahia, A.; Laur, V. Characterization of ferrite tunability at microwave frequencies: Application to VHF tunable antennas. In Proceedings of the 2019 IEEE Asia-Pacific Microwave Conference (APMC), Singapore, 10–13 December 2019. [Google Scholar]
- Berro, R.; Bories, S.; Delaveaud, C. Transmission Line Model For Lossy Inverted F Antenna Miniaturization. In Proceedings of the 2019 International Conference on Electromagnetics in Advanced Applications (ICEAA), Granada, Spain, 9–13 September 2019; pp. 0797–0802. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).