Structural, Optical, Magnetic and Electrical Properties of Sputtered ZnO and ZnO:Fe Thin Films: The Role of Deposition Power
Abstract
:1. Introduction
- simultaneous co-sputtering from two targets (ZO and Fe) [17];
- radio-frequency (RF) magnetron sputtering.
2. Materials and Methods
3. Results
3.1. Elemental Analysis
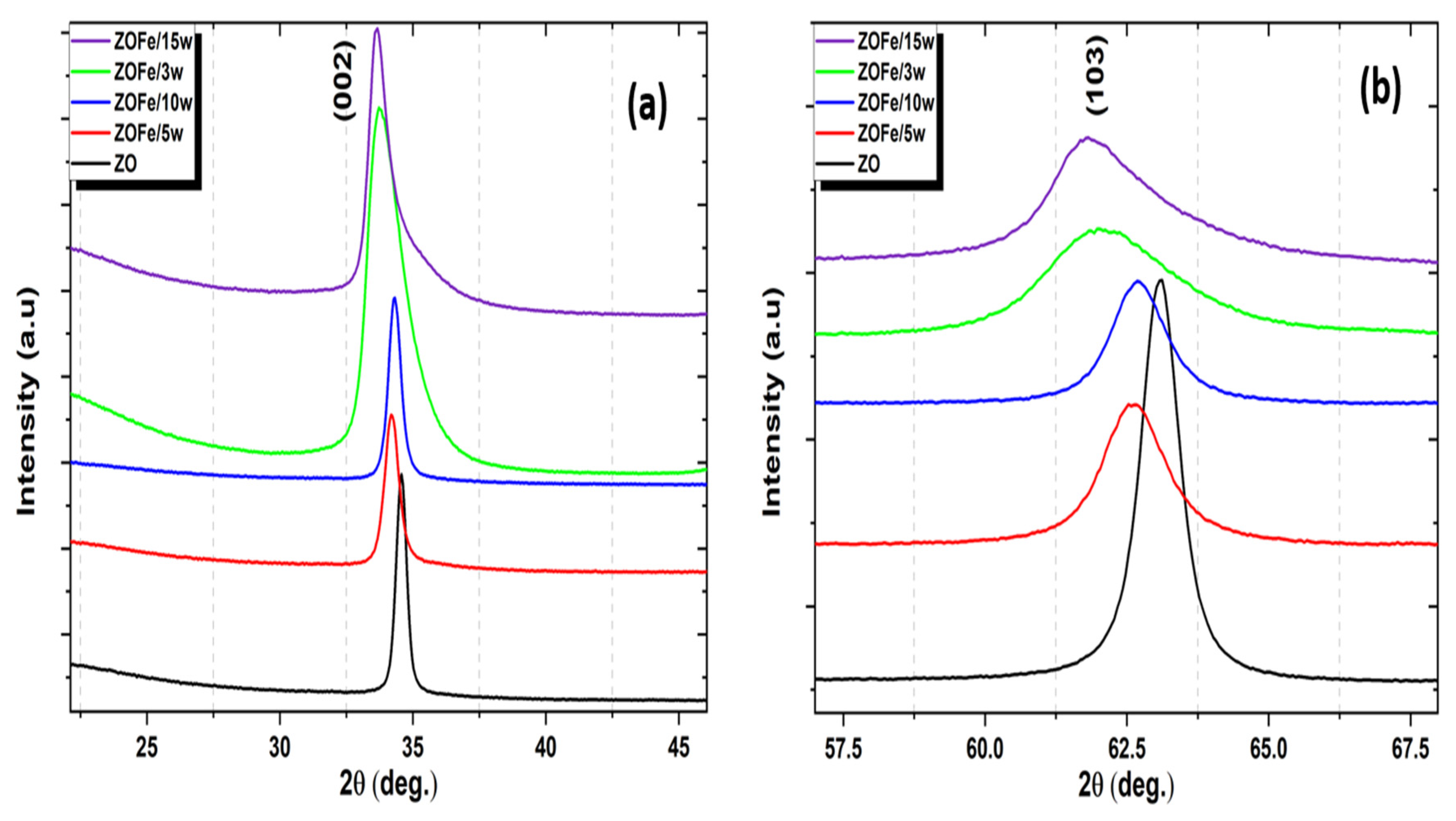
3.2. GIXRD Analysis
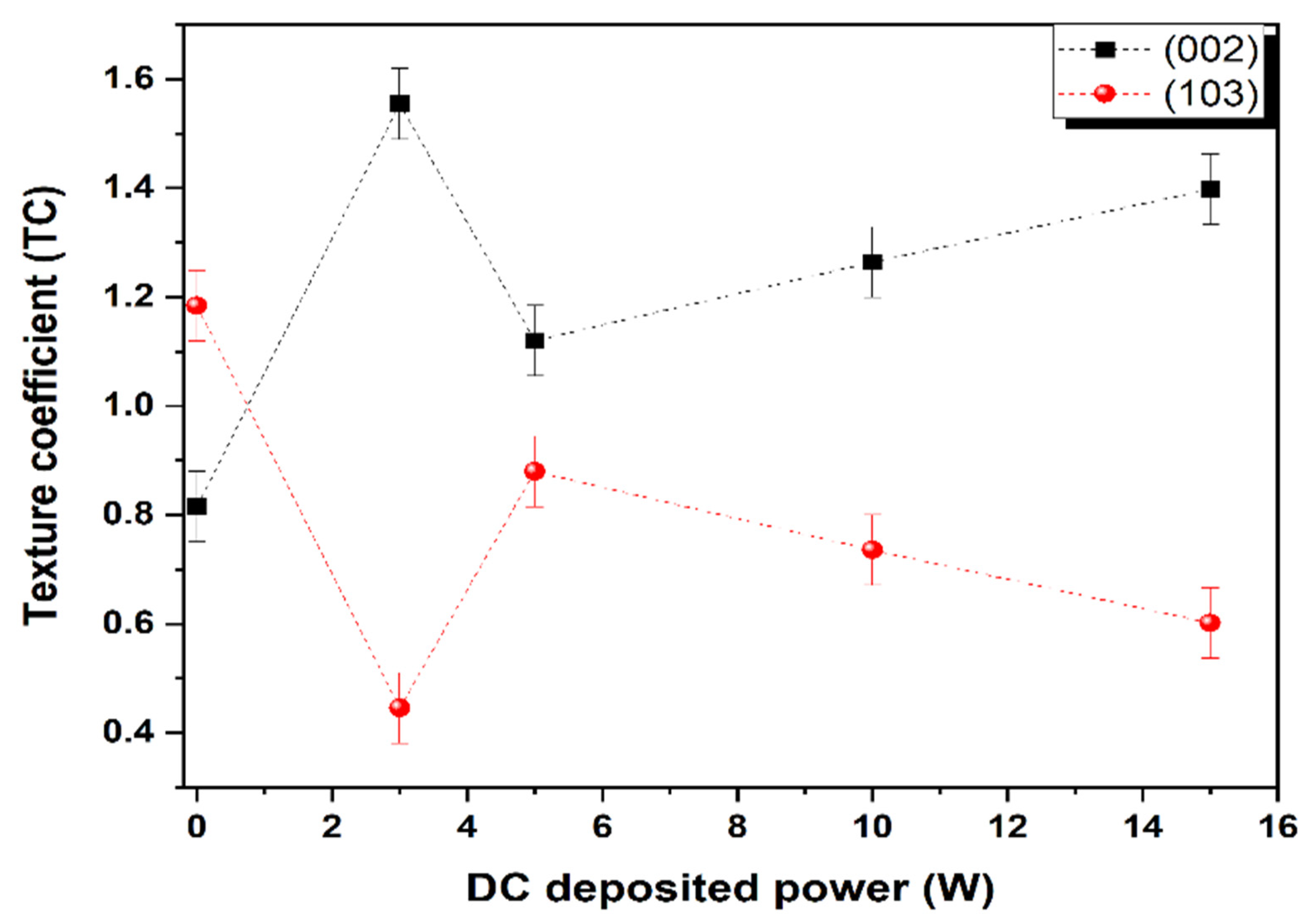
3.3. Microstructural Analysis
3.4. Optical Properties
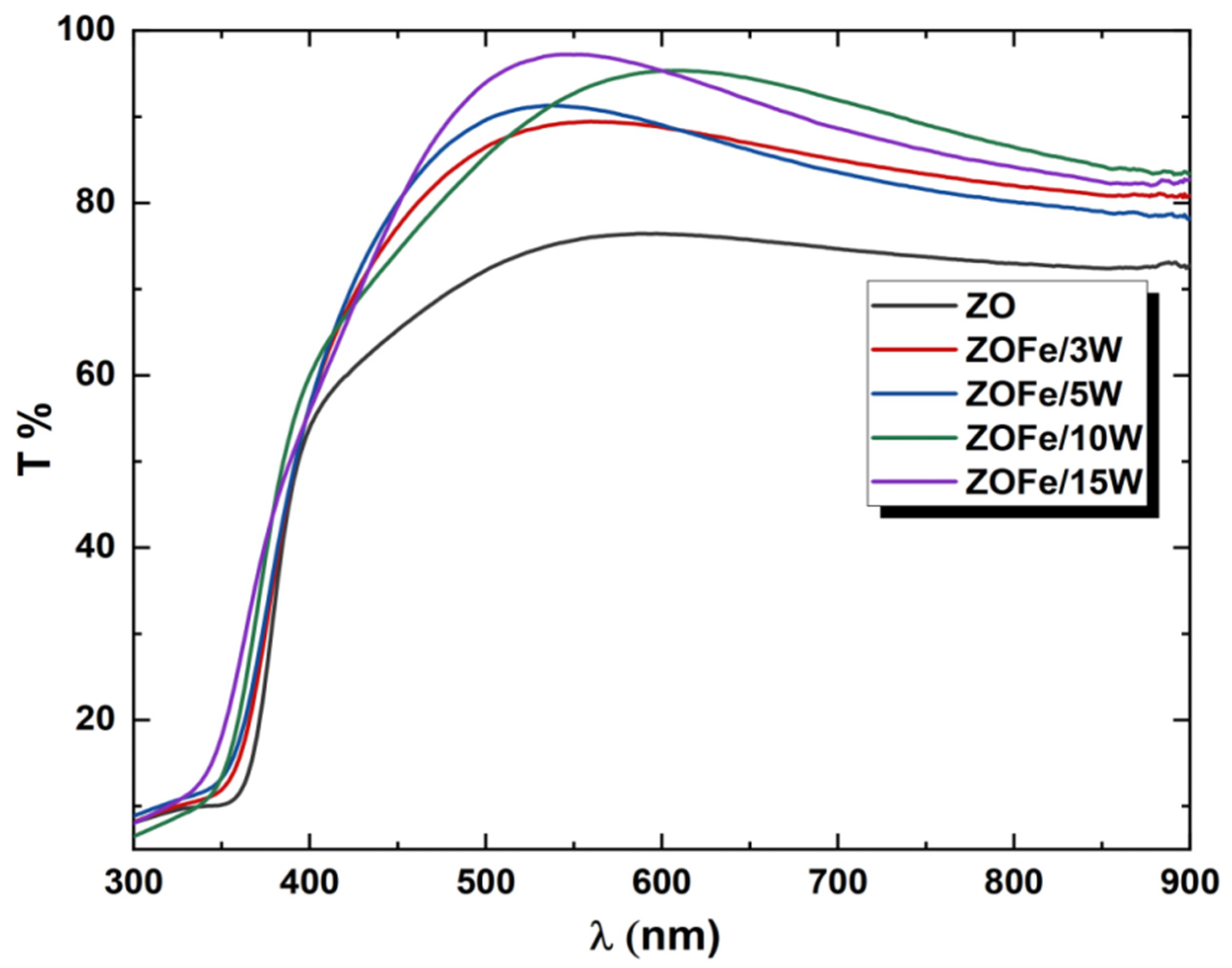
3.4.1. Transmittance Spectra
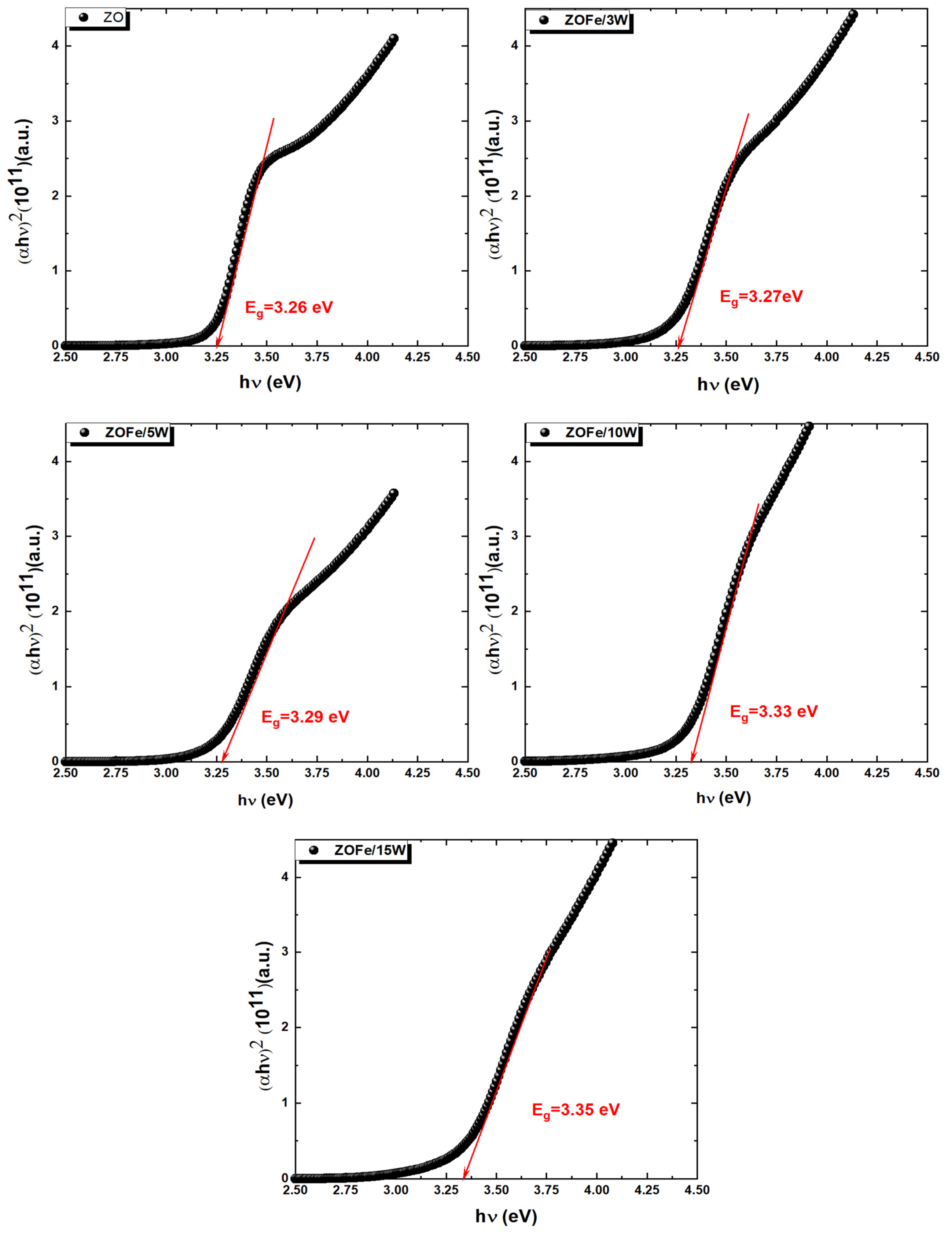
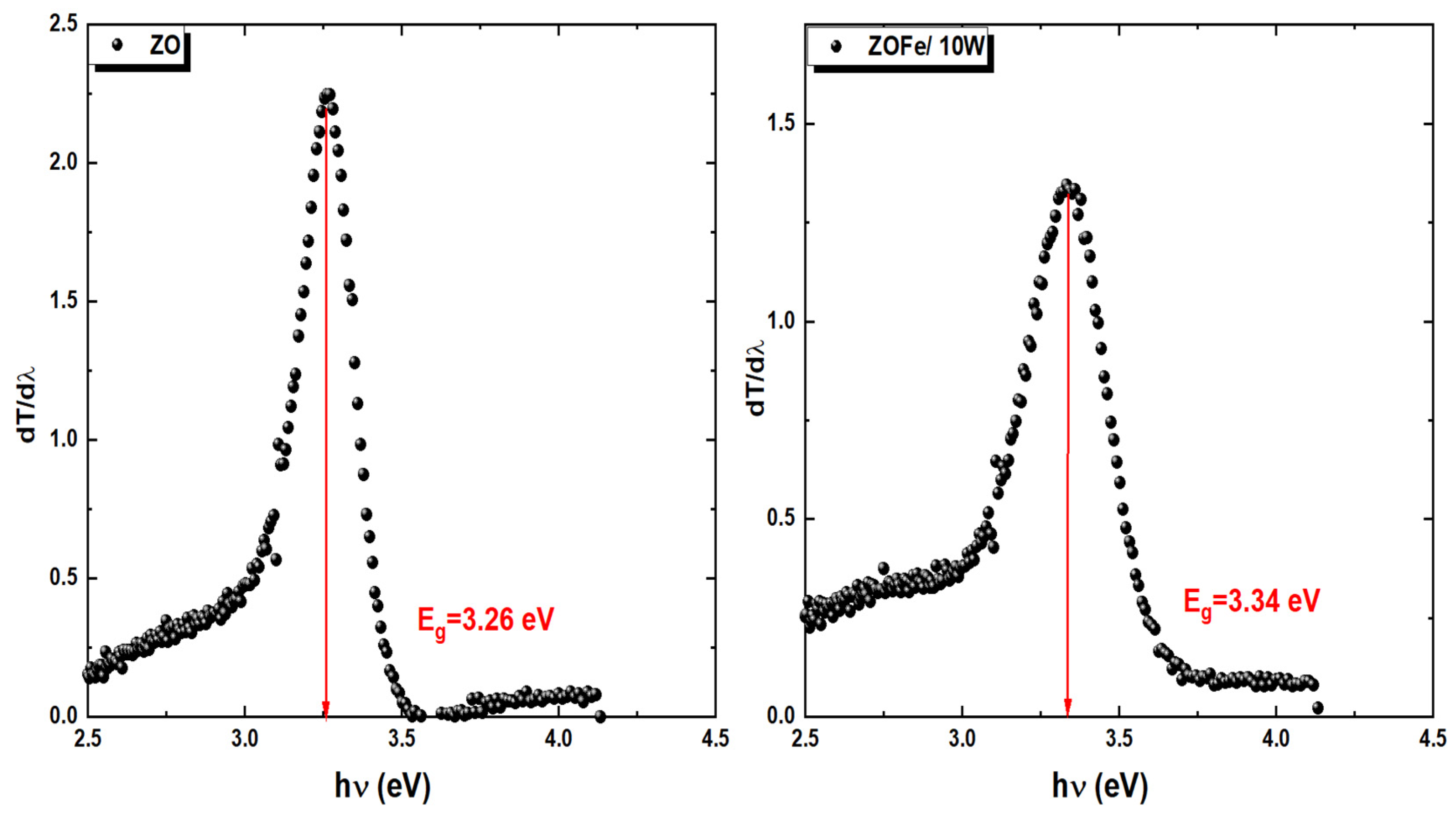
3.4.2. Optical Band Gap
- (A)
- Tauc method:
- (B)
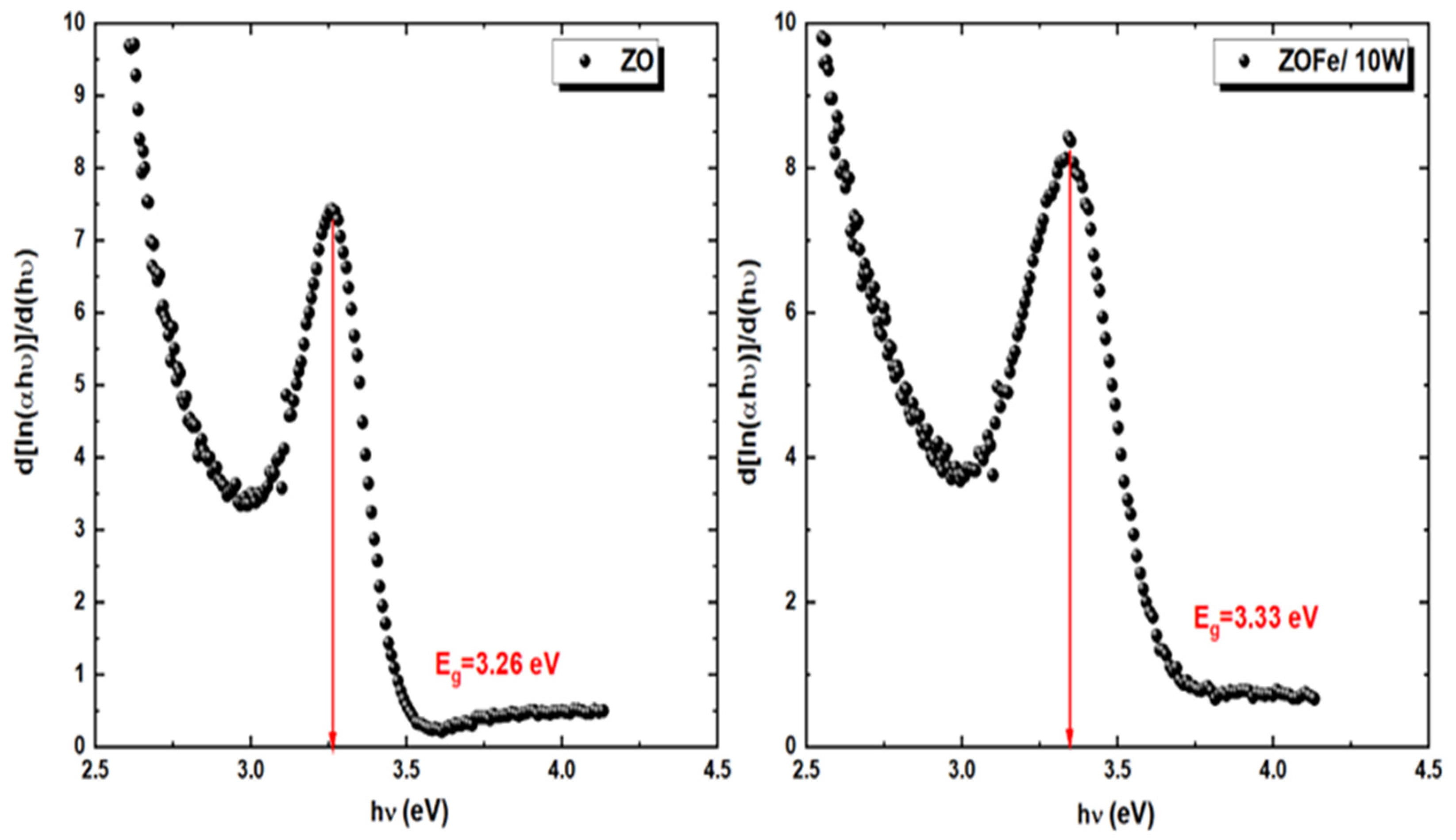
- The derivative of transmittance (T) against photon energy (hν)
- (C)
- The derivative of transmittance (T) against wavelength (λ)
- (D)
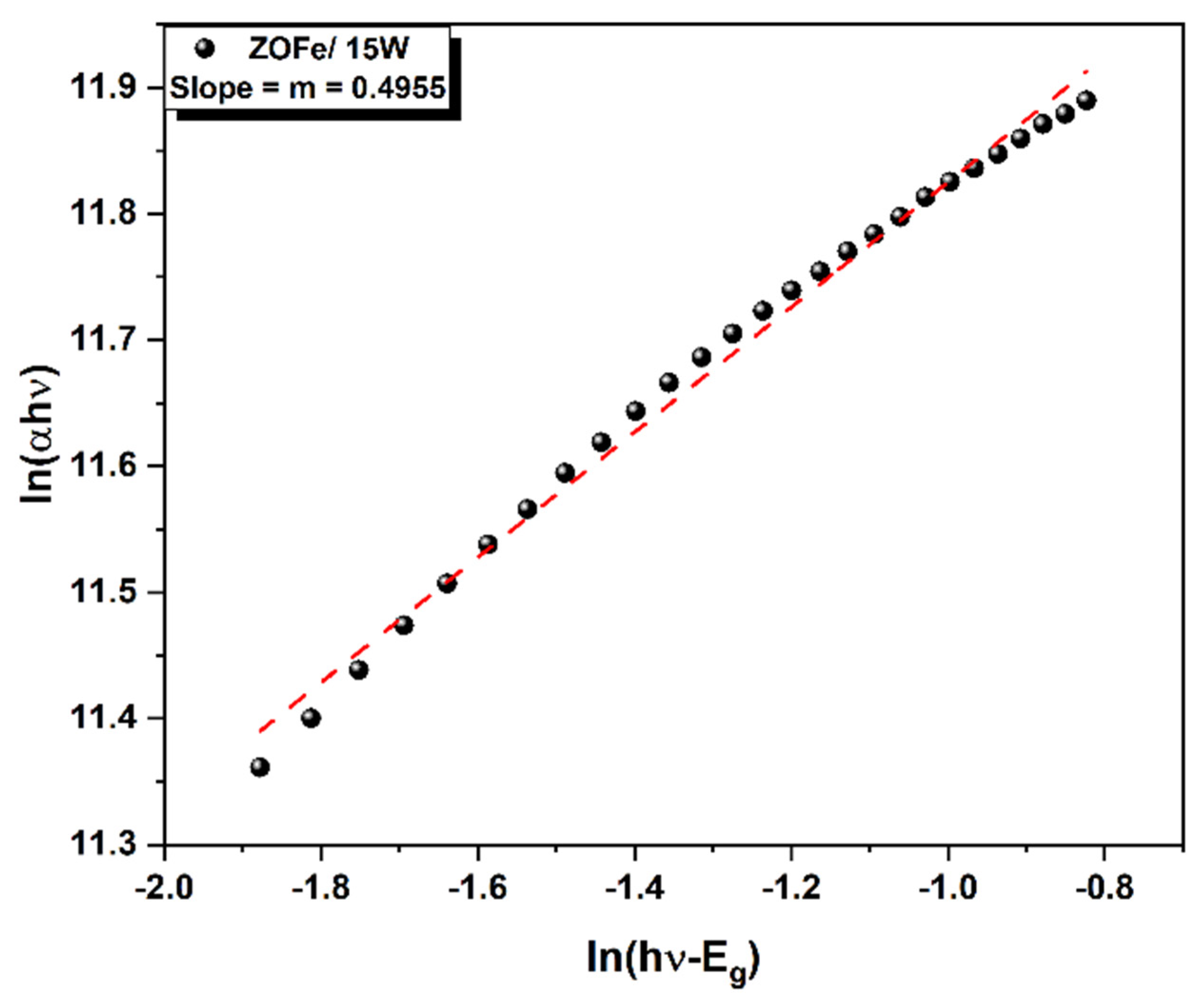
- Logarithmic derivative (LD) method:
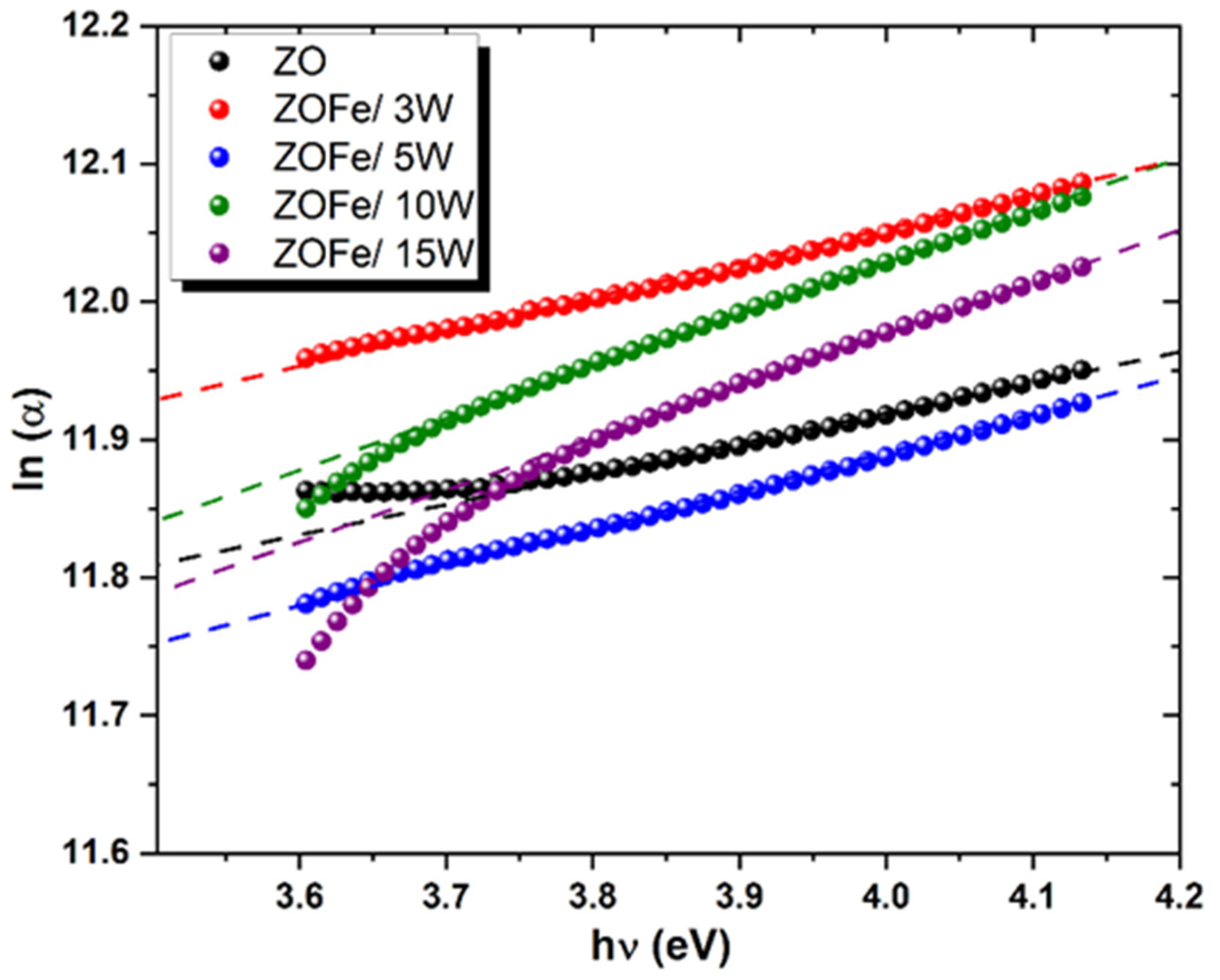
3.4.3. Urbach Energy
3.4.4. Refractive Index
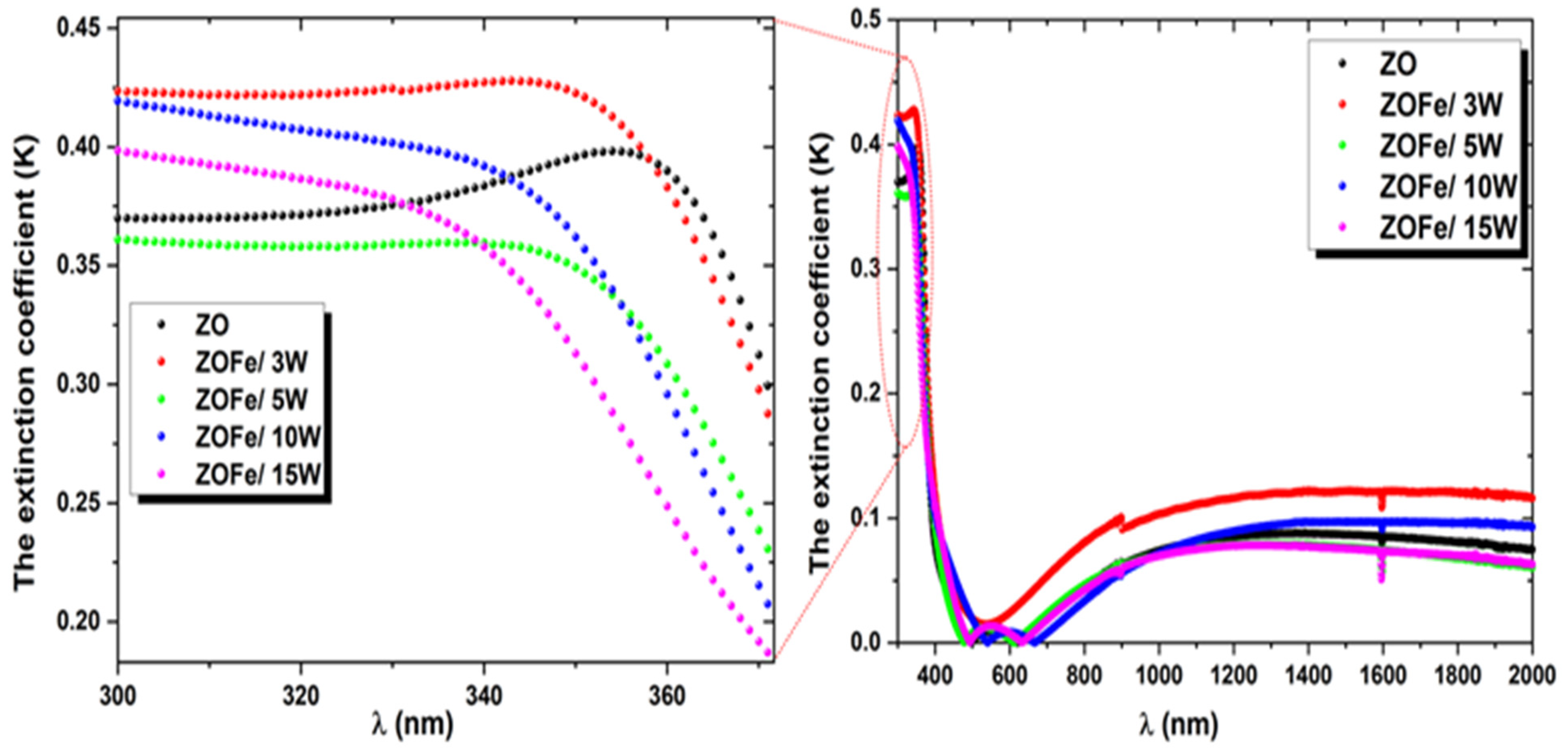
3.4.5. The Extinction Coefficient
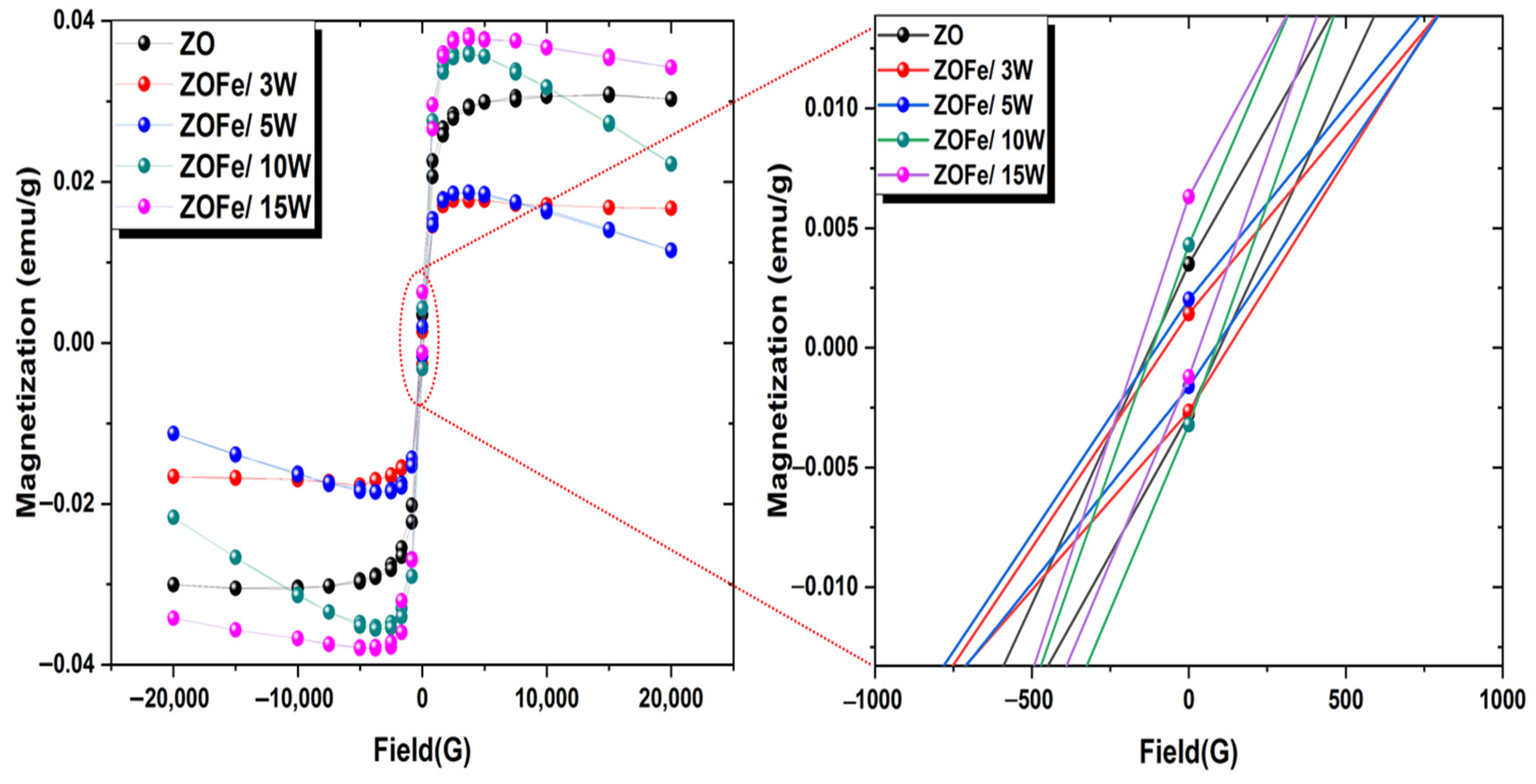
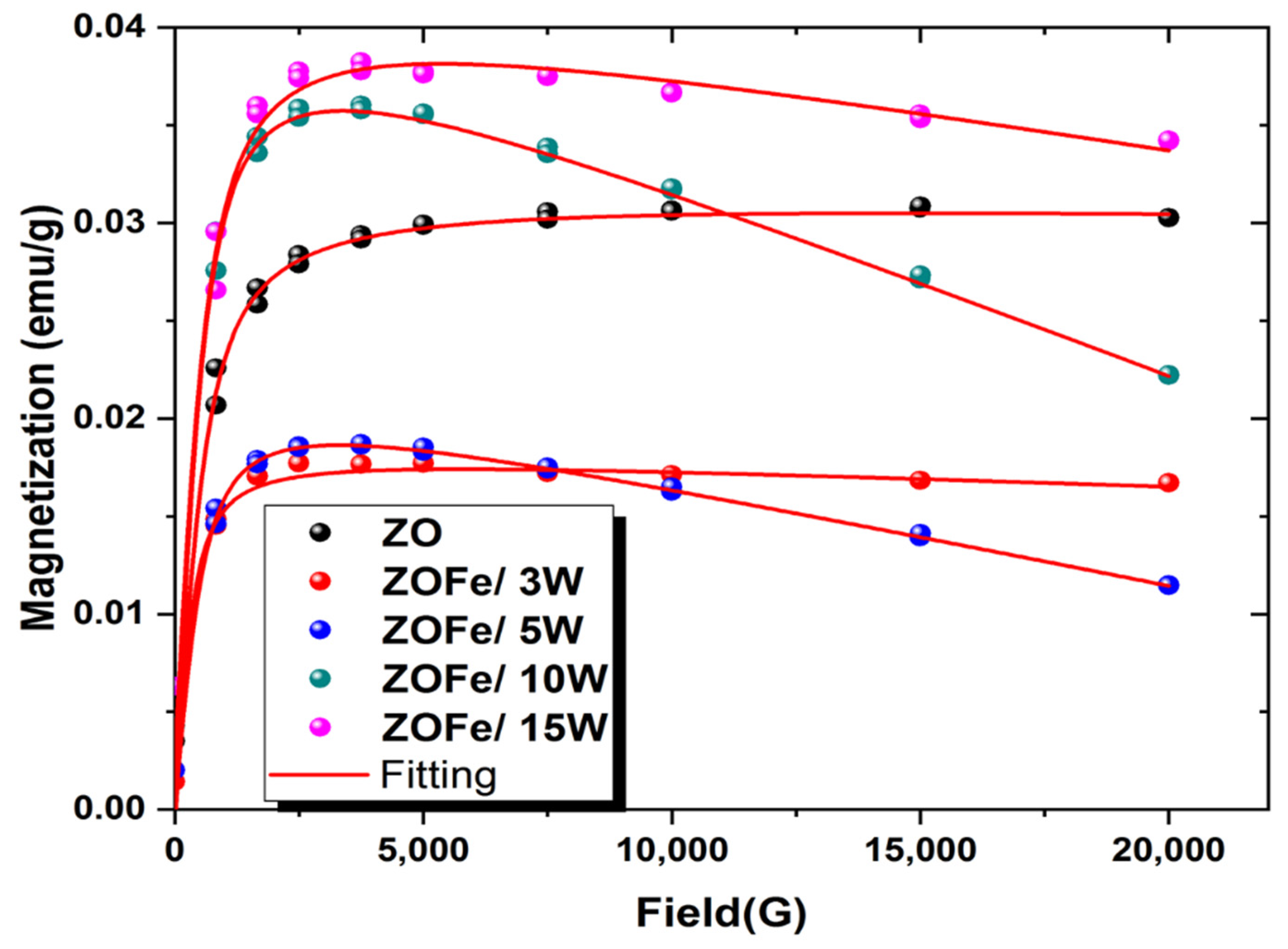
3.5. Magnetic Properties
3.5.1. Magnetic Behavior of the Films
3.5.2. The Magnetic Parameters
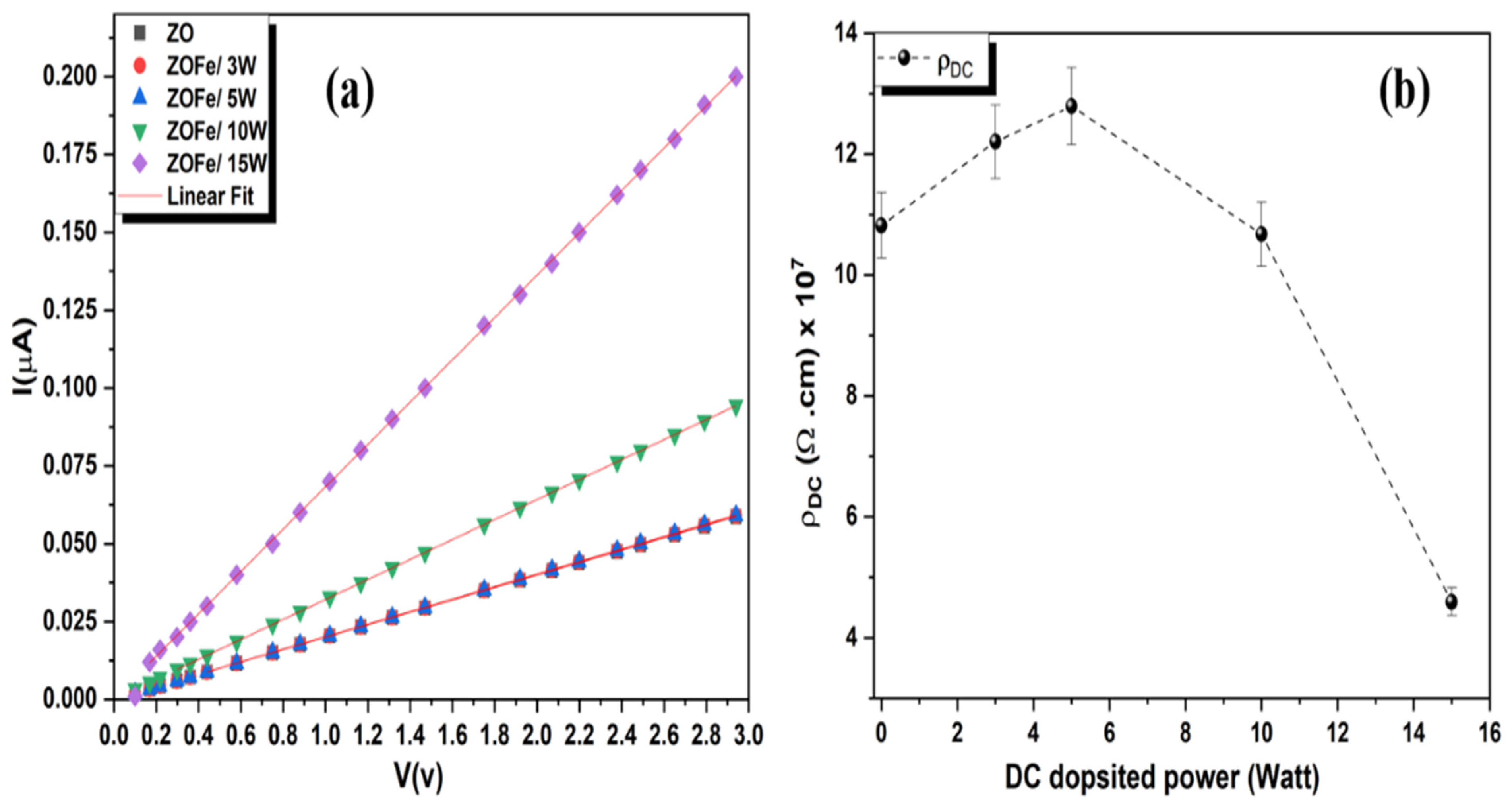
3.6. Electrical Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Theerthagiri, J.; Salla, S.; Senthil, R.A.; Nithyadharseni, P.; Madankumar, A.; Arunachalam, P.; Maiyalagan, T.; Kim, H.S. A review on ZnO nanostructured materials: Energy, environmental and biological applications. Nanotechnology 2019, 30, 392001. [Google Scholar] [CrossRef] [PubMed]
- Tereshchenko, A.; Bechelany, M.; Viter, R.; Khranovskyy, V.; Smyntyna, V.; Starodub, N.; Yakimova, R. Optical biosensors based on ZnO nanostructures: Advantages and perspectives. A review. Sens. Actuators B Chem. 2016, 229, 664–677. [Google Scholar] [CrossRef] [Green Version]
- Hwang, D.K.; Oh, M.S.; Lim, J.H.; Park, S.J. ZnO thin films and light-emitting diodes. J. Phys. D Appl. Phys. 2007, 40, R387–R412. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, G.; Al-Dossary, O.; Umar, A. ZnO nanostructured thin films: Depositions, properties and applications—A review. Mater. Express 2015, 5, 3–23. [Google Scholar] [CrossRef]
- Hamid, S.B.A.; Teh, S.J.; Lai, C.W. Photocatalytic Water Oxidation on ZnO: A Review. Catalysts 2017, 7, 93. [Google Scholar] [CrossRef] [Green Version]
- Prellier, W.; Fouchet, A.; Mercey, B. Oxide-diluted magnetic semiconductors: A review of the experimental status. J. Physics Condens. Matter 2003, 15, R1583–R1601. [Google Scholar] [CrossRef]
- Rong, P.; Ren, S.; Yu, Q. Fabrications and Applications of ZnO Nanomaterials in Flexible Functional Devices-A Review. Crit. Rev. Anal. Chem. 2018, 49, 336–349. [Google Scholar] [CrossRef]
- Dietl, T. Zener Model Description of Ferromagnetism in Zinc-Blende Magnetic Semiconductors. Science 2000, 287, 1019–1022. [Google Scholar] [CrossRef] [Green Version]
- Castro-Lopes, S.; Guerra, Y.; Silva-Sousa, A.; Oliveira, D.M.; Gonçalves, L.A.P.; Franco, A.; Padrón-Hernández, E.; Peña-Garcia, R. Influence of pH on the structural and magnetic properties of Fe-doped ZnO nanoparticles synthesized by sol gel method. Solid State Sci. 2020, 109, 106438. [Google Scholar] [CrossRef]
- Soares, A.S.; Castro-Lopes, S.; Cabrera-Baez, M.; Milani, R.; Padrón-Hernández, E.; Farias, B.V.; Soares, J.M.; Gusmão, S.S.; Viana, B.C.; Guerra, Y.; et al. The role of pH on the vibrational, optical and electronic properties of the Zn1-xFexO compound synthesized via sol gel method. Solid State Sci. 2022, 128, 106880. [Google Scholar] [CrossRef]
- Liu, C.; Yun, F.; Morkoç, H. Ferromagnetism of ZnO and GaN: A Review. J. Mater. Sci. Mater. Electron. 2005, 16, 555–597. [Google Scholar] [CrossRef]
- Wang, Y.S.; Thomas, P.J.; O’Brien, P. Optical properties of ZnO nanocrystals doped with Cd, Mg, Mn, and Fe ions. J. Phys. Chem. B 2006, 110, 21412–21415. [Google Scholar] [CrossRef]
- Aghgonbad, M.M.; Sedghi, H. Optical and Electronic Analysis of Pure and Fe-Doped ZnO Thin Films Using Spectroscopic Ellipsometry and Kramers–Kronig Method. Int. J. Nanosci. 2019, 18, 1850013. [Google Scholar] [CrossRef]
- Bousslama, W.; Elhouichet, H.; Férid, M. Enhanced photocatalytic activity of Fe doped ZnO nanocrystals under sunlight irradiation. Optik Stuttg. 2017, 134, 88–98. [Google Scholar] [CrossRef]
- Wang, L.; Meng, L.; Teixeira, V.; Song, S.; Xu, Z.; Xu, X. Structure and optical properties of ZnO:V thin films with different doping concentrations. Thin Solid Films 2009, 517, 3721–3725. [Google Scholar] [CrossRef] [Green Version]
- Kamalianfar, A.; Halim, S.A.; Behzad, K.; Naseri, M.G.; Navasery, M.; Din, F.U.; Zahedi, J.A.M.; Lim, K.P.; Chen, S.K.; Sidek, H.A.A. Effect of thickness on structural, optical and magnetic properties of Co doped ZnO thin film by pulsed laser deposition. J. Optoelectron. Adv. Mater. 2013, 15, 239–243. [Google Scholar]
- Wang, L.M.; Liao, J.-W.; Peng, Z.-A.; Lai, J.-H. Doping Effects on the Characteristics of Fe:ZnO Films: Valence Transition and Hopping Transport. J. Electrochem. Soc. 2009, 156, H138. [Google Scholar] [CrossRef]
- Al-Kuhaili, M.F.; Durrani, S.M.A.; El-Said, A.S.; Heller, R. Influence of iron doping on the structural, chemical, and optoelectronic properties of sputtered zinc oxide thin films. J. Mater. Res. 2016, 31, 3230–3239. [Google Scholar] [CrossRef]
- Wang, X.B.; Song, C.; Li, D.M.; Geng, K.W.; Zeng, F.; Pan, F. The influence of different doping elements on microstructure, piezoelectric coefficient and resistivity of sputtered ZnO film. Appl. Surf. Sci. 2006, 253, 1639–1643. [Google Scholar] [CrossRef]
- Chu, W.-T.; Mayer, J.W.; Nicolet, M. Backscattering Spectrometry; Acadamic Press, INC.: London, UK, 1978. [Google Scholar] [CrossRef] [Green Version]
- Fujimura, N.; Nishihara, T.; Goto, S.; Xu, J.; Ito, T. Control of preferred orientation for ZnOx films: Control of self-texture. J. Cryst. Growth 1993, 130, 269–279. [Google Scholar] [CrossRef]
- Hammad, A.H.; Abdel-wahab, M.S.; Vattamkandathil, S.; Ansari, A.R. Structural and optical properties of ZnO thin films prepared by RF sputtering at different thicknesses. Phys. B Condens. Matter. 2018, 540, 1–8. [Google Scholar] [CrossRef]
- Akl, A.A.; Mahmoud, S.A.; L-Shomar, S.M.A.; Hassanien, A.S. Improving microstructural properties and minimizing crystal imperfections of nanocrystalline Cu2O thin films of different solution molarities for solar cell applications. Mater. Sci. Semicond. Process. 2018, 74, 183–192. [Google Scholar] [CrossRef]
- Debye, P.; Scherrer, P. Interferenz an regellos orientierten Teilchen im Röntgenlicht I. Phys. Z. 1916, 17, 277. [Google Scholar]
- Köseoğlu, Y. Rapid synthesis of room temperature ferromagnetic Fe and Co co-doped ZnO DMS nanoparticles. Ceram. Int. 2015, 41, 11655–11661. [Google Scholar] [CrossRef]
- Allen, J.A.; Murugesan, D.; Viswanathan, C. Circumferential growth of zinc oxide nanostructure anchored over carbon fabric and its photocatalytic performance towards p-nitrophenol. Superlattices Microstruct. 2019, 125, 159–167. [Google Scholar] [CrossRef]
- Shaban, M.; El Sayed, A.M. Influences of lead and magnesium co-doping on the nanostructural, optical properties and wettability of spin coated zinc oxide films. Mater. Sci. Semicond. Process. 2015, 39, 136–147. [Google Scholar] [CrossRef]
- Maniv, S.; Westwood, W.D.; Colombini, E. Pressure and Angle of Incidence Effects in Reactive Planar Magnetron Sputtered ZnO layers. J. Vac. Sci. Technol. 1982, 20, 162–170. [Google Scholar] [CrossRef]
- Hur, T.B.; Hwang, Y.H.; Kim, H.K.; Lee, I.J.J. Strain effects in ZnO thin films and nanoparticles. J. Appl. Phys. 2006, 99, 64308. [Google Scholar] [CrossRef]
- Patsalas, P.; Gravalidis, C.; Logothetidis, S. Surface kinetics and subplantation phenomena affecting the texture, morphology, stress, and growth evolution of titanium nitride films. J. Appl. Phys. 2004, 96, 6234–6235. [Google Scholar] [CrossRef]
- Ulutas, C.; Gunes, M.; Gumus, C. Influence of post-deposition annealing on the structural and optical properties of γ-MnS thin film. Optik Stuttg. 2018, 164, 78–83. [Google Scholar] [CrossRef]
- Yusuf, Y.; Azis, R.S.; Mustaffa, M.S. Spin-Coating Technique for Fabricating Nickel Zinc Nanoferrite (Ni0.3Zn0.7Fe2O4) Thin Films. In Coatings and Thin-Film Technologies; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Tauc, J.; Grigorovici, R.; Vancu, A. Optical Properties and Electronic Structure of Amorphous Germanium. Phys. Status Solidi 1966, 15, 627–637. [Google Scholar] [CrossRef]
- Che, H.; Huso, J.; Morrison, J.L.; Thapa, D.; Huso, M.; Yeh, W.J.; Tarun, M.C.; McCluskey, M.D.; Bergman, L. Optical properties of ZnO-alloyed nanocrystalline films. J. Nanomater. 2012, 2012, 963485. [Google Scholar] [CrossRef] [Green Version]
- Marotti, R. Bandgap energy tuning of electrochemically grown ZnO thin films by thickness and electrodeposition potential. Sol. Energy Mater. Sol. Cells 2004, 82, 85–103. [Google Scholar] [CrossRef]
- McLean, T.P. The absorption edge spectrum of semiconductors. Prog. Semicond. 1960, 5, 53–102. [Google Scholar]
- Hammad, A.H.; Abdelghany, A.M.; Okasha, A.; Marzouk, S.Y. The influence of fluorine and nickel ions on the structural, spectroscopic, and optical properties of (100 − x)[15NaF–5CaF2–80B2O3]-xNiO glasses. J. Mater. Sci. Mater. Electron. 2017, 28, 8662–8668. [Google Scholar] [CrossRef]
- Parra-Palomino, A.; Perales–Perez, O.; Singhal, R.K.; Tomar, M.S.; Hwang, J.; Voyles, P. Structural, optical, and magnetic characterization of monodisperse Fe-doped ZnO nanocrystals. J. Appl. Phys. 2008, 103, 07D121. [Google Scholar] [CrossRef] [Green Version]
- Salem, M.; Akir, S.; Ghrib, T.; Daoudi, K.; Gaidi, M. Fe-doping effect on the photoelectrochemical properties enhancement of ZnO films. J. Alloys Compd. 2016, 685, 107–113. [Google Scholar] [CrossRef]
- Shanmuganathan, G.; Banu, I.B.S. Influence of Codoping on the Optical Properties of ZnO Thin Films Synthesized on Glass Substrate by Chemical Bath Deposition Method. Adv. Condens. Matter Phys. 2014, 2014, 761960. [Google Scholar] [CrossRef] [Green Version]
- Dhiman, P.; Chand, J.; Kumar, A.; Kotnala, R.K.; Batoo, K.M.; Singh, M. Synthesis and characterization of novel Fe@ZnO nanosystem. J. Alloys Compd. 2013, 578, 235–241. [Google Scholar] [CrossRef]
- Chen, Z.C.; Zhuge, L.J.; Wu, X.M.; Meng, Y.D. Initial study on the structure and optical properties of Zn1-xFexO films. Thin Solid Films 2007, 515, 5462–5465. [Google Scholar] [CrossRef]
- Wang, C.; Chen, Z.; He, Y.; Li, L.; Zhang, D. Structure, morphology and properties of Fe-doped ZnO films prepared by facing-target magnetron sputtering system. Appl. Surf. Sci. 2009, 255, 6881–6887. [Google Scholar] [CrossRef]
- Shaban, M.; El Sayed, A.M. Effects of lanthanum and sodium on the structural, optical and hydrophilic properties of sol-gel derived ZnO films: A comparative study. Mater. Sci. Semicond. Process. 2016, 41, 323–334. [Google Scholar] [CrossRef]
- Shaban, M.; Zayed, M.; Hamdy, H. Nanostructured ZnO thin films for self-cleaning applications. RSC Adv. 2017, 7, 617–631. [Google Scholar] [CrossRef]
- Moss, T.S. Relations between the Refractive Index and Energy Gap of Semiconductors. Phys. Status Solidi. 1985, 131, 415–427. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, J.K. Model for calculating the refractive index of different materials. Indian J. Pure Appl. Phys. 2010, 48, 571–574. [Google Scholar]
- Ravindra, N.M.; Srivastava, V.K. Variation of refractive index with energy gap in semiconductors. Infrared Phys. 1979, 19, 603–604. [Google Scholar] [CrossRef]
- Dimitrov, V.; Sakka, S. Linear and nonlinear optical properties of simple oxides. II. J. Appl. Phys. 1996, 79, 1741–1745. [Google Scholar] [CrossRef] [Green Version]
- Rumpf, K.; Granitzer, P.; Krenn, H. Porous Silicon/Metal Hybrid System with Ferro and Paramagnetic Behavior. IEEE Trans. Magn. 2008, 44, 2753–2755. [Google Scholar] [CrossRef]
- Zener, C. Interaction between the d-shells in the transition metals. II. Ferromagnetic compounds of manganese with Perovskite structure. Phys. Rev. 1951, 82, 403–405. [Google Scholar] [CrossRef]
- Anderson, P.W. New approach to the theory of superexchange interactions. Phys. Rev. 1959, 115, 2–13. [Google Scholar] [CrossRef]
- Katayama-Yoshida, H.; Sato, K.; Fukushima, T.; Toyoda, M.; Kizaki, H.; Dinh, V.A.; Dederichs, P.H. Theory of ferromagnetic semiconductors. Phys. Status Solidi Appl. Mater. Sci. 2007, 204, 15–32. [Google Scholar] [CrossRef]
- Pan, H.; Yi, J.B.; Shen, L.; Wu, R.Q.; Yang, J.H.; Lin, J.Y.; Feng, Y.P.; Ding, J.; Van, L.H.; Yin, J.H. Room-Temperature Ferromagnetism in Carbon-Doped ZnO. Phys. Rev. Lett. 2007, 99, 127201. [Google Scholar] [CrossRef] [PubMed]
- Özgür, Ü.; Alivov, Y.I.; Liu, C.; Teke, A.; Reshchikov, M.A.; Doǧan, S.; Avrutin, V.; Cho, S.J.; Morkoç, H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 041301. [Google Scholar] [CrossRef] [Green Version]
- Sundaresan, A.; Bhargavi, R.; Rangarajan, N.; Siddesh, U.; Rao, C.N.R. Ferromagnetism as a universal feature of nanoparticles of the otherwise nonmagnetic oxides. Phys. Rev. B-Condens. Matter Mater. Phys. 2006, 74, 161306. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, J.; Liu, Z.Z.; Liu, Z.Z. Structural, optical and magnetic properties of Zn 1-x Fe x O powders by sol-gel method. Appl. Surf. Sci. 2013, 284, 49–52. [Google Scholar] [CrossRef] [Green Version]
- Murugaraj, R. Room temperature ferromagnetism in Ist group elements co–doped ZnO:Fe nanoparticles by co-precipitation method. Phys. B Phys. Condens. Matter. 2016, 487, 102–108. [Google Scholar] [CrossRef]
- Kittilstved, K.R.; Schwartz, D.A.; Tuan, A.C.; Heald, S.M.; Chambers, S.A.; Gamelin, D.R. Direct kinetic correlation of carriers and ferromagnetism in Co2+:ZnO. Phys. Rev. Lett. 2006, 97, 2–5. [Google Scholar] [CrossRef] [PubMed]
- Vettumperumal, R.; Kalyanaraman, S.; Santoshkumar, B.; Thangavel, R. Magnetic properties of high Li doped ZnO sol-gel thin films. Mater. Res. Bull. 2014, 50, 7–11. [Google Scholar] [CrossRef]
- Ariyakkani, P.; Suganya, L.; Sundaresan, B. Investigation of the structural, optical and magnetic properties of Fe doped ZnO thin films coated on glass by sol-gel spin coating method. J. Alloys Compd. 2017, 695, 3467–3475. [Google Scholar] [CrossRef]
- Wang, D.; Chen, Z.Q.; Wang, D.D.; Gong, J.; Cao, C.Y.; Tang, Z.; Huang, L.R. Effect of thermal annealing on the structure and magnetism of Fe-doped ZnO nanocrystals synthesized by solid state reaction. J. Magn. Magn. Mater. 2010, 322, 3642–3647. [Google Scholar] [CrossRef]
- Kumar, S.; Kim, Y.J.; Koo, B.H.; Sharma, S.K.; Vargas, J.M.; Knobel, M.; Gautam, S.; Chae, K.H.; Kim, D.K.; Kim, Y.K.; et al. Structural and magnetic properties of chemically synthesized Fe doped ZnO. J. Appl. Phys. 2009, 105, 07C520. [Google Scholar] [CrossRef]
- Sattar, A.A.; Elsayed, H.M.; Faramawy, A.M. Comparative study of structure and magnetic properties of micro- and nano-sized GdxY3−xFe5O12 garnet. J. Magn. Magn. Mater. 2016, 412, 172–180. [Google Scholar] [CrossRef]
- Limaye, M.V.; Singh, S.B.; Das, R.; Poddar, P.; Kulkarni, S.K. Room temperature ferromagnetism in undoped and Fe doped ZnO nanorods: Microwave-assisted synthesis. J. Solid State Chem. 2011, 184, 391–400. [Google Scholar] [CrossRef]
- Faramawy, A.M.; Mattei, G.; Scian, C.; Elsayed, H.; Ismail, M.I.M. Cr3+ substituted aluminum cobalt ferrite nanoparticles: Influence of cation distribution on structural and magnetic properties. Phys. Scr. 2021, 96, 125849. [Google Scholar] [CrossRef]
- Ueda, K.; Tabata, H.; Kawai, T. Magnetic and electric properties of transition-metal-doped ZnO films. Appl. Phys. Lett. 2001, 79, 988–990. [Google Scholar] [CrossRef]
- Chaabouni, F.; Abaab, M.; Rezig, B. Effect of the substrate temperature on the properties of ZnO films grown by RF magnetron sputtering. Mater. Sci. Eng. B Solid-State Mater. Adv. Technol. 2004, 109, 236–240. [Google Scholar] [CrossRef]
- Cherifi, Y.; Chaouchi, A.; Lorgoilloux, Y.; Rguiti, M.; Kadri, A.; Courtois, C. Electrical, dielectric and photocatalytic properties of Fe-doped ZnO nanomaterials synthesized by sol gel method. Process. Appl. Ceram. 2016, 10, 125–135. [Google Scholar] [CrossRef] [Green Version]
- Cheng, W.; Ma, X. Structural, optical and magnetic properties of Fe-doped ZnO. J. Phys. Conf. Ser. 2009, 152, 012039. [Google Scholar] [CrossRef]
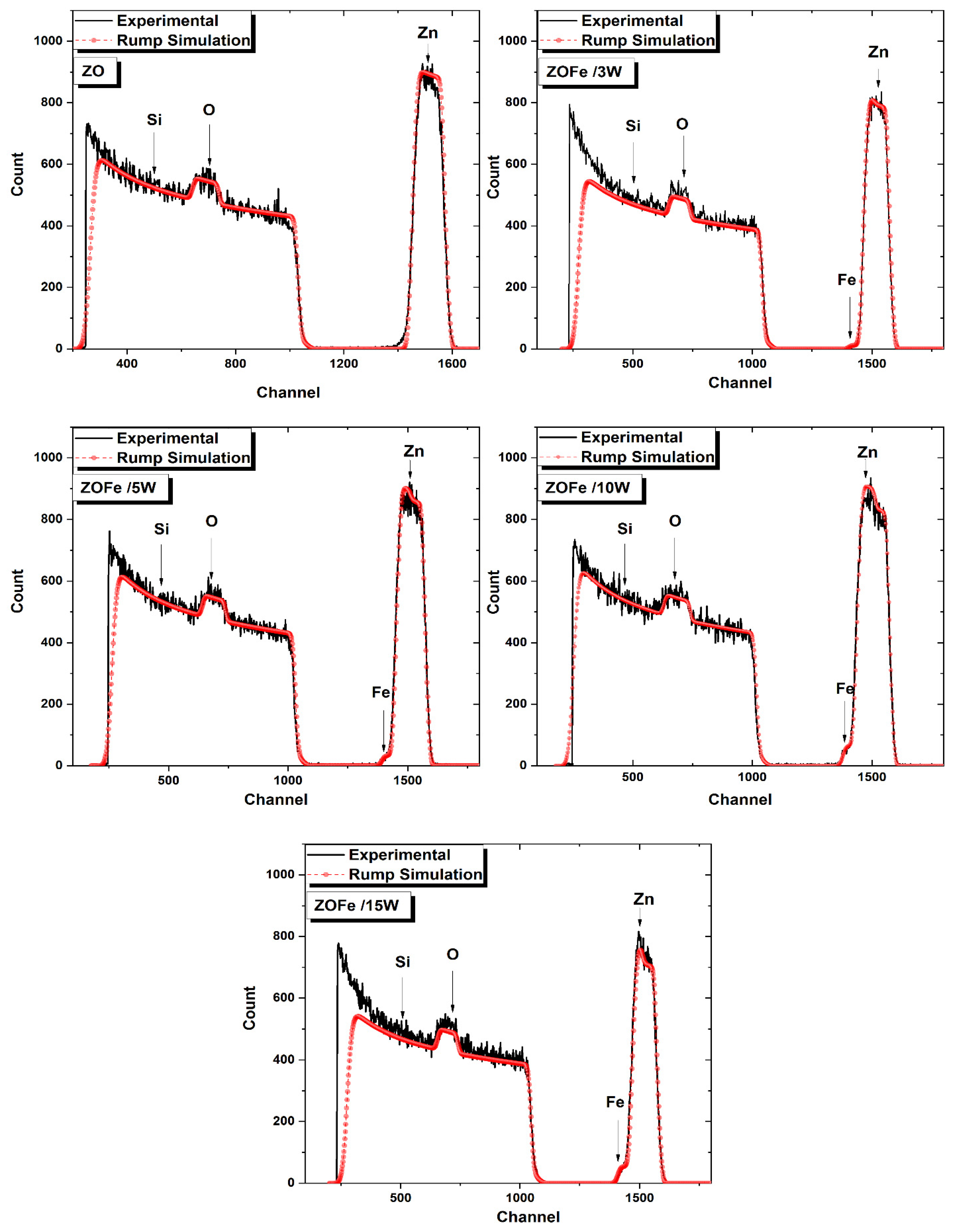
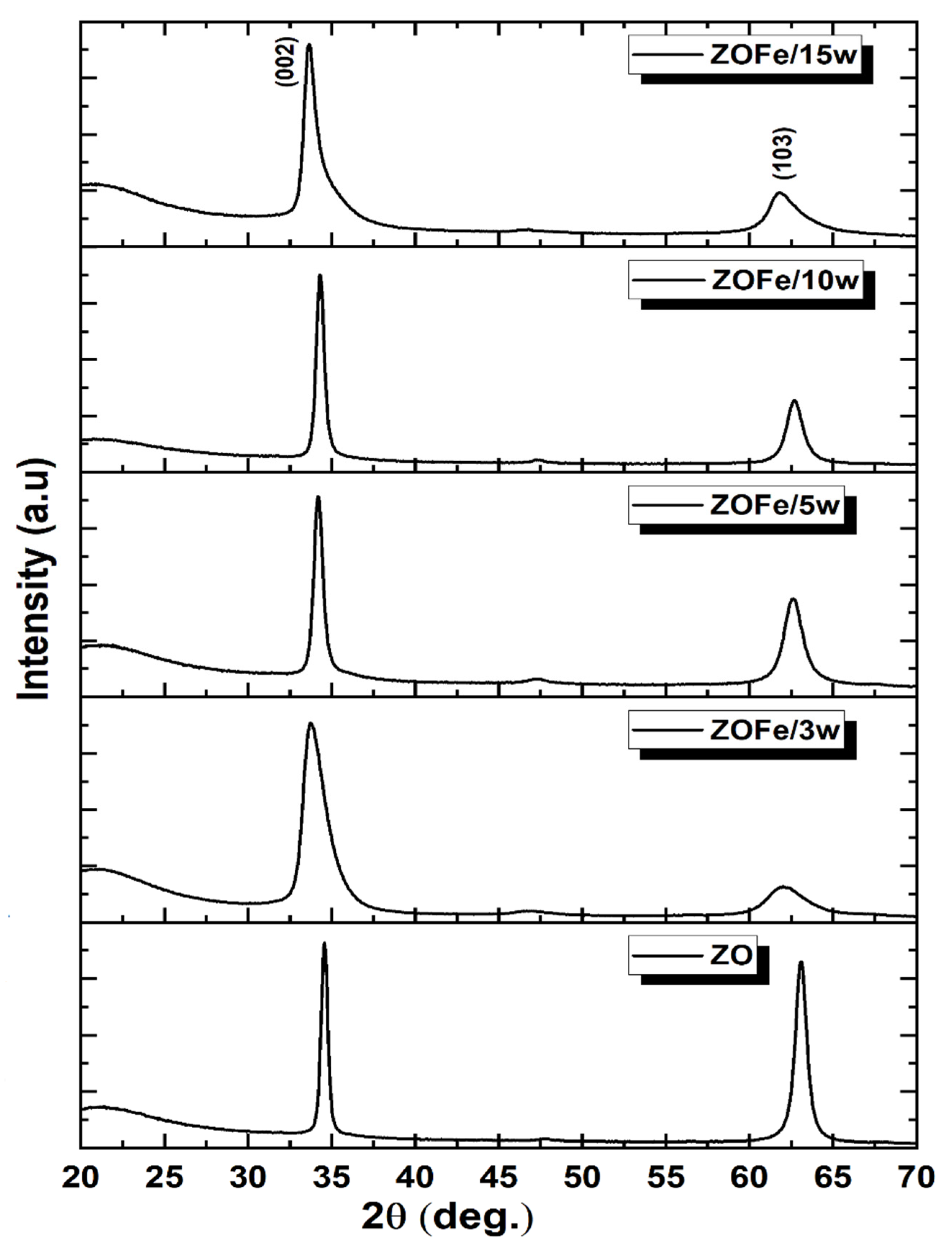

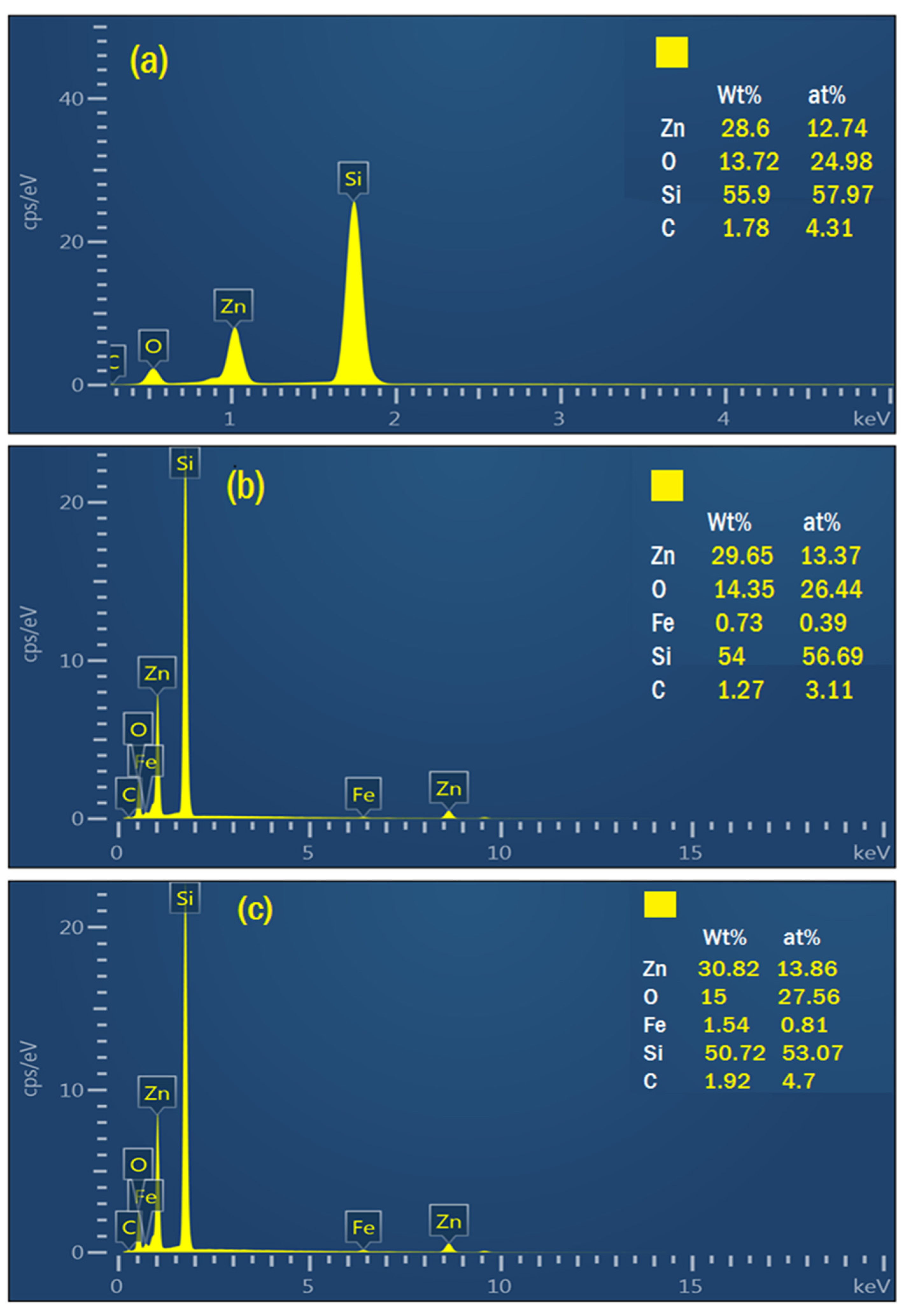

| Pre-sputtering pressure (mbar) | 1.5 × 10−6 |
| Sputtering pressure (mbar) | 50 × 10−4 |
| Ar gas pressure (mTorr) | 0.5 |
| Ar gas flow (sccm) | 20 |
| Sputtering time (min) | 17 |
| Sputtering voltage (V) | VDC ≈ 350 V, VRF ≈ 390 V |
| RBS Fluency (1015 at./cm2) | The Contents Percentage (% at.) | ||||
|---|---|---|---|---|---|
| Film | Zn | O | Fe | ZnO | Fe |
| ZO | 620 | 620 | 0 | 100 | 0 |
| ZOFe/3 W | 555 | 555 | 11 | 99 | 1 |
| ZOFe/5 W | 630 | 630 | 30 | 97.6 | 2.4 |
| ZOFe/10 W | 650 | 650 | 65 | 95.2 | 4.8 |
| ZOFe/15 W | 473 | 516 | 52 | 95 | 5 |
| Film | 2θ (o) | d-Spacing (Å) | Peak Intensity, I (a.u.) | Crystallite Size, D (nm) | Texture Coefficient |
|---|---|---|---|---|---|
| Plane (002) | TC(002) | ||||
| ZO | 34.57 | 2.59 | 54,621 | 40 | 0.815 |
| ZOFe/3 W | 33.28 | 2.69 | 88,247 | 6 | 1.554 |
| ZOFe/5 W | 34.20 | 2.62 | 39,271 | 19 | 1.120 |
| ZOFe/10 W | 34.13 | 2.61 | 45,609 | 25 | 1.264 |
| ZOFe/15 W | 33.67 | 2.65 | 72,050 | 11 | 1.398 |
| Plane (103) | TC(103) | ||||
| ZO | 63.08 | 0.52 | 49,566 | - | 1.184 |
| ZOFe/3 W | 62.08 | 0.52 | 15,787 | - | 0.445 |
| ZOFe/5 W | 62.61 | 0.52 | 19,252 | - | 0.879 |
| ZOFe/10 W | 62.69 | 0.52 | 16,571 | - | 0.735 |
| ZOFe/15 W | 61.87 | 0.52 | 19,353 | - | 0.601 |
| Film | a (Å) | c (Å) | V (Å3) | U | L (Å) | ezz × 10−3 | σ × 109 (GaP) |
|---|---|---|---|---|---|---|---|
| ZO | 2.993 | 5.183 | 40.201 | 0.361 | 1.871 | −4.152 | 1.868 |
| ZOFe/3 W | 3.015 | 5.378 | 41.908 | 0.361 | 1.942 | 3.329 | −14.981 |
| ZOFe/5 W | 3.024 | 5.237 | 41.420 | 0.361 | 1.891 | 6.236 | −2.806 |
| ZOFe/10 W | 3.015 | 5.221 | 41.091 | 0.361 | 1.885 | 3.316 | −1.411 |
| ZOFe/15 W | 3.071 | 5.318 | 43.416 | 0.361 | 1.921 | 2.172 | −9.775 |
| Film | Tauc | dT/dE | dT/dλ | LD |
|---|---|---|---|---|
| ZO | 3.26 | 3.26 | 3.26 | 3.26 |
| ZOFe/3 W | 3.27 | 3.27 | 3.27 | 3.27 |
| ZOFe/5 W | 3.29 | 3.28 | 3.29 | 3.28 |
| ZOFe/10 W | 3.33 | 3.34 | 3.34 | 3.33 |
| ZOFe/15 W | 3.35 | 3.39 | 3.40 | 3.40 |
| Film | Optical Band Gap, Eg (eV) | Eu (meV) | no [Moss] | no [Ravindra and Srivastava] | no [Dimitrov and Sakka] |
|---|---|---|---|---|---|
| ZO | 3.26 | 255 | 2.323 | 2.399 | 2.330 |
| ZOFe/3 W | 3.27 | 236 | 2.321 | 2.397 | 2.327 |
| ZOFe/5 W | 3.29 | 263 | 2.318 | 2.393 | 2.323 |
| ZOFe/10 W | 3.33 | 400 | 2.311 | 2.386 | 2.313 |
| ZOFe/15 W | 3.35 | 403 | 2.307 | 2.382 | 2.308 |
| Film | Magnetization × 10−4 emu/g | Coercivity (G) | Remanence × 10−3 emu/g |
|---|---|---|---|
| ZO | 3.16 ± 0.04 | 110.7 ± 2 | 3.12 ± 0.2 |
| ZOFe/3 W | 1.84 ± 0.03 | 100.3 ± 1 | 2.05 ± 0.1 |
| ZOFe/5 W | 2.20 ± 0.02 | 94.3 ± 1 | 1.82 ± 0.1 |
| ZOFe/10 W | 4.24 ± 0.05 | 101.3 ± 1 | 3.76 ± 0.2 |
| ZOFe/15 W | 4.26 ± 0.06 | 95.7 ± 1 | 3.77 ± 0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faramawy, A.; Elsayed, H.; Scian, C.; Mattei, G. Structural, Optical, Magnetic and Electrical Properties of Sputtered ZnO and ZnO:Fe Thin Films: The Role of Deposition Power. Ceramics 2022, 5, 1128-1153. https://doi.org/10.3390/ceramics5040080
Faramawy A, Elsayed H, Scian C, Mattei G. Structural, Optical, Magnetic and Electrical Properties of Sputtered ZnO and ZnO:Fe Thin Films: The Role of Deposition Power. Ceramics. 2022; 5(4):1128-1153. https://doi.org/10.3390/ceramics5040080
Chicago/Turabian StyleFaramawy, Ahmed, Hamada Elsayed, Carlo Scian, and Giovanni Mattei. 2022. "Structural, Optical, Magnetic and Electrical Properties of Sputtered ZnO and ZnO:Fe Thin Films: The Role of Deposition Power" Ceramics 5, no. 4: 1128-1153. https://doi.org/10.3390/ceramics5040080
APA StyleFaramawy, A., Elsayed, H., Scian, C., & Mattei, G. (2022). Structural, Optical, Magnetic and Electrical Properties of Sputtered ZnO and ZnO:Fe Thin Films: The Role of Deposition Power. Ceramics, 5(4), 1128-1153. https://doi.org/10.3390/ceramics5040080









