NMR Spectra Particularities in LiNbO3 Crystals with a Near-Stoichiometric Composition
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
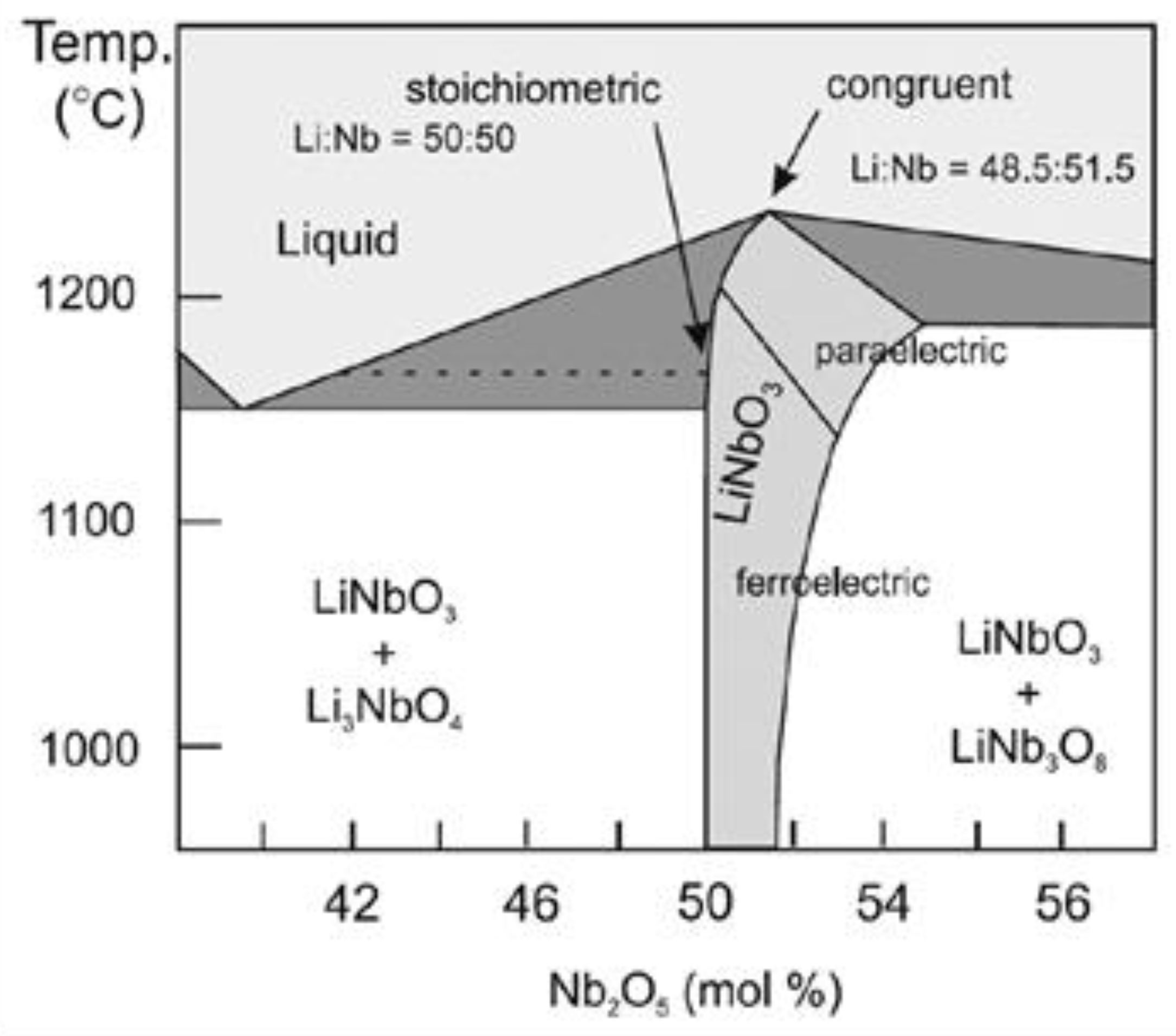
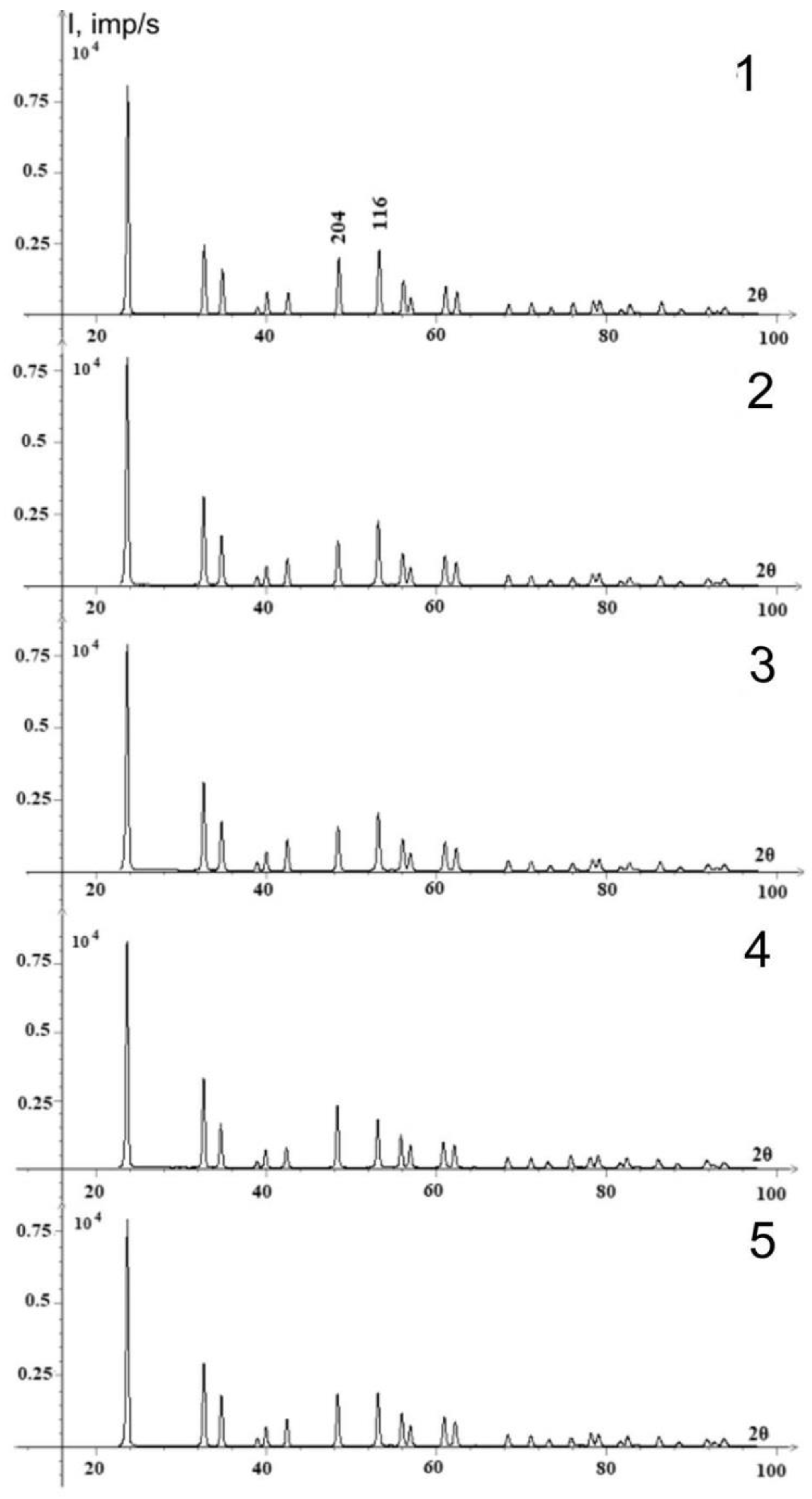
3.1. Analysis of Composition of Real LN Crystals by Means of IR Spectroscopy
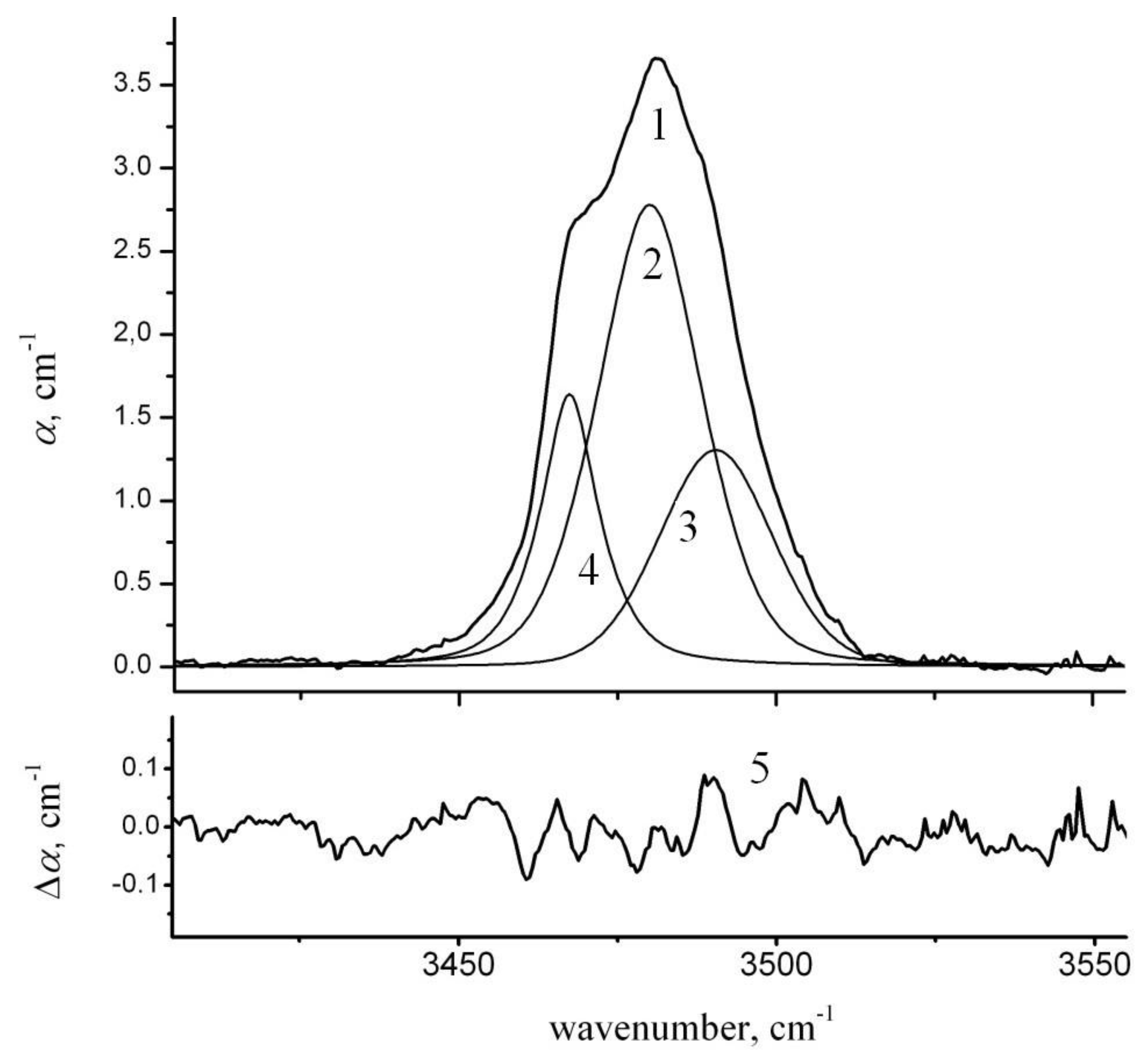
- (a)
- Each spectral band was represented by the Lorentz distribution (L-L-L);
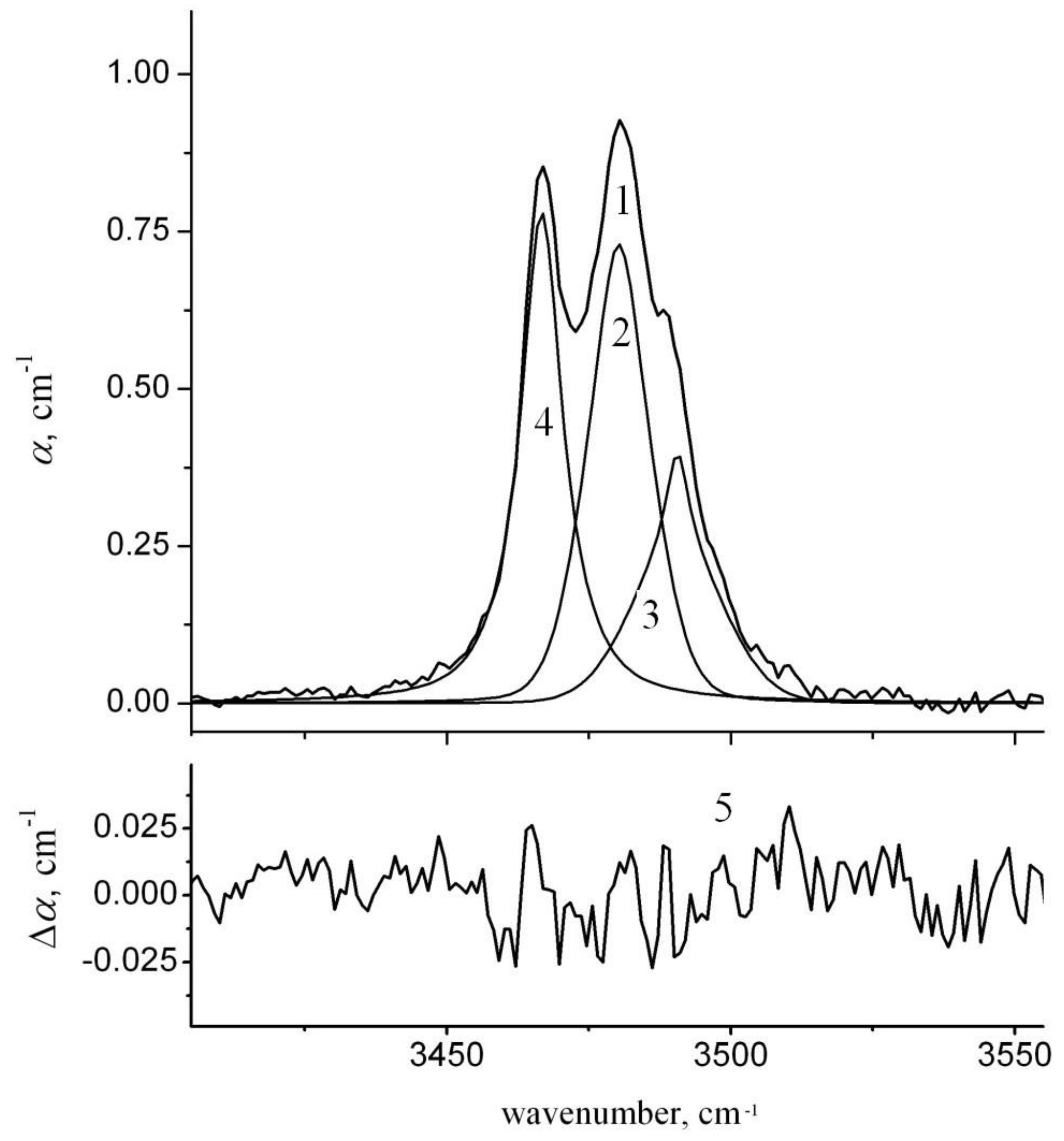
- (b)
- = 3466 сm−1 and = 3490 сm−1 bands were represented by the Lorentz distribution; = 3480 сm−1 band was represented by the Gaussian distribution (L-G-L);
- (c)
- All bands were represented by Voigt pseudo distribution (PV-PV-PV).
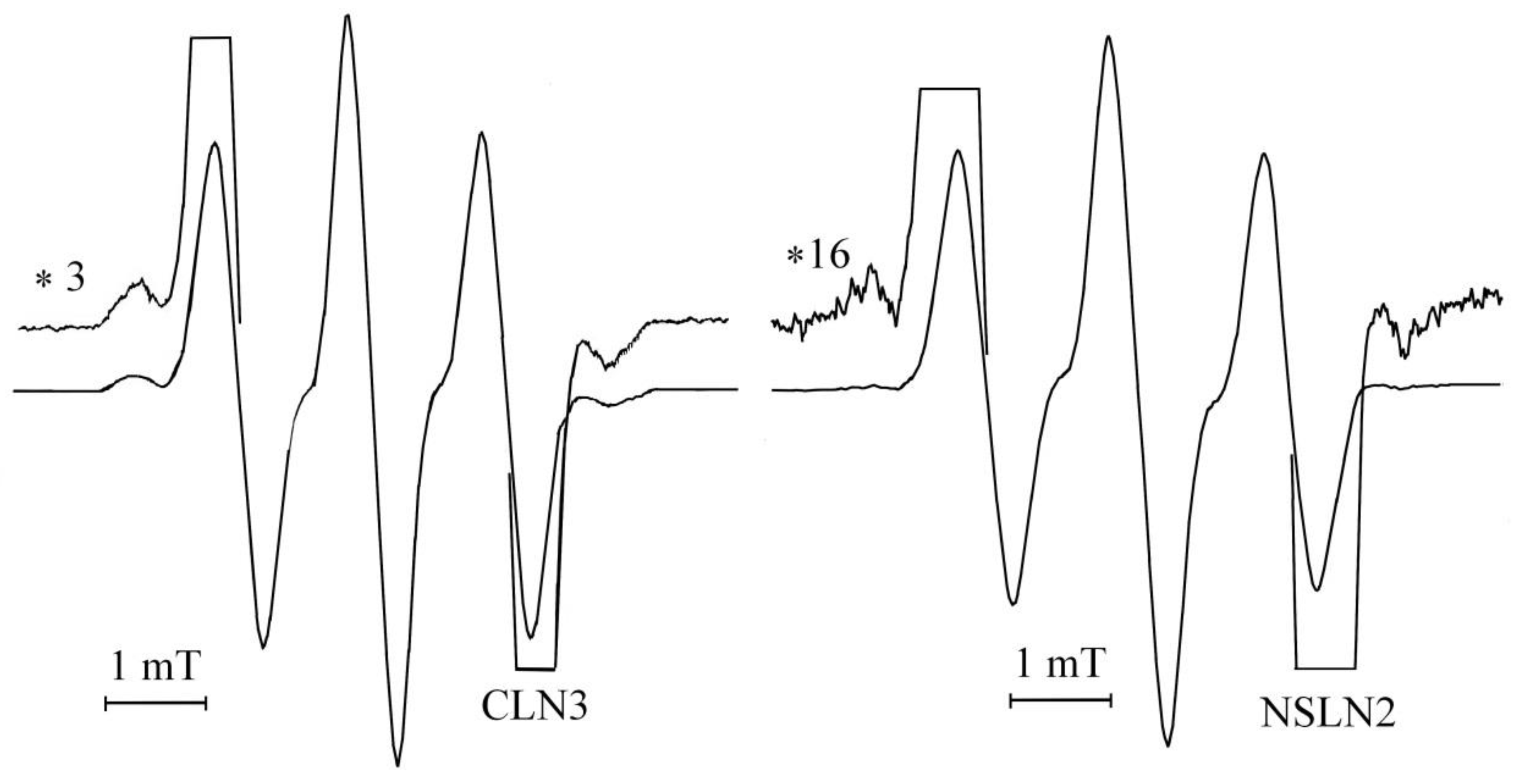
3.2. Analysis of NMR Spectra in NSLN Samples
3.3. Substantiation of the Applicability of Models Explaining the Complex Structure of the 7Li and 93Nb NMR Spectra of the LN Crystal and the Concentration Range of These Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Volk, T.R.; Wöhlecke, M. Lithium Niobate. Defects, Photorefraction and Ferroelectric Switching; Springer: Berlin, Germany, 2008. [Google Scholar]
- Abrahams, S.C. Properties of Lithium Niobate; INSPEC, The Institution of Engineering and Technology: New York, NY, USA, 1989; 234p. [Google Scholar]
- Gunter, P.; Huignard, J.P. Photorefractive Materials and Their Applications. Part 1; Springer: Berlin, Germany, 2006; 243p. [Google Scholar]
- Prokhorov, A.M.; Kuzminov, Y.S. Physics and Chemistry of Crystalline Lithium Niobate; Adam Hilger: New York, NY, USA, 1990; 237p. [Google Scholar]
- Lines, M.E.; Glass, A.M. Principles and Application of Ferroelectrics and Related Materials; Clarendon Press: Oxford, UK, 1977; p. 680. [Google Scholar]
- Lengyel, K.; Péter, A.; Kovács, L.; Corradi, G.; Pálfalvi, L.; Hebling, J.; Unferdorben, M.; Dravecz, G.; Hajdara, I.; Szaller, Z.; et al. Growth, defect structure, and THz application of stoichiometric lithium niobate. Appl. Phys. Rev. 2015, 2, 040601. [Google Scholar] [CrossRef]
- Slichter, C.P. Principles of Magnetic Resonance, 3rd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1996. [Google Scholar]
- Peterson, G.E.; Carruthers, J.R. 93Nb NMR as a sensitive and accurate probe of stoichiometry in LiNbO3 crystals. J. Solid St. Chem. 1969, 1, 98–99. [Google Scholar] [CrossRef]
- Peterson, G.E.; Carruthers, J.R.; Carnevale, A. 93Nb NMR study of the LiNbO3–LiTaO3 solid-solution system. J. Chem. Phys. 1970, 53, 2436–2442. [Google Scholar] [CrossRef]
- Charnaya, E.V.; Gabrielyan, V.T.; Kasperovich, V.S.; Klimko, S. Li7 NMR in LiNbO3 crystals with different nonstoichiometry. Ferroelectrics 1997, 202, 115–119. [Google Scholar] [CrossRef]
- Malovichko, G.; Grachev, V.; Schirmer, O. Interrelation of intrinsic and extrinsic defects—Congruent, stoichiometric, and regularly ordered lithium niobate. Appl. Phys. B 1999, 68, 785–793. [Google Scholar] [CrossRef]
- Peterson, G.E.; Carnevale, A. 93Nb NMR linewidths in nonstoichiometric lithium niobate. J. Chem. Phys. 1972, 56, 4848–4851. [Google Scholar] [CrossRef]
- Yatsenko, A.V.; Ivanova-Maksimova, H.M.; Sergeev, N.A. NMR study of intrinsic defects in congruent LiNbO3. 2. Overlapping defects. Phys. B 1998, 254, 256–259. [Google Scholar] [CrossRef]
- Yatsenko, A.V.; Yevdokimov, S.V.; Sugak, D.Y.; Solskii, I.M. Investigation of the defect complexes in highly Mg-doped LiNbO3 crystals by 93Nb NMR method. Func. Mater. 2014, 21, 31–35. [Google Scholar] [CrossRef]
- Yatsenko, A.V.; Ivanova, E.N.; Sergeev, N.A. NMR study of intrinsic defects in congruent LiNbO3. 1. Unoverlapping defects. Phys. B 1998, 240, 254–262. [Google Scholar] [CrossRef]
- Palatnikov, M.N.; Sidorov, N.V.; Kadetova, A.V.; Teplyakova, N.A.; Makarova, O.V.; Manukovskaya, D.V. Concentration threshold in optically nonlinear LiNbO3:Tb crystals. Opt. Las. Technol. 2021, 137, 106821. [Google Scholar] [CrossRef]
- Palatnikov, M.N.; Kadetova, A.V.; Aleshina, L.A.; Sidorova, O.V.; Sidorov, N.V.; Biryukova, I.V.; Makarova, O.V. Growth, structure, physical and chemical characteristics in a series of LiNbO3:Er crystals of different composition grown in one technological cycle. Opt. Las. Techol. 2022, 147, 107671. [Google Scholar] [CrossRef]
- Fedorova, E.P.; Aleshina, L.A.; Sidorov, N.V.; Chufyrev, P.G.; Yanichev, A.A.; Palatnikov, M.N.; Voskresenskii, V.M.; Kalinnikov, V.T. Stoichiometry and doping effects on cation ordering in LiNbO3 crystals. Inorg. Mater. 2010, 46, 206–211. [Google Scholar] [CrossRef]
- Serrano, M.D.; Bermudez, V.; Arizmendi, L.; Dieguez, E. Determination of the Li/Nb ratio in LiNbO3 crystals grown by Czochralski method with K2O added to the melt. J. Cryst. Growth 2000, 210, 670. [Google Scholar] [CrossRef]
- Polgar, K.; Peter, A.; Foldvari, I. Crystal growth and stoichiometry of LiNbO3 prepared by the flux method. Opt. Mater. 2002, 19, 7. [Google Scholar] [CrossRef]
- Yatsenko, A.V.; Yevdokimov, S.V. A nuclear magnetic resonance probe for testing substances with large values of T1. Instrum. Exp. Tech. 2003, 46, 57–59. [Google Scholar] [CrossRef]
- Kovács, L.; Shalay, V.; Capelletti, R. Stoichiometry dependence of the OH- absorption band in LiNbO3 crystals. Sol. St. Comm. 1984, 52, 1029–1984. [Google Scholar] [CrossRef]
- Chen, H.; Shi, L.; Yan, W.; Chen, G.; Shen, J.; Li, Y. OH− absorption bands of LiNbO3 with varying composition. Chin. Phys. B 2009, 18, 2372. [Google Scholar] [CrossRef]
- Sidorov, N.V.; Smirnov, M.V.; Teplyakova, N.A.; Palatnikov, M.N. Photoluminescence and particular features of the defect structure of congruent and near-stoichiometric lithium niobate crystals obtained using different technologies. Opt. Spectrosc. 2020, 128, 635–641. [Google Scholar] [CrossRef]
- Bäumer, C.; David, C.; Betzler, K.; Hesse, H.; Lengyel, K.; Kovács, L.; Wöhlecke, M. Composition dependence of the OH-stretch-mode spectrum in lithium tantalate. Phys. Stat. Sol. A 2004, 201, R13–R16. [Google Scholar] [CrossRef]
- Salloum, M.Y.; Grunsky, O.S.; Man’shina, A.A.; Tver’yanovich, A.S.; Tver’yanovich, Y.S. Investigation of lithium niobate composition by optical spectroscopy methods. Russ. Chem. Bull. 2009, 58, 2228–2232. [Google Scholar] [CrossRef]
- Kovács, L.; Wöhlecke, M.; Jovanović, A.; Polgar, K.; Kapphan, S. Infrared absorption study of the OH− vibrational band in LiNbO3 crystals. J. Phys. Chem. Sol. 1991, 52, 797–803. [Google Scholar] [CrossRef]
- Köhler, T.; Mehner, E.; Hanzig, J.; Gärtner, G.; Stöcker, H.; Leisegang, T.; Meyer, D.C. Real structure influencing the hydrogen defect chemistry in congruent LiNbO3 and LiTaO3. J. Sol. St. Chem. 2016, 244, 108–115. [Google Scholar] [CrossRef]
- Klauer, S.; Wöhlecke, M.; Kapphan, S. Influence of H-D isotopic substitution on the protonic conductivity of LiNbO3. Phys. Rev. B 1992, 45, 2786–2799. [Google Scholar] [CrossRef]
- Hennel, J.W.; Klinowski, J. Fundamentals of Nuclear Magnetic Resonance; Longman Scientific & Technical: Essex, UK; John Wiley & Sons: New York, NY, USA, 1993; p. 288. [Google Scholar]
- Kind, R.; Gränicher, H.; Derighetti, B.; Waldner, F.; Brun, E. NMR of 93Nb in ferroelectric LiNbO3. Sol. St. Comm. 1968, 6, 439–440. [Google Scholar] [CrossRef]
- Peterson, G.E.; Bridenbaugh, P.M. NMR study of ferroelectric LiNbO3 and LiTaO3. II. J. Chem. Phys. 1968, 48, 3402–3406. [Google Scholar] [CrossRef]
- Yatsenko, A.V.; Palatnikov, M.N.; Sidorov, N.V. Investigation of the intrinsic defects of LiTaO3 crystals by NMR spectroscopy. Cryst. Rep. 2019, 64, 36–40. [Google Scholar] [CrossRef]
- Kim, S.; Gopalan, V.; Kitamura, K.; Furukawa, Y. Domain reversal and nonstoichiometry in lithium tantalate. J. Appl. Phys. 2001, 90, 2949. [Google Scholar] [CrossRef]
- Gopalan, V.; Dierolf, V.; Scrymgeour, D. Defect–domain wall interactions in trigonal ferroelectrics. Annu. Rev. Mater. Res. 2007, 37, 449. [Google Scholar] [CrossRef] [Green Version]





| Impurity Concentration, wt% | |||
|---|---|---|---|
| Impurity | In the Charge | In NSLN1 | In NSLN2 |
| Mn, V, Mg, Sn, Cu | <2 × 10−4 | <3 × 10−4 | <4 × 10−4 |
| Pb, Ni, Cr | <2 × 10−4 | <3 × 10−4 | <2 × 10−4 |
| Co, Mo | <3 × 10−4 | <4 × 10−4 | <3 × 10−4 |
| Si, Fe | <3 × 10−4 | <3 × 10−4 | <3 × 10−4 |
| Ti | <3 × 10−4 | <4 × 10−4 | <5 × 10−4 |
| Al | <8 × 10−4 | <7 × 10−4 | <6 × 10−4 |
| Zr | <5 × 10−4 | <6 × 10−4 | <7 × 10−4 |
| Ca | <4 × 10−4 | <6 × 10−4 | <5 × 10−4 |
| Te, Sb | <4 × 10−4 | <5 × 10−4 | <4 × 10−4 |
| Bi | <3 × 10−4 | <4 × 10−4 | <4 × 10−4 |
| Sample | К2О in charge, wt% | Li2O mol% | N’, % | ||
|---|---|---|---|---|---|
| A | B | A | B | ||
| CLN3 | - | 48.6 | 48.6 | 1.08 | 1.08 |
| NSLN1 | 5.0 | 49.55 | 49.66 | 0.298 | 0.216 |
| NSLN2 | 5.5 | 49.7 | 49.77 | 0.199 | 0.153 |
| Sample | I3466, cm−2 | I3480, cm−2 | I3490, cm−2 | Function | μ, % | M, % | |
|---|---|---|---|---|---|---|---|
| A | B | ||||||
| CLN1 | 60.24 | 132.09 | 118.32 | G-G-G | 3.1 | 48.86 | 49.31 |
| 34.13 | 217.48 | 65.53 | L-G-L | 2.4 | 46.70 | 48.61 | |
| 51.72 | 154.81 | 108.46 | PV-G-G | 1.3 | 48.45 | 49.14 | |
| 45.99 | 149.44 | 119.03 | PV-PV-PV | 0.9 | 48.31 | 49.02 | |
| CLN2 | 34.8 | 58.49 | 31.27 | L-L-L | 6.2 | 49.13 | 49.56 |
| 28.57 | 58.99 | 32.06 | L-G-L | 2.0 | 48.93 | 49.46 | |
| 33.36 | 39.64 | 41.7 | PV-G-G | 1.4 | 48.38 | 49.59 | |
| 23.94 | 62.60 | 30.67 | PV-PV-PV | 0.6 | 48.64 | 49.35 | |
| NSLN1 | 8.33 | 15.71 | 4.06 | L-L-L | 3.7 | 49.02 | 49.6 |
| 8.21 | 9.18 | 7.22 | L-G-L | 2.6 | 49.42 | 49.66 | |
| 10.31 | 10.69 | 6.02 | PV-PV-PV | 1.0 | 49.46 | 49.72 | |
| NSLN2 | 52.94 | 23.65 | 12.66 | L-G-L | 4.4 | 49.71 | 49.88 |
| 46.72 | 39.15 | 7.11 | L-L-L | 3.1 | 49.57 | 49.83 | |
| 47.76 | 32.59 | 8.74 | PV-PV-PV | 1.1 | 49.64 | 49.85 | |
| Sample | R | δνo, kHz | δν1, kHz | (M2)o, kHz2 | (M2)1,2, kHz2 | N, % |
|---|---|---|---|---|---|---|
| CLN3 | 0.946 | 8.3 ± 0.2 | 8.8 ± 0.2 | 13.9 ± 0.5 | 19.2 ± 0.5 | 5 ± 1 |
| NSLN1 | ~0.978 | 8.3 ± 0.3 | 8.6 ± 0.3 | 13.8 ± 0.7 | 16.0 ± 0.9 | 0.8 ± 0.2 |
| NSLN2 | ~0.985 | 8.3 ± 0.3 | 8.5 ± 0.3 | 14.2 ± 0.7 | 15.8 ± 0.8 | 0.7 ± 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yatsenko, A.; Yevdokimov, S.; Palatnikov, M.; Sidorov, N. NMR Spectra Particularities in LiNbO3 Crystals with a Near-Stoichiometric Composition. Ceramics 2023, 6, 432-446. https://doi.org/10.3390/ceramics6010025
Yatsenko A, Yevdokimov S, Palatnikov M, Sidorov N. NMR Spectra Particularities in LiNbO3 Crystals with a Near-Stoichiometric Composition. Ceramics. 2023; 6(1):432-446. https://doi.org/10.3390/ceramics6010025
Chicago/Turabian StyleYatsenko, Alexander, Sergey Yevdokimov, Mikhail Palatnikov, and Nikolay Sidorov. 2023. "NMR Spectra Particularities in LiNbO3 Crystals with a Near-Stoichiometric Composition" Ceramics 6, no. 1: 432-446. https://doi.org/10.3390/ceramics6010025
APA StyleYatsenko, A., Yevdokimov, S., Palatnikov, M., & Sidorov, N. (2023). NMR Spectra Particularities in LiNbO3 Crystals with a Near-Stoichiometric Composition. Ceramics, 6(1), 432-446. https://doi.org/10.3390/ceramics6010025








