Characterization of Bipolar Transport in Hf(Te1−xSex)2 Thermoelectric Alloys
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
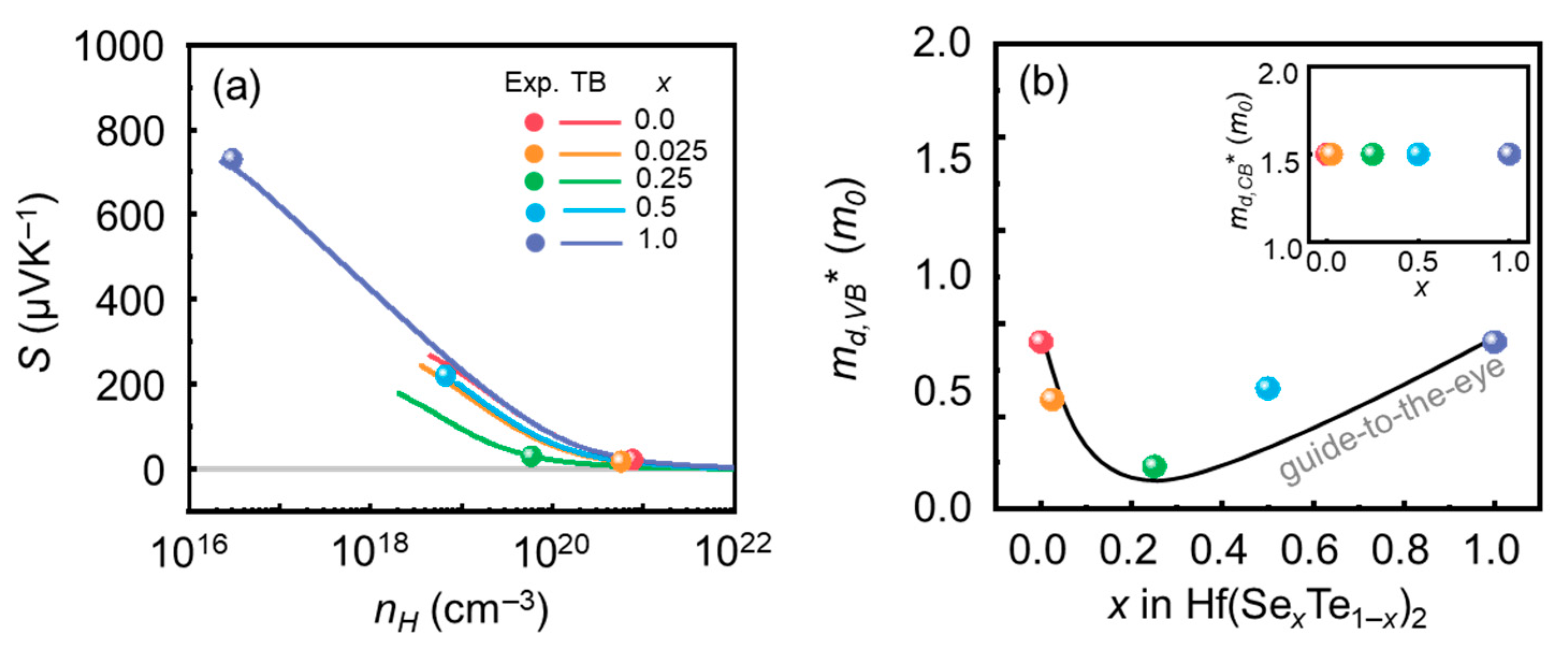
3.1. Estimation of the md,i* (i = VB, CB) Via the TB Model
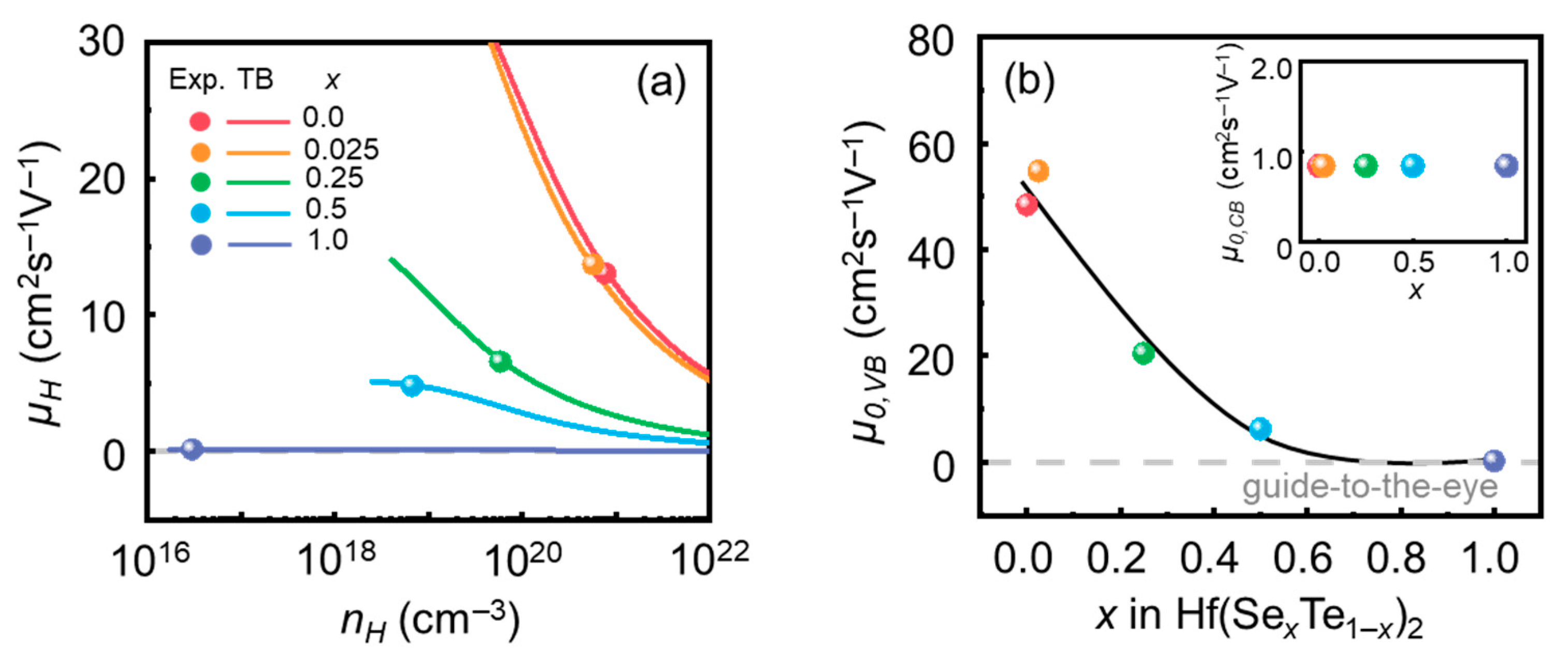
3.2. Estimation of the μ0,i (i = VB, CB) Via the TB Model
3.3. Estimation of the μW,i (i = VB, CB) Via the TB Model
3.4. Estimation of the Bipolar Thermal Conductivity (κb) Via the TB Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Petsagkourakis, I.; Tybrandt, K.; Crispin, X.; Ohkubo, I.; Satoh, N.; Mori, T. Thermoelectric materials and applications for energy harvesting power generation. Sci. Technol. Adv. Mater. 2018, 19, 836–862. [Google Scholar] [CrossRef]
- Tritt, T.M.; Subramanian, M.A. Thermoelectric Materials, Phenomena, and Applications: A Bird’s Eye View. MRS Bull. 2006, 31, 188–198. [Google Scholar] [CrossRef]
- Caballero-Calero, O.; Ares, J.R.; Martín-González, M. Environmentally Friendly Thermoelectric Materials: High Performance from Inorganic Components with Low Toxicity and Abundance in the Earth. Adv. Sustain. Syst. 2021, 5, 2100095. [Google Scholar] [CrossRef]
- Rosi, F.D. Thermoelectricity and thermoelectric power generation. Solid State Electron. 1968, 11, 833–868. [Google Scholar] [CrossRef]
- Liu, W.; Jie, Q.; Kim, H.S.; Ren, Z. Current progress and future challenges in thermoelectric power generation: From materials to devices. Acta Mater. 2015, 87, 357–376. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef]
- Lee, K.H.; Kim, Y.M.; Park, C.O.; Shin, W.H.; Kim, S.W.; Kim, H.S.; Kim, S.i. Cumulative defect structures for experimentally attainable low thermal conductivity in thermoelectric (Bi,Sb)2Te3 alloys. Mater. Today Energy 2021, 21, 100795. [Google Scholar] [CrossRef]
- Feng, Y.; Li, J.; Li, Y.; Ding, T.; Zhang, C.; Hu, L.; Liu, F.; Ao, W.; Zhang, C. Band convergence and carrier-density fine-tuning as the electronic origin of high-average thermoelectric performance in Pb-doped GeTe-based alloys. J. Mater. Chem. A 2020, 8, 11370–11380. [Google Scholar] [CrossRef]
- Kim, H.-S.; Heinz, N.A.; Gibbs, Z.M.; Tang, Y.; Kang, S.D.; Snyder, G.J. High thermoelectric performance in (Bi0.25Sb0.75)2Te3 due to band convergence and improved by carrier concentration control. Mater. Today 2017, 20, 452–459. [Google Scholar] [CrossRef]
- Hong, T.; Wang, D.; Qin, B.; Zhang, X.; Chen, Y.; Gao, X.; Zhao, L.-D. Band convergence and nanostructure modulations lead to high thermoelectric performance in SnPb0.04Te-y% AgSbTe2. Mater. Today Phys. 2021, 21, 100505. [Google Scholar] [CrossRef]
- Moshwan, R.; Liu, W.-D.; Shi, X.-L.; Wang, Y.-P.; Zou, J.; Chen, Z.-G. Realizing high thermoelectric properties of SnTe via synergistic band engineering and structure engineering. Nano Energy 2019, 65, 104056. [Google Scholar] [CrossRef]
- Wang, N.; Li, M.; Xiao, H.; Gao, Z.; Liu, Z.; Zu, X.; Li, S.; Qiao, L. Band degeneracy enhanced thermoelectric performance in layered oxyselenides by first-principles calculations. Npj Comput. Mater. 2021, 7, 18. [Google Scholar] [CrossRef]
- Dangić, Đ.; Hellman, O.; Fahy, S.; Savić, I. The origin of the lattice thermal conductivity enhancement at the ferroelectric phase transition in GeTe. Npj Comput. Mater. 2021, 7, 57. [Google Scholar] [CrossRef]
- Chhowalla, M.; Shin, H.S.; Eda, G.; Li, L.-J.; Loh, K.P.; Zhang, H. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 2013, 5, 263–275. [Google Scholar] [CrossRef] [PubMed]
- Muratore, C.; Varshney, V.; Gengler, J.J.; Hu, J.J.; Bultman, J.E.; Smith, T.M.; Shamberger, P.J.; Qiu, B.; Ruan, X.; Roy, A.K.; et al. Cross-plane thermal properties of transition metal dichalcogenides. Appl. Phys. Lett. 2013, 102, 081604. [Google Scholar] [CrossRef]
- Isomäki, H.; Boehm, J.v. Bonding and Band Structure of ZrS2 and ZrSe2. Phys. Scr. 1981, 24, 465. [Google Scholar] [CrossRef]
- Gaiser, C.; Zandt, T.; Krapf, A.; Serverin, R.; Janowitz, C.; Manzke, R. Band-gap engineering with HfSxSe2-x. Phys. Rev. B 2004, 69, 075205. [Google Scholar] [CrossRef]
- Bilc, D.I.; Benea, D.; Pop, V.; Ghosez, P.; Verstraete, J. Electronic and Thermoelectric Properties of Transition-Metal Dichalcogenides. J. Phys. Chem. C B 2021, 125, 27084–27097. [Google Scholar] [CrossRef]
- Ge, Y.; Wan, W.; Ren, Y.; Liu, Y. Large thermoelectric power factor of high-mobility transition-metal dichalcogenides with 1T’’ phase. Phys. Rev. Res. 2020, 2, 013134. [Google Scholar] [CrossRef]
- Bharadwaj, S.; Ramasubramaniam, A.; Ram-Mohan, L.R. Lateral transition-metal dichalcogenide heterostructures for high efficiency thermoelectric devices. Nanoscale 2022, 14, 11750–11759. [Google Scholar] [CrossRef]
- Yumnam, G.; Pandey, T.; Singh, A.K. High temperature thermoelectric properties of Zr and Hf based transition metal dichalcogenides: A first principles study. J. Chem. Phys. 2015, 143, 234704. [Google Scholar] [CrossRef] [PubMed]
- Bang, J.; Kim, H.-S.; Kim, D.H.; Lee, S.W.; Park, O.; Kim, S.-I. Phase formation behavior and electronic transport properties of HfSe2-HfTe2 solid solution system. J. Alloys Compd. 2022, 920, 166028. [Google Scholar] [CrossRef]
- May, A.F.; Snyder, G.J. Introduction to Modeling Thermoelectric Transport at High Temperatures. In Materials, Preparation, and Characterization in Thermoelectrics; CRC Press: Boca Raton, FL, USA, 2012; pp. 1–18. [Google Scholar]
- Goldsmid, H.J.; Sharp, J.W. Estimation of the thermal band gap of a semiconductor from seebeck measurements. J. Electron. Mater. 1999, 28, 869–872. [Google Scholar] [CrossRef]
- Gibbs, Z.M.; Kim, H.-S.; Wang, H.; Snyder, G.J. Band gap estimation from temperature dependent Seebeck measurement—Deviations from the 2e|S|maxTmax relation. Appl. Phys. Lett. 2015, 106, 022112. [Google Scholar] [CrossRef]
- Foster, S.; Neophytou, N. Effectiveness of nanoinclusions for reducing bipolar effects in thermoelectric materials. Com. Mat. Sci. 2019, 164, 91–98. [Google Scholar] [CrossRef]
- Graziosi, P.; Neophytou, N. Bipolar conduction asymmetries lead to ultra-high thermoelectric power factor. Appl. Phys. Lett. 2022, 120, 072102. [Google Scholar] [CrossRef]
- Hong, M.; Chen, Z.-G.; Yang, L.; Zou, J. Enhancing thermoelectric performance of Bi2Te3-based nanostructures through rational structure design. Nanoscle 2016, 8, 8681–8686. [Google Scholar] [CrossRef]
- Bahk, J.-H.; Shakouri, A. Enhancing the thermoelectric figure of merit through the reduction of bipolar thermal conductivity with heterostructure barriers. Appl. Phys. Lett. 2014, 105, 052106. [Google Scholar] [CrossRef]
- Burke, P.G.; Curtin, B.M.; Bowers, J.E.; Gossard, A.C. Minority carrier barrier heterojunctions for improved thermoelectric efficiency. Nano Energy 2015, 12, 735–741. [Google Scholar] [CrossRef]
- Muzaffar, M.U.; Zhu, B.; Yang, Q.; Zhou, Y.; Zhang, S.; Zhang, Z.; He, J. Suppressing bipolar effect to broadening the optimum range of thermoelectric performance for p-type bismuth telluride–based alloys via calcium doping. Mater. Today Phys. 2019, 9, 100130. [Google Scholar] [CrossRef]
- Parker, D.; Singh, D.J. Thermoelectric properties of AgGaTe2 and related chalcopyrite structure materials. Phys. Rev. B 2012, 85, 125209. [Google Scholar] [CrossRef]
- Zhang, L.; Xiao, P.; Shi, L.; Henkelman, G.; Goodenough, J.B.; Zhou, J. Suppressing the bipolar contribution to the thermoelectric properties of Mg2Si0.4Sn0.6 by Ge substitution. J. Appl. Phys. 2015, 117, 155103. [Google Scholar] [CrossRef]

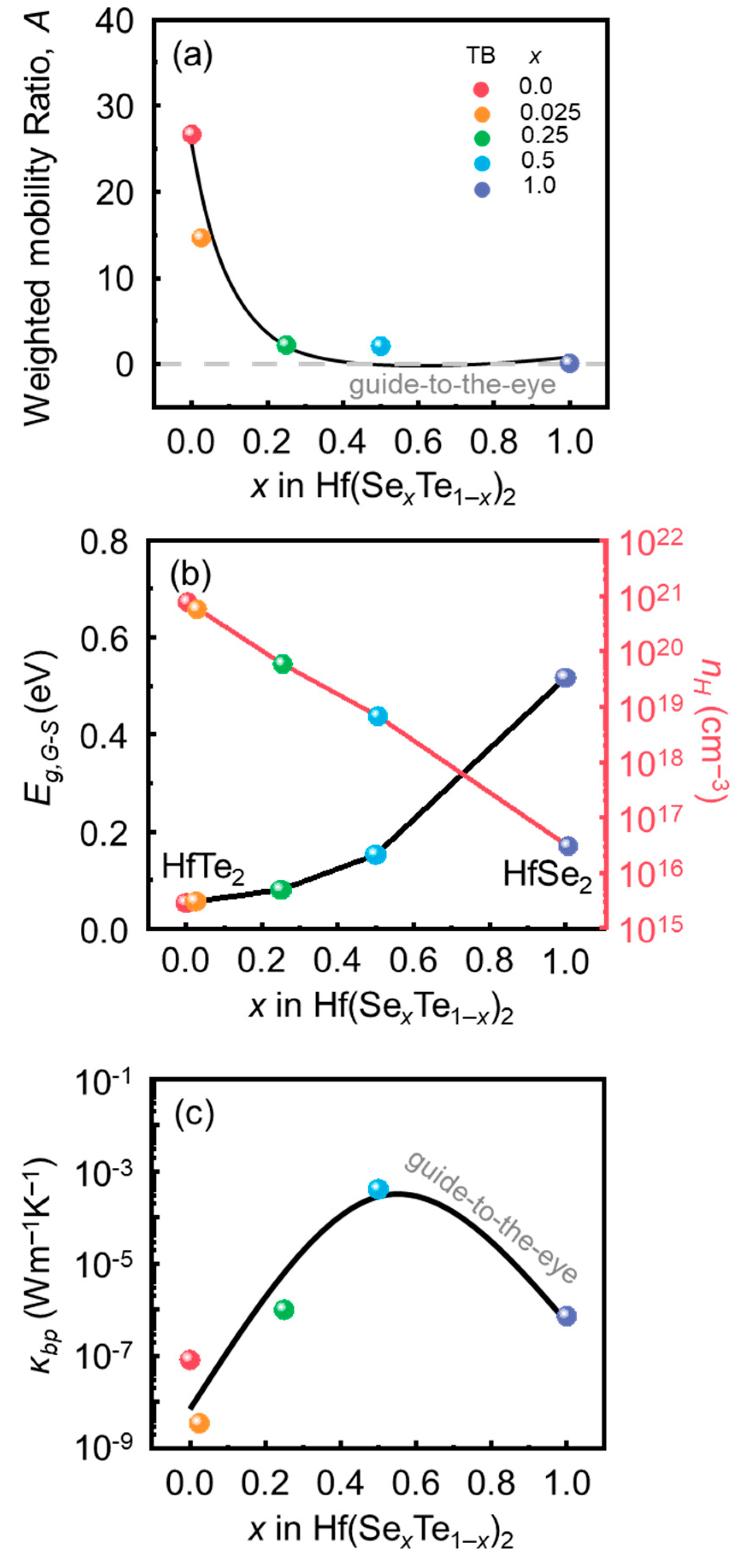
| x in Hf(Te1−xSex)2 | εg (Band gap/kBT) |
|---|---|
| 0.0 | 2.06 |
| 0.025 | 2.19 |
| 0.25 | 3.12 |
| 0.5 | 5.92 |
| 1.0 | 20.00 |
| x in Hf(Te1−xSex)2 | md,VB* (m0) | μ0,VB (cm2 V−1 s−1) | Edef,VB (eV) |
|---|---|---|---|
| 0.0 | 0.9 | 48.39 | 0.051 |
| 0.025 | 0.59 | 54.78 | 0.081 |
| 0.25 | 0.23 | 20.45 | 0.43 |
| 0.5 | 0.65 | 6.19 | 0.21 |
| 1.0 | 0.9 | 0.17 | 0.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, S.-M.; Kim, S.-i.; Kim, J.-Y.; Heo, M.; Kim, H.-S. Characterization of Bipolar Transport in Hf(Te1−xSex)2 Thermoelectric Alloys. Ceramics 2023, 6, 538-547. https://doi.org/10.3390/ceramics6010032
Hwang S-M, Kim S-i, Kim J-Y, Heo M, Kim H-S. Characterization of Bipolar Transport in Hf(Te1−xSex)2 Thermoelectric Alloys. Ceramics. 2023; 6(1):538-547. https://doi.org/10.3390/ceramics6010032
Chicago/Turabian StyleHwang, Seong-Mee, Sang-il Kim, Jeong-Yeon Kim, Minsu Heo, and Hyun-Sik Kim. 2023. "Characterization of Bipolar Transport in Hf(Te1−xSex)2 Thermoelectric Alloys" Ceramics 6, no. 1: 538-547. https://doi.org/10.3390/ceramics6010032
APA StyleHwang, S.-M., Kim, S.-i., Kim, J.-Y., Heo, M., & Kim, H.-S. (2023). Characterization of Bipolar Transport in Hf(Te1−xSex)2 Thermoelectric Alloys. Ceramics, 6(1), 538-547. https://doi.org/10.3390/ceramics6010032







