An Investigation into the Approximations Used in Wave Packet Molecular Dynamics for the Study of Warm Dense Matter
Abstract
:1. Introduction
2. Materials and Methods
2.1. Introduction to Wave-Packet Molecular Dynamics
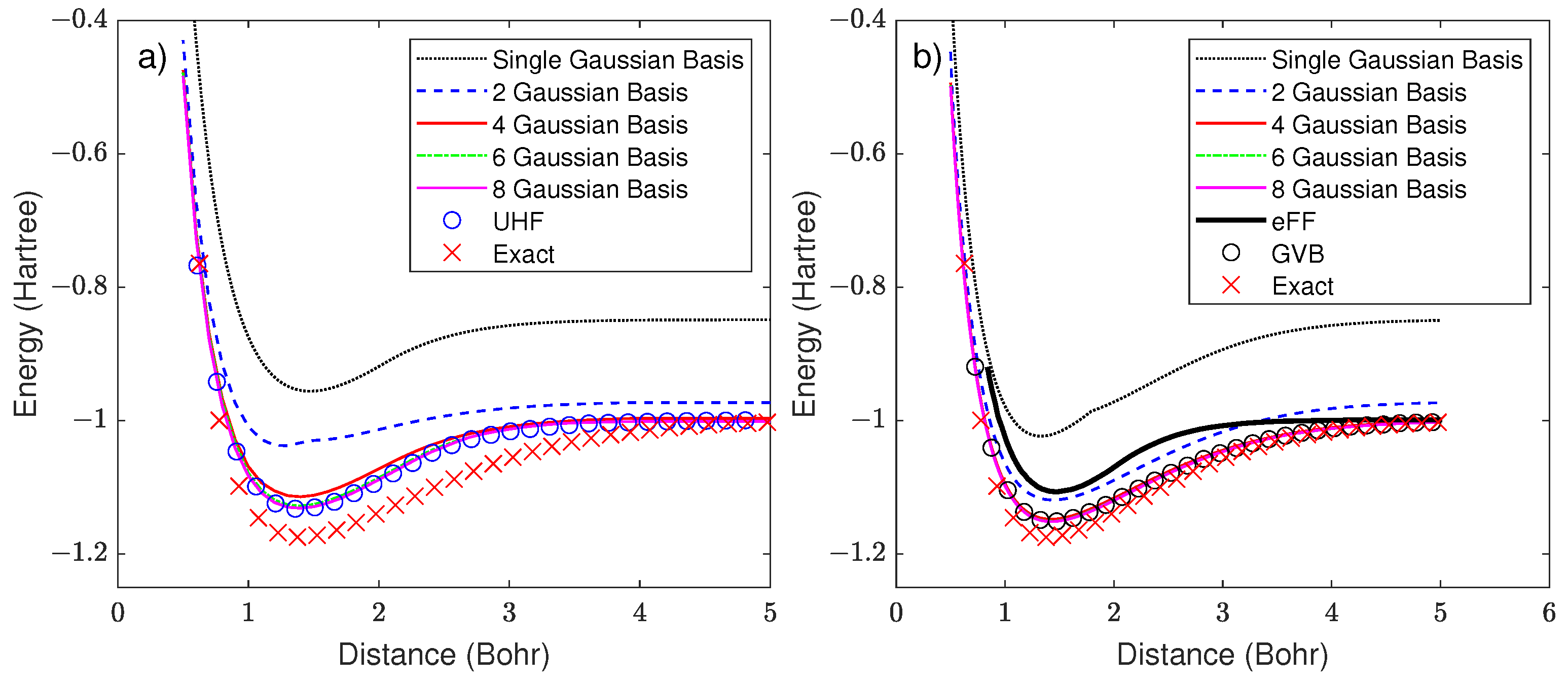
2.2. Extension to Multiple Gaussians
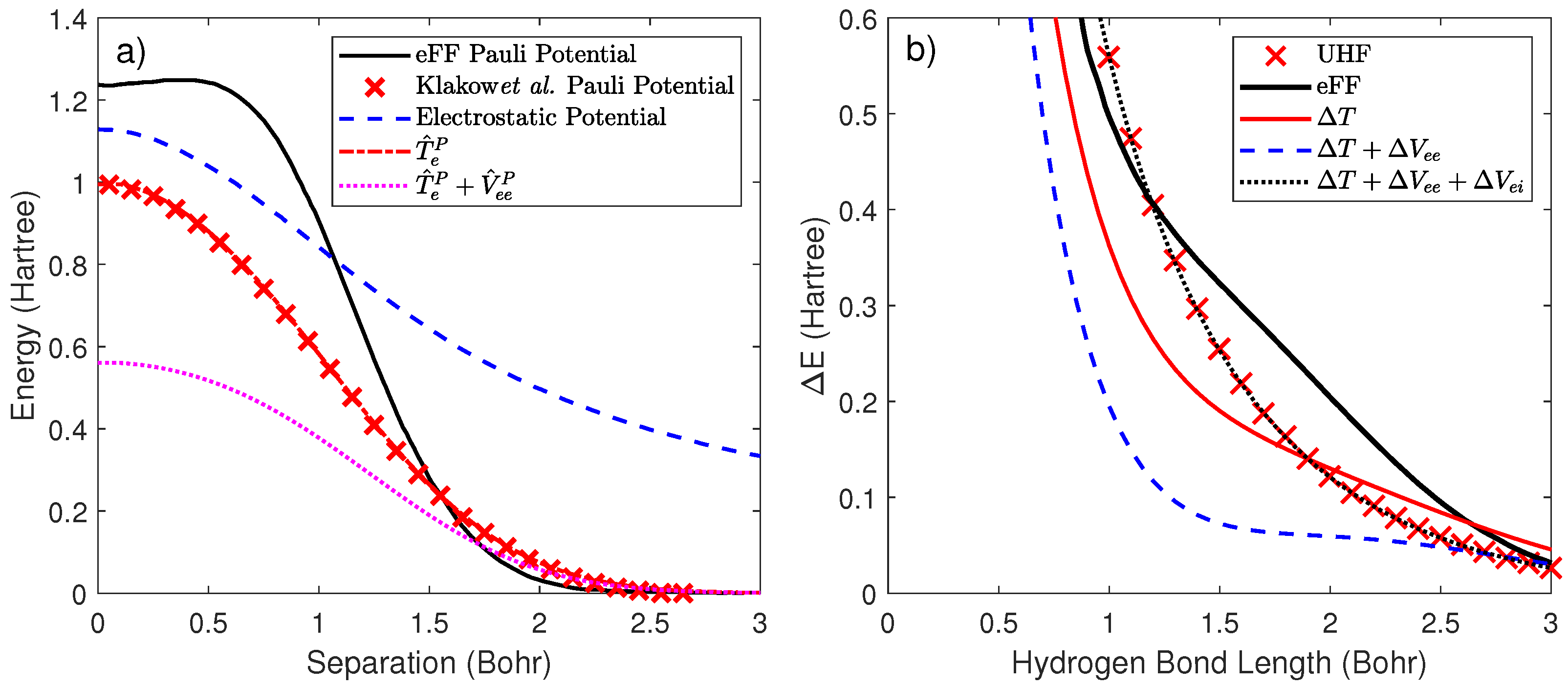
2.3. Development of a Pairwise Pauli and Correlation Potential
2.4. The Implementation of Periodic Boundary Conditions
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guillot, T. A Comparison of the Interiors of Jupiter and Saturn. Planet. Space Sci. 1999, 47, 1183–1200. [Google Scholar] [CrossRef] [Green Version]
- Paquette, C.; Pelletier, C.; Fontaine, G.; Michaud, G. Diffusion Coefficients for Stellar Plasmas. ApJS 1986, 61, 177–195. [Google Scholar] [CrossRef]
- Atzeni, S.; Meyer-ter-Vehn, J. Thermonuclear Fusion and Confinement. In The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter, 1st ed.; Clarendon Press: Oxford, UK, 2004; Volume 125, pp. 31–36. [Google Scholar]
- Ichimaru, S. Strongly Coupled Plasmas: High-Density Classical Plasmas and Degenerate Electron Liquids. Rev. Mod. Phys. 1982, 54, 1017–1059. [Google Scholar] [CrossRef]
- Davis, R.A.; Angermeier, W.A.; Hermsmeier, R.K.T.; White, T.G. Ion Modes in Dense Ionized Plasmas through Nonadiabatic Molecular Dynamics. Phys. Rev. Res. 2020, 2, 043139. [Google Scholar] [CrossRef]
- Yao, Y.; Zeng, Q.; Chen, K.; Kang, D.; Hou, Y.; Ma, Q.; Dai, J. Reduced Ionic Diffusion by the Dynamic Electron–Ion Collisions in Warm Dense Hydrogen. Phys. Plasmas 2021, 28, 012704. [Google Scholar] [CrossRef]
- Lorenzen, W.; Becker, A.; Redmer, R. Progress in Warm Dense Matter and Planetary Physics. In Frontiers and Challenges in Warm Dense Matter; Graziani, F., Desjarlais, M.P., Redmer, R., Trickey, S.B., Eds.; Lecture Notes in Computational Science and Engineering; Springer International Publishing: Cham, Switzerland, 2014; pp. 203–234. [Google Scholar]
- Grabowski, P.E.; Hansen, S.B.; Murillo, M.S.; Stanton, L.G.; Graziani, F.R.; Zylstra, A.B.; Baalrud, S.D.; Arnault, P.; Baczewski, A.D.; Benedict, L.X.; et al. Review of the First Charged-Particle Transport Coefficient Comparison Workshop. High Energy Density Phys. 2020, 37, 100905. [Google Scholar] [CrossRef]
- Salin, G.; Caillol, J.M. Equilibrium Molecular Dynamics Simulations of the Transport Coefficients of the Yukawa One Component Plasma. Phys. Plasmas 2003, 10, 1220–1230. [Google Scholar] [CrossRef]
- White, T.G.; Richardson, S.; Crowley, B.J.B.; Pattison, L.K.; Harris, J.W.O.; Gregori, G. Orbital-Free Density-Functional Theory Simulations of the Dynamic Structure Factor of Warm Dense Aluminum. Phys. Rev. Lett. 2013, 111, 175002. [Google Scholar] [CrossRef] [Green Version]
- Mabey, P.; Richardson, S.; White, T.G.; Fletcher, L.B.; Glenzer, S.H.; Hartley, N.J.; Vorberger, J.; Gericke, D.O.; Gregori, G. A Strong Diffusive Ion Mode in Dense Ionized Matter Predicted by Langevin Dynamics. Nat. Commun. 2017, 8, 14125. [Google Scholar] [CrossRef] [Green Version]
- Graziani, F.R.; Batista, V.S.; Benedict, L.X.; Castor, J.I.; Chen, H.; Chen, S.N.; Fichtl, C.A.; Glosli, J.N.; Grabowski, P.E.; Graf, A.T.; et al. Large-Scale Molecular Dynamics Simulations of Dense Plasmas: The Cimarron Project. High Energy Density Phys. 2012, 8, 105–131. [Google Scholar] [CrossRef]
- Rüter, H.R.; Redmer, R. Ab Initio Simulations for the Ion-Ion Structure Factor of Warm Dense Aluminum. Phys. Rev. Lett. 2014, 112, 145007. [Google Scholar] [CrossRef]
- Kang, D.; Hou, Y.; Zeng, Q.; Dai, J. Unified First-Principles Equations of State of Deuterium-Tritium Mixtures in the Global Inertial Confinement Fusion Region. Matter Radiat. Extrem. 2020, 5, 055401. [Google Scholar] [CrossRef]
- Clérouin, J.; Robert, G.; Arnault, P.; Ticknor, C.; Kress, J.D.; Collins, L.A. Evidence for Out-of-Equilibrium States in Warm Dense Matter Probed by x-Ray Thomson Scattering. Phys. Rev. E 2015, 91, 011101. [Google Scholar] [CrossRef] [Green Version]
- Dai, J.; Yuan, J. Large-Scale Efficient Langevin Dynamics, and Why It Works. EPL 2009, 88, 20001. [Google Scholar] [CrossRef]
- Tamm, A.; Caro, M.; Caro, A.; Samolyuk, G.; Klintenberg, M.; Correa, A.A. Langevin Dynamics with Spatial Correlations as a Model for Electron-Phonon Coupling. Phys. Rev. Lett. 2018, 120, 185501. [Google Scholar] [CrossRef] [Green Version]
- Duffy, D.M.; Rutherford, A.M. Including the Effects of Electronic Stopping and Electron–Ion Interactions in Radiation Damage Simulations. J. Phys. Condens. Matter 2007, 19, 016207. [Google Scholar] [CrossRef]
- Rutherford, A.M.; Duffy, D.M. The Effect of Electron–Ion Interactions on Radiation Damage Simulations. J. Phys. Condens. Matter 2007, 19, 496201. [Google Scholar] [CrossRef]
- Larder, B.; Gericke, D.O.; Richardson, S.; Mabey, P.; White, T.G.; Gregori, G. Fast Nonadiabatic Dynamics of Many-Body Quantum Systems. Sci. Adv. 2019, 5, eaaw1634. [Google Scholar] [CrossRef] [Green Version]
- Moldabekov, Z.A.; Dornheim, T.; Gregori, G.; Graziani, F.; Bonitz, M.; Cangi, A. The Quantum Bohm Potential for Many-Fermion Systems. arXiv 2021, arXiv:2103.08523. [Google Scholar]
- Klakow, D.; Toepffer, C. Hydrogen under Extreme Conditions. Phys. Lett. A 1994, 192, 55–59. [Google Scholar] [CrossRef]
- Knaup, M.; Zwicknagel, G.; Reinhard, P.G.; Toepffer, C. Wave Packet Molecular Dynamics Simulations of Hydrogen under Extreme Conditions. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 464, 267–270. [Google Scholar] [CrossRef]
- Jakob, B.; Reinhard, P.G.; Toepffer, C.; Zwicknagel, G. Wave Packet Simulation of Dense Hydrogen. Phys. Rev. E 2007, 76, 036406. [Google Scholar] [CrossRef]
- Su, J.T.; Goddard, W.A. Excited Electron Dynamics Modeling of Warm Dense Matter. Phys. Rev. Lett. 2007, 99, 185003. [Google Scholar] [CrossRef] [Green Version]
- Lavrinenko, Y.S.; Morozov, I.V.; Valuev, I.A. Thermodynamic Properties of the Nonideal Hydrogen Plasmas: Comparison of Different Simulation Techniques. J. Phys. Conf. Ser. 2018, 946, 012097. [Google Scholar] [CrossRef]
- Jaramillo-Botero, A.; Su, J.; Qi, A.; Goddard, W.A. Large-Scale, Long-Term Nonadiabatic Electron Molecular Dynamics for Describing Material Properties and Phenomena in Extreme Environments. J. Comput. Chem. 2011, 32, 497–512. [Google Scholar] [CrossRef]
- Kim, H.; Su, J.T.; Goddard, W.A. High-Temperature High-Pressure Phases of Lithium from Electron Force Field (eFF) Quantum Electron Dynamics Simulations. Proc. Natl. Acad. Sci. USA 2011, 108, 15101–15105. [Google Scholar] [CrossRef] [Green Version]
- Ma, Q.; Dai, J.; Kang, D.; Murillo, M.S.; Hou, Y.; Zhao, Z.; Yuan, J. Extremely Low Electron-Ion Temperature Relaxation Rates in Warm Dense Hydrogen: Interplay between Quantum Electrons and Coupled Ions. Phys. Rev. Lett. 2019, 122, 015001. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Tully, J.C.; Schlegel, H.B.; Frisch, M.J. Ab Initio Ehrenfest Dynamics. J. Chem. Phys. 2005, 123, 084106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feldmeier, H.; Schnack, J. Molecular Dynamics for Fermions. Rev. Mod. Phys. 2000, 72, 655–688. [Google Scholar] [CrossRef] [Green Version]
- Su, J.T.; Goddard, W.A. The Dynamics of Highly Excited Electronic Systems: Applications of the Electron Force Field. J. Chem. Phys. 2009, 131, 244501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grabowski, P.E. A Review of Wave Packet Molecular Dynamics. In Frontiers and Challenges in Warm Dense Matter; Graziani, F., Desjarlais, M.P., Redmer, R., Trickey, S.B., Eds.; Lecture Notes in Computational Science and Engineering; Springer International Publishing: Cham, Switzerland, 2014; pp. 265–282. [Google Scholar]
- Boal, D.H.; Glosli, J.N. Quasiparticle Model for Nuclear Dynamics Studies: Ground-State Properties. Phys. Rev. C 1988, 38, 1870–1878. [Google Scholar] [CrossRef] [PubMed]
- Morozov, I.V.; Valuev, I.A. Localization Constraints in Gaussian Wave Packet Molecular Dynamics of Nonideal Plasmas. J. Phys. A Math. Theory 2009, 42, 214044. [Google Scholar] [CrossRef]
- Grabowski, P.E.; Markmann, A.; Morozov, I.V.; Valuev, I.A.; Fichtl, C.A.; Richards, D.F.; Batista, V.S.; Graziani, F.R.; Murillo, M.S. Wave Packet Spreading and Localization in Electron-Nuclear Scattering. Phys. Rev. E 2013, 87, 063104. [Google Scholar] [CrossRef] [Green Version]
- Xiao, H.; Jaramillo-Botero, A.; Theofanis, P.L.; Goddard, W.A. Non-Adiabatic Dynamics Modeling Framework for Materials in Extreme Conditions. Mech. Mater. 2015, 90, 243–252. [Google Scholar] [CrossRef] [Green Version]
- Lan, M.; Yang, Z.H.; Wang, X. Displacement Damage in Silicon Studied by the Electronic Force Field Method in the keV Regime. Comput. Mater. Sci. 2020, 179, 109697. [Google Scholar] [CrossRef]
- Fletcher, L.B.; Lee, H.J.; Döppner, T.; Galtier, E.; Nagler, B.; Heimann, P.; Fortmann, C.; Lepape, S.; Ma, T.; Millot, M.; et al. Ultrabright X-Ray Laser Scattering for Dynamic Warm Dense Matter Physics. Nat. Photonics 2015, 9, 274–279. [Google Scholar] [CrossRef]
- Knaup, M.; Reinhard, P.G.; Toepffer, C.; Zwicknagel, G. Wave Packet Molecular Dynamics Simulations of Hydrogen at Mbar Pressures. Comput. Phys. Commun. 2002, 147, 202–204. [Google Scholar] [CrossRef]
- Knaup, M.; Reinhard, P.G.; Toepffer, C.; Zwicknagel, G. Wave Packet Molecular Dynamics Simulations of Warm Dense Hydrogen. J. Phys. A Math. Gen. 2003, 36, 6165–6171. [Google Scholar] [CrossRef]
- Morozov, I.V.; Valuev, I.A. Improvement of Wave Packet Molecular Dynamics Using Packet Splitting. Contrib. Plasma Phys. 2012, 52, 140–144. [Google Scholar] [CrossRef]
- Valuev, I.A.; Morozov, I.V. Extension of the Wave Packet Molecular Dynamics Method towards the Accurate Quantum Simulations of Electron Dynamics. J. Phys. Conf. Ser. 2015, 653, 012153. [Google Scholar] [CrossRef] [Green Version]
- Cohen-Tannoudji, C.; Diu, B.; Laloë, F. Quantum Mechanics, Volume 1: Basic Concepts, Tools, and Applications, 1st ed.; Wiley: New York, NY, USA, 1977; Volume 1. [Google Scholar]
- Xiao, H. First Principles Based Multiparadigm Modeling of Electronic Structures and Dynamics. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2015. [Google Scholar] [CrossRef]
- Boys, S.F.; Egerton, A.C. Electronic Wave Functions—I. A General Method of Calculation for the Stationary States of Any Molecular System. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1950, 200, 542–554. [Google Scholar] [CrossRef]
- Littlejohn, R.G. The Semiclassical Evolution of Wave Packets. Phys. Rep. 1986, 138, 193–291. [Google Scholar] [CrossRef] [Green Version]
- Zwicknagel, G.; Pschiwul, T. WPMD Simulations of a Two-Component Plasma. J. Phys. A Math. Gen. 2006, 39, 4359–4364. [Google Scholar] [CrossRef]
- Löwdin, P.O. Quantum Theory of Many-Particle Systems. III. Extension of the Hartree-Fock Scheme to Include Degenerate Systems and Correlation Effects. Phys. Rev. 1955, 97, 1509–1520. [Google Scholar] [CrossRef]
- Lavrinenko, Y.S.; Morozov, I.V.; Valuev, I.A. Wave Packet Molecular Dynamics–Density Functional Theory Method for Non-Ideal Plasma and Warm Dense Matter Simulations. Contrib. Plasma Phys. 2019, 59, e201800179. [Google Scholar] [CrossRef]
- Chachiyo, T.; Chachiyo, H. Understanding Electron Correlation Energy through Density Functional Theory. Comput. Theor. Chem. 2020, 1172, 112669. [Google Scholar] [CrossRef] [Green Version]
- Lavrinenko, Y.S.; Morozov, I.V.; Valuev, I.A. High Performance Wave Packet Molecular Dynamics with Density Functional Exchange-Correlation Term for Non-Ideal Plasma Simulations. J. Phys. Conf. Ser. 2021, 1787, 012043. [Google Scholar] [CrossRef]
- Su, J.T.l. An Electron Force Field for Simulating Large Scale Excited Electron Dynamics. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2007. [Google Scholar] [CrossRef]
- Izvekov, S.; Swanson, J.M.J.; Voth, G.A. Coarse-Graining in Interaction Space: A Systematic Approach for Replacing Long-Range Electrostatics with Short-Range Potentials. J. Phys. Chem. B 2008, 112, 4711–4724. [Google Scholar] [CrossRef]
- Dickenson, G.D.; Niu, M.L.; Salumbides, E.J.; Komasa, J.; Eikema, K.S.E.; Pachucki, K.; Ubachs, W. Fundamental Vibration of Molecular Hydrogen. Phys. Rev. Lett. 2013, 110, 193601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics: Volume 5, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Loubeyre, P.; LeToullec, R.; Hausermann, D.; Hanfland, M.; Hemley, R.J.; Mao, H.K.; Finger, L.W. X-Ray Diffraction and Equation of State of Hydrogen at Megabar Pressures. Nature 1996, 383, 702–704. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angermeier, W.A.; White, T.G. An Investigation into the Approximations Used in Wave Packet Molecular Dynamics for the Study of Warm Dense Matter. Plasma 2021, 4, 294-308. https://doi.org/10.3390/plasma4020020
Angermeier WA, White TG. An Investigation into the Approximations Used in Wave Packet Molecular Dynamics for the Study of Warm Dense Matter. Plasma. 2021; 4(2):294-308. https://doi.org/10.3390/plasma4020020
Chicago/Turabian StyleAngermeier, William A., and Thomas G. White. 2021. "An Investigation into the Approximations Used in Wave Packet Molecular Dynamics for the Study of Warm Dense Matter" Plasma 4, no. 2: 294-308. https://doi.org/10.3390/plasma4020020
APA StyleAngermeier, W. A., & White, T. G. (2021). An Investigation into the Approximations Used in Wave Packet Molecular Dynamics for the Study of Warm Dense Matter. Plasma, 4(2), 294-308. https://doi.org/10.3390/plasma4020020





