Evaluating the Drought Code Using In Situ Drying Timelags of Feathermoss Duff in Interior Alaska
Abstract
:1. Introduction
2. Objectives
- 1
- Determine the depth, bulk density, weight, and water storage capacity of black spruce-feathermoss duff from Wilmore’s measurements.
- 2
- Determine the properties of the soil represented by the water balance model of the DC by using measurements of water storage capacity, in situ drying timelag of the duff profile, and known soil attributes. Sequentially, this process is:
- 2.1
- Determine the drying timelag of a black spruce-feathermoss forest floor using a time series of in situ measurements of water storage and the relationships in Equation (1). Similarly calculate timelags of the DC over the same drying periods.
- 2.2
- Determine the potential evaporation rate at the surface of the forest floor from measurements of the water storage capacity (Obj. 1) and in situ drying timelag (Obj. 2.1) using Equation (1).
- 2.3
- Use the potential evaporation rate at the forest floor from Obj. 2.2 to determine the water storage capacity of the “DC equivalent soil” by setting the timelag in Equation (1) equal to the corresponding timelag of the DC.
- 2.4
- Determine the depth of the “DC equivalent soil” using its water storage capacity (Obj. 2.3) and measurements of component horizon bulk density, thickness, and maximum gravimetric moisture content from Obj. 1 using Equation (4).
3. Methods
3.1. Study Site
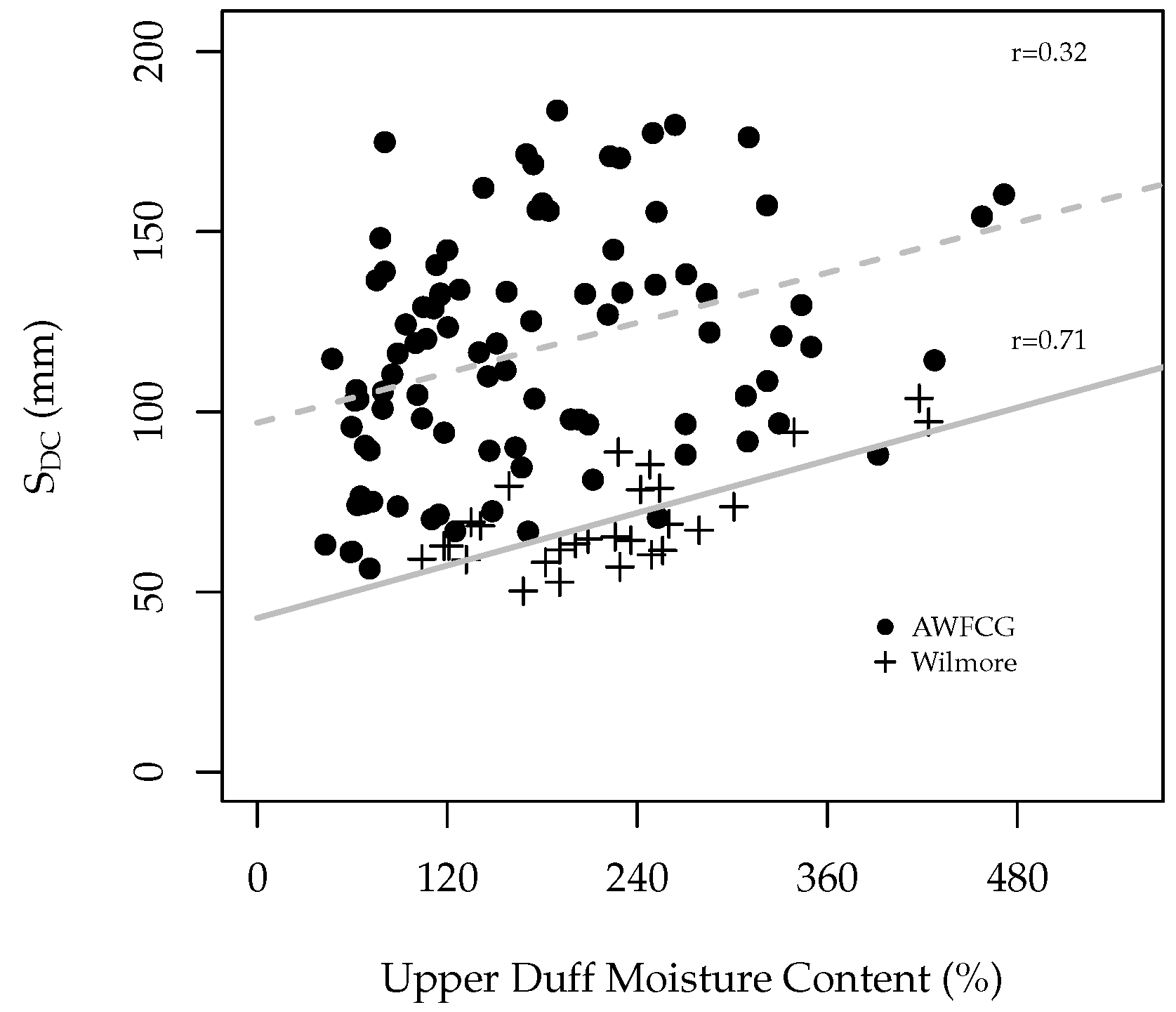
3.2. Soil Attributes (Obj. 1)
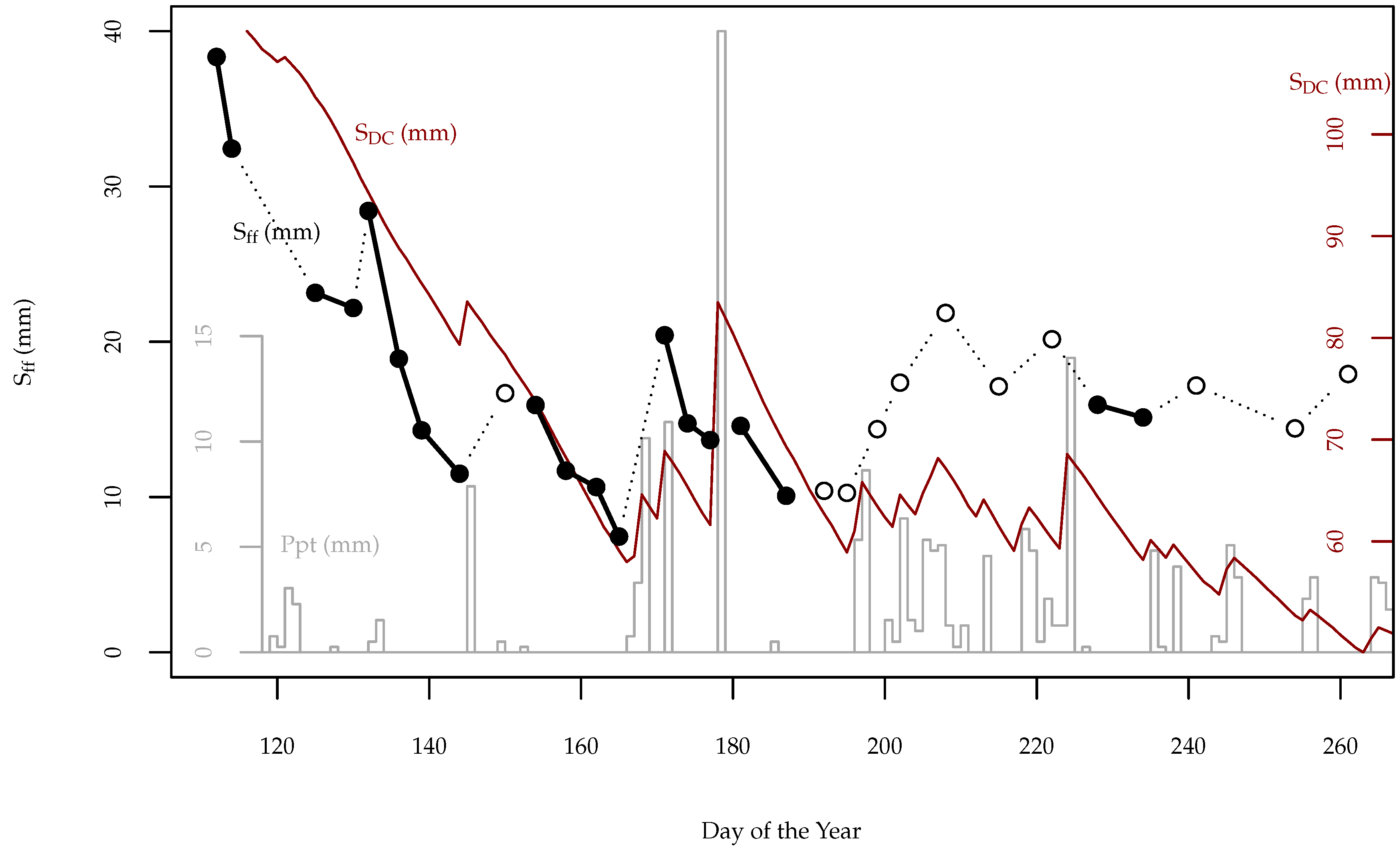
3.3. Determination of Timelags (Obj. 2.1)
3.4. Estimation of the Attributes of the “DC equivalent soil” (Obj. 2.2–2.4)
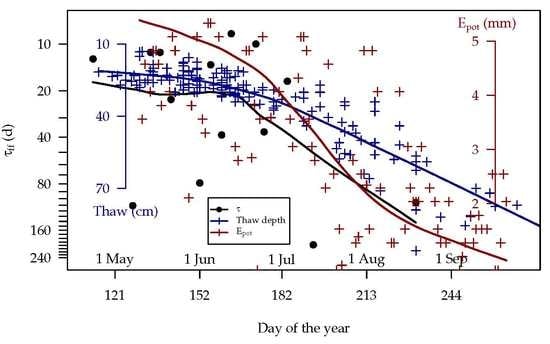
3.5. Evaporimeter and Thaw Depth Measurements
4. Results
4.1. Soil Attributes (Obj. 1)
4.2. Duff Timelag (Obj. 2.1)
4.3. Attributes of the “DC Equivalent Soil” (Obj. 2.2–2.4)
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| Abbreviations | |
| DC | Drought Code |
| DMC | Duff Moisture Code |
| FFMC | Fine Fuel Moisture Code |
| FWI | Canadian Forest Fire Weather Index System |
| Variables | |
| D | Drought Code (Unitless) |
| Actual evaporation (mm) | |
| Potential evaporation (mm) | |
| Gravimetric moisture content (%) | |
| Volumetric moisture content (mm3 mm−3 or mm mm−1) | |
| S | Water storage depth (mm) |
| t | Elapsed time (d) |
| w | Soil weight (mg mm−2) |
| Depth or thickness (mm) | |
| Soil bulk density (mg mm−3) | |
| Density of water (mg mm−3) | |
| Timelag (d) | |
| Subscripts | |
| Initial or yesterday’s value | |
| Of the DC | |
| Of the “DC equivalent soil” | |
| Of the in situ forest floor soil | |
| Equilibrium | |
| Maximum | |
| Conversions | |
| w | 1 mg mm−2 = 1 kg m−2 |
| 1000 mm = 1 m | |
| 1 mg mm−3 = 1000 kg m−3 |
References
- Byram, G.M.; Nelson, R.M. An Analysis of the Drying Process in Forest Fuel Material; Technical Report; e-General Technical Report SRS-200; U.S. Forest Service, Southern Research Station: Asheville, NC, USA, 2015.
- Nelson, R.M. Some Factors Affecting the Moisture Timelags of Woody Materials; Technical Report; Research Paper SE-44; U.S. Forest Service, Southeastern Forest Experiment Station: Asheville, NC, USA, 1969.
- Van Wagner, C.E. A laboratory study of weather effects on the drying rate of jack pine litter. Can. J. For. Res. 1979, 9, 267–275. [Google Scholar] [CrossRef]
- Van Wagner, C.E. Development and Structure of the Canadian Forest Fire Weather Index System; Technical Report; Forestry Technical Report 35; Canadian Forestry Service: Ottawa, ON, Canada, 1987.
- Van Wagner, C.E. Drought, timelag, and fire danger rating. In Eighth Conference on Fire and Forest Meteorology; Society of American Foresters: Detroit, MI, USA, 1985; pp. 178–185. [Google Scholar]
- Miller, E.A. Moisture sorption models for fuel beds of standing dead grass in Alaska. Fire 2019, 2, 2. [Google Scholar] [CrossRef] [Green Version]
- Mutch, R.W.; Gastineau, O.W. Timelag and Equilibrium Moisture Content of Reindeer Lichen; Technical Report; Research Paper INT-76; U.S. Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1970.
- Stocks, B.J.; Lawson, B.D.; Alexander, M.E.; Van Wagner, C.E.; McAlpine, R.S.; Lynham, T.J.; Dube, D.E. The Canadian Forest Fire Danger Rating System: An overview. For. Chron. 1989, 65, 450–457. [Google Scholar] [CrossRef]
- Turner, J.A. The Stored Moisture Index: A Guide to Slash Burning; Technical Report; British Columbia Forest Service, Protection Division: Powell River, BC, Canada, 1966.
- Turner, J.A. The Drought Code Component of the Canadian Forest Fire Behavior System; Technical Report; Publication No. 1316; Environment Canada, Canadian Forestry Service, Headquarters: Ottawa, ON, Canada, 1972.
- Hanks, R.J.; Ashcroft, G.L. Applied Soil Physics: Soil Water and Temperature Applications; OCLC: 5029519; Springer: Berlin, Germany; New York, NY, USA, 1980. [Google Scholar]
- Miller, E.A. A Conceptual Interpretation of the Drought Code of the Canadian Forest Fire Weather Index System. Fire 2020, 3, 23. [Google Scholar] [CrossRef]
- Rorig, M.; Furguson, S.; Sandberg, D. Fire weather indexes and fuel condition in Alaska. In Proceedings of Fire Conference 2000: The First National Congress on Fire Ecology, Prevention, and Management; Galley, K., Klinger, R., Sugihara, N., Eds.; Tall Timbers Research Station: Tallahasee, FL, USA, 2003; pp. 202–210. [Google Scholar]
- Jandt, R.; Allen, J.; Horschel, E. Forest Floor Moisture Content and Fire Danger Indices in Alaska; Technical Report; Alaska Technical Report 54; U. S. Department of the Interior, Bureau of Land Management: Anchorage, AK, USA, 2005.
- Barnes, J.; Miller, E.; Saperstein, L. Duff Fuel Moisture and FWI Codes, 2012–2014; Summit on the Canadian Forest Fire Danger Rating System in Alaska: Fort Wainwright, AK, USA, 2014.
- Miller, E.; Barnes, J. Duff Moisture to Code Conversion Equations For Alaska; Summit on the Canadian Forest Fire Danger Rating System in Alaska: Fort Wainwright, AK, USA, 2014.
- Wilmore, B. Duff Moisture Dynamics in Black Spruce Feather Moss Stands and Their Relation to the Canadian Forest Fire Danger Rating System. Master’s Thesis, University of Alaska Fairbanks, Fairbanks, AK, USA, 2001. [Google Scholar]
- AWFCG. Alaska Interagency Records of Duff Moisture Content; Technical Report; Alaska Wildland Fire Coordinating Group, Bureau of Land Management, Alaska Fire Service: Fort Wainwright, AK, USA, 2019.
- Brandt, J.P. The extent of the North American boreal zone. Environ. Rev. 2009, 17, 101–161. [Google Scholar] [CrossRef]
- Brown, J.; Ferrians, O.; Heginbottom, J.A.; Melnikov, E. Circum-Arctic Map of Permafrost and Ground-Ice Conditions; Version 2; US Geological Survey Reston: Reston, VA, USA, 2002.
- Muraro, S.; Lawson, B. Prediction of Duff Moisture Distribution for Prescribed Burning; Technical Report; Information Report BC-X-046; Government of Canada, Department of Fisheries and Forestry, Forest Research Laboratory: Victoria, BC, Canada, 1970.
- Van Wagner, C.E. An Index to Estimate the Current Moisture Content of the Forest Floor; Technical Report; Publication No. 1288; Canadian Forest Service: Ottawa, ON, Canada, 1970.
- Taylor, S.W.; Alexander, M.E. Field guide to the Canadian Forest Fire Behavior Prediction (FBP) System, 3rd ed.; Special Report 11; Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 2018.
- Farnsworth, R.K.; Thompson, E.S. Mean Monthly, Seasonal, and Annual Pan Evaporation for the United States; Technical Report; NOAA Technical Report NWS 34; U.S. National Oceanic and Atmospheric Association, National Weather Service: Washington, DC, USA, 1982.
- White, J.D.; Koepke, B.E.; Swanson, D.K. Soil Survey of North Star Area, Alaska; Technical Report; U.S. Department of Agriculture, National Resources Conservation Service: Washington, DC, USA, 2000.
- McMahon, T.A.; Peel, M.C.; Lowe, L.; Srikanthan, R.; McVicar, T.R. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 1331–1363. [Google Scholar] [CrossRef] [Green Version]
- Heijmans, M.M.P.D.; Arp, W.J.; Chapin, F.S. Controls on moss evaporation in a boreal black spruce forest. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef]
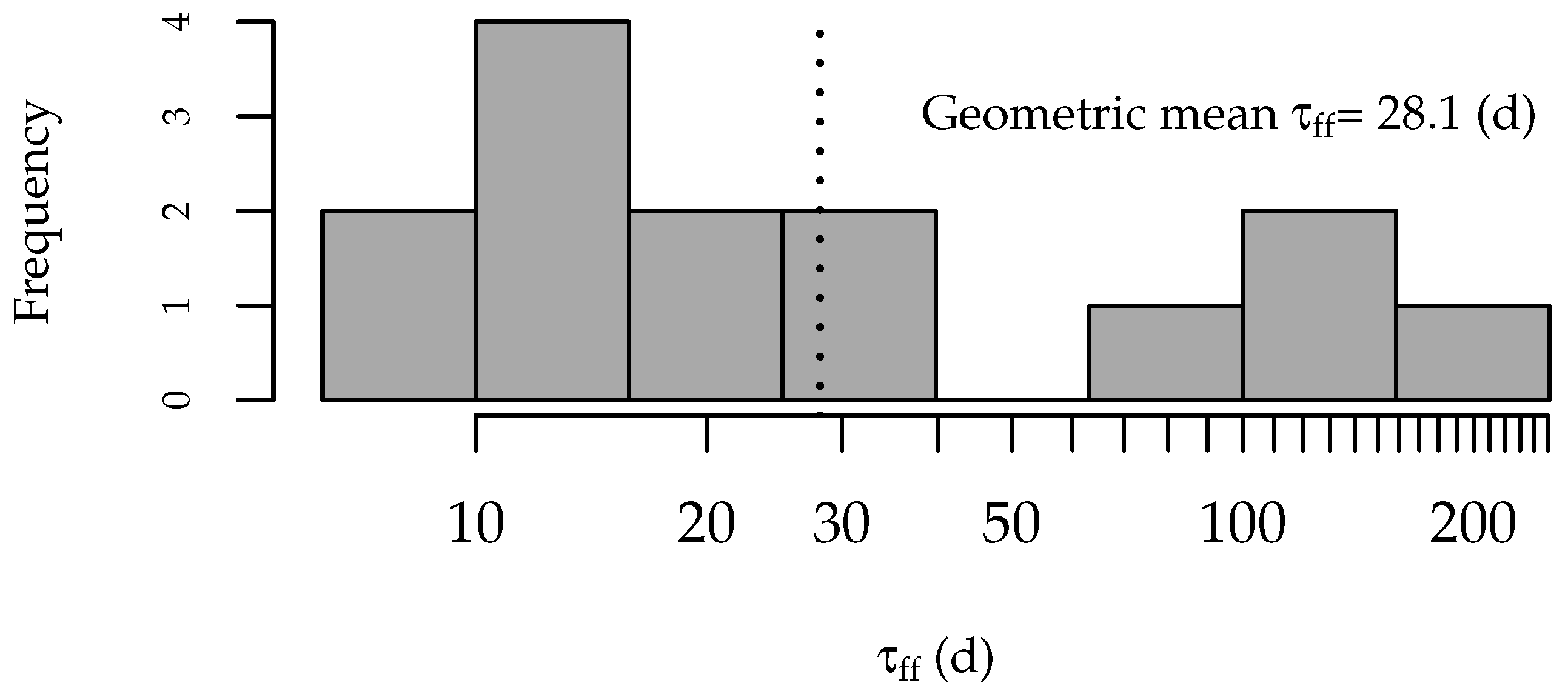
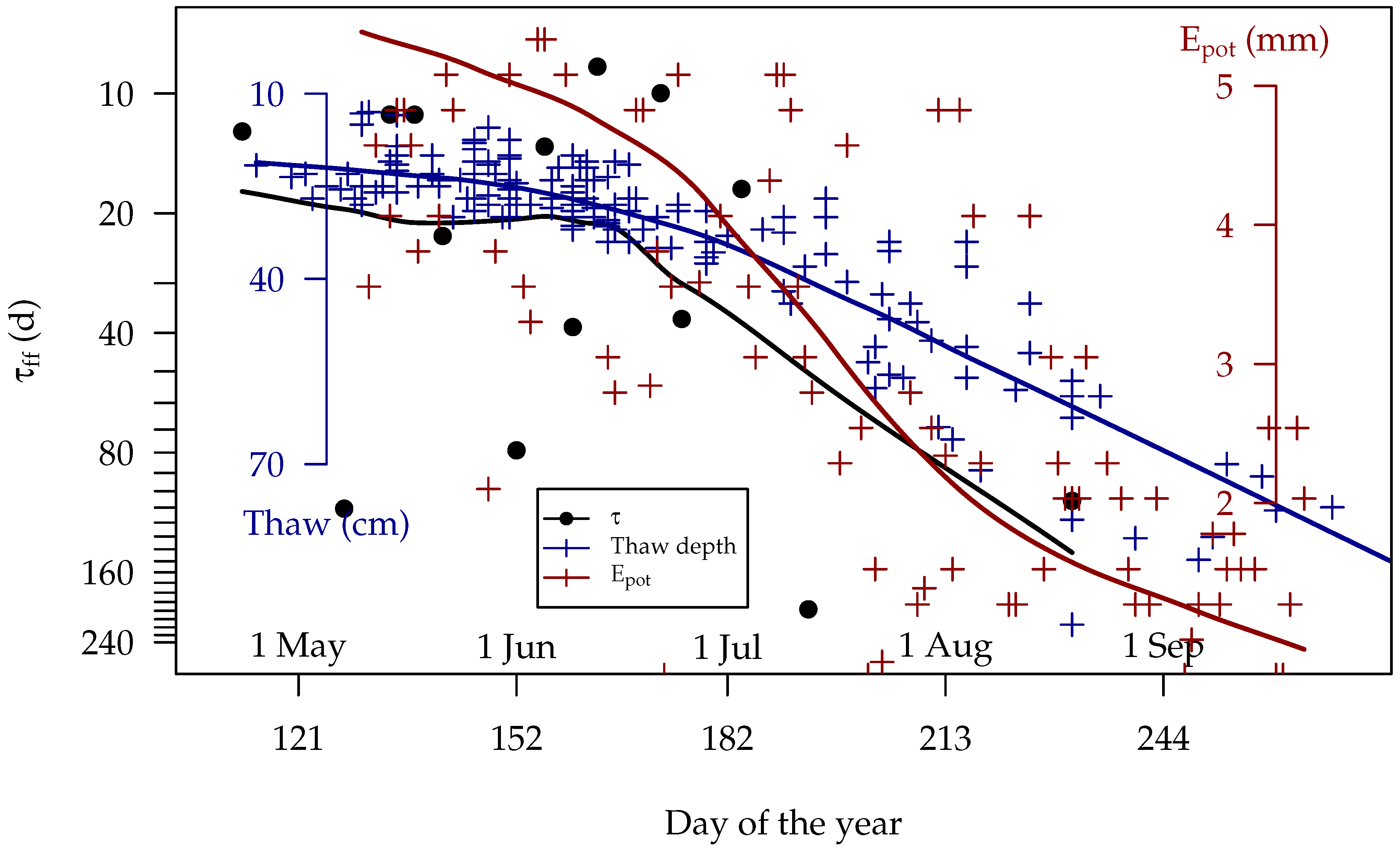
| Moisture Code | (mm) | Timelag (d) | Depth (mm) | Weight (mg mm−2) |
|---|---|---|---|---|
| FFMC | 0.6 | 0.67 | 12 | 0.25 |
| DMC | 15 | 12 | 70 | 5 |
| DC | 100 | 52 | 180 | 25 |
| Duff | Approximate | Corresponding |
|---|---|---|
| Horizon | Thickness (mm) [18] | Moisture Code |
| Live Moss | 0–30 | FFMC |
| Dead Moss | 30–80 | DMC |
| Upper Duff | 80–150 | DC |
| Lower Duff | 150–200 | – |
| Mineral soil | 200+ | – |
| Soil Type | Horizon | Bulk Density | Thickness | Weight | |
|---|---|---|---|---|---|
| (mm) | (mg mm−3) | (mm) | (mg mm−2) | (mm) | |
| Organic | 0–50 | 0.017 | 50 | 0.85 | 3.4 |
| 50–100 | 0.025 | 50 | 1.25 | 5.0 | |
| 100–150 | 0.042 | 50 | 2.10 | 8.4 | |
| 150–200 | 0.070 | 50 | 3.50 | 14.0 | |
| Mineral | Each 50 mm | 1.40 | 50 | 70 | 10.5 |
| Soil Type | Profile | Bulk Density | Weight | ||
|---|---|---|---|---|---|
| (mm) | (mg mm−3) | (mg mm−2) | (%) | (mm) | |
| Organic | 0–50 | 0.017 | 0.85 | 400 | 3.4 |
| 0–100 | 0.021 | 2.1 | 400 | 8.4 | |
| 0–150 | 0.028 | 4.2 | 400 | 17 | |
| 0–200 | 0.039 | 7.7 | 400 | 31 | |
| Organic + Mineral | 0–366 | 0.62 | 227 | 29 | 66 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miller, E.A.; Wilmore, B. Evaluating the Drought Code Using In Situ Drying Timelags of Feathermoss Duff in Interior Alaska. Fire 2020, 3, 25. https://doi.org/10.3390/fire3020025
Miller EA, Wilmore B. Evaluating the Drought Code Using In Situ Drying Timelags of Feathermoss Duff in Interior Alaska. Fire. 2020; 3(2):25. https://doi.org/10.3390/fire3020025
Chicago/Turabian StyleMiller, Eric A., and Brenda Wilmore. 2020. "Evaluating the Drought Code Using In Situ Drying Timelags of Feathermoss Duff in Interior Alaska" Fire 3, no. 2: 25. https://doi.org/10.3390/fire3020025
APA StyleMiller, E. A., & Wilmore, B. (2020). Evaluating the Drought Code Using In Situ Drying Timelags of Feathermoss Duff in Interior Alaska. Fire, 3(2), 25. https://doi.org/10.3390/fire3020025