The Post-Fire Assembly Processes of Tree Communities Based on Spatial Analysis of a Sierra Nevada Mixed-Conifer Forest
Abstract
:1. Introduction
2. Materials and Methods
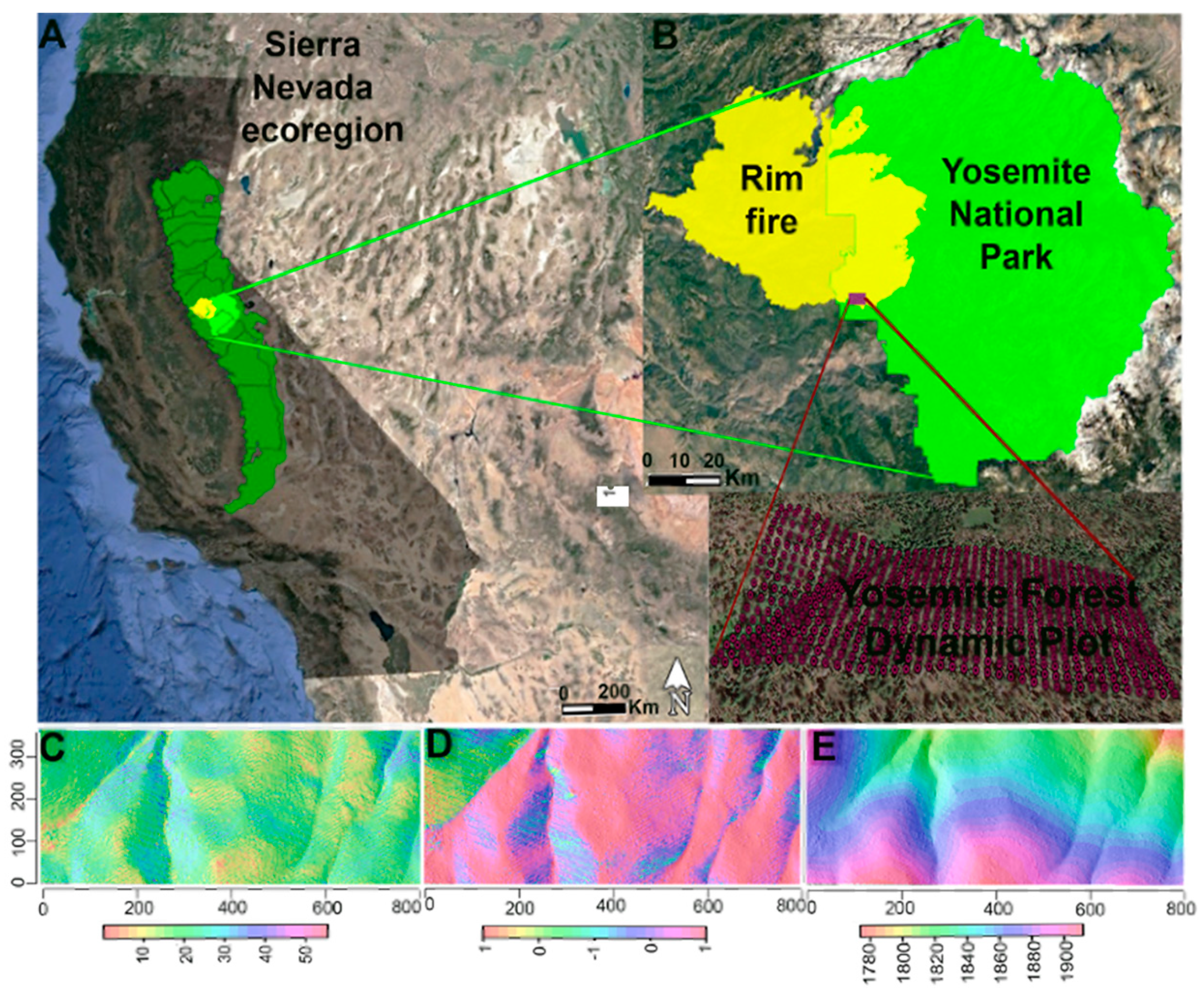
2.1. Study Area
2.2. Field Methods
2.3. Data Analysis
2.3.1. Null Models and Spatial Point Process Models
2.3.2. Complete Spatial Randomness (CSR)
2.3.3. Inhomogeneous Poisson Process (IPP)
2.3.4. Homogeneous Thomas Process (HTP)
2.3.5. Contributions of Habitat Heterogeneity and Dispersal Limitation at Different Scales
2.3.6. Antecedent Conditions Null Model
2.3.7. Assessing Spatial Pattern
2.3.8. Conspecific Negative Density Dependence
2.3.9. Edge Correction
3. Results
3.1. Topographic Effect (Heterogeneous Poisson Process)
3.2. Dispersal Limitation Effect (Homogeneous Thomas Process)
3.3. Contributions of Habitat Heterogeneity and Dispersal Limitation
3.4. Spatial Patterns of Juvenile and Adult Trees
3.5. Overall Changes in Tree Spatial Patterns
3.6. Conspecific Negative Density Dependence
4. Discussion
4.1. Effect of Random Process, Habitat Heterogeneity, and Dispersal Limitation on the Formation of the Spatial Patterns of Abundant Species
4.2. Biotic Interactions of the Four Abundant Species
4.3. Effect of Disturbance on the Spatial Pattern of Juveniles Regeneration and Large-Diameter Trees
4.4. Effect of Conspecific Negative Density Dependence in Regulating Dominant Tree Species Spatial Pattern
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Whitfield, J. Neutrality versus the Niche. Nature 2002, 417, 480–481. [Google Scholar] [CrossRef]
- Hubbell, S.P. The Unified Neutral Theory of Biodiversity and Biogeography; Princton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Zhou, S.; Zhang, D. Neutral theory in community ecology. Front. Biol. China 2008, 3, 1–8. [Google Scholar] [CrossRef]
- Condit, R.; Ashton, P.S.; Baker, P.; Bunyavejchewin, S.; Gunatilleke, S.; Gunatilleke, N.; Hubbell, S.P.; Foster, R.B.; Itoh, A.; LaFrankie, J.V. Spatial patterns in the distribution of tropical tree species. Science 2000, 288, 1414–1418. [Google Scholar] [CrossRef]
- Zhang, Z.-H.; Hu, G.; Ni, J. Effects of topographical and edaphic factors on the distribution of plant communities in two subtropical karst forests, southwestern China. J. Mt. Sci. 2013, 10, 95–104. [Google Scholar] [CrossRef]
- Engone Obiang, N.L.; Kenfack, D.; Picard, N.; Lutz, J.A.; Bissiengou, P.; Memiaghe, H.R.; Alonso, A. Determinants of spatial patterns of canopy tree species in a tropical evergreen forest in Gabon. J. Veg. Sci. 2019, 30, 929–939. [Google Scholar] [CrossRef]
- Harms, K.E.; Condit, R.; Hubbell, S.P.; Foster, R.B. Habitat associations of trees and shrubs in a 50-ha neotropical forest plot. J. Ecol. 2001, 89, 947–959. [Google Scholar] [CrossRef]
- Queenborough, S.A.; Burslem, D.F.; Garwood, N.C.; Valencia, R. Habitat niche partitioning by 16 species of Myristicaceae in Amazonian Ecuador. Plant Ecol. 2007, 192, 193–207. [Google Scholar] [CrossRef]
- Valencia, R.; Foster, R.B.; Villa, G.; Condit, R.; Svenning, J.C.; Hernández, C.; Romoleroux, K.; Losos, E.; Magård, E.; Balslev, H. Tree species distributions and local habitat variation in the Amazon: Large forest plot in eastern Ecuador. J. Ecol. 2004, 92, 214–229. [Google Scholar] [CrossRef]
- Briggs, J.M.; Gibson, D.J. Effect of fire on tree spatial patterns in a tallgrass prairie landscape. Bull. Torrey Bot. Club 1992, 119, 300–307. [Google Scholar] [CrossRef]
- Pillay, T.; Ward, D. Spatial pattern analysis and competition between Acacia karroo trees in humid savannas. Plant Ecol. 2012, 213, 1609–1619. [Google Scholar] [CrossRef]
- Das, A.J.; Larson, A.J.; Lutz, J.A. Individual species–area relationships in temperate coniferous forests. J. Veg. Sci. 2018, 29, 317–324. [Google Scholar] [CrossRef]
- Wang, H.; Peng, H.; Hui, G.; Hu, Y.; Zhao, Z. Large trees are surrounded by more heterospecific neighboring trees in Korean pine broad-leaved natural forests. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Dalling, J.W.; Hubbell, S.P. Seed size, growth rate and gap microsite conditions as determinants of recruitment success for pioneer species. J. Ecol. 2002, 90, 557–568. [Google Scholar] [CrossRef]
- Plotkin, J.B.; Chave, J.; Ashton, P.S. Cluster analysis of spatial patterns in Malaysian tree species. Am. Nat. 2002, 160, 629–644. [Google Scholar] [CrossRef] [PubMed]
- Kinloch, B.B., Jr.; Scheuner, W.H. Pinus lambertiana Dougl. Sugar pine. Silvics of North America, Conifers. In Agriculture Handbook; US Department of Agriculture: Washington, DC, USA, 1990; pp. 370–379. [Google Scholar]
- Vander Wall, S.B. Effects of seed size of wind-dispersed pines (Pinus) on secondary seed dispersal and the caching behavior of rodents. Oikos 2003, 100, 25–34. [Google Scholar] [CrossRef]
- Zouhar, K.L. Abies Concolor. Fire effects Information System (Online). US Department of Agriculture, Forest Service, Rocky Mountain Research, Fire Science Laboratory (Producer). 2001. Available online: https://www.feis-crs.org/feis (accessed on 15 December 2020).
- Furniss, T.J.; Larson, A.J.; Kane, V.R.; Lutz, J.A. Multi-scale assessment of post-fire tree mortality models. Int. J. Wildland Fire 2019, 28, 46–61. [Google Scholar] [CrossRef]
- Furniss, T.J.; Larson, A.J.; Kane, V.R.; Lutz, J.A. Wildfire and drought moderate the spatial elements of tree mortality. Ecosphere 2020, 11, e03214. [Google Scholar] [CrossRef]
- Furniss, T.J.; Kane, V.R.; Larson, A.J.; Lutz, J.A. Detecting tree mortality with Landsat-derived spectral indices: Improving ecological accuracy by examining uncertainty. Remote Sens. Environ. 2020, 237, 111497. [Google Scholar] [CrossRef]
- Lutz, J.A.; Furniss, T.J.; Johnson, D.J.; Davies, S.J.; Allen, D.; Alonso, A.; Anderson-Teixeira, K.J.; Andrade, A.; Baltzer, J.; Becker, K.M. Global importance of large-diameter trees. Glob. Ecol. Biogeogr. 2018, 27, 849–864. [Google Scholar] [CrossRef] [Green Version]
- Lutz, J.A.; Larson, A.J.; Swanson, M.E.; Freund, J.A. Ecological importance of large-diameter trees in a temperate mixed-conifer forest. PLoS ONE 2012, 7, e36131. [Google Scholar] [CrossRef]
- Lutz, J.A.; Larson, A.J.; Freund, J.A.; Swanson, M.E.; Bible, K.J. The importance of large-diameter trees to forest structural heterogeneity. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lutz, J.A.; Struckman, S.; Furniss, T.J.; Cansler, C.A.; Germain, S.J.; Yocom, L.L.; McAvoy, D.J.; Kolden, C.A.; Smith, A.M.; Swanson, M.E. Large-diameter trees dominate snag and surface biomass following reintroduced fire. Ecol. Process. 2020, 9, 1–13. [Google Scholar] [CrossRef]
- Neary, D.G.; Ryan, K.C.; DeBano, L.F. Wildland Fire in Ecosystems: Effects of Fire on Soils and Water; General Technical Report RMRS-GTR-42-vol. 4; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 2005; p. 42.
- Blomdahl, E.M.; Kolden, C.A.; Meddens, A.J.; Lutz, J.A. The importance of small fire refugia in the central Sierra Nevada, California, USA. For. Ecol. Manag. 2019, 432, 1041–1052. [Google Scholar] [CrossRef]
- Murphy, J.; Johnson, D.; Miller, W.W.; Walker, R.F.; Blank, R.R. Prescribed fire effects on forest floor and soil nutrients in a Sierra Nevada forest. Soil Sci. 2006, 171, 181–199. [Google Scholar] [CrossRef]
- Covington, W.W.; Sackett, S.S. The effect of a prescribed burn in southwestern ponderosa pine on organic matter and nutrients in woody debris and forest floor. For. Sci. 1984, 30, 183–192. [Google Scholar]
- Zhu, W.-Z.; Xiang, J.-S.; Wang, S.-G.; Li, M.-H. Resprouting ability and mobile carbohydrate reserves in an oak shrubland decline with increasing elevation on the eastern edge of the Qinghai–Tibet Plateau. For. Ecol. Manag. 2012, 278, 118–126. [Google Scholar] [CrossRef]
- Saha, S.; Kuehne, C.; Bauhus, J. Intra-and interspecific competition differently influence growth and stem quality of young oaks (Quercus robur L. and Quercus petraea (Mattuschka) Liebl.). Ann. For. Sci. 2014, 71, 381–393. [Google Scholar] [CrossRef] [Green Version]
- Liao, J.; Bogaert, J.; Nijs, I. Species interactions determine the spatial mortality patterns emerging in plant communities after extreme events. Sci. Rep. 2015, 5, 11229. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.-Z.; Zhang, W.-H.; He, Q.-Y. Effects of intraspecific competition on growth, architecture and biomass allocation of Quercus Liaotungensis. J. Plant Interact. 2019, 14, 284–294. [Google Scholar] [CrossRef] [Green Version]
- Pardos, M.; Montes, F.; Aranda, I.; Cañellas, I. Influence of environmental conditions on germinant survival and diversity of Scots pine (Pinus sylvestris L.) in central Spain. Eur. J. For. Res. 2007, 126, 37–47. [Google Scholar] [CrossRef]
- Janzen, D.H. Escape of juvenile Dioclea megacarpa (Leguminosae) vines from predators in a deciduous tropical forest. Am. Nat. 1971, 105, 97–112. [Google Scholar] [CrossRef]
- Belmecheri, S.; Babst, F.; Wahl, E.R.; Stahle, D.W.; Trouet, V. Multi-century evaluation of Sierra Nevada snowpack. Nat. Clim. Chang. 2016, 6, 2–3. [Google Scholar] [CrossRef]
- Andivia, E.; Madrigal-González, J.; Villar-Salvador, P.; Zavala, M.A. Do adult trees increase conspecific juvenile resilience to recurrent droughts? Implications for forest regeneration. Ecosphere 2018, 9, e02282. [Google Scholar] [CrossRef]
- Janzen, D.H. Herbivores and the number of tree species in tropical forests. Am. Nat. 1970, 104, 501–528. [Google Scholar] [CrossRef]
- Inman-Narahari, F.; Ostertag, R.; Hubbell, S.P.; Giardina, C.P.; Cordell, S.; Sack, L. Density-dependent seedling mortality varies with light availability and species abundance in wet and dry Hawaiian forests. J. Ecol. 2016, 104, 773–780. [Google Scholar] [CrossRef]
- Anderson-Teixeira, K.J.; Davies, S.J.; Bennett, A.C.; Gonzalez-Akre, E.B.; Muller-Landau, H.C.; Joseph Wright, S.; Abu Salim, K.; Almeyda Zambrano, A.M.; Alonso, A.; Baltzer, J.L.; et al. CTFS-Forest GEO: A worldwide network monitoring forests in an era of global change. Glob. Chang. Biol. 2015, 21, 528–549. [Google Scholar] [CrossRef] [Green Version]
- Lutz, J.A. The evolution of long-term data for forestry: Large temperate research plots in an era of global change. Northwest Sci. 2015, 89, 255–269. [Google Scholar] [CrossRef] [Green Version]
- Lutz, J.A.; Van Wagtendonk, J.W.; Franklin, J.F. Climatic water deficit, tree species ranges, and climate change in Yosemite National Park. J. Biogeogr. 2010, 37, 936–950. [Google Scholar] [CrossRef]
- Van Wagtendonk, J.W.; Moore, P.E.; Yee, J.L.; Lutz, J.A. The distribution of woody species in relation to climate and fire in Yosemite National Park, California, USA. Fire Ecol. 2020, 16, 1–23. [Google Scholar] [CrossRef]
- Stavros, E.N.; Tane, Z.; Kane, V.R.; Veraverbeke, S.; McGaughey, R.J.; Lutz, J.A.; Ramirez, C.; Schimel, D. Unprecedented remote sensing data over King and Rim megafires in the Sierra Nevada Mountains of California. Ecology 2016, 97, 3244. [Google Scholar] [CrossRef]
- Lutz, J.A.; Matchett, J.R.; Tarnay, L.W.; Smith, D.F.; Becker, K.M.; Furniss, T.J.; Brooks, M.L. Fire and the distribution and uncertainty of carbon sequestered as aboveground tree biomass in Yosemite and Sequoia & Kings Canyon National Parks. Land 2017, 6, 10. [Google Scholar] [CrossRef] [Green Version]
- Cansler, C.A.; Swanson, M.E.; Furniss, T.J.; Larson, A.J.; Lutz, J.A. Fuel dynamics after reintroduced fire in an old-growth Sierra Nevada mixed-conifer forest. Fire Ecol. 2019, 15, 16. [Google Scholar] [CrossRef] [Green Version]
- Stoyan, D.; Stoyan, H. Fractals, Random Shapes, and Point Fields: Methods of Geometrical Statistics; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1994; Volume 302. [Google Scholar]
- Illian, J.; Penttinen, A.; Stoyan, H.; Stoyan, D. Statistical Analysis and Modelling of Spatial Point Patterns; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 70. [Google Scholar]
- Goreaud, F.; Pélissier, R. Avoiding misinterpretation of biotic interactions with the intertype K12-function: Population independence vs. random labelling hypotheses. J. Veg. Sci. 2003, 14, 681–692. [Google Scholar] [CrossRef]
- Harvey, P.H.; Colwell, R.K.; Silvertown, J.W.; May, R.M. Null models in ecology. Annu. Rev. Ecol. Syst. 1983, 14, 189–211. [Google Scholar] [CrossRef]
- Google Earth Pro 7.3. (December 8, 2017). Yosemite Forest Dynamic Plot, California, USA. 37.77° N, 119.92° W. Available online: http://www.google.com/earth/index.html (accessed on 21 July 2020).
- Wiegand, T.; Moloney, A.; Rings, K. Circles, and null-models for point pattern analysis in ecology. Oikos 2004, 104, 209–229. [Google Scholar] [CrossRef]
- Wiegand, T.; Gunatilleke, C.S.; Gunatilleke, I.N.; Huth, A. How individual species structure diversity in tropical forests. Proc. Natl. Acad. Sci. USA 2007, 104, 19029–19033. [Google Scholar] [CrossRef] [Green Version]
- Yetemen, O.; Istanbulluoglu, E.; Duvall, A.R. Solar radiation as a global driver of hillslope asymmetry: Insights from an ecogeomorphic landscape evolution model. Water Resour. Res. 2015, 51, 9843–9861. [Google Scholar] [CrossRef] [Green Version]
- Gibbons, J.; Newbery, D. Drought avoidance and the effect of local topography on trees in the understorey of Bornean lowland rain forest. Plant Ecol. 2003, 164, 1–18. [Google Scholar] [CrossRef]
- Stage, A.R.; Salas, C. Interactions of elevation, aspect, and slope in models of forest species composition and productivity. For. Sci. 2007, 53, 486–492. [Google Scholar]
- Baddeley, A.; Diggle, P.J.; Hardegen, A.; Lawrence, T.; Milne, R.K.; Nair, G. Spatial Point Patterns On tests of spatial pattern based on simulation envelopes. Ecol. Monogr. 2014, 84, 477–489. [Google Scholar] [CrossRef] [Green Version]
- Baddeley, A.; Rubak, E.; Turner, R. Spatial Point Pattern: Methodology and Applications with R.; Chapman and Hall CRC: London, UK, 2015; Available online: http://www.crcpress.com/Spatial-Point-Patterns-Methodology-and-Applications-with-R/Baddeley-Rubak-Turner/9781482210200/ (accessed on 15 November 2020).
- R Core Team. R: A Language and Environment for Statistical Computing. Version 3.6.3.; R Core Team: Vienna, Austria, 2020. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. nlme: Linear and Nonlinear Mixed Effects Models. R Package Version 3.1-144. 2020. Available online: https://cran.r-project.org/web/packages/nlme/index.html (accessed on 15 November 2020).
- Batllori, E.; Camarero, J.J.; Gutiérrez, E. Current regeneration patterns at the tree line in the Pyrenees indicate similar recruitment processes irrespective of the past disturbance regime. J. Biogeogr. 2010, 37, 1938–1950. [Google Scholar] [CrossRef]
- Furniss, T.J.; Larson, A.J.; Lutz, J.A. Reconciling niches and neutrality in a subalpine temperate forest. Ecosphere 2017, 8, e01847. [Google Scholar] [CrossRef]
- Loosmore, N.B.; Ford, E.D. Statistical inference using the G or K point pattern spatial statistics. Ecology 2006, 87, 1925–1931. [Google Scholar] [CrossRef] [Green Version]
- De la Cruz Rot, M. Ecespa: Functions for Spatial Point Pattern Analysis. R Package Version 1.1-11. Available online: https://cran.r-project.org/web/packages/ecespa/index.html (accessed on 27 March 2020).
- Hubbell, S.P. Tree dispersion, abundance, and diversity in a tropical dry forest. Science 1979, 203, 1299–1309. [Google Scholar] [CrossRef] [Green Version]
- Habeck, R. Pinus lambertiana. Fire Effects Information System (Online); US Department of Agriculture, Forest Service, Rocky Mountain Research Station, Fire Sciences Laboratory (Producer). 1992. Available online: https://www.fs.fed.us/database/feis/plants/shrub/spibet/all.html (accessed on 15 November 2020).
- Hardy, O.J.; Sonké, B. Spatial pattern analysis of tree species distribution in a tropical rain forest of Cameroon: Assessing the role of limited dispersal and niche differentiation. For. Ecol. Manag. 2004, 197, 191–202. [Google Scholar] [CrossRef]
- Seidler, T.G.; Plotkin, J.B. Seed dispersal and spatial pattern in tropical trees. PLoS Biol. 2006, 4, e344. [Google Scholar] [CrossRef]
- Wang, X.; Ye, J.; Li, B.; Zhang, J.; Lin, F.; Hao, Z. Spatial distributions of species in an old-growth temperate forest, northeastern China. Can. J. For. Res. 2010, 40, 1011–1019. [Google Scholar] [CrossRef] [Green Version]
- Tamjidi, J.; Lutz, J.A. Soil Enzyme Activity and Soil Nutrients Jointly Influence Post-Fire Habitat Models in Mixed-Conifer Forests of Yosemite National Park, USA. Fire 2020, 3, 54. [Google Scholar] [CrossRef]
- Madrigal-González, J.; Zavala, M.A. Competition and tree age modulated last century pine growth responses to high frequency of dry years in a water limited forest ecosystem. Agric. For. Meteorol. 2014, 192, 18–26. [Google Scholar] [CrossRef]
- Molina, R.; O’Dell, T.; Luoma, D.; Amaranthus, M.; Castellano, M.; Russell, K. Biology, Ecology, and Social Aspects of Wild Edible Mushrooms in the Forests of the Pacific Northwest: A Preface to Managing Commercial Harvest; USDA Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 1993; Volume 309.
- Johnson, D.J.; Clay, K.; Phillips, R.P. Mycorrhizal associations and the spatial structure of an old-growth forest community. Oecologia 2018, 186, 195–204. [Google Scholar] [CrossRef]
- Das, A.; Battles, J.; van Mantgem, P.J.; Stephenson, N.L. Spatial elements of mortality risk in old-growth forests. Ecology 2008, 89, 1744–1756. [Google Scholar] [CrossRef] [PubMed]
- Martínez, I.; Wiegand, T.; González-Taboada, F.; Obeso, J.R. Spatial associations among tree species in a temperate forest community in North-western Spain. For. Ecol. Manag. 2010, 260, 456–465. [Google Scholar] [CrossRef]
- Teste, F.P.; Simard, S.W.; Durall, D.M. Role of mycorrhizal networks and tree proximity in ectomycorrhizal colonization of planted seedlings. Fungal Ecol. 2009, 2, 21–30. [Google Scholar] [CrossRef]
- Lutz, J.; Larson, A.; Swanson, M. Advancing fire science with large forest plots and a long-term multidisciplinary approach. Fire 2018, 1, 5. [Google Scholar] [CrossRef] [Green Version]
- Larson, A.J.; Cansler, C.A.; Cowdery, S.G.; Hiebert, S.; Furniss, T.J.; Swanson, M.E.; Lutz, J.A. Post-fire morel (Morchella) mushroom abundance, spatial structure, and harvest sustainability. For. Ecol. Manag. 2016, 377, 16–25. [Google Scholar] [CrossRef]
- Jeronimo, S.M.; Lutz, J.A.; Kane, V.R.; Larson, A.J.; Franklin, J.F. Burn weather and three-dimensional fuel structure determine post-fire tree mortality. Landsc. Ecol. 2020, 35, 859–878. [Google Scholar] [CrossRef]
- Kane, V.R.; Cansler, C.A.; Povak, N.A.; Kane, J.T.; McGaughey, R.J.; Lutz, J.A.; Churchill, D.J.; North, M.P. Mixed severity fire effects within the Rim fire: Relative importance of local climate, fire weather, topography, and forest structure. For. Ecol. Manag. 2015, 358, 62–79. [Google Scholar] [CrossRef] [Green Version]
- Jeronimo, S.M.; Kane, V.R.; Churchill, D.J.; Lutz, J.A.; North, M.P.; Asner, G.P.; Franklin, J.F. Forest structure and pattern vary by climate and landform across active-fire landscapes in the montane Sierra Nevada. For. Ecol. Manag. 2019, 437, 70–86. [Google Scholar] [CrossRef]
- Ng, J.; North, M.P.; Arditti, A.J.; Cooper, M.R.; Lutz, J.A. Topographic variation in tree group and gap structure in Sierra Nevada mixed-conifer forests with active fire regimes. For. Ecol. Manag. 2020, 472, 118220. [Google Scholar] [CrossRef]
- Churchill, D.J.; Larson, A.J.; Dahlgreen, M.C.; Franklin, J.F.; Hessburg, P.F.; Lutz, J.A. Restoring forest resilience: From reference spatial patterns to silvicultural prescriptions and monitoring. For. Ecol. Manag. 2013, 291, 442–457. [Google Scholar] [CrossRef]
- Zald, H.S.; Gray, A.N.; North, M.; Kern, R.A. Initial tree regeneration responses to fire and thinning treatments in a Sierra Nevada mixed-conifer forest, USA. For. Ecol. Manag. 2008, 256, 168–179. [Google Scholar] [CrossRef]
- Johnson, P.S.; Shifley, S.R.; Rogers, R.; Dey, D.C.; Kabrick, J.M. The Ecology and Silviculture of Oaks; Cabi: Boston, MA, USA, 2019. [Google Scholar]
- Green, S.R.; Arthur, M.A.; Blankenship, B.A. Oak and red maple seedling survival and growth following periodic prescribed fire on xeric ridgetops on the Cumberland Plateau. For. Ecol. Manag. 2010, 259, 2256–2266. [Google Scholar] [CrossRef]
- Van Wilgen, B.W.; Richardson, D.M.; Kruger, F.J.; van Hensbergen, H.J. Fire in South African Mountain Fynbos: Ecosystem, Community and Species Response at Swartboskloof; Springer Science & Business Media: Berlin, Germany, 2012; Volume 93. [Google Scholar]
- Owen, S.M.; Sieg, C.H.; Meador, A.J.S.; Fulé, P.Z.; Iniguez, J.M.; Baggett, L.S.; Fornwalt, P.J.; Battaglia, M.A. Spatial patterns of ponderosa pine regeneration in high-severity burn patches. For. Ecol. Manag. 2017, 405, 134–149. [Google Scholar] [CrossRef]
- Ziegler, J.P.; Hoffman, C.M.; Fornwalt, P.J.; Sieg, C.H.; Battaglia, M.A.; Chambers, M.E.; Iniguez, J.M. Tree Regeneration Spatial Patterns in Ponderosa Pine Forests Following Stand-Replacing Fire: Influence of Topography and Neighbors. Forests 2017, 8, 391. [Google Scholar] [CrossRef] [Green Version]
- Fulé, P.Z.; Covington, W.W. Spatial patterns of Mexican pine-oak forests under different recent fire regimes. Plant Ecol. 1998, 134, 197–209. [Google Scholar] [CrossRef]
- Becker, K.M.; Lutz, J.A. Can low-severity fire reverse compositional change in montane forests of the Sierra Nevada, California, USA? Ecosphere 2016, 7, e01484. [Google Scholar] [CrossRef]
- Armesto, J.; Mitchell, J.; Villagran, C. A comparison of spatial patterns of trees in some tropical and temperate forests. Biotropica 1986, 18, 1–11. [Google Scholar] [CrossRef]
- Le, N.; Thi, D.; Van Thinh, N.; Mitlöhner, R. Effect of disturbance regimes on spatial patterns of tree species in three sites in a tropical evergreen forest in Vietnam. Int. J. For. 2016, 2016, 16. [Google Scholar]
- Larson, A.J.; Lutz, J.A.; Donato, D.C.; Freund, J.A.; Swanson, M.E.; HilleRisLambers, J.; Sprugel, D.G.; Franklin, J.F. Spatial aspects of tree mortality strongly differ between young and old-growth forests. Ecology 2015, 96, 2855–2861. [Google Scholar] [CrossRef] [Green Version]
- Bär, A.; Michaletz, S.T.; Mayr, S. Fire effects on tree physiology. New Phytol. 2019, 223, 1728–1741. [Google Scholar] [CrossRef] [Green Version]
- Davis, M.A.; Curran, C.; Tietmeyer, A.; Miller, A. Dynamic tree aggregation patterns in a species-poor temperate woodland disturbed by fire. J. Veg. Sci. 2005, 16, 167–174. [Google Scholar] [CrossRef]
- Hood, S.; Sala, A.; Heyerdahl, E.K.; Boutin, M. Low-severity fire increases tree defense against bark beetle attacks. Ecology 2015, 96, 1846–1855. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| Analysis | Null hypothesis | Results | Explanation |
|---|---|---|---|
| Complete Spatial randomness | Trees are randomly distributed. | Aggregation of trees (Figure 2). | Tree aggregation may be caused by seed dispersal, environmental heterogeneity, interaction, fire, and density dependence. |
| Inhomogeneous Poisson Process | Trees are spatially aggregated due to habitat preference. | Aggregation of all trees at scales ≤ 15 m (Figure 2). | Tree aggregations are based on habitat heterogeneity. |
| Homogeneous Thomas process | Trees are spatially aggregated at smaller distances due to seed dispersal limitations, especially in species with known restricted seed dispersal. | Spatial aggregation at scales < 5 m especially in species with restricted seed dispersal (Figure 2). | Tree aggregations are based on species dispersal limitations. |
| Antecedent condition null model | Juveniles are spatially aggregated around conspecific adults. | Juveniles are spatially aggregated around conspecific and heterospecific adults (Figure 4). | Facilitation due to habitat suitability, resilience promotion, mycorrhizal fungi, and reduced competition. |
| Random labeling | Conspecific density-dependent mortality exists among species. | Conspecific density- dependence mortality in Pinus lambertiana and positive density-dependence in Abies concolor at scales < 4 m (Figure 7). | Density-dependent mortality due to strong intraspecific competition, lower allocation on defense mechanisms, increased susceptibility to bark beetles and drought stress. |
| Best Model | <2 m | 2–5 m | 5–10 m | 10–20 m | 20–40 m | 40–60 m |
|---|---|---|---|---|---|---|
| Homogeneous Poisson process | 0% | 0% | 0% | 0% | 0% | 0% |
| Inhomogeneous Poisson process | 0% | 0% | 67% | 100% | 100% | 100% |
| Homogeneous Thomas process | 100% | 100% | 33% | 0% | 0% | 0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamjidi, J.; Lutz, J.A. The Post-Fire Assembly Processes of Tree Communities Based on Spatial Analysis of a Sierra Nevada Mixed-Conifer Forest. Fire 2020, 3, 72. https://doi.org/10.3390/fire3040072
Tamjidi J, Lutz JA. The Post-Fire Assembly Processes of Tree Communities Based on Spatial Analysis of a Sierra Nevada Mixed-Conifer Forest. Fire. 2020; 3(4):72. https://doi.org/10.3390/fire3040072
Chicago/Turabian StyleTamjidi, Jelveh, and James A. Lutz. 2020. "The Post-Fire Assembly Processes of Tree Communities Based on Spatial Analysis of a Sierra Nevada Mixed-Conifer Forest" Fire 3, no. 4: 72. https://doi.org/10.3390/fire3040072
APA StyleTamjidi, J., & Lutz, J. A. (2020). The Post-Fire Assembly Processes of Tree Communities Based on Spatial Analysis of a Sierra Nevada Mixed-Conifer Forest. Fire, 3(4), 72. https://doi.org/10.3390/fire3040072






